 数Ⅱ
数Ⅱ
 数Ⅱ
数Ⅱ
福田の数学〜青山学院大学2022年理工学部第3問〜関数の増減と極値

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#微分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
関数
$f(x)=\sqrt{1-2\cos x}-\frac{1}{2}x$
について以下の問いに答えよ。
(1)$f'(x)$を求めよ。
(2)$f'(x) \gt 0$ となるxの値の範囲を求めよ。
(3)f(x)の増減を調べ、極値を求めよ。
2022青山学院大学理工学部過去問
この動画を見る
関数
$f(x)=\sqrt{1-2\cos x}-\frac{1}{2}x$
について以下の問いに答えよ。
(1)$f'(x)$を求めよ。
(2)$f'(x) \gt 0$ となるxの値の範囲を求めよ。
(3)f(x)の増減を調べ、極値を求めよ。
2022青山学院大学理工学部過去問
【解答にミスあり概要欄】大学入試問題#322 慶應義塾大学(2021) #三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$-\displaystyle \frac{\pi}{2} \leqq \theta \leqq \displaystyle \frac{\pi}{2}$
$4\cos\displaystyle \frac{\theta}{2}(\cos\displaystyle \frac{\theta}{2}+\sin\displaystyle \frac{\theta}{2})$のとき
$\sin\theta$の値を求めよ。
出典:2021年慶應義塾大学 入試問題
この動画を見る
$-\displaystyle \frac{\pi}{2} \leqq \theta \leqq \displaystyle \frac{\pi}{2}$
$4\cos\displaystyle \frac{\theta}{2}(\cos\displaystyle \frac{\theta}{2}+\sin\displaystyle \frac{\theta}{2})$のとき
$\sin\theta$の値を求めよ。
出典:2021年慶應義塾大学 入試問題
俺のアイデアを聞いて
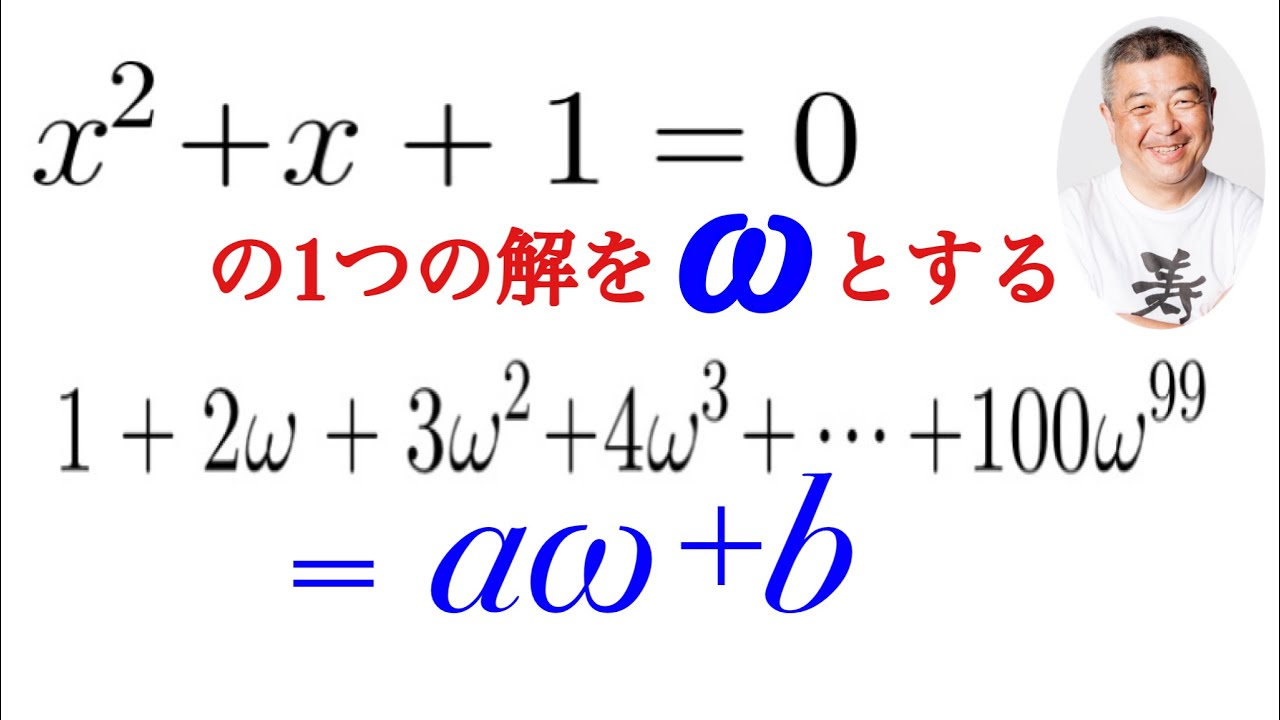
単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^2+x+1=$の1つの解を$\omega$とする.
$1+2\omega+3\omega^2+4\omega^3+…+100\omega^{99}=a\omega+b$である.a.bの値を求めよ.
この動画を見る
$ x^2+x+1=$の1つの解を$\omega$とする.
$1+2\omega+3\omega^2+4\omega^3+…+100\omega^{99}=a\omega+b$である.a.bの値を求めよ.
【数Ⅱ】積分で定義された関数【積分区間を見て、計算結果を考えよう。】
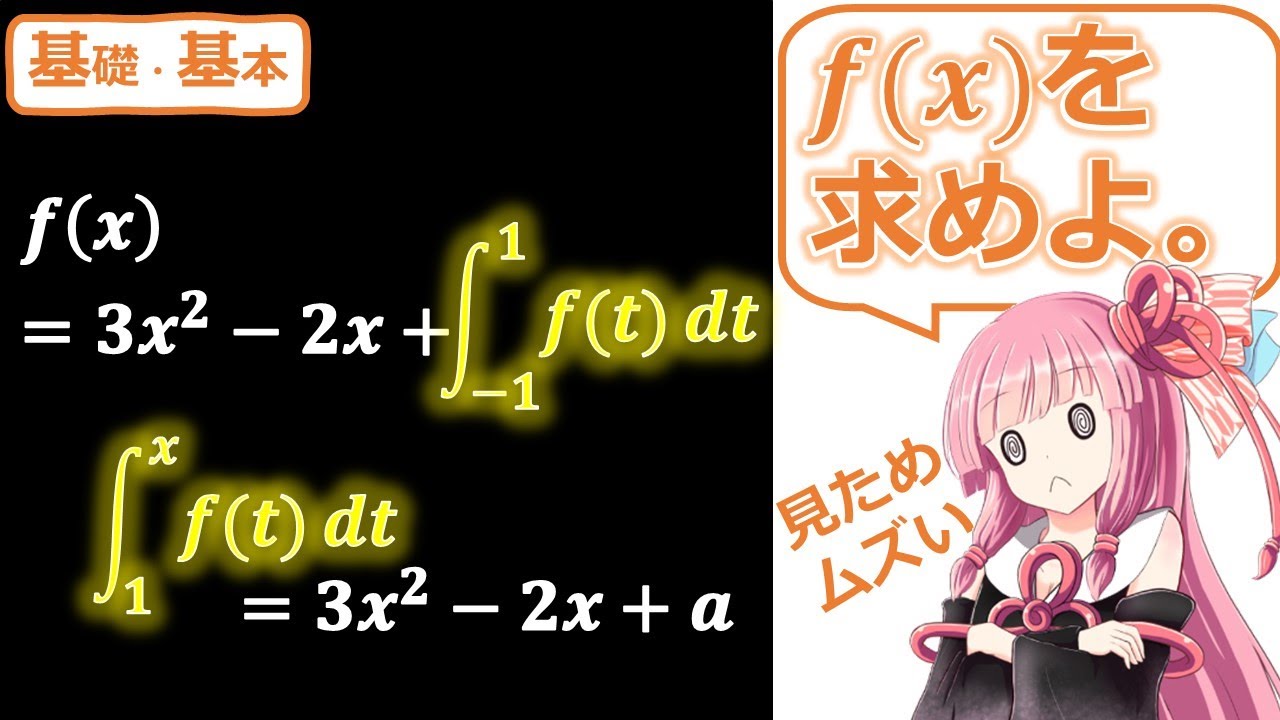
単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1)f(x)=3x^2-2x+ \displaystyle \int_{-1}^{1}f(t)dtを満たす関数f(x)を求めよ.$
$(2)f(x)=3x+\displaystyle \int_{0}^{1}(x+t)f(t)dtを満たす関数f(x)を求めよ.$
$(3)y=\displaystyle \int_{1}^{x}(t^2-2t-3)dtの極値を求めよ.$
$(4)\displaystyle \int_{1}^{x}f(t)dt=3x^2-2x+aを満たす関数f(x)と定数aを求めよ.$
この動画を見る
$(1)f(x)=3x^2-2x+ \displaystyle \int_{-1}^{1}f(t)dtを満たす関数f(x)を求めよ.$
$(2)f(x)=3x+\displaystyle \int_{0}^{1}(x+t)f(t)dtを満たす関数f(x)を求めよ.$
$(3)y=\displaystyle \int_{1}^{x}(t^2-2t-3)dtの極値を求めよ.$
$(4)\displaystyle \int_{1}^{x}f(t)dt=3x^2-2x+aを満たす関数f(x)と定数aを求めよ.$
福田の数学〜立教大学2022年経済学部第3問〜放物線と円と直線で囲まれた面積

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#微分法と積分法#円と方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
Oを原点とする座標平面上の放物線$C:y=x^2$とC上の点P$(\frac{\sqrt3}{2}, \ \frac{3}{4})$がある。
PにおけるCの接線をlとし、また、Pを通りlと直交する直線をmとする。
さらに、mとx軸の交点をQとする。このとき、次の問いに答えよ。
(1)mの方程式を$y=px+q$とするとき、定数p,qの値を求めよ。
(2)Qの座標を$(a,\ 0)$とするとき、aの値を求めよ。
(3)Qを中心とする半径rの円Dがlとただ1つの共有点を持つとき、rの値を求めよ。
(4)(1)で定めたp,qの値に対して、次の連立不等式の表す領域の面積S_1を求めよ。
$x \geqq 0,\ \ \ y \geqq 0,\ \ \ y \leqq px+q,\ \ \ y \leqq x^2$
(5)(2)で定めたaの値と(3)で定めたrの値に対して、次の連立不等式の表す領域
の面積S_2を求めよ。
$0 \leqq x \leqq \frac{\sqrt3}{2},\ \ \ y \geqq 0,\ \ \ y \leqq x^2,\ \ \ (x-a)^2+y^2 \geqq r^2$
2022立教学部経済学部過去問
この動画を見る
Oを原点とする座標平面上の放物線$C:y=x^2$とC上の点P$(\frac{\sqrt3}{2}, \ \frac{3}{4})$がある。
PにおけるCの接線をlとし、また、Pを通りlと直交する直線をmとする。
さらに、mとx軸の交点をQとする。このとき、次の問いに答えよ。
(1)mの方程式を$y=px+q$とするとき、定数p,qの値を求めよ。
(2)Qの座標を$(a,\ 0)$とするとき、aの値を求めよ。
(3)Qを中心とする半径rの円Dがlとただ1つの共有点を持つとき、rの値を求めよ。
(4)(1)で定めたp,qの値に対して、次の連立不等式の表す領域の面積S_1を求めよ。
$x \geqq 0,\ \ \ y \geqq 0,\ \ \ y \leqq px+q,\ \ \ y \leqq x^2$
(5)(2)で定めたaの値と(3)で定めたrの値に対して、次の連立不等式の表す領域
の面積S_2を求めよ。
$0 \leqq x \leqq \frac{\sqrt3}{2},\ \ \ y \geqq 0,\ \ \ y \leqq x^2,\ \ \ (x-a)^2+y^2 \geqq r^2$
2022立教学部経済学部過去問
これで5分短縮!共通テスト数学IIB【第2問 微分積分】(増減表は不要)

単元:
#数Ⅱ#大学入試過去問(数学)#共通テスト#その他#勉強法#数B
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
$y=x^3-3x^2+2x$を求めよ
この動画を見る
$y=x^3-3x^2+2x$を求めよ
3次方程式の解と係数の関係 あっという間に出す方法もあるよ

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^3-2x^2+3x+4=0$の3つの解を$\alpha,\beta,\delta$とする.
$\alpha^2,\beta^2,\delta^2$を解にもつ方程式を1つ例示せよ.
この動画を見る
$ x^3-2x^2+3x+4=0$の3つの解を$\alpha,\beta,\delta$とする.
$\alpha^2,\beta^2,\delta^2$を解にもつ方程式を1つ例示せよ.
どっちがでかい?

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ (2+3)(2^2+3^2)(2^4+3^4)(2^8+3^8)(2^{16}+3^{16})$
$(2^{32}+3^{32})$と,
$3^{64}$はどちらが大きいか?
この動画を見る
$ (2+3)(2^2+3^2)(2^4+3^4)(2^8+3^8)(2^{16}+3^{16})$
$(2^{32}+3^{32})$と,
$3^{64}$はどちらが大きいか?
どっちがでかい?

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$(2+3)(2^2+3^2)(2^4+3^4)(2^8+3^8)(2^{16}+3^{16})(2^{32}+3^{32})$ VS $3^{64}$
この動画を見る
どちらが大きいか?
$(2+3)(2^2+3^2)(2^4+3^4)(2^8+3^8)(2^{16}+3^{16})(2^{32}+3^{32})$ VS $3^{64}$
電卓のeの意味は!?

指数の連立方程式
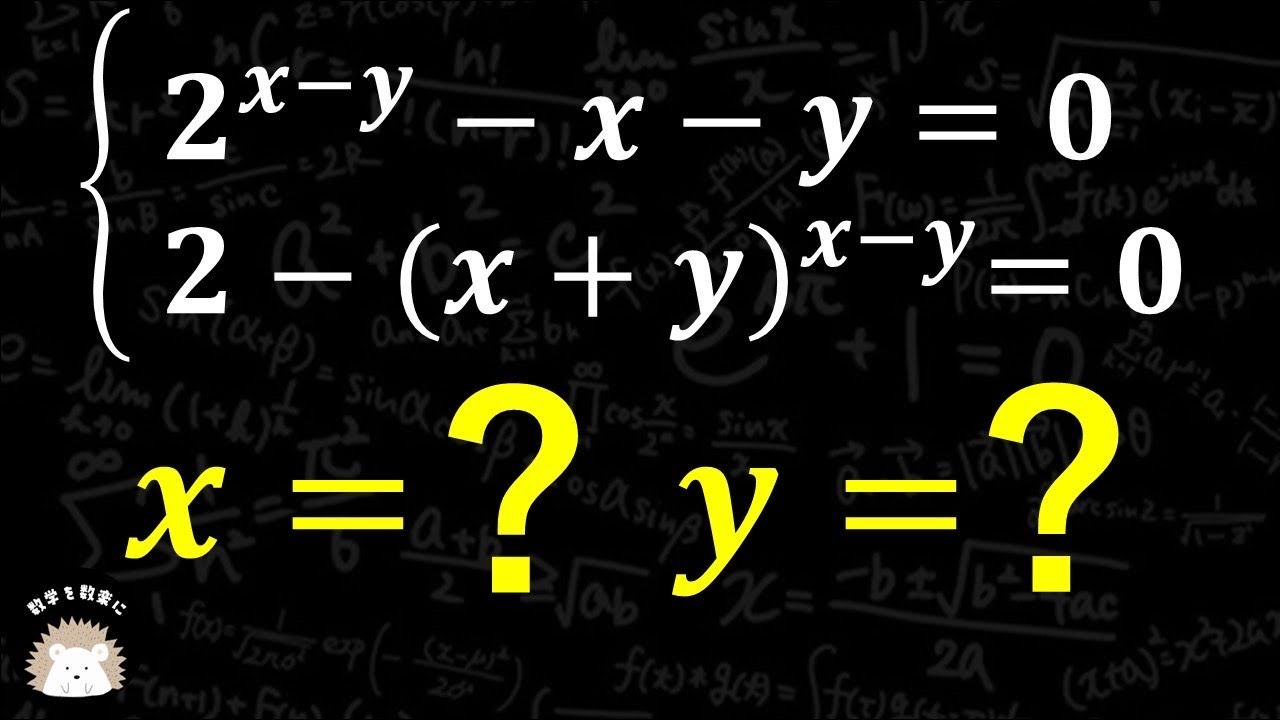
単元:
#数学(中学生)#中2数学#連立方程式#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
2^{x-y}-x-y=0 \\
2-(x+y)^{x-y} = 0
\end{array}
\right.
\end{eqnarray}
x=? y=?
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
2^{x-y}-x-y=0 \\
2-(x+y)^{x-y} = 0
\end{array}
\right.
\end{eqnarray}
x=? y=?
【数学IIB】コレだけやれば50点はとれます【最短で50点突破】(共通テスト)

単元:
#数Ⅱ#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学IIB】点数獲得できる勉強法紹介動画です
この動画を見る
【数学IIB】点数獲得できる勉強法紹介動画です
福田の数学〜立教大学2022年経済学部第1問(3)〜整式の割り算と余り

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
aを定数とする。
3次式 $F(x)=x^3-6x+a$を2次式$G(x)=x^2 -3x+2$で割った余りを$R(x)$ とする。
G(x)がR(x)で割り切れるようなaの値をすべて求めよ。
2022立教大学経済学部過去問
この動画を見る
aを定数とする。
3次式 $F(x)=x^3-6x+a$を2次式$G(x)=x^2 -3x+2$で割った余りを$R(x)$ とする。
G(x)がR(x)で割り切れるようなaの値をすべて求めよ。
2022立教大学経済学部過去問
【数Ⅱ】放物線と面積 1/3・1/6・1/12の公式を使いこなせ【定積分をせずに面積を求める】

単元:
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1)y=x^2-2x+2とy=2x-1で囲われた図形の面積を求めよ.$
$(2)y=x^2-2x+2とy=-x^2+4x+2で囲われた図形の面積を求めよ.$
$(3)y= \vert x^2-1 \vertとx軸,x=0,x=2で囲われた図形の面積を求めよ.$
$(4)放物線C:y=x^2+3x+1上の点(-3,1)における接線と$
$放物線C,y軸で囲われた図形の面積を求めよ.$
$(5)放物線C:y=x^2-x+3と点A(1,-1)からこの放物線に引いた接線で$
$囲われた図形の面積を求めよ.$
この動画を見る
$(1)y=x^2-2x+2とy=2x-1で囲われた図形の面積を求めよ.$
$(2)y=x^2-2x+2とy=-x^2+4x+2で囲われた図形の面積を求めよ.$
$(3)y= \vert x^2-1 \vertとx軸,x=0,x=2で囲われた図形の面積を求めよ.$
$(4)放物線C:y=x^2+3x+1上の点(-3,1)における接線と$
$放物線C,y軸で囲われた図形の面積を求めよ.$
$(5)放物線C:y=x^2-x+3と点A(1,-1)からこの放物線に引いた接線で$
$囲われた図形の面積を求めよ.$
放物線 栃木県(改) 正答率5%!?
工夫が大事!積分と確率の融合問題【一橋大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
サイコロを3回投げて出た目を順に$a,b,c$とするとき,
$ \displaystyle \int_{a-3}^{a+3} (x-b)(x-c)dx=0 $
となる確率を求めよ。
一橋大過去問
この動画を見る
サイコロを3回投げて出た目を順に$a,b,c$とするとき,
$ \displaystyle \int_{a-3}^{a+3} (x-b)(x-c)dx=0 $
となる確率を求めよ。
一橋大過去問
分からないので教えてください!ふさわしくない解は?

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x-\dfrac{4}{x}=\sqrt x+\dfrac{2}{\sqrt x}$
これを解け.
この動画を見る
$ x-\dfrac{4}{x}=\sqrt x+\dfrac{2}{\sqrt x}$
これを解け.
福田の数学〜立教大学2022年理学部第3問〜接線法線と囲まれた部分の面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#円と方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$t$を正の実数とする。座標平面上に放物線$C_1:y=x^2$とその上の点$P(t,\ t^2)$がある。
Pにおける$C_1$の接線を$l$とし、法線を$m$とする。$l$とx軸との交点をQとする。
Pにおいて$l$に接し、さらにx軸にも接する円で、中心のx座標がt以下であるものを$C_2$
とする。$C_2$の中心をAとし、$C_2$とx軸の接点をBとする。
(1)lの方程式を求めよ。
(2)mの方程式を求めよ。
(3)$\angle BAP=\frac{\pi}{3}$であるとき、tの値を求めよ。
(4)(3)のとき、Aの座標を求めよ。
(5)(3)のとき、四角形ABQPの面積を求めよ。
2022立教大学理学部過去問
この動画を見る
$t$を正の実数とする。座標平面上に放物線$C_1:y=x^2$とその上の点$P(t,\ t^2)$がある。
Pにおける$C_1$の接線を$l$とし、法線を$m$とする。$l$とx軸との交点をQとする。
Pにおいて$l$に接し、さらにx軸にも接する円で、中心のx座標がt以下であるものを$C_2$
とする。$C_2$の中心をAとし、$C_2$とx軸の接点をBとする。
(1)lの方程式を求めよ。
(2)mの方程式を求めよ。
(3)$\angle BAP=\frac{\pi}{3}$であるとき、tの値を求めよ。
(4)(3)のとき、Aの座標を求めよ。
(5)(3)のとき、四角形ABQPの面積を求めよ。
2022立教大学理学部過去問
指数
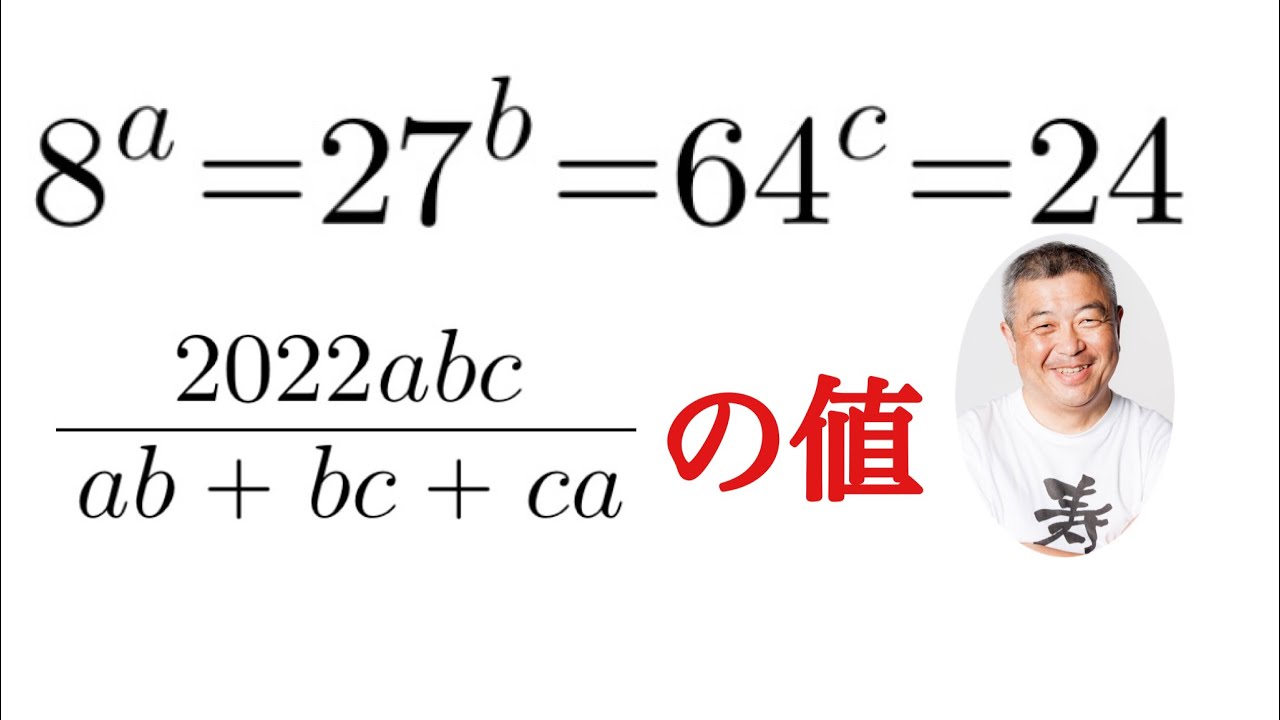
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 8^a=27^b=64^c=24,\dfrac{2022 abc}{ab+bc+ca}$
の値を求めよ.
この動画を見る
$ 8^a=27^b=64^c=24,\dfrac{2022 abc}{ab+bc+ca}$
の値を求めよ.
福田の数学〜立教大学2022年理学部第1問(4)〜解と係数の関係

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
2次方程式$2x^2+4x+1=0$の解を$\alpha,\ \beta(\alpha\lt \beta)$とする。実数$p,q$に対して、
2次方程式$x^2+px+q=0$の解が$\alpha^3,\ \beta^3$であるならば、
$p=\boxed{オ},\ q=\boxed{カ}$である。
2022立教大学理学部過去問
この動画を見る
2次方程式$2x^2+4x+1=0$の解を$\alpha,\ \beta(\alpha\lt \beta)$とする。実数$p,q$に対して、
2次方程式$x^2+px+q=0$の解が$\alpha^3,\ \beta^3$であるならば、
$p=\boxed{オ},\ q=\boxed{カ}$である。
2022立教大学理学部過去問
4次方程式

単元:
#数Ⅱ#式と証明#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ (x^2-x-1)^2-x^3=5$
これを解け.
この動画を見る
$ (x^2-x-1)^2-x^3=5$
これを解け.
【数Ⅱ】積分をイチから理解。面積を求めよう【まずは計算方法をマスターする】

単元:
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1)微分するとx^2+4x+3となる関数を求めよ.$
$(2)\displaystyle \int_{1}^{2} (x^2+4x+3)dxを計算せよ. $
$(3)y=x^2-4x+3とx軸で囲われた図形の面積を求めよ.$
$(4)y=x^3-5x^2+6xとx軸で囲われた2つの図形の面積の和を求めよ.$
この動画を見る
$(1)微分するとx^2+4x+3となる関数を求めよ.$
$(2)\displaystyle \int_{1}^{2} (x^2+4x+3)dxを計算せよ. $
$(3)y=x^2-4x+3とx軸で囲われた図形の面積を求めよ.$
$(4)y=x^3-5x^2+6xとx軸で囲われた2つの図形の面積の和を求めよ.$
福田の数学〜立教大学2022年理学部第1問(2)〜余事象と確率の加法定理

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#確率#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
下図のように1から9までの数字が1つずつ記入された、9枚のカードがある。
$\boxed{1}\ \ \ \boxed{2}\ \ \ \boxed{3}\ \ \ \boxed{4}\ \ \ \boxed{5}\ \ \ \boxed{6}\ \ \ \boxed{7}\ \ \ \boxed{8}\ \ \ \boxed{9}$
これら9枚のカードから同時に取り出した3枚のカードの数字の積が
10で割り切れる確率は$\boxed{イ}$である。
2022立教大学理学部過去問
この動画を見る
下図のように1から9までの数字が1つずつ記入された、9枚のカードがある。
$\boxed{1}\ \ \ \boxed{2}\ \ \ \boxed{3}\ \ \ \boxed{4}\ \ \ \boxed{5}\ \ \ \boxed{6}\ \ \ \boxed{7}\ \ \ \boxed{8}\ \ \ \boxed{9}$
これら9枚のカードから同時に取り出した3枚のカードの数字の積が
10で割り切れる確率は$\boxed{イ}$である。
2022立教大学理学部過去問
福田の数学〜立教大学2022年理学部第1問(1)〜対数方程式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}(1)$実数$x$に関する方程式
$2\log(1-x)-\log(5-x)=\log 2$
を解くと$x=\boxed{ア}$である.
立教大学2022年理学部過去問
この動画を見る
$\boxed{1}(1)$実数$x$に関する方程式
$2\log(1-x)-\log(5-x)=\log 2$
を解くと$x=\boxed{ア}$である.
立教大学2022年理学部過去問
東大数学科が解説!球の体積の公式を微分すると面積公式になるのはなぜ?

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
球の体積の公式を微分すると面積公式になるのはなぜか解説します
この動画を見る
球の体積の公式を微分すると面積公式になるのはなぜか解説します
【数Ⅱ】三角関数:3倍角の公式笑っちゃう覚え方

福田の数学〜明治大学2022年理工学部第3問〜平行六面体の対角線を軸とした回転体の体積

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#微分法と積分法#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#不定積分・定積分#面積、体積#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
右の図(※動画参照)のような平行六面体OABC-DEFGにおいて、
すべての辺の長さは1であり、$\overrightarrow{ OA },\ \overrightarrow{ OC },\ \overrightarrow{ OD }$のどの
2つのなす角も$\frac{\pi}{3}$であるとする。
(1)$\overrightarrow{ OF }$を$\overrightarrow{ OA },\ \overrightarrow{ OC },\ \overrightarrow{ OD }$を用いて表すと、
$\overrightarrow{ OF }= \boxed{き}$である。
(2)$|\overrightarrow{ OF }|,\ \cos \angle AOF$を求めると$|\overrightarrow{ OF }|= \boxed{く},$
$\ \cos \angle AOF=\boxed{け}$である。
(3)三角形ACDを底面とする三角錐OACDを、直線OFの周りに1回転して
できる円錐の体積は$\boxed{こ}$である。
(4)対角線OF上に点Pをとり、$|\overrightarrow{ OP }|=t$とおく。点Pを通り、$\overrightarrow{ OF }$に垂直な平面
をHとする。平行六面体$OABC-DEFG$を平面Hで切った時の断面が六角形
となるようなtの範囲は$\boxed{さ}$である。このとき、平面Hと辺AEの交点をQ
として、$|\overrightarrow{ AQ }|$をtの式で表すと$|\overrightarrow{ AQ }|=\boxed{し}$である。
また、$|\overrightarrow{ PQ }|^2$を$t$の式で表すと
$|\overrightarrow{ PQ }|^2=|\overrightarrow{ OQ }|^2-|\overrightarrow{ OP }|^2=\boxed{す}$
である。
(5)平行六面体$OABC-DEFG$を、直線OFの周りに1回転してできる回転体
の体積は$\boxed{こ}$である。
2022明治大学理工学部過去問
この動画を見る
右の図(※動画参照)のような平行六面体OABC-DEFGにおいて、
すべての辺の長さは1であり、$\overrightarrow{ OA },\ \overrightarrow{ OC },\ \overrightarrow{ OD }$のどの
2つのなす角も$\frac{\pi}{3}$であるとする。
(1)$\overrightarrow{ OF }$を$\overrightarrow{ OA },\ \overrightarrow{ OC },\ \overrightarrow{ OD }$を用いて表すと、
$\overrightarrow{ OF }= \boxed{き}$である。
(2)$|\overrightarrow{ OF }|,\ \cos \angle AOF$を求めると$|\overrightarrow{ OF }|= \boxed{く},$
$\ \cos \angle AOF=\boxed{け}$である。
(3)三角形ACDを底面とする三角錐OACDを、直線OFの周りに1回転して
できる円錐の体積は$\boxed{こ}$である。
(4)対角線OF上に点Pをとり、$|\overrightarrow{ OP }|=t$とおく。点Pを通り、$\overrightarrow{ OF }$に垂直な平面
をHとする。平行六面体$OABC-DEFG$を平面Hで切った時の断面が六角形
となるようなtの範囲は$\boxed{さ}$である。このとき、平面Hと辺AEの交点をQ
として、$|\overrightarrow{ AQ }|$をtの式で表すと$|\overrightarrow{ AQ }|=\boxed{し}$である。
また、$|\overrightarrow{ PQ }|^2$を$t$の式で表すと
$|\overrightarrow{ PQ }|^2=|\overrightarrow{ OQ }|^2-|\overrightarrow{ OP }|^2=\boxed{す}$
である。
(5)平行六面体$OABC-DEFG$を、直線OFの周りに1回転してできる回転体
の体積は$\boxed{こ}$である。
2022明治大学理工学部過去問
福田の数学〜明治大学2022年理工学部第2問〜平面図形の計量

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#英語(高校生)#平面図形#大学入試過去問(英語)#学校別大学入試過去問解説(英語)#明治大学#数学(高校生)#明治大学
指導講師:
福田次郎
問題文全文(内容文):
平面上の長さ3の線分AB上に、$AP=t\ (0 \lt t \lt 3)$を満たす点Pをとる。
中心を$O$とする半径1の円Oが、線分ABと点Pで接しているとする。
$\alpha=\angle OAB,\ \beta=\angle OBA$
とおく。$\tan\alpha,\ \tan\beta,\tan(\alpha+\beta)$を$t$で表すと、
$\tan\alpha=\boxed{あ},\ \tan\beta=\boxed{い},$
$\ \tan(\alpha+\beta)=\boxed{う}$である。
$0 \lt \alpha+\beta \lt \frac{\pi}{2}$であるようなtの範囲は$\boxed{え}$である。
tは$\boxed{え}$の範囲にあるとする。点$A,\ B$から円Oに引いた接線の接点のうち、
Pでないものをそれぞれ$Q,\ R$とすると、$\angle QAB+\angle RBA \lt \pi$である。
したがって、線分AQのQの方への延長と線分BRのRの方への延長は交わり、
その交点をCとすると、円Oは三角形ABCの内接円である。
このとき、線分CQの長さをtで表すと$\ \boxed{お}$である。
また、$t$が$\boxed{え}$の範囲を動くとき、三角形ABCの面積Sの取り得る値の範囲は$\boxed{か}$である。
2022明治大学理工学部過去問
この動画を見る
平面上の長さ3の線分AB上に、$AP=t\ (0 \lt t \lt 3)$を満たす点Pをとる。
中心を$O$とする半径1の円Oが、線分ABと点Pで接しているとする。
$\alpha=\angle OAB,\ \beta=\angle OBA$
とおく。$\tan\alpha,\ \tan\beta,\tan(\alpha+\beta)$を$t$で表すと、
$\tan\alpha=\boxed{あ},\ \tan\beta=\boxed{い},$
$\ \tan(\alpha+\beta)=\boxed{う}$である。
$0 \lt \alpha+\beta \lt \frac{\pi}{2}$であるようなtの範囲は$\boxed{え}$である。
tは$\boxed{え}$の範囲にあるとする。点$A,\ B$から円Oに引いた接線の接点のうち、
Pでないものをそれぞれ$Q,\ R$とすると、$\angle QAB+\angle RBA \lt \pi$である。
したがって、線分AQのQの方への延長と線分BRのRの方への延長は交わり、
その交点をCとすると、円Oは三角形ABCの内接円である。
このとき、線分CQの長さをtで表すと$\ \boxed{お}$である。
また、$t$が$\boxed{え}$の範囲を動くとき、三角形ABCの面積Sの取り得る値の範囲は$\boxed{か}$である。
2022明治大学理工学部過去問
英国数学オリンピック 高校入試レベルの問題

単元:
#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
すべてのxで次の式が成り立つ整数(a,b,c)をすべて求めよ.
$(x-10)(x-a)+1=(x+a)(x+c)$
英国数学オリンピック過去問
この動画を見る
すべてのxで次の式が成り立つ整数(a,b,c)をすべて求めよ.
$(x-10)(x-a)+1=(x+a)(x+c)$
英国数学オリンピック過去問
『log』の解説を30秒でします

