 数Ⅱ
数Ⅱ
 数Ⅱ
数Ⅱ
高専数学 微積I #226(3) 媒介変数表示の面積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq \dfrac{\pi}{2}$
曲線$x=\cos t,\cos 2t+1$
$x$軸,直線$x=1$で囲まれた図形の
面積$S$を求めよ.
この動画を見る
$0\leqq t\leqq \dfrac{\pi}{2}$
曲線$x=\cos t,\cos 2t+1$
$x$軸,直線$x=1$で囲まれた図形の
面積$S$を求めよ.
ε N論法 #7 a_n ≧ b_n
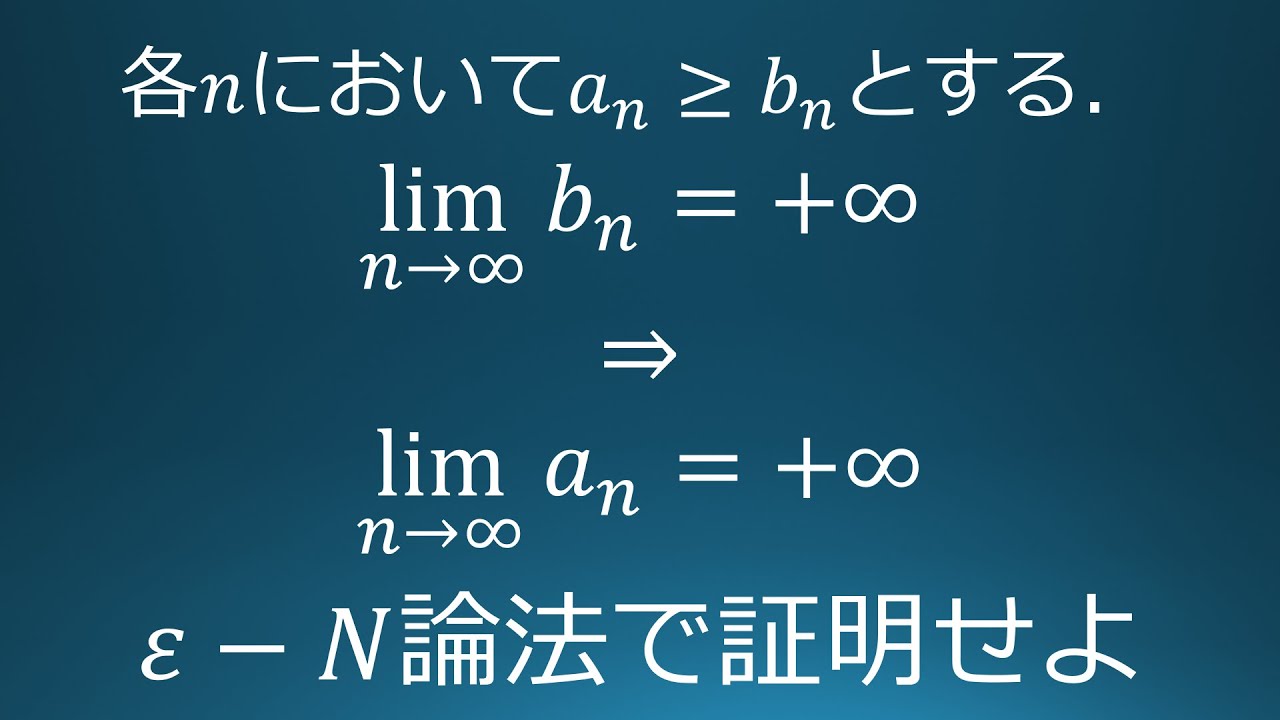
単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
数列{$a_n$},{$b_n$}は各$n$において
$a_n \geqq b_n$をみたす
$\displaystyle \lim_{n\to\infty} b_n=+\infty$
$\displaystyle \lim_{n\to\infty} a_n=+\infty$
$ε N$論法で証明せよ.
この動画を見る
数列{$a_n$},{$b_n$}は各$n$において
$a_n \geqq b_n$をみたす
$\displaystyle \lim_{n\to\infty} b_n=+\infty$
$\displaystyle \lim_{n\to\infty} a_n=+\infty$
$ε N$論法で証明せよ.
高専数学 微積I #226(2) 媒介変数表示の面積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq \dfrac{\pi}{4}$とする.
曲線$x=\tan t,y=\sin t+1$と
$x$軸,$y$軸,直線$x=1$で囲まれた図形の
面積$S$を求めよ.
この動画を見る
$0\leqq t\leqq \dfrac{\pi}{4}$とする.
曲線$x=\tan t,y=\sin t+1$と
$x$軸,$y$軸,直線$x=1$で囲まれた図形の
面積$S$を求めよ.
指数タワー どっちがでかいの?

ε N論法 #6 1-n^2(n→∞)

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{n\to\infty}(1-n^2)=-\infty$
$ε N$論法で証明せよ.
この動画を見る
$\displaystyle \lim_{n\to\infty}(1-n^2)=-\infty$
$ε N$論法で証明せよ.
ε N論法 #5 √n(n→∞)

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{n\to\infty} \sqrt n=+\infty$
$ε N$論法で証明せよ.
この動画を見る
$\displaystyle \lim_{n\to\infty} \sqrt n=+\infty$
$ε N$論法で証明せよ.
高専数学 微積I #226(1) 媒介変数表示の面積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq 1$とする.
曲線$x=t^2,y=t^2-2t+1$
$x$軸,$y$軸で囲まれた図形の
面積$S$を求めよ.
この動画を見る
$0\leqq t\leqq 1$とする.
曲線$x=t^2,y=t^2-2t+1$
$x$軸,$y$軸で囲まれた図形の
面積$S$を求めよ.
兵庫県教員採用試験(数学:練習問題 解の個数)

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$a\gt 0$とする.
$x^a=a^x$を満たす正の解の
個数を調べよ.
この動画を見る
$a\gt 0$とする.
$x^a=a^x$を満たす正の解の
個数を調べよ.
【数Ⅱ】 微分法と積分法:2021年高3第1回K塾記述模試

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数f(x)を次の式で定める。ただし、kは正の定数である。$f(x)=kx^3-4x^2+x+k^2$ 原点をOとする座標平面上において、曲線$C:y=f(x)$とy軸の交点をAとし、Aにお けるCの接線と垂直でAを通る直線をlとする。
(1)lの方程式を求めよ。
(2)Cとlが A以外に2点で交わるとする。このとき、kの値の範囲を求めよ。
(3)(2)のとき、CとlのA以外の2交点をP、Qとし、三角形OPQの面積をSとする。kが(2)で求めた範 囲を変化するとき、Sの最大値を求めよ。
この動画を見る
関数f(x)を次の式で定める。ただし、kは正の定数である。$f(x)=kx^3-4x^2+x+k^2$ 原点をOとする座標平面上において、曲線$C:y=f(x)$とy軸の交点をAとし、Aにお けるCの接線と垂直でAを通る直線をlとする。
(1)lの方程式を求めよ。
(2)Cとlが A以外に2点で交わるとする。このとき、kの値の範囲を求めよ。
(3)(2)のとき、CとlのA以外の2交点をP、Qとし、三角形OPQの面積をSとする。kが(2)で求めた範 囲を変化するとき、Sの最大値を求めよ。
【数Ⅱ】三角関数:2021年高3第1回K塾記述模試

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
aは実数の定数とし、$0\leqq\theta\lt 2\pi$とする。次の2つの式を考える。
$8a\cos\theta- 8\cos2\theta=a^2+7$…①
$\sin\theta-\cos\theta\gt-1$…②
(1)a=1のとき、方程式①を解け。
(2)不等式②を 解け。
(3)(2)で求めた範囲に①の異なる解がちょうど3個存在するようなaの値の 範囲を求めよ。
この動画を見る
aは実数の定数とし、$0\leqq\theta\lt 2\pi$とする。次の2つの式を考える。
$8a\cos\theta- 8\cos2\theta=a^2+7$…①
$\sin\theta-\cos\theta\gt-1$…②
(1)a=1のとき、方程式①を解け。
(2)不等式②を 解け。
(3)(2)で求めた範囲に①の異なる解がちょうど3個存在するようなaの値の 範囲を求めよ。
高専数学 微積I #218 曲線の長さの最小値 (九州大学類題)
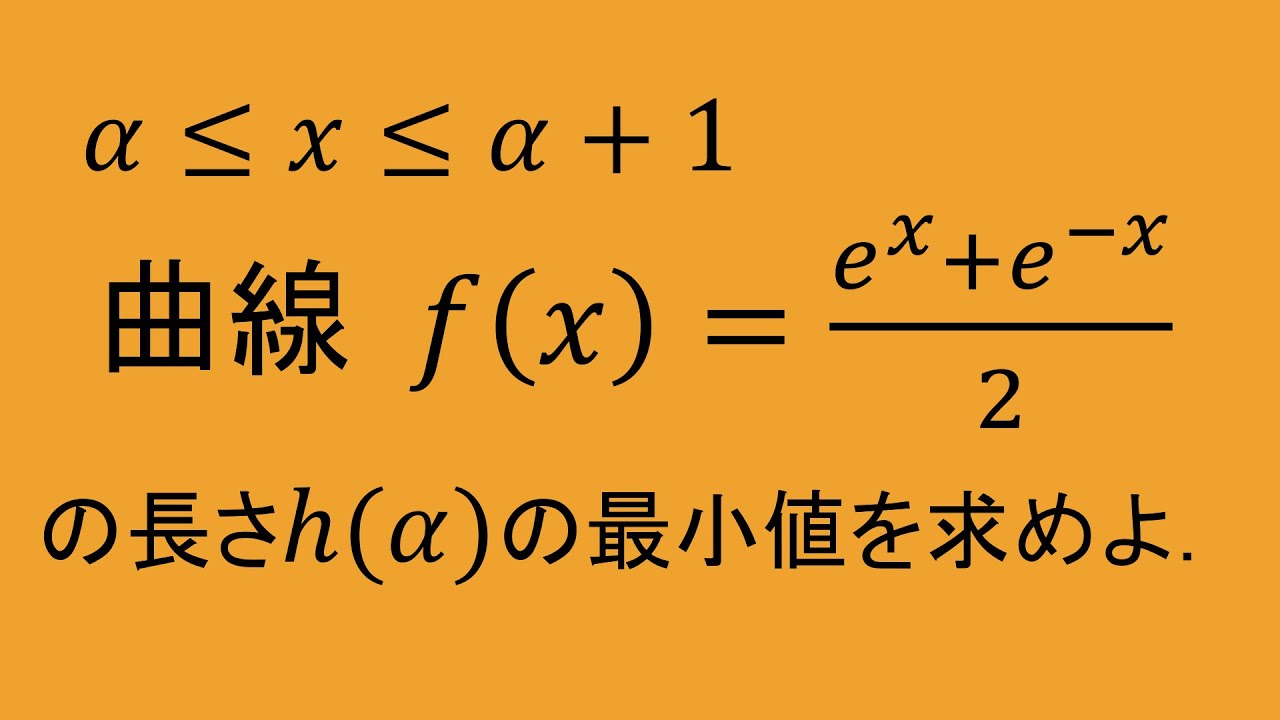
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\dfrac{e^x+e^{-x}}{2} \ (\alpha \leqq x \leqq \alpha+1)$
の曲線の長さ$k(\alpha)$の最小値を求めよ.
この動画を見る
$f(x)=\dfrac{e^x+e^{-x}}{2} \ (\alpha \leqq x \leqq \alpha+1)$
の曲線の長さ$k(\alpha)$の最小値を求めよ.
16和歌山県教員採用試験(数学:6番 対数の不等式)

単元:
#数Ⅰ#数Ⅱ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
$2\log_3 x-4\log_x 27 \leqq 5$を解け.
この動画を見る
$\boxed{6}$
$2\log_3 x-4\log_x 27 \leqq 5$を解け.
福田のわかった数学〜高校2年生030〜円と放物線の位置関係(2)

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{II} 円と放物線の位置関係(2)\\
\\
\left\{\begin{array}{1}
円\ x^2+(y-r)^2=r^2 (r \gt 0)\\
放物線\ y=x^2
\end{array}\right.\\
\\
の共有点が原点のみとなるrの範囲
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{II} 円と放物線の位置関係(2)\\
\\
\left\{\begin{array}{1}
円\ x^2+(y-r)^2=r^2 (r \gt 0)\\
放物線\ y=x^2
\end{array}\right.\\
\\
の共有点が原点のみとなるrの範囲
\end{eqnarray}
11滋賀県教員採用試験(数学:1-(4) 剰余・因数定理系)

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}-(4)$
$f(x)=x^4+px^2+gx-8$は
$(x+1)^2$で割り切れるとき,
$p,q$の値を求めよ.
この動画を見る
$\boxed{1}-(4)$
$f(x)=x^4+px^2+gx-8$は
$(x+1)^2$で割り切れるとき,
$p,q$の値を求めよ.
高専数学 微積I #211 体積

単元:
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
半径$r$の直円柱を底面の直径$AB$を通り
底面と$\dfrac{\pi}{6}$の角をなす平面で切るとき,
底面と平面の間の部分の体積$V$を求めよ.
この動画を見る
半径$r$の直円柱を底面の直径$AB$を通り
底面と$\dfrac{\pi}{6}$の角をなす平面で切るとき,
底面と平面の間の部分の体積$V$を求めよ.
福田の数学〜早稲田大学2021年商学部第1問(3)〜相加相乗平均

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$
(3)正の実数$x,y,z$が
$\dfrac{1}{x}+\dfrac{2}{y}+\dfrac{3}{z}=1$
を満たすとき、$(x-1)(y-2)(z-3)$の最小値は$\boxed{\ \ ウ\ \ }$である。
2021早稲田大学商学部過去問
この動画を見る
${\Large\boxed{1}}$
(3)正の実数$x,y,z$が
$\dfrac{1}{x}+\dfrac{2}{y}+\dfrac{3}{z}=1$
を満たすとき、$(x-1)(y-2)(z-3)$の最小値は$\boxed{\ \ ウ\ \ }$である。
2021早稲田大学商学部過去問
高専数学 微積I #210(2) 曲線の長さ
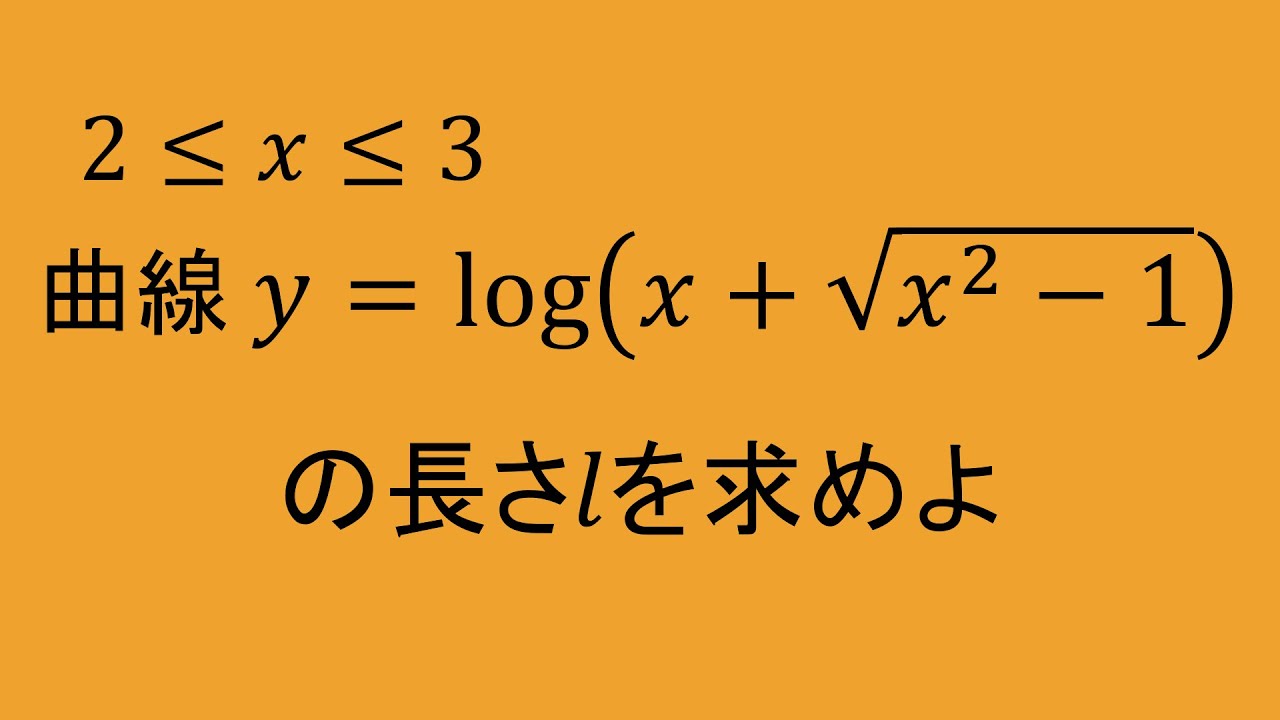
単元:
#数Ⅱ#平面上の曲線#微分法と積分法#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$2\leqq x\leqq 3$
曲線$y=\log (x+\sqrt{x^2-1})$の長さ$\ell$を求めよ.
この動画を見る
$2\leqq x\leqq 3$
曲線$y=\log (x+\sqrt{x^2-1})$の長さ$\ell$を求めよ.
高専数学 微積I #210(1) 曲線の長さ

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
曲線$y=(x-1)^{\frac{3}{2}} \ (1\leq x \leq 6)$
の長さ$\ell$を求めよ.
この動画を見る
曲線$y=(x-1)^{\frac{3}{2}} \ (1\leq x \leq 6)$
の長さ$\ell$を求めよ.
【数Ⅱ】図形と方程式:5分で学ぶファクシミリ論法

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
教材:
#チャート式#黄チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ファクシミリ論法を5分で解説!
この動画を見る
ファクシミリ論法を5分で解説!
福田の数学〜早稲田大学2021年商学部第1問(1)〜三角形と三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$
(1)三角形$\rm ABC$において、$\rm \angle B=2\alpha, \angle C=2\beta$とする。
$\tan\alpha\tan\beta=x, \rm \dfrac{AB+AC}{BC}=y$
とするとき、$y$を$x$で表すと、$y=\boxed{ア}$となる。
2021早稲田大学商学部過去問
この動画を見る
${\Large\boxed{1}}$
(1)三角形$\rm ABC$において、$\rm \angle B=2\alpha, \angle C=2\beta$とする。
$\tan\alpha\tan\beta=x, \rm \dfrac{AB+AC}{BC}=y$
とするとき、$y$を$x$で表すと、$y=\boxed{ア}$となる。
2021早稲田大学商学部過去問
福田のわかった数学〜高校3年生理系030〜極限(30)関数の極限、三角関数の極限(10)

単元:
#数Ⅱ#三角関数#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 三角関数の極限(10)
$\displaystyle \lim_{x \to 0}\frac{\sqrt{9-8x+7\cos2x}-(a+bx)}{x^2}$
が有限の値となる$a,b$とそのときの極限値
この動画を見る
数学$\textrm{III}$ 三角関数の極限(10)
$\displaystyle \lim_{x \to 0}\frac{\sqrt{9-8x+7\cos2x}-(a+bx)}{x^2}$
が有限の値となる$a,b$とそのときの極限値
どっちがでかい?

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?$ e\fallingdotseq 2,71$
$6^{\sqrt7}$ VS $7^{\sqrt6}$
この動画を見る
どちらが大きいか?$ e\fallingdotseq 2,71$
$6^{\sqrt7}$ VS $7^{\sqrt6}$
ε-N論法 #3 lim n/n+2 =1
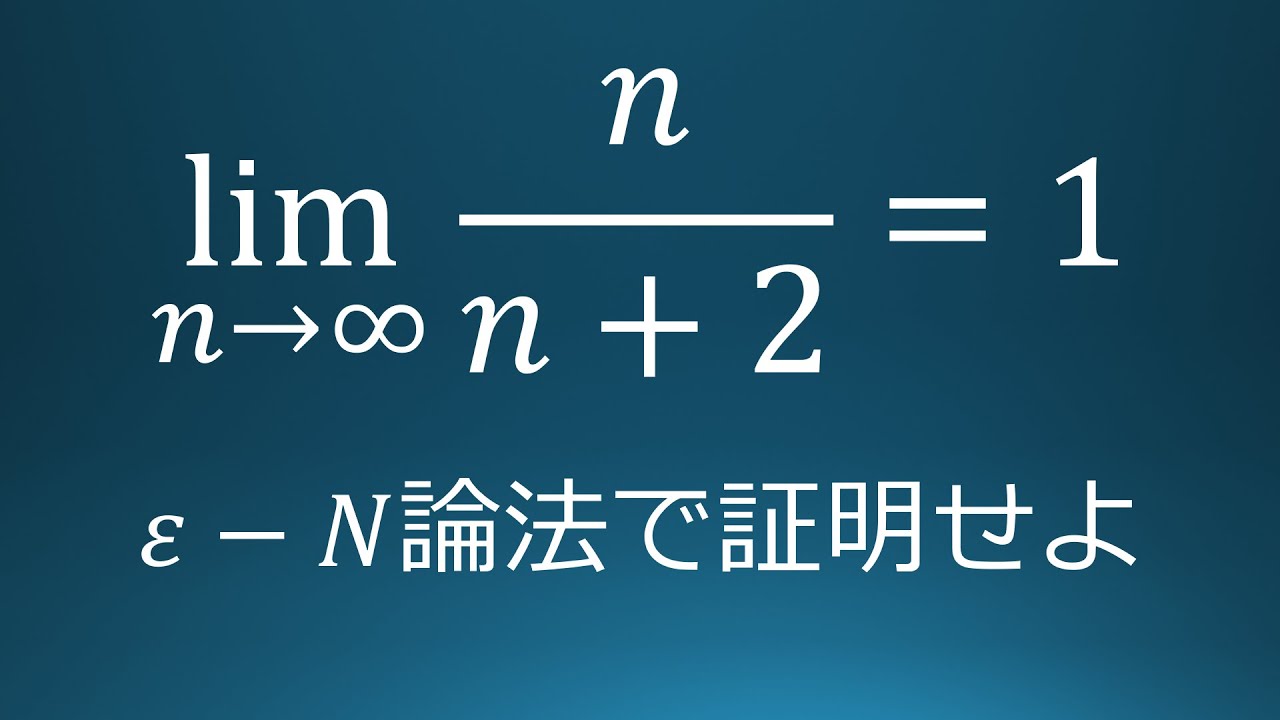
単元:
#数Ⅱ#式と証明#微分法と積分法#恒等式・等式・不等式の証明#平均変化率・極限・導関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{n\to\infty} \dfrac{n}{n+2}=1$を
$ε-N$論法を利用して示せ.
この動画を見る
$\displaystyle \lim_{n\to\infty} \dfrac{n}{n+2}=1$を
$ε-N$論法を利用して示せ.
ε-N論法 #2 lim 1/n^2=0
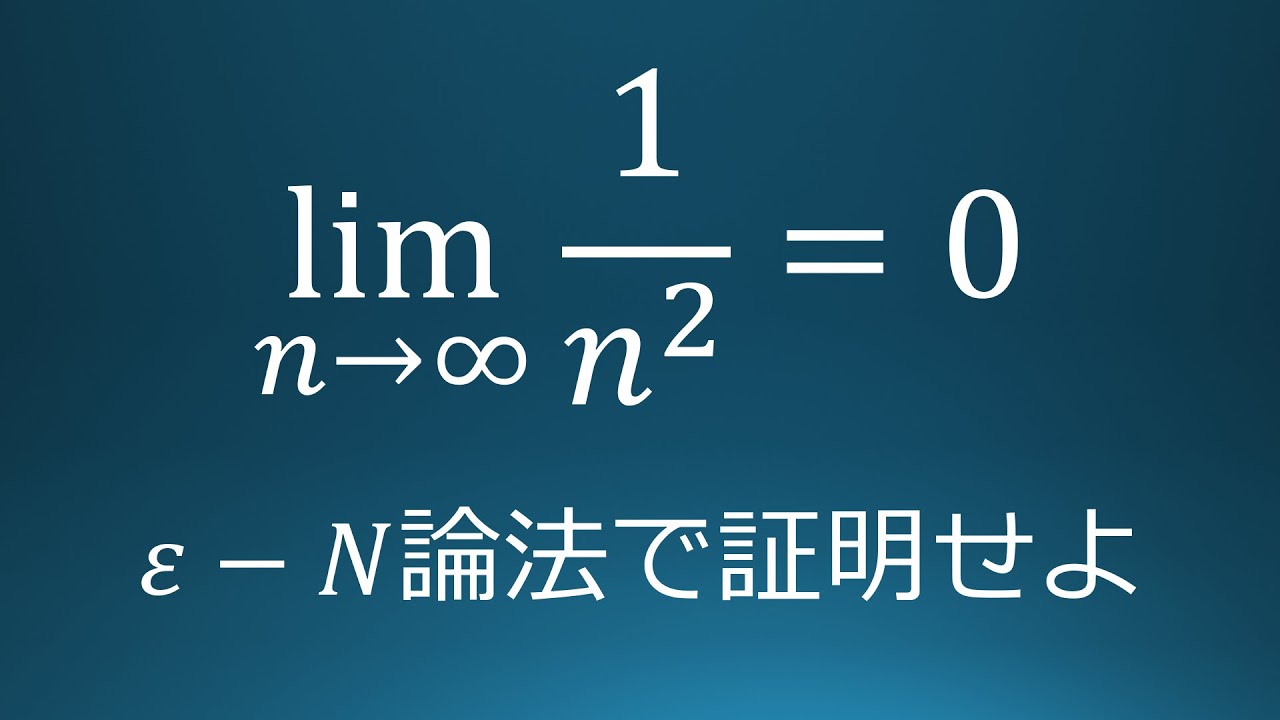
単元:
#数Ⅱ#式と証明#微分法と積分法#恒等式・等式・不等式の証明#平均変化率・極限・導関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{n\to\infty} \dfrac{1}{n^2}=0$を
$ε-N$論法を利用して示せ.
この動画を見る
$\displaystyle \lim_{n\to\infty} \dfrac{1}{n^2}=0$を
$ε-N$論法を利用して示せ.
福田のわかった数学〜高校2年生029〜円と放物線の位置関係(1)

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{II} 円と放物線の位置関係(1)\\
\left\{\begin{array}{1}
円\ x^2+y^2=r^2 (r \gt 0)\\
放物線\ y=x^2-1
\end{array}\right.\\
\\
の共有点の個数を調べよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{II} 円と放物線の位置関係(1)\\
\left\{\begin{array}{1}
円\ x^2+y^2=r^2 (r \gt 0)\\
放物線\ y=x^2-1
\end{array}\right.\\
\\
の共有点の個数を調べよ。
\end{eqnarray}
高専数学 微積I #207 体積

単元:
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
点$x(0\lt x\lt \pi)$で$x$軸に垂直な平面で切った切り口が,
辺の長さが$x,\sin x$の長方形である立体の体積$V$を求めよ.
この動画を見る
点$x(0\lt x\lt \pi)$で$x$軸に垂直な平面で切った切り口が,
辺の長さが$x,\sin x$の長方形である立体の体積$V$を求めよ.
ε-N論法 #1 lim1/n=0
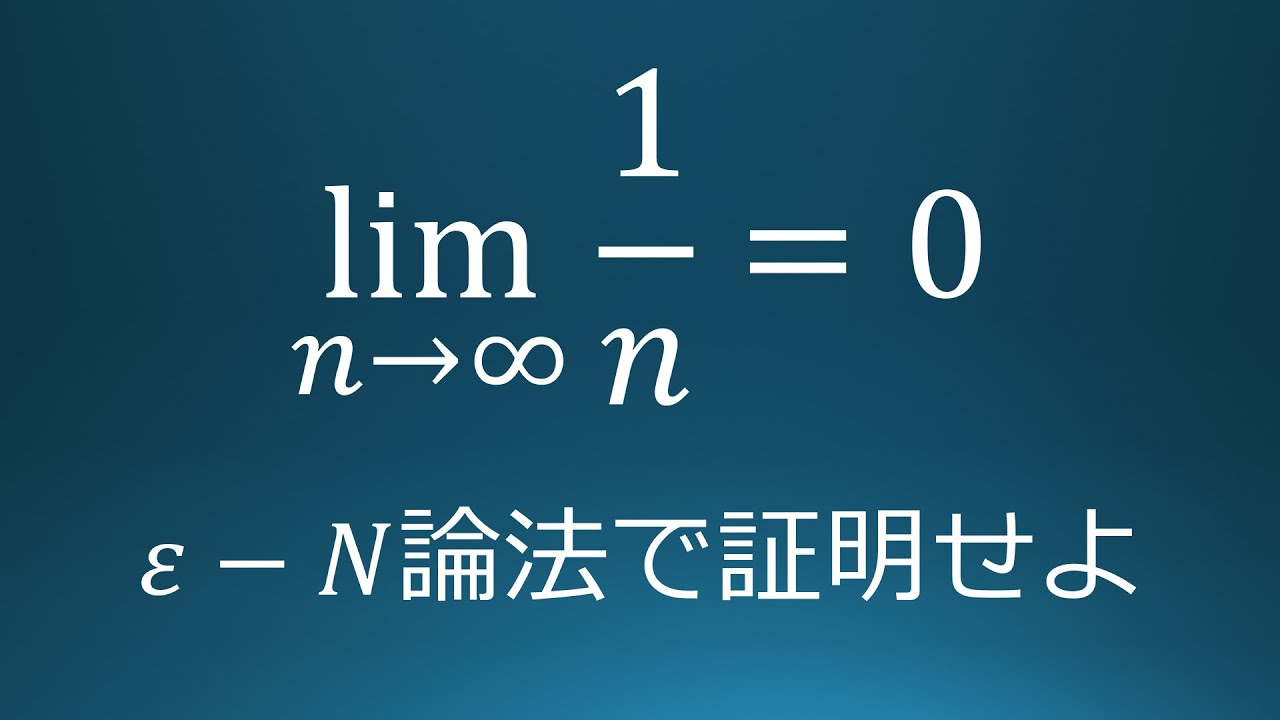
単元:
#数Ⅱ#式と証明#微分法と積分法#恒等式・等式・不等式の証明#平均変化率・極限・導関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{n\to\infty} \dfrac{1}{n}=0$を
$ε-N$論法を利用して示せ.
この動画を見る
$\displaystyle \lim_{n\to\infty} \dfrac{1}{n}=0$を
$ε-N$論法を利用して示せ.
ε-N論法 #4 はさみうちの原理

単元:
#数Ⅱ#式と証明#微分法と積分法#恒等式・等式・不等式の証明#平均変化率・極限・導関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
各自然数$n$で$a_n \leqq b_n \leqq c_n$を
満たす任意の数列
{$a_n$},{$b_n$},{$c_n$}に対して
$\displaystyle \lim_{n\to\infty} a_n=A=\displaystyle \lim_{n\to\infty} c_n$
ならば
$\displaystyle \lim_{n\to\infty} b_n=A$
ε-N論法で証明せよ.
この動画を見る
各自然数$n$で$a_n \leqq b_n \leqq c_n$を
満たす任意の数列
{$a_n$},{$b_n$},{$c_n$}に対して
$\displaystyle \lim_{n\to\infty} a_n=A=\displaystyle \lim_{n\to\infty} c_n$
ならば
$\displaystyle \lim_{n\to\infty} b_n=A$
ε-N論法で証明せよ.
高専数学 微積I #206 体積

単元:
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
3辺の長さが3,4,5の三角形を底面とする高さが
10の三角錐の体積$V$を求めよ.
この動画を見る
3辺の長さが3,4,5の三角形を底面とする高さが
10の三角錐の体積$V$を求めよ.
福田の数学〜早稲田大学2021年社会科学部第1問〜三角関数で表された点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#三角関数#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ a,bを定数とし、関数$f(x)=x^2+ax+b$ とする。方程式$f(x)=0$の2つの解$\alpha,\beta\\$
が次式で与えられている。
$\alpha=\frac{\sin\theta}{1+\cos\theta}$, $\beta=\frac{\sin\theta}{1-\cos\theta}\\$
ここで$\theta$は、$0 \lt \theta \lt \pi$の定数である。次の問いに答えよ。
$(1)a,b$を$\theta$を用いて表せ。
$(2)\theta$が$0$ $\lt \theta \pi$で変化するとき、放物線$y=f(x)$の頂点の軌跡を求めよ。
$(3)\int_0^{2\sin\theta}f(x)dx=0$ となる$\theta$の値を全て求めよ。
2021早稲田大学社会科学部過去問
この動画を見る
${\Large\boxed{1}}$ a,bを定数とし、関数$f(x)=x^2+ax+b$ とする。方程式$f(x)=0$の2つの解$\alpha,\beta\\$
が次式で与えられている。
$\alpha=\frac{\sin\theta}{1+\cos\theta}$, $\beta=\frac{\sin\theta}{1-\cos\theta}\\$
ここで$\theta$は、$0 \lt \theta \lt \pi$の定数である。次の問いに答えよ。
$(1)a,b$を$\theta$を用いて表せ。
$(2)\theta$が$0$ $\lt \theta \pi$で変化するとき、放物線$y=f(x)$の頂点の軌跡を求めよ。
$(3)\int_0^{2\sin\theta}f(x)dx=0$ となる$\theta$の値を全て求めよ。
2021早稲田大学社会科学部過去問
