 数Ⅱ
数Ⅱ
 数Ⅱ
数Ⅱ
2021 神戸大(文)複素数の累乗

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
①$(3+i)^n$
$n=2,3,4,5$の値と虚部の整数を$10$で割った余りを求めよ.
②$(3+i)^n$は虚数であることを示せ.($n$は自然数)
2021神戸大(文)
この動画を見る
①$(3+i)^n$
$n=2,3,4,5$の値と虚部の整数を$10$で割った余りを求めよ.
②$(3+i)^n$は虚数であることを示せ.($n$は自然数)
2021神戸大(文)
04岡山県教員採用試験(数学:6-(2) 積分)

単元:
#数Ⅱ#微分法と積分法#その他#不定積分・定積分#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6} - (2)$
$\displaystyle \int_{}^{} (\sin^{-1} x)^2 \ dx$を計算せよ.
この動画を見る
$\boxed{6} - (2)$
$\displaystyle \int_{}^{} (\sin^{-1} x)^2 \ dx$を計算せよ.
cosの積 華麗な解法で綺麗な答え

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\displaystyle \prod_{k=1}^7 \cos\dfrac{\pi}{15}\pi=$
$\cos\dfrac{\pi}{15}\cos\dfrac{2\pi}{15}\cos\dfrac{3\pi}{15}\cos\dfrac{4\pi}{15}\cos\dfrac{5\pi}{15}\cos\dfrac{6\pi}{15}\cos\dfrac{7\pi}{15}$
この動画を見る
これを解け.
$\displaystyle \prod_{k=1}^7 \cos\dfrac{\pi}{15}\pi=$
$\cos\dfrac{\pi}{15}\cos\dfrac{2\pi}{15}\cos\dfrac{3\pi}{15}\cos\dfrac{4\pi}{15}\cos\dfrac{5\pi}{15}\cos\dfrac{6\pi}{15}\cos\dfrac{7\pi}{15}$
複素関数論⑬ 高専数学*4(複素積分の極限)
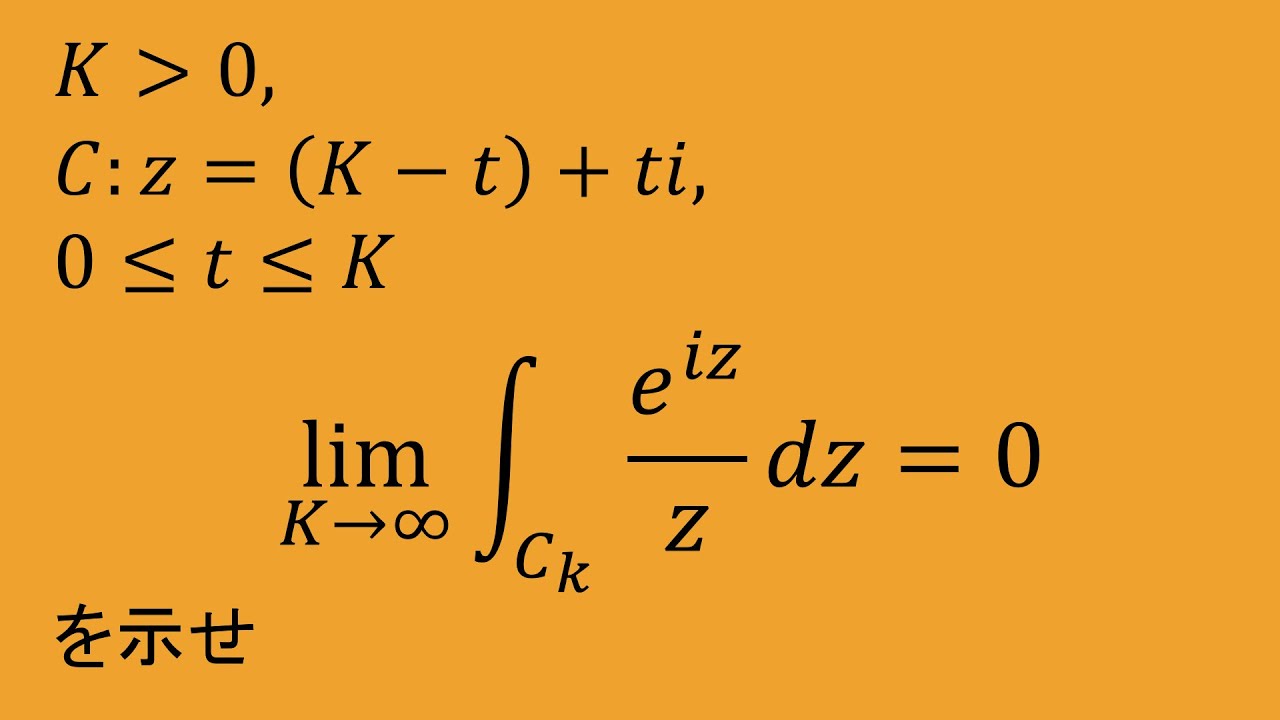
単元:
#数Ⅱ#複素数と方程式#微分法と積分法#複素数#平均変化率・極限・導関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$k\gt 0$,$C_k:z=(k-t)+it$であり,
$0\leqq t\leqq k$とするとき,以下を解け.
(1)$\vert z\vert \geqq \dfrac{k}{\sqrt2},\left\vert\dfrac{e^{iz}}{z}\right\vert \leqq \dfrac{\sqrt2 e^{-t}}{k}$
(2)$\displaystyle \lim_{k\to\infty} \displaystyle \int_{c_k}^{} \dfrac{e^{iz}}{z} dz=0$
この動画を見る
$k\gt 0$,$C_k:z=(k-t)+it$であり,
$0\leqq t\leqq k$とするとき,以下を解け.
(1)$\vert z\vert \geqq \dfrac{k}{\sqrt2},\left\vert\dfrac{e^{iz}}{z}\right\vert \leqq \dfrac{\sqrt2 e^{-t}}{k}$
(2)$\displaystyle \lim_{k\to\infty} \displaystyle \int_{c_k}^{} \dfrac{e^{iz}}{z} dz=0$
04岡山県教員採用試験(数学:4番 積分)

単元:
#数Ⅱ#微分法と積分法#その他#不定積分・定積分#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
$\displaystyle \int_{}^{} \sin^{-1}x \ dx$を計算せよ.
この動画を見る
$\boxed{6}$
$\displaystyle \int_{}^{} \sin^{-1}x \ dx$を計算せよ.
方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$x$を実数とする.
$\sqrt{x^2+3x+2}-\sqrt{x^2+2x+5}=3-x$
この動画を見る
これを解け.$x$を実数とする.
$\sqrt{x^2+3x+2}-\sqrt{x^2+2x+5}=3-x$
04京都府教員採用試験(数学:6番 ネピアの数の性質)

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$n\in IN$,$\displaystyle \lim_{n\to\infty} \left(1+\dfrac{1}{n}\right)^n=e$
を満たすとき,
$x\in IR$,$\displaystyle \lim_{x\to\infty}\left(1+\dfrac{1}{x}\right)^n=e$
を示せ.
この動画を見る
$n\in IN$,$\displaystyle \lim_{n\to\infty} \left(1+\dfrac{1}{n}\right)^n=e$
を満たすとき,
$x\in IR$,$\displaystyle \lim_{x\to\infty}\left(1+\dfrac{1}{x}\right)^n=e$
を示せ.
複素関数論⑫:複素積分の絶対値の評価(高専数学)
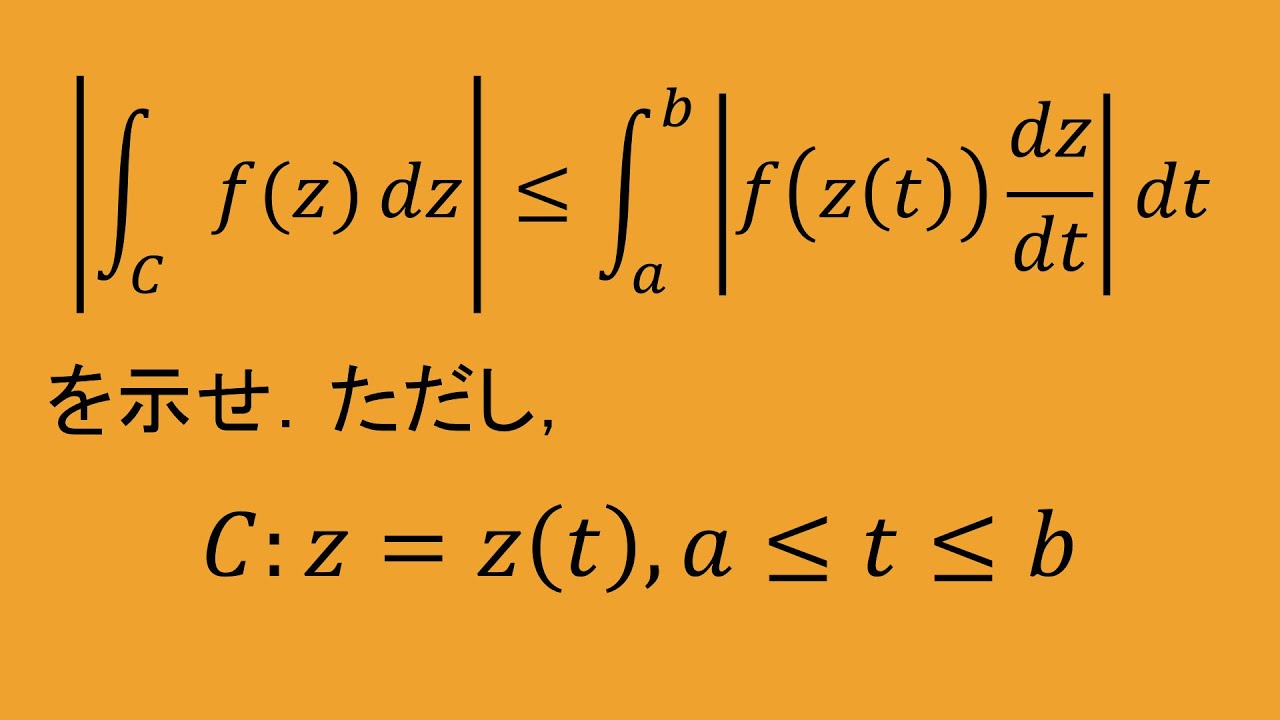
単元:
#数Ⅱ#複素数と方程式#微分法と積分法#複素数#不定積分・定積分#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$C:z=z(t),a\leqq t\leqq b$とする.
$\vert \displaystyle \int_{c}^{} f(z)dz \vert\leqq \displaystyle \int_{a}^{b} \vert f(z(t)\dfrac{dz}{dt}\vert dt $
を示せ.
この動画を見る
$C:z=z(t),a\leqq t\leqq b$とする.
$\vert \displaystyle \int_{c}^{} f(z)dz \vert\leqq \displaystyle \int_{a}^{b} \vert f(z(t)\dfrac{dz}{dt}\vert dt $
を示せ.
とある奈良県教員採用試験の問題(数学:接線の数)

単元:
#数A#数Ⅱ#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#微分法と積分法#接線と増減表・最大値・最小値#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
点$P(a,0)$を通り,
曲線$y=\dfrac{x}{\log_x}\ (x\gt 1)$に接する直線が
2本引けるように$a$の値の範囲を求めよ.
この動画を見る
点$P(a,0)$を通り,
曲線$y=\dfrac{x}{\log_x}\ (x\gt 1)$に接する直線が
2本引けるように$a$の値の範囲を求めよ.
16京都府教員採用試験(数学:1番 積分)

単元:
#数Ⅱ#微分法と積分法#その他#不定積分・定積分#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}$
$n \in IN$とする.
$2(\sqrt{n+1}-1)\lt 1+\dfrac{1}{\sqrt 2}+\dfrac{1}{\sqrt 3}+・・・+\dfrac{1}{\sqrt n}$
これを解け.
この動画を見る
$\boxed{1}$
$n \in IN$とする.
$2(\sqrt{n+1}-1)\lt 1+\dfrac{1}{\sqrt 2}+\dfrac{1}{\sqrt 3}+・・・+\dfrac{1}{\sqrt n}$
これを解け.
いつかの奈良県教員採用試験(数学:バームクーヘンの定理)

単元:
#数Ⅱ#微分法と積分法#その他#面積、体積#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$y=\sin x\ (0\leqq x \leqq \pi)$と
$x$軸で囲まれた部分を$y$軸を中心として
回転させる体積$V$を求めよ.
この動画を見る
$y=\sin x\ (0\leqq x \leqq \pi)$と
$x$軸で囲まれた部分を$y$軸を中心として
回転させる体積$V$を求めよ.
【数Ⅱ】微分法と積分法:2021年度東大文科第1問を典型解法で攻略!

単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
aを正の実数とする。座標平面上の曲線Cを$y=ax^3-2x$で定める。原点を中心とする半径1の円とCの共有点の個数が6個であるようなaの範囲を求めよ。
この動画を見る
aを正の実数とする。座標平面上の曲線Cを$y=ax^3-2x$で定める。原点を中心とする半径1の円とCの共有点の個数が6個であるようなaの範囲を求めよ。
09愛知県教員採用試験(数学:3番 指数・対数)

単元:
#数Ⅱ#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
$25^{\log_5 3^x}-4\sqrt3・3^x=-9$を解け.
この動画を見る
$\boxed{3}$
$25^{\log_5 3^x}-4\sqrt3・3^x=-9$を解け.
複素関数論⑪ 三角形の周の複素積分 高専数学*3(3)
16愛知県教員採用試験(数学:5番 三角関数)

単元:
#数Ⅱ#三角関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
$0\leqq x\leqq \pi$とする.
$\sin 2x-2(\sin x+\cos x)-k=0$の
実数解の個数を調べよ.
この動画を見る
$\boxed{3}$
$0\leqq x\leqq \pi$とする.
$\sin 2x-2(\sin x+\cos x)-k=0$の
実数解の個数を調べよ.
30度 45度 60度の直線の式 A 慶應義塾 2021
単元:
#数学(中学生)#数Ⅱ#三角関数#三角関数とグラフ#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
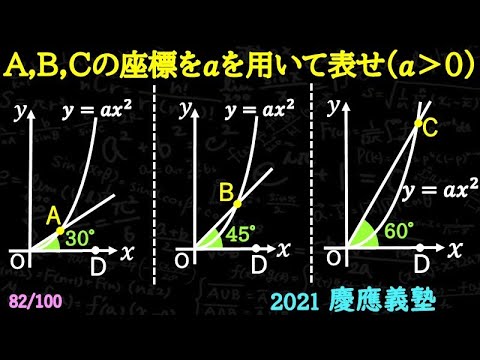
A,B,Cの座標をaを用いて表せ
*図は動画内参照
2021慶應義塾高等学校
この動画を見る
A,B,Cの座標をaを用いて表せ
*図は動画内参照
2021慶應義塾高等学校
15愛知県教員採用試験(数学:6番 三角関数)

単元:
#数Ⅱ#三角関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
$\left(\sin\theta+\dfrac{1}{2}\right)^2+\left(\cos\theta+\dfrac{1}{2}\right)^2=2$のとき,
$\sin\theta,\cos\theta$を解にもつ二次方程式も1つを求めよ.
この動画を見る
$\boxed{6}$
$\left(\sin\theta+\dfrac{1}{2}\right)^2+\left(\cos\theta+\dfrac{1}{2}\right)^2=2$のとき,
$\sin\theta,\cos\theta$を解にもつ二次方程式も1つを求めよ.
京都大2021 素数という条件は必要か

2021京都大 秒殺整数問題

複素関数論⑩ 高専数学 複素積分*ex2, *2
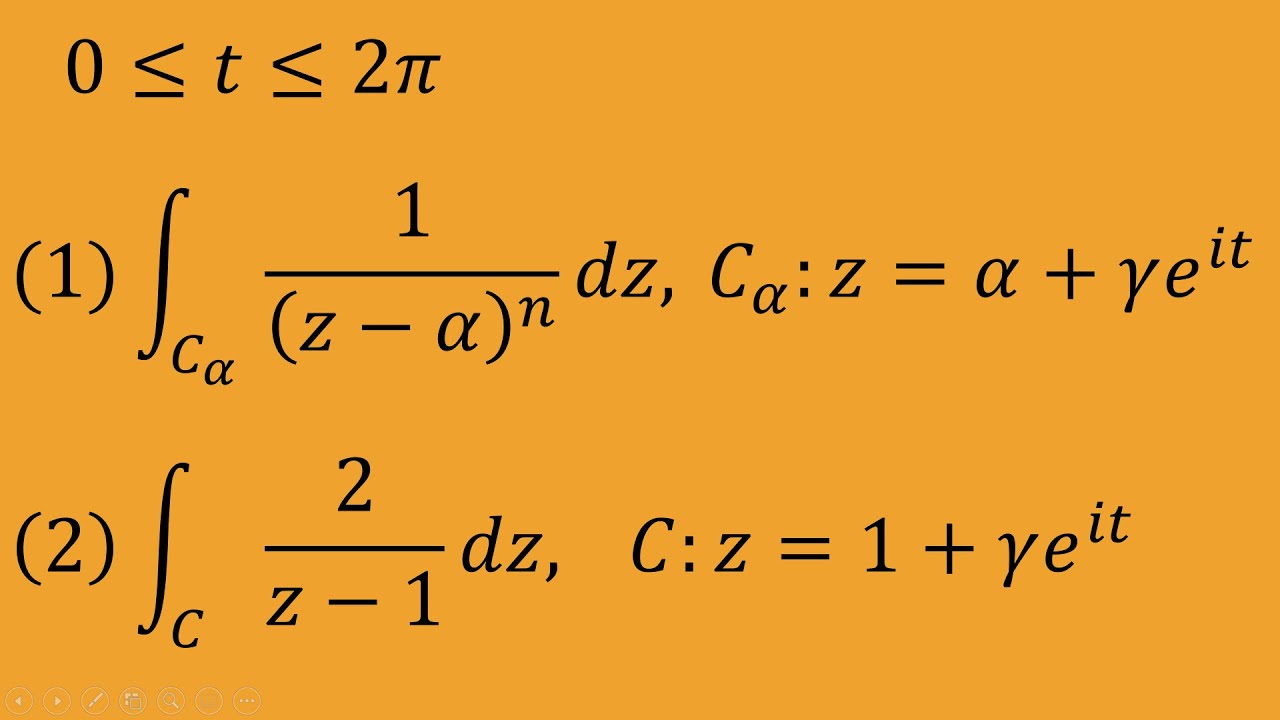
単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
これを解け.
(1)$C_{\alpha}:Z=\alpha+re^{it} \ (0\leqq t\leqq 2\pi)$
$ \displaystyle \int_{C\alpha}^{} \ \dfrac{1}{(Z-\alpha)^n}\ \alpha_Z$
(2) $C_{\alpha}:Z=1+re^{it} \ (0\leqq t\leqq 2\pi)$
$ \displaystyle \int_{C}^{} \ \dfrac{2}{Z-1}\ \alpha_Z$
この動画を見る
これを解け.
(1)$C_{\alpha}:Z=\alpha+re^{it} \ (0\leqq t\leqq 2\pi)$
$ \displaystyle \int_{C\alpha}^{} \ \dfrac{1}{(Z-\alpha)^n}\ \alpha_Z$
(2) $C_{\alpha}:Z=1+re^{it} \ (0\leqq t\leqq 2\pi)$
$ \displaystyle \int_{C}^{} \ \dfrac{2}{Z-1}\ \alpha_Z$
福田の数学〜慶應義塾大学2021年理工学部第5問〜ベクトルの図形への応用

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#図形と方程式#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{5}}$ 座標平面上で、原点$O$を通り、$\overrightarrow{ u }=(\cos\theta, \sin\theta)$を方向ベクトルとする直線を
lとおく。ただし、$-\displaystyle \frac{\pi}{2} \lt \theta \leqq \displaystyle \frac{\pi}{2}$とする。
(1)$\theta \neq \displaystyle \frac{\pi}{2}$とする。直線lの法線ベクトルで、$y$成分が正であり、大きさが
1のベクトルを$\ \overrightarrow{ n }\ $とおく。点$P(1,1)$に対し、$\overrightarrow{ OP }=s\ \overrightarrow{ u }+t\ \overrightarrow{ n }$と表す。$a=\cos\theta,$
$b=\sin\theta$として、$s,t$のそれぞれを$a,b$についての1次式で表すと、$s=\boxed{\ \ テ\ \ },$
$t=\boxed{\ \ ト\ \ }$である。
点$P(1,1)$から直線lに垂線を下ろし、直線$l$との交点を$Q$とする。ただし、点$P$
が直線$l$上にあるときは、点$Q$は$P$とする。以下では$-\displaystyle \frac{\pi}{2} \lt \theta \leqq \displaystyle \frac{\pi}{2}$とする。
(2)線分$PQ$の長さは、$\theta=\boxed{\ \ ナ\ \ }$のとき最大となる。
さらに、点$R(-3,1)$から直線$l$に垂線を下ろし、直線$l$との交点を$S$とする。
ただし、点$R$が直線$l$上にあるときは、点$S$は$R$とする。
(3)線分$QS$を$1:3$に内分する点を$T$とおく。$\theta$が$-\displaystyle \frac{\pi}{2} \lt \theta \leqq \displaystyle \frac{\pi}{2}$を満たしながら
動くとき、点$T(x,y)$が描く軌跡の方程式は$\boxed{\ \ ニ\ \ }=0$である。
(4)$PQ^2+RS^2$の最大値は$\boxed{\ \ ヌ\ \ }$である。
2021慶應義塾大学理工学部過去問
この動画を見る
${\Large\boxed{5}}$ 座標平面上で、原点$O$を通り、$\overrightarrow{ u }=(\cos\theta, \sin\theta)$を方向ベクトルとする直線を
lとおく。ただし、$-\displaystyle \frac{\pi}{2} \lt \theta \leqq \displaystyle \frac{\pi}{2}$とする。
(1)$\theta \neq \displaystyle \frac{\pi}{2}$とする。直線lの法線ベクトルで、$y$成分が正であり、大きさが
1のベクトルを$\ \overrightarrow{ n }\ $とおく。点$P(1,1)$に対し、$\overrightarrow{ OP }=s\ \overrightarrow{ u }+t\ \overrightarrow{ n }$と表す。$a=\cos\theta,$
$b=\sin\theta$として、$s,t$のそれぞれを$a,b$についての1次式で表すと、$s=\boxed{\ \ テ\ \ },$
$t=\boxed{\ \ ト\ \ }$である。
点$P(1,1)$から直線lに垂線を下ろし、直線$l$との交点を$Q$とする。ただし、点$P$
が直線$l$上にあるときは、点$Q$は$P$とする。以下では$-\displaystyle \frac{\pi}{2} \lt \theta \leqq \displaystyle \frac{\pi}{2}$とする。
(2)線分$PQ$の長さは、$\theta=\boxed{\ \ ナ\ \ }$のとき最大となる。
さらに、点$R(-3,1)$から直線$l$に垂線を下ろし、直線$l$との交点を$S$とする。
ただし、点$R$が直線$l$上にあるときは、点$S$は$R$とする。
(3)線分$QS$を$1:3$に内分する点を$T$とおく。$\theta$が$-\displaystyle \frac{\pi}{2} \lt \theta \leqq \displaystyle \frac{\pi}{2}$を満たしながら
動くとき、点$T(x,y)$が描く軌跡の方程式は$\boxed{\ \ ニ\ \ }=0$である。
(4)$PQ^2+RS^2$の最大値は$\boxed{\ \ ヌ\ \ }$である。
2021慶應義塾大学理工学部過去問
14愛知県教員採用試験(数学:5番 三角関数)

単元:
#数Ⅱ#三角関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
$0\leqq \theta \leqq \dfrac{\pi}{2}$
$\sin3\theta+\sqrt 3\cos3\theta=\sqrt2$を解け.
この動画を見る
$\boxed{5}$
$0\leqq \theta \leqq \dfrac{\pi}{2}$
$\sin3\theta+\sqrt 3\cos3\theta=\sqrt2$を解け.
練習問題18 どっかの教採の問題

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$f(\theta)=\sin2\theta+\sin\theta-\cos\theta+k\ (0\leqq \theta\leqq \pi)$
$f(\theta)=0$が異なる3つの解をもつような$k$の範囲を求めよ.
この動画を見る
$f(\theta)=\sin2\theta+\sin\theta-\cos\theta+k\ (0\leqq \theta\leqq \pi)$
$f(\theta)=0$が異なる3つの解をもつような$k$の範囲を求めよ.
約束記号 C 慶應義塾 2021
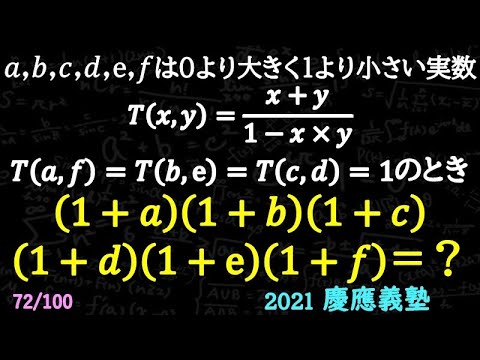
単元:
#数学(中学生)#数Ⅱ#三角関数#加法定理とその応用#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a,b,c,d,e,fは0より大きく1より小さい実数
$T(x,y)=\frac{x+y}{1-x \times y}$
$T(a,f) = T(b,e) = T(c,d) = 1$のとき
$(1+a)(1+b)(1+c)(1+d)(1+e)(1+f) =$
2021慶應義塾高等学校
この動画を見る
a,b,c,d,e,fは0より大きく1より小さい実数
$T(x,y)=\frac{x+y}{1-x \times y}$
$T(a,f) = T(b,e) = T(c,d) = 1$のとき
$(1+a)(1+b)(1+c)(1+d)(1+e)(1+f) =$
2021慶應義塾高等学校
複素関数論⑨ 高専数学 複素積分*1(1)-(3)

いろいろな方法で解こう

単元:
#数Ⅱ#指数関数と対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\left(\dfrac{1}{2021}\right)$ VS $\left(\dfrac{1}{2022}\right)^{2021}$
どちらが大きいか?
この動画を見る
$\left(\dfrac{1}{2021}\right)$ VS $\left(\dfrac{1}{2022}\right)^{2021}$
どちらが大きいか?
07大阪府教員採用試験(数学:1番 三角関数と極限)

単元:
#数Ⅱ#三角関数#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}$
$x-2\sin\theta-\cos2\theta$
$y=\displaystyle \sum_{n=1}^{\infty} \left(\dfrac{x}{6}\right)^n$のとりうる値の範囲を求めよ.
この動画を見る
$\boxed{1}$
$x-2\sin\theta-\cos2\theta$
$y=\displaystyle \sum_{n=1}^{\infty} \left(\dfrac{x}{6}\right)^n$のとりうる値の範囲を求めよ.
2021同志社大 4次方程式4つの虚数解

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$c$は実数であり,定数である.
$x^4+cx^3+cx^2+cx+1=0$の$4$つの解がすべて虚数となる.$c$の必要十分条件である.
$4$つの虚数解が複素平面上で正方形になる$c$の値を求めよ.
2021同志社過去問
この動画を見る
$c$は実数であり,定数である.
$x^4+cx^3+cx^2+cx+1=0$の$4$つの解がすべて虚数となる.$c$の必要十分条件である.
$4$つの虚数解が複素平面上で正方形になる$c$の値を求めよ.
2021同志社過去問
複素関数論⑧ 逆関数 高専数学 *25(1)-(4), *26
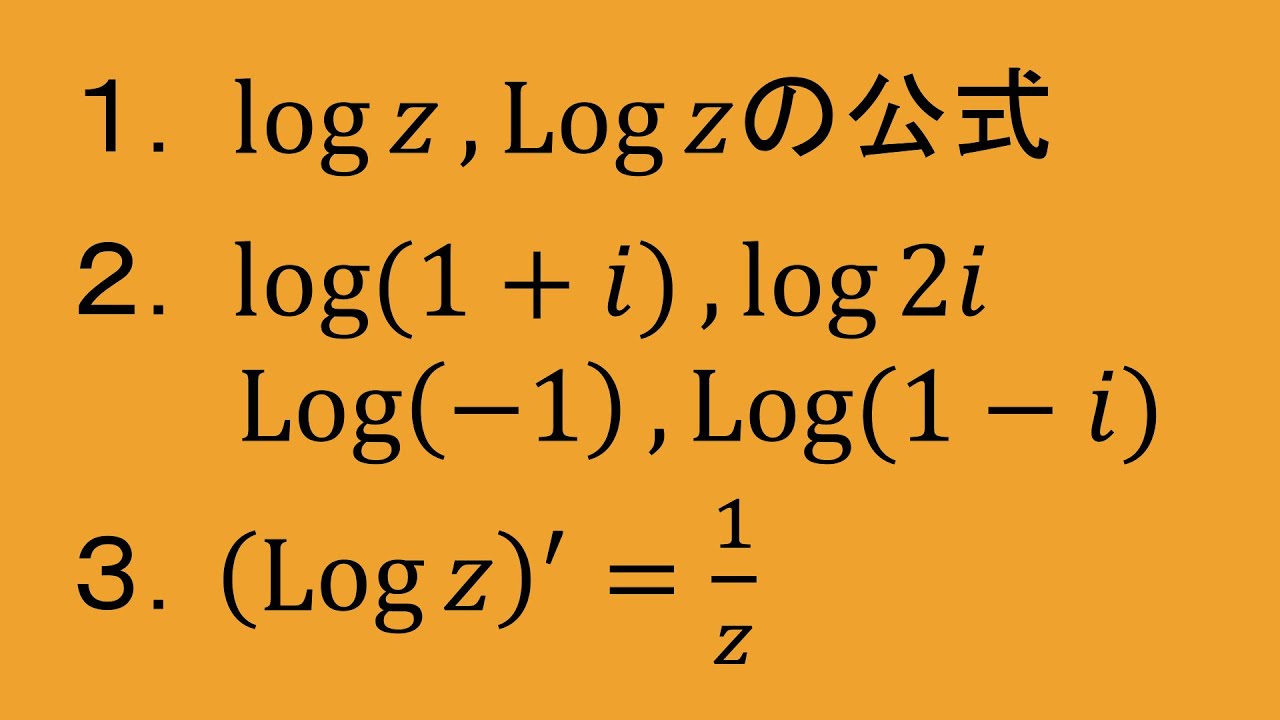
単元:
#数Ⅱ#複素数と方程式#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
複素関数論⑧ 逆関数に関して解説します.
この動画を見る
複素関数論⑧ 逆関数に関して解説します.
福田の数学〜慶應義塾大学2021年理工学部第2問〜複素数と多項式の商と余り

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$ (1)複素数$\alpha$は$\alpha^2+3\alpha+3=0$ を満たすとする。このとき、$(\alpha+1)^2(\alpha+2)^5=\boxed{\ \ キ\ \ }$
である。また、$(\alpha+2)^s(\alpha+3)^t=3$となる整数$s,t$の組を全て求めよ。
(2)多項式$(x+1)^3(x+2)^2$を$x^2+3x+3$で割った時の商は$\boxed{\ \ ク\ \ }$、余りは$\boxed{\ \ ケ\ \ }$である。
また、$(x+1)^{2021}$を$x^2+3x+3$で割った時の余りは$\boxed{\ \ コ\ \ }$である。
2021慶應義塾大学理工学部過去問
この動画を見る
${\Large\boxed{2}}$ (1)複素数$\alpha$は$\alpha^2+3\alpha+3=0$ を満たすとする。このとき、$(\alpha+1)^2(\alpha+2)^5=\boxed{\ \ キ\ \ }$
である。また、$(\alpha+2)^s(\alpha+3)^t=3$となる整数$s,t$の組を全て求めよ。
(2)多項式$(x+1)^3(x+2)^2$を$x^2+3x+3$で割った時の商は$\boxed{\ \ ク\ \ }$、余りは$\boxed{\ \ ケ\ \ }$である。
また、$(x+1)^{2021}$を$x^2+3x+3$で割った時の余りは$\boxed{\ \ コ\ \ }$である。
2021慶應義塾大学理工学部過去問
