 数列とその和(等差・等比・階差・Σ)
数列とその和(等差・等比・階差・Σ)
 数列とその和(等差・等比・階差・Σ)
数列とその和(等差・等比・階差・Σ)
福田の1.5倍速演習〜合格する重要問題065〜中央大学2019年度理工学部第3問〜反復試行と確率漸化式

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$ Oを原点とする平面上の動点Rが$R_0$(1, 0)から出発して、単位円の周上を1秒ごとに反時計周りに移動する。移動するときの動径ORの回転角は、確率$\frac{1}{2}$で$\frac{\pi}{6}$、確率$\frac{1}{2}$で$\frac{\pi}{3}$である。n秒後のRの位置を$R_n$とする。以下の問いに答えよ。
(1)$R_5$が(-1, 0)である確率を求めよ。
(2)$R_9$がx軸上にある確率を求めよ。
次に、$R_n$がx軸上またはy軸上にある確率を$p_n$(n≧1)とする。
(3)$p_{n+1}$を$p_n$を用いて表せ。
(4)$p_n$を求めよ。
2019中央大学理工学部過去問
この動画を見る
$\boxed{3}$ Oを原点とする平面上の動点Rが$R_0$(1, 0)から出発して、単位円の周上を1秒ごとに反時計周りに移動する。移動するときの動径ORの回転角は、確率$\frac{1}{2}$で$\frac{\pi}{6}$、確率$\frac{1}{2}$で$\frac{\pi}{3}$である。n秒後のRの位置を$R_n$とする。以下の問いに答えよ。
(1)$R_5$が(-1, 0)である確率を求めよ。
(2)$R_9$がx軸上にある確率を求めよ。
次に、$R_n$がx軸上またはy軸上にある確率を$p_n$(n≧1)とする。
(3)$p_{n+1}$を$p_n$を用いて表せ。
(4)$p_n$を求めよ。
2019中央大学理工学部過去問
無限等比級数

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} +\frac{1}{16} +\frac{1}{32} + \cdots =?$
この動画を見る
$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} +\frac{1}{16} +\frac{1}{32} + \cdots =?$
福田の1.5倍速演習〜合格する重要問題039〜早稲田大学2019年度理工学部第2問〜正n角形の周の長さと極限

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
nは3以上の自然数とする。面積1の正n角形$P_n$を考え、その周の
長さを$L_n$とする。次の問いに答えよ。
(1)$(L_n)^2$を求めよ。
(2)$\lim_{n \to \infty}L_n$を求めよ。
(3)$n \lt k$ならば$(L_n)^2 \gt (L_k)^2$となることを示せ。
2019早稲田大学理工学部過去問
この動画を見る
nは3以上の自然数とする。面積1の正n角形$P_n$を考え、その周の
長さを$L_n$とする。次の問いに答えよ。
(1)$(L_n)^2$を求めよ。
(2)$\lim_{n \to \infty}L_n$を求めよ。
(3)$n \lt k$ならば$(L_n)^2 \gt (L_k)^2$となることを示せ。
2019早稲田大学理工学部過去問
福田の1.5倍速演習〜合格する重要問題035〜東京大学2017年度理系第4問〜数列の帰納的定義と最大公約数

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#数学的帰納法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$p=2+\sqrt5$とおき、自然数$n=1,2,3,\cdots$対して
$a_n=p^n+\left(-\frac{1}{p}\right)^n$
と定める。以下の問いに答えよ。(1)は結論のみを書けばよい。
(1)$a_1,a_2$の値を求めよ。
(2)$n \geqq 2$とする。積$a_1a_n$を、$a_{n+1}$と$a_{n-1}$を用いて表せ。
(3)$a_n$は自然数であることを示せ。
(4)$a_{n+1}$と$a_n$の最大公約数を求めよ。
2017東京大学理系過去問
この動画を見る
$p=2+\sqrt5$とおき、自然数$n=1,2,3,\cdots$対して
$a_n=p^n+\left(-\frac{1}{p}\right)^n$
と定める。以下の問いに答えよ。(1)は結論のみを書けばよい。
(1)$a_1,a_2$の値を求めよ。
(2)$n \geqq 2$とする。積$a_1a_n$を、$a_{n+1}$と$a_{n-1}$を用いて表せ。
(3)$a_n$は自然数であることを示せ。
(4)$a_{n+1}$と$a_n$の最大公約数を求めよ。
2017東京大学理系過去問
【高校数学】数列の和と一般項の例題 3-11【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
初項から第n項までの和SnがSn = n² + 3nで表される数列{a_n}の一般項を求めよ。
この動画を見る
初項から第n項までの和SnがSn = n² + 3nで表される数列{a_n}の一般項を求めよ。
【高校数学】数列の和と一般項~理解して覚えようね~ 3-10【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
数列の和と一般項の関係について解説しています。
この動画を見る
数列の和と一般項の関係について解説しています。
高知大(医)3項間漸化式

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#高知大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a_1=1,a_2=5,a_{n+2}=4a_{n+1}-3a_n-4$
の一般項$a_n$を求めよ.
高知大(医)過去問
この動画を見る
$ a_1=1,a_2=5,a_{n+2}=4a_{n+1}-3a_n-4$
の一般項$a_n$を求めよ.
高知大(医)過去問
室蘭工業大 漸化式基本

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a_1=2,a_{n+1}=\dfrac{1}{2}a_n+\dfrac{4n+2^n}{2^{n+1}}$である.
$a_n\lt a_{n+1}$を満たす最大の自然数$n$を求めよ.
室蘭工業大過去問
この動画を見る
$ a_1=2,a_{n+1}=\dfrac{1}{2}a_n+\dfrac{4n+2^n}{2^{n+1}}$である.
$a_n\lt a_{n+1}$を満たす最大の自然数$n$を求めよ.
室蘭工業大過去問
記号は大学数学でも頑張れば中学生でもできる
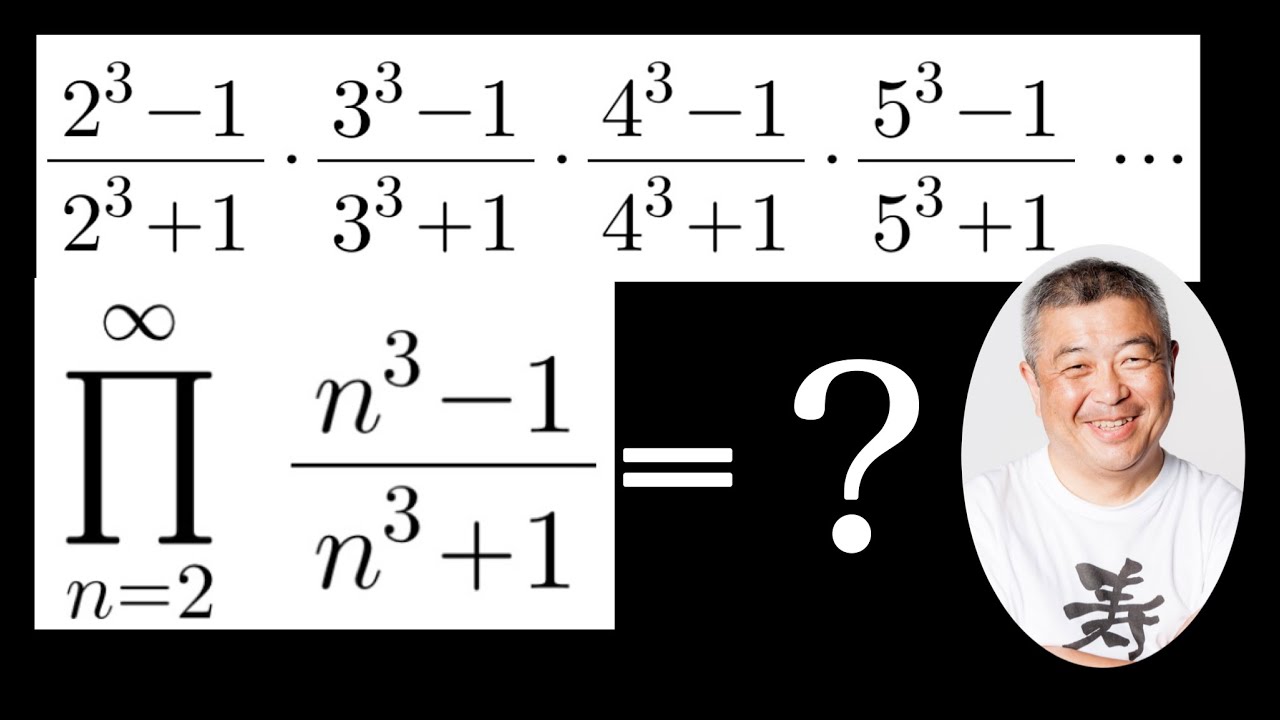
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{2^3-1}{2^3+1}・\dfrac{3^3-1}{3^3+1}・\dfrac{4^3-1}{4^3+1}・\dfrac{5^3-1}{5^3+1}…$
$\displaystyle \prod_{n=2}^{\infty} \dfrac{n^3-1}{n^3+1}=?$
これを解け.
この動画を見る
$\dfrac{2^3-1}{2^3+1}・\dfrac{3^3-1}{3^3+1}・\dfrac{4^3-1}{4^3+1}・\dfrac{5^3-1}{5^3+1}…$
$\displaystyle \prod_{n=2}^{\infty} \dfrac{n^3-1}{n^3+1}=?$
これを解け.
福田の数学〜立教大学2022年経済学部第1問(5)〜群数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
自然数n が 2n-1 個続く、初項が1の次のような数列がある。
1,2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5,…
このとき、自然数 m が初めて現れるのは第何項か。
また第 2022項はいくつか。
2022立教学部経済学部過去問
この動画を見る
自然数n が 2n-1 個続く、初項が1の次のような数列がある。
1,2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5,…
このとき、自然数 m が初めて現れるのは第何項か。
また第 2022項はいくつか。
2022立教学部経済学部過去問
階乗の方程式
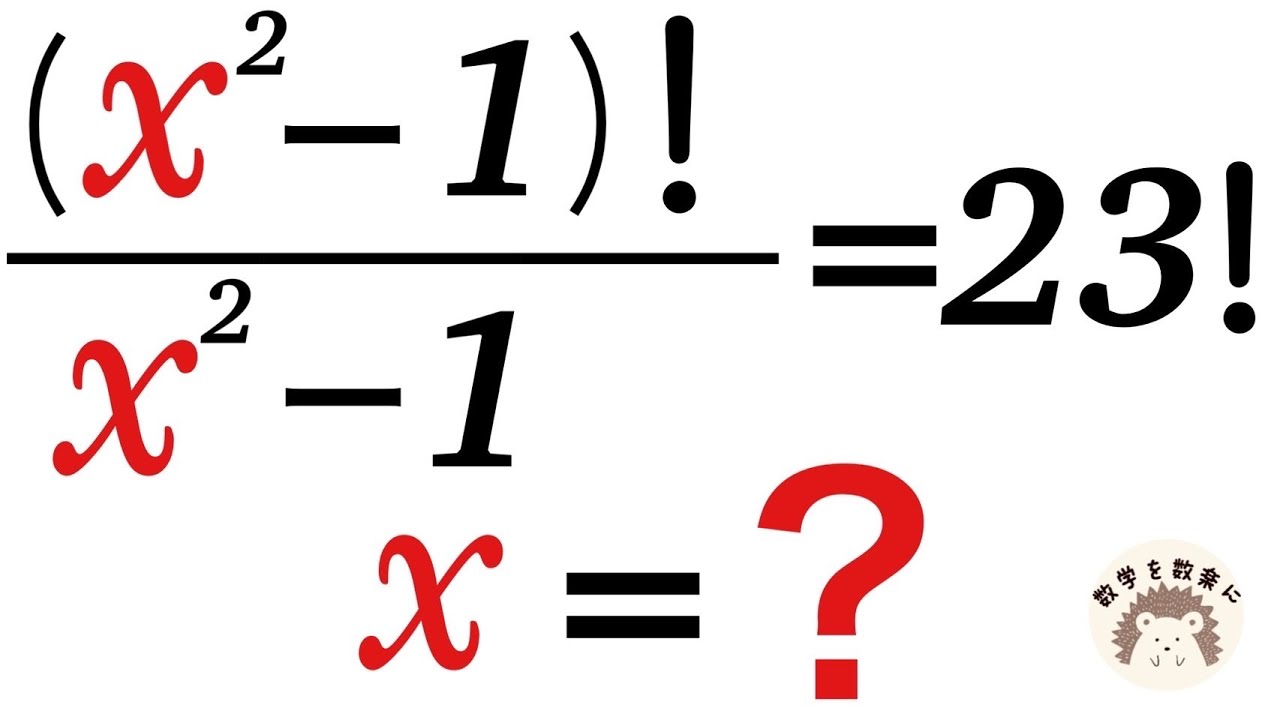
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{(x^2-1)!}{x^2-1} = 23!$のとき
x=?
この動画を見る
$\frac{(x^2-1)!}{x^2-1} = 23!$のとき
x=?
ガウス記号×数列!難しそうに見えるけど・・・【一橋大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
実数$x$に対し,$x$を超えない最大の整数を$\lbrack x \rbrack$で表す。数列{$a_k$}を
$a_k=2^{[\sqrt{k}]}$ $(k=1,2,3,・・・)
で定義する。正の整数$n$に対して
$b_n$=$\displaystyle \sum_{k=1}^n^{2} a_k$ を求めよ。
一橋大過去問
この動画を見る
実数$x$に対し,$x$を超えない最大の整数を$\lbrack x \rbrack$で表す。数列{$a_k$}を
$a_k=2^{[\sqrt{k}]}$ $(k=1,2,3,・・・)
で定義する。正の整数$n$に対して
$b_n$=$\displaystyle \sum_{k=1}^n^{2} a_k$ を求めよ。
一橋大過去問
等比数列の和
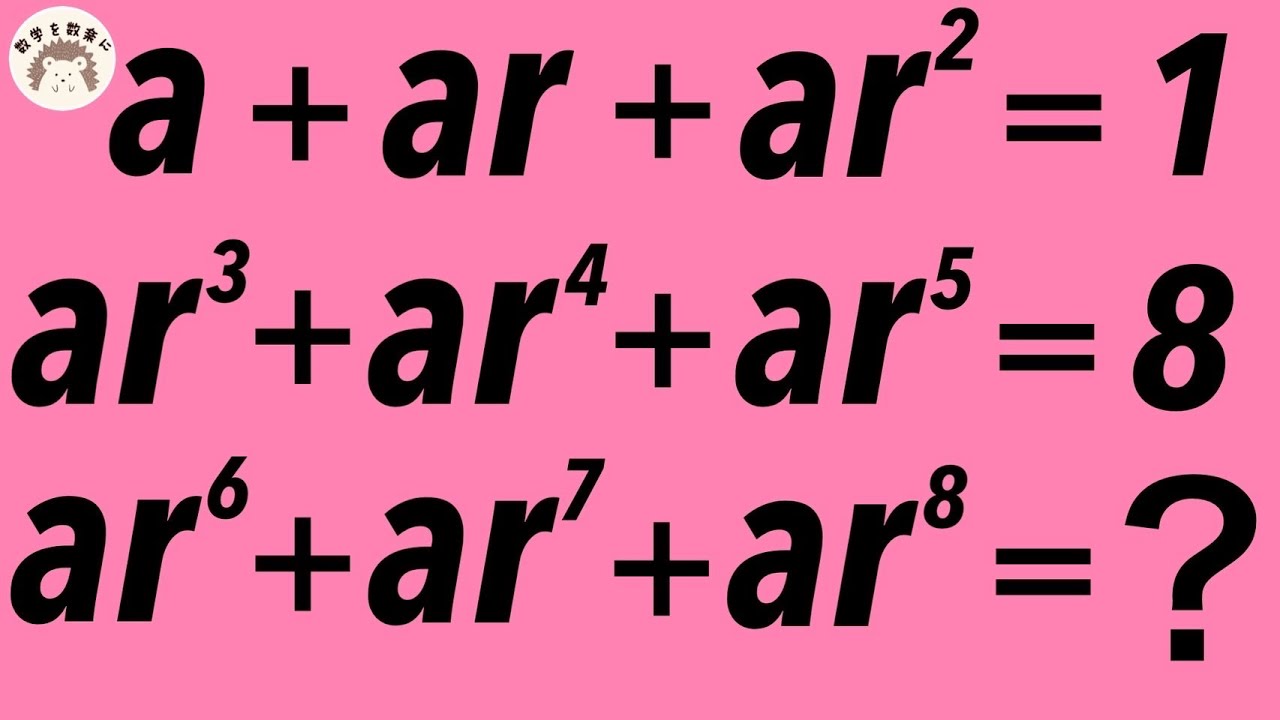
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$a+ar+ar^2=1$
$ar^3+ar^4+ar^5=8$
$ar^6+ar^7+ar^8=?$
この動画を見る
$a+ar+ar^2=1$
$ar^3+ar^4+ar^5=8$
$ar^6+ar^7+ar^8=?$
福田の数学〜早稲田大学2022年商学部第1問(3)〜漸化式で与えられた数列の項の値

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(3)$a$を実数とする。
数列$\left\{a_n\right\}$が次の条件を満たしている。
$(\textrm{i})a_1=a$
$(\textrm{ii})a_{n+1}=a_n^2-2a_n-3(n=1,2,3,\ldots)$
このとき、すべての正の整数$n$に対して、$a_n \leqq 10$となるような
$a$の最小値は$\boxed{\ \ ウ\ \ }$である。
2022早稲田大学商学部過去問
この動画を見る
${\large\boxed{1}}$(3)$a$を実数とする。
数列$\left\{a_n\right\}$が次の条件を満たしている。
$(\textrm{i})a_1=a$
$(\textrm{ii})a_{n+1}=a_n^2-2a_n-3(n=1,2,3,\ldots)$
このとき、すべての正の整数$n$に対して、$a_n \leqq 10$となるような
$a$の最小値は$\boxed{\ \ ウ\ \ }$である。
2022早稲田大学商学部過去問
差がつく問題!記号が多くても焦らずに解けば大丈夫!【お茶の水女子大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$m$を2以上の自然数,$n$を自然数とするとき,次の不等式
${}_{mn} \mathrm {C}_n≧m^n>\displaystyle \sum_{i=0}^{n-1} m^i$
が成り立つことを示せ。
お茶の水女子大過去問
この動画を見る
$m$を2以上の自然数,$n$を自然数とするとき,次の不等式
${}_{mn} \mathrm {C}_n≧m^n>\displaystyle \sum_{i=0}^{n-1} m^i$
が成り立つことを示せ。
お茶の水女子大過去問
階乗に関する問題!! 24で割った余り

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
1!+2!+3!+・・・+2022!
24で割った余りは?
この動画を見る
1!+2!+3!+・・・+2022!
24で割った余りは?
福田の数学〜早稲田大学2022年人間科学部第1問(1)〜命題の真偽とカードの裏表

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(1)表面にアルファベットが、裏面には自然数が書かれている5枚のカードが、
次のように置かれている。
${\large\boxed{P}}\hspace{45pt}{\large\boxed{Q}}\hspace{45pt}{\large\boxed{1}}\hspace{45pt}{\large\boxed{3}}\hspace{45pt}{\large\boxed{6}}$
これら5枚のカードに対する命題「表面がアルファベットPならば、裏面は
素数である」の審議を調べるために、できるだけ少ない枚数のカードを裏返
して確認したい。左からn番目の位置にあるカードを裏返す必要があるとき
には$a_n=1$、必要のないときには$a_n=0$とするとき
$\sum_{k=1}^5 a_k2^{k-1}=\boxed{\ \ ア\ \ }$
である。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{1}}$(1)表面にアルファベットが、裏面には自然数が書かれている5枚のカードが、
次のように置かれている。
${\large\boxed{P}}\hspace{45pt}{\large\boxed{Q}}\hspace{45pt}{\large\boxed{1}}\hspace{45pt}{\large\boxed{3}}\hspace{45pt}{\large\boxed{6}}$
これら5枚のカードに対する命題「表面がアルファベットPならば、裏面は
素数である」の審議を調べるために、できるだけ少ない枚数のカードを裏返
して確認したい。左からn番目の位置にあるカードを裏返す必要があるとき
には$a_n=1$、必要のないときには$a_n=0$とするとき
$\sum_{k=1}^5 a_k2^{k-1}=\boxed{\ \ ア\ \ }$
である。
2022早稲田大学人間科学部過去問
福田の数学〜慶應義塾大学2022年看護医療学部第2問(2)〜漸化式と和に関する不等式

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}$(2)$a_1=4,\ \ \ 4a_{n+1}=2a_n+3(n=1,2,3,\ldots)$で与えられる
数列$\left\{a_n\right\}$の一般項は$a_n=\boxed{\ \ ア\ \ }$である。
また$\sum_{n=1}^la_n \geqq 20$
を満たす最小の自然数lは$\boxed{\ \ イ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{2}}$(2)$a_1=4,\ \ \ 4a_{n+1}=2a_n+3(n=1,2,3,\ldots)$で与えられる
数列$\left\{a_n\right\}$の一般項は$a_n=\boxed{\ \ ア\ \ }$である。
また$\sum_{n=1}^la_n \geqq 20$
を満たす最小の自然数lは$\boxed{\ \ イ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
【高校数学】階差数列の問題演習~標準的な問題~ 3-9.5【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
一般項$a_{n}$を求めよ。
-5,1,8,17,29,45,66,...
この動画を見る
一般項$a_{n}$を求めよ。
-5,1,8,17,29,45,66,...
福田の数学〜慶應義塾大学2022年総合政策学部第1問〜ガウス記号を含む数列の和

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$実数xに対して、x以下の最大の整数を$[x]$と表すことにする。
いま、数列$\left\{a_n\right\}$を
$a_n=[\sqrt{2n}+\frac{1}{2}]$
と定義すると
$a_1=\boxed{\ \ ア\ \ },\ \ \ \ a_2=\boxed{\ \ イ\ \ },\ \ \ \ a_3=\boxed{\ \ ウ\ \ },\ \ \ \ a_4=\boxed{\ \ エ\ \ },\ \ \ \ a_5=\boxed{\ \ オ\ \ },a_6=\boxed{\ \ カ\ \ },$
となる。このとき、$a_n=10$となるのは、$\boxed{\ \ キク\ \ } \leqq n \leqq \boxed{\ \ ケコ\ \ }$の場合に限られる。
また、$\sum_{n=1}^{\boxed{\ \ ケコ\ \ }}a_n=\boxed{\ \ サシスセ\ \ }$である。
2022慶應義塾大学総合政策学部過去問
この動画を見る
${\Large\boxed{1}}$実数xに対して、x以下の最大の整数を$[x]$と表すことにする。
いま、数列$\left\{a_n\right\}$を
$a_n=[\sqrt{2n}+\frac{1}{2}]$
と定義すると
$a_1=\boxed{\ \ ア\ \ },\ \ \ \ a_2=\boxed{\ \ イ\ \ },\ \ \ \ a_3=\boxed{\ \ ウ\ \ },\ \ \ \ a_4=\boxed{\ \ エ\ \ },\ \ \ \ a_5=\boxed{\ \ オ\ \ },a_6=\boxed{\ \ カ\ \ },$
となる。このとき、$a_n=10$となるのは、$\boxed{\ \ キク\ \ } \leqq n \leqq \boxed{\ \ ケコ\ \ }$の場合に限られる。
また、$\sum_{n=1}^{\boxed{\ \ ケコ\ \ }}a_n=\boxed{\ \ サシスセ\ \ }$である。
2022慶應義塾大学総合政策学部過去問
『Σ』の記号の意味を理解させます

【高校数学】階差数列の問題演習~基礎的な問題~ 3-9.5【数学B】

単元:
#数Ⅱ#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
\begin{eqnarray}
一般項a_nを求めよ
\end{eqnarray}
\begin{eqnarray}
(1)\,\,1,\,7,\,17,\,31,\,71,\,…
\end{eqnarray}
\begin{eqnarray}
(2)\,\,2,\,3,\,5,\,9,\,17,\,…
\end{eqnarray}
この動画を見る
\begin{eqnarray}
一般項a_nを求めよ
\end{eqnarray}
\begin{eqnarray}
(1)\,\,1,\,7,\,17,\,31,\,71,\,…
\end{eqnarray}
\begin{eqnarray}
(2)\,\,2,\,3,\,5,\,9,\,17,\,…
\end{eqnarray}
シグマΣの記号について~中学生でも理解させます~

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
\begin{eqnarray}
(1)
\displaystyle \sum_{k=1}^{100} k
\end{eqnarray}
この動画を見る
\begin{eqnarray}
(1)
\displaystyle \sum_{k=1}^{100} k
\end{eqnarray}
無限等比級数
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
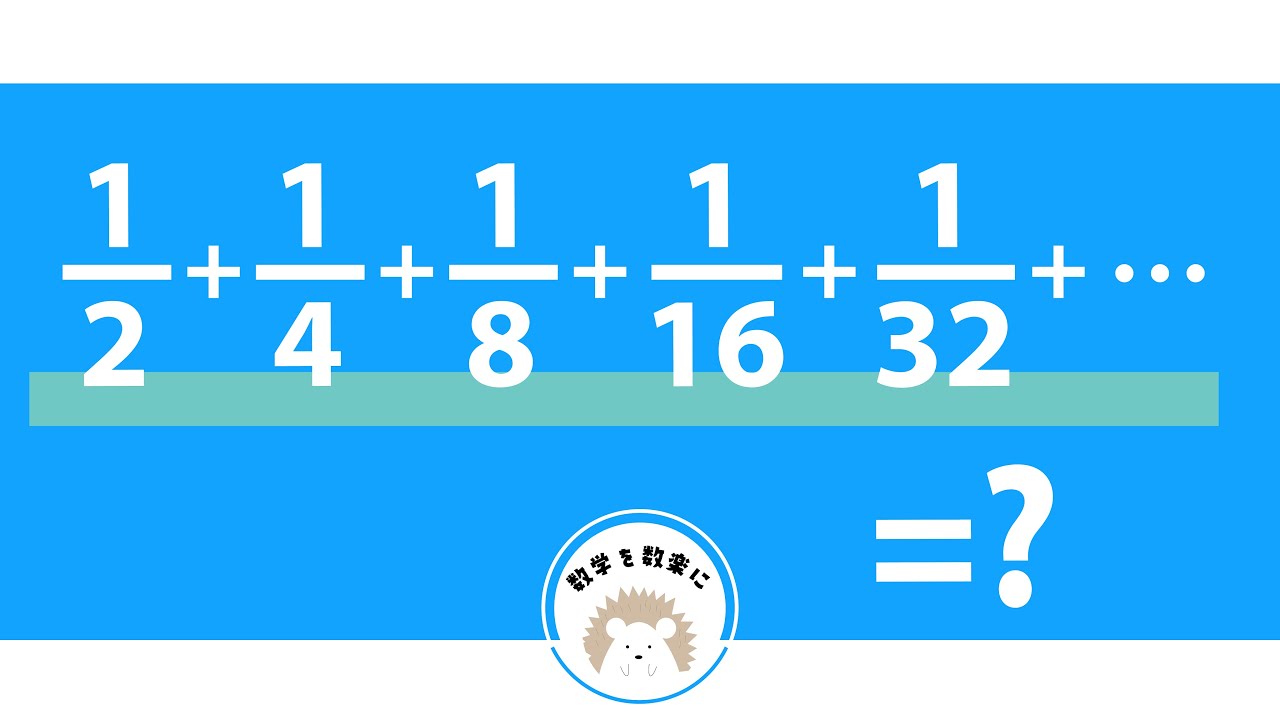
$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+ \cdots = ?$
この動画を見る
$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+ \cdots = ?$
【高校数学】階差数列の一般項~どこよりも丁寧に~ 3-9【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\displaystyle
a_{n}=a_{1}+\sum_{k=1}^{n-1}b_{k}
$
この動画を見る
$\displaystyle
a_{n}=a_{1}+\sum_{k=1}^{n-1}b_{k}
$
【群数列ニガテな人は見て!!】群数列はこれさえ出来れば大丈夫!〔数学、高校数学〕

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
3rd School
問題文全文(内容文):
2から順に偶数を並べた数列で、 各郡に含まれる数が、1、3、5$\cdots$個と なるような数列を考える。
2|4,6,8|10,12,14,16,18|20,$\cdots$
このとき、第n郡の初項と末項を求めよ
この動画を見る
2から順に偶数を並べた数列で、 各郡に含まれる数が、1、3、5$\cdots$個と なるような数列を考える。
2|4,6,8|10,12,14,16,18|20,$\cdots$
このとき、第n郡の初項と末項を求めよ
【等比数列の和はこれで一撃!】等比数列の和の公式は覚えなくていいです〔数学、高校数学〕

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
3rd School
問題文全文(内容文):
5,10,20,40,80$\cdots$
で表される等比数列の第n項までの和を求めよ。
この動画を見る
5,10,20,40,80$\cdots$
で表される等比数列の第n項までの和を求めよ。
【階差数列の攻略法はこれ!】階差数列の一般項の求め方を解説しました〔数学、高校数学〕

福田の数学〜千葉大学2022年理系第7問〜不定方程式の自然数解と漸化式で与えられた数列

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$x,y$についての方程式
$x^2-6xy+y^2=9 \ldots\ldots(*)$
に関する次の問いに答えよ。
(1)$x,y$がともに正の整数であるような(*)の解のうち、yが最小であるものを
求めよ。
(2)数列$a_1,a_2,a_3,\ldots$が漸化式
$a_{n+2}-6a_{n+1}+a_n=0 (n=1,2,3,\ldots)$
を満たすとする。このとき、$(x,y)=(a_{n+1},a_n)$が(*)を満たすならば、
$(x,y)=(a_{n+2},a_{n+1})$も(*)を満たすことを示せ。
(3)(*)の整数解(x,y)は無数に存在することを示せ。
2022千葉大学理系過去問
この動画を見る
$x,y$についての方程式
$x^2-6xy+y^2=9 \ldots\ldots(*)$
に関する次の問いに答えよ。
(1)$x,y$がともに正の整数であるような(*)の解のうち、yが最小であるものを
求めよ。
(2)数列$a_1,a_2,a_3,\ldots$が漸化式
$a_{n+2}-6a_{n+1}+a_n=0 (n=1,2,3,\ldots)$
を満たすとする。このとき、$(x,y)=(a_{n+1},a_n)$が(*)を満たすならば、
$(x,y)=(a_{n+2},a_{n+1})$も(*)を満たすことを示せ。
(3)(*)の整数解(x,y)は無数に存在することを示せ。
2022千葉大学理系過去問
【超難問】2-1が難しすぎる世界

単元:
#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#数学(高校生)#数B#数Ⅲ
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
深読みしすぎた2-1の計算紹介動画です
この動画を見る
深読みしすぎた2-1の計算紹介動画です
