 漸化式
漸化式
 漸化式
漸化式
これの説明できますか?

二項定理を使ってあることに気付ける?【2017年一橋大学】

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#式の計算(整式・展開・因数分解)#恒等式・等式・不等式の証明#数列#漸化式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数B
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ P(0)=1,P(x+1)-P(x)=2x$を満たす整式$P(x)$を求めよ。
2017一橋大過去問
この動画を見る
$ P(0)=1,P(x+1)-P(x)=2x$を満たす整式$P(x)$を求めよ。
2017一橋大過去問
福田の数学〜京都大学2022年文系第2問〜条件を満たす経路の総数と漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
下図(※動画参照)の三角柱ABC-DEFにおいて、Aを始点として、辺に沿って
頂点をn回移動する。すなわち、この移動経路
$P_0 \to P_1 \to P_2 \to \ldots \to P_{n-1} \to P_n$ (ただし$P_0=A$)
において、$P_0P_1,P_1P_2,\ldots,P_{n-1}P_n$は全て辺であるとする。
また、同じ頂点を何度通ってよいものとする。このような移動経路で、終点$P_n$がA,B,Cの
いずれかとなるものの総数$a_n$を求めよ。
2022京都大学文系過去問
この動画を見る
下図(※動画参照)の三角柱ABC-DEFにおいて、Aを始点として、辺に沿って
頂点をn回移動する。すなわち、この移動経路
$P_0 \to P_1 \to P_2 \to \ldots \to P_{n-1} \to P_n$ (ただし$P_0=A$)
において、$P_0P_1,P_1P_2,\ldots,P_{n-1}P_n$は全て辺であるとする。
また、同じ頂点を何度通ってよいものとする。このような移動経路で、終点$P_n$がA,B,Cの
いずれかとなるものの総数$a_n$を求めよ。
2022京都大学文系過去問
福田の入試問題解説〜東京大学2022年文系第3問〜漸化式と最大公約数

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師:
問題文全文(内容文):
数列$\left\{a_n\right\}$を次のように定める。
$a_1=4, a_{n+1}=a_n^2+n(n+2)$
(1)$a_{2022}$を3で割った余りを求めよ。
(2)$a_{2022},a_{2023},a_{2024}$の最大公約数を求めよ。
2022東京大学文系過去問
この動画を見る
数列$\left\{a_n\right\}$を次のように定める。
$a_1=4, a_{n+1}=a_n^2+n(n+2)$
(1)$a_{2022}$を3で割った余りを求めよ。
(2)$a_{2022},a_{2023},a_{2024}$の最大公約数を求めよ。
2022東京大学文系過去問
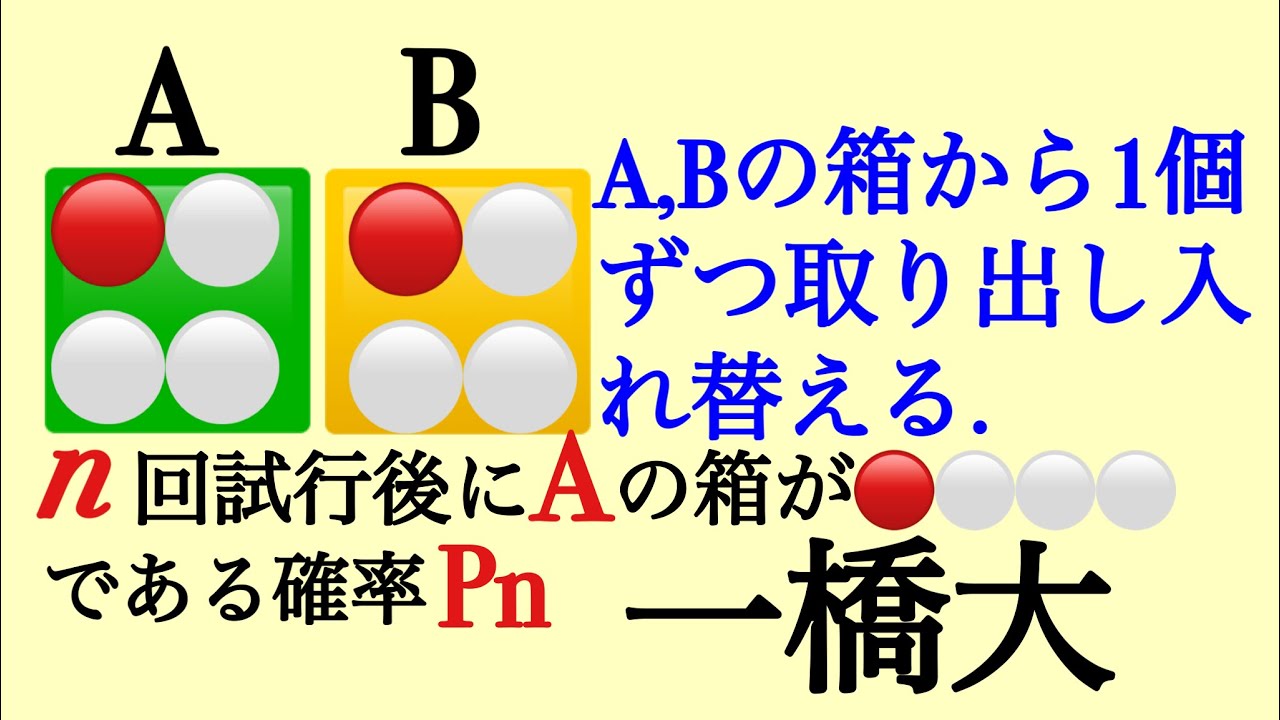
一橋大 漸化式
単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#漸化式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
同時に1個ずつ取り出して入れかえる.
n回後にAがA,Bである確率を求めよ.
2022一橋大過去問
この動画を見る
同時に1個ずつ取り出して入れかえる.
n回後にAがA,Bである確率を求めよ.
2022一橋大過去問
福田の数学〜京都大学2022年理系第6問〜漸化式の解法

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列$\left\{x_n\right\}, \left\{y_n\right\}$を次の式
$x_1=0, x_{n+1}=x_n+n+2\cos\frac{2\pi x_n}{3} (n=1,2,3,\ldots)$
$y_{3m+1}=3m, y_{3m+2}=3m+2, y_{3m+3}=3m+4 (m=0,1,2,3,\ldots)$
により定める。このとき、数列$\left\{x_n-y_n\right\}$の一般項を求めよ。
2022京都大学理系過去問
この動画を見る
数列$\left\{x_n\right\}, \left\{y_n\right\}$を次の式
$x_1=0, x_{n+1}=x_n+n+2\cos\frac{2\pi x_n}{3} (n=1,2,3,\ldots)$
$y_{3m+1}=3m, y_{3m+2}=3m+2, y_{3m+3}=3m+4 (m=0,1,2,3,\ldots)$
により定める。このとき、数列$\left\{x_n-y_n\right\}$の一般項を求めよ。
2022京都大学理系過去問
福田の入試問題解説〜北海道大学2022年理系第2問〜ベクトルと漸化式

単元:
#大学入試過去問(数学)#平面上のベクトル#数列#平面上のベクトルと内積#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
aは$a\neq 1$を満たす正の実数とする。xy平面上の点$P_1,P_2,\ldots\ldots,P_n,\ldots\ldots$および
$Q_1,Q_2,\ldots\ldots,Q_n,\ldots\ldots$が、すべての自然数nについて
$\overrightarrow{ P_nP_{n+1} }=(1-a)\overrightarrow{ P_nQ_n }, \overrightarrow{ Q_nQ_{n+1} }=(0, \frac{a^{-n}}{1-a})$
を満たしているとする。また$P_n$の座標を$(x_n,y_n)$とする。
(1)$x_{n+2}$を$a, x_n, x_{n+1}$で表せ。
(2)$x_1=0, x_2=1$のとき、数列$\left\{x_n\right\}$の一般項を求めよ。
(3)$y_1=\frac{a}{(1-a)^2}, y_2-y_1=1$のとき数列$\left\{y_n\right\}$の一般項を求めよ。
2022北海道大学理系過去問
この動画を見る
aは$a\neq 1$を満たす正の実数とする。xy平面上の点$P_1,P_2,\ldots\ldots,P_n,\ldots\ldots$および
$Q_1,Q_2,\ldots\ldots,Q_n,\ldots\ldots$が、すべての自然数nについて
$\overrightarrow{ P_nP_{n+1} }=(1-a)\overrightarrow{ P_nQ_n }, \overrightarrow{ Q_nQ_{n+1} }=(0, \frac{a^{-n}}{1-a})$
を満たしているとする。また$P_n$の座標を$(x_n,y_n)$とする。
(1)$x_{n+2}$を$a, x_n, x_{n+1}$で表せ。
(2)$x_1=0, x_2=1$のとき、数列$\left\{x_n\right\}$の一般項を求めよ。
(3)$y_1=\frac{a}{(1-a)^2}, y_2-y_1=1$のとき数列$\left\{y_n\right\}$の一般項を求めよ。
2022北海道大学理系過去問
高校入試だけど確率漸化式!?西大和学園2022入試問題解説100問解説!!58問目
単元:
#数学(中学生)#中2数学#確率#数列#漸化式#高校入試過去問(数学)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
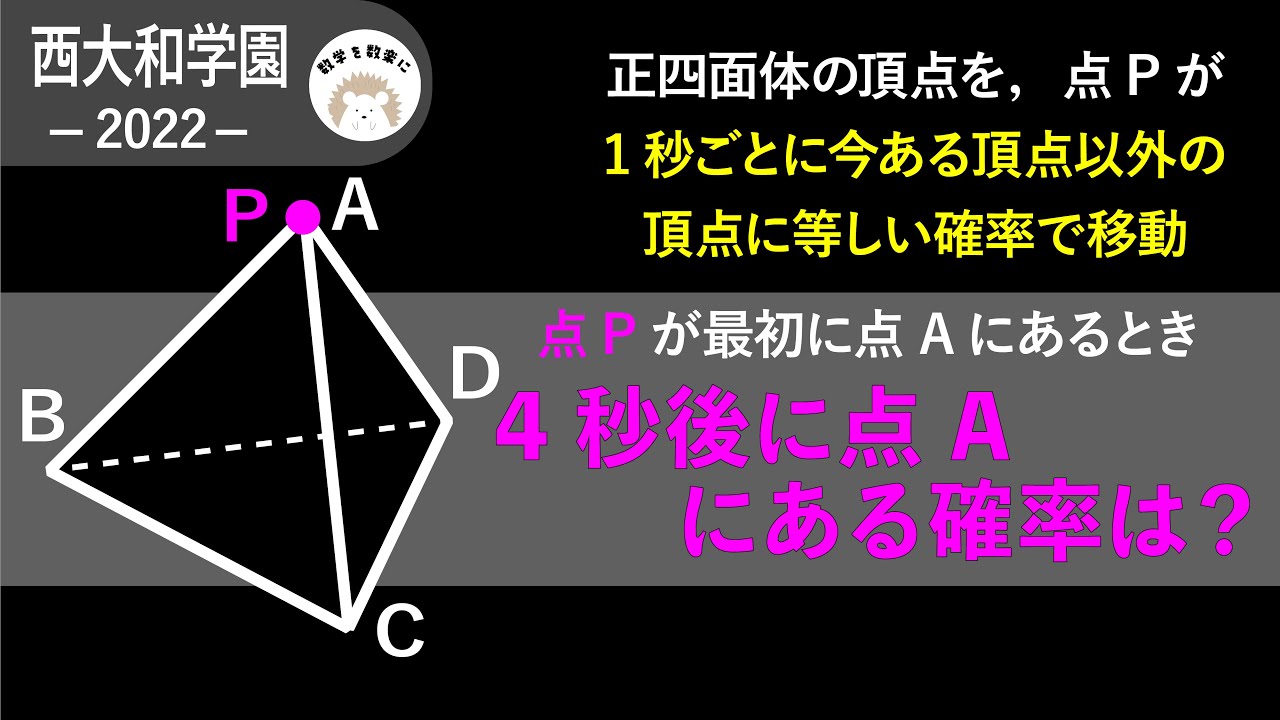
正四面体の頂点を、点Pが1秒ごとに今ある頂点以外の頂点に等しい確率で移動する
点Pが最初に点Aにあるとき4秒後に点Aにある確率は?
*図は動画内参照
2022西大和学園高等学校
この動画を見る
正四面体の頂点を、点Pが1秒ごとに今ある頂点以外の頂点に等しい確率で移動する
点Pが最初に点Aにあるとき4秒後に点Aにある確率は?
*図は動画内参照
2022西大和学園高等学校
大学入試問題#105 京都大学(2003) 数列
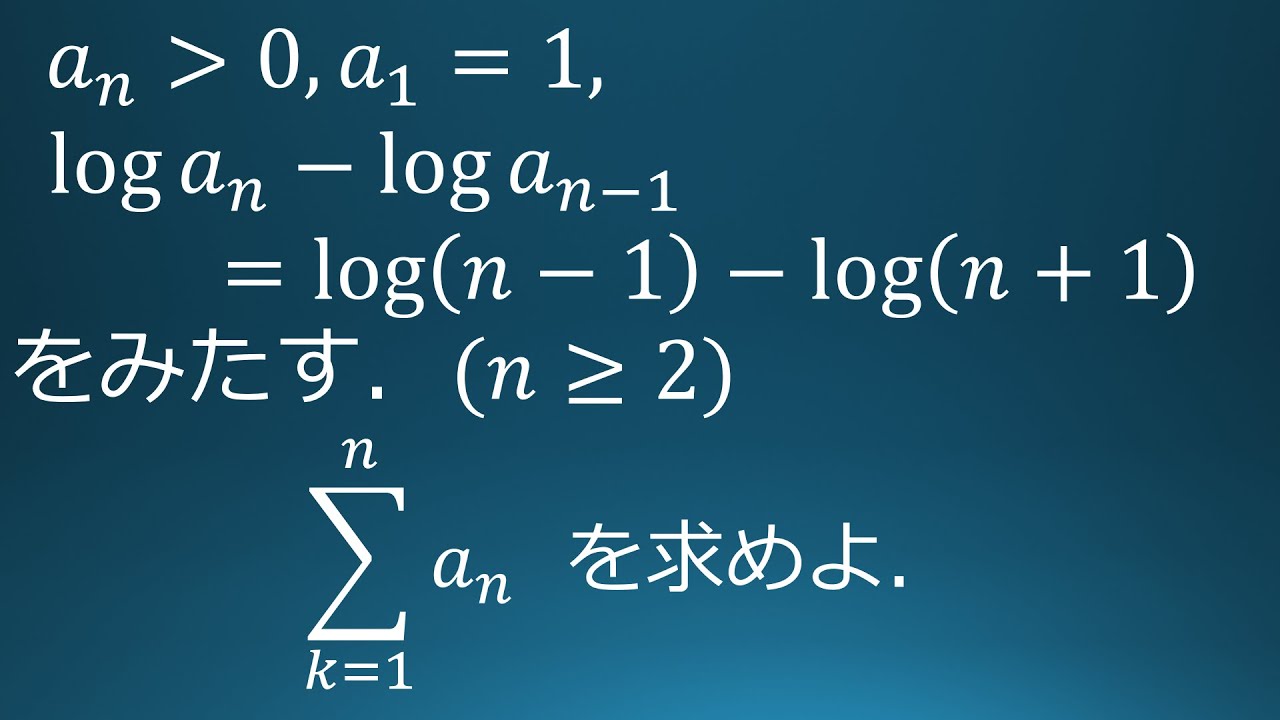
単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_n \gt 0,\ a_1=1$
$n \geqq 2$のとき
$log\ a_n-log\ a_{n-1}=log(n-1)-log(n+1)$である。
$\displaystyle \sum_{k=1}^n a_k$を求めよ
出典:2003年京都大学 入試問題
この動画を見る
$a_n \gt 0,\ a_1=1$
$n \geqq 2$のとき
$log\ a_n-log\ a_{n-1}=log(n-1)-log(n+1)$である。
$\displaystyle \sum_{k=1}^n a_k$を求めよ
出典:2003年京都大学 入試問題
福田の共通テスト直前演習〜2021年共通テスト数学ⅡB問題4。数列の問題。

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
以下のように、歩行者と自転車が自宅を出発して移動と停止を繰り返してい
る。歩行者と自転車の動きについて、数学的に考えてみよう。
自宅を原点とする数直線を考え、歩行者と自転車をその数直線上を動く点とみ
なす。数直線上の点の座標がyであるとき、その点は位置にあるということに
する。また、歩行者が自宅を出発してからx分経過した時点を時刻xと表す。歩
行者は時刻0に自宅を出発し、正の向きに毎分1の速さで歩き始める。自転車は
時刻2に自宅を出発し、毎分2の速さで歩行者を追いかける。自転車が歩行者に
追いつくと、歩行者と自転車はともに1分だけ停止する。その後、歩行者は再び
正の向きに毎分1の速さで歩き出し、自転車は毎分2の速さで自宅に戻る。自転
車は自宅に到着すると、1分だけ停止した後、再び毎分2の速さで歩行者を追い
かける。これを繰り返し、自転車は自宅と歩行者の間を往復する。
$x=a_n$を自転車がn回目に自宅を出発する時刻とし、$y=b_n$をそのときの歩
行者の位置とする。
(1) 花子さんと太郎さんは、数列$\left\{a_n\right\}, \left\{b_n\right\}$の一般項を求めるために、歩行者
と自転車について、時刻において位置yにいることをOを原点とする座標
平面上の点(x,y)で表すことにした。
$a_1=2,b_1=2$により、自転車が最初に自宅を出発するときの時刻と自転
車の位置を表す点の座標は(2,0)であり、その時の時刻と歩行者の位置を
表す点の座標は(2,2)である。また、自転車が最初に歩行者に追いつくとき
の時刻と位置を表す点の座標は$(\boxed{\ \ ア\ \ },\boxed{\ \ ア\ \ })$である。よって
$a_2=\boxed{\ \ イ\ \ }, b_2=\boxed{\ \ ウ\ \ }$
である。
花子:数列$\left\{a_n\right\}, \left\{b_n\right\}$の一般項について考える前に、
$(\boxed{\ \ ア\ \ },\boxed{\ \ ア\ \ })$の求め方について整理してみようか。
太郎:花子さんはどうやって求めたの?
花子:自転車が歩行者を追いかけるときに、間隔が1分間に1ずつ縮まっていくこと
を利用したよ。
太郎:歩行者と自転車の動きをそれぞれ直線の方程式で表して、交点を
計算して求めることもできるね。
自転車がn回目に自宅を出発するときの時刻と自転車の位置を表す点の座標
は$(a_n,0)$であり、そのときの時刻と歩行者の位置を表す点の座標は
$(a_n,b_n)$である。よって、n回目に自宅を出発した自転車が次に歩行者に
追いつくときの時刻と位置を表す点の座標は、$a_n,b_n$を用いて、
$(\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ })$と表せる。
$\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
⓪$a_n$ ①$b_n$ ②$2a_n$
③$a_n+b_n$ ④$2b_n$ ⑤$3a_n$
⑥$2a_n+b_n$ ⑦$a_n+2b_n$ ⑧$3b_n$
以上から、数列$\left\{a_n\right\}, \left\{b_n\right\}$について、自然数nに対して、関係式
$a_{n+1}=a_n+\boxed{\ \ カ\ \ }\ b_n+\boxed{\ \ キ\ \ } \ldots①$
$b_{n+1}=3b_n+\boxed{\ \ ク\ \ } \ldots②$
が成り立つことが分かる。まず、$b_1=2$と②から
$b_n=\boxed{\ \ ケ\ \ } (n=1,2,3,\ldots)$
を得る。この結果と、$a_1=2$および1から
$a_n=\boxed{\ \ コ\ \ } (n=1,2,3,\ldots)$
がわかる。
$\boxed{\ \ ケ\ \ }, \boxed{\ \ コ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
⓪$3^{n-1}+1$ ①$\frac{1}{2}・3^n+\frac{1}{2}$
②$3^{n-1}+n$ ③$\frac{1}{2}・3^n+n-\frac{1}{2}$
④$3^{n-1}+n^2$ ⑤$\frac{1}{2}・3^n+n^2-\frac{1}{2}$
⑥$2・3^{n-1}$ ⑦$\frac{5}{2}・3^{n-1}-\frac{1}{2}$
⑧$2・3^{n-1}+n-1$ ⑨$\frac{5}{2}・3^{n-1}+n-\frac{3}{2}$
ⓐ$2・3^{n-1}+n^2-1$ ⓑ$\frac{5}{2}・3^{n-1}+n^2-\frac{3}{2}$
(2)歩行者が$y=300$の位置に到着するときまでに、自転車が装甲車に追いつく
回数は$\boxed{\ \ サ\ \ }$回である。また、$\boxed{\ \ サ\ \ }$回目に自転車が歩行者に追いつく
時刻は、$x=\boxed{\ \ シスセ\ \ }$である。
2022共通テスト数学過去問
この動画を見る
以下のように、歩行者と自転車が自宅を出発して移動と停止を繰り返してい
る。歩行者と自転車の動きについて、数学的に考えてみよう。
自宅を原点とする数直線を考え、歩行者と自転車をその数直線上を動く点とみ
なす。数直線上の点の座標がyであるとき、その点は位置にあるということに
する。また、歩行者が自宅を出発してからx分経過した時点を時刻xと表す。歩
行者は時刻0に自宅を出発し、正の向きに毎分1の速さで歩き始める。自転車は
時刻2に自宅を出発し、毎分2の速さで歩行者を追いかける。自転車が歩行者に
追いつくと、歩行者と自転車はともに1分だけ停止する。その後、歩行者は再び
正の向きに毎分1の速さで歩き出し、自転車は毎分2の速さで自宅に戻る。自転
車は自宅に到着すると、1分だけ停止した後、再び毎分2の速さで歩行者を追い
かける。これを繰り返し、自転車は自宅と歩行者の間を往復する。
$x=a_n$を自転車がn回目に自宅を出発する時刻とし、$y=b_n$をそのときの歩
行者の位置とする。
(1) 花子さんと太郎さんは、数列$\left\{a_n\right\}, \left\{b_n\right\}$の一般項を求めるために、歩行者
と自転車について、時刻において位置yにいることをOを原点とする座標
平面上の点(x,y)で表すことにした。
$a_1=2,b_1=2$により、自転車が最初に自宅を出発するときの時刻と自転
車の位置を表す点の座標は(2,0)であり、その時の時刻と歩行者の位置を
表す点の座標は(2,2)である。また、自転車が最初に歩行者に追いつくとき
の時刻と位置を表す点の座標は$(\boxed{\ \ ア\ \ },\boxed{\ \ ア\ \ })$である。よって
$a_2=\boxed{\ \ イ\ \ }, b_2=\boxed{\ \ ウ\ \ }$
である。
花子:数列$\left\{a_n\right\}, \left\{b_n\right\}$の一般項について考える前に、
$(\boxed{\ \ ア\ \ },\boxed{\ \ ア\ \ })$の求め方について整理してみようか。
太郎:花子さんはどうやって求めたの?
花子:自転車が歩行者を追いかけるときに、間隔が1分間に1ずつ縮まっていくこと
を利用したよ。
太郎:歩行者と自転車の動きをそれぞれ直線の方程式で表して、交点を
計算して求めることもできるね。
自転車がn回目に自宅を出発するときの時刻と自転車の位置を表す点の座標
は$(a_n,0)$であり、そのときの時刻と歩行者の位置を表す点の座標は
$(a_n,b_n)$である。よって、n回目に自宅を出発した自転車が次に歩行者に
追いつくときの時刻と位置を表す点の座標は、$a_n,b_n$を用いて、
$(\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ })$と表せる。
$\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
⓪$a_n$ ①$b_n$ ②$2a_n$
③$a_n+b_n$ ④$2b_n$ ⑤$3a_n$
⑥$2a_n+b_n$ ⑦$a_n+2b_n$ ⑧$3b_n$
以上から、数列$\left\{a_n\right\}, \left\{b_n\right\}$について、自然数nに対して、関係式
$a_{n+1}=a_n+\boxed{\ \ カ\ \ }\ b_n+\boxed{\ \ キ\ \ } \ldots①$
$b_{n+1}=3b_n+\boxed{\ \ ク\ \ } \ldots②$
が成り立つことが分かる。まず、$b_1=2$と②から
$b_n=\boxed{\ \ ケ\ \ } (n=1,2,3,\ldots)$
を得る。この結果と、$a_1=2$および1から
$a_n=\boxed{\ \ コ\ \ } (n=1,2,3,\ldots)$
がわかる。
$\boxed{\ \ ケ\ \ }, \boxed{\ \ コ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
⓪$3^{n-1}+1$ ①$\frac{1}{2}・3^n+\frac{1}{2}$
②$3^{n-1}+n$ ③$\frac{1}{2}・3^n+n-\frac{1}{2}$
④$3^{n-1}+n^2$ ⑤$\frac{1}{2}・3^n+n^2-\frac{1}{2}$
⑥$2・3^{n-1}$ ⑦$\frac{5}{2}・3^{n-1}-\frac{1}{2}$
⑧$2・3^{n-1}+n-1$ ⑨$\frac{5}{2}・3^{n-1}+n-\frac{3}{2}$
ⓐ$2・3^{n-1}+n^2-1$ ⓑ$\frac{5}{2}・3^{n-1}+n^2-\frac{3}{2}$
(2)歩行者が$y=300$の位置に到着するときまでに、自転車が装甲車に追いつく
回数は$\boxed{\ \ サ\ \ }$回である。また、$\boxed{\ \ サ\ \ }$回目に自転車が歩行者に追いつく
時刻は、$x=\boxed{\ \ シスセ\ \ }$である。
2022共通テスト数学過去問
無題
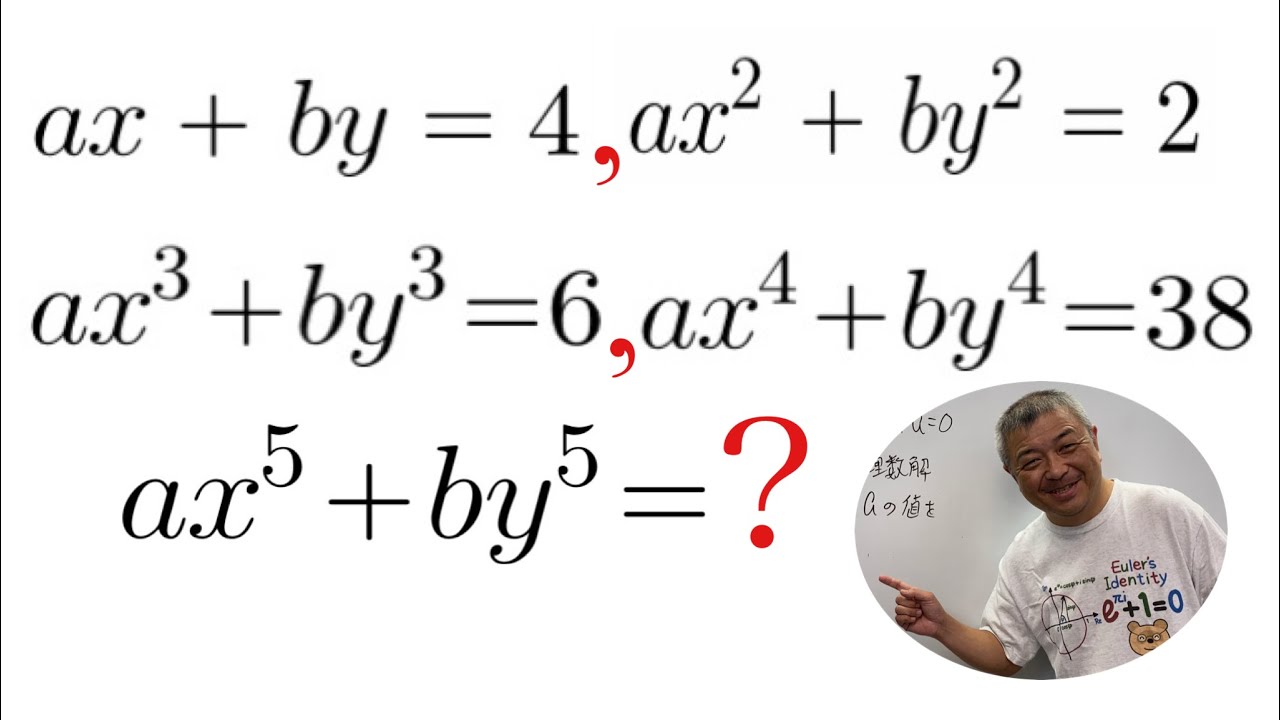
単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ax+by=4$
$ax^2+by^2=2$
$ax^3+by^3=6$
$ax^4+by^4=38$
$ax^5+by^5=\Box$
これを解け.
この動画を見る
$ax+by=4$
$ax^2+by^2=2$
$ax^3+by^3=6$
$ax^4+by^4=38$
$ax^5+by^5=\Box$
これを解け.
【数学B/数列】an+1=pan+q型の漸化式(特性方程式)

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次のように定義される数列{$a_n$}の一般項$a_n$を求めよ。
$a_1=2,$ $a_{n+1}=3a_n-2$
この動画を見る
次のように定義される数列{$a_n$}の一般項$a_n$を求めよ。
$a_1=2,$ $a_{n+1}=3a_n-2$
【数学B/数列】漸化式の基本

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次のように定義される数列${a_n}$の一般項$a_n$を求めよ。
(1)
$a_1=1,$ $a_{n+1}=a_n+3$
(2)
$a_1=2,$ $a_{n+1}=3a_n$
(3)
$a_1=-1,$ $a_{n+1}=a_n+6n-2$
(4)
$a_1=1,$ $a_{n+1}=a_n+2^{n-1}$
この動画を見る
次のように定義される数列${a_n}$の一般項$a_n$を求めよ。
(1)
$a_1=1,$ $a_{n+1}=a_n+3$
(2)
$a_1=2,$ $a_{n+1}=3a_n$
(3)
$a_1=-1,$ $a_{n+1}=a_n+6n-2$
(4)
$a_1=1,$ $a_{n+1}=a_n+2^{n-1}$
大学入試問題#77 京都大学(2002) 数列と極限

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_1=1,\displaystyle \lim_{ n \to \infty }S_n=1$
$n(n-2)a_{n+1}=s_n$のとき
一般項$a_n$を求めよ。
出典:2002年京都大学 入試問題
この動画を見る
$a_1=1,\displaystyle \lim_{ n \to \infty }S_n=1$
$n(n-2)a_{n+1}=s_n$のとき
一般項$a_n$を求めよ。
出典:2002年京都大学 入試問題
【概要欄に正確な文章と説明の補足】大学入試問題#76 京都大学(2007) 数列と極限

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x,y$:異なる正の実数
$a_1=0$
$a_{n+1}=x a_n=s\ a_n+y^{n+1}$のとき
$\displaystyle \lim_{ n \to \infty }a_n \lt \infty$となるような$(x,y)$の範囲を図示せよ。
出典:2007年京都大学 入試問題
この動画を見る
$x,y$:異なる正の実数
$a_1=0$
$a_{n+1}=x a_n=s\ a_n+y^{n+1}$のとき
$\displaystyle \lim_{ n \to \infty }a_n \lt \infty$となるような$(x,y)$の範囲を図示せよ。
出典:2007年京都大学 入試問題
大学入試問題#74 神戸大学(1991) 数列と極限
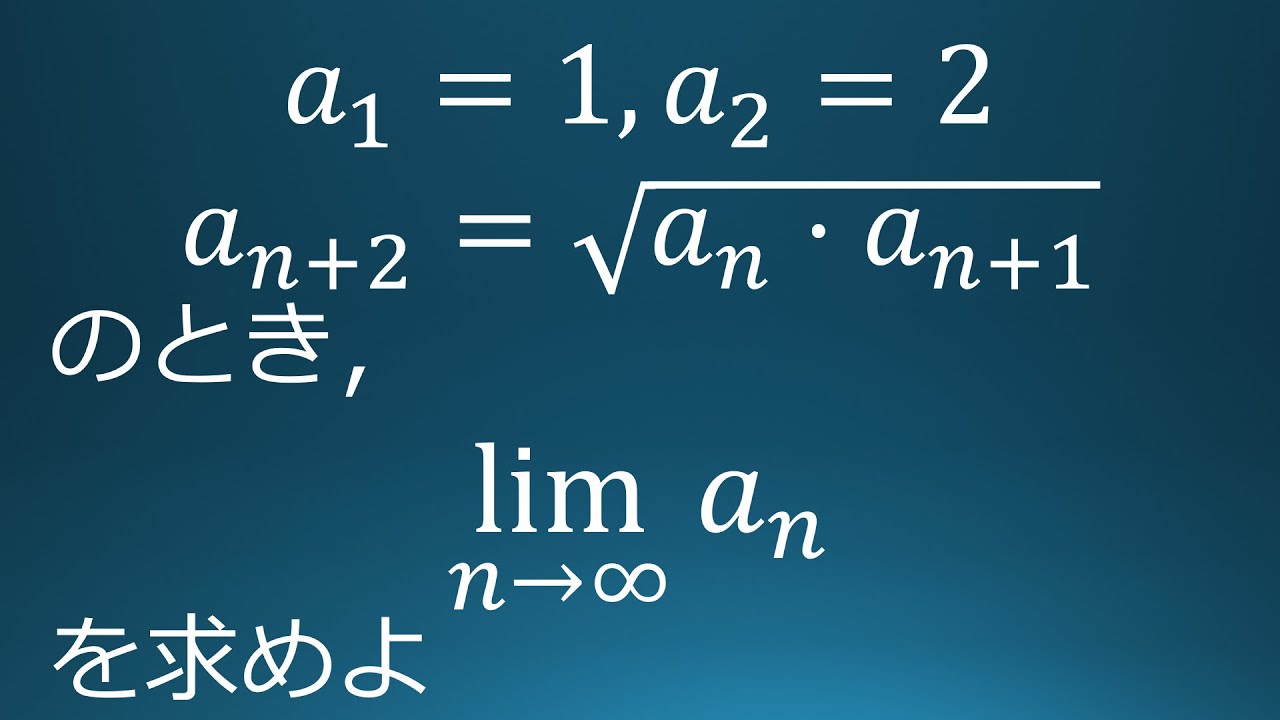
単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_1=1,\ a_2=2$
$a_{n+2}=\sqrt{ a_n\ a_{n+1} }$のとき
$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
出典:1991年神戸大学 入試問題
この動画を見る
$a_1=1,\ a_2=2$
$a_{n+2}=\sqrt{ a_n\ a_{n+1} }$のとき
$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
出典:1991年神戸大学 入試問題
もっちゃんと数学 映画「あなたの番です」で横浜流星が呟いた数式

大学入試問題#69 高知大学(2012) 数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#高知大学#数B
指導講師:
ますただ
問題文全文(内容文):
各自然数$n$に対して
$a_n \gt 0$
$S_n=\displaystyle \frac{1}{2}a_n^2+\displaystyle \frac{1}{2}a_n-1$をみたす一般項$a_n$を求めよ。
出典:2012年高知大学 入試問題
この動画を見る
各自然数$n$に対して
$a_n \gt 0$
$S_n=\displaystyle \frac{1}{2}a_n^2+\displaystyle \frac{1}{2}a_n-1$をみたす一般項$a_n$を求めよ。
出典:2012年高知大学 入試問題
大学入試問題#61 大阪工業大学(2021) 数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#大阪工業大学
指導講師:
ますただ
問題文全文(内容文):
$S_n=\displaystyle \frac{n+3}{2}a_n-6$を満たすとき
一般項$a_n$を求めよ。
出典:2021年大阪工業大学 入試問題
この動画を見る
$S_n=\displaystyle \frac{n+3}{2}a_n-6$を満たすとき
一般項$a_n$を求めよ。
出典:2021年大阪工業大学 入試問題
福田の数学〜立教大学2021年経済学部第2問〜2項間の漸化式の解法

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$次の条件によって定められる数列$\left\{a_n\right\}$がある。
$a_1=1, a_{n+1}=3a_n+4n (n=1,2,3,\ldots)$
また、$n$に無関係な定数$p,q$に対し、
$b_n=a_n+pn+q (n=1,2,3,\ldots)$
とおく。このとき次の問いに答えよ。
(1)$n,p,q$に無関係な定数$A,B,C,D,E$が
$b_{n+1}=Ab_n+(Bp+C)n+(Dp+Eq) (n=1,2,3,\ldots)$
を満たすとき、A,B,C,D,Eの値をそれぞれ求めよ。
(2)Aを(1)で求めた値とする。数列$\left\{b_n\right\}$が公比$A$の等比数列となるような
$p,q$の値をそれぞれ求めよ。
(3)(2)で求めた$p,q$の値に対して、数列$\left\{b_n\right\}$の一般項を求めよ。
2021立教大学経済学部過去問
この動画を見る
${\Large\boxed{3}}$次の条件によって定められる数列$\left\{a_n\right\}$がある。
$a_1=1, a_{n+1}=3a_n+4n (n=1,2,3,\ldots)$
また、$n$に無関係な定数$p,q$に対し、
$b_n=a_n+pn+q (n=1,2,3,\ldots)$
とおく。このとき次の問いに答えよ。
(1)$n,p,q$に無関係な定数$A,B,C,D,E$が
$b_{n+1}=Ab_n+(Bp+C)n+(Dp+Eq) (n=1,2,3,\ldots)$
を満たすとき、A,B,C,D,Eの値をそれぞれ求めよ。
(2)Aを(1)で求めた値とする。数列$\left\{b_n\right\}$が公比$A$の等比数列となるような
$p,q$の値をそれぞれ求めよ。
(3)(2)で求めた$p,q$の値に対して、数列$\left\{b_n\right\}$の一般項を求めよ。
2021立教大学経済学部過去問
福田の数学〜立教大学2021年経済学部第1問(5)〜対数方程式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#数列#漸化式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(5)$x$についての方程式
$(\log_2x)^2+5\log_2x+2=0$
の2つの解を$\alpha,\beta$とおくと、$\alpha\beta=\boxed{キ}$である。
2021立教大学経済学部過去問
この動画を見る
${\Large\boxed{1}}$(5)$x$についての方程式
$(\log_2x)^2+5\log_2x+2=0$
の2つの解を$\alpha,\beta$とおくと、$\alpha\beta=\boxed{キ}$である。
2021立教大学経済学部過去問
福田の数学〜立教大学2021年理学部第3問〜定積分の漸化式と回転体の体積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#数列#漸化式#学校別大学入試過去問解説(数学)#不定積分・定積分#立教大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$nを0以上の整数とする。定積分
$I_n=\int_1^e\frac{(\log x)^n}{x^2}\ dx$
について、次の問(1)~(4)に答えよ。ただし、$e$は自然対数の底である。
(1)$I_0, I_1$の値をそれぞれ求めよ。
(2)$I_{n+1}$を$I_n$と$n$を用いて表せ。
(3)$x \gt 0$とする。関数$f(x)=\frac{(\log x)^2}{x}$の増減表を書け。
ただし、極値も増減表に記入すること。
(4)座標平面上の曲線$y=\frac{(\log x)^2}{x}$, x軸と直線$x=e$とで囲まれた図形を、
x軸の周りに1回転させてできる立体の体積Vを求めよ。
2021立教大学理工学部過去問
この動画を見る
${\Large\boxed{3}}$nを0以上の整数とする。定積分
$I_n=\int_1^e\frac{(\log x)^n}{x^2}\ dx$
について、次の問(1)~(4)に答えよ。ただし、$e$は自然対数の底である。
(1)$I_0, I_1$の値をそれぞれ求めよ。
(2)$I_{n+1}$を$I_n$と$n$を用いて表せ。
(3)$x \gt 0$とする。関数$f(x)=\frac{(\log x)^2}{x}$の増減表を書け。
ただし、極値も増減表に記入すること。
(4)座標平面上の曲線$y=\frac{(\log x)^2}{x}$, x軸と直線$x=e$とで囲まれた図形を、
x軸の周りに1回転させてできる立体の体積Vを求めよ。
2021立教大学理工学部過去問
福田のわかった数学〜高校1年生063〜場合の数(2)完全順列

単元:
#数A#場合の数と確率#場合の数#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(2) 完全順列
1,2,3,4を1列に並べたものを$a_1a_2a_3a_4$とする。
$a_1\neq 1,a_2\neq 2,a_3\neq 3,a_4\neq 4$を満たす並べ方は何通りあるか。
この動画を見る
数学$\textrm{I}$ 場合の数(2) 完全順列
1,2,3,4を1列に並べたものを$a_1a_2a_3a_4$とする。
$a_1\neq 1,a_2\neq 2,a_3\neq 3,a_4\neq 4$を満たす並べ方は何通りあるか。
広島大2002漸化式 最大項を求める

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_{1}=-30$であり,$9a_{a+1}=a_n-\dfrac{4}{3^n}$である.
$a_n$が最大となる自然数$n$を求めよ.
広島大過去問
この動画を見る
$a_{1}=-30$であり,$9a_{a+1}=a_n-\dfrac{4}{3^n}$である.
$a_n$が最大となる自然数$n$を求めよ.
広島大過去問
ちょっと複雑な漸化式

3つの解法・漸化式
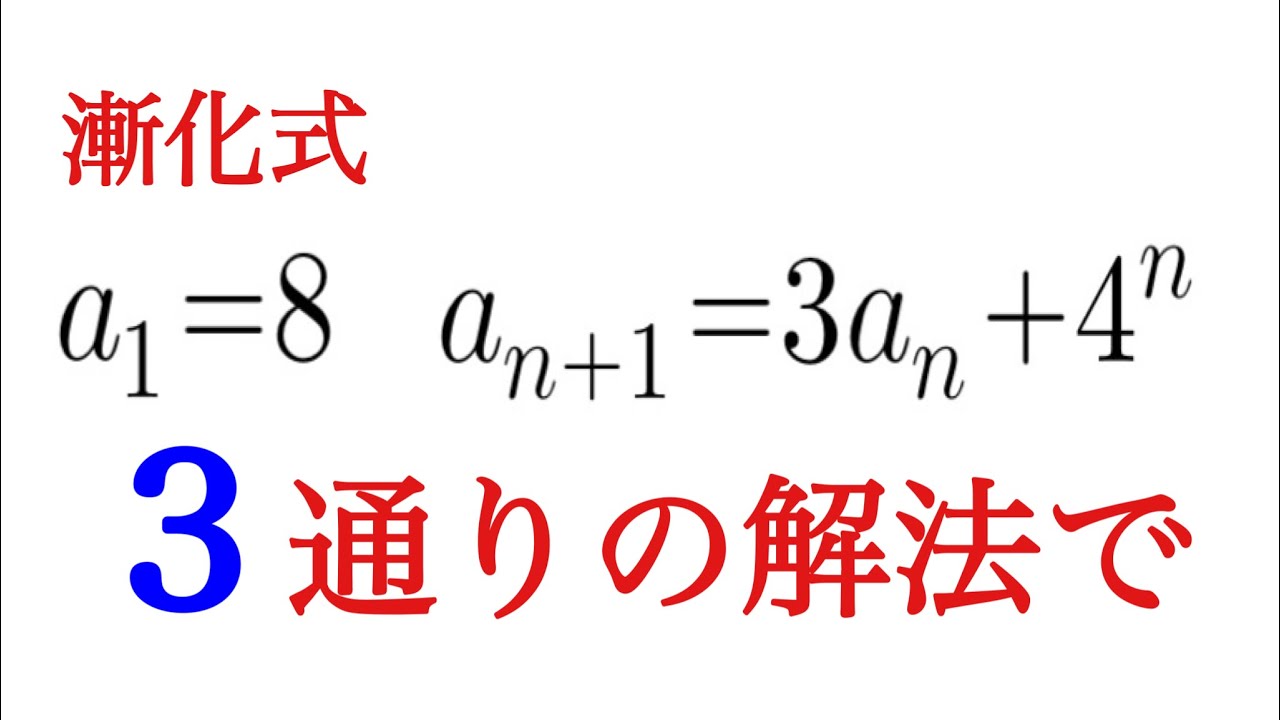
福田のわかった数学〜高校3年生理系076〜平均値の定理(4)数列の極限の問題

単元:
#数列#漸化式#関数と極限#微分とその応用#数列の極限#接線と法線・平均値の定理#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$平均値の定理(4)
微分可能な関数$f(x)$が$f(1)=1, 0 \lt f'(x) \leqq \frac{1}{2}$を満たしている。
$a_{n+1}=f(a_n)$で定義される数列$\left\{a_n\right\}$について、
$\lim_{n \to \infty}a_n=1$であることを示せ。
この動画を見る
数学$\textrm{III}$平均値の定理(4)
微分可能な関数$f(x)$が$f(1)=1, 0 \lt f'(x) \leqq \frac{1}{2}$を満たしている。
$a_{n+1}=f(a_n)$で定義される数列$\left\{a_n\right\}$について、
$\lim_{n \to \infty}a_n=1$であることを示せ。
福田の数学〜明治大学2021年全学部統一入試IⅡAB第1問(1)〜連立型の漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(1)数列$\left\{a_n\right\},\ \left\{b_n\right\}$について次の条件が与えられている。
$\left\{
\begin{array}{1}
a_{n+1}=7a_n-10b_n\\
b_{n+1}=2a_n-2b_n
\end{array}
\right. (n=1,2,3,\ldots)$
ただし、$a_1=11,\ b_1=4$とする。このとき、
$\left\{
\begin{array}{1}
c_n=a_n-2b_n \\
d_n=2a_n-5b_n
\end{array}
\right. (n=1,2,3,\ldots)$
とおくと、$c_n=\boxed{\ \ ア\ \ }^n, d_n=\boxed{\ \ イ\ \ }^n$であり、これより$\left\{a_n\right\},\ \left\{b_n\right\}$
の一般項は
$\left\{
\begin{array}{1}
a_n=\boxed{\ \ ウ\ \ }・\boxed{\ \ ア\ \ }^n-\boxed{\ \ エ\ \ }・\boxed{\ \ イ\ \ }^n\\
b_n=\boxed{\ \ オ\ \ }・\boxed{\ \ ア\ \ }^n-\boxed{\ \ イ\ \ }^n \\
\end{array}
\right.$
である。
2021明治大学全統過去問
この動画を見る
${\Large\boxed{1}}$(1)数列$\left\{a_n\right\},\ \left\{b_n\right\}$について次の条件が与えられている。
$\left\{
\begin{array}{1}
a_{n+1}=7a_n-10b_n\\
b_{n+1}=2a_n-2b_n
\end{array}
\right. (n=1,2,3,\ldots)$
ただし、$a_1=11,\ b_1=4$とする。このとき、
$\left\{
\begin{array}{1}
c_n=a_n-2b_n \\
d_n=2a_n-5b_n
\end{array}
\right. (n=1,2,3,\ldots)$
とおくと、$c_n=\boxed{\ \ ア\ \ }^n, d_n=\boxed{\ \ イ\ \ }^n$であり、これより$\left\{a_n\right\},\ \left\{b_n\right\}$
の一般項は
$\left\{
\begin{array}{1}
a_n=\boxed{\ \ ウ\ \ }・\boxed{\ \ ア\ \ }^n-\boxed{\ \ エ\ \ }・\boxed{\ \ イ\ \ }^n\\
b_n=\boxed{\ \ オ\ \ }・\boxed{\ \ ア\ \ }^n-\boxed{\ \ イ\ \ }^n \\
\end{array}
\right.$
である。
2021明治大学全統過去問
福田の数学〜中央大学2021年経済学部第1問(5)〜漸化式の解法

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(5)次の条件によって定められる数列$\left\{a_n\right\}$の一般項を求めよ。
$a_1=-1, a_{n+1}=a_n+2・3^{n-1} (n=1,2,3,\ldots)$
2021中央大学経済学部過去問
この動画を見る
${\Large\boxed{1}}$(5)次の条件によって定められる数列$\left\{a_n\right\}$の一般項を求めよ。
$a_1=-1, a_{n+1}=a_n+2・3^{n-1} (n=1,2,3,\ldots)$
2021中央大学経済学部過去問
福田の数学〜中央大学2021年理工学部第2問〜3項間の漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$コインを繰り返し,連続した3回が順に,表→裏→表,あるいは,裏→表→裏,というパターンが出たときにコイン投げを終了する.$n\geqq 3$に対し,コインをちょうど$n$回投げて終了する確率を$p_n$とする.
以下の手順により$p_n$を求める.コインを$n$回投げて,「まだ終了していないが$n+1$回目に表が出たら終了する」または「まだ終了してないが$n+1$回目に裏が出たら終了する.」という状態にある確率を$r_n$とする.またコインを$n$回投げて「まだ終了しておらず,$n+1$回目に表が出ても裏が出ても終了しない」という状態にある確率を$s_n$とする.
このとき,$r_3=\dfrac{1}{4},s_3=\boxed{ク},r_4=\dfrac{1}{4},s_4=\boxed{ケ}$である.
ここで,$r_{n+4}$と$r_{n},s_n$を用いて表すと,それぞれ$r_{n+1}=\boxed{コ}$,$s_{n+1}=\boxed{サ}$となる.
この動画を見る
$\boxed{2}$コインを繰り返し,連続した3回が順に,表→裏→表,あるいは,裏→表→裏,というパターンが出たときにコイン投げを終了する.$n\geqq 3$に対し,コインをちょうど$n$回投げて終了する確率を$p_n$とする.
以下の手順により$p_n$を求める.コインを$n$回投げて,「まだ終了していないが$n+1$回目に表が出たら終了する」または「まだ終了してないが$n+1$回目に裏が出たら終了する.」という状態にある確率を$r_n$とする.またコインを$n$回投げて「まだ終了しておらず,$n+1$回目に表が出ても裏が出ても終了しない」という状態にある確率を$s_n$とする.
このとき,$r_3=\dfrac{1}{4},s_3=\boxed{ク},r_4=\dfrac{1}{4},s_4=\boxed{ケ}$である.
ここで,$r_{n+4}$と$r_{n},s_n$を用いて表すと,それぞれ$r_{n+1}=\boxed{コ}$,$s_{n+1}=\boxed{サ}$となる.
