 漸化式
漸化式
 漸化式
漸化式
千葉大 漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数$n\geqq 2$であり,$a_n=\dfrac{(1+\sqrt3)^n+(1-\sqrt3)^n}{4}$である.
$a_n$は整数であり,$a_n$を$3$で割った余りは$2$であることを示せ.
2013千葉大過去問
この動画を見る
整数$n\geqq 2$であり,$a_n=\dfrac{(1+\sqrt3)^n+(1-\sqrt3)^n}{4}$である.
$a_n$は整数であり,$a_n$を$3$で割った余りは$2$であることを示せ.
2013千葉大過去問
福井大(医)漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=1,a_2=3$であり,$n\geqq 2$とする.
$a_{n+1}-\dfrac{4n+2}{n+1}an+\dfrac{4n-4}{n}a_{n-1}=0$
(1)$b_n=a_{n+1}-\dfrac{2n}{n+1}a_n(n\geqq 1)$,$b_n$を$n$で表せ.
(2)$a_n$を求めよ.
福井大(医)過去問
この動画を見る
$a_1=1,a_2=3$であり,$n\geqq 2$とする.
$a_{n+1}-\dfrac{4n+2}{n+1}an+\dfrac{4n-4}{n}a_{n-1}=0$
(1)$b_n=a_{n+1}-\dfrac{2n}{n+1}a_n(n\geqq 1)$,$b_n$を$n$で表せ.
(2)$a_n$を求めよ.
福井大(医)過去問
東京海洋大 漸化式と3次関数

単元:
#数列#漸化式#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数B#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数とする.
$a_1=1$であり,$a_{n+1}=27^{n^2-3n-9}a_n$とする.
(1)一般項$a_n$を求めよ.
(2)$a_n$が最小となる値を求めよ.
2013東京海洋大過去問
この動画を見る
$n$は自然数とする.
$a_1=1$であり,$a_{n+1}=27^{n^2-3n-9}a_n$とする.
(1)一般項$a_n$を求めよ.
(2)$a_n$が最小となる値を求めよ.
2013東京海洋大過去問
東大 漸化式 整式の剰余
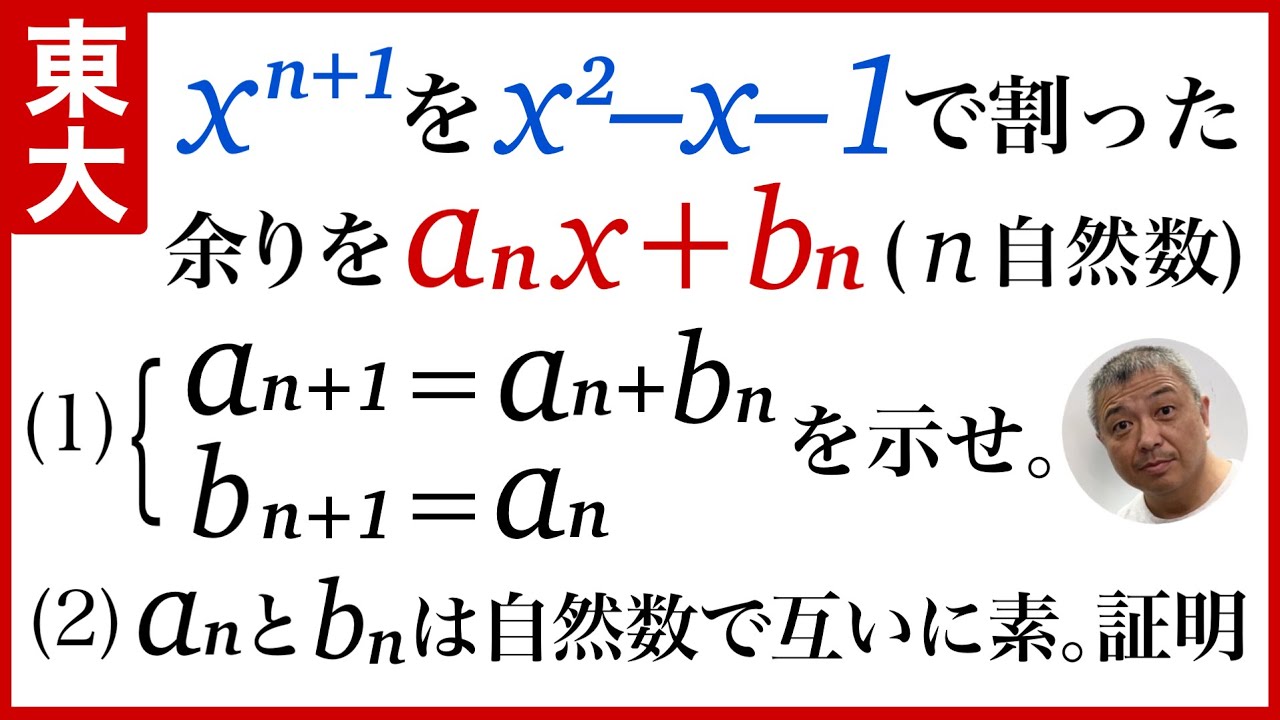
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$を自然数とする.
$x^{n+1}$を$x^2-x-1$で割った余りを$a_n x+b_n$とする.
(1)$\begin{eqnarray}
\left\{
\begin{array}{l}
a_{n+1}=a_n+b_n \\
b_{n+1}=a_n
\end{array}
\right.
\end{eqnarray}$ を示せ.
(2)$a_n$と$b_n$は自然数で,互いに素であることを示せ.
東大過去問
この動画を見る
$n$を自然数とする.
$x^{n+1}$を$x^2-x-1$で割った余りを$a_n x+b_n$とする.
(1)$\begin{eqnarray}
\left\{
\begin{array}{l}
a_{n+1}=a_n+b_n \\
b_{n+1}=a_n
\end{array}
\right.
\end{eqnarray}$ を示せ.
(2)$a_n$と$b_n$は自然数で,互いに素であることを示せ.
東大過去問
練習問題2(数検1級1次レベル? 3項間漸化式)

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_1=-1,a_2=1$
$a_{n+2}+2a_{n+1}+4a_n=0$
一般項$a_n$を求めよ
この動画を見る
$a_1=-1,a_2=1$
$a_{n+2}+2a_{n+1}+4a_n=0$
一般項$a_n$を求めよ
04兵庫県教員採用試験(数学:2番 数列と帰納法)

単元:
#数列#漸化式#数学的帰納法#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$a_1=\frac{1}{2}$ , $a_{n+1}=\frac{1}{2-a_n}$
一般項$a_n$を求めよ
この動画を見る
$a_1=\frac{1}{2}$ , $a_{n+1}=\frac{1}{2-a_n}$
一般項$a_n$を求めよ
東大 三角比と漸化式

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a=\sin^2\dfrac{\pi}{5}$であり,$b=\sin^2\dfrac{2\pi}{5}$である.
(1)$a+b,ab$は有理数であることを示せ.
(2)$(a^{-n}+b^{-n})(a+b)^n$は整数であることを示せ.($n$は自然数)
1994東大過去問
この動画を見る
$a=\sin^2\dfrac{\pi}{5}$であり,$b=\sin^2\dfrac{2\pi}{5}$である.
(1)$a+b,ab$は有理数であることを示せ.
(2)$(a^{-n}+b^{-n})(a+b)^n$は整数であることを示せ.($n$は自然数)
1994東大過去問
07神奈川県教員採用試験(数学:7番 数列の極限)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
7⃣$a_1=\frac{1}{3}$ , $3^{n+1}a_{n+1}=3^na_n+1$
$\displaystyle \lim_{ n \to \infty } S_n$を求めよ
この動画を見る
7⃣$a_1=\frac{1}{3}$ , $3^{n+1}a_{n+1}=3^na_n+1$
$\displaystyle \lim_{ n \to \infty } S_n$を求めよ
【数B】数列:基礎からわかる確率漸化式!!四面体の頂点を移動する点がn秒後に他の頂点にいる確率

単元:
#数列#漸化式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
四面体OABCの頂点を移動する点Pがある。 点Pは1つの頂点に達してから1秒後に、他の3つの頂点の いずれかに各々確率1/3で移動する。 最初に頂点Oにいた点Pがn秒後に頂点Aにいる確率Pnを求めよ。
この動画を見る
四面体OABCの頂点を移動する点Pがある。 点Pは1つの頂点に達してから1秒後に、他の3つの頂点の いずれかに各々確率1/3で移動する。 最初に頂点Oにいた点Pがn秒後に頂点Aにいる確率Pnを求めよ。
漸化式と素数

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=1$であり,$a_{n+1}=2a_n+1$である.
$a_n$が素数なら$n$は素数であることを示せ.
この動画を見る
$a_1=1$であり,$a_{n+1}=2a_n+1$である.
$a_n$が素数なら$n$は素数であることを示せ.
弘前大 漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=2$,$a_{n+1}=\dfrac{n+2}{n}a_n+1$
一般項を求めよ.
弘前大過去問
この動画を見る
$a_1=2$,$a_{n+1}=\dfrac{n+2}{n}a_n+1$
一般項を求めよ.
弘前大過去問
漸化式と整数の融合問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=2$,$a_{n+1}=2^{n^2+2n-1}・a^2_n$
$a_n$の1の位が2になるのは$a_1$のみであることを示せ.
この動画を見る
$a_1=2$,$a_{n+1}=2^{n^2+2n-1}・a^2_n$
$a_n$の1の位が2になるのは$a_1$のみであることを示せ.
漸化式と整数問題の融合

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数である.
$a_1=10,a_{n+1}=2a_n+3^{n+1}$
$a_n$が7の倍数となるような$n$を求めよ.
この動画を見る
$n$は自然数である.
$a_1=10,a_{n+1}=2a_n+3^{n+1}$
$a_n$が7の倍数となるような$n$を求めよ.
一橋大 漸化式&対数

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
数列$a_n,a_1=5,a_{n+1}=2,a_n+3^n$がある.
(1)$a_n$を求めよ.
(2)$a_n\lt 10^{10}$を満たす最大の$n$を求めよ.
$\log_{10}2=0.3010,\log_{10}3=0.4771$
1998一橋大過去問
この動画を見る
数列$a_n,a_1=5,a_{n+1}=2,a_n+3^n$がある.
(1)$a_n$を求めよ.
(2)$a_n\lt 10^{10}$を満たす最大の$n$を求めよ.
$\log_{10}2=0.3010,\log_{10}3=0.4771$
1998一橋大過去問
16神奈川県教員採用試験(数学:8番 数列の極限)

単元:
#数列#漸化式#関数と極限#数列の極限#数学(高校生)#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
8⃣ $3S_n=a_n+6n+1$のとき$\displaystyle \lim_{ n \to \infty } a_n$を求めよ。
この動画を見る
8⃣ $3S_n=a_n+6n+1$のとき$\displaystyle \lim_{ n \to \infty } a_n$を求めよ。
【数B】数列:隣接三項間型(重解) 次の条件によって定められる数列{an}の一般項を求めよ。a[1]=1,a[2]=5,a[n+2]+8a[n+1]+16a[n]=0

単元:
#数列#漸化式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の条件によって定められる数列${an}$の一般項を求めよ。
$a_1=1,a_2=5,a_{n+2}+8a_{n+1}-16a_n=0$
この動画を見る
次の条件によって定められる数列${an}$の一般項を求めよ。
$a_1=1,a_2=5,a_{n+2}+8a_{n+1}-16a_n=0$
【数B】数列:隣接三項間型(解2つ) 次の条件によって定められる数列{an}の一般項を求めよ。a1=1,a2=4,a[n+2]+a[n+1]-2a[n]=0

単元:
#数列#漸化式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の条件によって定められる数列${an}$の一般項を求めよ。
$a_1=1,a_2=4,a_{n+2}+a_{n+1}-2a_n=0$
この動画を見る
次の条件によって定められる数列${an}$の一般項を求めよ。
$a_1=1,a_2=4,a_{n+2}+a_{n+1}-2a_n=0$
【数B】確率漸化式:ある地方では雨が降った日の翌日に雨が降る確率は60%、雨が降らなかった日の翌日に雨が降る確率は30%であるという。今日雨が降っている時、n日後も雨が降る確率P[n]を求めよ。

単元:
#数列#漸化式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある地方では雨が降った日の翌日に雨が降る確率は60%、雨が降らなかった日の翌日に雨が降る確率は30%であるという。今日雨が降っている時、n日後も雨が降る確率$P_n$を求めよ。
この動画を見る
ある地方では雨が降った日の翌日に雨が降る確率は60%、雨が降らなかった日の翌日に雨が降る確率は30%であるという。今日雨が降っている時、n日後も雨が降る確率$P_n$を求めよ。
【数B】確率漸化式:3つの数字2,3,4をn個並べてn桁の整数をつくる。その中で、各位の数字の和が偶数であるものの個数をa[n]とする。(1)a[n+1]をa[n]の式で表せ。(2)a[n]を求めよ

単元:
#数列#漸化式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
3つの数字2,3,4をn個並べてn桁の整数をつくる。その中で、各位の数字の和が偶数であるものの個数を$a_n$とする。
(1)$a_{n+1}$を$a_n$の式で表せ。
(2)$a_n$を求めよ
この動画を見る
3つの数字2,3,4をn個並べてn桁の整数をつくる。その中で、各位の数字の和が偶数であるものの個数を$a_n$とする。
(1)$a_{n+1}$を$a_n$の式で表せ。
(2)$a_n$を求めよ
【数B】確率漸化式:1回の試行で事象Aの起こる確率が1/3であるとする。この試行をn回行うときに奇数回Aが起こる確率をP[n]とする。(1)P[n+1]をP[n]の式で表せ。(2)P[n]を求めよ。

単元:
#数列#漸化式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
1回の試行で事象Aの起こる確率が$\dfrac{1}{3}$であるとする。この試行をn回行うときに奇数回Aが起こる確率を$P_n$とする。
(1)$P_{n+1}$を$P_n$の式で表せ。
(2)$P_n$を求めよ。
この動画を見る
1回の試行で事象Aの起こる確率が$\dfrac{1}{3}$であるとする。この試行をn回行うときに奇数回Aが起こる確率を$P_n$とする。
(1)$P_{n+1}$を$P_n$の式で表せ。
(2)$P_n$を求めよ。
【数B】確率漸化式:さいころをn回投げたとき1の目が偶数回出る確率をp[n]とする(中略) (1)p1を求めよ。(2)p[n+1]をp[n]で表せ。(3)p[n] (n=1,2,3,..)を求めよ。

単元:
#数列#漸化式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
さいころをn回投げたとき1の目が偶数回出る確率を$p_n$とする。ただし、1の目が1回も出なかった場合は偶数回出たと考えることにする。
(1)$p_1$を求めよ。
(2)$p_{n+1}$を$p_n$で表せ。
(3)$p_n$ (n=1,2,3,..)を求めよ。
この動画を見る
さいころをn回投げたとき1の目が偶数回出る確率を$p_n$とする。ただし、1の目が1回も出なかった場合は偶数回出たと考えることにする。
(1)$p_1$を求めよ。
(2)$p_{n+1}$を$p_n$で表せ。
(3)$p_n$ (n=1,2,3,..)を求めよ。
13奈良県教員採用試験(数学:1-2番 数列)

単元:
#数列#漸化式#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(2)
$a_1$=3 , $a_2$=2
$a_n=\frac{2a_{n+1}・a_{n-1}}{a_{n+1}+a_{n-1}}$のとき$a_n$を求めよ。
この動画を見る
1⃣-(2)
$a_1$=3 , $a_2$=2
$a_n=\frac{2a_{n+1}・a_{n-1}}{a_{n+1}+a_{n-1}}$のとき$a_n$を求めよ。
北里大2020 分数型漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=2,a_{n+1}=\dfrac{4a_2+2}{a_n+5}$
一般項を求めよ.
2020北里大過去問
この動画を見る
$a_1=2,a_{n+1}=\dfrac{4a_2+2}{a_n+5}$
一般項を求めよ.
2020北里大過去問
三乗根と漸化式(類)一橋:順天堂(医)

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数とする.
$\alpha=\sqrt[3]{9+4\sqrt5},\beta=\sqrt[3]{9-4\sqrt5}$
$a_n=\alpha^{2n-1}+\beta^{2n-1}$である.
$a_{n+4}-a_n$が7の倍数であることを示せ.
一橋:順天堂(医)過去問
この動画を見る
$n$は自然数とする.
$\alpha=\sqrt[3]{9+4\sqrt5},\beta=\sqrt[3]{9-4\sqrt5}$
$a_n=\alpha^{2n-1}+\beta^{2n-1}$である.
$a_{n+4}-a_n$が7の倍数であることを示せ.
一橋:順天堂(医)過去問
首都大学東京 漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \sum_{k=1}^n a_k=n^4+6n^3+11n^2+6n$
①$a_n$を$n$の式で表せ.
②$\displaystyle \sum_{k=1}^{\infty}\dfrac{1}{a_k}$
2018首都大学東京過去問
この動画を見る
$\displaystyle \sum_{k=1}^n a_k=n^4+6n^3+11n^2+6n$
①$a_n$を$n$の式で表せ.
②$\displaystyle \sum_{k=1}^{\infty}\dfrac{1}{a_k}$
2018首都大学東京過去問
広島県立大 漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_n \gt 0,S_n=\displaystyle \sum_{k=1}^n a_k$
$a_1^3+a_2^3・・・・・・+a_n^3=2S_n^2$とする.
(1)$a_n^2+2a_n=4S_n$を示せ.
(2)$a_n$を$n$の式で表せ.
1996広島県立大過去問
この動画を見る
$a_n \gt 0,S_n=\displaystyle \sum_{k=1}^n a_k$
$a_1^3+a_2^3・・・・・・+a_n^3=2S_n^2$とする.
(1)$a_n^2+2a_n=4S_n$を示せ.
(2)$a_n$を$n$の式で表せ.
1996広島県立大過去問
群馬大(医)漸化式
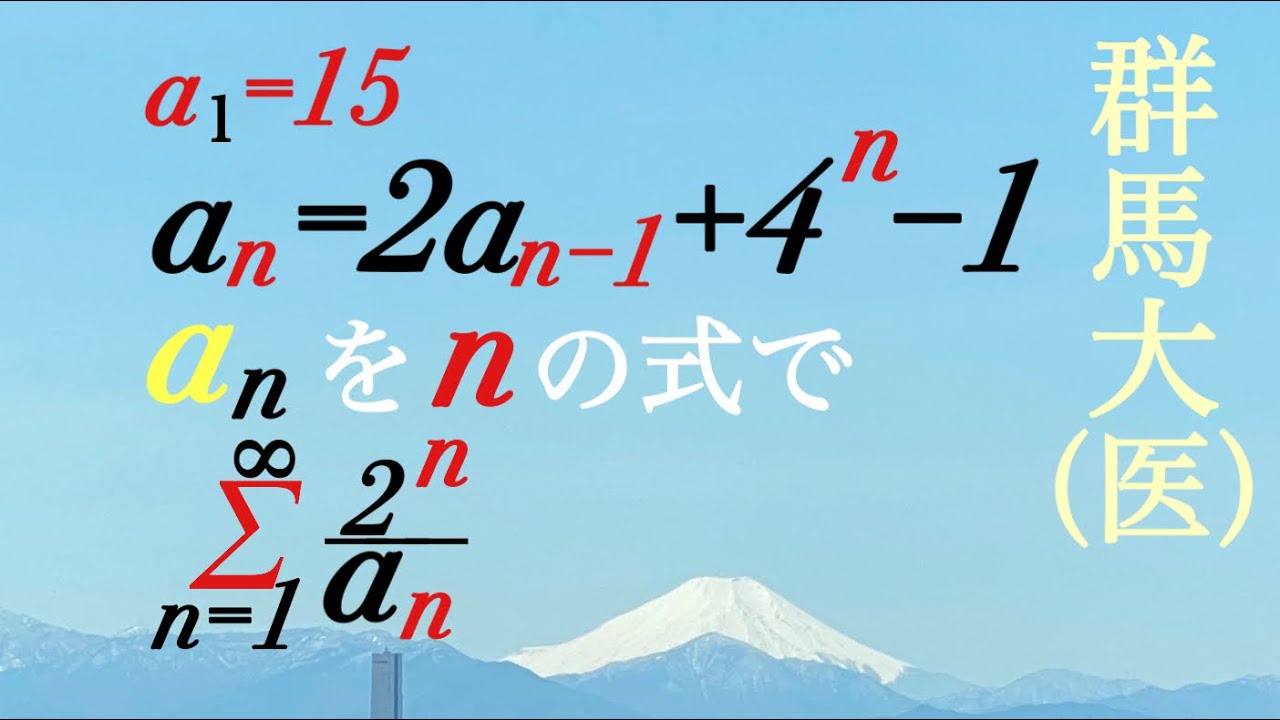
単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=15$であり,$n$を自然数とする.
$a_n-2a_{n-1}+4^n-1$
(1)$a_n$を$n$の式で表せ.
(2)$\displaystyle \sum_{n=1}^{\infty}\dfrac{2^n}{a_n}$
1992群馬大(医)過去問
この動画を見る
$a_1=15$であり,$n$を自然数とする.
$a_n-2a_{n-1}+4^n-1$
(1)$a_n$を$n$の式で表せ.
(2)$\displaystyle \sum_{n=1}^{\infty}\dfrac{2^n}{a_n}$
1992群馬大(医)過去問
順天堂大(医)漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_n=(\sqrt2+1)^{2n-1}-(\sqrt2-1)^{2n-1}$
$a_{n+4}-a_n$が6の倍数であることを示せ.
順天堂(医)過去問
この動画を見る
$a_n=(\sqrt2+1)^{2n-1}-(\sqrt2-1)^{2n-1}$
$a_{n+4}-a_n$が6の倍数であることを示せ.
順天堂(医)過去問
自治医科大 食塩水漸化式

単元:
#数列#漸化式#売買損益と食塩水#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$A$には16%の食塩水400gある.$B$には4%の食塩水200gある.
100gずつ取り出して入れかえる.$n$回後の$A,B$の濃度$a_n,b_n$を$n$の式で表せ.
1992自治医大過去問
この動画を見る
$A$には16%の食塩水400gある.$B$には4%の食塩水200gある.
100gずつ取り出して入れかえる.$n$回後の$A,B$の濃度$a_n,b_n$を$n$の式で表せ.
1992自治医大過去問
【数B】数列:N次式型の漸化式! a1=1,a[n+1]=2a[n]-n²+2nで定められる数列{an}の一般項を求めよ。

単元:
#数列#漸化式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$a_1=1,a_{n+1}=2a_n-n²+2n$で定められる数列${an}$の一般項を求めよ。
この動画を見る
$a_1=1,a_{n+1}=2a_n-n²+2n$で定められる数列${an}$の一般項を求めよ。
