 確率分布
確率分布
 確率分布
確率分布
【数B】【数列】1個のさいころを2回続けて投げる次の3つの事象A, B, Cは互いに独立であるか。A: 1回目に偶数の目が出る。B: 2回目に奇数の目が出る。C: 1回目と2回目の目の和が奇数である。

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
1個のさいころを2回続けて投げるとき、次の3つの事象A, B, Cは互いに独立であるか。
A: 1回目に偶数の目が出る。
B: 2回目に奇数の目が出る。
C: 1回目と2回目の目の和が奇数である。
この動画を見る
1個のさいころを2回続けて投げるとき、次の3つの事象A, B, Cは互いに独立であるか。
A: 1回目に偶数の目が出る。
B: 2回目に奇数の目が出る。
C: 1回目と2回目の目の和が奇数である。
福田の数学〜慶應義塾大学薬学部2025第2問〜薬の効果を検定する

単元:
#大学入試過去問(数学)#確率分布と統計的な推測#確率分布#学校別大学入試過去問解説(数学)#標本調査#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
薬を病気にかかっている患者に投与すると、
投与された患者のうちの$40$% に治療の効果が認められる。
この薬に対し、新しく開発した薬$\beta$の方が
治療の効果が認められる割合が高いかどうか、
有意水準$5$%で検定を行う。
病気$X$にかかっている患者から無作為に抽出した$1000$人に
薬を投与したとき、
$n$人以上に治療の効果が認められると、
薬$\alpha$よりも薬$\beta$の方が効果が認められる割合が高いと判断される。
ただし、薬の治療効果の標本比率を$R$、母比率を$p$とする。
(1) 帰無仮説$H_0$と対立仮説$H_1$に設定する式は
$H_0:\boxed{チ},H_1:\boxed{ツ}$である。
$H_0$が正しいと仮定するとき、
$R$は近似的に正規分布$N(\boxed{テ},\boxed{ト})$に従う。
(2) (1) をふまえ、
$n$のとりうる最小の値を求めなさい。
ただし、解答に
「標準正規分布」と「棄却域」という言葉を含めなさい。
なお、
$\sqrt{2}=1.4,\sqrt3=1.7,\sqrt5 = 2.2$として計算し、
必要に応じて正規分布表を用いなさい。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{2}$
薬を病気にかかっている患者に投与すると、
投与された患者のうちの$40$% に治療の効果が認められる。
この薬に対し、新しく開発した薬$\beta$の方が
治療の効果が認められる割合が高いかどうか、
有意水準$5$%で検定を行う。
病気$X$にかかっている患者から無作為に抽出した$1000$人に
薬を投与したとき、
$n$人以上に治療の効果が認められると、
薬$\alpha$よりも薬$\beta$の方が効果が認められる割合が高いと判断される。
ただし、薬の治療効果の標本比率を$R$、母比率を$p$とする。
(1) 帰無仮説$H_0$と対立仮説$H_1$に設定する式は
$H_0:\boxed{チ},H_1:\boxed{ツ}$である。
$H_0$が正しいと仮定するとき、
$R$は近似的に正規分布$N(\boxed{テ},\boxed{ト})$に従う。
(2) (1) をふまえ、
$n$のとりうる最小の値を求めなさい。
ただし、解答に
「標準正規分布」と「棄却域」という言葉を含めなさい。
なお、
$\sqrt{2}=1.4,\sqrt3=1.7,\sqrt5 = 2.2$として計算し、
必要に応じて正規分布表を用いなさい。
$2025$年慶應義塾大学薬学部過去問題
【数B】【確率分布と統計的な推測】独立な確率変数と期待値、分散 ※問題文は概要欄

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
2つの事象A,Bが独立であって,P(A)=1/2,P(B)=1/3であるとき,次の問いに答えよ。
(1)A,Bのうち少なくとも一方が起こる確率を求めよ。
(2) A,Bのうちどちらか一方のみが起こる確率を求めよ。
2,4,6の目が2面ずつ書かれた3個のさいころを同時に投げるとき,出る目の積の期待値を求めよ。
1つの面には1,2つの面には2,3つの面には3が書かれているさいころを2回投げて,1回目に出た目の数を十の位,2回目に出た目の数を一の位として得られる2桁の数をXとする。
(1)Xの確率分布を求めよ。
(2)Xの期待値と分散を求めよ。
この動画を見る
2つの事象A,Bが独立であって,P(A)=1/2,P(B)=1/3であるとき,次の問いに答えよ。
(1)A,Bのうち少なくとも一方が起こる確率を求めよ。
(2) A,Bのうちどちらか一方のみが起こる確率を求めよ。
2,4,6の目が2面ずつ書かれた3個のさいころを同時に投げるとき,出る目の積の期待値を求めよ。
1つの面には1,2つの面には2,3つの面には3が書かれているさいころを2回投げて,1回目に出た目の数を十の位,2回目に出た目の数を一の位として得られる2桁の数をXとする。
(1)Xの確率分布を求めよ。
(2)Xの期待値と分散を求めよ。
【数B】【確率分布と統計的な推測】確率変数の和と期待値 ※問題文は概要欄

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
トランプのハート13枚を裏返しにしてよく混ぜてから,まずAが3枚抜き,抜いたカードはもとに戻さずに,続けてBが1枚抜くとき,A,Bが抜いた絵札の枚数を,それぞれX,Yとする。XとYの同時分布を求めよ。
100本のくじの中に30本の当たりくじがある。このくじから10本のくじを続けて引くとき,その中の当たりくじの本数をYとする。確率変数Yの期待値を求めよ。ただし,引いたくじはもとに戻さないとする。
この動画を見る
トランプのハート13枚を裏返しにしてよく混ぜてから,まずAが3枚抜き,抜いたカードはもとに戻さずに,続けてBが1枚抜くとき,A,Bが抜いた絵札の枚数を,それぞれX,Yとする。XとYの同時分布を求めよ。
100本のくじの中に30本の当たりくじがある。このくじから10本のくじを続けて引くとき,その中の当たりくじの本数をYとする。確率変数Yの期待値を求めよ。ただし,引いたくじはもとに戻さないとする。
【数B】【確率分布と統計的な推測】確率変数の期待値と分散3 ※問題文は概要欄

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
1と書かれたカードが2枚,2と書かれたカードが2枚,4と書かれたカードが1枚,計5枚のカードがある。この中から2枚のカードを取り出し,それらに書かれている数の和をXとするとき,確率変数Xの期待値と分散を求めよ。
この動画を見る
1と書かれたカードが2枚,2と書かれたカードが2枚,4と書かれたカードが1枚,計5枚のカードがある。この中から2枚のカードを取り出し,それらに書かれている数の和をXとするとき,確率変数Xの期待値と分散を求めよ。
【数B】【確率分布と統計的な推測】確率変数の期待値と分散2 ※問題文は概要欄

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
白玉6個と赤玉4個が入っている袋から玉を次の方法で取り出す。白玉の出た回数をXとするとき,Xの期待値と分散をそれぞれ求めよ。
(1)1個ずつ,もとに戻さず2回続けて取り出す。
(2)1個ずつ,2回取り出す。ただし,取り出した玉は毎回もとに戻す。
この動画を見る
白玉6個と赤玉4個が入っている袋から玉を次の方法で取り出す。白玉の出た回数をXとするとき,Xの期待値と分散をそれぞれ求めよ。
(1)1個ずつ,もとに戻さず2回続けて取り出す。
(2)1個ずつ,2回取り出す。ただし,取り出した玉は毎回もとに戻す。
【数B】【確率分布と統計的な推測】確率変数と確率分布 ※問題文は概要欄

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
4枚の硬貨を同時に投げる試行を4回繰り返すとき,2枚が表で2枚が裏となる回数をXとする。P(X=k)(k=0,1,2,3,4)の式を求めよ。
4つの箱があり、その箱に,それぞれ1,2,3,4の番号がつけられている。1,2,3,4の番号がつけられている4枚のカードを1つの箱に1枚ずつ入れるとき,カードの番号と箱の番号が一致したものの個数をXとする。このとき,Xの確率分布と,P(X>2), P(X≦2)を求めよ。
この動画を見る
4枚の硬貨を同時に投げる試行を4回繰り返すとき,2枚が表で2枚が裏となる回数をXとする。P(X=k)(k=0,1,2,3,4)の式を求めよ。
4つの箱があり、その箱に,それぞれ1,2,3,4の番号がつけられている。1,2,3,4の番号がつけられている4枚のカードを1つの箱に1枚ずつ入れるとき,カードの番号と箱の番号が一致したものの個数をXとする。このとき,Xの確率分布と,P(X>2), P(X≦2)を求めよ。
324 コイン投げの結果を度数分布表にまとめる:ばらつきを可視化しよう!
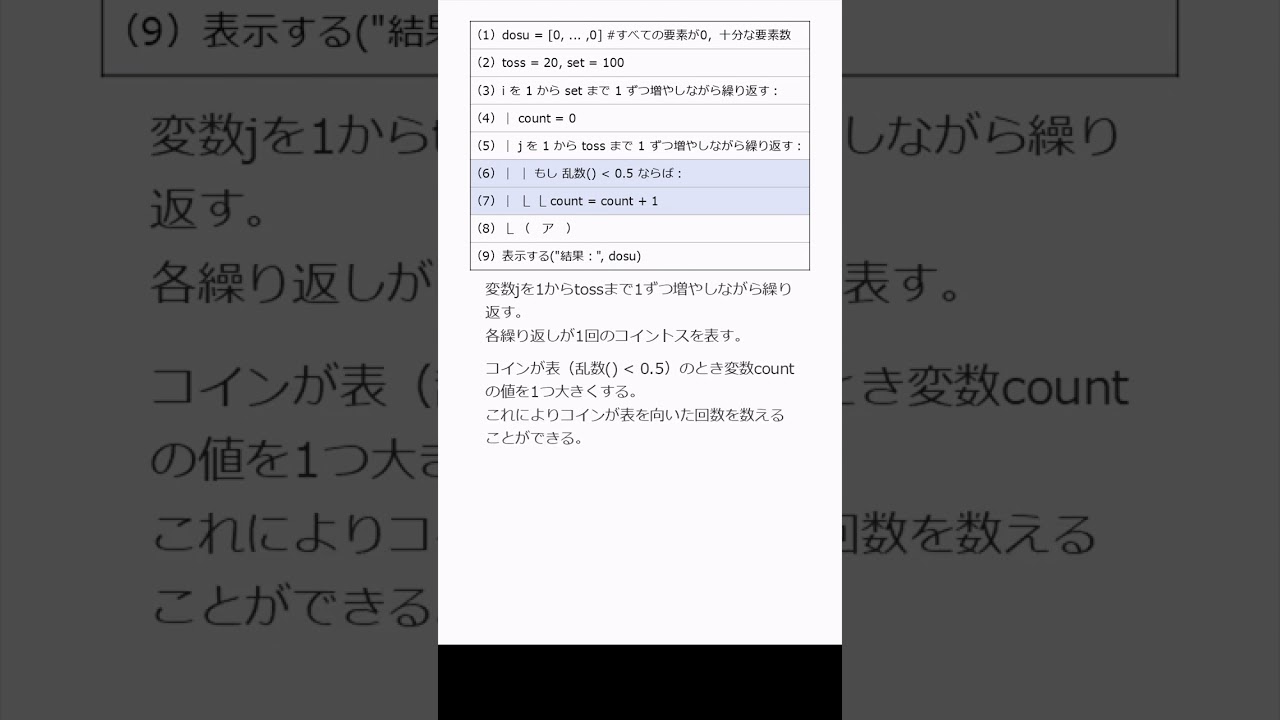
男女比率どうなる?

単元:
#数A#場合の数と確率#確率#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ある国では人々は生まれてくる子には男の子だけを欲しがりました。そのため、どの家庭も男の子を生むまで子供を作り続けました。この国では男の子と女の子の人口比率はどうなりますか?
この動画を見る
ある国では人々は生まれてくる子には男の子だけを欲しがりました。そのため、どの家庭も男の子を生むまで子供を作り続けました。この国では男の子と女の子の人口比率はどうなりますか?
【短時間でポイントチェック!!】aX+bの確率変数の期待値・分散・標準偏差〔現役講師解説、数学〕

【短時間でポイントチェック!!】確率変数の期待値・分散・標準偏差〔現役講師解説、数学〕

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
3rd School
問題文全文(内容文):
1から6までの番号をつけてある6枚のカードがある。
この中から2枚のカードを同時に引くとき、引いたカードの番号の大きい方を$X$とする。
①$X$の期待値を求めよ
②$X$の分散を求めよ
③$X$の標準偏差を求めよ
この動画を見る
1から6までの番号をつけてある6枚のカードがある。
この中から2枚のカードを同時に引くとき、引いたカードの番号の大きい方を$X$とする。
①$X$の期待値を求めよ
②$X$の分散を求めよ
③$X$の標準偏差を求めよ
【統計分野、演習編】データを加えた時の相関係数の変化【数学b】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
3rd School
問題文全文(内容文):
変量$x,y$の値の組
$(-1,-1),(-1,1),(1,-1),(1,1)$をデータ$W$とする。
データ$W$と$x$と$y$の相関係数は0である。
データ$W$に、新たに1個のデータを加えたときの相関係数について調べる。
なお、必要に応じて、以下の表を用いて良い。
$a$を実数とする。
データ$W$の$x$の平均値$\vec{ x }$は(ア)で、$W$の$x$と$y$の共分散の値は(イ)である。
(ア)(イ)を求めよ
この動画を見る
変量$x,y$の値の組
$(-1,-1),(-1,1),(1,-1),(1,1)$をデータ$W$とする。
データ$W$と$x$と$y$の相関係数は0である。
データ$W$に、新たに1個のデータを加えたときの相関係数について調べる。
なお、必要に応じて、以下の表を用いて良い。
$a$を実数とする。
データ$W$の$x$の平均値$\vec{ x }$は(ア)で、$W$の$x$と$y$の共分散の値は(イ)である。
(ア)(イ)を求めよ
【統計分野、演習編】確率密度関数と面積の関係の確認【数学b】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
3rd School
問題文全文(内容文):
確率変数$X$の確率密度関数$f(x)$が次の式で表されるとき、確率$P(0 \leqq x \leqq 2)$を求めよ
$f(x)=\displaystyle \frac{1}{8}x(0 \leqq x \leqq 4)$
この動画を見る
確率変数$X$の確率密度関数$f(x)$が次の式で表されるとき、確率$P(0 \leqq x \leqq 2)$を求めよ
$f(x)=\displaystyle \frac{1}{8}x(0 \leqq x \leqq 4)$
【統計分野】正規分布ってなんだろう?ついて解説しました!【数学b】

【高校数学】正規分布はこれ1本でマスター!統計的な推測 2週間完成【④正規分布】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
・1000人の生徒に数学のテストを行ったところ、その成績は平均48点、標準偏差15点であった。成績が正規分布に従うものとするとき、次の問いに答えよ。
(1) ある生徒の点数が78点以上である確率を求めよ。
(2) 78点以上の生徒は約何人いると考えられるか。
(3) 30点以下の生徒は約何人いると考えられるか。
・ある植物の種子の発芽率は80%であるという。この植物の種子を900個まいたとき、次の問いに答えよ。
(1) 750個以上の種子が発芽する確率を求めよ。
(2) 900個のうちn個以上の種子が発芽する確率が80%以上となるようなnの最大値を求めよ。
この動画を見る
・1000人の生徒に数学のテストを行ったところ、その成績は平均48点、標準偏差15点であった。成績が正規分布に従うものとするとき、次の問いに答えよ。
(1) ある生徒の点数が78点以上である確率を求めよ。
(2) 78点以上の生徒は約何人いると考えられるか。
(3) 30点以下の生徒は約何人いると考えられるか。
・ある植物の種子の発芽率は80%であるという。この植物の種子を900個まいたとき、次の問いに答えよ。
(1) 750個以上の種子が発芽する確率を求めよ。
(2) 900個のうちn個以上の種子が発芽する確率が80%以上となるようなnの最大値を求めよ。
【高校数学】模試に向けて今からでも間に合う!統計的な推測 2週間完成【③二項分布】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
・次の二項分布の平均、分散と標準偏差を求めよ。
$\displaystyle B(5,\frac{1}{6})$
・1個のさいころを8回投げるとき、4以上の目が出る回数をXとする。
(1) 4以上の目が3回以上出る確率を求めよ。
(2) 確率変数Xの期待値と標準偏差を求めよ。
この動画を見る
・次の二項分布の平均、分散と標準偏差を求めよ。
$\displaystyle B(5,\frac{1}{6})$
・1個のさいころを8回投げるとき、4以上の目が出る回数をXとする。
(1) 4以上の目が3回以上出る確率を求めよ。
(2) 確率変数Xの期待値と標準偏差を求めよ。
【高校数学】統計的な推測 2週間完成【②同時分布、確率変数の和の期待値、独立な確率変数】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
・500円硬貨2枚と100円硬貨1枚を同時に投げる。表の出た硬貨の金額の和の期待値を求めよ。
・Aは2枚、Bは3枚の硬貨を同時に投げ、表の出た枚数をそれぞれX,Yとするとき、積XYの期待値を求めよ。
この動画を見る
・500円硬貨2枚と100円硬貨1枚を同時に投げる。表の出た硬貨の金額の和の期待値を求めよ。
・Aは2枚、Bは3枚の硬貨を同時に投げ、表の出た枚数をそれぞれX,Yとするとき、積XYの期待値を求めよ。
【高校数学】模試に向けて今からでも間に合う!統計的な推測 2週間完成【①確率変数と確率分布、期待値、分散、標準偏差、確率変数の変換】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
・3枚の硬貨を同時に投げるとき、表の出る枚数をXとする。確率変数Xの確率分布を求めよ。
・1個のサイコロを1回投げるとき、出る目の数をXとする。Xの期待値、分散、標準偏差を求めよ。
この動画を見る
・3枚の硬貨を同時に投げるとき、表の出る枚数をXとする。確率変数Xの確率分布を求めよ。
・1個のサイコロを1回投げるとき、出る目の数をXとする。Xの期待値、分散、標準偏差を求めよ。
数Bの統計分野はどう勉強していけばいい!?

単元:
#確率分布と統計的な推測#確率分布#統計的な推測#その他#勉強法#数学(高校生)#数B
指導講師:
3rd School
問題文全文(内容文):
数Bの統計分野 今後の勉強法について説明動画です
この動画を見る
数Bの統計分野 今後の勉強法について説明動画です
数学どうにかしたい人へ

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#集合と命題(集合・命題と条件・背理法)#2次方程式と2次不等式#2次関数とグラフ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#データの分析#整数の性質#場合の数#確率#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和(等差・等比・階差・Σ)#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体(オイラーの法則)#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
告白の成功率を上げるには?

福田の数学〜2023年共通テスト速報〜数学IIB第3問確率分布〜正規分布と二項分布

単元:
#大学入試過去問(数学)#確率分布と統計的な推測#確率分布#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト#数B
指導講師:
福田次郎
問題文全文(内容文):
第3問
以下の問題を解答するにあたっては、必要に応じて43ページの正規分布表を用いてもよい。
(1)ある生産地で生産されるピーマン全体を母集団とし、この母集団におけるピーマン1個の重さ(単位はg)を表す確率変数をXとする。mとσを正の実数とし、Xは正規分布N(m, $\sigma^2$)に従うとする。
(i)この母集団から1個のピーマンを無作為に抽出したとき、重さがm g以上である確率P(X≧m)は
P(X≧m)=P$\left(\frac{X-m}{\sigma}\geqq \boxed{\ \ ア\ \ }\right)$=$\frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }}$
である。
(ii)母集団から無作為に抽出された大きさnの標本$X_1$, $X_2$, ..., $X_n$の標本平均を$\bar{X}$とする。$\bar{X}$の平均(期待値)と標準偏差はそれぞれ
E($\bar{X}$)=$\boxed{\boxed{\ \ エ\ \ }}$, σ($\bar{X}$)=$\boxed{\boxed{\ \ オ\ \ }}$
となる。
n=400, 標本平均が30.0g, 標本の標準偏差が3.6gのとき、mの信頼度90%の信頼区間を次の方針で求めよう。
方針:Zを標準正規分布N(0,1)に従う確率変数として、P($-z_0 \leqq Z \leqq z_0$)=0.901 となる$z_0$を正規分布表から求める。この$z_0$を用いるとmの信頼度90.1%の信頼区間が求められるが、これを信頼度90%の信頼区間とみなして考える。
方針において、$z_0$=$\boxed{\ \ カ\ \ }$.$\boxed{\ \ キク\ \ }$である。
一般に、標本の大きさnが大きいときには、母標準偏差の代わりに、標本の標準偏差を用いてよいことが知られている。n=400は十分に大きいので、方針に基づくと、mの信頼度90%の信頼区間は$\boxed{\boxed{\ \ ケ\ \ }}$となる。
$\boxed{\boxed{\ \ エ\ \ }}, \boxed{\boxed{\ \ オ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪σ ①$\sigma^2$ ②$\frac{\sigma}{\sqrt n}$ ③$\frac{\sigma^2}{n}$
④m ⑤2m ⑥$m^2$ ⑦$\sqrt m$
⑧$\frac{\sigma}{n}$ ⑨$n\sigma $ⓐ$nm$ ⓑ$\frac{m}{n}$
$\boxed{\boxed{\ \ ケ\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪28.6≦m≦31.4 ①28.7≦m≦31.3 ②28.9≦m≦31.1
③29.6≦m≦30.4 ④29.7≦m≦30.3 ⑤29.9≦m≦30.1
(2)(1)の確率変数Xにおいて、m=30.0, σ=3.6とした母集団から無作為にピーマンを1個ずつ抽出し、ピーマン2個を1組にしたものを袋に入れていく。このようにしてピーマン2個を1組にしたものを25袋作る。その際、1袋ずつの重さの分数を小さくするために、次のピーマン分類法を考える。
ピーマン分類法:無作為に抽出したいくつかのピーマンについて、重さが30.0g以下のときをSサイズ、30.0gを超えるときはLサイズと分類する。そして、分類されたピーマンからSサイズとLサイズのピーマンを一つずつ選び、ピーマン2個を1組とした袋を作る。
(i)ピーマンを無作為に50個抽出した時、ピーマン分類法で25袋作ることができる確率$p_0$を考えよう。無作為に1個抽出したピーマンがSサイズである確率は$\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。ピーマンを無作為に50個抽出したときのSサイズのピーマンの個数を表す確率変数を$U_0$とすると、$U_0$は二項分布$B\left(50, \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)$に従うので
$p_0$=${}_{50}C_{\boxed{シス}}×\left(\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)^{\boxed{シス}}×\left(1-\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)^{50-\boxed{シス}}$
となる。
$p_0$を計算すると、$p_0$=0.1122...となることから、ピーマンを無作為に50個抽出したとき、25袋作ることができる確率は0.11程度とわかる。
(ii)ピーマン分類法で25袋作ることができる確率が0.95以上となるようなピーマンの個数を考えよう。
kを自然数とし、ピーマンを無作為に(50+k)個抽出したとき、Sサイズのピーマンの個数を表す確率変数を$U_k$とすると、$U_k$は二項分布$B\left(50+k, \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)$に従う。
(50+k)は十分に大きいので、$U_k$は近似的に正規分布$N\left(\boxed{\boxed{\ \ セ\ \ }}, \boxed{\boxed{\ \ ソ\ \ }}\right)$に従い、$Y=\frac{U_k-\boxed{\boxed{\ \ セ\ \ }}}{\sqrt{\boxed{\boxed{\ \ ソ\ \ }}}}$とすると、Yは近似的に標準正規分布N(0,1)に従う。
よって、ピーマン分類法で、25袋作ることができる確率を$p_k$とすると
$p_k$=$P(25 \leqq U_k \leqq 25+k)$=$P\left(-\frac{\boxed{\boxed{\ \ タ\ \ }}}{\sqrt{50+k}} \leqq Y \leqq \frac{\boxed{\boxed{\ \ タ\ \ }}}{\sqrt{50+k}}\right)$
となる。
$\boxed{\boxed{\ \ タ\ \ }}$=a, $\sqrt{50+k}$=$\beta$とおく。
$p_k$≧0.95になるような$\frac{\alpha}{\beta}$について、正規分布表から$\frac{\alpha}{\beta}$≧1.96を満たせばよいことが分かる。ここでは
$\frac{\alpha}{\beta}$≧2 ...①
を満たす自然数kを考えることとする。①の両辺は正であるから、$\alpha^2$≧4$\beta^2$を満たす最小のkを$k_0$とすると、$k_0$=$\boxed{\ \ チツ\ \ }$であることがわかる。ただし、$\boxed{\ \ チツ\ \ }$の計算においては、$\sqrt{51}=7.14$を用いてもよい。
したがって、少なくとも(50+$\boxed{\ \ チツ\ \ }$)個のピーマンを抽出しておけば、ピーマン分類法で25袋作ることができる確率は0.95以上となる。
$\boxed{\boxed{\ \ セ\ \ }}$~$\boxed{\boxed{\ \ タ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪k ①2k ②3k ③$\frac{50+k}{2}$
④$\frac{25+k}{2}$ ⑤25+k ⑥$\frac{\sqrt{50+k}}{2}$ ⑦$\frac{50+k}{4}$
2023共通テスト過去問
この動画を見る
第3問
以下の問題を解答するにあたっては、必要に応じて43ページの正規分布表を用いてもよい。
(1)ある生産地で生産されるピーマン全体を母集団とし、この母集団におけるピーマン1個の重さ(単位はg)を表す確率変数をXとする。mとσを正の実数とし、Xは正規分布N(m, $\sigma^2$)に従うとする。
(i)この母集団から1個のピーマンを無作為に抽出したとき、重さがm g以上である確率P(X≧m)は
P(X≧m)=P$\left(\frac{X-m}{\sigma}\geqq \boxed{\ \ ア\ \ }\right)$=$\frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }}$
である。
(ii)母集団から無作為に抽出された大きさnの標本$X_1$, $X_2$, ..., $X_n$の標本平均を$\bar{X}$とする。$\bar{X}$の平均(期待値)と標準偏差はそれぞれ
E($\bar{X}$)=$\boxed{\boxed{\ \ エ\ \ }}$, σ($\bar{X}$)=$\boxed{\boxed{\ \ オ\ \ }}$
となる。
n=400, 標本平均が30.0g, 標本の標準偏差が3.6gのとき、mの信頼度90%の信頼区間を次の方針で求めよう。
方針:Zを標準正規分布N(0,1)に従う確率変数として、P($-z_0 \leqq Z \leqq z_0$)=0.901 となる$z_0$を正規分布表から求める。この$z_0$を用いるとmの信頼度90.1%の信頼区間が求められるが、これを信頼度90%の信頼区間とみなして考える。
方針において、$z_0$=$\boxed{\ \ カ\ \ }$.$\boxed{\ \ キク\ \ }$である。
一般に、標本の大きさnが大きいときには、母標準偏差の代わりに、標本の標準偏差を用いてよいことが知られている。n=400は十分に大きいので、方針に基づくと、mの信頼度90%の信頼区間は$\boxed{\boxed{\ \ ケ\ \ }}$となる。
$\boxed{\boxed{\ \ エ\ \ }}, \boxed{\boxed{\ \ オ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪σ ①$\sigma^2$ ②$\frac{\sigma}{\sqrt n}$ ③$\frac{\sigma^2}{n}$
④m ⑤2m ⑥$m^2$ ⑦$\sqrt m$
⑧$\frac{\sigma}{n}$ ⑨$n\sigma $ⓐ$nm$ ⓑ$\frac{m}{n}$
$\boxed{\boxed{\ \ ケ\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪28.6≦m≦31.4 ①28.7≦m≦31.3 ②28.9≦m≦31.1
③29.6≦m≦30.4 ④29.7≦m≦30.3 ⑤29.9≦m≦30.1
(2)(1)の確率変数Xにおいて、m=30.0, σ=3.6とした母集団から無作為にピーマンを1個ずつ抽出し、ピーマン2個を1組にしたものを袋に入れていく。このようにしてピーマン2個を1組にしたものを25袋作る。その際、1袋ずつの重さの分数を小さくするために、次のピーマン分類法を考える。
ピーマン分類法:無作為に抽出したいくつかのピーマンについて、重さが30.0g以下のときをSサイズ、30.0gを超えるときはLサイズと分類する。そして、分類されたピーマンからSサイズとLサイズのピーマンを一つずつ選び、ピーマン2個を1組とした袋を作る。
(i)ピーマンを無作為に50個抽出した時、ピーマン分類法で25袋作ることができる確率$p_0$を考えよう。無作為に1個抽出したピーマンがSサイズである確率は$\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。ピーマンを無作為に50個抽出したときのSサイズのピーマンの個数を表す確率変数を$U_0$とすると、$U_0$は二項分布$B\left(50, \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)$に従うので
$p_0$=${}_{50}C_{\boxed{シス}}×\left(\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)^{\boxed{シス}}×\left(1-\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)^{50-\boxed{シス}}$
となる。
$p_0$を計算すると、$p_0$=0.1122...となることから、ピーマンを無作為に50個抽出したとき、25袋作ることができる確率は0.11程度とわかる。
(ii)ピーマン分類法で25袋作ることができる確率が0.95以上となるようなピーマンの個数を考えよう。
kを自然数とし、ピーマンを無作為に(50+k)個抽出したとき、Sサイズのピーマンの個数を表す確率変数を$U_k$とすると、$U_k$は二項分布$B\left(50+k, \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)$に従う。
(50+k)は十分に大きいので、$U_k$は近似的に正規分布$N\left(\boxed{\boxed{\ \ セ\ \ }}, \boxed{\boxed{\ \ ソ\ \ }}\right)$に従い、$Y=\frac{U_k-\boxed{\boxed{\ \ セ\ \ }}}{\sqrt{\boxed{\boxed{\ \ ソ\ \ }}}}$とすると、Yは近似的に標準正規分布N(0,1)に従う。
よって、ピーマン分類法で、25袋作ることができる確率を$p_k$とすると
$p_k$=$P(25 \leqq U_k \leqq 25+k)$=$P\left(-\frac{\boxed{\boxed{\ \ タ\ \ }}}{\sqrt{50+k}} \leqq Y \leqq \frac{\boxed{\boxed{\ \ タ\ \ }}}{\sqrt{50+k}}\right)$
となる。
$\boxed{\boxed{\ \ タ\ \ }}$=a, $\sqrt{50+k}$=$\beta$とおく。
$p_k$≧0.95になるような$\frac{\alpha}{\beta}$について、正規分布表から$\frac{\alpha}{\beta}$≧1.96を満たせばよいことが分かる。ここでは
$\frac{\alpha}{\beta}$≧2 ...①
を満たす自然数kを考えることとする。①の両辺は正であるから、$\alpha^2$≧4$\beta^2$を満たす最小のkを$k_0$とすると、$k_0$=$\boxed{\ \ チツ\ \ }$であることがわかる。ただし、$\boxed{\ \ チツ\ \ }$の計算においては、$\sqrt{51}=7.14$を用いてもよい。
したがって、少なくとも(50+$\boxed{\ \ チツ\ \ }$)個のピーマンを抽出しておけば、ピーマン分類法で25袋作ることができる確率は0.95以上となる。
$\boxed{\boxed{\ \ セ\ \ }}$~$\boxed{\boxed{\ \ タ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪k ①2k ②3k ③$\frac{50+k}{2}$
④$\frac{25+k}{2}$ ⑤25+k ⑥$\frac{\sqrt{50+k}}{2}$ ⑦$\frac{50+k}{4}$
2023共通テスト過去問
はじめしゃちょーの宝くじ710万円購入210万円当選を数学的に考える

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
はじめしゃちょーの宝くじ710万円購入210万円当選を数学的に考えていきます.
この動画を見る
はじめしゃちょーの宝くじ710万円購入210万円当選を数学的に考えていきます.
福田の数学〜上智大学2022年TEAP理系型第3問〜最後の目が得点になる確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#確率分布と統計的な推測#確率分布#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
各頂点に1から4までの数が1つずつ書いてあり、振るとそれらの1つが等し
い確率で得られる正四面体の形のさいころTがある。これを用いて、2人のプレイ
ヤA, B が以下のようなゲームをする。それぞれの枠内に記したルールに従い、各
プレイヤがTを1回以上振って、最後に出た数をそのプレイヤの得点とし、得点の
多い方を勝ちとする。ここで、同点のときには常にBの勝ちとする。また、振り直
すかどうかは、各プレイヤーとも自分が勝つ確率を最大にするように選択するとす
る。このとき、Aが勝つ確率pについて答えよ。ただし、以下のそれぞれの場合に
ついて、pは0以上の整数k, nを用いて$p =\frac{2k+1}{2^n}$と表せるので、このk, nを
答えよ。
(1)$A, B$がそれぞれ1回ずつTを振る
このときpを表すk, nは、$k=\boxed{ケ} ,\ n=\boxed{コ}$である。
(2)先にAが一回振る。次にBが2回まで振ってよい(Aの得点を知っている状
況で、1回振り直してよい)
このときpを表すk,nは、$k=\boxed{サ} ,\ n=\boxed{シ}$である。
(3)先にAが2回まで振ってよい(Bの得点がまだわからない状況で、1回振り直
してよい)。次にBが1回振る。
このときpを表すk,nは、$k=\boxed{ス} ,\ n=\boxed{セ }$である。
(4)先にAが2回まで振ってよい(Bの得点がまだわからない状況で、1回振り直
してよい)。次にBが2回まで振ってよい(Aの得点を知っている状況で、1回
振り直してよい)
このときpを表すk,nは、$k=\boxed{ソ} ,\ n=\boxed{タ}$である。
(5)先にAが3回まで振ってよい(Bの得点がまだわからない状況で、2回まで振
り直してよい)。次にBが2回まで振ってよい(Aの得点を知っている状況で、
1回振り直してよい)
このときpを表すk,nは、$k=\boxed{チ} ,\ n=\boxed{ツ}$である。
2022上智大学理系過去問
この動画を見る
各頂点に1から4までの数が1つずつ書いてあり、振るとそれらの1つが等し
い確率で得られる正四面体の形のさいころTがある。これを用いて、2人のプレイ
ヤA, B が以下のようなゲームをする。それぞれの枠内に記したルールに従い、各
プレイヤがTを1回以上振って、最後に出た数をそのプレイヤの得点とし、得点の
多い方を勝ちとする。ここで、同点のときには常にBの勝ちとする。また、振り直
すかどうかは、各プレイヤーとも自分が勝つ確率を最大にするように選択するとす
る。このとき、Aが勝つ確率pについて答えよ。ただし、以下のそれぞれの場合に
ついて、pは0以上の整数k, nを用いて$p =\frac{2k+1}{2^n}$と表せるので、このk, nを
答えよ。
(1)$A, B$がそれぞれ1回ずつTを振る
このときpを表すk, nは、$k=\boxed{ケ} ,\ n=\boxed{コ}$である。
(2)先にAが一回振る。次にBが2回まで振ってよい(Aの得点を知っている状
況で、1回振り直してよい)
このときpを表すk,nは、$k=\boxed{サ} ,\ n=\boxed{シ}$である。
(3)先にAが2回まで振ってよい(Bの得点がまだわからない状況で、1回振り直
してよい)。次にBが1回振る。
このときpを表すk,nは、$k=\boxed{ス} ,\ n=\boxed{セ }$である。
(4)先にAが2回まで振ってよい(Bの得点がまだわからない状況で、1回振り直
してよい)。次にBが2回まで振ってよい(Aの得点を知っている状況で、1回
振り直してよい)
このときpを表すk,nは、$k=\boxed{ソ} ,\ n=\boxed{タ}$である。
(5)先にAが3回まで振ってよい(Bの得点がまだわからない状況で、2回まで振
り直してよい)。次にBが2回まで振ってよい(Aの得点を知っている状況で、
1回振り直してよい)
このときpを表すk,nは、$k=\boxed{チ} ,\ n=\boxed{ツ}$である。
2022上智大学理系過去問
福田の共通テスト直前演習〜2021年共通テスト数学ⅡB問題3。確率分布、統計の問題。

単元:
#大学入試過去問(数学)#確率分布と統計的な推測#確率分布#統計的な推測#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
(1)A地区で保護されるジャガイモには1個の重さが200gを超えるものが
25%含まれることが経験的にわかっている。花子さんはA地区で収穫された
ジャガイモから400個を無作為に抽出し、重さを計測した。そのうち、重さが
200gを超えるジャガイモの個数を表す確率変数をZとする。このときZは
二項分布B($400,0,\boxed{\ \ アイ\ \ }$)に従うから、Zの平均(期待値)は$\boxed{\ \ ウエオ\ \ }$である。
(2)Zを(1)の確率変数とし、A地区で収穫されたジャガイモ400個からなる標本において
重さが200gを超えていたジャガイモの標本における比率を
$R=\frac{Z}{400}$とする。このとき、Rの標準偏差は$\sigma(R)=\boxed{\ \ カ\ \ }$である。
標本の大きさ400は十分に大きいので、Rは近似的に正規分布
$N(0,\boxed{\ \ アイ\ \ },(\boxed{\ \ カ\ \ })^2)$に従う。
したがって、$P(R \geqq x)=0.0465$となるようなxの値は$\boxed{\ \ キ\ \ }$となる。
ただし、$\boxed{\ \ キ\ \ }$の計算においては$\sqrt3=1.73$とする。
$\boxed{\ \ カ\ \ }$の解答群
⓪$\frac{3}{6400}$ ①$\frac{\sqrt3}{4}$ ②$\frac{\sqrt3}{80}$ ③$\frac{3}{40}$
$\boxed{\ \ キ\ \ }$については、最も適当なものを、次の⓪~③のうちから一つ選べ。
⓪0.209 ①0.251 ②0.286 ③0.395
(3)B地区で収穫され、出荷される予定のジャガイモ1個の重さは100gから
300gの間に分布している。B地区で収穫され、出荷される予定のジャガイモ
1個の重さを表す確率変数をXとするとき、Xは連続型確率変数であり、X
の取り得る値xの範囲は$100 \leqq x \leqq 300$である。
花子さんは、B地区で収穫され、出荷される予定の全てのジャガイモのうち、
重さが200g以上のものの割合を見積もりたいと考えた。そのために花子さんは
Xの確率密度関数f(x)として適当な関数を定め、それを用いて割合を
見積もるという方針を立てた。
B地区で収穫され、出荷される予定のジャガイモから206個を無作為に抽出
したところ、重さの標本平均は180gであった。
図1(※動画参照)はこの標本のヒストグラムである。
花子さんは図1のヒストグラムにおいて、重さxの増加とともに度数がほぼ
一定の割合で減少している傾向に着目し、Xの確率密度関数f(x)として、1次関数
$f(x)=ax+b (100 \leqq x \leqq 300)$
を考えることにした。ただし、$100 \leqq x \leqq 300$の範囲で$f(x) \geqq 0$とする。
このとき、$P(100 \leqq X \leqq 300)=\boxed{\ \ ク\ \ }$であることから
$\boxed{\ \ ケ\ \ }・10^4a+\boxed{\ \ コ\ \ }・10^2b=\boxed{\ \ ク\ \ } \ldots①$
である。
花子さんは、Xの平均(期待値)が重さの標本平均180gと等しくなるように
確率密度関数を定める方法を用いることにした。
連続型確率変数Xの取り得る値xの範囲が$100 \leqq x \leqq 300$で、その
確率密度関数がf(x)のとき、Xの平均(期待値)mは
$m=\int_{100}^{300}xf(x)dx$
で定義される。この定義と花子さんの採用した方法から
$m=\frac{26}{3}・10^5a+4・10^4b=180 \ldots②$
となる。①と②により、確率密度関数は
$f(x)=-\ \boxed{\ \ サ\ \ }・10^{-5}x+\boxed{\ \ シス\ \ }・10^{-3} \ldots③$
と得られる。このようにして得られた③のf(x)は、$100 \leqq x \leqq 300$の範囲で
$f(x) \geqq 0$を満たしており、確かに確率密度関数として適当である。
したがって、この花子さんお方針に基づくと、B地区で収穫され、出荷される
予定の全てのジャガイモのうち、重さが200g以上のものは$\boxed{\ \ セ\ \ }%$
あると見積もることができる。
$\boxed{\ \ セ\ \ }$については、最も適当なものを、次の⓪~③のうちから一つ選べ。
⓪33 ①34 ②35 ③36
2022共通テスト数学過去問
この動画を見る
(1)A地区で保護されるジャガイモには1個の重さが200gを超えるものが
25%含まれることが経験的にわかっている。花子さんはA地区で収穫された
ジャガイモから400個を無作為に抽出し、重さを計測した。そのうち、重さが
200gを超えるジャガイモの個数を表す確率変数をZとする。このときZは
二項分布B($400,0,\boxed{\ \ アイ\ \ }$)に従うから、Zの平均(期待値)は$\boxed{\ \ ウエオ\ \ }$である。
(2)Zを(1)の確率変数とし、A地区で収穫されたジャガイモ400個からなる標本において
重さが200gを超えていたジャガイモの標本における比率を
$R=\frac{Z}{400}$とする。このとき、Rの標準偏差は$\sigma(R)=\boxed{\ \ カ\ \ }$である。
標本の大きさ400は十分に大きいので、Rは近似的に正規分布
$N(0,\boxed{\ \ アイ\ \ },(\boxed{\ \ カ\ \ })^2)$に従う。
したがって、$P(R \geqq x)=0.0465$となるようなxの値は$\boxed{\ \ キ\ \ }$となる。
ただし、$\boxed{\ \ キ\ \ }$の計算においては$\sqrt3=1.73$とする。
$\boxed{\ \ カ\ \ }$の解答群
⓪$\frac{3}{6400}$ ①$\frac{\sqrt3}{4}$ ②$\frac{\sqrt3}{80}$ ③$\frac{3}{40}$
$\boxed{\ \ キ\ \ }$については、最も適当なものを、次の⓪~③のうちから一つ選べ。
⓪0.209 ①0.251 ②0.286 ③0.395
(3)B地区で収穫され、出荷される予定のジャガイモ1個の重さは100gから
300gの間に分布している。B地区で収穫され、出荷される予定のジャガイモ
1個の重さを表す確率変数をXとするとき、Xは連続型確率変数であり、X
の取り得る値xの範囲は$100 \leqq x \leqq 300$である。
花子さんは、B地区で収穫され、出荷される予定の全てのジャガイモのうち、
重さが200g以上のものの割合を見積もりたいと考えた。そのために花子さんは
Xの確率密度関数f(x)として適当な関数を定め、それを用いて割合を
見積もるという方針を立てた。
B地区で収穫され、出荷される予定のジャガイモから206個を無作為に抽出
したところ、重さの標本平均は180gであった。
図1(※動画参照)はこの標本のヒストグラムである。
花子さんは図1のヒストグラムにおいて、重さxの増加とともに度数がほぼ
一定の割合で減少している傾向に着目し、Xの確率密度関数f(x)として、1次関数
$f(x)=ax+b (100 \leqq x \leqq 300)$
を考えることにした。ただし、$100 \leqq x \leqq 300$の範囲で$f(x) \geqq 0$とする。
このとき、$P(100 \leqq X \leqq 300)=\boxed{\ \ ク\ \ }$であることから
$\boxed{\ \ ケ\ \ }・10^4a+\boxed{\ \ コ\ \ }・10^2b=\boxed{\ \ ク\ \ } \ldots①$
である。
花子さんは、Xの平均(期待値)が重さの標本平均180gと等しくなるように
確率密度関数を定める方法を用いることにした。
連続型確率変数Xの取り得る値xの範囲が$100 \leqq x \leqq 300$で、その
確率密度関数がf(x)のとき、Xの平均(期待値)mは
$m=\int_{100}^{300}xf(x)dx$
で定義される。この定義と花子さんの採用した方法から
$m=\frac{26}{3}・10^5a+4・10^4b=180 \ldots②$
となる。①と②により、確率密度関数は
$f(x)=-\ \boxed{\ \ サ\ \ }・10^{-5}x+\boxed{\ \ シス\ \ }・10^{-3} \ldots③$
と得られる。このようにして得られた③のf(x)は、$100 \leqq x \leqq 300$の範囲で
$f(x) \geqq 0$を満たしており、確かに確率密度関数として適当である。
したがって、この花子さんお方針に基づくと、B地区で収穫され、出荷される
予定の全てのジャガイモのうち、重さが200g以上のものは$\boxed{\ \ セ\ \ }%$
あると見積もることができる。
$\boxed{\ \ セ\ \ }$については、最も適当なものを、次の⓪~③のうちから一つ選べ。
⓪33 ①34 ②35 ③36
2022共通テスト数学過去問
【数B】確率分布:母平均の推定、信頼区間とは??

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
母平均の推定、標準化と信頼度の関係は??信頼区間の公式までを説明します!
この動画を見る
母平均の推定、標準化と信頼度の関係は??信頼区間の公式までを説明します!
【数B】確率分布:正規分布表を用いて確率を求めよう!~標本平均編(実際に計算してみよう)

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある生物の体長が$N(50,3^2)$に従っている。このとき、大きさ4の標本の標本平均をYとし、$P(Y\geqq 53)$を求めよ。
この動画を見る
ある生物の体長が$N(50,3^2)$に従っている。このとき、大きさ4の標本の標本平均をYとし、$P(Y\geqq 53)$を求めよ。
【数B】確率分布:正規分布表を用いて確率を求めよう!~標本平均編(何で大きさが大切なの?)

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
母集団から大きさ4の標本を取り出すとき、何で標準偏差は$\sqrt4$で割るのか?
問題(青チャートより抜粋)ある生物の体長が$N(50,3^2)$の正規分布に従っている。
(1)$P(47\leqq X\leqq 56)$
(2)大きさ4の標本を取り出し標本平均を$\var(X)$とするとき、$P(\var(x)\geqq 53)$
この動画を見る
母集団から大きさ4の標本を取り出すとき、何で標準偏差は$\sqrt4$で割るのか?
問題(青チャートより抜粋)ある生物の体長が$N(50,3^2)$の正規分布に従っている。
(1)$P(47\leqq X\leqq 56)$
(2)大きさ4の標本を取り出し標本平均を$\var(X)$とするとき、$P(\var(x)\geqq 53)$
【数B】正規分布表を用いて確率を求めよう!~標準化の計算

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題(青チャートより抜粋)ある生物の体長が$N(50,3^2)$の正規分布に従っている。
(1)$P(47\leqq X\leqq 56)$
この動画を見る
問題(青チャートより抜粋)ある生物の体長が$N(50,3^2)$の正規分布に従っている。
(1)$P(47\leqq X\leqq 56)$
【数B】確率分布と統計的推測:正規分布ー標準化の置き方とは?

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
データ数が多いものは疑似的に正規分布に直すことが出来る。正規分布→標準正規分布に直す計算とは?またその逆も解説します!
この動画を見る
データ数が多いものは疑似的に正規分布に直すことが出来る。正規分布→標準正規分布に直す計算とは?またその逆も解説します!
