 数B
数B
 数B
数B
東京電機大 複素数のべき乗

単元:
#複素数と方程式#複素数#指数関数#数列
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(1+2i)^n=x_n+y_ni$
(1)$x^2_n+y^2_n$を求めよ.
(2)$x_{n+2}$を$x_{n+1}$と$x_n$で表せ.
(3)$x_n$と$y_n$の最大公約数を求めよ.
東京電機大過去問
この動画を見る
$(1+2i)^n=x_n+y_ni$
(1)$x^2_n+y^2_n$を求めよ.
(2)$x_{n+2}$を$x_{n+1}$と$x_n$で表せ.
(3)$x_n$と$y_n$の最大公約数を求めよ.
東京電機大過去問
福田の数学〜神戸大学2022年理系第1問〜3項間の漸化式と極限

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数列$\left\{a_n\right\}$を$a_1=1,a_2=2,a_{n+2}=\sqrt{a_{n+1}・a_n} (n=1,2,3,\ldots)$によって定める。
以下の問いに答えよ。
(1)全ての自然数$n$について$a_{n+1}=\frac{2}{\sqrt{a_n}}$が成り立つことを示せ。
(2)数列$\left\{b_n\right\}$を$b_n=\log a_n (n=1,2,3,\ldots)$によって定める。
$b_n$の値を$n$を用いて表せ。
(3)極限値$\lim_{n \to \infty}a_n$を求めよ。
2022神戸大学理系過去問
この動画を見る
数列$\left\{a_n\right\}$を$a_1=1,a_2=2,a_{n+2}=\sqrt{a_{n+1}・a_n} (n=1,2,3,\ldots)$によって定める。
以下の問いに答えよ。
(1)全ての自然数$n$について$a_{n+1}=\frac{2}{\sqrt{a_n}}$が成り立つことを示せ。
(2)数列$\left\{b_n\right\}$を$b_n=\log a_n (n=1,2,3,\ldots)$によって定める。
$b_n$の値を$n$を用いて表せ。
(3)極限値$\lim_{n \to \infty}a_n$を求めよ。
2022神戸大学理系過去問
あれですよ、あれ

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \dfrac{3}{1!+2!+3!}+ \dfrac{4}{2!+3!+4!}+\dfrac{5}{3!+4!+5!}+$
$・・・・・・+\dfrac{2022}{2020!+2021!+2022!}$
これを解け.
この動画を見る
$ \dfrac{3}{1!+2!+3!}+ \dfrac{4}{2!+3!+4!}+\dfrac{5}{3!+4!+5!}+$
$・・・・・・+\dfrac{2022}{2020!+2021!+2022!}$
これを解け.
あれですよ、あれ

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\dfrac{3}{1!+2!+3!}+\dfrac{4}{2!+3!+4!}+\dfrac{5}{3!+4!+5!}+・・・・・・+\dfrac{2022}{2020!+2021!+2022!}$
この動画を見る
これを解け.
$\dfrac{3}{1!+2!+3!}+\dfrac{4}{2!+3!+4!}+\dfrac{5}{3!+4!+5!}+・・・・・・+\dfrac{2022}{2020!+2021!+2022!}$
cos1°は有理数か【数学 入試問題】【チェビシェフ多項式】

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#集合と命題(集合・命題と条件・背理法)#三角関数#加法定理とその応用#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数B
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(1)$n$を自然数とする。
$cos(n+2)\theta+cos n\theta=2cos(n+1)\theta cos\theta$を示せ。
(2)自然数$n$に対し、$cosn\theta=T_n(cos\theta)$を満たす整数係数の$n$次の整式$T_n(x)$が存在することを示せ。
(3)$cos1°$が無理数であることを証明せよ。
数学入試問題過去問
この動画を見る
(1)$n$を自然数とする。
$cos(n+2)\theta+cos n\theta=2cos(n+1)\theta cos\theta$を示せ。
(2)自然数$n$に対し、$cosn\theta=T_n(cos\theta)$を満たす整数係数の$n$次の整式$T_n(x)$が存在することを示せ。
(3)$cos1°$が無理数であることを証明せよ。
数学入試問題過去問
福田の数学〜大阪大学2022年理系第4問〜漸化式とはさみうちの原理

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#関数の極限#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=\log(x+1)+1$とする。以下の問いに答えよ。
(1)方程式$f(x)=x$は、$x \gt 0$の範囲でただ1つの解を
もつことを示せ。
(2)(1)の解を$\alpha$とする。実数$x$が$0 \lt x \lt \alpha$を満たすならば、
次の不等式が成り立つことを示せ。
$0 \lt \frac{\alpha-f(x)}{\alpha-x} \lt f'(x)$
(3)数列$\left\{x_n\right\}$を
$x_1=1, x_{n+1}=f(x_n) (n=1,2,3,\ldots\ldots)$
で定める。このとき、全ての自然数nに対して
$\alpha -x_{n+1} \lt \frac{1}{2}(\alpha -x_n)$
が成り立つことを示せ。
(4)(3)の数列$\left\{x_n\right\}$について、$\lim_{n \to \infty}x_n=\alpha$を示せ。
2022大阪大学理系過去問
この動画を見る
$f(x)=\log(x+1)+1$とする。以下の問いに答えよ。
(1)方程式$f(x)=x$は、$x \gt 0$の範囲でただ1つの解を
もつことを示せ。
(2)(1)の解を$\alpha$とする。実数$x$が$0 \lt x \lt \alpha$を満たすならば、
次の不等式が成り立つことを示せ。
$0 \lt \frac{\alpha-f(x)}{\alpha-x} \lt f'(x)$
(3)数列$\left\{x_n\right\}$を
$x_1=1, x_{n+1}=f(x_n) (n=1,2,3,\ldots\ldots)$
で定める。このとき、全ての自然数nに対して
$\alpha -x_{n+1} \lt \frac{1}{2}(\alpha -x_n)$
が成り立つことを示せ。
(4)(3)の数列$\left\{x_n\right\}$について、$\lim_{n \to \infty}x_n=\alpha$を示せ。
2022大阪大学理系過去問
福田の数学〜一橋大学2022年文系第5問〜確率漸化式

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
中身の見えない2つの箱があり、1つの箱には赤玉2つと白玉1つが入っており、
もう1つの箱には赤玉1つと白玉2つが入っている。どちらかの箱を選び、選んだ
箱の中から玉を1つ取り出して元に戻す、という操作を繰り返す。
(1) 1回目は箱を無作為に選び、2回目以降は、前回取り出した玉が赤玉なら前回
と同じ箱、前回取り出した玉が白玉なら前回とは異なる箱を選ぶ。n回目に赤玉
を取り出す確率$p_n$を求めよ。
(2)1回目は箱を無作為に選び、2回目以降は、前回取り出した玉が赤玉なら前回
と同じ箱、前回取り出した玉が白玉なら箱を無作為に選ぶ。n回目に赤玉を取り
出す確率 $q_n$を求めよ。
2022一橋大学文系過去問
この動画を見る
中身の見えない2つの箱があり、1つの箱には赤玉2つと白玉1つが入っており、
もう1つの箱には赤玉1つと白玉2つが入っている。どちらかの箱を選び、選んだ
箱の中から玉を1つ取り出して元に戻す、という操作を繰り返す。
(1) 1回目は箱を無作為に選び、2回目以降は、前回取り出した玉が赤玉なら前回
と同じ箱、前回取り出した玉が白玉なら前回とは異なる箱を選ぶ。n回目に赤玉
を取り出す確率$p_n$を求めよ。
(2)1回目は箱を無作為に選び、2回目以降は、前回取り出した玉が赤玉なら前回
と同じ箱、前回取り出した玉が白玉なら箱を無作為に選ぶ。n回目に赤玉を取り
出す確率 $q_n$を求めよ。
2022一橋大学文系過去問
これの説明できますか?

二項定理を使ってあることに気付ける?【2017年一橋大学】

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#式の計算(整式・展開・因数分解)#恒等式・等式・不等式の証明#数列#漸化式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数B
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ P(0)=1,P(x+1)-P(x)=2x$を満たす整式$P(x)$を求めよ。
2017一橋大過去問
この動画を見る
$ P(0)=1,P(x+1)-P(x)=2x$を満たす整式$P(x)$を求めよ。
2017一橋大過去問
これ説明できる?

【概要欄に問題掲載】大学入試問題#167 岡山県立大学2020 数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$S_n=2a_n-n^2$のとき
一般項$a_n$を求めよ。
出典:2020年岡山県立大学 入試問題
この動画を見る
$S_n=2a_n-n^2$のとき
一般項$a_n$を求めよ。
出典:2020年岡山県立大学 入試問題
!
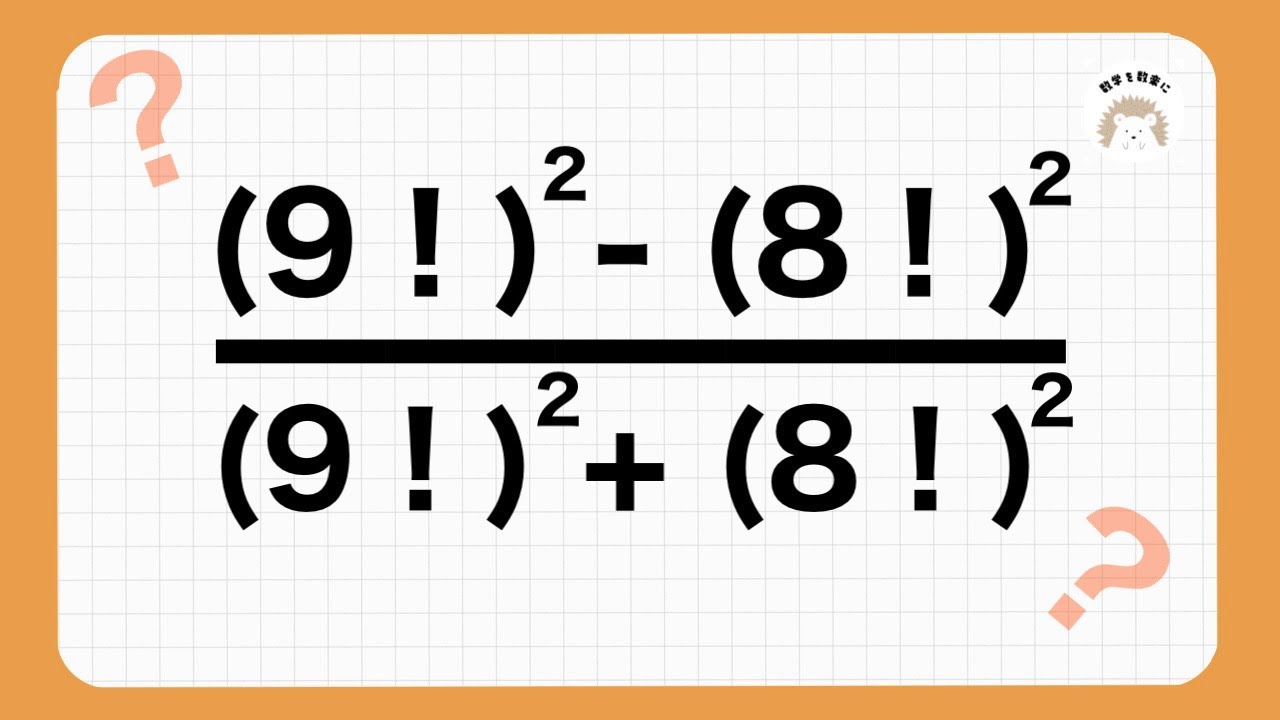
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{(9!)^2 - (8!)^2} {(9!)^2 + (8!)^2} $
この動画を見る
$\frac{(9!)^2 - (8!)^2} {(9!)^2 + (8!)^2} $
20和歌山県教員採用試験 数列、整数問題

単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{15}{8},\displaystyle \frac{165}{11},\displaystyle \frac{315}{14},\displaystyle \frac{465}{17},・・・$の一般項$a_n$が自然数となるもののうち最大となるときの$n$を求めよ。
出典:2020年教育採用試験和歌山
この動画を見る
$\displaystyle \frac{15}{8},\displaystyle \frac{165}{11},\displaystyle \frac{315}{14},\displaystyle \frac{465}{17},・・・$の一般項$a_n$が自然数となるもののうち最大となるときの$n$を求めよ。
出典:2020年教育採用試験和歌山
❗️

福田の入試問題解説〜北海道大学2022年文系第2問〜数列の一般項の最小と部分和の最小

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数B
指導講師:
福田次郎
問題文全文(内容文):
$\left\{a_n\right\}$を$a_1=-15$および
$a_{n+1}=a_n+\frac{n}{5}-2 (n=1,2,3,\ldots)$
を満たす数列とする。
(1)$a_n$が最小となる自然数nを全て求めよ。
(2)$\left\{a_n\right\}$の一般項を求めよ。
(3)$\sum_{k=1}^na_k$が最小となる自然数nを全て求めよ。
2022北海道大学文系過去問
この動画を見る
$\left\{a_n\right\}$を$a_1=-15$および
$a_{n+1}=a_n+\frac{n}{5}-2 (n=1,2,3,\ldots)$
を満たす数列とする。
(1)$a_n$が最小となる自然数nを全て求めよ。
(2)$\left\{a_n\right\}$の一般項を求めよ。
(3)$\sum_{k=1}^na_k$が最小となる自然数nを全て求めよ。
2022北海道大学文系過去問
階乗に関する問題 巣鴨高校(改)

単元:
#数学(中学生)#数列#数列とその和(等差・等比・階差・Σ)#高校入試過去問(数学)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$1!+2!+3!+4!+5!+\cdots +18!+19!+20!$
を計算した結果の下2ケタを求めよ。
巣鴨高等学校(改)
この動画を見る
$1!+2!+3!+4!+5!+\cdots +18!+19!+20!$
を計算した結果の下2ケタを求めよ。
巣鴨高等学校(改)
ざ・見掛け倒し

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \sum_{n=1}^{2022}n^{2022}=$
$1^{2022}+2^{2022}+3^{2022}+$
$・・・・・・+2021^{2022}+2022^{2022}$を13で割った余りを求めよ.
この動画を見る
$\displaystyle \sum_{n=1}^{2022}n^{2022}=$
$1^{2022}+2^{2022}+3^{2022}+$
$・・・・・・+2021^{2022}+2022^{2022}$を13で割った余りを求めよ.
福田の数学〜京都大学2022年文系第2問〜条件を満たす経路の総数と漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
下図(※動画参照)の三角柱ABC-DEFにおいて、Aを始点として、辺に沿って
頂点をn回移動する。すなわち、この移動経路
$P_0 \to P_1 \to P_2 \to \ldots \to P_{n-1} \to P_n$ (ただし$P_0=A$)
において、$P_0P_1,P_1P_2,\ldots,P_{n-1}P_n$は全て辺であるとする。
また、同じ頂点を何度通ってよいものとする。このような移動経路で、終点$P_n$がA,B,Cの
いずれかとなるものの総数$a_n$を求めよ。
2022京都大学文系過去問
この動画を見る
下図(※動画参照)の三角柱ABC-DEFにおいて、Aを始点として、辺に沿って
頂点をn回移動する。すなわち、この移動経路
$P_0 \to P_1 \to P_2 \to \ldots \to P_{n-1} \to P_n$ (ただし$P_0=A$)
において、$P_0P_1,P_1P_2,\ldots,P_{n-1}P_n$は全て辺であるとする。
また、同じ頂点を何度通ってよいものとする。このような移動経路で、終点$P_n$がA,B,Cの
いずれかとなるものの総数$a_n$を求めよ。
2022京都大学文系過去問
【高校数学】シグマの例題演習~文字の扱いが難しい~ 3-8.5【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$$1,1+2,1+2+3,\cdots,1+2+3+\cdots+n,\cdots$$
となる数列の初項から第k項までの 総和を求めなさい。
この動画を見る
$$1,1+2,1+2+3,\cdots,1+2+3+\cdots+n,\cdots$$
となる数列の初項から第k項までの 総和を求めなさい。
東京大2022理系

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
数列{$a_n$}を次のように定める。
$a_1=1$ , $a_{n+1}={a_n}^2+1(n=1,2,3\cdots)$
(1)正の整数nが3の倍数のとき$a_n$は5の倍数となることを示せ。
(2)$a_n$が$a_k$の倍数となる必要十分条件をk,nを用いて示せ。(k,n:正の整数)
(3)$a_{2022}$と$(a_{8091})^2$の最大公約数を求めよ。
2022東京大学理系
この動画を見る
数列{$a_n$}を次のように定める。
$a_1=1$ , $a_{n+1}={a_n}^2+1(n=1,2,3\cdots)$
(1)正の整数nが3の倍数のとき$a_n$は5の倍数となることを示せ。
(2)$a_n$が$a_k$の倍数となる必要十分条件をk,nを用いて示せ。(k,n:正の整数)
(3)$a_{2022}$と$(a_{8091})^2$の最大公約数を求めよ。
2022東京大学理系
福田の入試問題解説〜東京大学2022年文系第3問〜漸化式と最大公約数

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師:
問題文全文(内容文):
数列$\left\{a_n\right\}$を次のように定める。
$a_1=4, a_{n+1}=a_n^2+n(n+2)$
(1)$a_{2022}$を3で割った余りを求めよ。
(2)$a_{2022},a_{2023},a_{2024}$の最大公約数を求めよ。
2022東京大学文系過去問
この動画を見る
数列$\left\{a_n\right\}$を次のように定める。
$a_1=4, a_{n+1}=a_n^2+n(n+2)$
(1)$a_{2022}$を3で割った余りを求めよ。
(2)$a_{2022},a_{2023},a_{2024}$の最大公約数を求めよ。
2022東京大学文系過去問
一橋大 漸化式
単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#漸化式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
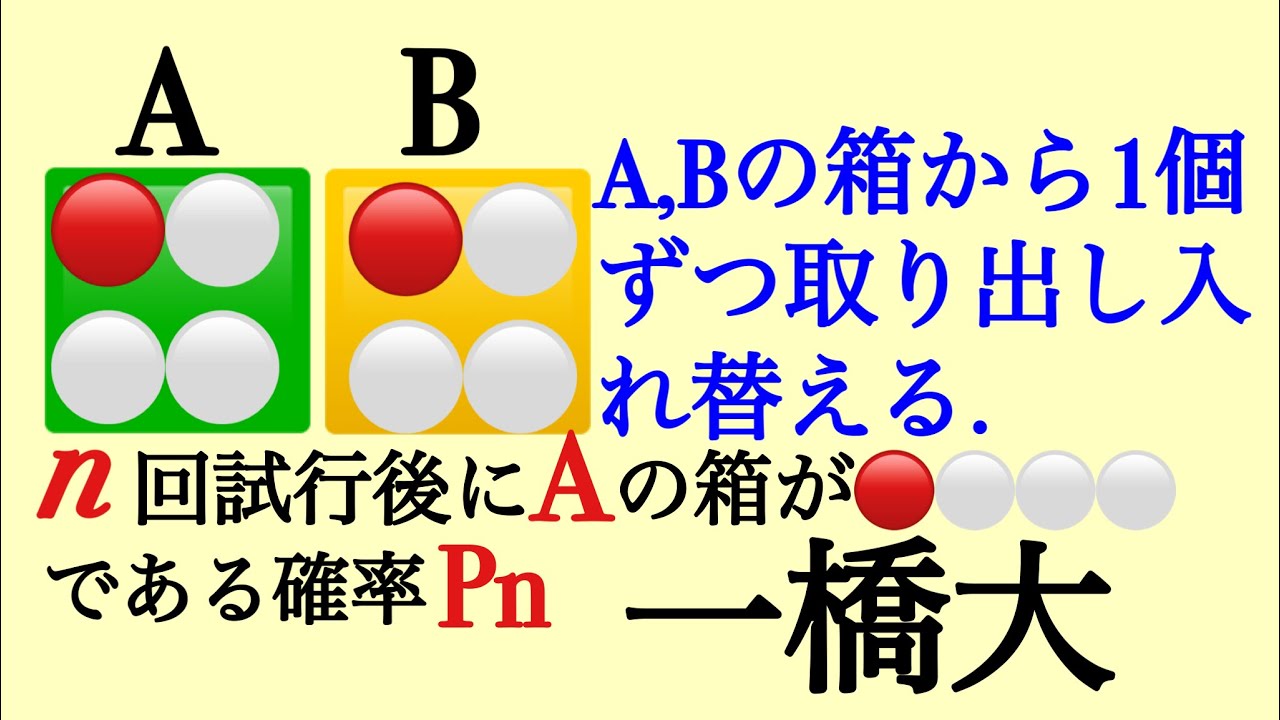
同時に1個ずつ取り出して入れかえる.
n回後にAがA,Bである確率を求めよ.
2022一橋大過去問
この動画を見る
同時に1個ずつ取り出して入れかえる.
n回後にAがA,Bである確率を求めよ.
2022一橋大過去問
大学入試問題#141 島根大学(2020) 数列
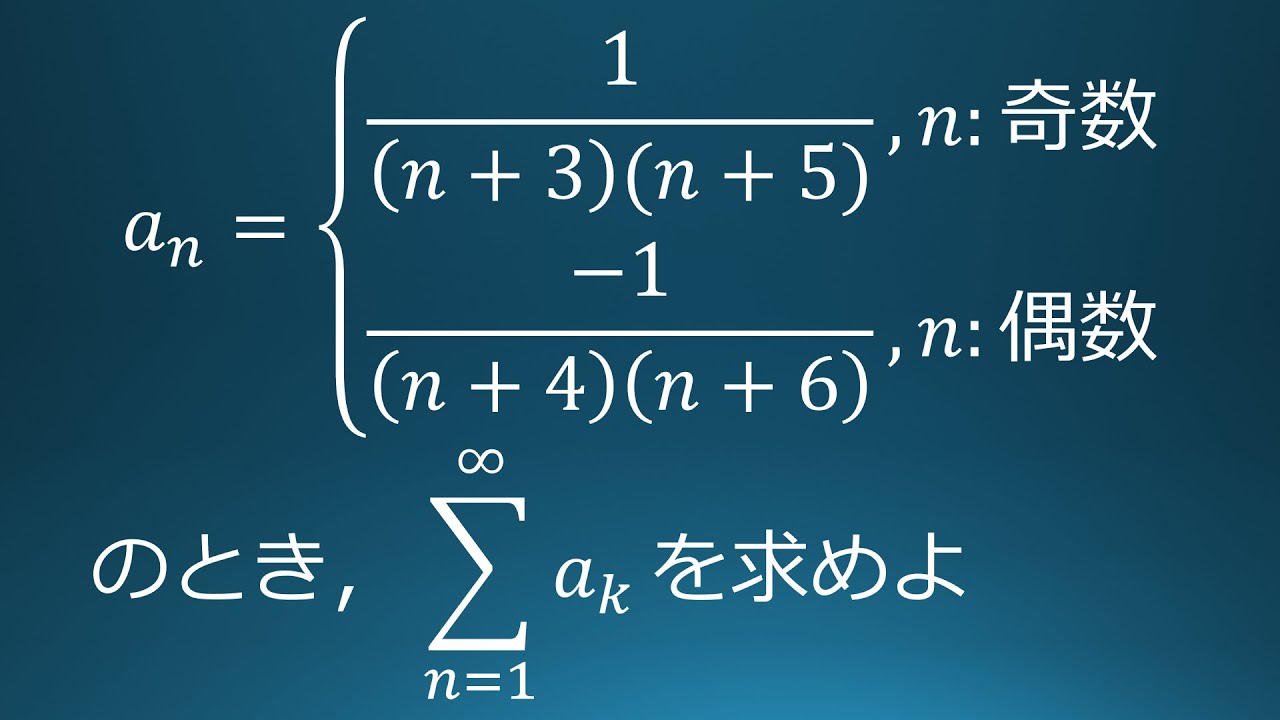
単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#島根大学#数B
指導講師:
ますただ
問題文全文(内容文):
$a_n=\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{1}{(n+3)(n+5))},n:奇数 \\
\displaystyle \frac{1}{(n+4)(n+6)},n:偶数
\end{array}
\right.
\end{eqnarray}$
$\displaystyle \sum_{n=1}^{\infty}a_k$を求めよ。
出典:2020年島根大学 入試問題
この動画を見る
$a_n=\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{1}{(n+3)(n+5))},n:奇数 \\
\displaystyle \frac{1}{(n+4)(n+6)},n:偶数
\end{array}
\right.
\end{eqnarray}$
$\displaystyle \sum_{n=1}^{\infty}a_k$を求めよ。
出典:2020年島根大学 入試問題
【高校数学】計算のテクニック~シグマの例題演習~ 3-8.5【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
次の和を求めよ。
$$1^{ 2 }・2+2^{ 2 }・3+3^{ 2 }・4+\cdots+n^{ 2 }・(n+1)$$
この動画を見る
次の和を求めよ。
$$1^{ 2 }・2+2^{ 2 }・3+3^{ 2 }・4+\cdots+n^{ 2 }・(n+1)$$
どっかの都道府県の教採の問題 数列 個人的に数列では過去一の難問
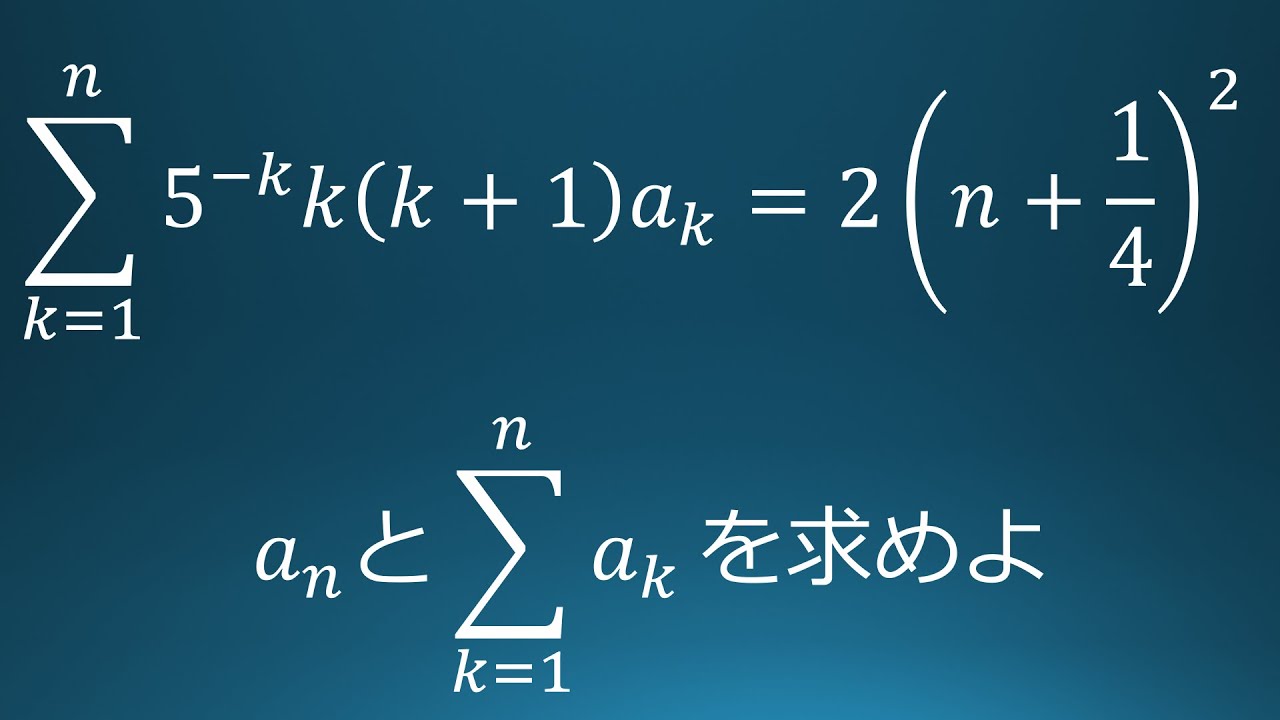
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \sum_{k=1}^n5^{-k}k(k+1)a_k=2(n+\displaystyle \frac{1}{4})^2$
(1)$a_n$を求めよ。
(2)$\displaystyle \sum_{k=1}^na_k$を求めよ。
この動画を見る
$\displaystyle \sum_{k=1}^n5^{-k}k(k+1)a_k=2(n+\displaystyle \frac{1}{4})^2$
(1)$a_n$を求めよ。
(2)$\displaystyle \sum_{k=1}^na_k$を求めよ。
福田の数学〜京都大学2022年理系第6問〜漸化式の解法

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列$\left\{x_n\right\}, \left\{y_n\right\}$を次の式
$x_1=0, x_{n+1}=x_n+n+2\cos\frac{2\pi x_n}{3} (n=1,2,3,\ldots)$
$y_{3m+1}=3m, y_{3m+2}=3m+2, y_{3m+3}=3m+4 (m=0,1,2,3,\ldots)$
により定める。このとき、数列$\left\{x_n-y_n\right\}$の一般項を求めよ。
2022京都大学理系過去問
この動画を見る
数列$\left\{x_n\right\}, \left\{y_n\right\}$を次の式
$x_1=0, x_{n+1}=x_n+n+2\cos\frac{2\pi x_n}{3} (n=1,2,3,\ldots)$
$y_{3m+1}=3m, y_{3m+2}=3m+2, y_{3m+3}=3m+4 (m=0,1,2,3,\ldots)$
により定める。このとき、数列$\left\{x_n-y_n\right\}$の一般項を求めよ。
2022京都大学理系過去問
福田の入試問題解説〜北海道大学2022年理系第2問〜ベクトルと漸化式

単元:
#大学入試過去問(数学)#平面上のベクトル#数列#平面上のベクトルと内積#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
aは$a\neq 1$を満たす正の実数とする。xy平面上の点$P_1,P_2,\ldots\ldots,P_n,\ldots\ldots$および
$Q_1,Q_2,\ldots\ldots,Q_n,\ldots\ldots$が、すべての自然数nについて
$\overrightarrow{ P_nP_{n+1} }=(1-a)\overrightarrow{ P_nQ_n }, \overrightarrow{ Q_nQ_{n+1} }=(0, \frac{a^{-n}}{1-a})$
を満たしているとする。また$P_n$の座標を$(x_n,y_n)$とする。
(1)$x_{n+2}$を$a, x_n, x_{n+1}$で表せ。
(2)$x_1=0, x_2=1$のとき、数列$\left\{x_n\right\}$の一般項を求めよ。
(3)$y_1=\frac{a}{(1-a)^2}, y_2-y_1=1$のとき数列$\left\{y_n\right\}$の一般項を求めよ。
2022北海道大学理系過去問
この動画を見る
aは$a\neq 1$を満たす正の実数とする。xy平面上の点$P_1,P_2,\ldots\ldots,P_n,\ldots\ldots$および
$Q_1,Q_2,\ldots\ldots,Q_n,\ldots\ldots$が、すべての自然数nについて
$\overrightarrow{ P_nP_{n+1} }=(1-a)\overrightarrow{ P_nQ_n }, \overrightarrow{ Q_nQ_{n+1} }=(0, \frac{a^{-n}}{1-a})$
を満たしているとする。また$P_n$の座標を$(x_n,y_n)$とする。
(1)$x_{n+2}$を$a, x_n, x_{n+1}$で表せ。
(2)$x_1=0, x_2=1$のとき、数列$\left\{x_n\right\}$の一般項を求めよ。
(3)$y_1=\frac{a}{(1-a)^2}, y_2-y_1=1$のとき数列$\left\{y_n\right\}$の一般項を求めよ。
2022北海道大学理系過去問
福田の数学〜慶應義塾大学2022年薬学部第2問〜二項定理と数列の部分和

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列$\left\{a_n\right\}$の初項から第n項までの和$S_n$、数列$\left\{b_n\right\}$の初項から第n項までの和$T_n$
はそれぞれ
$S_n=\sum_{k=1}^n {}_n \mathrm{ C }_k, T_n=\sum_{k=1}^n k・{}_n \mathrm{ C }_k$
で表される。
(1)$x \gt y \geqq 1$を満たす自然数x,yについて、
${}_x \mathrm{ C }_y={}_{x-1} \mathrm{ C }_y+{}_i \mathrm{ C }_j, y・{}_x \mathrm{ C }_y=x・{}_p \mathrm{ C }_q,$
が成り立つ。i,j,p,qをそれぞれx,yを用いて表すと、$i=\boxed{\ \ ス\ \ },j=\boxed{\ \ セ\ \ },$
$p=\boxed{\ \ ソ\ \ },q=\boxed{\ \ タ\ \ }$である。
(2)$a_2,b_4$の値をそれぞれ求めると$a_2=\boxed{\ \ チ\ \ },b_4=\boxed{\ \ ツ\ \ }$である。
(3)$S_n,a_n$をそれぞれnの式で表すと、$S_n=\boxed{\ \ テ\ \ },a_n=\boxed{\ \ ト\ \ }$である。
(4)$b_n$をnの式で表すと、$b_n=\boxed{\ \ ナ\ \ }$である。
2022慶應義塾大学薬学部過去問
この動画を見る
数列$\left\{a_n\right\}$の初項から第n項までの和$S_n$、数列$\left\{b_n\right\}$の初項から第n項までの和$T_n$
はそれぞれ
$S_n=\sum_{k=1}^n {}_n \mathrm{ C }_k, T_n=\sum_{k=1}^n k・{}_n \mathrm{ C }_k$
で表される。
(1)$x \gt y \geqq 1$を満たす自然数x,yについて、
${}_x \mathrm{ C }_y={}_{x-1} \mathrm{ C }_y+{}_i \mathrm{ C }_j, y・{}_x \mathrm{ C }_y=x・{}_p \mathrm{ C }_q,$
が成り立つ。i,j,p,qをそれぞれx,yを用いて表すと、$i=\boxed{\ \ ス\ \ },j=\boxed{\ \ セ\ \ },$
$p=\boxed{\ \ ソ\ \ },q=\boxed{\ \ タ\ \ }$である。
(2)$a_2,b_4$の値をそれぞれ求めると$a_2=\boxed{\ \ チ\ \ },b_4=\boxed{\ \ ツ\ \ }$である。
(3)$S_n,a_n$をそれぞれnの式で表すと、$S_n=\boxed{\ \ テ\ \ },a_n=\boxed{\ \ ト\ \ }$である。
(4)$b_n$をnの式で表すと、$b_n=\boxed{\ \ ナ\ \ }$である。
2022慶應義塾大学薬学部過去問
例の“あれ”を使うだけの問題

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ f(n)=\dfrac{1}{2^n}+\dfrac{1}{3^n}+\dfrac{1}{4^n}+…+\dfrac{1}{2022^n}$
$ \displaystyle \sum_{n=2}^{\infty}f(n)=?$これを解け.
この動画を見る
$ f(n)=\dfrac{1}{2^n}+\dfrac{1}{3^n}+\dfrac{1}{4^n}+…+\dfrac{1}{2022^n}$
$ \displaystyle \sum_{n=2}^{\infty}f(n)=?$これを解け.
2022都立入試 整数問題証明(11の倍数)

単元:
#数学(中学生)#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#数列#数列とその和(等差・等比・階差・Σ)#高校入試過去問(数学)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
2022都立入試 整数問題証明に関して解説していきます.
この動画を見る
2022都立入試 整数問題証明に関して解説していきます.
