 数B
数B
 数B
数B
福田の数学〜慶應義塾大学2021年商学部第4問〜数列の文章題

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$座標平面上でx座標とy座標がいずれも整数である点を格子点と呼ぶ。それぞれ
の正の整数nについて、4つの格子点$A_n(n,n),\ B_n(-n,n),\ C_n(-n,-n),\ D_n(n,-n)$
が作る正方形をJ_nとする。また、$(n-1,n)$にある格子点を$P_n$とする。
$\left\{a_k\right\}$を初項$a_1$が$-56$で、交差が$\frac{1}{4}$の等差数列とし、数列$\left\{a_k\right\}$の各項を以下の
ようにして格子点上順番に割り当てていく。
1.初項$a_1$は格子点$P_1$に割り当てる。
2.$a_l$が正方形$J_m$の周上にある格子点で$A_m$以外の点に割り当てられているときには、
$J_m$の周上でその点から半時計回り(右図(※動画参照)での矢印が示す方向)に一つ移動
した格子点に$a_{l+1}$を割り当てる。
3$.a_l$が格子点$A_m$に割り当てられているときには、$a_{l+1}$を格子点$P_{m+1}$に割り当てる。
全体としては、図に示されているようにして、格子点をたどっていくことになる。
(1)格子点$P_n$に割り当てられる数列$\left\{a_k\right\}$の項を$p_n$とし、格子点$C_n$に割り当て
られる数列$\left\{a_k\right\}$の項を$c_n$とする。
このとき、$p_4=-\boxed{\ \ アイ\ \ }, c_4=-\frac{\boxed{\ \ ウエオ\ \ }}{\boxed{\ \ カ\ \ }}$である。
(2)上で定めた$p_n$を用いて、$q_n$を数列$\left\{p_n\right\}$の初項$p_1$から第n項$p_n$までの和とする。
$q_n$をnを使って表すと、$q_n=\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}n^3-\frac{\boxed{\ \ ケコサ\ \ }}{\boxed{\ \ シ\ \ }}n$である。
(3)上で定めた$q_n$が最小値を取るのは、$n=\boxed{\ \ ス\ \ }$または$n=\boxed{\ \ セ\ \ }$のときであり、
その値は#$-\boxed{\ \ ソタチ\ \ }$である。
2021慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{4}}$座標平面上でx座標とy座標がいずれも整数である点を格子点と呼ぶ。それぞれ
の正の整数nについて、4つの格子点$A_n(n,n),\ B_n(-n,n),\ C_n(-n,-n),\ D_n(n,-n)$
が作る正方形をJ_nとする。また、$(n-1,n)$にある格子点を$P_n$とする。
$\left\{a_k\right\}$を初項$a_1$が$-56$で、交差が$\frac{1}{4}$の等差数列とし、数列$\left\{a_k\right\}$の各項を以下の
ようにして格子点上順番に割り当てていく。
1.初項$a_1$は格子点$P_1$に割り当てる。
2.$a_l$が正方形$J_m$の周上にある格子点で$A_m$以外の点に割り当てられているときには、
$J_m$の周上でその点から半時計回り(右図(※動画参照)での矢印が示す方向)に一つ移動
した格子点に$a_{l+1}$を割り当てる。
3$.a_l$が格子点$A_m$に割り当てられているときには、$a_{l+1}$を格子点$P_{m+1}$に割り当てる。
全体としては、図に示されているようにして、格子点をたどっていくことになる。
(1)格子点$P_n$に割り当てられる数列$\left\{a_k\right\}$の項を$p_n$とし、格子点$C_n$に割り当て
られる数列$\left\{a_k\right\}$の項を$c_n$とする。
このとき、$p_4=-\boxed{\ \ アイ\ \ }, c_4=-\frac{\boxed{\ \ ウエオ\ \ }}{\boxed{\ \ カ\ \ }}$である。
(2)上で定めた$p_n$を用いて、$q_n$を数列$\left\{p_n\right\}$の初項$p_1$から第n項$p_n$までの和とする。
$q_n$をnを使って表すと、$q_n=\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}n^3-\frac{\boxed{\ \ ケコサ\ \ }}{\boxed{\ \ シ\ \ }}n$である。
(3)上で定めた$q_n$が最小値を取るのは、$n=\boxed{\ \ ス\ \ }$または$n=\boxed{\ \ セ\ \ }$のときであり、
その値は#$-\boxed{\ \ ソタチ\ \ }$である。
2021慶應義塾大学商学部過去問
【高校数学】等差数列の性質~等差数列の証明と等差中項~ 3-3【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
a,6,2aが等差数列のとき、aの値を求めよ
この動画を見る
a,6,2aが等差数列のとき、aの値を求めよ
【数B】確率分布:<分散の計算に注意!>2つの確率変数の和の期待値・分散

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
(2つの確率の和の期待値・分散の求め方と例)
赤のコイン2枚投げて表の出た枚数をX,青のコイン1枚投げて表の出た枚数をYとするとき、X+Yの期待値・分散を求めよう
この動画を見る
(2つの確率の和の期待値・分散の求め方と例)
赤のコイン2枚投げて表の出た枚数をX,青のコイン1枚投げて表の出た枚数をYとするとき、X+Yの期待値・分散を求めよう
14三重県教員採用試験(数学:6番 数列)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
$a_1=7,a_{n+1}=2a_n-2n-1$
一般項を求めよ.
この動画を見る
$\boxed{6}$
$a_1=7,a_{n+1}=2a_n-2n-1$
一般項を求めよ.
【数B】数列:種々の数列格子点

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
座標平面上の曲線$y=-nx^2+2n^2x$とx軸で囲まれた図形(境界を含む)をDnとし、図形Dnにある格子点の個数をAnとする。
(1)$A_1、A_2$の値を求めよ。
(2)図形Dnの格子点のうち、x座標の値が$x=k(k=0,1,2,・・・,2n)$である格子点の個数をBkとする。Bkをnとkの式で表せ。
(3)Anをnの式で表せ。
この動画を見る
座標平面上の曲線$y=-nx^2+2n^2x$とx軸で囲まれた図形(境界を含む)をDnとし、図形Dnにある格子点の個数をAnとする。
(1)$A_1、A_2$の値を求めよ。
(2)図形Dnの格子点のうち、x座標の値が$x=k(k=0,1,2,・・・,2n)$である格子点の個数をBkとする。Bkをnとkの式で表せ。
(3)Anをnの式で表せ。
【高校数学】等差数列の一般項の例題2第~一緒に解こう~ 3-2.5【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
次の等差数列の一般項を求めよ。
また、その第8項を求めよ。
23,17,11,5,…
2⃣
第5項が-5,第10項が15である等差数列{an}がある。
この数列の一般項を求めよ。
この動画を見る
1⃣
次の等差数列の一般項を求めよ。
また、その第8項を求めよ。
23,17,11,5,…
2⃣
第5項が-5,第10項が15である等差数列{an}がある。
この数列の一般項を求めよ。
福田の数学〜慶應義塾大学2021年経済学部第4問〜対数不等式と数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$
$k$を実数の定数とする。実数$x$は不等式
(*)$2\log_5x-\log_5(6x-5^k) \lt k-1$
を満たすとする。
(1)不等式(*)を満たすxの値の範囲を、$k$を用いて表せ。
(2)$k$を自然数とする。(*)を満たす$x$のうち奇数の個数を$a_k$とし
$S_n=\sum_{k=1}^na_k (n=1,2,3,\ldots)$
とおく。$a_k$を$k$の式で表し、さらに$S_n$を$n$の式で表せ。
(3)(2)の$S_n$に対して、$S_n+n$が10桁の整数となるような自然数$n$
の値を求めよ。なお、必要があれば$0.30 \lt \log_{10}2 \lt 0.31$を用いよ。
2021慶應義塾大学経済学過去問
この動画を見る
${\Large\boxed{4}}$
$k$を実数の定数とする。実数$x$は不等式
(*)$2\log_5x-\log_5(6x-5^k) \lt k-1$
を満たすとする。
(1)不等式(*)を満たすxの値の範囲を、$k$を用いて表せ。
(2)$k$を自然数とする。(*)を満たす$x$のうち奇数の個数を$a_k$とし
$S_n=\sum_{k=1}^na_k (n=1,2,3,\ldots)$
とおく。$a_k$を$k$の式で表し、さらに$S_n$を$n$の式で表せ。
(3)(2)の$S_n$に対して、$S_n+n$が10桁の整数となるような自然数$n$
の値を求めよ。なお、必要があれば$0.30 \lt \log_{10}2 \lt 0.31$を用いよ。
2021慶應義塾大学経済学過去問
福田の数学〜慶應義塾大学2021年経済学部第3問〜数列の部分和と一般項の関係

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$ 数列$\left\{a_n\right\}$に対して、
$S_n=\sum_{k=1}^na_k (n=1,2,3,\ldots)$
とおく。$\left\{a_n\right\}$は、$a_2=1,a_6=2$および
(*)$S_n=\frac{(n-2)(n+1)^2}{4}a_{n+1} (n=1,2,3,\ldots)$
を満たすとする。
(1)$a_1=-\boxed{\ \ ア\ \ }$である。(*)で$n=4,5$とすると、$a_3+a_4$と$a_5$の関係が2通り定まり、
$a_5=\boxed{\ \ イ\ \ }$と求まる。さらに(*)で$n=3$として、$a_3=\boxed{\ \ ウエ\ \ },a_4=\boxed{\ \ オカ\ \ }$と求まる。
(2)$n \geqq 2$に対して$a_n=S_n-S_{n-1}$であるから(*)とあわせて
$(n-\boxed{\ \ キ\ \ })(n+\boxed{\ \ ク\ \ })^2a_{n+1}=(n^3-\boxed{\ \ ケ\ \ }n^2+\boxed{\ \ コ\ \ })a_n (n=2,3,\ldots)$
ゆえに、$n \geqq 3$ならば$(n+\boxed{\ \ サ\ \ })a_{n+1}=(n-\boxed{\ \ シ\ \ })a_n$となる。そこで、$n \geqq 3$に
対して$b_n=(n-r)(n-s)(n-t)a_n$とおくと、漸化式
$b_{n+1}=b_n (nz-3,4,5,\ldots)$
が成り立つ。ただしここに、$r \lt s \lt t$として$r=\boxed{\ \ ス\ \ },s=\boxed{\ \ セ\ \ },t=\boxed{\ \ ソ\ \ }$である。
したがって、$n \geqq 4$に対して
$a_n=\frac{\boxed{\ \ ソ\ \ }a_4}{(n-r)(n-s)(n-t)}$
となる。この式は$n=3$の時も成立する。
(3)$n \geqq 2$に対して
$S_n=\frac{\boxed{\ \ チツ\ \ }(n+\boxed{\ \ テ\ \ })(n-\boxed{\ \ ト\ \ })}{n(n-\boxed{\ \ ナ\ \ })}$
であるから、$S_n \geqq 59$となる最小の$n$は$n=\boxed{\ \ ニヌ\ \ }$である。
2021慶應義塾大学経済学部過去問
この動画を見る
${\Large\boxed{3}}$ 数列$\left\{a_n\right\}$に対して、
$S_n=\sum_{k=1}^na_k (n=1,2,3,\ldots)$
とおく。$\left\{a_n\right\}$は、$a_2=1,a_6=2$および
(*)$S_n=\frac{(n-2)(n+1)^2}{4}a_{n+1} (n=1,2,3,\ldots)$
を満たすとする。
(1)$a_1=-\boxed{\ \ ア\ \ }$である。(*)で$n=4,5$とすると、$a_3+a_4$と$a_5$の関係が2通り定まり、
$a_5=\boxed{\ \ イ\ \ }$と求まる。さらに(*)で$n=3$として、$a_3=\boxed{\ \ ウエ\ \ },a_4=\boxed{\ \ オカ\ \ }$と求まる。
(2)$n \geqq 2$に対して$a_n=S_n-S_{n-1}$であるから(*)とあわせて
$(n-\boxed{\ \ キ\ \ })(n+\boxed{\ \ ク\ \ })^2a_{n+1}=(n^3-\boxed{\ \ ケ\ \ }n^2+\boxed{\ \ コ\ \ })a_n (n=2,3,\ldots)$
ゆえに、$n \geqq 3$ならば$(n+\boxed{\ \ サ\ \ })a_{n+1}=(n-\boxed{\ \ シ\ \ })a_n$となる。そこで、$n \geqq 3$に
対して$b_n=(n-r)(n-s)(n-t)a_n$とおくと、漸化式
$b_{n+1}=b_n (nz-3,4,5,\ldots)$
が成り立つ。ただしここに、$r \lt s \lt t$として$r=\boxed{\ \ ス\ \ },s=\boxed{\ \ セ\ \ },t=\boxed{\ \ ソ\ \ }$である。
したがって、$n \geqq 4$に対して
$a_n=\frac{\boxed{\ \ ソ\ \ }a_4}{(n-r)(n-s)(n-t)}$
となる。この式は$n=3$の時も成立する。
(3)$n \geqq 2$に対して
$S_n=\frac{\boxed{\ \ チツ\ \ }(n+\boxed{\ \ テ\ \ })(n-\boxed{\ \ ト\ \ })}{n(n-\boxed{\ \ ナ\ \ })}$
であるから、$S_n \geqq 59$となる最小の$n$は$n=\boxed{\ \ ニヌ\ \ }$である。
2021慶應義塾大学経済学部過去問
12高知県教員採用試験(数学:3番 数列)
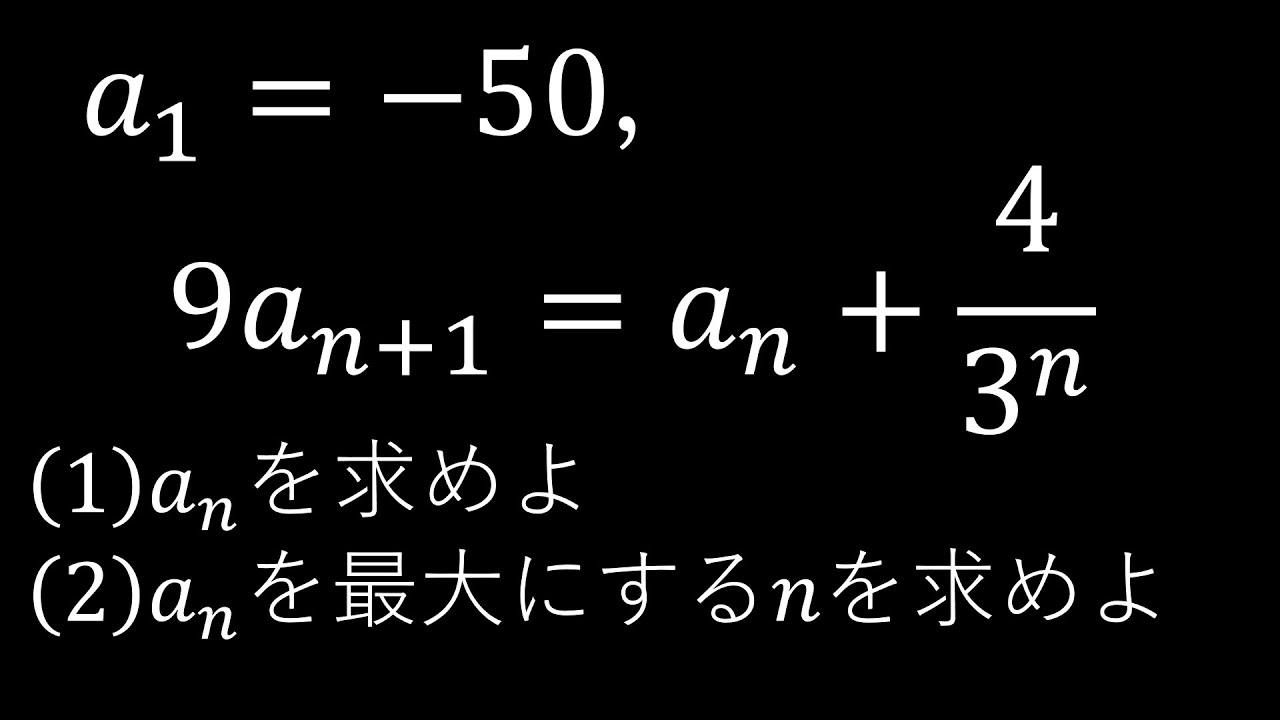
単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
$a_1=-50,9a_{n+1}=a_n+\dfrac{4}{3^n}$
(1)一般項$a_n$を求めよ.
(2)$a_n$を最大にする$n$の値を求めよ.
この動画を見る
$\boxed{3}$
$a_1=-50,9a_{n+1}=a_n+\dfrac{4}{3^n}$
(1)一般項$a_n$を求めよ.
(2)$a_n$を最大にする$n$の値を求めよ.
チャレンジ問題(複雑なパズル)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数列#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$\dfrac{1}{1}=?,\ \dfrac{2\cdot 3}{1\cdot 3}=?,\ \dfrac{3\cdot 5\cdot 6}{1\cdot 3\cdot 5}=?$
$\dfrac{4 \cdot 7 \cdot 9 \cdot 10}{1 \cdot 3 \cdot 5 \cdot 7}=?,\ \dfrac{5 \cdot 9 \cdot 12 \cdot 14 \cdot 15}{1 \cdot 3 \cdot 5 \cdot 7 \cdot 4}=?$
(1)各式の右辺を計算せよ.
(2)式の両辺がどのように続くか予想せよ.
(3)(2)の予想を示せ.
この動画を見る
$\dfrac{1}{1}=?,\ \dfrac{2\cdot 3}{1\cdot 3}=?,\ \dfrac{3\cdot 5\cdot 6}{1\cdot 3\cdot 5}=?$
$\dfrac{4 \cdot 7 \cdot 9 \cdot 10}{1 \cdot 3 \cdot 5 \cdot 7}=?,\ \dfrac{5 \cdot 9 \cdot 12 \cdot 14 \cdot 15}{1 \cdot 3 \cdot 5 \cdot 7 \cdot 4}=?$
(1)各式の右辺を計算せよ.
(2)式の両辺がどのように続くか予想せよ.
(3)(2)の予想を示せ.
【高校数学】等差数列の一般項~理解すると忘れない~ 3-2【数学B】

福田の数学〜慶應義塾大学2021年医学部第2問〜データの分析、共分散と相関係数

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$
$n$人のクラス(ただし$n \gt 1$)で英語と理科のテストを実施する。ただしどちらの科目にも同順位の者はいないとする。出席番号$i(i=1,2,\ldots,n)$の生徒について、その英語の順位$x$と理科の順位$y$の組を$(x_i,y_i)$で表す。
(1)変量$x$の平均値$\bar{ x }$と分散$s_x^2$をそれぞれ求めると$\bar{ x }=\boxed{\ \ (あ)\ \ },s_x^2=\boxed{\ \ (い)\ \ }$である。
(2)変量$x,y$の共分散$s_{xy}$とする。クラスの人数$n$が奇数の2倍であるとき、$s_{xy}\neq 0$であることを示しなさい。
(3)$i=1,2,\ldots,n$に対して$d_i=x_i-y_i$とおく。変量$x,y$の相関係数を$r$とするとき、$r$は$n$と$d_1,d_2,\ldots,d_n$を用いて$r=1-\dfrac{6}{\boxed{\ \ (う)\ \ }}\boxed{\ \ (え)\ \ }$と表される。
(4)$x_i$と$y_i$の間に$y_i=\boxed{\ \ (お)\ \ }(i=1,2,\ldots,n)$の関係があるとき$r$は最大値$\boxed{\ \ (か)\ \ }$をとり$y_i=\boxed{\ \ (き)\ \ }(i=1,2,\ldots,n)$の関係があるとき$r$は最小値$\boxed{\ \ (く)\ \ }$をとる。
2021慶應義塾大学医学部過去問
この動画を見る
${\Large\boxed{2}}$
$n$人のクラス(ただし$n \gt 1$)で英語と理科のテストを実施する。ただしどちらの科目にも同順位の者はいないとする。出席番号$i(i=1,2,\ldots,n)$の生徒について、その英語の順位$x$と理科の順位$y$の組を$(x_i,y_i)$で表す。
(1)変量$x$の平均値$\bar{ x }$と分散$s_x^2$をそれぞれ求めると$\bar{ x }=\boxed{\ \ (あ)\ \ },s_x^2=\boxed{\ \ (い)\ \ }$である。
(2)変量$x,y$の共分散$s_{xy}$とする。クラスの人数$n$が奇数の2倍であるとき、$s_{xy}\neq 0$であることを示しなさい。
(3)$i=1,2,\ldots,n$に対して$d_i=x_i-y_i$とおく。変量$x,y$の相関係数を$r$とするとき、$r$は$n$と$d_1,d_2,\ldots,d_n$を用いて$r=1-\dfrac{6}{\boxed{\ \ (う)\ \ }}\boxed{\ \ (え)\ \ }$と表される。
(4)$x_i$と$y_i$の間に$y_i=\boxed{\ \ (お)\ \ }(i=1,2,\ldots,n)$の関係があるとき$r$は最大値$\boxed{\ \ (か)\ \ }$をとり$y_i=\boxed{\ \ (き)\ \ }(i=1,2,\ldots,n)$の関係があるとき$r$は最小値$\boxed{\ \ (く)\ \ }$をとる。
2021慶應義塾大学医学部過去問
階乗(❗️)に関する問題 常総学院

単元:
#数学(中学生)#数列#数列とその和(等差・等比・階差・Σ)#高校入試過去問(数学)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{(n+2)!}{n!} = 20$のときn=?
常総学院高等学校(改)
この動画を見る
$\frac{(n+2)!}{n!} = 20$のときn=?
常総学院高等学校(改)
【数B】確率分布:変量の変換公式 こう覚えておけばOK!

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
XからYに確率変数を$Y=aX+b$で変換する場合の期待値、分散、標準偏差の公式
この動画を見る
XからYに確率変数を$Y=aX+b$で変換する場合の期待値、分散、標準偏差の公式
14和歌山県教員採用試験(数学:4番 数列)
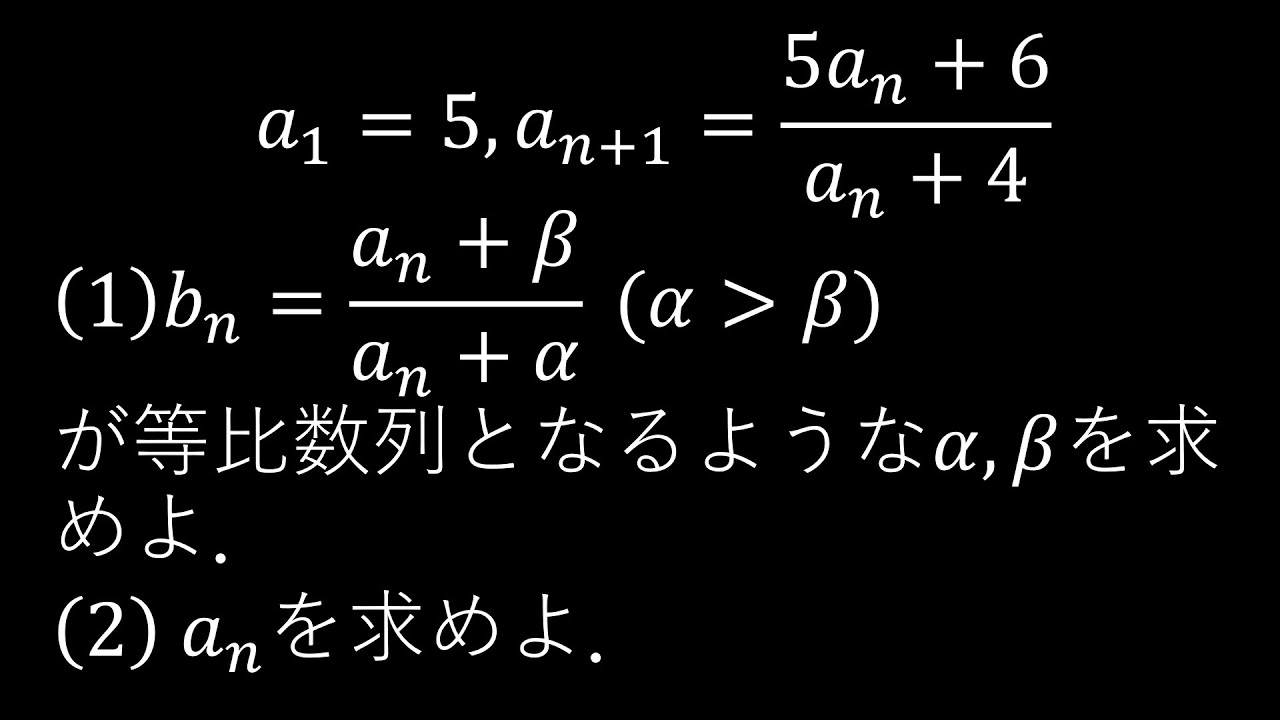
単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{4}$
$a_1=5,a_{n+1}=\dfrac{5a_n+6}{a_4+4}$とする.
(1)$b_n=\dfrac{a_n+\beta}{a_n+\alpha}\ (\alpha \gt \beta)$
$b_n$が等比数列となるような$\alpha,\beta$の値を求めよ.
(2)$a_n$を求めよ.
この動画を見る
$\boxed{4}$
$a_1=5,a_{n+1}=\dfrac{5a_n+6}{a_4+4}$とする.
(1)$b_n=\dfrac{a_n+\beta}{a_n+\alpha}\ (\alpha \gt \beta)$
$b_n$が等比数列となるような$\alpha,\beta$の値を求めよ.
(2)$a_n$を求めよ.
数学「大学入試良問集」【17−4 漸化式と等比数列・極限】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#東京農工大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次のように定義された数列を$\{a_n\}$とする。
$a_1=r^2,a_2=1,2a_n=(r+3)a_{n-1}-(r+1)a_{n-2}(n \geqq 3)$
このとき、次の各問いに答えよ。
(1)$b_n=a_{n+1}-a_n$とおくとき、$b_n$を$n$と$r$を用いて表せ。
(2)$a_n$を求めよ。
(3)数列$\{a_n\}$が収束するような$r$の範囲およびそのときの極限値を求めよ。
この動画を見る
次のように定義された数列を$\{a_n\}$とする。
$a_1=r^2,a_2=1,2a_n=(r+3)a_{n-1}-(r+1)a_{n-2}(n \geqq 3)$
このとき、次の各問いに答えよ。
(1)$b_n=a_{n+1}-a_n$とおくとき、$b_n$を$n$と$r$を用いて表せ。
(2)$a_n$を求めよ。
(3)数列$\{a_n\}$が収束するような$r$の範囲およびそのときの極限値を求めよ。
福田の数学〜早稲田大学2021年人間科学部第5問〜漸化式の作成と値の評価

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{5}}$ 半径$r_1=2$の円$O_1$に接する平行でない$2$つの直線がある。接点を$A,B$とし、$2$つの直線の交点を$P$とし、$\angle APB=\frac{\pi}{3}$とする。$O_1$より半径が小さく、$O_1$の中心を通り、直線$AP$と直線$BP$に接する円を$O_2$とする。同様に自然数$n$に対して、$O_n$より半径が小さく、$O_n$の中心を通り、直線$AP$と直線$BP$に接する円を$O_{n+1}$とする。$O_n$の半径を$r_n$とするとき、$\frac{r_n}{r_{n+1}}=\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハ\ \ }}$ となる。次に、$n$個の円$O_1,O_2,\ldots,O_n$の面積の和を$S_n$とするとき、$S_{10}$の整数部分は$\boxed{\ \ ヒ\ \ }$である。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{5}}$ 半径$r_1=2$の円$O_1$に接する平行でない$2$つの直線がある。接点を$A,B$とし、$2$つの直線の交点を$P$とし、$\angle APB=\frac{\pi}{3}$とする。$O_1$より半径が小さく、$O_1$の中心を通り、直線$AP$と直線$BP$に接する円を$O_2$とする。同様に自然数$n$に対して、$O_n$より半径が小さく、$O_n$の中心を通り、直線$AP$と直線$BP$に接する円を$O_{n+1}$とする。$O_n$の半径を$r_n$とするとき、$\frac{r_n}{r_{n+1}}=\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハ\ \ }}$ となる。次に、$n$個の円$O_1,O_2,\ldots,O_n$の面積の和を$S_n$とするとき、$S_{10}$の整数部分は$\boxed{\ \ ヒ\ \ }$である。
2021早稲田大学人間科学部過去問
田の数学〜早稲田大学2021年人間科学部第3問〜格子点の個数

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$
自然数$n$について、連立不等式
$\left\{\begin{array}{1}
x \geqq 0\\
\displaystyle\frac{1}{4}x+\frac{1}{5}|y| \leqq n\\
\end{array}\right.$
を満たす整数の組$(x, y)$の個数は、$n=1$のときは$\boxed{\ \ シ\ \ }$であり、$n$の式で表すと$\boxed{\ \ ス\ \ }n^2+\boxed{\ \ セ\ \ }n+\boxed{\ \ ソ\ \ }$となる。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{3}}$
自然数$n$について、連立不等式
$\left\{\begin{array}{1}
x \geqq 0\\
\displaystyle\frac{1}{4}x+\frac{1}{5}|y| \leqq n\\
\end{array}\right.$
を満たす整数の組$(x, y)$の個数は、$n=1$のときは$\boxed{\ \ シ\ \ }$であり、$n$の式で表すと$\boxed{\ \ ス\ \ }n^2+\boxed{\ \ セ\ \ }n+\boxed{\ \ ソ\ \ }$となる。
2021早稲田大学人間科学部過去問
【高校数学】数列の基礎・言葉の確認~知らないとヤバい知識~ 3-1【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1,4,9,16,25…この一般項を求めよ。
この動画を見る
1,4,9,16,25…この一般項を求めよ。
数学「大学入試良問集」【13−15 格子点の解法】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数B
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の問いに答えよ。
(1)
$k$を$0$以上の整数とするとき、$\displaystyle \frac{x}{3}+\displaystyle \frac{y}{2} \leqq k$をみたす$0$以上の整数$x,y$の組$(x,y)$の個数を$a_k$とする。
$a_k$を$k$の式で表せ。
(2)
$n$を$0$以上の整数とするとき
$\displaystyle \frac{x}{3}+\displaystyle \frac{y}{2}+z \leqq n$
をみたす$0$以上の整数$x,y,z$の組$(x,y,z)$の個数を$b_n$とする。
$b_n$を$n$の式で表せ。
この動画を見る
次の問いに答えよ。
(1)
$k$を$0$以上の整数とするとき、$\displaystyle \frac{x}{3}+\displaystyle \frac{y}{2} \leqq k$をみたす$0$以上の整数$x,y$の組$(x,y)$の個数を$a_k$とする。
$a_k$を$k$の式で表せ。
(2)
$n$を$0$以上の整数とするとき
$\displaystyle \frac{x}{3}+\displaystyle \frac{y}{2}+z \leqq n$
をみたす$0$以上の整数$x,y,z$の組$(x,y,z)$の個数を$b_n$とする。
$b_n$を$n$の式で表せ。
数学「大学入試良問集」【13−14 確率漸化式の基本】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数B
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
袋の中に$1~9$までの異なる数字を1つずつ書いた9枚のカードが入っている。
この中から1枚を取り出し、数字を調べて袋に戻す。
この試行を$n$回繰り返したとき、調べた$n$枚のカードの数字の和が偶数になる確率を$P_n$とする。
このとき、次の各問いに答えよ。
(1)$P_2,P_3$の値を求めよ。
(2)$P_{n+1}$を$P_n$を用いて表せ。
(3)$P_n$を$n$を用いて表せ。
この動画を見る
袋の中に$1~9$までの異なる数字を1つずつ書いた9枚のカードが入っている。
この中から1枚を取り出し、数字を調べて袋に戻す。
この試行を$n$回繰り返したとき、調べた$n$枚のカードの数字の和が偶数になる確率を$P_n$とする。
このとき、次の各問いに答えよ。
(1)$P_2,P_3$の値を求めよ。
(2)$P_{n+1}$を$P_n$を用いて表せ。
(3)$P_n$を$n$を用いて表せ。
数学「大学入試良問集」【13−12 数列と二項定理】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#静岡大学#数学(高校生)#数B
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の問いに答えよ。
(1)
$k$を2以上の自然数とする。
$x$の整式$(1+x)^k$において$x^2$の係数を求めよ。
(2)
$n$を2以上の自然数とする。
$x$の整式$\displaystyle \sum_{k=1}^n(1+x)^k$において$x^2$の係数を$a_n$とする。
(ⅰ)$a_n$を求めよ。
(ⅱ)$S_n=\displaystyle \frac{1}{a_2}+\displaystyle \frac{1}{a_3}+・・・+\displaystyle \frac{1}{a_n}$を求めよ。
この動画を見る
次の問いに答えよ。
(1)
$k$を2以上の自然数とする。
$x$の整式$(1+x)^k$において$x^2$の係数を求めよ。
(2)
$n$を2以上の自然数とする。
$x$の整式$\displaystyle \sum_{k=1}^n(1+x)^k$において$x^2$の係数を$a_n$とする。
(ⅰ)$a_n$を求めよ。
(ⅱ)$S_n=\displaystyle \frac{1}{a_2}+\displaystyle \frac{1}{a_3}+・・・+\displaystyle \frac{1}{a_n}$を求めよ。
数学「大学入試良問集」【13−11 ガウス記号とその戦略】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学#数B
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
実数$x$に対し、$[x]$を$x$以下の最大の整数とする。
たとえば、$[2]=2,\left[ \dfrac{ 7 }{ 5 } \right]=1$である。
数列$\{a_n\}$を$a_k=\left[ \dfrac{ 3k }{ 5 } \right](k=1,2,・・・)$と定めるとき、以下の問いに答えよ。
(1)$a_1,a_2,a_3,a_4,a_5$を求めよ。
(2)$a_{k+5}=a_k+3(k=1,2,・・・)$を示せ。
(3)自然数$n$に対して、$\displaystyle \sum_{k=1}^{5n} a_k$を求めよ。
この動画を見る
実数$x$に対し、$[x]$を$x$以下の最大の整数とする。
たとえば、$[2]=2,\left[ \dfrac{ 7 }{ 5 } \right]=1$である。
数列$\{a_n\}$を$a_k=\left[ \dfrac{ 3k }{ 5 } \right](k=1,2,・・・)$と定めるとき、以下の問いに答えよ。
(1)$a_1,a_2,a_3,a_4,a_5$を求めよ。
(2)$a_{k+5}=a_k+3(k=1,2,・・・)$を示せ。
(3)自然数$n$に対して、$\displaystyle \sum_{k=1}^{5n} a_k$を求めよ。
数学「大学入試良問集」【13−9 数学的帰納法(累積帰納法)】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数B
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
数列$a_0,a_1,a_2,・・・a_n・・・$を次のように定義する。
$a_0=\displaystyle \frac{1}{2},a_{n+1}\displaystyle \sum_{k=0}^n a_k a_{n-k}n=0,1,2,・・・)$
以下の問いに答えよ。
(1)$a_1,a_2,a_3$を求めよ。
(2)一般項$a_n$を求めよ。
(3)$b_n=\displaystyle \sum_{k=0}^n\displaystyle \frac{n!}{k!(n-k)!}a_ka_{n-k}(n=0,1,2,・・・)$を求めよ。
この動画を見る
数列$a_0,a_1,a_2,・・・a_n・・・$を次のように定義する。
$a_0=\displaystyle \frac{1}{2},a_{n+1}\displaystyle \sum_{k=0}^n a_k a_{n-k}n=0,1,2,・・・)$
以下の問いに答えよ。
(1)$a_1,a_2,a_3$を求めよ。
(2)一般項$a_n$を求めよ。
(3)$b_n=\displaystyle \sum_{k=0}^n\displaystyle \frac{n!}{k!(n-k)!}a_ka_{n-k}(n=0,1,2,・・・)$を求めよ。
数学「大学入試良問集」【13−8 数学的帰納法(不等式の証明)】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数B
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$n$が自然数のとき、次の各問いに答えよ。
(1)不等式$n! \geqq 2^{n-1}$が成り立つことを証明せよ。
(2)不等式$1+\displaystyle \frac{1}{1!}+\displaystyle \frac{1}{2!}+・・・+\displaystyle \frac{1}{n!} \lt 3$が成り立つことを証明せよ。
この動画を見る
$n$が自然数のとき、次の各問いに答えよ。
(1)不等式$n! \geqq 2^{n-1}$が成り立つことを証明せよ。
(2)不等式$1+\displaystyle \frac{1}{1!}+\displaystyle \frac{1}{2!}+・・・+\displaystyle \frac{1}{n!} \lt 3$が成り立つことを証明せよ。
数学「大学入試良問集」【13−7 数学的帰納法(13の倍数の証明)】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数B
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$n$を自然数とするとき、$4^{2n-1}+3^{n+1}$は$13$の倍数であることを示せ。
この動画を見る
$n$を自然数とするとき、$4^{2n-1}+3^{n+1}$は$13$の倍数であることを示せ。
福田の数学〜早稲田大学2021年教育学部第4問〜三角形の個数を数える

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}} $
1辺の長さが$1$の正三角形を下図(※動画参照)のように積んでいく。図の中には大きさの異なったいくつかの正三角形が含まれているが、底辺が下側にあるものを「上向きの正三角形」、底辺が上側にあるものを「下向きを正三角形」とよぶことにする。例えば、この図(※動画参照)は1辺の長さが1の正三角形を4段積んだものであり、1辺の長さが1の上向きの正三角形は10個あり、1辺の長さが2の上向き正三角形は6個ある。
また1辺の長さが1の下向きの正三角形は6個ある。上向きの正三角形の総数は20であり、下向きの正三角形の総数は7である。こうした正三角形の個数に関して次の問いに答えよ。
(1)1辺の長さが1の正三角形を$5$段積んだとき、上向きと下向きとを合わせた正三角形の総数を求めよ。
(2)1辺の長さが1の正三角形を$n$段(ただし$n$は自然数)積んだとき、上向きの正三角形の総数を求めよ。
(3)1辺の長さが1の正三角形を$n$段(ただし$n$は自然数)積んだとき、下向きの正三角形の総数を求めよ。
この動画を見る
${\Large\boxed{4}} $
1辺の長さが$1$の正三角形を下図(※動画参照)のように積んでいく。図の中には大きさの異なったいくつかの正三角形が含まれているが、底辺が下側にあるものを「上向きの正三角形」、底辺が上側にあるものを「下向きを正三角形」とよぶことにする。例えば、この図(※動画参照)は1辺の長さが1の正三角形を4段積んだものであり、1辺の長さが1の上向きの正三角形は10個あり、1辺の長さが2の上向き正三角形は6個ある。
また1辺の長さが1の下向きの正三角形は6個ある。上向きの正三角形の総数は20であり、下向きの正三角形の総数は7である。こうした正三角形の個数に関して次の問いに答えよ。
(1)1辺の長さが1の正三角形を$5$段積んだとき、上向きと下向きとを合わせた正三角形の総数を求めよ。
(2)1辺の長さが1の正三角形を$n$段(ただし$n$は自然数)積んだとき、上向きの正三角形の総数を求めよ。
(3)1辺の長さが1の正三角形を$n$段(ただし$n$は自然数)積んだとき、下向きの正三角形の総数を求めよ。
🟨=❓ 解けたら天才⁉️
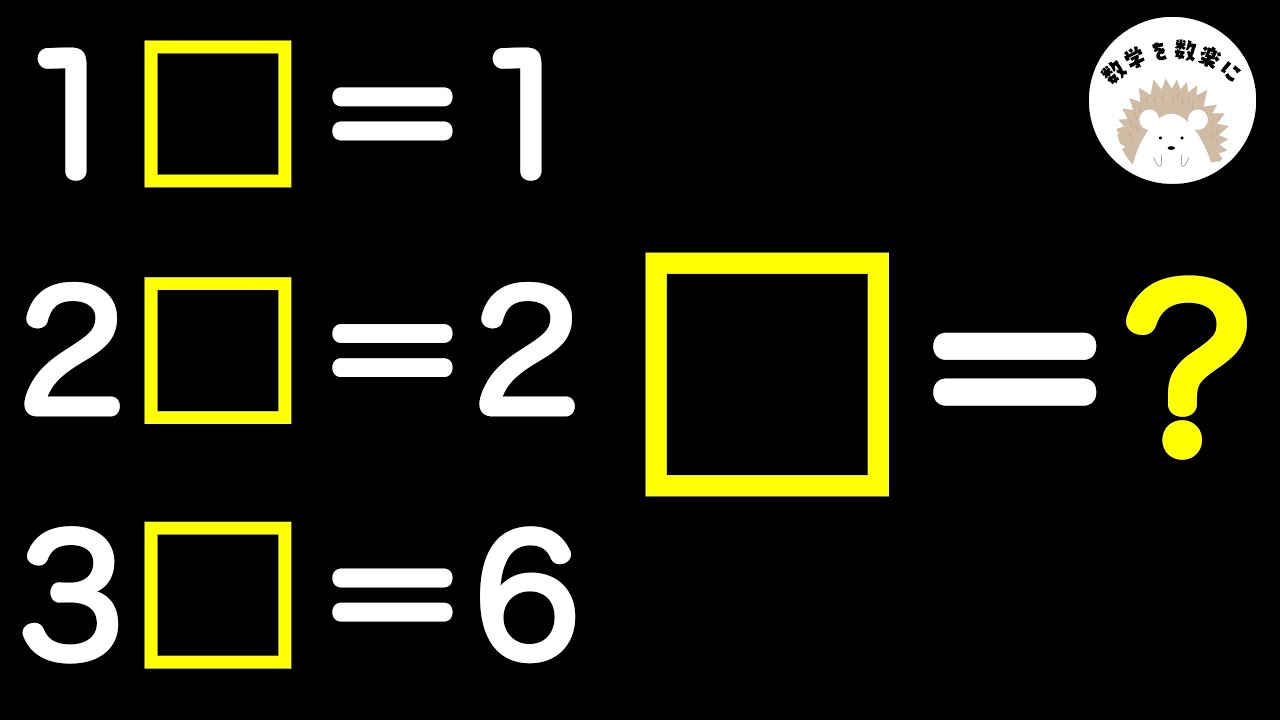
数学「大学入試良問集」【13−6 連立漸化式】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の条件によって定められる数列$\{x_n\},\{y_n\}$を考える。
$x_1=1,y_1=5$ $x_{n+1}=x_n+y_n$ $y_{n+1}=5x_n+y_n(n=1,2,・・・)$
次の問いに答えよ。
(1)
$a_n=x_n+cy_n$とおいたとき、数列$\{a_n\}$が等比数列となるように定数$c$の値を定め、$a_n$を$n$の式で表せ。
(2)
$x_n$および$y_n$を$n$の式で表せ。
この動画を見る
次の条件によって定められる数列$\{x_n\},\{y_n\}$を考える。
$x_1=1,y_1=5$ $x_{n+1}=x_n+y_n$ $y_{n+1}=5x_n+y_n(n=1,2,・・・)$
次の問いに答えよ。
(1)
$a_n=x_n+cy_n$とおいたとき、数列$\{a_n\}$が等比数列となるように定数$c$の値を定め、$a_n$を$n$の式で表せ。
(2)
$x_n$および$y_n$を$n$の式で表せ。
【25分で総復習】最初から『数列①』等差数列、等比数列(数学B)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
1⃣
初項が-1、公差が2の等差数列について、以下の問いに答えよ。
(1)一般項を求めよ。
(2)第10項を求めよ。
(3)初項から第$n$項までの和を求めよ。
2⃣
等比数列3,-6,12…について、以下の問いに答えよ。
(1)一般項を求めよ。
(2)初項から第$n$項までの和を求めよ。
この動画を見る
1⃣
初項が-1、公差が2の等差数列について、以下の問いに答えよ。
(1)一般項を求めよ。
(2)第10項を求めよ。
(3)初項から第$n$項までの和を求めよ。
2⃣
等比数列3,-6,12…について、以下の問いに答えよ。
(1)一般項を求めよ。
(2)初項から第$n$項までの和を求めよ。
