数B
数B
福田の数学〜立教大学2025経済学部第1問(3)〜等差中項と等比中項
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(3)$x,y,z$は実数であり、$x\lt y$を満たすとする。
$3$つの数$3,x,y$がこの順に等差数列となり、
さらに$4$つの数$4,x,y,z$がこの順に
等差数列となるとき、
$x=\boxed{ウ}、\boxed{エ}、\boxed{オ}$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(3)$x,y,z$は実数であり、$x\lt y$を満たすとする。
$3$つの数$3,x,y$がこの順に等差数列となり、
さらに$4$つの数$4,x,y,z$がこの順に
等差数列となるとき、
$x=\boxed{ウ}、\boxed{エ}、\boxed{オ}$である。
$2025$年立教大学経済学部過去問題
福田のおもしろ数学505〜フィボナッチ数列の性質
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
フィボナッチ数列$\{f_n\}$
$f_1=f_2=1,f_{n+2}=f_{n+1}+f_n$
に対し、
$f_m･f_n=mn$
を満たす自然数の組$(m,n)$をすべて求めて下さい。
この動画を見る
フィボナッチ数列$\{f_n\}$
$f_1=f_2=1,f_{n+2}=f_{n+1}+f_n$
に対し、
$f_m･f_n=mn$
を満たす自然数の組$(m,n)$をすべて求めて下さい。
福田の数学〜慶應義塾大学2025経済学部第2問〜数列の和から一般項を求める
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
数列$\{a_n\}$に対して
$T_n=\displaystyle \sum_{k=1}^n \dfrac{(k+2)!}{(k-1)!}a_k (n=1,2,3,\cdots)$
とおくとき、
$T_n=\left(n-\dfrac{1}{2}\right)^2 (n=1,2,3,\cdots)$
が成り立つとする。ただし、$0!=1$である。
(1)$a_1=\dfrac{\boxed{ア}}{\boxed{イウ}},a_2=\dfrac{\boxed{エ}}{\boxed{オ}}$である。
(2)$n\geqq 2$に対して$T_n-T_{n-1}=\boxed{カ}n-\boxed{キ}$が
成り立つから、
$a_n=r^n\dfrac{n-\boxed{ク}}{(n+s)(n+t)(n+u)} (n=2,3,4,\cdots)$
である。ただし、ここに$r=\boxed{ケ}$であり、
$s\lt t \lt u$として$s=\boxed{コ},t=\boxed{サ},u=\boxed{シ}$である。
$2025$年慶應義塾大学経済学部過去問題
この動画を見る
$\boxed{2}$
数列$\{a_n\}$に対して
$T_n=\displaystyle \sum_{k=1}^n \dfrac{(k+2)!}{(k-1)!}a_k (n=1,2,3,\cdots)$
とおくとき、
$T_n=\left(n-\dfrac{1}{2}\right)^2 (n=1,2,3,\cdots)$
が成り立つとする。ただし、$0!=1$である。
(1)$a_1=\dfrac{\boxed{ア}}{\boxed{イウ}},a_2=\dfrac{\boxed{エ}}{\boxed{オ}}$である。
(2)$n\geqq 2$に対して$T_n-T_{n-1}=\boxed{カ}n-\boxed{キ}$が
成り立つから、
$a_n=r^n\dfrac{n-\boxed{ク}}{(n+s)(n+t)(n+u)} (n=2,3,4,\cdots)$
である。ただし、ここに$r=\boxed{ケ}$であり、
$s\lt t \lt u$として$s=\boxed{コ},t=\boxed{サ},u=\boxed{シ}$である。
$2025$年慶應義塾大学経済学部過去問題
福田のおもしろ数学499〜1分チャレンジ！数値計算
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\dfrac{(4\times 7+2)(6\times 9+2)(8\times 11+2)\cdots}{(5\times 8 +2)(7\times 10 +2)(9\times 12 +2)\cdots }$
$\dfrac{\cdots (100\times 103+2)}{\cdots (99\times 102+2)}$
を計算して下さい。
この動画を見る
$\dfrac{(4\times 7+2)(6\times 9+2)(8\times 11+2)\cdots}{(5\times 8 +2)(7\times 10 +2)(9\times 12 +2)\cdots }$
$\dfrac{\cdots (100\times 103+2)}{\cdots (99\times 102+2)}$
を計算して下さい。
福田の数学〜東京科学大学(旧・東京工業大学)2025理系第4問〜フィボナッチ数列と無限級数の和
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
数列$\{a_n\}$を
$a_1=a_2=1,a_{n+2}=a_{n+1}+a_n (n=1,2,3,\cdots)$
により定め、数列$\{b_n\}$を
$\tan b_n=\dfrac{1}{a_n}$
により定める。
ただし、$0\lt b_n \lt \dfrac{\pi}{2}$であるものとする。
(1)$n\geqq 2$に対して、$a_{n+1}a_{n-1}-{a_n}^2$を求めよ。
(2)$m\geqq 1$($m$は整数)に対して、
$a_{2ｍ}･\tan(b_{2m+1}+b_{2m+2})$を求めよ。
(3)無限級数$\displaystyle \sum_{m=0}^{\infty} b_{2m+1}$を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
この動画を見る
$\boxed{4}$
数列$\{a_n\}$を
$a_1=a_2=1,a_{n+2}=a_{n+1}+a_n (n=1,2,3,\cdots)$
により定め、数列$\{b_n\}$を
$\tan b_n=\dfrac{1}{a_n}$
により定める。
ただし、$0\lt b_n \lt \dfrac{\pi}{2}$であるものとする。
(1)$n\geqq 2$に対して、$a_{n+1}a_{n-1}-{a_n}^2$を求めよ。
(2)$m\geqq 1$($m$は整数)に対して、
$a_{2ｍ}･\tan(b_{2m+1}+b_{2m+2})$を求めよ。
(3)無限級数$\displaystyle \sum_{m=0}^{\infty} b_{2m+1}$を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
【暗記じゃない…！】数列：興南高等学校～全国入試問題解法
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
1/1,1/2,2/2,1/3,2/3,3/3,1/4,2/4,3/4,4/4,・・・
の時、左から85番目の分数？
この動画を見る
1/1,1/2,2/2,1/3,2/3,3/3,1/4,2/4,3/4,4/4,・・・
の時、左から85番目の分数？
福田の数学〜東京科学大学(旧・東京工業大学)2025理系第3問〜確率漸化式と無限級数の和
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
$0\lt p\lt 1$とする。
表が出る確率が$p$、裏が出る確率が$1-p$である
$1$枚のコインを使って次のゲームを行う。
・ゲームの開始時点で点数は$0$点
・コインを投げ続け、表が出るごとに$1$点加算し、
裏が出たときは点数はそのまま
・$2$回続けて裏が出たらゲームは終了。
$0$以上の整数$n$に対し、ゲームが終わったときに
$n$点となっている確率を$Q_n$とする。
(1)$Q_1,Q_2$を$p$を用いて表せ。
(2)$Q_2$を$n$と$p$を用いて表せ。
(3)$0\lt x\lt 1$を満たす実数$x$に対して次式が
成り立つことを示せ。
$\dfrac{1}{(1-x)^2}=\displaystyle \sum_{k=0}^{\infty}(n+1)x^n$
必要ならば$0\lt x \lt 1$のとき
$\displaystyle \lim_{n\to\infty} nx^n=0$であることを
証明なしで使ってもよい。
(4)無限級数$\displaystyle \sum_{n=0}^{\infty} nQn$を$p$を用いて表せ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
この動画を見る
$\boxed{3}$
$0\lt p\lt 1$とする。
表が出る確率が$p$、裏が出る確率が$1-p$である
$1$枚のコインを使って次のゲームを行う。
・ゲームの開始時点で点数は$0$点
・コインを投げ続け、表が出るごとに$1$点加算し、
裏が出たときは点数はそのまま
・$2$回続けて裏が出たらゲームは終了。
$0$以上の整数$n$に対し、ゲームが終わったときに
$n$点となっている確率を$Q_n$とする。
(1)$Q_1,Q_2$を$p$を用いて表せ。
(2)$Q_2$を$n$と$p$を用いて表せ。
(3)$0\lt x\lt 1$を満たす実数$x$に対して次式が
成り立つことを示せ。
$\dfrac{1}{(1-x)^2}=\displaystyle \sum_{k=0}^{\infty}(n+1)x^n$
必要ならば$0\lt x \lt 1$のとき
$\displaystyle \lim_{n\to\infty} nx^n=0$であることを
証明なしで使ってもよい。
(4)無限級数$\displaystyle \sum_{n=0}^{\infty} nQn$を$p$を用いて表せ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
福田の数学〜一橋大学2025文系第5問〜確率漸化式と条件付き確率
単元：
#数A#場合の数と確率#確率#数列#漸化式#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{5}$
$5$点$A,B,C,D$が
下図のように線分で結ばれている。
点$P_1,P_2,P_3,\cdots $を次のように定めていく。
$P_1$を$A$とする。
正の整数$n$に対して、$P_n$を端点とする線分を
ひとつ無作為にえらび、その線分の$P_n$とは
異なる端点$P_{n+1}$とする。
(1)$P_n$が$A$または$B$である確率$p_n$を求めよ。
(2)$P_n$が$A$または$B$であるとき、
$k=1,2,\cdots ,n$のいずれに対しても$P_k=E$とは
ならない条件付き確率$q_n$を求めよ。
図は動画内参照
$2025$年一橋大学文系過去問題
この動画を見る
$\boxed{5}$
$5$点$A,B,C,D$が
下図のように線分で結ばれている。
点$P_1,P_2,P_3,\cdots $を次のように定めていく。
$P_1$を$A$とする。
正の整数$n$に対して、$P_n$を端点とする線分を
ひとつ無作為にえらび、その線分の$P_n$とは
異なる端点$P_{n+1}$とする。
(1)$P_n$が$A$または$B$である確率$p_n$を求めよ。
(2)$P_n$が$A$または$B$であるとき、
$k=1,2,\cdots ,n$のいずれに対しても$P_k=E$とは
ならない条件付き確率$q_n$を求めよ。
図は動画内参照
$2025$年一橋大学文系過去問題
福田の数学〜慶應義塾大学看護医療学部2025第2問(3)〜数学的帰納法
単元：
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
(3)自然数$n$に対して、
$3^n-2n-1$が
$4$の倍数であることの数学的帰納法を
用いた証明を記述しなさい。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{2}$
(3)自然数$n$に対して、
$3^n-2n-1$が
$4$の倍数であることの数学的帰納法を
用いた証明を記述しなさい。
$2025$年慶應義塾大学看護医療学部過去問題
福田のおもしろ数学484〜漸化式で定まる数列の連続する正の項の最大個数
単元：
#数列#漸化式#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
実数列$a_1,a_2,a_3,\cdots $が
$a_n=a_{n-1}-a_{n+2} (n=1,2,3,4\cdots)$
を満たしている。
この数列の連続する要素のうちで、
すべてが正となるものの最大個数はいくつか？
この動画を見る
実数列$a_1,a_2,a_3,\cdots $が
$a_n=a_{n-1}-a_{n+2} (n=1,2,3,4\cdots)$
を満たしている。
この数列の連続する要素のうちで、
すべてが正となるものの最大個数はいくつか？
【数B】【数列】自然数の式の証明3 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$n$は自然数とする。
$6^n+4= (5+1)^n+4$と変形することで、$6^n+4$が$5$の倍数であることを、二項定理を利用して証明せよ。
この動画を見る
$n$は自然数とする。
$6^n+4= (5+1)^n+4$と変形することで、$6^n+4$が$5$の倍数であることを、二項定理を利用して証明せよ。
【数B】【数列】自然数の式の証明2 ※問題文は概要欄
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$n$は整数とする。
(1)連続する2個の整数には、必ず$2$の倍数が含まれることを利用して、 $n^2+3n$が$2$の倍数であることを証明せよ。
(2)連続する3個の整数には、必ず$3$の倍数が含まれることを利用して、 $4n^3+3n^2+2n$が$3$の倍数であることを証明せよ。
この動画を見る
$n$は整数とする。
(1)連続する2個の整数には、必ず$2$の倍数が含まれることを利用して、 $n^2+3n$が$2$の倍数であることを証明せよ。
(2)連続する3個の整数には、必ず$3$の倍数が含まれることを利用して、 $4n^3+3n^2+2n$が$3$の倍数であることを証明せよ。
【数B】【数列】自然数の式の証明1 ※問題文は概要欄
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
理数個別チャンネル
問題文全文(内容文)：
(1) 整数$n$を$2$で割った余りで分類することで、$3n^2-n$が$2$の倍数であることを証明せよ。
(2) 整数$n$を$3$で割った余りで分類することで、 $n^3-n+9$が$3$の倍数であることを証明せよ。
この動画を見る
(1) 整数$n$を$2$で割った余りで分類することで、$3n^2-n$が$2$の倍数であることを証明せよ。
(2) 整数$n$を$3$で割った余りで分類することで、 $n^3-n+9$が$3$の倍数であることを証明せよ。
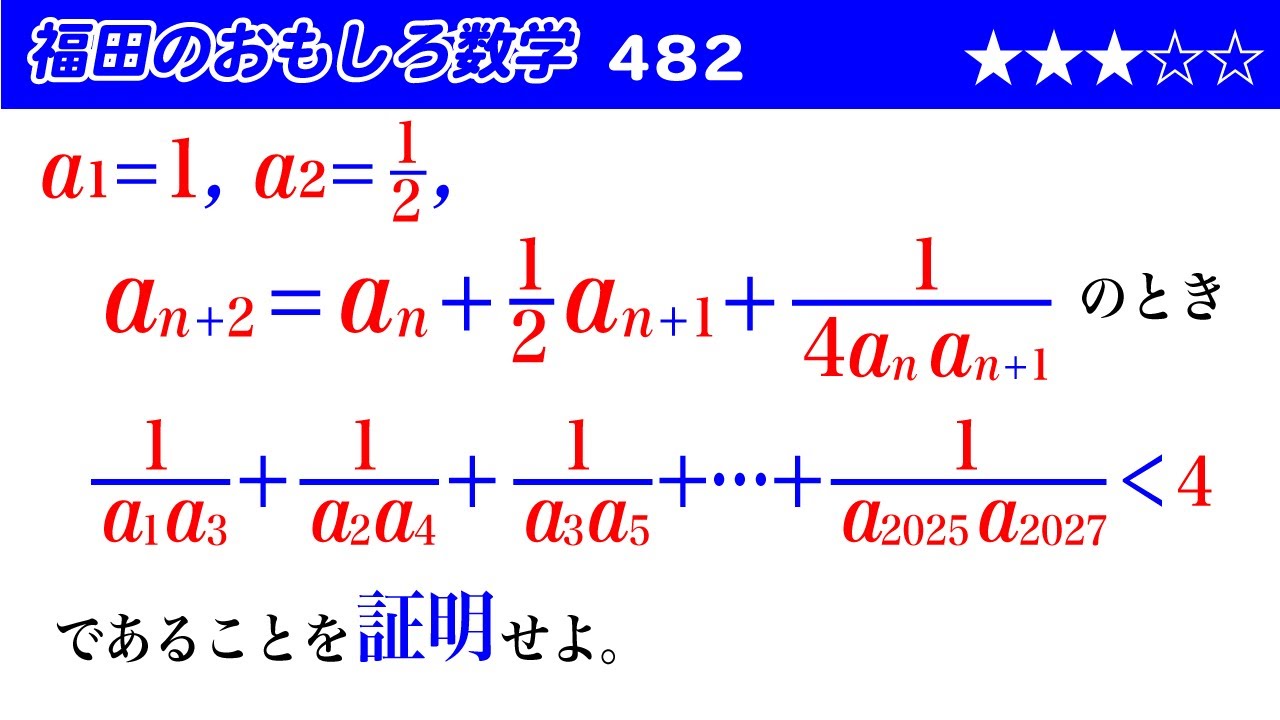
福田のおもしろ数学482〜漸化式で定まる数列に関する不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数列#漸化式#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$a_1=1,a_2=\dfrac{1}{2},$
$a_{n+2}=a_n+\dfrac{1}{2}a_{n+1}+\dfrac{1}{4a_na_{n+1}}$のとき、
$\dfrac{1}{a_1a_3}+\dfrac{1}{a_2a_4}+\dfrac{1}{a_3a_5}+\cdots +\dfrac{1}{a_{2025}a_{2027}}\lt 4$
であることを証明せよ。
この動画を見る
$a_1=1,a_2=\dfrac{1}{2},$
$a_{n+2}=a_n+\dfrac{1}{2}a_{n+1}+\dfrac{1}{4a_na_{n+1}}$のとき、
$\dfrac{1}{a_1a_3}+\dfrac{1}{a_2a_4}+\dfrac{1}{a_3a_5}+\cdots +\dfrac{1}{a_{2025}a_{2027}}\lt 4$
であることを証明せよ。
【数B】【数列】数学的帰納法4 ※問題文は概要欄
単元：
#数列#漸化式#数学(高校生)#数B
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#中高教材#数列
指導講師：
理数個別チャンネル
問題文全文(内容文)：
条件$a_1=3,{a_n}^2=(n+1)a_{n+1}+1$
によって定められる数列$\{a_n\}$がある。
(1) $a_2,a_3,a_4$を求めよ。
(2) 第$n$項$a_n$を推測して、
その結果を数学的帰納法によって証明せよ。
この動画を見る
条件$a_1=3,{a_n}^2=(n+1)a_{n+1}+1$
によって定められる数列$\{a_n\}$がある。
(1) $a_2,a_3,a_4$を求めよ。
(2) 第$n$項$a_n$を推測して、
その結果を数学的帰納法によって証明せよ。
【数B】【数列】数学的帰納法3 ※問題文は概要欄
単元：
#数列#漸化式#数学(高校生)#数B
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#中高教材#数列
指導講師：
理数個別チャンネル
問題文全文(内容文)：
(1) $n$は自然数とする。
$5^{n+1}+6^{2n-1}$は31で割り切れることを、
数学的帰納法によって証明せよ。
(2) $n$は2以上の自然数とする。
$2^{3n}-7n-1$は49で割り切れることを、
数学的帰納法によって証明せよ。
この動画を見る
(1) $n$は自然数とする。
$5^{n+1}+6^{2n-1}$は31で割り切れることを、
数学的帰納法によって証明せよ。
(2) $n$は2以上の自然数とする。
$2^{3n}-7n-1$は49で割り切れることを、
数学的帰納法によって証明せよ。
【数B】【数列】数学的帰納法2 ※問題文は概要欄
単元：
#数列#漸化式#数学(高校生)#数B
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#中高教材#数列
指導講師：
理数個別チャンネル
問題文全文(内容文)：
数学的帰納法によって次の不等式を証明せよ。
(1) $n$が自然数のとき$1^2+2^2+3^2+\cdots+n^2< \dfrac{(n+1)^3}3$
(2) $n$が4以上の自然数のとき$2^n>3n+1$
(3) $n$が3以上の自然数、$h>0$のとき$(1+h)^n> 1+nh^2$
この動画を見る
数学的帰納法によって次の不等式を証明せよ。
(1) $n$が自然数のとき$1^2+2^2+3^2+\cdots+n^2< \dfrac{(n+1)^3}3$
(2) $n$が4以上の自然数のとき$2^n>3n+1$
(3) $n$が3以上の自然数、$h>0$のとき$(1+h)^n> 1+nh^2$
【数B】【数列】数学的帰納法1 ※問題文は概要欄
単元：
#数列#漸化式#数学(高校生)#数B
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#中高教材#数列
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$n$は自然数とする。数学的帰納法によって、次の等式を証明せよ。
(1) $1+2\cdot\dfrac32+\cdots+n(\dfrac32)^{n-1}=2(n-2)(\dfrac32)^n+4$
(2) $(n+1)(n+2)(n+3)\cdots(2n)=2^n\cdot1\cdot3\cdot5\cdots(2n-1)$
この動画を見る
$n$は自然数とする。数学的帰納法によって、次の等式を証明せよ。
(1) $1+2\cdot\dfrac32+\cdots+n(\dfrac32)^{n-1}=2(n-2)(\dfrac32)^n+4$
(2) $(n+1)(n+2)(n+3)\cdots(2n)=2^n\cdot1\cdot3\cdot5\cdots(2n-1)$
福田の数学〜早稲田大学理工学部2025第3問〜完全順列と漸化式
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
$1$から$n$までの異なる自然数が$1$つずつ書かれた
$n$枚のカードが一列に並んでいる。
このとき、
どのカードも現在とは異なる位置に移動するよう
並べ替えてできる順列の総数を$a_n$で表し、
並べ方の総数$n!$に閉める$a_n$の割合を$p_n$で表す。
例えば、$a_1=0,p_1=0,a_2=1,p_2=\dfrac{1}{2},$
$a_3=2,p_3=\dfrac{1}{3}$である。
(1)$a_4$の値を求めよ。
(2)$n\geqq 3$のとき、$a_n$を$a_{n-1}$と
$a_{n-2}$を用いて表せ。
(3)$n\geqq 2$のとき、$p_n-p_{n-1}$を
$n$を用いて表せ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{3}$
$1$から$n$までの異なる自然数が$1$つずつ書かれた
$n$枚のカードが一列に並んでいる。
このとき、
どのカードも現在とは異なる位置に移動するよう
並べ替えてできる順列の総数を$a_n$で表し、
並べ方の総数$n!$に閉める$a_n$の割合を$p_n$で表す。
例えば、$a_1=0,p_1=0,a_2=1,p_2=\dfrac{1}{2},$
$a_3=2,p_3=\dfrac{1}{3}$である。
(1)$a_4$の値を求めよ。
(2)$n\geqq 3$のとき、$a_n$を$a_{n-1}$と
$a_{n-2}$を用いて表せ。
(3)$n\geqq 2$のとき、$p_n-p_{n-1}$を
$n$を用いて表せ。
$2025$年早稲田大学理工学部過去問題
【数B】【数列】漸化式8 ※問題文は概要欄
単元：
#数列#漸化式#数学(高校生)#数B
指導講師：
理数個別チャンネル
問題文全文(内容文)：
表の出る確率が1/3である硬貨を投げて、
表が出たら点数を1点増やし、
裏が出たら点数はそのままとするゲームについて考える。
0点から始めて、硬貨を$n$回投げたときの点数が偶数である確率$P_n$を求めよ。
ただし、0は偶数と考える。
この動画を見る
表の出る確率が1/3である硬貨を投げて、
表が出たら点数を1点増やし、
裏が出たら点数はそのままとするゲームについて考える。
0点から始めて、硬貨を$n$回投げたときの点数が偶数である確率$P_n$を求めよ。
ただし、0は偶数と考える。
【数B】【数列】漸化式7 ※問題文は概要欄
単元：
#数列#漸化式#数学(高校生)#数B
指導講師：
理数個別チャンネル
問題文全文(内容文)：
図のように、1辺の長さ1の正方形の各辺を2:1に内分する
4点を結んでできる正方形の面積を$S_1$とする。
同様に、新しくできた正方形の各辺を2:1に内分する
4点を結んでできる正方形の面積を$S_2$とする。
以下同様に、この操作を$n$回行った後にできる
正方形の面積を$S_n$とする。
(1) $S_n$をnの式で表せ。
(2) $\displaystyle \sum_{k=1}^n S_n$を求めよ。
この動画を見る
図のように、1辺の長さ1の正方形の各辺を2:1に内分する
4点を結んでできる正方形の面積を$S_1$とする。
同様に、新しくできた正方形の各辺を2:1に内分する
4点を結んでできる正方形の面積を$S_2$とする。
以下同様に、この操作を$n$回行った後にできる
正方形の面積を$S_n$とする。
(1) $S_n$をnの式で表せ。
(2) $\displaystyle \sum_{k=1}^n S_n$を求めよ。
福田の数学〜慶應義塾大学理工学部2025第3問〜確率漸化式
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
点$P, Q$を数直線の原点におき、
$1$個のさいころを投げて
出た目に応じて$P, Q$を動かす。
偶数の目が出たときは$P$を正の向きに$1$だけ動かし、
$5$または$6$の目が出たときは
$Q$を正の向きに$1$だけ動かす。
たとえば、$6$の目が出たときは$P, Q$をともに
正の向きに$1$だけ動かす。
$P$と$Q$の距離が初めて$2$となるまで
さいころを投げ続けることとし、
$P$と$Q$の距離が$2$となったら、
それ以降はさいころを投げない。
$n$回さいころを投げて$P$と$Q$の距離が
$2$となる確率を$p_n$とする。
(1)$P_2 = \boxed{シ}$である。
(2)$n$回さいころを投げて、
$P$が$Q$よりも正の向きに
$1$だけ進んでいる確率を$x_n$、
$P$と$Q$が同じ位置にある確率を$y_n$、
$Q$が$P$よりも正の向きに$1$だけ進んでいる確率を
$z_n$とすると、
$y_{n+1}=\boxed{ス}x_n+\boxed{セ}y_n+\boxed{ソ}z_n$
という関係式が成立する。
また、$x_n=\boxed{タ}z_n$が成り立つ。
ただし、$\boxed{ス}$～$\boxed{タ}$には数を記入すること。
(3)関係式
$z_{n+1}+\alpha y_{n+1}=\beta(z_n+\alpha y_n)$
を満たす定数の組$(\alpha,\beta)$は$\boxed{チ}$と$\boxed{ツ}$の$2$組ある。
(4)$p_n$を$n$を用いて表すと$p_n=\boxed{テ}$となる。
$2025$年慶應義塾大学理工学部過去問題
この動画を見る
$\boxed{3}$
点$P, Q$を数直線の原点におき、
$1$個のさいころを投げて
出た目に応じて$P, Q$を動かす。
偶数の目が出たときは$P$を正の向きに$1$だけ動かし、
$5$または$6$の目が出たときは
$Q$を正の向きに$1$だけ動かす。
たとえば、$6$の目が出たときは$P, Q$をともに
正の向きに$1$だけ動かす。
$P$と$Q$の距離が初めて$2$となるまで
さいころを投げ続けることとし、
$P$と$Q$の距離が$2$となったら、
それ以降はさいころを投げない。
$n$回さいころを投げて$P$と$Q$の距離が
$2$となる確率を$p_n$とする。
(1)$P_2 = \boxed{シ}$である。
(2)$n$回さいころを投げて、
$P$が$Q$よりも正の向きに
$1$だけ進んでいる確率を$x_n$、
$P$と$Q$が同じ位置にある確率を$y_n$、
$Q$が$P$よりも正の向きに$1$だけ進んでいる確率を
$z_n$とすると、
$y_{n+1}=\boxed{ス}x_n+\boxed{セ}y_n+\boxed{ソ}z_n$
という関係式が成立する。
また、$x_n=\boxed{タ}z_n$が成り立つ。
ただし、$\boxed{ス}$～$\boxed{タ}$には数を記入すること。
(3)関係式
$z_{n+1}+\alpha y_{n+1}=\beta(z_n+\alpha y_n)$
を満たす定数の組$(\alpha,\beta)$は$\boxed{チ}$と$\boxed{ツ}$の$2$組ある。
(4)$p_n$を$n$を用いて表すと$p_n=\boxed{テ}$となる。
$2025$年慶應義塾大学理工学部過去問題
福田のおもしろ数学472〜漸化式で与えられた数列の逆数の和
単元：
#数列#数列とその和（等差・等比・階差・Σ）#漸化式#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$a_1=2,a_{n+1}={a_n}^2-a_n+1$のとき
$\dfrac{1}{a_1}+\dfrac{1}{a_2}+\dfrac{1}{a_3}+･･･+\dfrac{1}{a_{2025}}\lt 1$
を証明して下さい。
この動画を見る
$a_1=2,a_{n+1}={a_n}^2-a_n+1$のとき
$\dfrac{1}{a_1}+\dfrac{1}{a_2}+\dfrac{1}{a_3}+･･･+\dfrac{1}{a_{2025}}\lt 1$
を証明して下さい。
【数B】【数列】漸化式6 ※問題文は概要欄
単元：
#数列#漸化式#数学(高校生)#数B
指導講師：
理数個別チャンネル
問題文全文(内容文)：
平面上に$n$個の円があって、それらのどの2つも異なる2点で交わり、
またどの3つも1点で交わらないとする。
これらの$n$個の円が平面を$a_n$個の部分に分けるとき、$\{a_n\}$をnの式で表せ。
この動画を見る
平面上に$n$個の円があって、それらのどの2つも異なる2点で交わり、
またどの3つも1点で交わらないとする。
これらの$n$個の円が平面を$a_n$個の部分に分けるとき、$\{a_n\}$をnの式で表せ。
福田の数学〜慶應義塾大学薬学部2025第2問〜薬の効果を検定する
単元：
#大学入試過去問(数学)#確率分布と統計的な推測#確率分布#学校別大学入試過去問解説(数学)#標本調査#慶應義塾大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
薬を病気にかかっている患者に投与すると、
投与された患者のうちの$40$% に治療の効果が認められる。
この薬に対し、新しく開発した薬$\beta$の方が
治療の効果が認められる割合が高いかどうか、
有意水準$5$%で検定を行う。
病気$X$にかかっている患者から無作為に抽出した$1000$人に
薬を投与したとき、
$n$人以上に治療の効果が認められると、
薬$\alpha$よりも薬$\beta$の方が効果が認められる割合が高いと判断される。
ただし、薬の治療効果の標本比率を$R$、母比率を$p$とする。
(1) 帰無仮説$H_0$と対立仮説$H_1$に設定する式は
$H_0:\boxed{チ},H_1:\boxed{ツ}$である。
$H_0$が正しいと仮定するとき、
$R$は近似的に正規分布$N(\boxed{テ},\boxed{ト})$に従う。
(2) (1) をふまえ、
$n$のとりうる最小の値を求めなさい。
ただし、解答に
「標準正規分布」と「棄却域」という言葉を含めなさい。
なお、
$\sqrt{2}=1.4,\sqrt3=1.7,\sqrt5 = 2.2$として計算し、
必要に応じて正規分布表を用いなさい。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{2}$
薬を病気にかかっている患者に投与すると、
投与された患者のうちの$40$% に治療の効果が認められる。
この薬に対し、新しく開発した薬$\beta$の方が
治療の効果が認められる割合が高いかどうか、
有意水準$5$%で検定を行う。
病気$X$にかかっている患者から無作為に抽出した$1000$人に
薬を投与したとき、
$n$人以上に治療の効果が認められると、
薬$\alpha$よりも薬$\beta$の方が効果が認められる割合が高いと判断される。
ただし、薬の治療効果の標本比率を$R$、母比率を$p$とする。
(1) 帰無仮説$H_0$と対立仮説$H_1$に設定する式は
$H_0:\boxed{チ},H_1:\boxed{ツ}$である。
$H_0$が正しいと仮定するとき、
$R$は近似的に正規分布$N(\boxed{テ},\boxed{ト})$に従う。
(2) (1) をふまえ、
$n$のとりうる最小の値を求めなさい。
ただし、解答に
「標準正規分布」と「棄却域」という言葉を含めなさい。
なお、
$\sqrt{2}=1.4,\sqrt3=1.7,\sqrt5 = 2.2$として計算し、
必要に応じて正規分布表を用いなさい。
$2025$年慶應義塾大学薬学部過去問題
福田のおもしろ数学465〜最小公倍数を含んだ3項間漸化式
単元：
#数列#漸化式#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$x_1=19,x_2=95$
$x_{n+2}=1cm(x_{n+1},x_n)+x_n$
を満たす数列$\{x_n\}$に対して
$x_{2025}$と$x_{2026}$の最大公約数を求めよ。
＊$1cm(a,b)$は$a$と$b$の最小公倍数を表す。
この動画を見る
$x_1=19,x_2=95$
$x_{n+2}=1cm(x_{n+1},x_n)+x_n$
を満たす数列$\{x_n\}$に対して
$x_{2025}$と$x_{2026}$の最大公約数を求めよ。
＊$1cm(a,b)$は$a$と$b$の最小公倍数を表す。
【数B】【数列】漸化式5 ※問題文は概要欄
単元：
#数列#漸化式#数学(高校生)#数B
指導講師：
理数個別チャンネル
問題文全文(内容文)：
数列$\{a_n\}$の初項から第$n$項までの
和$S_n$が$S_n=2a_n-n$であるとき、
数列$\{a_n\}$の一般項を求めよ。
この動画を見る
数列$\{a_n\}$の初項から第$n$項までの
和$S_n$が$S_n=2a_n-n$であるとき、
数列$\{a_n\}$の一般項を求めよ。
【数B】【数列】漸化式4 ※問題文は概要欄
単元：
#数列#漸化式#数学(高校生)#数B
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#中高教材#数列
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の条件によって定められる
数列 $\{a_n\}$ の一般項を求めよ。
1) $a_1 = 1$, $\quad (n+1) a_{n+1} = n a_n$
(2) $a_1 = 1$, $n a_{n+1} = (n+1) a_n$
この動画を見る
次の条件によって定められる
数列 $\{a_n\}$ の一般項を求めよ。
1) $a_1 = 1$, $\quad (n+1) a_{n+1} = n a_n$
(2) $a_1 = 1$, $n a_{n+1} = (n+1) a_n$
【数B】【数列】漸化式3 ※問題文は概要欄
単元：
#数列#漸化式#数学(高校生)#数B
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#中高教材#数列
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の条件によって定められる
数列 $\{a_n\}$ の一般項を求めよ。
$a_1$ = $1$, $a_{n+1} = 2a_n + 3n $
この動画を見る
次の条件によって定められる
数列 $\{a_n\}$ の一般項を求めよ。
$a_1$ = $1$, $a_{n+1} = 2a_n + 3n $
【数B】【数列】漸化式2 ※問題文は概要欄
単元：
#数列#漸化式#数学(高校生)#数B
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#中高教材#数列
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の条件によって定められる
数列 $\{a_n\}$ の一般項を求めよ。
(1)$a_1 = 10$, $a_{n+1} = 2a_n + 2^{n+2}$
(2)$a_1 = 3$, $a_{n+1} = 6a_n + 3^{n+1}$
この動画を見る
次の条件によって定められる
数列 $\{a_n\}$ の一般項を求めよ。
(1)$a_1 = 10$, $a_{n+1} = 2a_n + 2^{n+2}$
(2)$a_1 = 3$, $a_{n+1} = 6a_n + 3^{n+1}$