 関数の変化(グラフ・最大最小・方程式・不等式)
関数の変化(グラフ・最大最小・方程式・不等式)
 関数の変化(グラフ・最大最小・方程式・不等式)
関数の変化(グラフ・最大最小・方程式・不等式)
【数Ⅲ】【微分とその応用】関数の最大と最小7 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数の最大値、最小値を求めよ。
(1) $ \displaystyle y= \frac{x-1}{x^2+1}$
(2) $y=x- \sqrt{x^2-1}$
(3) $y= \sqrt{x^2+1}+ \sqrt{(x-3)^2+4}$
(4) $y=|x|e^x$
この動画を見る
次の関数の最大値、最小値を求めよ。
(1) $ \displaystyle y= \frac{x-1}{x^2+1}$
(2) $y=x- \sqrt{x^2-1}$
(3) $y= \sqrt{x^2+1}+ \sqrt{(x-3)^2+4}$
(4) $y=|x|e^x$
【数Ⅲ】【微分とその応用】関数の最大と最小6 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数 $f(x)=x+ \dfrac{a}{x-1}$の極大値が$-1$となるように、定数$a$の値を定めよ。ただし、$a \neq 0$とする。
この動画を見る
関数 $f(x)=x+ \dfrac{a}{x-1}$の極大値が$-1$となるように、定数$a$の値を定めよ。ただし、$a \neq 0$とする。
【数Ⅲ】【微分とその応用】関数の最大と最小5 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1) 関数 $y=xe^{-x^2+x}$の極値を求めよ。
(2) $2$次関数 $f(x)=ax^2+bx+c$に対して、$F(x)=xe^{f(x)}$で定義された関数$y=F(x)$が極値を持つための、定数$a,b,c$についての必要十分条件を求めよ。
この動画を見る
(1) 関数 $y=xe^{-x^2+x}$の極値を求めよ。
(2) $2$次関数 $f(x)=ax^2+bx+c$に対して、$F(x)=xe^{f(x)}$で定義された関数$y=F(x)$が極値を持つための、定数$a,b,c$についての必要十分条件を求めよ。
福田のおもしろ数学395〜2変数関数の最大値

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$x\gt 0,y\gt 0$のとき、
$f(x,y=min \left(x,\dfrac{y}{x^2+y^2}\right)$
の最大値を求めて下さい。
*$min(a,b)$は$a,b$の大きくない方の値を
意味します。
この動画を見る
$x\gt 0,y\gt 0$のとき、
$f(x,y=min \left(x,\dfrac{y}{x^2+y^2}\right)$
の最大値を求めて下さい。
*$min(a,b)$は$a,b$の大きくない方の値を
意味します。
福田のおもしろ数学392〜2変数関数についての関数方程式

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
任意の正の整数$x,y$に対して定義された関数$f$は
$f(x,x)=x,f(x,y)=f(y,x)(x+y)f(x,y)=$
$yf(x,x+y)$
を満たしている。
このような関数$f(x,y)$をすべて求めよ。
この動画を見る
任意の正の整数$x,y$に対して定義された関数$f$は
$f(x,x)=x,f(x,y)=f(y,x)(x+y)f(x,y)=$
$yf(x,x+y)$
を満たしている。
このような関数$f(x,y)$をすべて求めよ。
福田のおもしろ数学391〜簡単な関数方程式

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
任意の実数$x,y$に対して$f(0)=1$、
$f(xy+1)=f(x)f(y)-f(y)-x+2$
が成り立つような実数値関数$f(x)$をすべて求めて下さい。
この動画を見る
任意の実数$x,y$に対して$f(0)=1$、
$f(xy+1)=f(x)f(y)-f(y)-x+2$
が成り立つような実数値関数$f(x)$をすべて求めて下さい。
【数Ⅲ】【微分とその応用】不等式の応用6 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
aは定数とする。次の方程式の異なる実数解の個数を求めよ。
(2)では、必要ならば$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x}{e^x} =0$を用いてよい。
(1) $x^3-ax+2a$=0
(2) $2x-1=ae^{ -x }$
この動画を見る
aは定数とする。次の方程式の異なる実数解の個数を求めよ。
(2)では、必要ならば$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x}{e^x} =0$を用いてよい。
(1) $x^3-ax+2a$=0
(2) $2x-1=ae^{ -x }$
【数Ⅲ】【微分とその応用】不等式の応用5 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
教材:
#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のことが成り立つことを証明せよ。
$0≦x≦1$のとき
$1-x+x²e^x≦e^x≦1+x+\displaystyle \frac{1}{2}
x²e^x$
この動画を見る
次のことが成り立つことを証明せよ。
$0≦x≦1$のとき
$1-x+x²e^x≦e^x≦1+x+\displaystyle \frac{1}{2}
x²e^x$
【数Ⅲ】【微分とその応用】不等式の応用4 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x→∞$のとき、$y=x$が$y=\log x$と比較して、
より急速に増大すること、すなわち
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x}{\log x} =\infty$
が成り立つことを証明せよ。
ただし、まずは次の①~③のどれか1つを証明し、それを利用せよ。
①$x≧4$のとき、$x^2>\log x$が成り立つ
②$x≧4$のとき、$x>\log x$が成り立つ
③$x≧4$のとき、$\sqrt{x}>\log x$が成り立つ
この動画を見る
$x→∞$のとき、$y=x$が$y=\log x$と比較して、
より急速に増大すること、すなわち
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x}{\log x} =\infty$
が成り立つことを証明せよ。
ただし、まずは次の①~③のどれか1つを証明し、それを利用せよ。
①$x≧4$のとき、$x^2>\log x$が成り立つ
②$x≧4$のとき、$x>\log x$が成り立つ
③$x≧4$のとき、$\sqrt{x}>\log x$が成り立つ
【数Ⅲ】【微分とその応用】不等式の応用3 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
すべての正の数xに対して、
不等式$\sqrt{x}>a\log x$が成り立つような定数aの値の範囲を求めよ。
この動画を見る
すべての正の数xに対して、
不等式$\sqrt{x}>a\log x$が成り立つような定数aの値の範囲を求めよ。
【数Ⅲ】【微分とその応用】不等式の応用2 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のことが成り立つことを証明せよ。
(1) $b≧a>0$のとき $logb-loga≧\displaystyle \frac{2(b-a)}{(b+a)}$
(2) $0<α<β≦\displaystyle \frac{π}{2}$のとき $\displaystyle \frac{α}{β}<\displaystyle \frac{sin α}{sin β}$
この動画を見る
次のことが成り立つことを証明せよ。
(1) $b≧a>0$のとき $logb-loga≧\displaystyle \frac{2(b-a)}{(b+a)}$
(2) $0<α<β≦\displaystyle \frac{π}{2}$のとき $\displaystyle \frac{α}{β}<\displaystyle \frac{sin α}{sin β}$
【数Ⅲ】【微分とその応用】不等式の応用1 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x>0$のとき、次の不等式を証明せよ。
(1) $sin x>x-\displaystyle \frac{x^2}{2}$
(2) $1-\displaystyle \frac{x}{2}<\displaystyle \frac{1}{\sqrt{1+x}}<1-\displaystyle \frac{x}{2}+\displaystyle \frac{3x^2}{8}$
この動画を見る
$x>0$のとき、次の不等式を証明せよ。
(1) $sin x>x-\displaystyle \frac{x^2}{2}$
(2) $1-\displaystyle \frac{x}{2}<\displaystyle \frac{1}{\sqrt{1+x}}<1-\displaystyle \frac{x}{2}+\displaystyle \frac{3x^2}{8}$
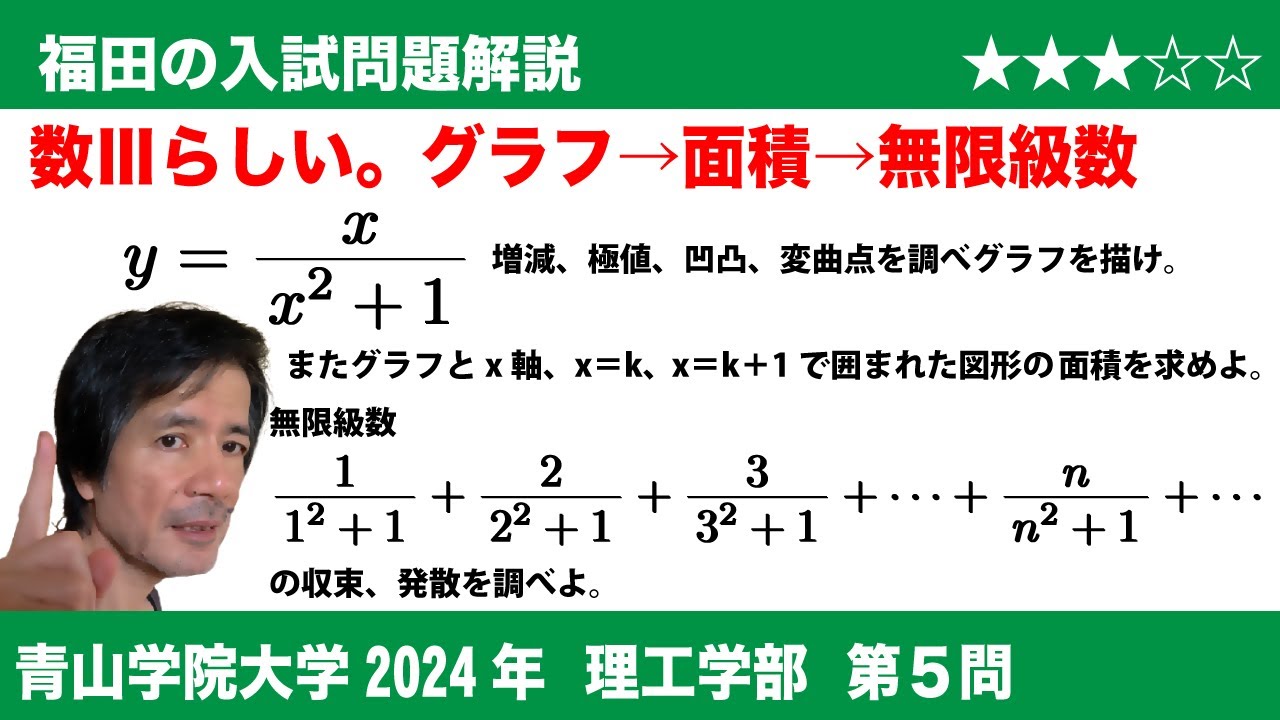
福田の数学〜青山学院大学2024理工学部第5問〜関数の増減と無限級数の収束発散の判定
単元:
#関数と極限#微分とその応用#積分とその応用#数列の極限#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
以下の問いに答えよ。
$(1)$ 関数 $\displaystyle{y=\frac{x}{x^2+1}}$ の増減、極値、グラフの凹凸および変曲点を調べて、そのグラフを描け。
$(2)$ $k$ を自然数とする。曲線 $\displaystyle{y=\frac{x}{x^2+1}}$ と $x$ 軸および2直線 $x=k$, $x=k+1$ で囲まれた図形の面積を $k$ を用いて表せ。
$(3)$ 無限級数
\begin{equation*}
\frac{1}{1^2+1}+\frac{2}{2^2+1}+\frac{3}{3^2+1}+\cdots+\frac{n}{n^2+1}+\cdots
\end{equation*}
の収束、発散を調べよ。
この動画を見る
以下の問いに答えよ。
$(1)$ 関数 $\displaystyle{y=\frac{x}{x^2+1}}$ の増減、極値、グラフの凹凸および変曲点を調べて、そのグラフを描け。
$(2)$ $k$ を自然数とする。曲線 $\displaystyle{y=\frac{x}{x^2+1}}$ と $x$ 軸および2直線 $x=k$, $x=k+1$ で囲まれた図形の面積を $k$ を用いて表せ。
$(3)$ 無限級数
\begin{equation*}
\frac{1}{1^2+1}+\frac{2}{2^2+1}+\frac{3}{3^2+1}+\cdots+\frac{n}{n^2+1}+\cdots
\end{equation*}
の収束、発散を調べよ。
福田の数学〜明治大学2024理工学部第2問〜三角関数の増減と面積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=\sin{3x}-\sqrt3\cos{2x}$とし、座標平面上の曲線$y=f(x)$を$C$とする。
(1) 点$(0,f(0))$における曲線$C$の接線の方程式は$y=\boxed{あ}$である。
(2) $t$についての整式$g(t)$で、$f'(x)=g(\sin x)\cos x$が成り立つものを求めると、$g(t)=\boxed{い}$である。
(3) $x>0$の範囲で、$f'(x)=0$となる$x$の値を小さい順に$x_1,x_2,x_3,\cdots$とすると、$x_1=\boxed{う},x_2=\boxed{え},x_3=\boxed{お}$である。
(4) $0\leqq x\leqq \pi$の範囲での$f(x)$の最大値は$\boxed{か}$、最小値は$\boxed{き}$である。
(5) (4)で定めた$x_1$と$x_3$に対して、2点$(x_1,f(x_1)),(x_3,f(x_3))$を通る直線を$l$とする。このとき、$x_1\leqq x\leqq x_3$の範囲において直線$l$と曲線$C$で囲まれた部分の面積は$\boxed{く}$である。
この動画を見る
$f(x)=\sin{3x}-\sqrt3\cos{2x}$とし、座標平面上の曲線$y=f(x)$を$C$とする。
(1) 点$(0,f(0))$における曲線$C$の接線の方程式は$y=\boxed{あ}$である。
(2) $t$についての整式$g(t)$で、$f'(x)=g(\sin x)\cos x$が成り立つものを求めると、$g(t)=\boxed{い}$である。
(3) $x>0$の範囲で、$f'(x)=0$となる$x$の値を小さい順に$x_1,x_2,x_3,\cdots$とすると、$x_1=\boxed{う},x_2=\boxed{え},x_3=\boxed{お}$である。
(4) $0\leqq x\leqq \pi$の範囲での$f(x)$の最大値は$\boxed{か}$、最小値は$\boxed{き}$である。
(5) (4)で定めた$x_1$と$x_3$に対して、2点$(x_1,f(x_1)),(x_3,f(x_3))$を通る直線を$l$とする。このとき、$x_1\leqq x\leqq x_3$の範囲において直線$l$と曲線$C$で囲まれた部分の面積は$\boxed{く}$である。
福田の数学〜中央大学2024理工学部第1問〜3つの関数の大小関係と絶対不等式

単元:
#数Ⅰ#2次関数#2次関数とグラフ#微分とその応用#積分とその応用#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$a$ を $1$ 以上の実数、$b$ を実数とし、関数 $f(x), \, g(x), \, h(x)$ を以下で定める。
$\displaystyle f(x)=-|2|x|-1|, \quad g(x)=ax+b, \quad h(x)=e^x$
$(1)$ すべての実数 $x$ に対して $f(x) \leq g(x)$ が成り立つ。$(a, \, b)$ の範囲は、条件 $a \geq 1$ の下では、$b \geq 1$ のとき $a \leq \fbox{ア}$ であり、$\frac{1}{2} \leq b \leq 1$ のとき $a \leq \fbox{イ}$ である。$b < \frac{1}{2}$ のとき条件を満たす $a$ は存在しない。
$(2)$ 実数$p$ に対し、$x=p$ における $y=h(x)$ の接線の方程式は $y=\fbox{ウ}$ である。したがって $a=e^p$ のとき、すべての実数 $x$ に対して $g(x) \leq h(x)$ が成り立つのは $b \leq \fbox{エ}$ のときであり、これは $a$ と $b$ の関係式として $b \leq \fbox{オ}$
$(3)$ すべての実数 $x$ に対し、$f(x) \leq g(x) \leq h(x)$ が成り立つような $(a, \, b)$ 全体のなす領域を $D$ とする。$D$ における $a$ の最大値は $\fbox{カ}$ である。また、$D$ の面積は $\fbox{キ}$ である。
この動画を見る
$a$ を $1$ 以上の実数、$b$ を実数とし、関数 $f(x), \, g(x), \, h(x)$ を以下で定める。
$\displaystyle f(x)=-|2|x|-1|, \quad g(x)=ax+b, \quad h(x)=e^x$
$(1)$ すべての実数 $x$ に対して $f(x) \leq g(x)$ が成り立つ。$(a, \, b)$ の範囲は、条件 $a \geq 1$ の下では、$b \geq 1$ のとき $a \leq \fbox{ア}$ であり、$\frac{1}{2} \leq b \leq 1$ のとき $a \leq \fbox{イ}$ である。$b < \frac{1}{2}$ のとき条件を満たす $a$ は存在しない。
$(2)$ 実数$p$ に対し、$x=p$ における $y=h(x)$ の接線の方程式は $y=\fbox{ウ}$ である。したがって $a=e^p$ のとき、すべての実数 $x$ に対して $g(x) \leq h(x)$ が成り立つのは $b \leq \fbox{エ}$ のときであり、これは $a$ と $b$ の関係式として $b \leq \fbox{オ}$
$(3)$ すべての実数 $x$ に対し、$f(x) \leq g(x) \leq h(x)$ が成り立つような $(a, \, b)$ 全体のなす領域を $D$ とする。$D$ における $a$ の最大値は $\fbox{カ}$ である。また、$D$ の面積は $\fbox{キ}$ である。
福田の数学〜筑波大学2024理系第4問〜媒介変数表示で表された曲線のグラフと面積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標平面において、媒介変数表示$x=-t(t-\dfrac32), y=\sin\pi t ~~ (0\leqq t \leqq 1)$で表される曲線を$C$とする。以下の問いに答えよ
(1) 定積分$\displaystyle \int_0^1 t\sin\pi t dt$を求めよ。
(2) 実数$a$に対し、曲線$C$と直線$x=a$の共有点の個数を求めよ。
(3) 曲線$C$と$x$軸で囲まれた図形の面積を求めよ。
この動画を見る
座標平面において、媒介変数表示$x=-t(t-\dfrac32), y=\sin\pi t ~~ (0\leqq t \leqq 1)$で表される曲線を$C$とする。以下の問いに答えよ
(1) 定積分$\displaystyle \int_0^1 t\sin\pi t dt$を求めよ。
(2) 実数$a$に対し、曲線$C$と直線$x=a$の共有点の個数を求めよ。
(3) 曲線$C$と$x$軸で囲まれた図形の面積を求めよ。
福田のおもしろ数学209〜無理不等式の解き方

単元:
#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#関数の変化(グラフ・最大最小・方程式・不等式)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt{x}+sqrt{x-2} < 3$を解いて下さい。
この動画を見る
$\sqrt{x}+sqrt{x-2} < 3$を解いて下さい。
【演習!】複雑な関数の最大値と最小値の求め方について解説しました!【数学III】

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
3rd School
問題文全文(内容文):
関数$f(x)=x-\sin 2x$における最大値と最小値を求めよ
この動画を見る
関数$f(x)=x-\sin 2x$における最大値と最小値を求めよ
福田のおもしろ数学151〜面積を2等分する直線が存在する証明

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
左の図形(※動画参照)の面積を2等分する直線が存在することを証明してください。
この動画を見る
左の図形(※動画参照)の面積を2等分する直線が存在することを証明してください。
福田の数学〜名古屋大学2024年理系第1問〜接線の本数と整数解

単元:
#微分とその応用#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 関数$f(x)$=$\sqrt x$+$\displaystyle\frac{2}{\sqrt x}$ ($x$>0)に対して、$y$=$f(x)$のグラフを$C$とする。
(1)$f(x)$の極値を求めよ。
(2)$x$軸上の点P($t$, 0)から$C$にちょうど2本の接線を引くことができるとする。
そのような実数$t$の値の範囲を求めよ。
(3)(2)において、$C$の2つの接点の$x$座標を$\alpha$, $\beta$($\alpha$<$\beta$)とする。$\alpha$, $\beta$がともに整数であるような組($\alpha$, $\beta$)をすべて求めよ。
この動画を見る
$\Large\boxed{1}$ 関数$f(x)$=$\sqrt x$+$\displaystyle\frac{2}{\sqrt x}$ ($x$>0)に対して、$y$=$f(x)$のグラフを$C$とする。
(1)$f(x)$の極値を求めよ。
(2)$x$軸上の点P($t$, 0)から$C$にちょうど2本の接線を引くことができるとする。
そのような実数$t$の値の範囲を求めよ。
(3)(2)において、$C$の2つの接点の$x$座標を$\alpha$, $\beta$($\alpha$<$\beta$)とする。$\alpha$, $\beta$がともに整数であるような組($\alpha$, $\beta$)をすべて求めよ。
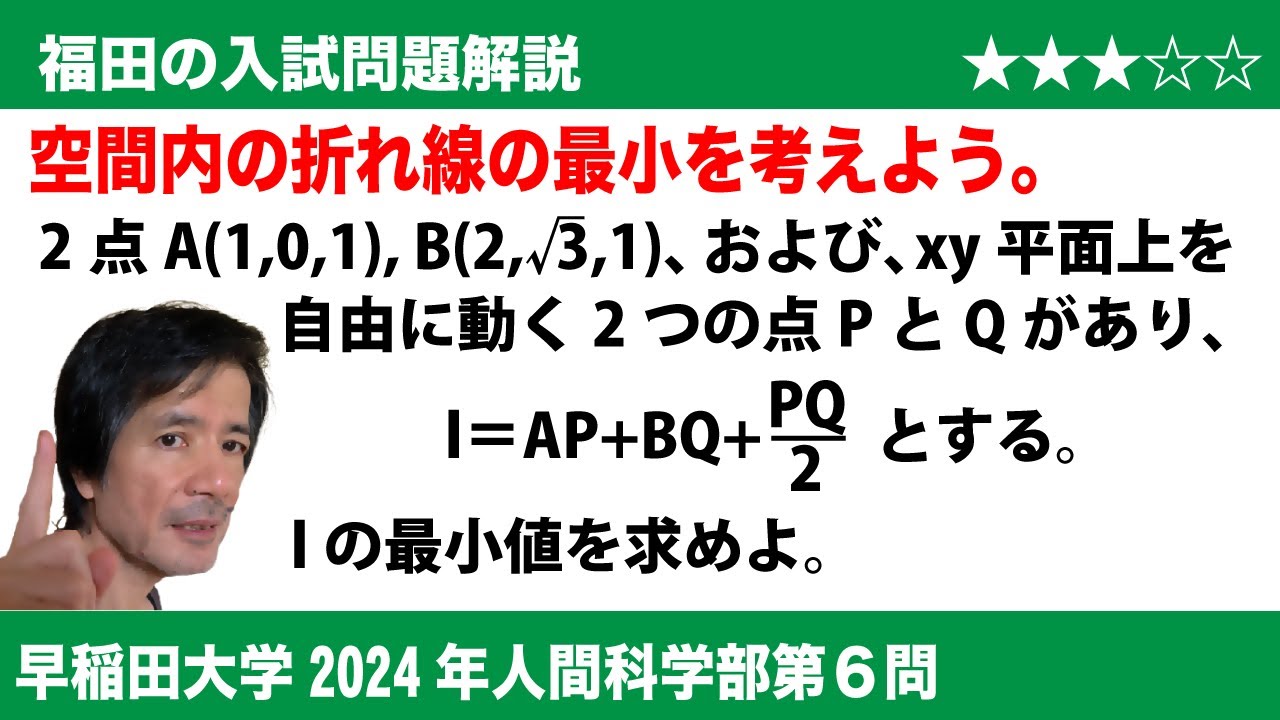
福田の数学〜早稲田大学2024年人間科学部第6問〜空間内の折れ線の長さの最小値
単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ 2点A(1,0,1)とB(2, $\sqrt 3$, 1)、および、$xy$平面上を自由に動く2つの点PとQがあり、$l$=AP+BQ+$\displaystyle\frac{\textrm{PQ}}{2}$とする。$l$が最小値をとるとき、点PとQを通る$xy$平面上の直線の方程式は$y$=$\sqrt{\boxed{\ \ ソ\ \ }\ x}$-$\sqrt{\boxed{\ \ タ\ \ }}$ であり、$l$の最小値は$\boxed{\ \ チ\ \ }$+$\sqrt{\boxed{\ \ ツ\ \ }}$ である。
この動画を見る
$\Large\boxed{6}$ 2点A(1,0,1)とB(2, $\sqrt 3$, 1)、および、$xy$平面上を自由に動く2つの点PとQがあり、$l$=AP+BQ+$\displaystyle\frac{\textrm{PQ}}{2}$とする。$l$が最小値をとるとき、点PとQを通る$xy$平面上の直線の方程式は$y$=$\sqrt{\boxed{\ \ ソ\ \ }\ x}$-$\sqrt{\boxed{\ \ タ\ \ }}$ であり、$l$の最小値は$\boxed{\ \ チ\ \ }$+$\sqrt{\boxed{\ \ ツ\ \ }}$ である。
福田のおもしろ数学120〜n変数の条件付き最大最小問題

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
実数$x_1$,$x_2$,...,$x_n$が$x_1^2$+$x_2^2$+...+$x_n^2$=1 を満たすとき、$x_1^2$+$2x_2^2$+...+$nx_n^2$ の最大値と最小値を求めよ。
この動画を見る
実数$x_1$,$x_2$,...,$x_n$が$x_1^2$+$x_2^2$+...+$x_n^2$=1 を満たすとき、$x_1^2$+$2x_2^2$+...+$nx_n^2$ の最大値と最小値を求めよ。
福田の数学〜東北大学2024年理系第5問〜関数の増減と方程式の整数解

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{5}}$ $x$≧2 を満たす実数$x$に対し、
$f(x)$=$\displaystyle\frac{\log(2x-3)}{x}$
とおく。必要ならば、$\displaystyle\lim_{t \to \infty}\frac{\log t}{t}$=0 であること、および自然対数の底$e$が2<$e$<3 を満たすことを証明なしで用いてもよい。
(1)$f'(x)$=$\displaystyle\frac{g(x)}{x^2(2x-3)}$ とおくとき、関数$g(x)$ ($x$≧2)を求めよ。
(2)(1)で求めた関数$g(x)$に対し、$g(\alpha)$=0 を満たす2以上の実数$\alpha$がただ一つ存在することを示せ。
(3)関数$f(x)$ ($x$≧2)の増減と極限$\displaystyle\lim_{t \to \infty}f(x)$ を調べ、$y$=$f(x)$ ($x$≧2)のグラフの概形を$xy$平面上に描け。ただし(2)の$\alpha$を用いてよい。グラフの凹凸は調べなくてよい。
(4)2≦$m$<$n$ を満たす整数$m$,$n$の組($m$,$n$)に対して、等式
(*)$(2m-3)^n$=$(2n-3)^m$
が成り立つとする。このような組($m$,$n$)をすべて求めよ。
この動画を見る
$\Large{\boxed{5}}$ $x$≧2 を満たす実数$x$に対し、
$f(x)$=$\displaystyle\frac{\log(2x-3)}{x}$
とおく。必要ならば、$\displaystyle\lim_{t \to \infty}\frac{\log t}{t}$=0 であること、および自然対数の底$e$が2<$e$<3 を満たすことを証明なしで用いてもよい。
(1)$f'(x)$=$\displaystyle\frac{g(x)}{x^2(2x-3)}$ とおくとき、関数$g(x)$ ($x$≧2)を求めよ。
(2)(1)で求めた関数$g(x)$に対し、$g(\alpha)$=0 を満たす2以上の実数$\alpha$がただ一つ存在することを示せ。
(3)関数$f(x)$ ($x$≧2)の増減と極限$\displaystyle\lim_{t \to \infty}f(x)$ を調べ、$y$=$f(x)$ ($x$≧2)のグラフの概形を$xy$平面上に描け。ただし(2)の$\alpha$を用いてよい。グラフの凹凸は調べなくてよい。
(4)2≦$m$<$n$ を満たす整数$m$,$n$の組($m$,$n$)に対して、等式
(*)$(2m-3)^n$=$(2n-3)^m$
が成り立つとする。このような組($m$,$n$)をすべて求めよ。
福田の数学〜慶應義塾大学2024年薬学部第1問(2)〜3次関数の増減と方程式の解の個数

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)$a$,$b$,$c$を実数とし、実数$x$の関数$f(x)$を$f(x)$=$x^3$+$ax^2$+$bx$+$c$ とおく。
$f(x)$は$x$=-1で極値3をとり、方程式$f(x)$=0は$x$=-2を解にもつ。
(i)$a$=$\boxed{\ \ ウ\ \ }$, $b$=$\boxed{\ \ エ\ \ }$, $c$=$\boxed{\ \ オ\ \ }$である。
(ii)Kを実数とする。方程式$f(x)$=$4x$+K が持つ異なる実数解の個数が2個となるとき、Kの値は$\boxed{\ \ カ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (2)$a$,$b$,$c$を実数とし、実数$x$の関数$f(x)$を$f(x)$=$x^3$+$ax^2$+$bx$+$c$ とおく。
$f(x)$は$x$=-1で極値3をとり、方程式$f(x)$=0は$x$=-2を解にもつ。
(i)$a$=$\boxed{\ \ ウ\ \ }$, $b$=$\boxed{\ \ エ\ \ }$, $c$=$\boxed{\ \ オ\ \ }$である。
(ii)Kを実数とする。方程式$f(x)$=$4x$+K が持つ異なる実数解の個数が2個となるとき、Kの値は$\boxed{\ \ カ\ \ }$である。
福田の数学〜東京大学2018年理系第1問〜関数の増減と極限の計算

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=\dfrac{x}{\sin x}+\cos x (0 \lt x \lt \pi)$のぞうげんひょうを作り、$x→+0,x→\pi-0$のときの極限を調べよ。
2018東京大学理過去問
この動画を見る
$f(x)=\dfrac{x}{\sin x}+\cos x (0 \lt x \lt \pi)$のぞうげんひょうを作り、$x→+0,x→\pi-0$のときの極限を調べよ。
2018東京大学理過去問
福田のおもしろ数学037〜相加相乗平均の罠〜2変数関数の最小値

単元:
#数Ⅰ#2次関数#式と証明#恒等式・等式・不等式の証明#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$x>1,y>1$のとき、
$x+y+\frac{2}{x+y}+\frac{1}{2xy}$の最小値を求めよ
この動画を見る
$x>1,y>1$のとき、
$x+y+\frac{2}{x+y}+\frac{1}{2xy}$の最小値を求めよ
福田の数学〜3次方程式の解の存在範囲に関する問題〜東京大学2018年文系第3問〜関数の増減と方程式の解

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
a>0とし、f(x)=$x^3-3a^2x$とおく。
( 1 )x$ \geqq 1$でf(x)が単調に増加するための aについての条件を求めよ。
( 2 )次の 2 条件を満たす点(a,b)の動きうる範囲を求め、座標平面上に図示せよ。
条件 1 :方程式f(x)=bは相異なる 3 実数解をもつ。
条件 2 :さらに方程式f(x)=bの解を$\alpha<\beta<\gamma$とすると、$\beta >1$ である。
2018東京大学文過去問
この動画を見る
a>0とし、f(x)=$x^3-3a^2x$とおく。
( 1 )x$ \geqq 1$でf(x)が単調に増加するための aについての条件を求めよ。
( 2 )次の 2 条件を満たす点(a,b)の動きうる範囲を求め、座標平面上に図示せよ。
条件 1 :方程式f(x)=bは相異なる 3 実数解をもつ。
条件 2 :さらに方程式f(x)=bの解を$\alpha<\beta<\gamma$とすると、$\beta >1$ である。
2018東京大学文過去問
福田の数学〜複数の絶対値に対応できるか〜東京大学2018年文系第1問(1)〜絶対値を含む関数の最小

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標平面上に放物線 C を$y=x^2-3x+4$ で定め、領域Dを$y \geqq x^2-3x+4$で定める。原点を通る 2 直線l, m は C に接する。
(1) 放物線 C 上を動く点 A と直線l, m の距離をそれぞれL,M とする。$\sqrt{ \mathstrut L } + \sqrt{ \mathstrut M }$が最小値をとるときの点 A の座標を求めよ。
2018東京大学文過去問
この動画を見る
座標平面上に放物線 C を$y=x^2-3x+4$ で定め、領域Dを$y \geqq x^2-3x+4$で定める。原点を通る 2 直線l, m は C に接する。
(1) 放物線 C 上を動く点 A と直線l, m の距離をそれぞれL,M とする。$\sqrt{ \mathstrut L } + \sqrt{ \mathstrut M }$が最小値をとるときの点 A の座標を求めよ。
2018東京大学文過去問
福田の数学〜この関数にピンときたら大正解〜北里大学2023年医学部第2問〜関数の増減と方程式の実数解の個数

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
関数$f(x)=2^x-x^2$について考える。必要ならば、$0.6 \lt \log 2 \lt 0.7,-0.4 \lt \log(\log2) \lt -0.3$を用いてよい。
(1)$f(x)$は区間 $x \geqq 4$で増加することを示せ。
(2)方程式$f'(x)=0$の異なる実数解の個数を求めよ。
(3)方程式$f(x)=0$の異なる実数解の個数を求めよ。
(4)方程式$f(x)=0$の実数解のうち、最小のものを$p$とする。
この時、曲線$y=f(x)$の$x \leq 0$の部分、放物線$y=-x^2+\dfrac{2}{\log2}x$、および2つの直線$x=p,x=0$で囲まれた図形の面積を求めよ。
2023北里大学医過去問
この動画を見る
関数$f(x)=2^x-x^2$について考える。必要ならば、$0.6 \lt \log 2 \lt 0.7,-0.4 \lt \log(\log2) \lt -0.3$を用いてよい。
(1)$f(x)$は区間 $x \geqq 4$で増加することを示せ。
(2)方程式$f'(x)=0$の異なる実数解の個数を求めよ。
(3)方程式$f(x)=0$の異なる実数解の個数を求めよ。
(4)方程式$f(x)=0$の実数解のうち、最小のものを$p$とする。
この時、曲線$y=f(x)$の$x \leq 0$の部分、放物線$y=-x^2+\dfrac{2}{\log2}x$、および2つの直線$x=p,x=0$で囲まれた図形の面積を求めよ。
2023北里大学医過去問
福田の数学〜陰関数を考える貴重な問題〜明治大学2023年全学部統一Ⅲ第4問〜陰関数のグラフの増減とグラフ

単元:
#大学入試過去問(数学)#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{4}}$ 座標空間において、2点(-2,0),(2,0)からの距離の積が4であるような点Pの軌跡を考える。点Pの座標を($x$,$y$)とすると、$x$,$y$は次の方程式を満たす。
$y^4$+$\boxed{\ \ ア\ \ }y^2$+$(\boxed{\ \ イ\ \ })^2$=16 ...(1)
方程式(1)が表す曲線を$C$とする。$C$の概形を描くことにしよう。まず、曲線$C$と$x$軸との共有点の$x$座標は$\boxed{\ \ ウ\ \ }$と$±\boxed{\ \ エ\ \ }\sqrt{\boxed{\ \ オ\ \ }}$である。次に、(1)を$y^2$に関する2次方程式とみて解けば、$y^2$≧0 であるので、
$y^2$=$\boxed{\ \ カ\ \ }$+$4\sqrt{\boxed{\ \ キ\ \ }}$ ...(2)
となり、また$x$のとりうる値の範囲は
$-\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$≦$x$≦$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$
となる。$x$≧0, $y$≧0とすれば、方程式(2)は0≦$x$≦$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$を定義域とする$x$の関数$y$を定める。このとき、0<$x$$\boxed{\ \ サ\ \ }$のとき共有点はなく、0≦$a$≦$\boxed{\ \ サ\ \ }$のとき共有点がある。
共有点の個数は、$a$=0のとき$\boxed{\ \ シ\ \ }$個、0<$a$<$\boxed{\ \ サ\ \ }$のとき$\boxed{\ \ ス\ \ }$個、$a$=$\boxed{\ \ サ\ \ }$のとき$\boxed{\ \ セ\ \ }$個となる。
$\boxed{\ \ ア\ \ }$、$\boxed{\ \ イ\ \ }$、$\boxed{\ \ カ\ \ }$、$\boxed{\ \ キ\ \ }$の解答群
⓪$x^2+1$ ①$-(x^2+1)$ ②$x^2-1$ ③$-(x^2-1)$ ④$x^2+4$
⑤$2(x^2+4)$ ⑥$x^2-4$ ⑦$2(x^2-4)$ ⑧$-(x^2+4)$ ⑨$-2(x^2-4)$
この動画を見る
$\Large{\boxed{4}}$ 座標空間において、2点(-2,0),(2,0)からの距離の積が4であるような点Pの軌跡を考える。点Pの座標を($x$,$y$)とすると、$x$,$y$は次の方程式を満たす。
$y^4$+$\boxed{\ \ ア\ \ }y^2$+$(\boxed{\ \ イ\ \ })^2$=16 ...(1)
方程式(1)が表す曲線を$C$とする。$C$の概形を描くことにしよう。まず、曲線$C$と$x$軸との共有点の$x$座標は$\boxed{\ \ ウ\ \ }$と$±\boxed{\ \ エ\ \ }\sqrt{\boxed{\ \ オ\ \ }}$である。次に、(1)を$y^2$に関する2次方程式とみて解けば、$y^2$≧0 であるので、
$y^2$=$\boxed{\ \ カ\ \ }$+$4\sqrt{\boxed{\ \ キ\ \ }}$ ...(2)
となり、また$x$のとりうる値の範囲は
$-\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$≦$x$≦$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$
となる。$x$≧0, $y$≧0とすれば、方程式(2)は0≦$x$≦$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$を定義域とする$x$の関数$y$を定める。このとき、0<$x$$\boxed{\ \ サ\ \ }$のとき共有点はなく、0≦$a$≦$\boxed{\ \ サ\ \ }$のとき共有点がある。
共有点の個数は、$a$=0のとき$\boxed{\ \ シ\ \ }$個、0<$a$<$\boxed{\ \ サ\ \ }$のとき$\boxed{\ \ ス\ \ }$個、$a$=$\boxed{\ \ サ\ \ }$のとき$\boxed{\ \ セ\ \ }$個となる。
$\boxed{\ \ ア\ \ }$、$\boxed{\ \ イ\ \ }$、$\boxed{\ \ カ\ \ }$、$\boxed{\ \ キ\ \ }$の解答群
⓪$x^2+1$ ①$-(x^2+1)$ ②$x^2-1$ ③$-(x^2-1)$ ④$x^2+4$
⑤$2(x^2+4)$ ⑥$x^2-4$ ⑦$2(x^2-4)$ ⑧$-(x^2+4)$ ⑨$-2(x^2-4)$
