 不定積分
不定積分
 不定積分
不定積分
福田のおもしろ数学549〜無理関数の不定積分その2

単元:
#関数と極限#積分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#不定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
不定積分
$I=\displaystyle \int \sqrt{x^2-1}dx \ (x\gt 1)$を
$x=\sqrt{x^2-1}=t$
と置き換えて求めて下さい。
この動画を見る
不定積分
$I=\displaystyle \int \sqrt{x^2-1}dx \ (x\gt 1)$を
$x=\sqrt{x^2-1}=t$
と置き換えて求めて下さい。
福田のおもしろ数学548〜無理関数の不定積分

単元:
#関数と極限#積分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#不定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
不定積分$I=\displaystyle \int \sqrt{x^2-1}dx \ (x\gt 1)$を
$x=\dfrac{1}{\cos\theta}$と
置き換えて求めて下さい。
この動画を見る
不定積分$I=\displaystyle \int \sqrt{x^2-1}dx \ (x\gt 1)$を
$x=\dfrac{1}{\cos\theta}$と
置き換えて求めて下さい。
福田の数学〜立教大学2025理学部第1問(3)〜定積分の計算

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(3)定積分$\displaystyle \int_{0}^{\frac{7}{6}\pi}\sin x \sin 2x \ dx$の値は
$\boxed{エ}$である。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{1}$
(3)定積分$\displaystyle \int_{0}^{\frac{7}{6}\pi}\sin x \sin 2x \ dx$の値は
$\boxed{エ}$である。
$2025$年立教大学理学部過去問題
福田のおもしろ数学454〜積分に関するシュワルツの不等式の証明と等号成立条件

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#積分とその応用#不定積分#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$p\leqq x \leqq q$で定義された連続関数$f(x),g(x)$に対して
$\left(\displaystyle \int_{p}^{q} f(x)^2 dx\right)\left(\displaystyle \int_{p}^{q}g(x)^2 dx \right) \geqq \left(\displaystyle \int_{p}^{q} f(x)g(x)dx\right)^2$
を証明して下さい。
また等号成立条件も調べて下さい。
この動画を見る
$p\leqq x \leqq q$で定義された連続関数$f(x),g(x)$に対して
$\left(\displaystyle \int_{p}^{q} f(x)^2 dx\right)\left(\displaystyle \int_{p}^{q}g(x)^2 dx \right) \geqq \left(\displaystyle \int_{p}^{q} f(x)g(x)dx\right)^2$
を証明して下さい。
また等号成立条件も調べて下さい。
【数Ⅲ】【積分とその応用】不定積分置換積分、部分積分3 ※問題文は概要欄

単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{\sqrt x}{\sqrt[4]{x^3}+1}~dx$
(2) $\displaystyle \int \frac{dx}{x\sqrt{x+1}}$
(3) $\displaystyle \int \log|x^2-1|~dx$
(4) $\displaystyle \int \frac{e^x}{e^x-e^{-x}}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \tan^4x~dx$
(2) $\displaystyle \int \frac{dx}{\sin{2x}}$
(3) $\displaystyle \int \frac{1}{1-\sin x}~dx$
(4) $\displaystyle \int (\sin^3x-\cos^3x)~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int e^x\cos x~dx$
(2) $\displaystyle \int e^{-x}\sin x~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \sin x\log(\cos x)~dx$
(2) $\displaystyle \int x\tan^2x~dx$
(3) $\displaystyle \int \frac{1}{1-e^x}~dx$
この動画を見る
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{\sqrt x}{\sqrt[4]{x^3}+1}~dx$
(2) $\displaystyle \int \frac{dx}{x\sqrt{x+1}}$
(3) $\displaystyle \int \log|x^2-1|~dx$
(4) $\displaystyle \int \frac{e^x}{e^x-e^{-x}}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \tan^4x~dx$
(2) $\displaystyle \int \frac{dx}{\sin{2x}}$
(3) $\displaystyle \int \frac{1}{1-\sin x}~dx$
(4) $\displaystyle \int (\sin^3x-\cos^3x)~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int e^x\cos x~dx$
(2) $\displaystyle \int e^{-x}\sin x~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \sin x\log(\cos x)~dx$
(2) $\displaystyle \int x\tan^2x~dx$
(3) $\displaystyle \int \frac{1}{1-e^x}~dx$
【数Ⅲ】【積分とその応用】不定積分置換積分、部分積分2 ※問題文は概要欄

単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{x^2+x+1}{x^2+1}~dx$
(2) $\displaystyle \int \frac{x^4}{x^2-1}~dx$
(1)次の等式が成り立つように、定数$a,b,c$の値を定めよ。
$\dfrac{3x+2}{x(x+1)^2}=\dfrac{a}{x}+\dfrac{b}{x+1}+\dfrac{c}{(x+1)^2}$
(2)不定積分$\displaystyle \int \dfrac{3x+2}{x(x+1)^2}~dx$を求めよ。
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{dx}{x(x^2-1)}$
(2) $\displaystyle \int \frac{dx}{x^2(x+2)}$
(3) $\displaystyle \int \frac{dx}{x(x^2+1)}$
(4) $\displaystyle \int \frac{x^2+1}{x^4-5x^2+4}~dx$
(5) $\displaystyle \int \frac{3x+2}{x(x+1)^3}~dx$
(6) $\displaystyle \int \frac{x^4}{x^3-3x+2}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{dx}{\sqrt{x+1}-\sqrt x}$
(2) $\displaystyle \int \frac{x}{\sqrt{3x+4}-2}~dx$
この動画を見る
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{x^2+x+1}{x^2+1}~dx$
(2) $\displaystyle \int \frac{x^4}{x^2-1}~dx$
(1)次の等式が成り立つように、定数$a,b,c$の値を定めよ。
$\dfrac{3x+2}{x(x+1)^2}=\dfrac{a}{x}+\dfrac{b}{x+1}+\dfrac{c}{(x+1)^2}$
(2)不定積分$\displaystyle \int \dfrac{3x+2}{x(x+1)^2}~dx$を求めよ。
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{dx}{x(x^2-1)}$
(2) $\displaystyle \int \frac{dx}{x^2(x+2)}$
(3) $\displaystyle \int \frac{dx}{x(x^2+1)}$
(4) $\displaystyle \int \frac{x^2+1}{x^4-5x^2+4}~dx$
(5) $\displaystyle \int \frac{3x+2}{x(x+1)^3}~dx$
(6) $\displaystyle \int \frac{x^4}{x^3-3x+2}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{dx}{\sqrt{x+1}-\sqrt x}$
(2) $\displaystyle \int \frac{x}{\sqrt{3x+4}-2}~dx$
【数Ⅲ】【積分とその応用】不定積分置換積分、部分積分1 ※問題文は概要欄

単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不定積分を求めよ。
(1) $\displaystyle \int x\sqrt[3]{1+x}~dx$
(2) $\displaystyle \int \sin x \cos^4x~dx$
(3) $\displaystyle \int \frac {dx}{\cos^4x}$
(4) $\displaystyle \int (2x+1)e^{x^2+x+5}~dx$
(5) $\displaystyle \int \frac{e^{2x}}{(e^x+2)^2}~dx$
(6) $\displaystyle \int \frac{\log x}{x(\log x-1)^2}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{x}{\cos^2x}~dx$
(2) $\displaystyle \int x\log(x-2)~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int x\log(x^2-2)~dx$
(2) $\displaystyle \int e^x\log(e^x+1)~dx$
不定積分$\displaystyle \int (\log x)^3~dx$を求めよ。
この動画を見る
次の不定積分を求めよ。
(1) $\displaystyle \int x\sqrt[3]{1+x}~dx$
(2) $\displaystyle \int \sin x \cos^4x~dx$
(3) $\displaystyle \int \frac {dx}{\cos^4x}$
(4) $\displaystyle \int (2x+1)e^{x^2+x+5}~dx$
(5) $\displaystyle \int \frac{e^{2x}}{(e^x+2)^2}~dx$
(6) $\displaystyle \int \frac{\log x}{x(\log x-1)^2}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{x}{\cos^2x}~dx$
(2) $\displaystyle \int x\log(x-2)~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int x\log(x^2-2)~dx$
(2) $\displaystyle \int e^x\log(e^x+1)~dx$
不定積分$\displaystyle \int (\log x)^3~dx$を求めよ。
福田の数学〜北里大学2024医学部第2問〜関数と不等式の証明

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(1)関数$y=\frac{1}{x}$の定積分を用いて、$n\geqq 2$を満たすすべての$n$に対して$f(x)\gt 0$が成り立つことを示せ。
(2)$f(x)=x+\frac{x}{1+x}-2\log (1+x)$とおく。すべての正の実数$x$に対して、$f(x)\gt 0$が成り立つことを証明せよ。さらに、すべての正の整数$n$に対して$\frac{1}{n}+\frac{1}{n+1}\gt 2\log (1+\frac{1}{n})$を示せ。
(3)$n\geqq 2$を満たすすべての整数$n$に対して$\displaystyle \sum_{k=1}^n \frac{1}{k}-\frac{1}{2}(1+\frac{1}{n})\gt \log n$が成り立つことを証明せよ。
この動画を見る
(1)関数$y=\frac{1}{x}$の定積分を用いて、$n\geqq 2$を満たすすべての$n$に対して$f(x)\gt 0$が成り立つことを示せ。
(2)$f(x)=x+\frac{x}{1+x}-2\log (1+x)$とおく。すべての正の実数$x$に対して、$f(x)\gt 0$が成り立つことを証明せよ。さらに、すべての正の整数$n$に対して$\frac{1}{n}+\frac{1}{n+1}\gt 2\log (1+\frac{1}{n})$を示せ。
(3)$n\geqq 2$を満たすすべての整数$n$に対して$\displaystyle \sum_{k=1}^n \frac{1}{k}-\frac{1}{2}(1+\frac{1}{n})\gt \log n$が成り立つことを証明せよ。
福田のおもしろ数学254〜ルートx2乗+1の不定積分

単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$
\{ \log(x+ \sqrt{x^2+1}) \}'= \frac{1}{ \sqrt{x^2+1}}
$
を使って
$
\int \sqrt{x^2+1}\ dx
$
を使って求めて下さい。
この動画を見る
$
\{ \log(x+ \sqrt{x^2+1}) \}'= \frac{1}{ \sqrt{x^2+1}}
$
を使って
$
\int \sqrt{x^2+1}\ dx
$
を使って求めて下さい。
#広島市立大学2024#不定積分_29#元高校教員

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{e^x}{e^{2x}-4} dx$
出典:2024年広島市立大学
この動画を見る
$\displaystyle \int \displaystyle \frac{e^x}{e^{2x}-4} dx$
出典:2024年広島市立大学
#高専#不定積分_19#元高専教員
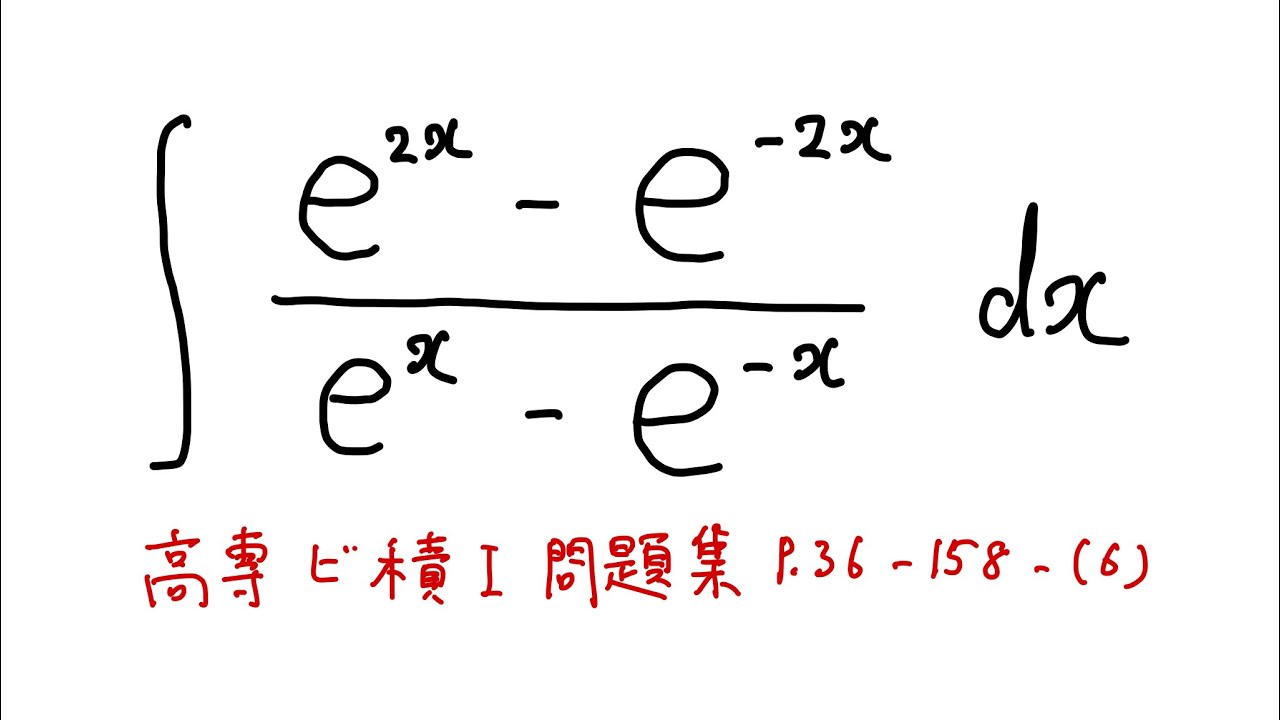
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#高専(高等専門学校)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{e^{2x}-e^{-2x}}{e^x-e^{-x}} dx$
出典:国立高等専門学校機構
この動画を見る
$\displaystyle \int \displaystyle \frac{e^{2x}-e^{-2x}}{e^x-e^{-x}} dx$
出典:国立高等専門学校機構
#高専#不定積分_18#元高専教員
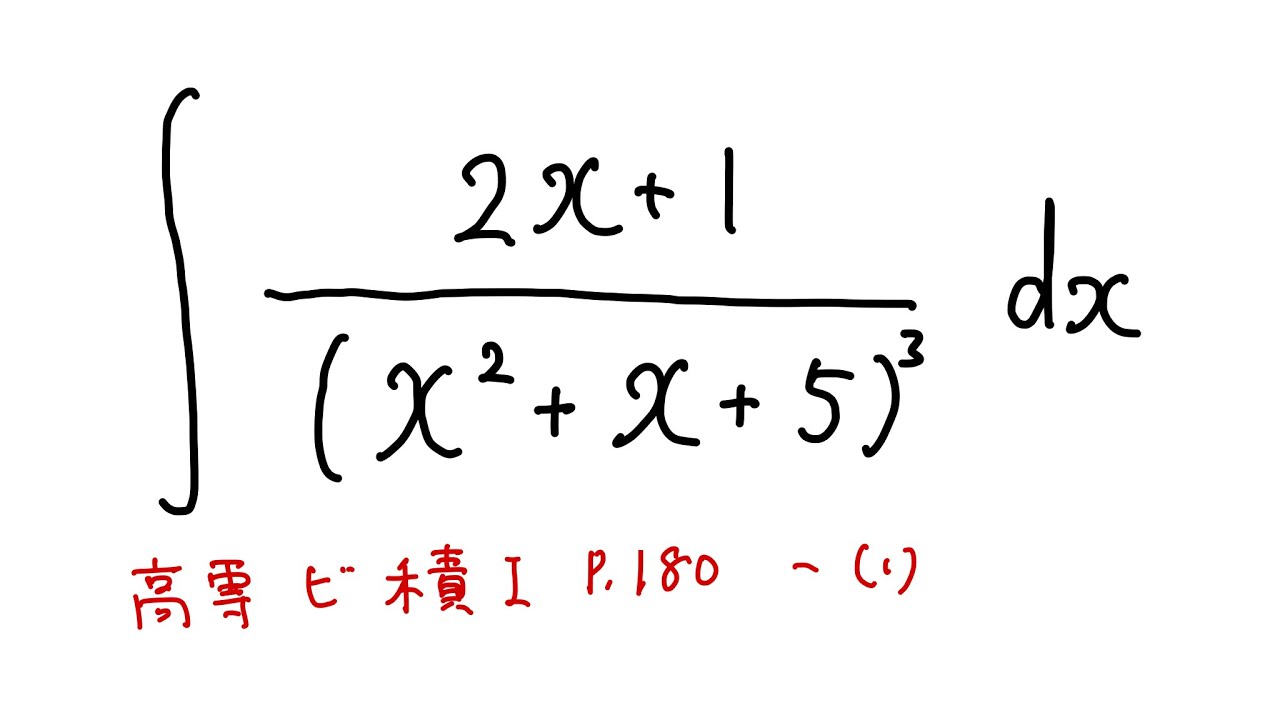
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#高専(高等専門学校)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int\displaystyle \frac{2x+1}{(x^2+x+5)^3} dx$
出典:国立高等専門学校機構
この動画を見る
$\displaystyle \int\displaystyle \frac{2x+1}{(x^2+x+5)^3} dx$
出典:国立高等専門学校機構
#高専#不定積分_17#元高専教員
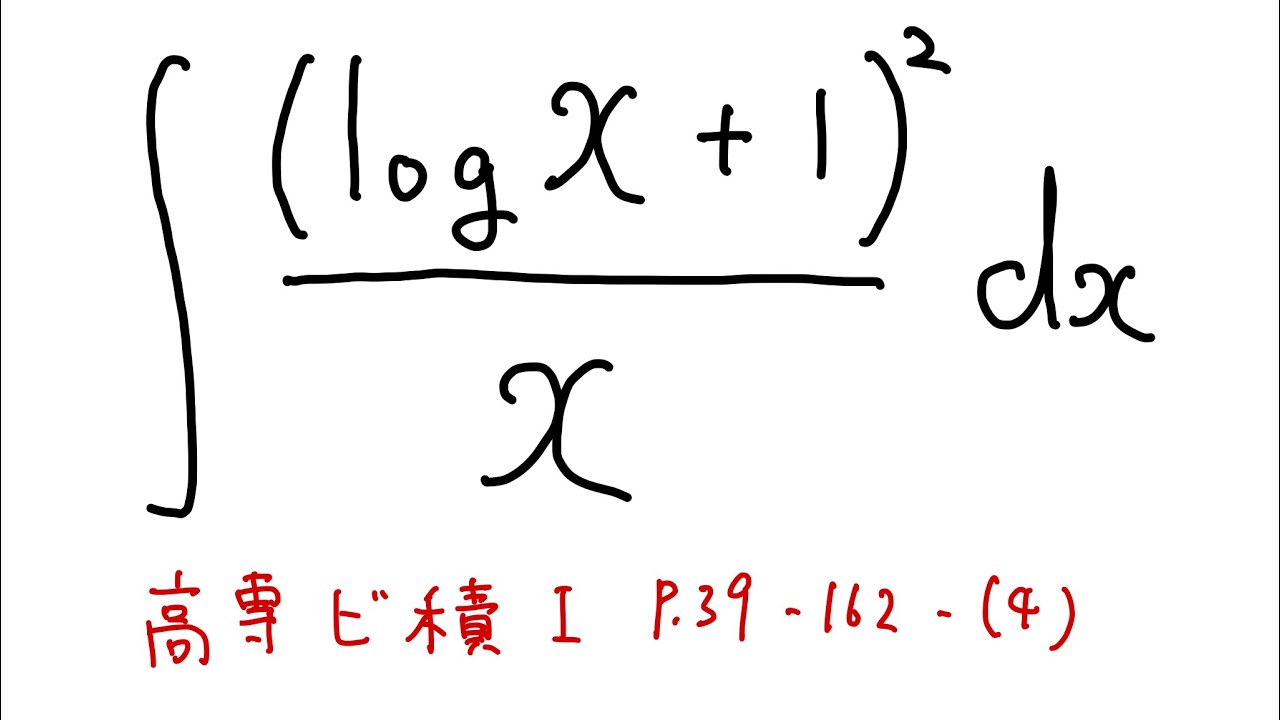
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#高専(高等専門学校)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int\displaystyle \frac{(logx+1)^2}{x} dx$
この動画を見る
$\displaystyle \int\displaystyle \frac{(logx+1)^2}{x} dx$
#高専#不定積分_16#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x-1}{\sqrt[ 3 ]{ x }-1} dx$
この動画を見る
$\displaystyle \int \displaystyle \frac{x-1}{\sqrt[ 3 ]{ x }-1} dx$
#高知工科大学2024#不定積分_23#元高校教員
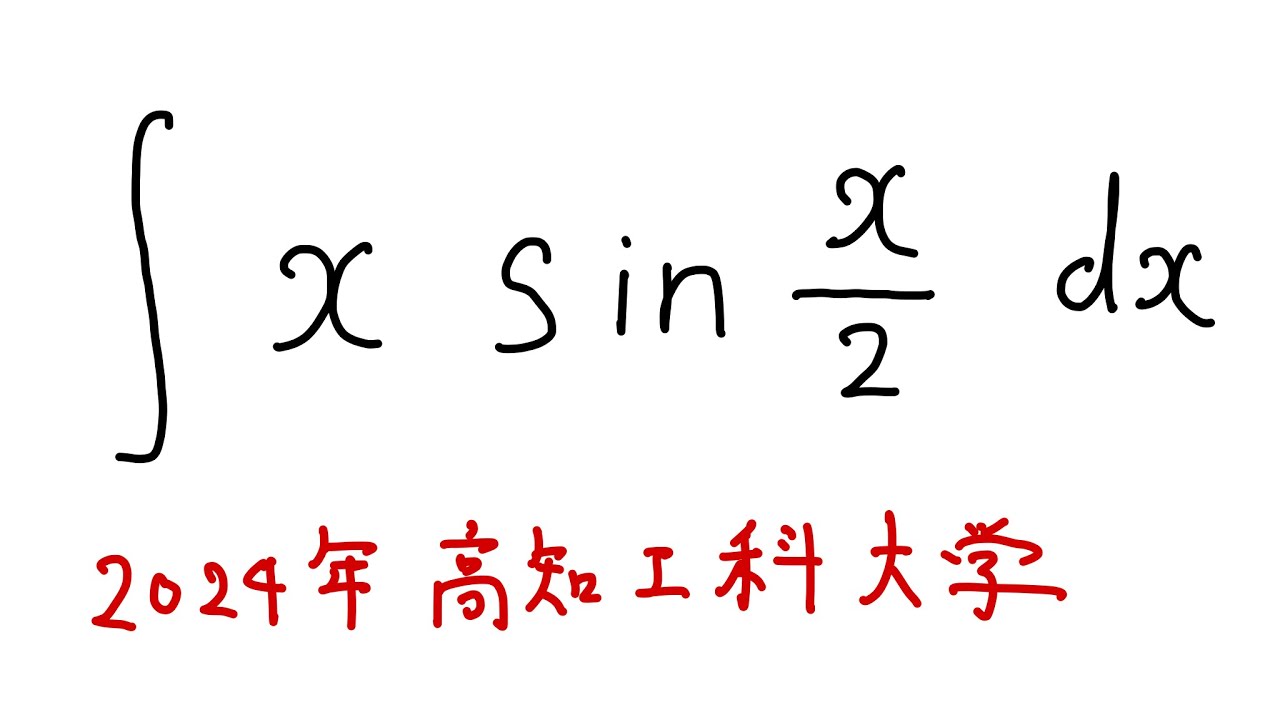
単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int x \sin\displaystyle \frac{x}{2} dx$
出典:2024年高知工科大学
この動画を見る
$\displaystyle \int x \sin\displaystyle \frac{x}{2} dx$
出典:2024年高知工科大学
#高専#ウォリス積分_15#元高専教員
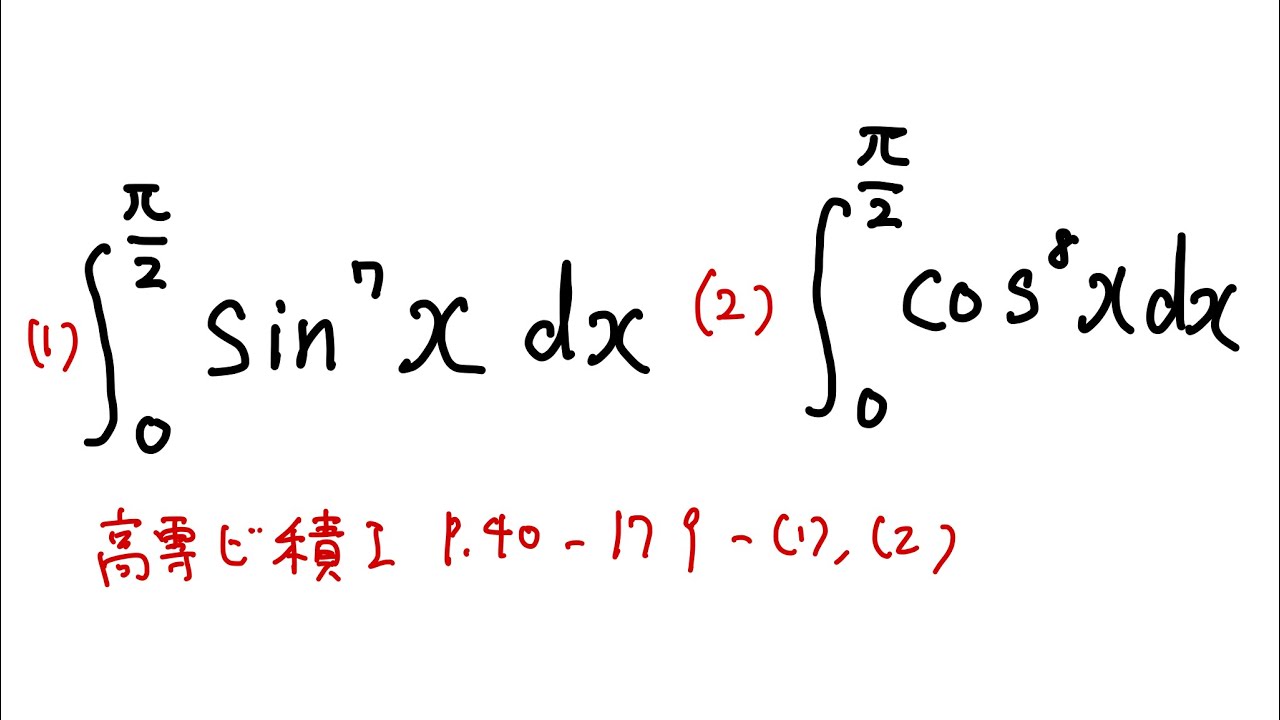
単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^7 x$ $dx$
(2)$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos^8 x$ $dx$
この動画を見る
(1)$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^7 x$ $dx$
(2)$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos^8 x$ $dx$
#広島市立大学2024#不定積分_22#元高校教員

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x}{e^{ \frac{x}{2}}} dx$
出典:2024年広島市立大学後期 不定積分問題
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{e^{ \frac{x}{2}}} dx$
出典:2024年広島市立大学後期 不定積分問題
大学入試問題#915「減点祭りの問題」 #京都大学1965 #積分方程式

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x \gt 1$とする。
$\displaystyle \int_{1}^{x} (x-t)f(t)dt=x^4-2x^2+1$を満たす整式$f(t)$を定めよ。
出典:1965年京都大学
この動画を見る
$x \gt 1$とする。
$\displaystyle \int_{1}^{x} (x-t)f(t)dt=x^4-2x^2+1$を満たす整式$f(t)$を定めよ。
出典:1965年京都大学
#高専数学#不定積分_13#元高専教員
単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
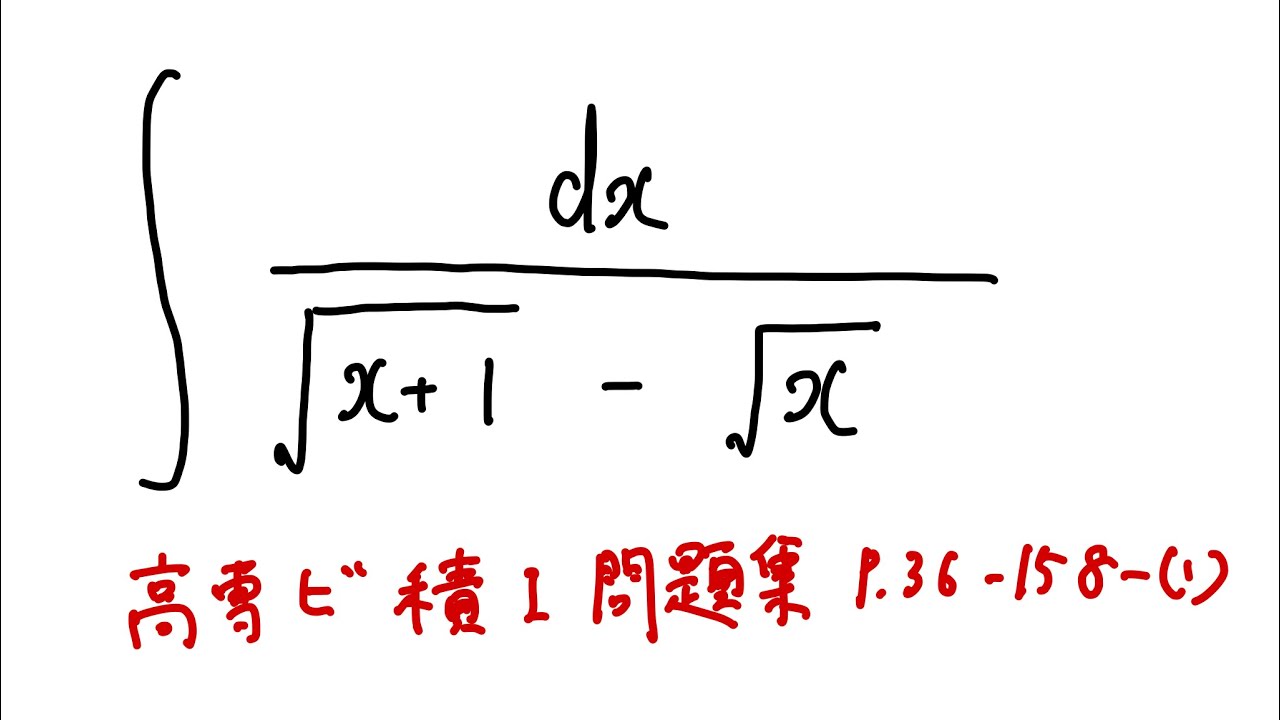
$\displaystyle \int \displaystyle \frac{dx}{\sqrt{ x+1 }-\sqrt{ x }}$
出典:高専数学 問題集
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{\sqrt{ x+1 }-\sqrt{ x }}$
出典:高専数学 問題集
#宮崎大学2024#不定積分_20#元高校教員
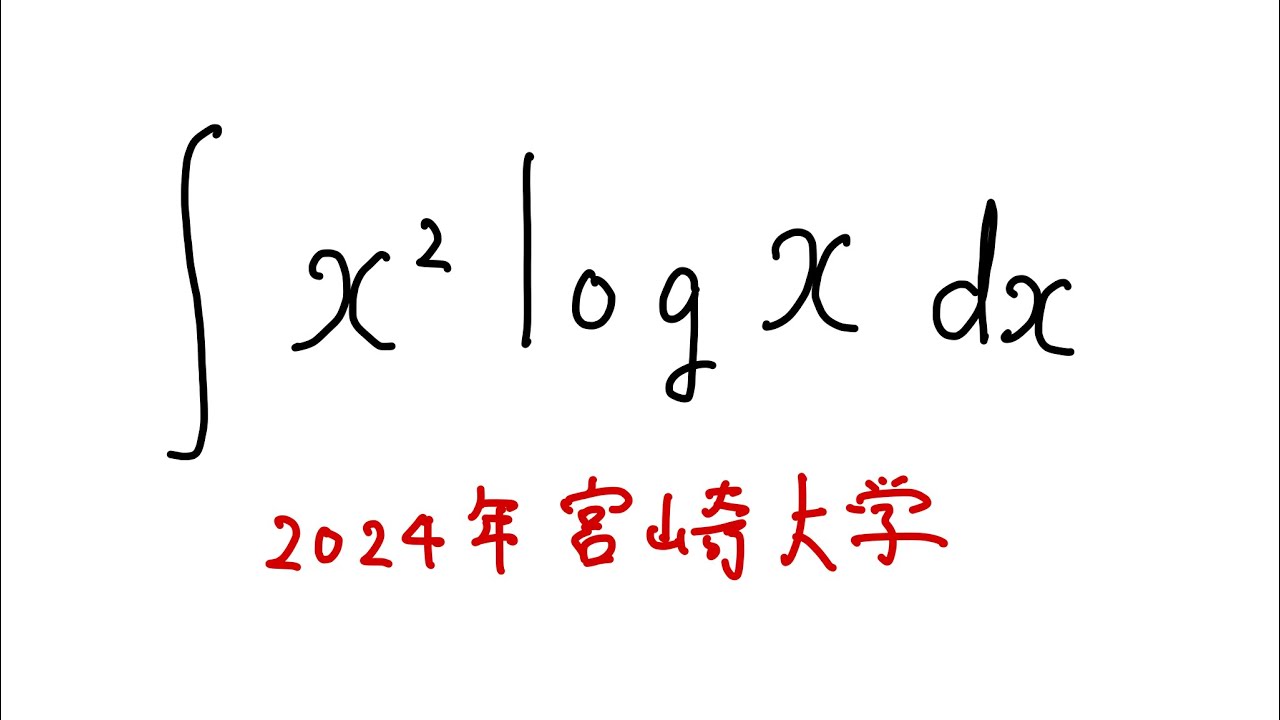
単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int x^2log$ $x$ $dx$
出典:2024年 宮崎大学
この動画を見る
$\displaystyle \int x^2log$ $x$ $dx$
出典:2024年 宮崎大学
#宮崎大学2024#不定積分_19#元高校教員
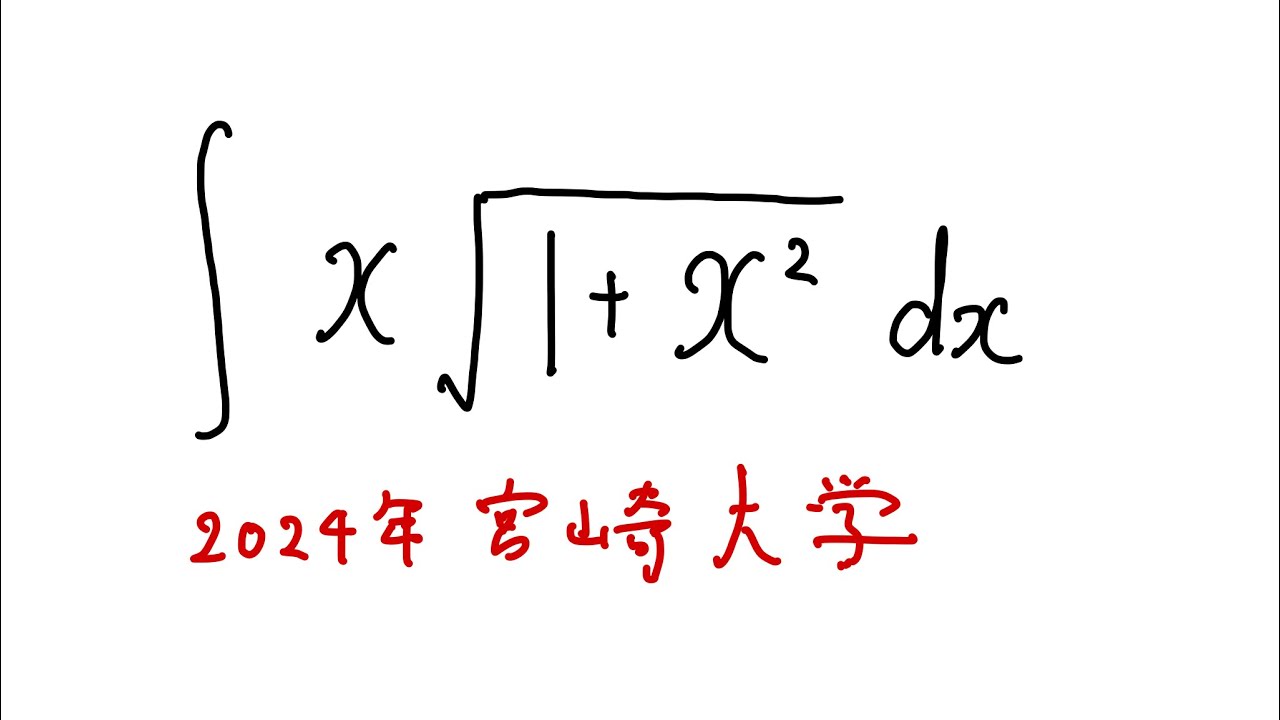
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int x \sqrt{ 1+x^2 }dx$
出典:2024年宮崎大学
この動画を見る
$\displaystyle \int x \sqrt{ 1+x^2 }dx$
出典:2024年宮崎大学
#名古屋工業大学2024#不定積分_18#元高校教員

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#名古屋大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int\sqrt{ 2 }$ $logx$ $dx$
出典:2024年 名古屋工業大学
この動画を見る
$\displaystyle \int\sqrt{ 2 }$ $logx$ $dx$
出典:2024年 名古屋工業大学
福田のおもしろ数学234〜区分求積の公式の変形その2

単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \frac{1}{n} \sum_{k=1}^{n} f(\frac{k}{n}) $$ = \displaystyle \int_0^1 f(x) dx $ である。では、$\displaystyle \lim_{ n \to \infty } \frac{1}{n+1} \sum_{k=n+2}^{4n+1} f(\frac{k}{n})$ は?
この動画を見る
$\displaystyle \lim_{ n \to \infty } \frac{1}{n} \sum_{k=1}^{n} f(\frac{k}{n}) $$ = \displaystyle \int_0^1 f(x) dx $ である。では、$\displaystyle \lim_{ n \to \infty } \frac{1}{n+1} \sum_{k=n+2}^{4n+1} f(\frac{k}{n})$ は?
どゆこと?
#高専数学#不定積分_12#元高専教員
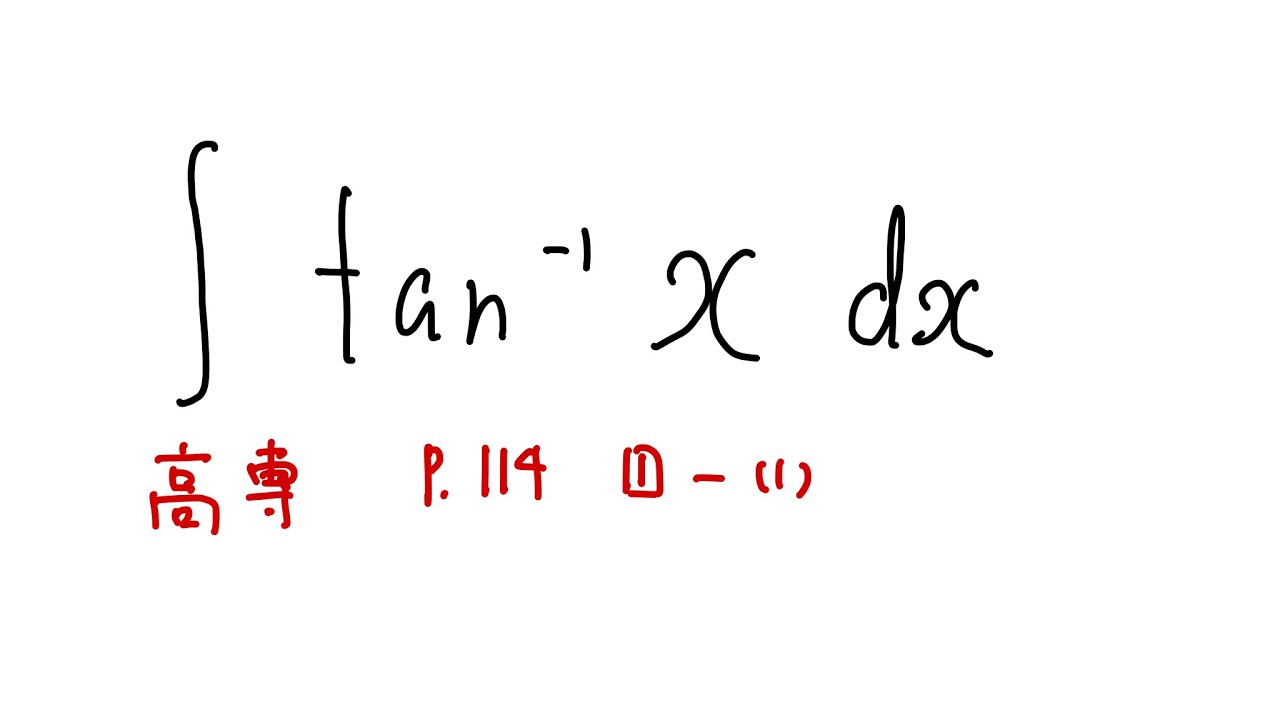
単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int fan^{-1}x$ $dx$
この動画を見る
$\displaystyle \int fan^{-1}x$ $dx$
#高専数学_10#不定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x}{(x-2)^2} dx$
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{(x-2)^2} dx$
#高専数学_9#不定積分#元高専教員
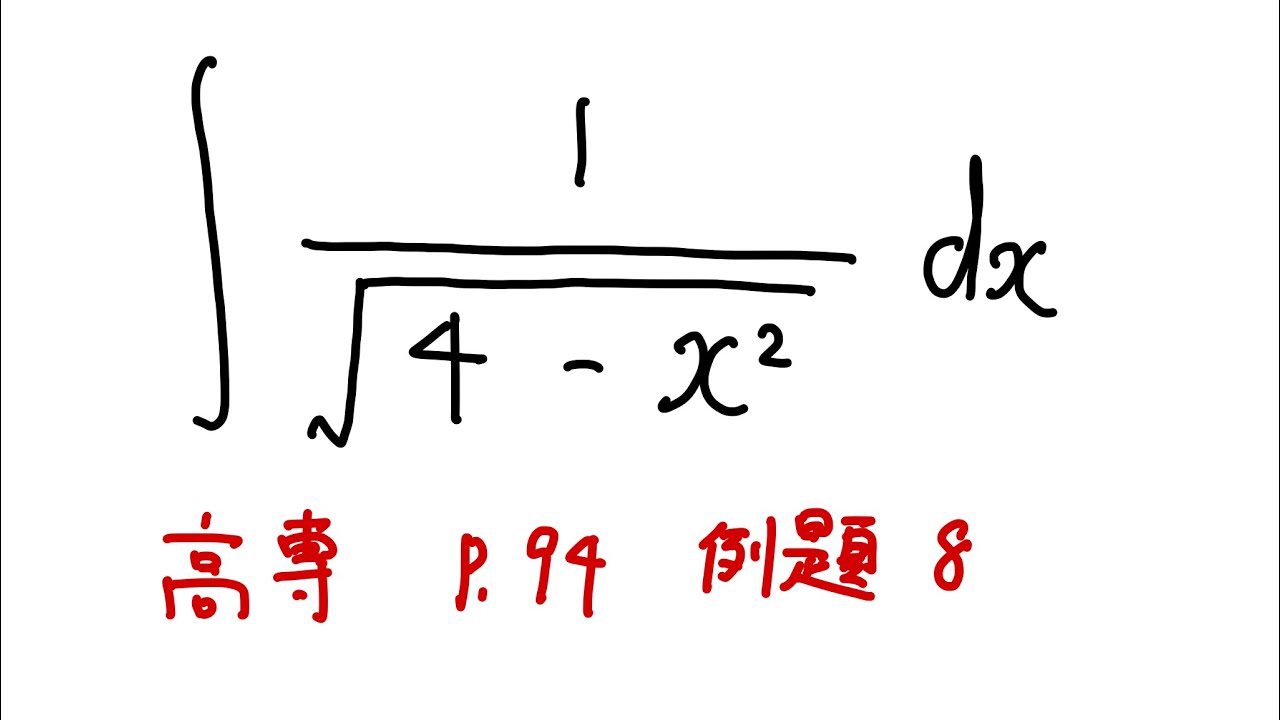
単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
下記の不定積分を解け。
$\displaystyle \int \displaystyle \frac{1}{\sqrt{ 4-x^2 }} dx$
この動画を見る
下記の不定積分を解け。
$\displaystyle \int \displaystyle \frac{1}{\sqrt{ 4-x^2 }} dx$
#高専_8#不定積分#元高専教員
単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
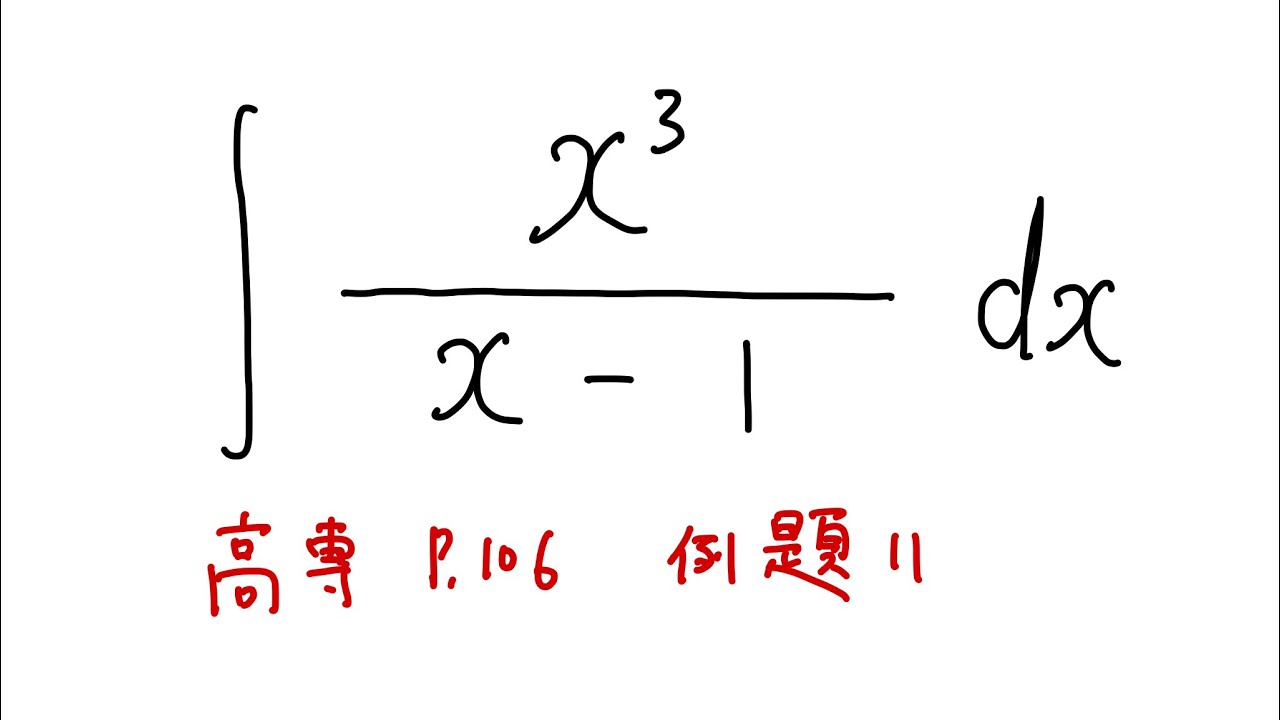
以下の不定積分を解け。
$\displaystyle \int \displaystyle \frac{x^3}{x-1}$ $dx$
この動画を見る
以下の不定積分を解け。
$\displaystyle \int \displaystyle \frac{x^3}{x-1}$ $dx$
#千葉大学2021#不定積分#元高専教員
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int x log(x^2-1) dx$
出典:2021年千葉大学
この動画を見る
以下の不定積分を解け。
$\displaystyle \int x log(x^2-1) dx$
出典:2021年千葉大学
#千葉大学2018#不定積分#数学者
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int \sin^3x \cos^2x$ $dx$
出典:2018年千葉大学
この動画を見る
以下の不定積分を解け。
$\displaystyle \int \sin^3x \cos^2x$ $dx$
出典:2018年千葉大学
