 定積分
定積分
 定積分
定積分
数学IIIのこの問題、解けるかな?

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
以下を満たすf(x)は?
f(x)=8x+2∫f(t)dt
この動画を見る
以下を満たすf(x)は?
f(x)=8x+2∫f(t)dt
定積分を含む関数f(x)を求める問題、解けてくれーー
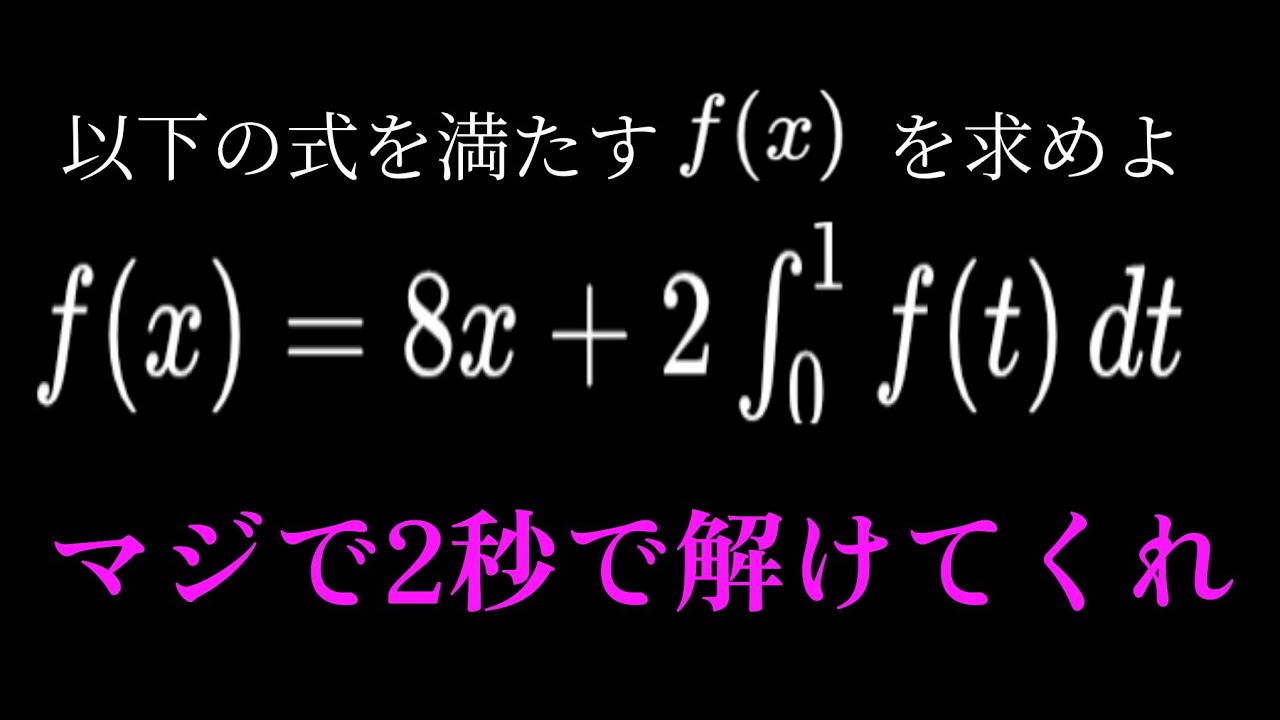
単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
以下を満たすf(x)は?
f(x)=8x+2∫f(t)dt
この動画を見る
以下を満たすf(x)は?
f(x)=8x+2∫f(t)dt
【数Ⅲ】【積分とその応用】シュワルツの不等式{∫[a→b]f(x)g(x)dx}²≦(∫[a→b]{f(x)}²dx)(∫[a→b]{g(x)}²dx) を利用して、次の不等式が成り立つことを証明せよ

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
シュワルツの不等式
\[
\left\{ \int_a^b f(x)g(x) \, dx \right\}^2 \leq
\left( \int_a^b \{ f(x) \}^2 dx \right)
\left( \int_a^b \{ g(x) \}^2 dx \right) \quad (a < b)
\]
を利用して、\( 0 < a < b, \, h(x) > 0 \) のとき、次の不等式が成り立つことを証明せよ。
(1)
\[
(b - a)^2 < \int_a^b x^2 \, dx \int_a^b \frac{dx}{x^2}
\]
(2)
\[
(b - a)^2 \leq \int_a^b h(x) \, dx \int_a^b \frac{dx}{h(x)}
\]
この動画を見る
シュワルツの不等式
\[
\left\{ \int_a^b f(x)g(x) \, dx \right\}^2 \leq
\left( \int_a^b \{ f(x) \}^2 dx \right)
\left( \int_a^b \{ g(x) \}^2 dx \right) \quad (a < b)
\]
を利用して、\( 0 < a < b, \, h(x) > 0 \) のとき、次の不等式が成り立つことを証明せよ。
(1)
\[
(b - a)^2 < \int_a^b x^2 \, dx \int_a^b \frac{dx}{x^2}
\]
(2)
\[
(b - a)^2 \leq \int_a^b h(x) \, dx \int_a^b \frac{dx}{h(x)}
\]
【数Ⅲ】【積分とその応用】次の極限値を求めよ。(1)lim[n→∞]{√(n+1)+√(n+2)+……+√(2n)}/{1+√2+√3+……+√n}他1問

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の極限値を求めよ。
(1) $\displaystyle \lim_{ n \to 0 }\dfrac{\sqrt{n+1}+\sqrt{n+2}+\sqrt{n+3}+…+\sqrt{2n}}{1+\sqrt{2}+\sqrt{3}+\sqrt{4}+…+\sqrt{n}}$
(2) $\displaystyle \lim_{ n \to 0 }\log{\sqrt[ n ]{ n+1 }}+\log{\sqrt[ n ]{ n+2 }}+\log{\sqrt[ n ]{ n+3 }}+…+\log{\sqrt[ n ]{ 2n }}-\log n$
この動画を見る
次の極限値を求めよ。
(1) $\displaystyle \lim_{ n \to 0 }\dfrac{\sqrt{n+1}+\sqrt{n+2}+\sqrt{n+3}+…+\sqrt{2n}}{1+\sqrt{2}+\sqrt{3}+\sqrt{4}+…+\sqrt{n}}$
(2) $\displaystyle \lim_{ n \to 0 }\log{\sqrt[ n ]{ n+1 }}+\log{\sqrt[ n ]{ n+2 }}+\log{\sqrt[ n ]{ n+3 }}+…+\log{\sqrt[ n ]{ 2n }}-\log n$
【数Ⅲ】【積分とその応用】次の極限値を求めよ。(1) lim[x→0]1/x∫[0→x]1/(1+cost)dt(2) lim[x→0]∫[0→x](1+sint)²/xdt他1問

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
導関数、定積分の定義を利用して、次の極限値を求めよ。
(1) $\displaystyle \lim_{ x \to 0 }\dfrac{1}{x}\int_0^x \dfrac{1}{1+cost}dt$
(2) $\displaystyle \lim_{ x \to 0 }\int_0^x \dfrac{(1+sint)^2}{x}dt$
(3) $\displaystyle \lim_{ x \to 0 }\int_0^{x^2} \dfrac{cos⁵t}{x}dt$
この動画を見る
導関数、定積分の定義を利用して、次の極限値を求めよ。
(1) $\displaystyle \lim_{ x \to 0 }\dfrac{1}{x}\int_0^x \dfrac{1}{1+cost}dt$
(2) $\displaystyle \lim_{ x \to 0 }\int_0^x \dfrac{(1+sint)^2}{x}dt$
(3) $\displaystyle \lim_{ x \to 0 }\int_0^{x^2} \dfrac{cos⁵t}{x}dt$
福田の数学〜立教大学2025理学部第1問(3)〜定積分の計算

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(3)定積分$\displaystyle \int_{0}^{\frac{7}{6}\pi}\sin x \sin 2x \ dx$の値は
$\boxed{エ}$である。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{1}$
(3)定積分$\displaystyle \int_{0}^{\frac{7}{6}\pi}\sin x \sin 2x \ dx$の値は
$\boxed{エ}$である。
$2025$年立教大学理学部過去問題
【数Ⅲ】【積分とその応用】定積分の種々の問題6 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の等式を満たす関数$f(x)$を求めよ。
(1) $\displaystyle f(x)=x+\int_0^2f(t)e^t~dt$
(2) $\displaystyle f(x)=\sin x-\int_0^\frac\pi3\{f(t)-\frac\pi3\}\sin t~dt$
この動画を見る
次の等式を満たす関数$f(x)$を求めよ。
(1) $\displaystyle f(x)=x+\int_0^2f(t)e^t~dt$
(2) $\displaystyle f(x)=\sin x-\int_0^\frac\pi3\{f(t)-\frac\pi3\}\sin t~dt$
【数Ⅲ】【積分とその応用】定積分の種々の問題5 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数$f(x)$の最大値、最小値を求めよ。
(1) $\displaystyle f(x)=\int_0^x(1+2\cos t)\sin t~dt~~(0\leqq x\leqq2\pi)$
(2) $\displaystyle f(x)=\int_1^x(2-t)\log t~dt~~(1\leqq x\leqq e)$
この動画を見る
次の関数$f(x)$の最大値、最小値を求めよ。
(1) $\displaystyle f(x)=\int_0^x(1+2\cos t)\sin t~dt~~(0\leqq x\leqq2\pi)$
(2) $\displaystyle f(x)=\int_1^x(2-t)\log t~dt~~(1\leqq x\leqq e)$
【数Ⅲ】【積分とその応用】定積分の種々の問題4 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数$\displaystyle f(x)=\int_0^{x}\sin 2t~dt~~(0\leqq x\leqq 2\pi)$
の極値を求めよ。
この動画を見る
関数$\displaystyle f(x)=\int_0^{x}\sin 2t~dt~~(0\leqq x\leqq 2\pi)$
の極値を求めよ。
【数Ⅲ】【積分とその応用】定積分の種々の問題3 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数$\displaystyle F(x)=\int_x^{2x^2}(x+t)\sin t~dt$
を$x$について微分せよ。
この動画を見る
関数$\displaystyle F(x)=\int_x^{2x^2}(x+t)\sin t~dt$
を$x$について微分せよ。
【数Ⅲ】【積分とその応用】定積分の種々の問題2 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数を$x$について微分せよ。
(1) $\displaystyle y=\int_x^{2x}\cos^2t~dt$
(2) $\displaystyle y=\int_x^{x^2}e^t\sin t~dt$
この動画を見る
次の関数を$x$について微分せよ。
(1) $\displaystyle y=\int_x^{2x}\cos^2t~dt$
(2) $\displaystyle y=\int_x^{x^2}e^t\sin t~dt$
【数Ⅲ】【積分とその応用】定積分の種々の問題1 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数を$x$について微分せよ。
(1) $\displaystyle F(x)=\int_0^x(x+t)e^t~dt$
(2) $\displaystyle F(x)=\int_1^x(t-x)\log t~dt$
この動画を見る
次の関数を$x$について微分せよ。
(1) $\displaystyle F(x)=\int_0^x(x+t)e^t~dt$
(2) $\displaystyle F(x)=\int_1^x(t-x)\log t~dt$
福田のおもしろ数学498〜定積分で定義された関数の極限

単元:
#関数と極限#積分とその応用#関数の極限#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$0\lt t \leqq 1$に対し、
$f(t)=\dfrac{1}{t} \displaystyle \int_{0}^{\frac{\pi}{2}t} \vert \cos 2x \vert dx$とする。
$\displaystyle \lim_{t\to 0} f(t)$を求めよ。
この動画を見る
$0\lt t \leqq 1$に対し、
$f(t)=\dfrac{1}{t} \displaystyle \int_{0}^{\frac{\pi}{2}t} \vert \cos 2x \vert dx$とする。
$\displaystyle \lim_{t\to 0} f(t)$を求めよ。
福田の数学〜慶應義塾大学薬学部2025第3問〜逆関数と定積分

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
実数$x$に対して、関数
$f(x)=\dfrac{1}{3}x+\sqrt{\dfrac{1}{9}x^2+8}$
がある。ただし、定義域は$x\geqq 0$である。
$y=f(x)$の逆関数を$y=g(x)$とする。
(1)$g(x)$を求めると、$g(x)=\boxed{ナ}$であり、
$g(x)$定義域は$\boxed{ニ}$である。
(2)$\displaystyle \int_{2\sqrt2}^{4}g(x)dx$を求めると$\boxed{ヌ}$である。
(3)$\displaystyle \int_{0}^{3} f(x) dx$を求めると$\boxed{ネ}$である。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{3}$
実数$x$に対して、関数
$f(x)=\dfrac{1}{3}x+\sqrt{\dfrac{1}{9}x^2+8}$
がある。ただし、定義域は$x\geqq 0$である。
$y=f(x)$の逆関数を$y=g(x)$とする。
(1)$g(x)$を求めると、$g(x)=\boxed{ナ}$であり、
$g(x)$定義域は$\boxed{ニ}$である。
(2)$\displaystyle \int_{2\sqrt2}^{4}g(x)dx$を求めると$\boxed{ヌ}$である。
(3)$\displaystyle \int_{0}^{3} f(x) dx$を求めると$\boxed{ネ}$である。
$2025$年慶應義塾大学薬学部過去問題
福田のおもしろ数学454〜積分に関するシュワルツの不等式の証明と等号成立条件

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#積分とその応用#不定積分#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$p\leqq x \leqq q$で定義された連続関数$f(x),g(x)$に対して
$\left(\displaystyle \int_{p}^{q} f(x)^2 dx\right)\left(\displaystyle \int_{p}^{q}g(x)^2 dx \right) \geqq \left(\displaystyle \int_{p}^{q} f(x)g(x)dx\right)^2$
を証明して下さい。
また等号成立条件も調べて下さい。
この動画を見る
$p\leqq x \leqq q$で定義された連続関数$f(x),g(x)$に対して
$\left(\displaystyle \int_{p}^{q} f(x)^2 dx\right)\left(\displaystyle \int_{p}^{q}g(x)^2 dx \right) \geqq \left(\displaystyle \int_{p}^{q} f(x)g(x)dx\right)^2$
を証明して下さい。
また等号成立条件も調べて下さい。
福田の数学〜北海道大学2025理系第3問〜部分積分と極限

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
実数$a$および自然数$n$に対して、定積分
$I(a,n)=\displaystyle \int_{0}^{2\pi} e^{ax} \sin (nx) dx$
を考える。ここで$e$は自然対数の底である。
(1)$I(a,n)$を求めよ。
(2)$a_n=\dfrac{\log _n}{2\pi} (n=1,2,3,\cdots)$のとき、
極限$\displaystyle \lim_{n\to\infty} I(a_n,n)$を求めよ。
ただし、$\log_n$は$n$の自然対数である。
また、必要ならば$\displaystyle \lim_{n\to\infty}\dfrac{\log_n}{n}=0$である
ことを用いてもよい。
$2025$年北海道大学理系過去問題
この動画を見る
$\boxed{3}$
実数$a$および自然数$n$に対して、定積分
$I(a,n)=\displaystyle \int_{0}^{2\pi} e^{ax} \sin (nx) dx$
を考える。ここで$e$は自然対数の底である。
(1)$I(a,n)$を求めよ。
(2)$a_n=\dfrac{\log _n}{2\pi} (n=1,2,3,\cdots)$のとき、
極限$\displaystyle \lim_{n\to\infty} I(a_n,n)$を求めよ。
ただし、$\log_n$は$n$の自然対数である。
また、必要ならば$\displaystyle \lim_{n\to\infty}\dfrac{\log_n}{n}=0$である
ことを用いてもよい。
$2025$年北海道大学理系過去問題
福田のおもしろ数学438〜定積分の値の評価

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\dfrac{2}{3} \lt \displaystyle \int_{0}^{1} e^{-x^2} dx \lt \dfrac{\pi}{4}$
を証明してください。
この動画を見る
$\dfrac{2}{3} \lt \displaystyle \int_{0}^{1} e^{-x^2} dx \lt \dfrac{\pi}{4}$
を証明してください。
【数Ⅲ】【積分とその応用】定積分部分積分 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
定積分$\displaystyle \int_0^1x^2e^{2x}~dx$を求めよ。
定積分$\displaystyle \int_0^\frac\pi2(ax-\sin x)^2~dx$を最小にする実数$a$の値を求めよ。
定積分$\displaystyle I=\int_0^\frac\pi2e^{-3x}\sin x~dx$を求めよ。
自然数$n$について、$\displaystyle I_n=\int_1^e(\log x)^n~dx$とする。
(1) $I_1$を求めよ。
(2) $I_{n+1}$を$I_n$を用いて表せ。
(3) $I_4$を求めよ。
この動画を見る
定積分$\displaystyle \int_0^1x^2e^{2x}~dx$を求めよ。
定積分$\displaystyle \int_0^\frac\pi2(ax-\sin x)^2~dx$を最小にする実数$a$の値を求めよ。
定積分$\displaystyle I=\int_0^\frac\pi2e^{-3x}\sin x~dx$を求めよ。
自然数$n$について、$\displaystyle I_n=\int_1^e(\log x)^n~dx$とする。
(1) $I_1$を求めよ。
(2) $I_{n+1}$を$I_n$を用いて表せ。
(3) $I_4$を求めよ。
【数Ⅲ】【積分とその応用】定積分置換積分 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の定積分を求めよ。
(1) $\displaystyle \int_{-1}^0 (x+2)\sqrt{3x+4}~dx$
(2) $\displaystyle \int_{0}^4 \frac{x^2}{\sqrt{x+1}}~dx$
(3) $\displaystyle \int_{0}^1 \frac{x^3}{\sqrt{1+x^2}}~dx$
(4) $\displaystyle \int_{1}^3 \frac{dx}{x\sqrt{x+1}}$
(5) $\displaystyle \int_{1}^2 \frac{dx}{e^x-1}$
(6) $\displaystyle \int_{0}^{\frac\pi4} \frac{\sin^3x}{\cos^2x}~dx$
次の定積分を求めよ。ただし、$a$は正の定数とする。
(1) $\displaystyle \int_{0}^1 \sqrt{2x-x^2}~dx$
(2) $\displaystyle \int_{1}^{\frac12} \frac{dx}{\sqrt{2x-x^2}}$
(3) $\displaystyle \int_{1}^{\frac a2} \frac{dx}{(a^2-x^2)^{\frac32}}$
(4) $\displaystyle \int_{1}^{2} \frac{dx}{x^2-2x+2}$
(5) $\displaystyle \int_{3}^{5} \frac{dx}{x^2-4x+4}$
(6) $\displaystyle \int_{6}^{12} \frac{dx}{x^2-3x-10}$
(7) $\displaystyle \int_{0}^{a} \frac{dx}{(x^2+a^2)^2}$
(8) $\displaystyle \int_{1}^{\sqrt3} \frac{2x+1}{x^2+1}~dx$
次のことが成り立つことを証明せよ。
(1) $\displaystyle \int_a^b f(x)~dx=\int_a^bf(a+b-x)~dx$
(2) $\displaystyle\int_{-a}^af(x)~dx=\int_0^a\{f(x)+f(-x)\}~dx$
(3) $\displaystyle \int_0^af(x)~dx=\int_0^{\frac a 2}\{f(x)+f(a-x)\}~dx$
(4) $f(a+x)=f(a-x)$のとき$\displaystyle \int_{a-b}^{a+b}f(x)~dx=2\int_a^{a+b}f(x)~dx$
この動画を見る
次の定積分を求めよ。
(1) $\displaystyle \int_{-1}^0 (x+2)\sqrt{3x+4}~dx$
(2) $\displaystyle \int_{0}^4 \frac{x^2}{\sqrt{x+1}}~dx$
(3) $\displaystyle \int_{0}^1 \frac{x^3}{\sqrt{1+x^2}}~dx$
(4) $\displaystyle \int_{1}^3 \frac{dx}{x\sqrt{x+1}}$
(5) $\displaystyle \int_{1}^2 \frac{dx}{e^x-1}$
(6) $\displaystyle \int_{0}^{\frac\pi4} \frac{\sin^3x}{\cos^2x}~dx$
次の定積分を求めよ。ただし、$a$は正の定数とする。
(1) $\displaystyle \int_{0}^1 \sqrt{2x-x^2}~dx$
(2) $\displaystyle \int_{1}^{\frac12} \frac{dx}{\sqrt{2x-x^2}}$
(3) $\displaystyle \int_{1}^{\frac a2} \frac{dx}{(a^2-x^2)^{\frac32}}$
(4) $\displaystyle \int_{1}^{2} \frac{dx}{x^2-2x+2}$
(5) $\displaystyle \int_{3}^{5} \frac{dx}{x^2-4x+4}$
(6) $\displaystyle \int_{6}^{12} \frac{dx}{x^2-3x-10}$
(7) $\displaystyle \int_{0}^{a} \frac{dx}{(x^2+a^2)^2}$
(8) $\displaystyle \int_{1}^{\sqrt3} \frac{2x+1}{x^2+1}~dx$
次のことが成り立つことを証明せよ。
(1) $\displaystyle \int_a^b f(x)~dx=\int_a^bf(a+b-x)~dx$
(2) $\displaystyle\int_{-a}^af(x)~dx=\int_0^a\{f(x)+f(-x)\}~dx$
(3) $\displaystyle \int_0^af(x)~dx=\int_0^{\frac a 2}\{f(x)+f(a-x)\}~dx$
(4) $f(a+x)=f(a-x)$のとき$\displaystyle \int_{a-b}^{a+b}f(x)~dx=2\int_a^{a+b}f(x)~dx$
【数Ⅲ】【積分とその応用】定積分置換積分、部分積分 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次を求めよ
(1) $\displaystyle \int_0^1 \sqrt{e^{1-t}}~dt$
(2) $\displaystyle \int_0^{\frac{\pi}2}\frac{\cos{2\theta}}{\sin \theta+\cos\theta}~d\theta$
(3) $\displaystyle\int_0^\pi \sin^4x~dx$
(4) $\displaystyle \int_1^2 \frac{\sqrt{x^2-4x+4}}{x}~dx$
次を求めよ
(1) $\displaystyle \int_0^\pi |\cos2\theta|~d\theta$
(2) $\displaystyle \int_0^\pi|\sin x+\cos x|~dx$
$m,n$は正の整数とする。次の定積分を求めよ。
(1) $\displaystyle \int_0^\pi \cos mx\cos nx~dx$
(2) $\displaystyle \int_0^\pi \sin mx\sin nx~dx$
(3) $\displaystyle \int_0^\pi \sin mx\cos nx~dx$
定積分$\displaystyle \int_0^\pi (1-a\sin x-b\sin2x)^2~dx$を最小にする定数$a,b$の値を求めよ。
この動画を見る
次を求めよ
(1) $\displaystyle \int_0^1 \sqrt{e^{1-t}}~dt$
(2) $\displaystyle \int_0^{\frac{\pi}2}\frac{\cos{2\theta}}{\sin \theta+\cos\theta}~d\theta$
(3) $\displaystyle\int_0^\pi \sin^4x~dx$
(4) $\displaystyle \int_1^2 \frac{\sqrt{x^2-4x+4}}{x}~dx$
次を求めよ
(1) $\displaystyle \int_0^\pi |\cos2\theta|~d\theta$
(2) $\displaystyle \int_0^\pi|\sin x+\cos x|~dx$
$m,n$は正の整数とする。次の定積分を求めよ。
(1) $\displaystyle \int_0^\pi \cos mx\cos nx~dx$
(2) $\displaystyle \int_0^\pi \sin mx\sin nx~dx$
(3) $\displaystyle \int_0^\pi \sin mx\cos nx~dx$
定積分$\displaystyle \int_0^\pi (1-a\sin x-b\sin2x)^2~dx$を最小にする定数$a,b$の値を求めよ。
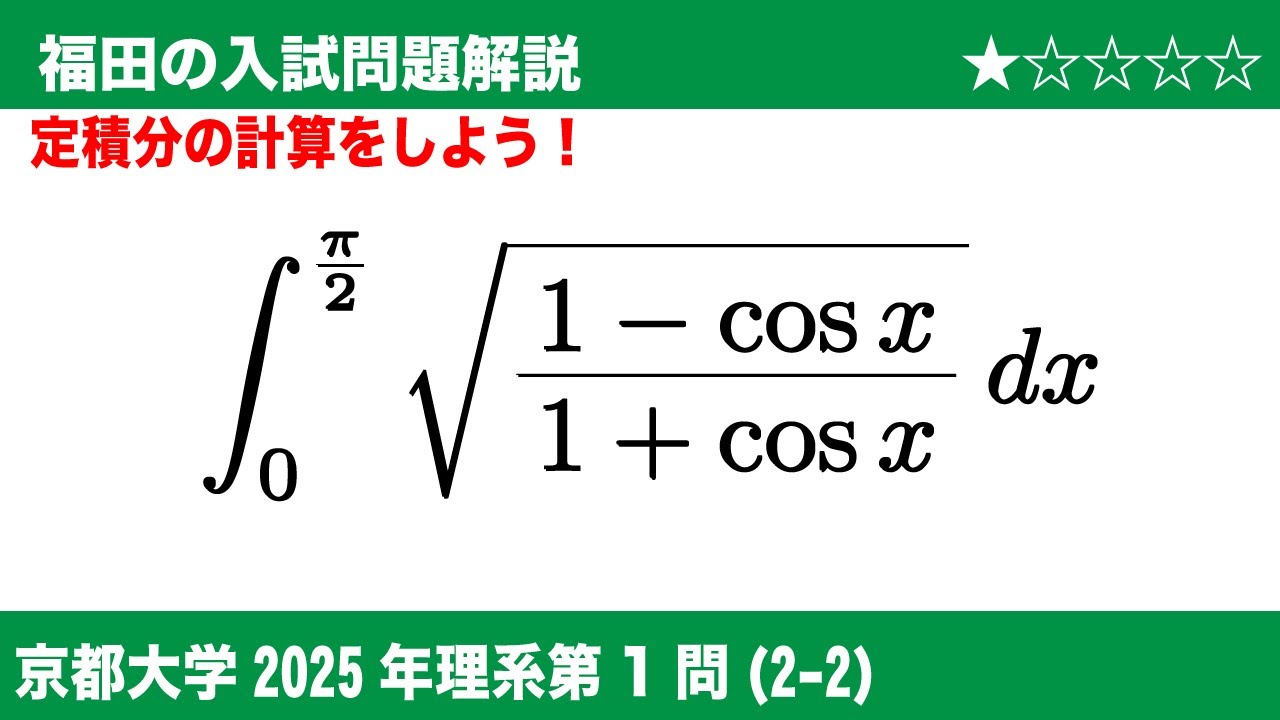
福田の数学〜京都大学2025理系第1問(2−2)〜定積分の計算
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(2-2)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{\dfrac{1-\cos x}{1+\cos x}}dx$
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{1}$
(2-2)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{\dfrac{1-\cos x}{1+\cos x}}dx$
$2025$年京都大学理系過去問題
福田のおもしろ数学380〜定積分の計算

福田のおもしろ数学363〜定積分の計算

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$
\int_0^\pi (1+2x)\frac{\sin^3{x}}{1+\cos ^2 x} \mathrm{d}x
$
を計算して下さい。
この動画を見る
$
\int_0^\pi (1+2x)\frac{\sin^3{x}}{1+\cos ^2 x} \mathrm{d}x
$
を計算して下さい。
福田のおもしろ数学362〜定積分の等式の証明

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\int_0^πx f(sin x) dx=\frac{π}{2}\int_0^π f(sinx) dx$
を証明してください。
この動画を見る
$\int_0^πx f(sin x) dx=\frac{π}{2}\int_0^π f(sinx) dx$
を証明してください。
福田のおもしろ数学358〜定積分の計算

単元:
#積分とその応用#定積分#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$I=\int_0^{\frac{\pi}{2}} \frac{\sin^3 x}{\sin x + \cos x} dx$の値を求めて下さい。
この動画を見る
$I=\int_0^{\frac{\pi}{2}} \frac{\sin^3 x}{\sin x + \cos x} dx$の値を求めて下さい。
福田のおもしろ数学358〜定積分の計算

単元:
#積分とその応用#定積分#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$I=\int_0^\frac{\pi}{2} \frac{\sin^3 x}{\sin x+\cos x} dx$の値を求めて下さい。
この動画を見る
$I=\int_0^\frac{\pi}{2} \frac{\sin^3 x}{\sin x+\cos x} dx$の値を求めて下さい。
福田のおもしろ数学357〜シグマで表された式の定積分の計算

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle\int_0^\pi (\sum_{k=1}^n \sin kx)^2 dx$ を計算して下さい。
この動画を見る
$\displaystyle\int_0^\pi (\sum_{k=1}^n \sin kx)^2 dx$ を計算して下さい。
福田のおもしろ数学337〜定積分の計算

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \int_{-1}^1\log(x+\sqrt{x^2+1})dx$
を計算して下さい。
この動画を見る
$\displaystyle \int_{-1}^1\log(x+\sqrt{x^2+1})dx$
を計算して下さい。
福田のおもしろ数学300〜絶対値の付いた式の定積分

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$
\displaystyle \int_{0}^{ \pi } |a \sin \ nx + b \cos nx| dx
\quad
$
(nは自然数)を求めよ
この動画を見る
$
\displaystyle \int_{0}^{ \pi } |a \sin \ nx + b \cos nx| dx
\quad
$
(nは自然数)を求めよ
この式はあれしかない!!どう解く?

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
多項式(x^100+1)^100+(x^2+1)^100+1は多項式x^2+x+1で割り切れるか。
この動画を見る
多項式(x^100+1)^100+(x^2+1)^100+1は多項式x^2+x+1で割り切れるか。
