 定積分
定積分
 定積分
定積分
#会津大学2023#定積分_9#元高校教員
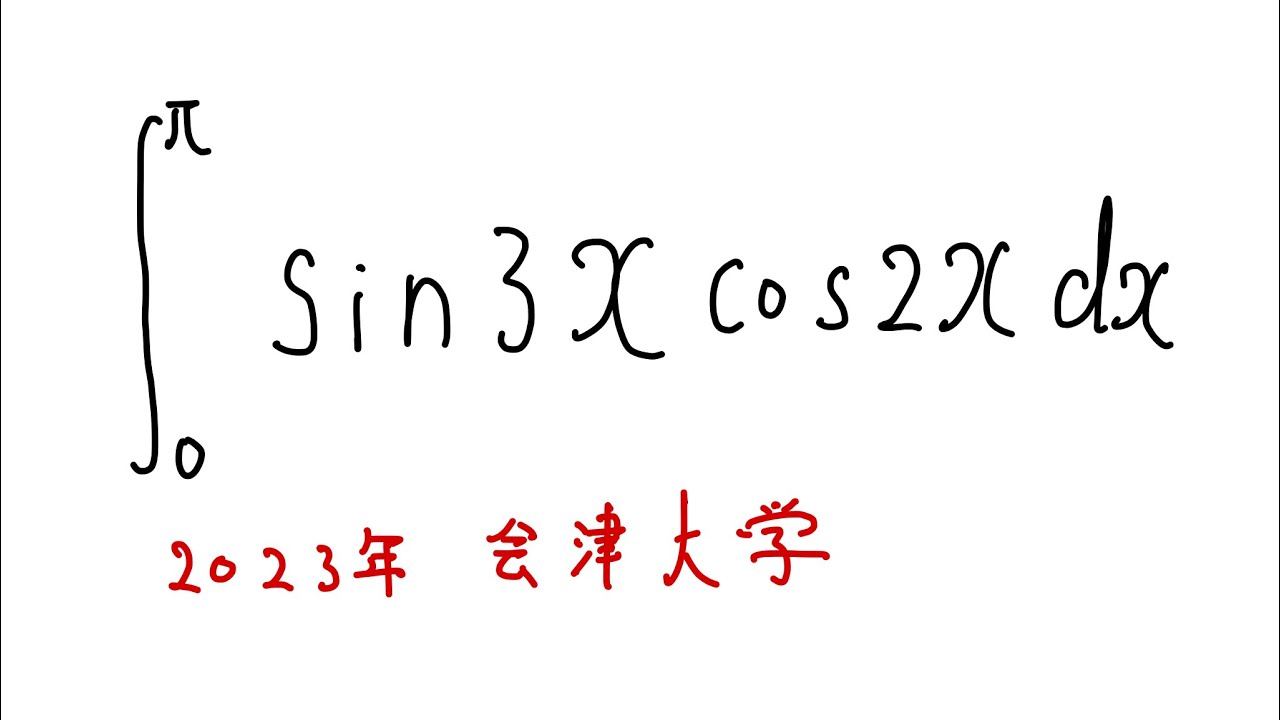
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\pi} \sin3x\cos2x$ $dx$
出典:2023年会津大学
この動画を見る
$\displaystyle \int_{0}^{\pi} \sin3x\cos2x$ $dx$
出典:2023年会津大学
#茨城大学2024#定積分_8#元高校教員

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos\theta\sin 2 \theta d \theta$
出典:2024年茨城大学後期
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos\theta\sin 2 \theta d \theta$
出典:2024年茨城大学後期
福田のおもしろ数学239〜定積分と不等式の関係

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$k>0$ のとき、
$\displaystyle
\frac{1}{2(k+1)}<\int^{1}_{0}\frac{1-x}{k+x}dx<\frac{1}{2k}
$
を示して下さい。
この動画を見る
$k>0$ のとき、
$\displaystyle
\frac{1}{2(k+1)}<\int^{1}_{0}\frac{1-x}{k+x}dx<\frac{1}{2k}
$
を示して下さい。
福田のおもしろ数学229〜置換積分の計算

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \int^3_2\dfrac{1}{1+x^2}dx$の値を求めよ。
この動画を見る
$\displaystyle \int^3_2\dfrac{1}{1+x^2}dx$の値を求めよ。
大学入試問題#908「正確に対応するだけ」 #信州大学理学部(2024) #積分方程式

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
次の等式を満たす関数$f(x)$を求めよ
$f(x)=x+\displaystyle \int_{0}^{\pi} f(t) \cos(x+t) dt$
出典:2024年信州大学理学部
この動画を見る
次の等式を満たす関数$f(x)$を求めよ
$f(x)=x+\displaystyle \int_{0}^{\pi} f(t) \cos(x+t) dt$
出典:2024年信州大学理学部
#茨城大学2024#定積分_7#元高校教員

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} e^x(e^{2x}+\frac{1}{e^{2x}}) dx$
出典:2024年茨城大学
この動画を見る
$\displaystyle \int_{0}^{1} e^x(e^{2x}+\frac{1}{e^{2x}}) dx$
出典:2024年茨城大学
#茨城大学後期2024#定積分_6#元高校教員

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{2}^{4} \displaystyle \frac{2}{x^2-1} dx$
出典:2024年茨城大学後期
この動画を見る
$\displaystyle \int_{2}^{4} \displaystyle \frac{2}{x^2-1} dx$
出典:2024年茨城大学後期
福田の数学〜中央大学202理工学部第4問〜sin(x)のn乗の定積分と極限

単元:
#関数と極限#積分とその応用#関数の極限#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$n=1,2,3,\cdots$に対し、$\displaystyle I_n=\int_0^{\frac{\pi}{2}}\sin^nxdx$とおく。また、$\displaystyle I_0=\int_0^{\frac{\pi}{2}}1dx$とする。
(1) $(n+1)I_{n+1}=nI_{n-1}$を示せ。
(2) $nI_nI_{n-1}$を求めよ。
(3) $I_{n+1} < I_n$を示せ。
(4) 極限$\displaystyle \lim_{n \to\infty}nI_n^2$を求めよ。
この動画を見る
$n=1,2,3,\cdots$に対し、$\displaystyle I_n=\int_0^{\frac{\pi}{2}}\sin^nxdx$とおく。また、$\displaystyle I_0=\int_0^{\frac{\pi}{2}}1dx$とする。
(1) $(n+1)I_{n+1}=nI_{n-1}$を示せ。
(2) $nI_nI_{n-1}$を求めよ。
(3) $I_{n+1} < I_n$を示せ。
(4) 極限$\displaystyle \lim_{n \to\infty}nI_n^2$を求めよ。
#茨城大学2024#区分求積法_5#元高校教員

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n^{3}}\displaystyle \sum_{k=1}^n (n-k)^2$
出典:2024年茨城大学
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n^{3}}\displaystyle \sum_{k=1}^n (n-k)^2$
出典:2024年茨城大学
#福島大学2024#定積分_4#元高校教員

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#福島大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} x\sqrt{ 1-x }$ $dx$
出典:2024年福島大学
この動画を見る
$\displaystyle \int_{0}^{1} x\sqrt{ 1-x }$ $dx$
出典:2024年福島大学
福田のおもしろ数学227〜極限と区分求積法

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \lim_{n\to\infty}\dfrac1n\sqrt[n]{_{2n}\mathrm{P}_n}$を求めよ
この動画を見る
$\displaystyle \lim_{n\to\infty}\dfrac1n\sqrt[n]{_{2n}\mathrm{P}_n}$を求めよ
#会津大学2024#定積分_3#元高校教員
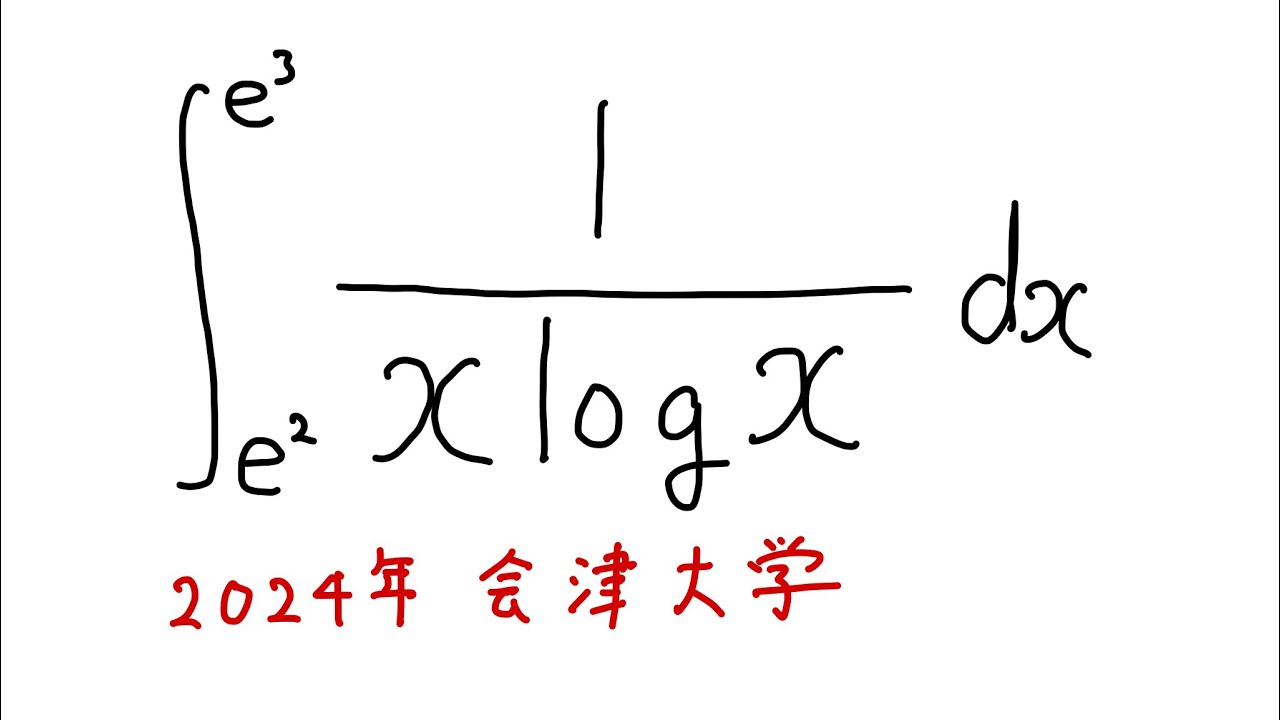
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
問題文全文(内容文):
$\displaystyle \int_{e^2}^{e^3} \displaystyle \frac{1}{x log x} dx$
出典:2024年会津大学
この動画を見る
$\displaystyle \int_{e^2}^{e^3} \displaystyle \frac{1}{x log x} dx$
出典:2024年会津大学
大学入試問題#905「基本変形の王道」 #信州大学教育学部(2024) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} (\cos x\cos 2x-\cos3x\sin4x) dx$
出典:2024年信州大学教育学部
この動画を見る
$\displaystyle \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} (\cos x\cos 2x-\cos3x\sin4x) dx$
出典:2024年信州大学教育学部
#高専数学_12#定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{3x^2+1} dx$
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{3x^2+1} dx$
#茨城大学2024#定積分_2#元高校教員
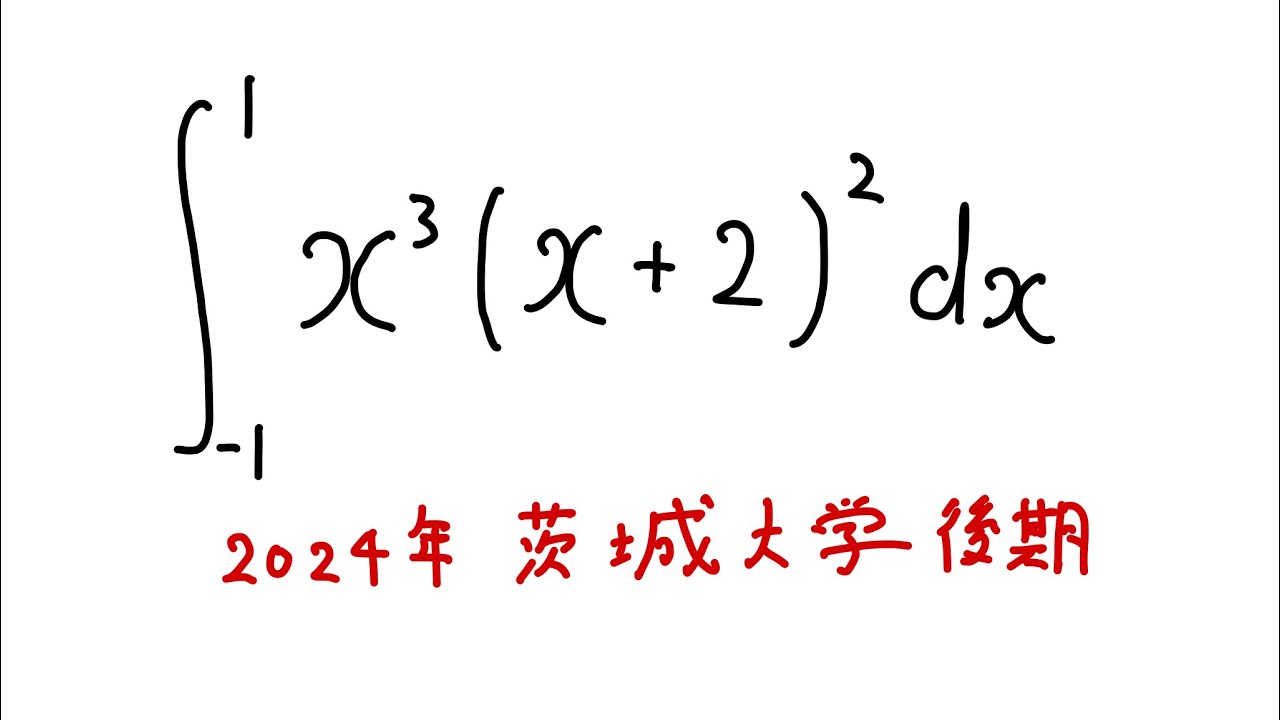
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1} x^3(x+2)^2 dx$
出典:2024年茨城大学後期
この動画を見る
$\displaystyle \int_{-1}^{1} x^3(x+2)^2 dx$
出典:2024年茨城大学後期
大学入試問題#616「これは理系が解くと逆にはまるかも」 名古屋大学(1963)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#名古屋大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x \gt y$とする
$x+y=6,\ xy=4$のとき
$\displaystyle \frac{\sqrt{ x }-\sqrt{ y }}{\sqrt{ x }+\sqrt{ y }}$の値を求めよ。
出典:1963年名古屋大学 入試問題
この動画を見る
$x \gt y$とする
$x+y=6,\ xy=4$のとき
$\displaystyle \frac{\sqrt{ x }-\sqrt{ y }}{\sqrt{ x }+\sqrt{ y }}$の値を求めよ。
出典:1963年名古屋大学 入試問題
#高専数学_11#定積分#元高専教員
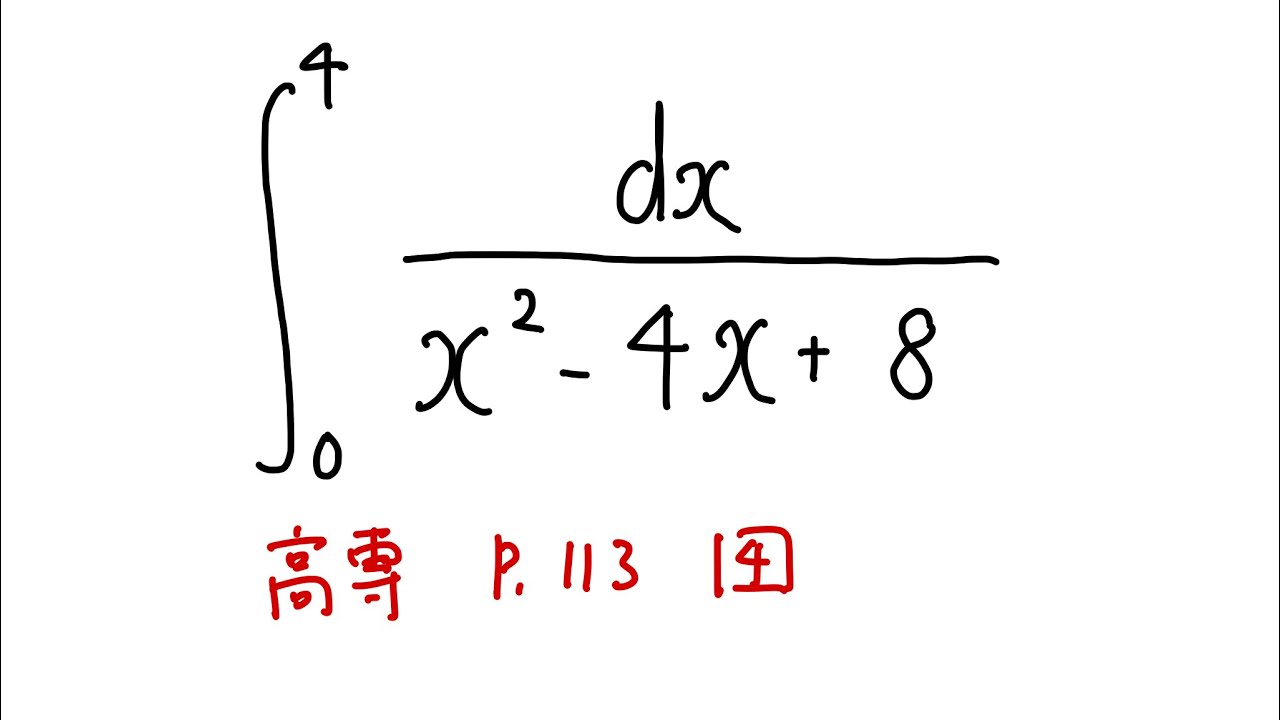
単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{4} \displaystyle \frac{dx}{x^2-4x+8}$
この動画を見る
$\displaystyle \int_{0}^{4} \displaystyle \frac{dx}{x^2-4x+8}$
#茨城大学2024_1#定積分
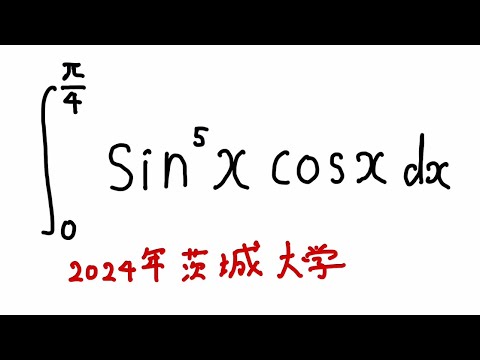
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}} \sin^5x\cos x$ $dx$
出典:2024年茨城大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} \sin^5x\cos x$ $dx$
出典:2024年茨城大学
#千葉大学2016#定積分#元高校教員

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \cos^3x$ $dx$
出典:2016年千葉大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \cos^3x$ $dx$
出典:2016年千葉大学
#高専_7#定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{\sqrt{ 2 }} \displaystyle \frac{1+2x}{\sqrt{ 4-x^2 }} dx$
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{\sqrt{ 2 }} \displaystyle \frac{1+2x}{\sqrt{ 4-x^2 }} dx$
#高専_3#定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1} (e^x-e^{-x})^2(e^x+e^{-x}) dx$
この動画を見る
$\displaystyle \int_{-1}^{1} (e^x-e^{-x})^2(e^x+e^{-x}) dx$
#高専_2#定積分

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (1-\sin^3x)\cos x$ $dx$
この動画を見る
$\displaystyle \int (1-\sin^3x)\cos x$ $dx$
#千葉大学2024#定積分
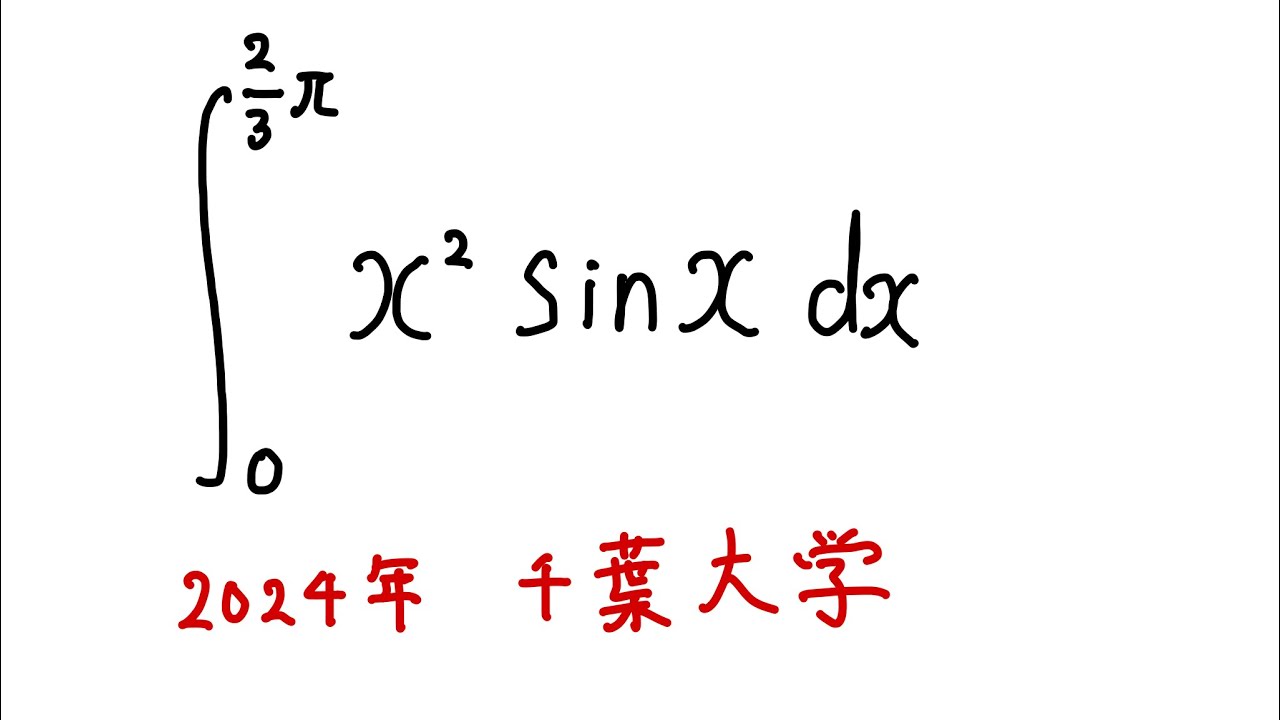
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{2}{3}\pi} x^2\sin x$ $dx$
出典:2024年千葉大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{2}{3}\pi} x^2\sin x$ $dx$
出典:2024年千葉大学
#千葉大学2023#定積分#ますただ
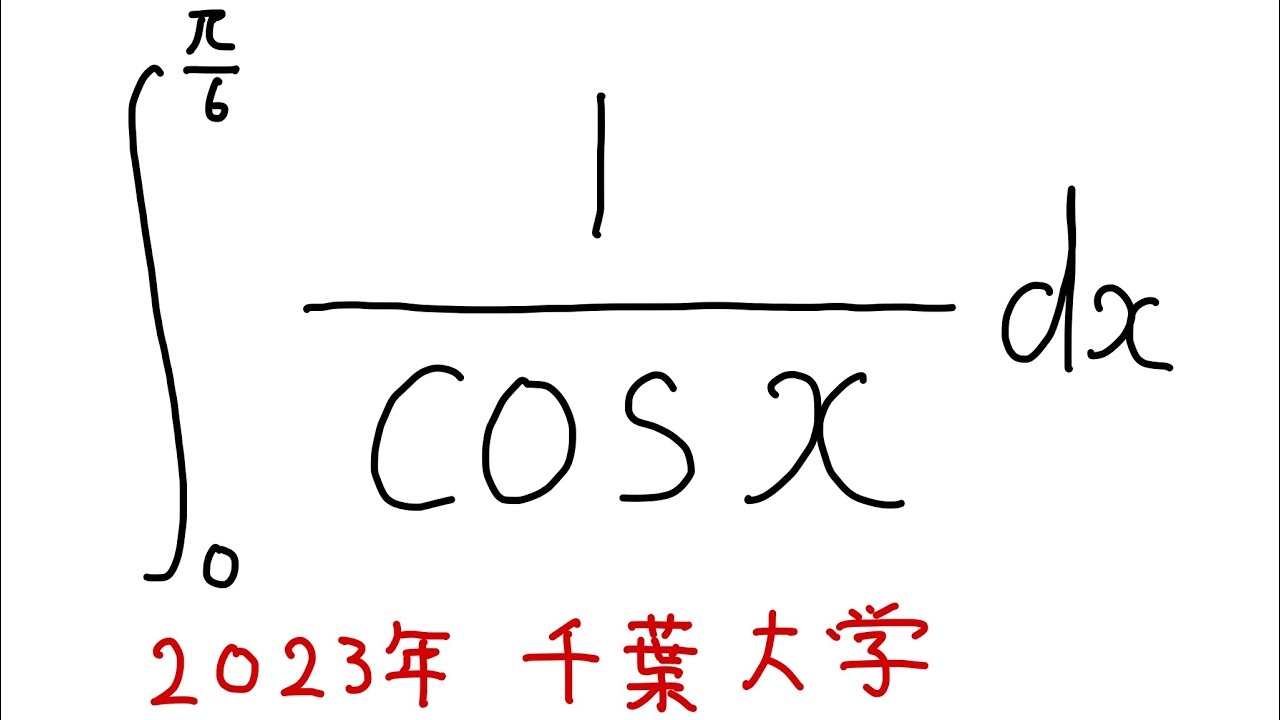
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{1}{\cos x} dx$
出典:2023年千葉大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{1}{\cos x} dx$
出典:2023年千葉大学
#千葉大学2023#定積分
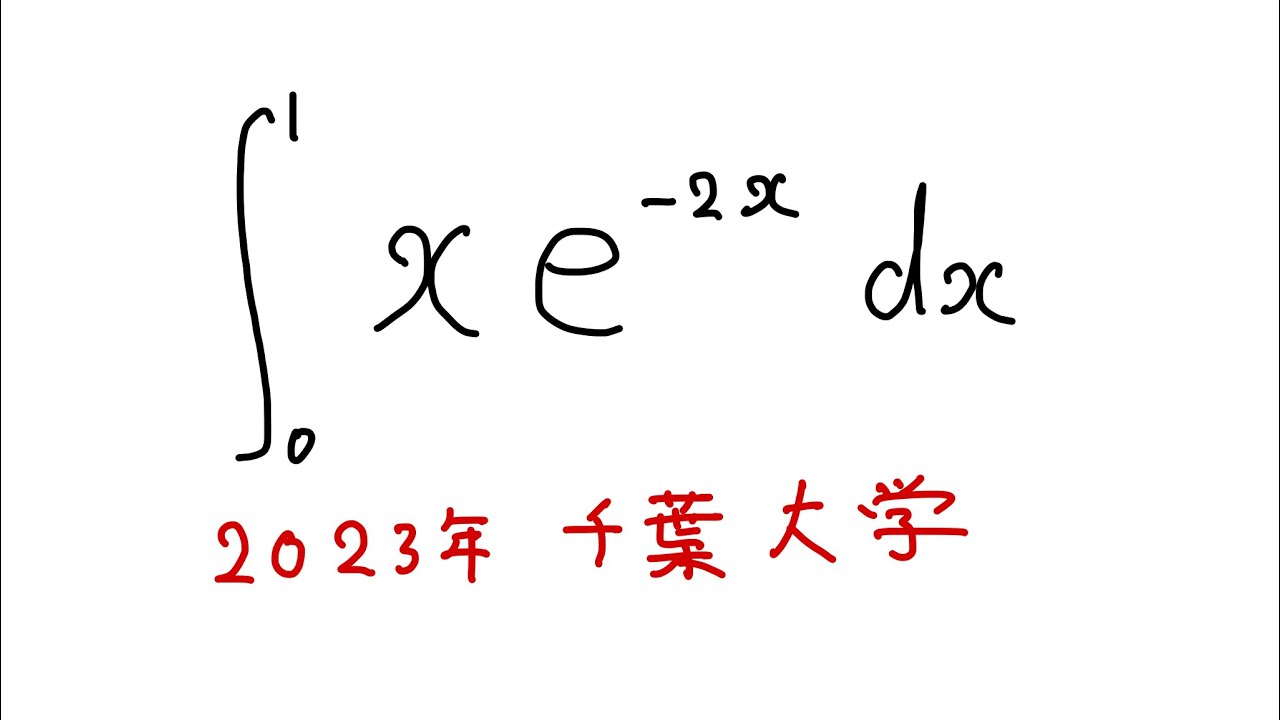
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
下記の定積分を解け
$\displaystyle \int_{0}^{1} xe^{-2x} dx$
出典:2023年千葉大学
この動画を見る
下記の定積分を解け
$\displaystyle \int_{0}^{1} xe^{-2x} dx$
出典:2023年千葉大学
#富山大学推薦2019#定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#富山大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{\sqrt{ 3 }} \displaystyle \frac{x}{x^2+1} dx$
出典:2019年富山大学推薦
この動画を見る
$\displaystyle \int_{1}^{\sqrt{ 3 }} \displaystyle \frac{x}{x^2+1} dx$
出典:2019年富山大学推薦
#電気通信大学2015#定積分#ますただ
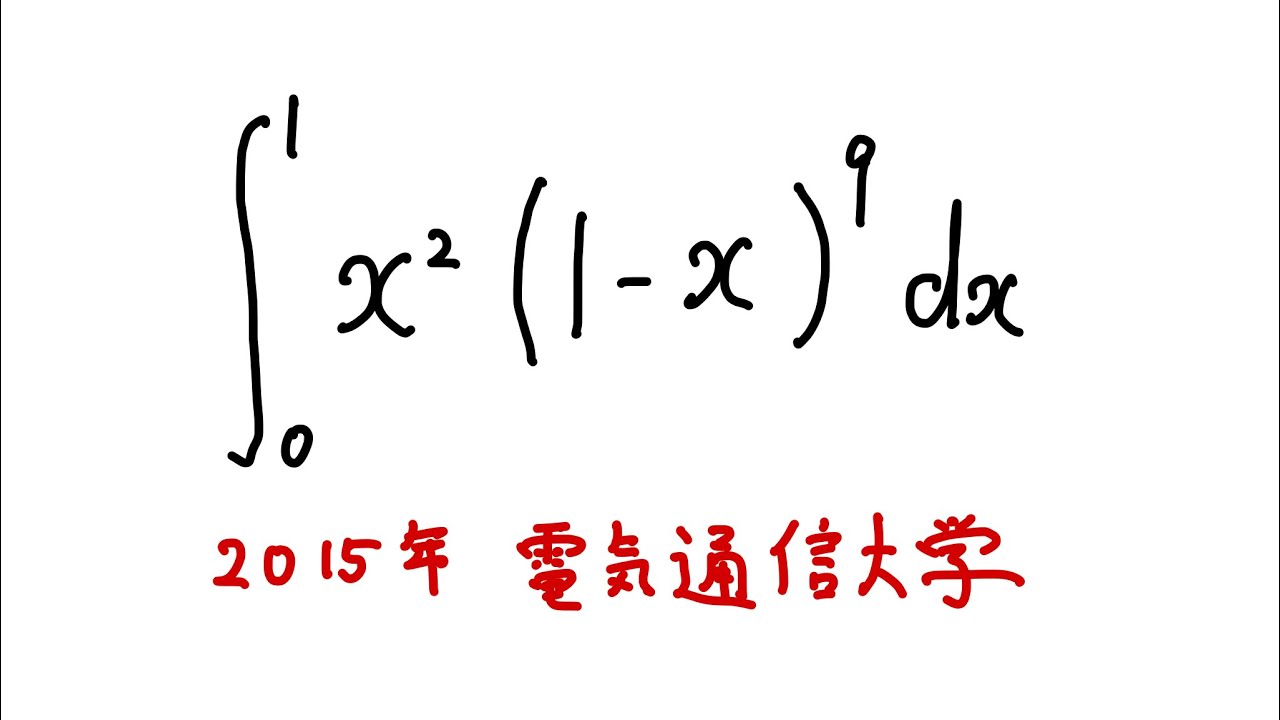
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} x^2(1-x)^9 dx$
出典:2015年電気通信大学
この動画を見る
$\displaystyle \int_{0}^{1} x^2(1-x)^9 dx$
出典:2015年電気通信大学
#藤田医科大学2023#定積分
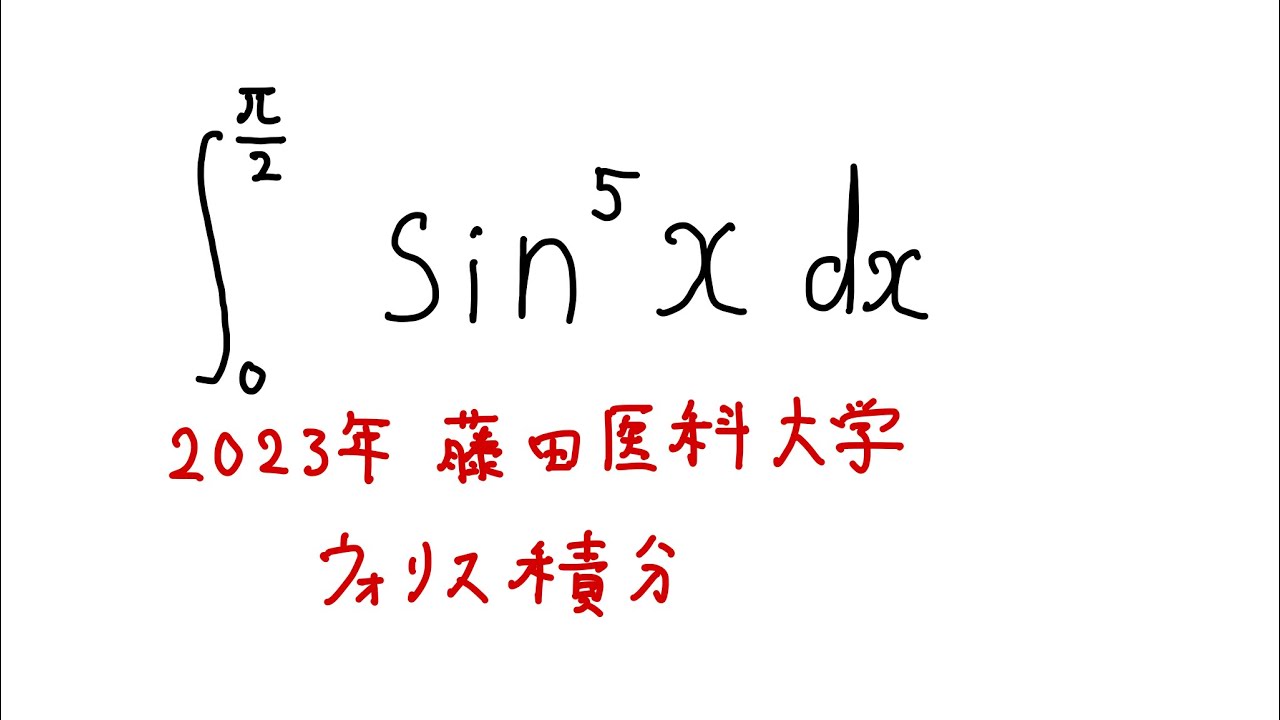
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#藤田医科大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^5x$ $dx$
出典:2023年藤田医科大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^5x$ $dx$
出典:2023年藤田医科大学
#数検準1級1次 #7
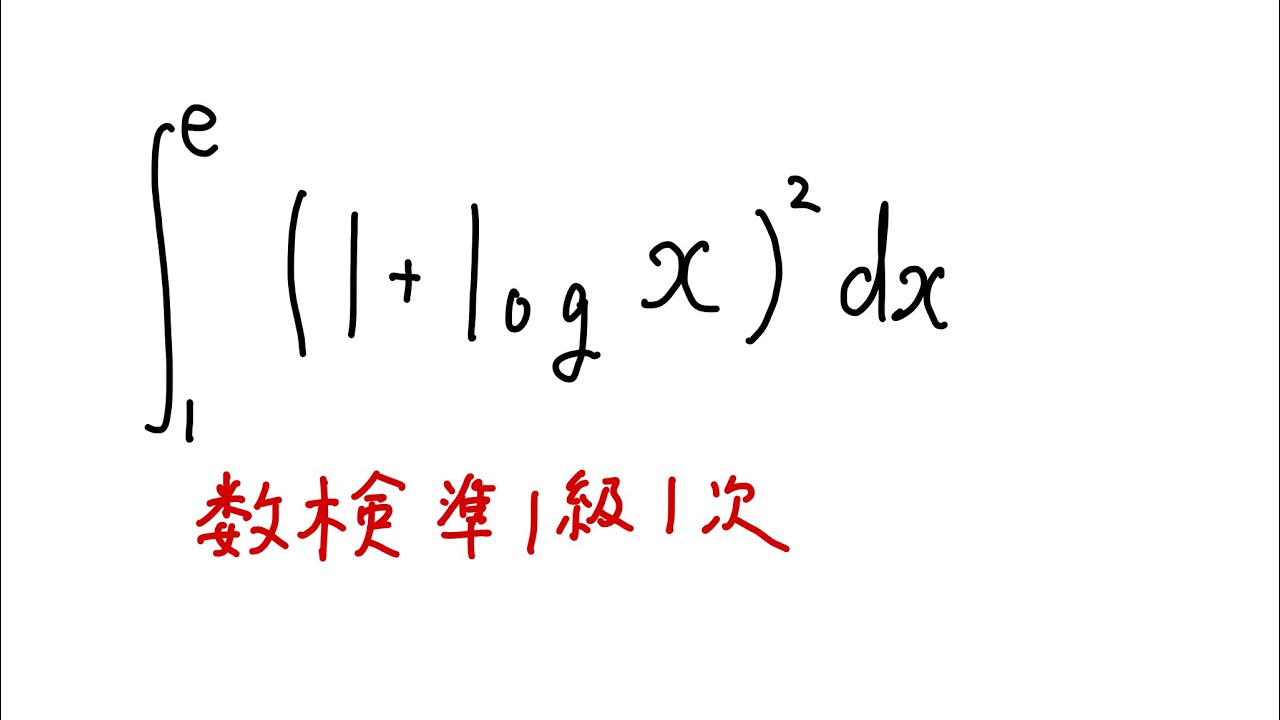
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e} (1+log x)^2$ $dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int_{1}^{e} (1+log x)^2$ $dx$
出典:数検準1級1次
#数検準1級1次-1 #定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{x^4+2x^2+1} dx$
出典:数検準1級1次
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{x^4+2x^2+1} dx$
出典:数検準1級1次
