 数Ⅲ
数Ⅲ
 数Ⅲ
数Ⅲ
大学入試問題#549「解き方は色々」 島根大学(2023) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#島根大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{2x-2}{2x^2-2x+1}dx$
出典:2023年島根大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{2x-2}{2x^2-2x+1}dx$
出典:2023年島根大学 入試問題
早稲田大 みんな大好きBBB

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \sum_{i=6}^{\infty} \dfrac{1800}{(n-5)(n-4)(n-1)n}$
これを求めよ。
早稲田大過去問
この動画を見る
$\displaystyle \sum_{i=6}^{\infty} \dfrac{1800}{(n-5)(n-4)(n-1)n}$
これを求めよ。
早稲田大過去問
【等比数列の極限!】無限等比級数の基礎と求め方を解説!【数学III】

大学院入試問題#1「間違えてたらすみません」 岡山大学大学院 #微分方程式

単元:
#微分とその応用#微分法#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$\displaystyle \frac{dy}{dx}=\displaystyle \frac{4y}{3x},\ x \gt 0$の一般項を求めよ
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{dy}{dx}=\displaystyle \frac{2y}{3x}+\displaystyle \frac{2x}{y},\ x \gt 0 \\
y(1)=3
\end{array}
\right.
\end{eqnarray}$を満たす解を求めよ
出典:岡山大学大学院 入試問題
この動画を見る
(1)
$\displaystyle \frac{dy}{dx}=\displaystyle \frac{4y}{3x},\ x \gt 0$の一般項を求めよ
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{dy}{dx}=\displaystyle \frac{2y}{3x}+\displaystyle \frac{2x}{y},\ x \gt 0 \\
y(1)=3
\end{array}
\right.
\end{eqnarray}$を満たす解を求めよ
出典:岡山大学大学院 入試問題
大学入試問題#546「もう飽きてると思います」 愛知教育大学(2023) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#愛知教育大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1} \displaystyle \frac{x^2}{1+e^x} dx$
出典:2023年愛知教育大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{1} \displaystyle \frac{x^2}{1+e^x} dx$
出典:2023年愛知教育大学 入試問題
大学入試だけど、中学生が解ける!?名城大

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
数学を数楽に
問題文全文(内容文):
$OA=OB=OC=1$
$AB=BC=CA=\sqrt 2$
四面体OABCの体積を求めよ
名城大学(改)
この動画を見る
$OA=OB=OC=1$
$AB=BC=CA=\sqrt 2$
四面体OABCの体積を求めよ
名城大学(改)
福田の数学〜東北大学2023年文系第3問〜軸の動く最大最小

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ aを実数とし、2次関数f(x)=$x^2$+2$ax$-3 を考える。実数xがa≦x≦a+3 の範囲を動くときのf(x)の最大値および最小値を、それぞれM(a), m(a)とする。
以下の問いに答えよ。
(1)M(a)をaを用いて表せ。
(2)m(a)をaを用いて表せ。
(3)aがすべての実数を動くとき、m(a)の最小値を求めよ。
2023東北大学文系過去問
この動画を見る
$\Large\boxed{3}$ aを実数とし、2次関数f(x)=$x^2$+2$ax$-3 を考える。実数xがa≦x≦a+3 の範囲を動くときのf(x)の最大値および最小値を、それぞれM(a), m(a)とする。
以下の問いに答えよ。
(1)M(a)をaを用いて表せ。
(2)m(a)をaを用いて表せ。
(3)aがすべての実数を動くとき、m(a)の最小値を求めよ。
2023東北大学文系過去問
大学入試問題#545「作成時間がありませんでした」 会津大学(2023) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} (2x+1)log(x+1)\ dx$
出典:2023年会津大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} (2x+1)log(x+1)\ dx$
出典:2023年会津大学 入試問題
福田の数学〜東北大学2023年理系第6問〜線分の通過範囲の面積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#微分法#接線と法線・平均値の定理#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ 関数$f(x)$=$-\frac{1}{2}x$$-\frac{4}{6x+1}$について、以下の問いに答えよ。
(1)曲線y=f(x)の接線で、傾きが1であり、かつ接点のx座標が正であるものの方程式を求めよ。
(2)座標平面上の2点P(x, f(x)), Q(x+1, f(x)+1)を考える。xが0≦x≦2の範囲を動くとき、線分PQが通過してできる図形Sの概形を描け。またSの面積を求めよ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{6}$ 関数$f(x)$=$-\frac{1}{2}x$$-\frac{4}{6x+1}$について、以下の問いに答えよ。
(1)曲線y=f(x)の接線で、傾きが1であり、かつ接点のx座標が正であるものの方程式を求めよ。
(2)座標平面上の2点P(x, f(x)), Q(x+1, f(x)+1)を考える。xが0≦x≦2の範囲を動くとき、線分PQが通過してできる図形Sの概形を描け。またSの面積を求めよ。
2023東北大学理系過去問
大学入試問題#543「見た目は次数だけ」 前橋工科大学(2023) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\sqrt[ 4 ]{ 3 }} (x^7-3x^3)e^{-\frac{x^4}{4}}\ dx$
出典:2023年前橋工科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\sqrt[ 4 ]{ 3 }} (x^7-3x^3)e^{-\frac{x^4}{4}}\ dx$
出典:2023年前橋工科大学 入試問題
大学入試問題#541「初手が大事」長崎大学(2023)定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#長崎大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2} \displaystyle \frac{x^2}{x^2+(3-x)^2} dx$
出典:2023年長崎大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2} \displaystyle \frac{x^2}{x^2+(3-x)^2} dx$
出典:2023年長崎大学 入試問題
大学入試問題#540「これは平均点の調整すらならないような」 京都大学(2023) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{4} \sqrt{ x }\ log(x^2)\ dx$
出典:2023年京都大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{4} \sqrt{ x }\ log(x^2)\ dx$
出典:2023年京都大学 入試問題
福田の数学〜東北大学2023年理系第2問〜三角方程式の解の個数とその極限

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#円と方程式#三角関数とグラフ#関数と極限#微分とその応用#関数の極限#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 関数f(x)=$\sin3x$+$\sin x$について、以下の問いに答えよ。
(1)f(x)=0 を満たす正の実数$x$のうち、最小のものを求めよ。
(2)正の整数$m$に対して、f(x)=0を満たす正の実数$x$のうち、$m$以下のものの個数を$p(m)$とする。極限値$\displaystyle\lim_{m \to \infty}\frac{p(m)}{m}$ を求めよ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{2}$ 関数f(x)=$\sin3x$+$\sin x$について、以下の問いに答えよ。
(1)f(x)=0 を満たす正の実数$x$のうち、最小のものを求めよ。
(2)正の整数$m$に対して、f(x)=0を満たす正の実数$x$のうち、$m$以下のものの個数を$p(m)$とする。極限値$\displaystyle\lim_{m \to \infty}\frac{p(m)}{m}$ を求めよ。
2023東北大学理系過去問
大学入試問題#539「これはよく出る」 佐賀大学(2023) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{d\theta}{\cos^3\theta}$
出典:2023年佐賀大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{d\theta}{\cos^3\theta}$
出典:2023年佐賀大学 入試問題
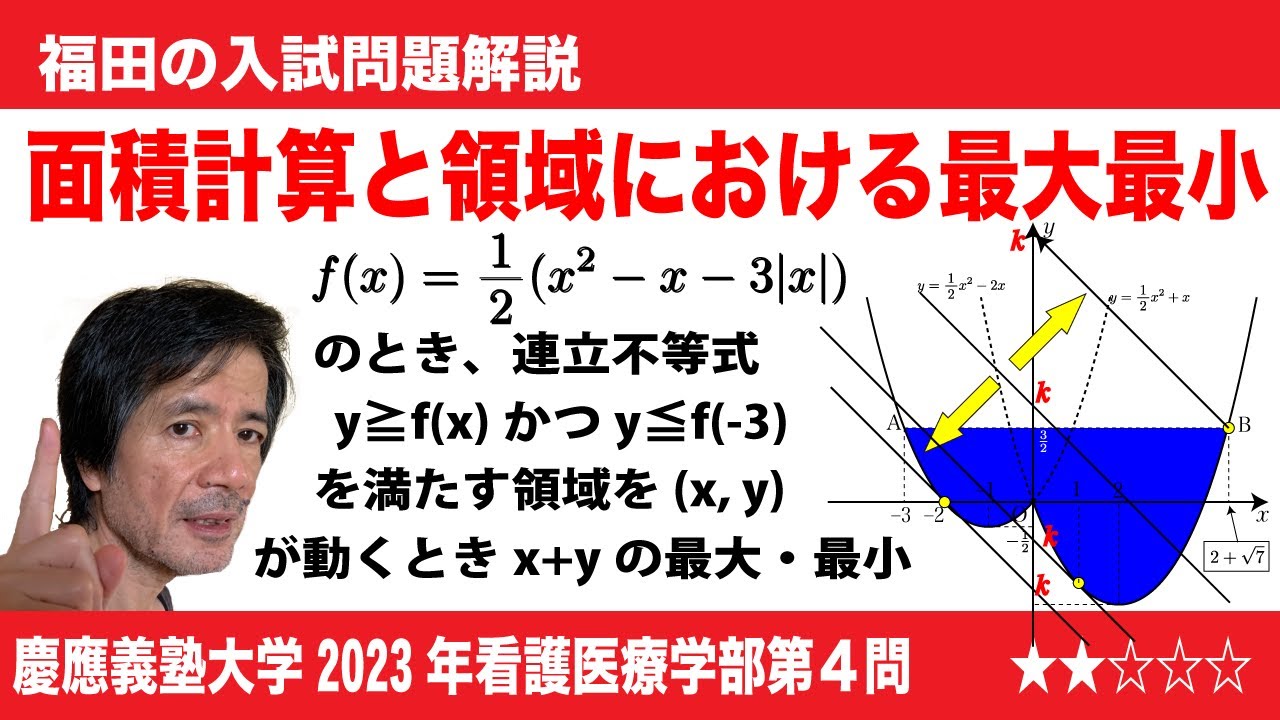
福田の数学〜慶應義塾大学2023年看護医療学部第4問〜絶対値の付いた関数と領域における最大最小
単元:
#大学入試過去問(数学)#図形と方程式#軌跡と領域#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 関数f(x)をf(x)=$\frac{1}{2}$($x^2$-$x$-3|$x$|)で定める。以下に答えなさい。
(1)y=f(x)のグラフをかきなさい。
(2)曲線y=f(x)上の点A(-3, f(-3))を通り、点Aにおける接線に垂直な直線lの方程式はy=$\boxed{\ \ ニ\ \ }$である。また、曲線と直線lは2つの共有点をもつが点Aとは異なる共有点の座標は$\boxed{\ \ ヌ\ \ }$である。さらに、曲線y=f(x)と直線lで囲まれた図形の面積は$\boxed{\ \ ネ\ \ }$である。
(3)連立不等式y≧f(x), y≦f(-3)の表す領域をDとする。点(x,y)がこの領域Dを動くとき、x+yは(x,y)=$\boxed{\ \ ノ\ \ }$のとき最大値$\boxed{\ \ ハ\ \ }$をとり、
(x,y)=$\boxed{\ \ ヒ\ \ }$のうち最小値$\boxed{\ \ フ\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 関数f(x)をf(x)=$\frac{1}{2}$($x^2$-$x$-3|$x$|)で定める。以下に答えなさい。
(1)y=f(x)のグラフをかきなさい。
(2)曲線y=f(x)上の点A(-3, f(-3))を通り、点Aにおける接線に垂直な直線lの方程式はy=$\boxed{\ \ ニ\ \ }$である。また、曲線と直線lは2つの共有点をもつが点Aとは異なる共有点の座標は$\boxed{\ \ ヌ\ \ }$である。さらに、曲線y=f(x)と直線lで囲まれた図形の面積は$\boxed{\ \ ネ\ \ }$である。
(3)連立不等式y≧f(x), y≦f(-3)の表す領域をDとする。点(x,y)がこの領域Dを動くとき、x+yは(x,y)=$\boxed{\ \ ノ\ \ }$のとき最大値$\boxed{\ \ ハ\ \ }$をとり、
(x,y)=$\boxed{\ \ ヒ\ \ }$のうち最小値$\boxed{\ \ フ\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
大学入試問題#536「計算力大事」 福島県立医科大学(2021) #微積の応用

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
すべての実数$x$に対して$f(x)=x+\displaystyle \int_{0}^{1} 2^{2t+x}f(t)\ dt$を満たすとき$f(0)$を求めよ
出典:2021年福島県立医科大学 入試問題
この動画を見る
すべての実数$x$に対して$f(x)=x+\displaystyle \int_{0}^{1} 2^{2t+x}f(t)\ dt$を満たすとき$f(0)$を求めよ
出典:2021年福島県立医科大学 入試問題
大学入試問題#535「解き方いろいろ」 岡山県立大学(2023) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{1}{2}} \displaystyle \frac{x^3}{\sqrt{ 1-x^2 }} dx$
出典:2023年岡山県立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{1}{2}} \displaystyle \frac{x^3}{\sqrt{ 1-x^2 }} dx$
出典:2023年岡山県立大学 入試問題
【数Ⅲ】積分で体積を求める【細かくちぎって足し合わせる、積分の原理】

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
めいちゃんねる
問題文全文(内容文):
(1)$ y=\sin x(0 \leqq x \leqq \pi)$上の点Pからx軸に下ろした垂線の足を点Qとする.
PQを1辺とするxy平面に垂直な正方形を作る.点Pが(0,0)から$ (\pi,0)$まで動くとき,
この正方形が通過する部分の体積を求めよ.
(2)$ y=x^2-3x $とx軸で囲まれた部分をx軸の周りに1回転させてできる立体の体積を求めよ.
この動画を見る
(1)$ y=\sin x(0 \leqq x \leqq \pi)$上の点Pからx軸に下ろした垂線の足を点Qとする.
PQを1辺とするxy平面に垂直な正方形を作る.点Pが(0,0)から$ (\pi,0)$まで動くとき,
この正方形が通過する部分の体積を求めよ.
(2)$ y=x^2-3x $とx軸で囲まれた部分をx軸の周りに1回転させてできる立体の体積を求めよ.
大学入試問題#534「みためがなんとも」日本大学 年度不明 #定積分
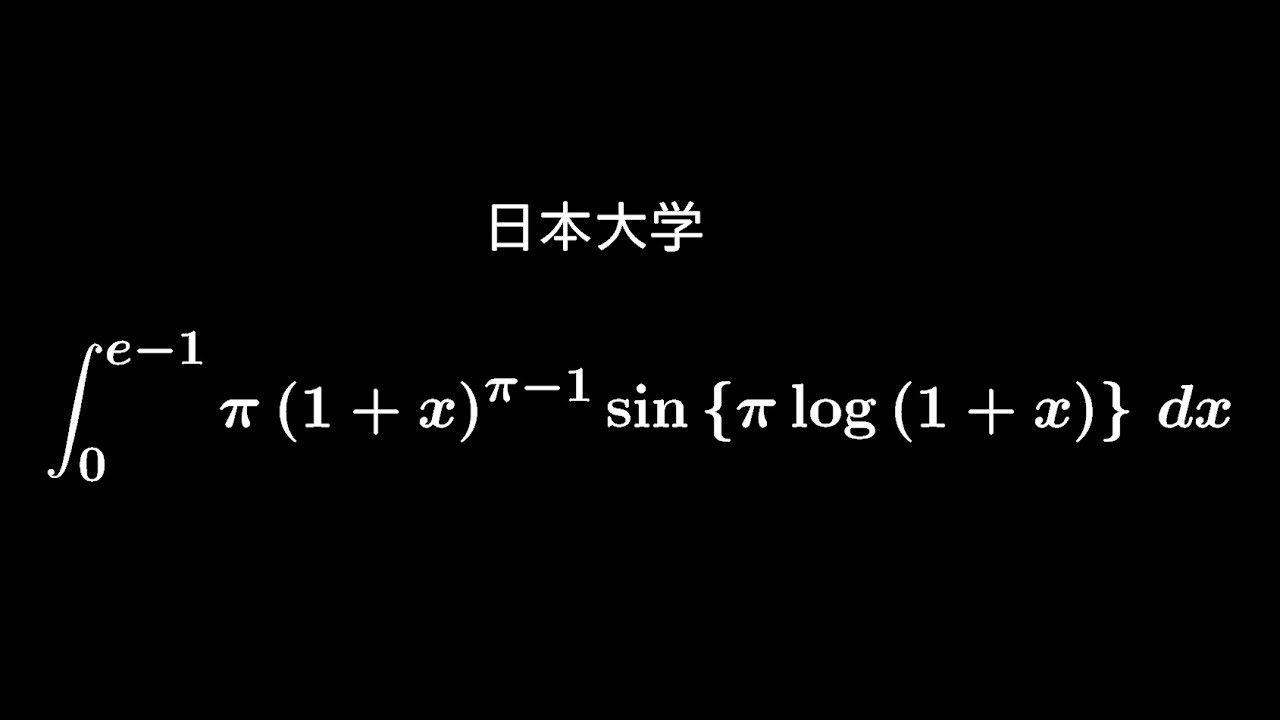
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#日本大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{e-1} \pi(1+x)^{\pi-1}\sin\{\pi\ log(1+x)\} dx$
出典:日本大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{e-1} \pi(1+x)^{\pi-1}\sin\{\pi\ log(1+x)\} dx$
出典:日本大学 入試問題
【和の極限】無限級数の基礎と求め方を解説!【数学III】

大学入試問題#533「もはや3分で1級の詰将棋」 信州大学1999 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{x\ \sin\ x}{3+\sin^2\ x} dx$
出典:1999年信州大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{x\ \sin\ x}{3+\sin^2\ x} dx$
出典:1999年信州大学 入試問題
大学入試問題#532「技をかける前の味付け」 By 英語orドイツ語さん #定積分

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (\sin\ x)log(1+e^x)\ dx$
この動画を見る
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (\sin\ x)log(1+e^x)\ dx$
神戸大 3次関数の最大最小

単元:
#大学入試過去問(数学)#式と証明#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$t\gt 0$とし,
$f(x)=x^3+3x^2-3(t^2-1)x+2t^3-3t^2+1$
$-1\leqq x \leqq 2$ における最大値と最小値を求めよ.
神戸大過去問
この動画を見る
$t\gt 0$とし,
$f(x)=x^3+3x^2-3(t^2-1)x+2t^3-3t^2+1$
$-1\leqq x \leqq 2$ における最大値と最小値を求めよ.
神戸大過去問
大学入試問題#530「定石どおり」 信州大学(2000) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} e^{\sin\ x}\sin2x\ dx$
出典:2000年信州大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} e^{\sin\ x}\sin2x\ dx$
出典:2000年信州大学 入試問題
大学入試問題#529「教科書に載ってそう」 北見工業大学(2012) #微積

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\cos\ x+\displaystyle \int_{0}^{x} e^{t-x}f(t)\ dt$のとき$f(x)$を求めよ
出典:2012年北見工業大学 入試問題
この動画を見る
$f(x)=\cos\ x+\displaystyle \int_{0}^{x} e^{t-x}f(t)\ dt$のとき$f(x)$を求めよ
出典:2012年北見工業大学 入試問題
大学入試問題#528「正面突破はしたくない」 福島県立医科大学② 改 (2021) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\pi} \sin^4x\ \cos^22x\ dx$
出典:2021年福島県立医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi} \sin^4x\ \cos^22x\ dx$
出典:2021年福島県立医科大学 入試問題
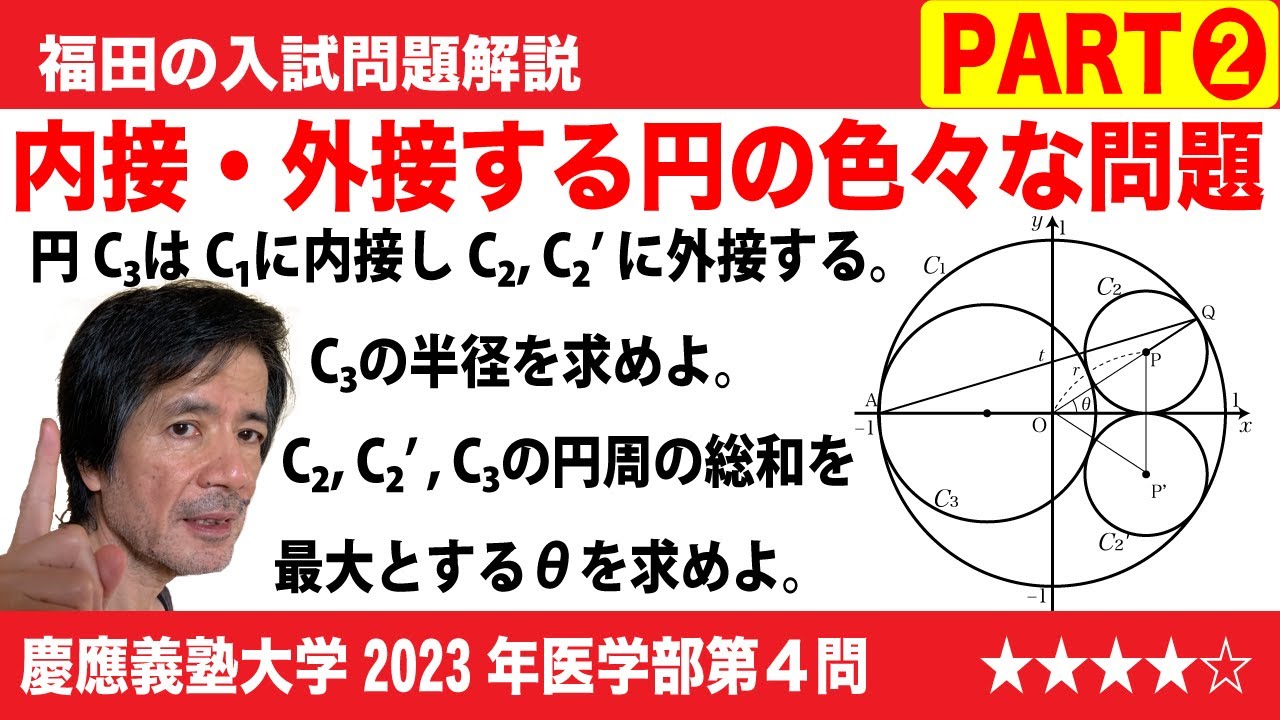
福田の数学〜慶應義塾大学2023年医学部第4問PART2〜円に内接する円の性質
単元:
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
大学入試問題#526「イカツイのは見た目だけ」 久留米大学医学部(2017) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#久留米大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{4}{x^7(x^{-6}+1)^{\frac{1}{3}}} dx$
出典:2017年久留米大学医学部 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{4}{x^7(x^{-6}+1)^{\frac{1}{3}}} dx$
出典:2017年久留米大学医学部 入試問題
大学入試問題#527「もうこのタイプは飽きた?」 福島県立医科大学① (2021) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\pi} \sin^2\ x\ \cos2x\ dx$
出典:2021年福島県立医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi} \sin^2\ x\ \cos2x\ dx$
出典:2021年福島県立医科大学 入試問題
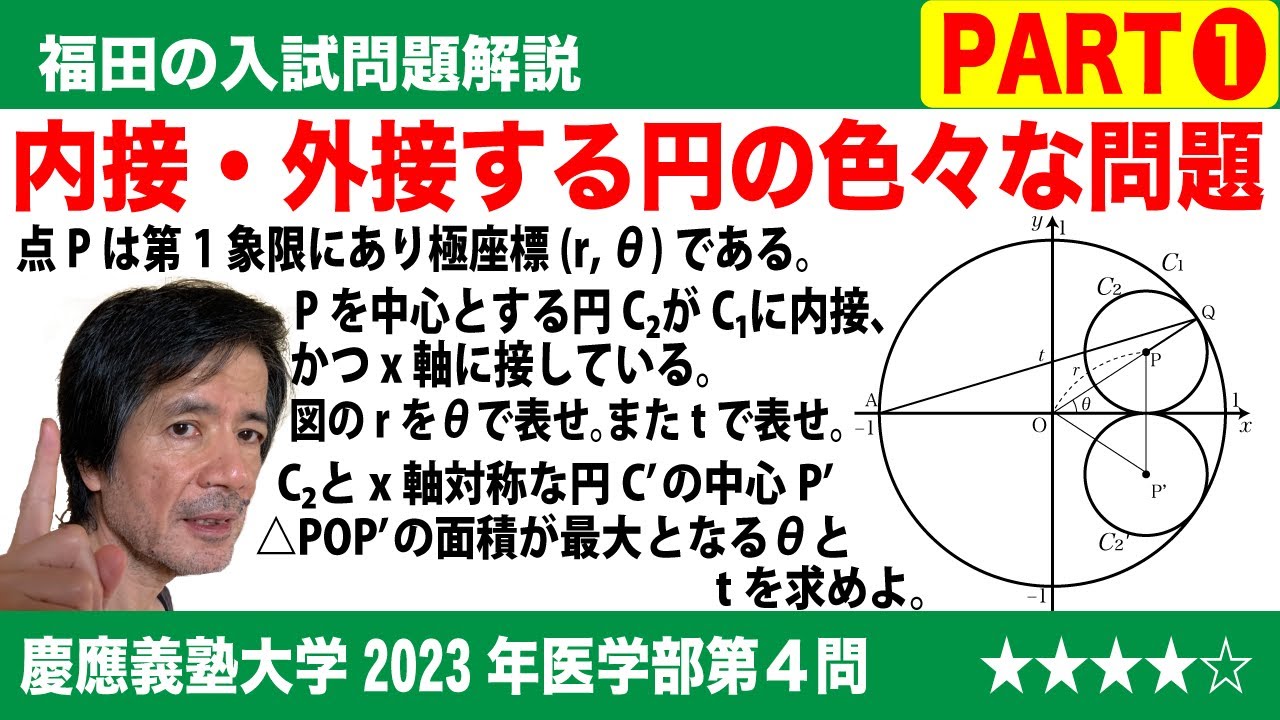
福田の数学〜慶應義塾大学2023年医学部第4問PART1〜円に内接する円の性質
単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#複素数平面#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#微分とその応用#複素数平面#図形への応用#微分法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
