数Ⅲ
数Ⅲ
大学入試問題#375「定跡どおり」 広島市立大学2015 #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}e^{-\sqrt{ 1-x }}dx$
出典：2015年広島市立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}e^{-\sqrt{ 1-x }}dx$
出典：2015年広島市立大学 入試問題
福田の1.5倍速演習〜合格する重要問題006〜名古屋大学2015年理系数学第１問
単元：
#大学入試過去問(数学)#微分とその応用#微分法#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
次の問いに答えよ。
(1)関数$f(x)=x^{-2}2^x(x≠0)$について、$f'(x) \gt 0$となるための
xに関する条件を求めよ。
(2)方程式$2^x=x^2$は相異なる3個の実数解をもつことを示せ。
(3)方程式$2^x=x^2$の解で有理数であるものを全て求めよ。
2015名古屋大学理系過去問
この動画を見る
次の問いに答えよ。
(1)関数$f(x)=x^{-2}2^x(x≠0)$について、$f'(x) \gt 0$となるための
xに関する条件を求めよ。
(2)方程式$2^x=x^2$は相異なる3個の実数解をもつことを示せ。
(3)方程式$2^x=x^2$の解で有理数であるものを全て求めよ。
2015名古屋大学理系過去問
大学入試問題#374「技をかける前の味付け」 富山県立大学(2015) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#富山県立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x}{3+4\cos^2x}dx$
出典：2015年富山県立大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x}{3+4\cos^2x}dx$
出典：2015年富山県立大学 入試問題
大学入試問題#373「結局いつもの唐揚げ定食」 横浜国立大学2012 #不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$a \gt 0$
$\displaystyle \int x^2\cos(a\ log\ x)dx$
出典：2012年横浜国立大学 入試問題
この動画を見る
$a \gt 0$
$\displaystyle \int x^2\cos(a\ log\ x)dx$
出典：2012年横浜国立大学 入試問題
大学入試問題#372「初手が命」 兵庫県立大学2015 #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫県立大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{3}}\displaystyle \frac{dx}{\cos^4x}$
出典：2015年兵庫県立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{3}}\displaystyle \frac{dx}{\cos^4x}$
出典：2015年兵庫県立大学 入試問題
大学入試問題#371「少し変わった置換積分」 京都大学 改 #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{\frac{2}{\sqrt{ 3 }}}^{2}\displaystyle \frac{dx}{x\sqrt{ x^2-1 }}$
出典：京都大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{2}{\sqrt{ 3 }}}^{2}\displaystyle \frac{dx}{x\sqrt{ x^2-1 }}$
出典：京都大学 入試問題
福田の1.5倍速演習〜合格する重要問題002〜京都大学2015年理系数学第１問〜回転体の体積
単元：
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
2つの関数$y = \sin(x+\frac{\pi}{8})$と$y=\sin2x$のグラフの$0\leqq x\leqq \frac{\pi}{2}$の部分で囲まれ
る領域を、x軸のまわりに1回転させてできる立体の体積を求めよ。
ただし、$x=0$と$x=\frac{\pi}{2}$は領域を囲む線とは考えない。
2015京都大学理系過去問
この動画を見る
2つの関数$y = \sin(x+\frac{\pi}{8})$と$y=\sin2x$のグラフの$0\leqq x\leqq \frac{\pi}{2}$の部分で囲まれ
る領域を、x軸のまわりに1回転させてできる立体の体積を求めよ。
ただし、$x=0$と$x=\frac{\pi}{2}$は領域を囲む線とは考えない。
2015京都大学理系過去問
大学入試問題#370「初手は好み」 滋賀医科大学2012 #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#滋賀医科大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}\displaystyle \frac{1+x}{1+x^2}dx$
出典：2012年滋賀医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{1+x}{1+x^2}dx$
出典：2012年滋賀医科大学 入試問題
大学入試問題#369「2種類準備しました」 広島市立大学2014 #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{\cos\ x}{\cos^2x+2\sin\ x-2}dx$
出典：2014年広島市立大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{\cos\ x}{\cos^2x+2\sin\ x-2}dx$
出典：2014年広島市立大学 入試問題
【数Ⅲ】三角関数・指数・対数の微分公式【合成関数との合せ技】
大学入試問題#368「よくみる積分」 防衛医科大学校2014 #不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{dx}{x^2+x+1}$
出典：2014年防衛医科大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x^2+x+1}$
出典：2014年防衛医科大学 入試問題
大学入試問題#367「これは、たぶん一撃で倒せる」 横浜国立大学2012 #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{2+\sin\ x}{1+\cos\ x}dx$
出典：2012年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{2+\sin\ x}{1+\cos\ x}dx$
出典：2012年横浜国立大学 入試問題
大学入試問題#366「これは有名問題」 静岡大学2014 #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#静岡大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\cos^3x}{\cos\ x+\sin\ x}dx$
出典：2014年静岡大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\cos^3x}{\cos\ x+\sin\ x}dx$
出典：2014年静岡大学 入試問題
大学入試問題#365「さすがに小問」 旭川医科大学(2014) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#旭川医科大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}log(x^2+1)dx$
出典：2014年旭川医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}log(x^2+1)dx$
出典：2014年旭川医科大学 入試問題
福田の数学〜東京理科大学2022年理工学部第１問(1)〜解と係数の関係と３次関数の最大最小
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#指数関数と対数関数#解と判別式・解と係数の関係#指数関数#接線と増減表・最大値・最小値#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
(1)mを実数とする。xについての2次方程式$x^2-(m+3)x+m^2-9=0$の
二つの解を$α,β$とする。$α,β$が実数であるための必要十分条件は$- \boxed{ア} \leqq m \leqq \boxed{イ}$である。
mが$- \boxed{ア} \leqq m \leqq \boxed{イ}$の範囲を動くときの
$α^3+β^3$の最小値は$\boxed{ウ}$、最大値は$\boxed{エオカ}$である。
この動画を見る
(1)mを実数とする。xについての2次方程式$x^2-(m+3)x+m^2-9=0$の
二つの解を$α,β$とする。$α,β$が実数であるための必要十分条件は$- \boxed{ア} \leqq m \leqq \boxed{イ}$である。
mが$- \boxed{ア} \leqq m \leqq \boxed{イ}$の範囲を動くときの
$α^3+β^3$の最小値は$\boxed{ウ}$、最大値は$\boxed{エオカ}$である。
大学入試問題#364「計算が大変でした」 岩手大学2014 #不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int x\ log(x+1)dx$
出典：2014年岩手大学 入試問題
この動画を見る
$\displaystyle \int x\ log(x+1)dx$
出典：2014年岩手大学 入試問題
大学入試問題#363「置換からの部分積分？」 横浜国立大学(2014) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\sqrt{ \frac{\pi}{2} }}x^3\cos(x^2)dx$
出典：2014年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\sqrt{ \frac{\pi}{2} }}x^3\cos(x^2)dx$
出典：2014年横浜国立大学 入試問題
大学入試問題#362「頻出問題ではないでしょうか？」 福島大学 改 2014 #定積分 #極限
単元：
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ a \to \infty } \displaystyle \int_{-a}^{a}\displaystyle \frac{dx}{(e^x+e^{-x})^2}$
出典：2014年福島大学 入試問題
この動画を見る
$\displaystyle \lim_{ a \to \infty } \displaystyle \int_{-a}^{a}\displaystyle \frac{dx}{(e^x+e^{-x})^2}$
出典：2014年福島大学 入試問題
大学入試問題#361「作成時間がありませんでした。」 横浜国立大学(2014) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{e}\displaystyle \frac{log\ x}{x^2}dx$
出典：2014年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e}\displaystyle \frac{log\ x}{x^2}dx$
出典：2014年横浜国立大学 入試問題
大学入試問題#360「もっとスマートな解答がありそう・・・」 宮崎大学2014 #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^3+3x^2}{x^2+3x+2}dx$
出典：2014年宮崎大学
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^3+3x^2}{x^2+3x+2}dx$
出典：2014年宮崎大学
大学入試問題#359「読みの入った部分積分で解いてみた」 神戸大学(2014) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{6}}\displaystyle \frac{2x\ sin\ x}{\cos^2x}dx$
出典：2014年神戸大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{6}}\displaystyle \frac{2x\ sin\ x}{\cos^2x}dx$
出典：2014年神戸大学 入試問題
極限
単元：
#関数と極限#関数の極限#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ \displaystyle \lim_{ x \to 1 } \dfrac{\sqrt x -1}{\sqrt[3]{x}-1}$,これを解け.
この動画を見る
$ \displaystyle \lim_{ x \to 1 } \dfrac{\sqrt x -1}{\sqrt[3]{x}-1}$,これを解け.
福田の数学〜中央大学2022年経済学部第１問(3)〜三角不等式
単元：
#大学入試過去問(数学)#三角関数#加法定理とその応用#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
(3)$0\leqq x\leqq \pi$のとき、次の不等式を解け。
$\sin^2x-\cos^2x+sinx \gt 0$
2022中央大学経済学部過去問
この動画を見る
(3)$0\leqq x\leqq \pi$のとき、次の不等式を解け。
$\sin^2x-\cos^2x+sinx \gt 0$
2022中央大学経済学部過去問
大学入試問題#358「チャートの例題に載ってもいいのかな？」 青山学院大学(2010) #定積分 #極限
単元：
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ a \to \infty } \displaystyle \int_{1}^{0}(\displaystyle \frac{x+1}{\sqrt{ x^2+2x }}-1)dx$
出典：2010年青山学院大学 入試問題
この動画を見る
$\displaystyle \lim_{ a \to \infty } \displaystyle \int_{1}^{0}(\displaystyle \frac{x+1}{\sqrt{ x^2+2x }}-1)dx$
出典：2010年青山学院大学 入試問題
【数Ⅲ】微分の公式 積・商・合成関数の微分【中身と外側を区別しよう】
【誘導あり：概要欄】大学入試問題#357「この大問は落とせないかな～～」 横浜国立大学2010 #定積分 #積分の応用
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
（1）
$0 \lt x \lt \pi$のとき
$\sin\ x-x\cos\ x \gt 0$を示せ
（2）
$0 \lt a \lt 1$
$I=\displaystyle \int_{0}^{\pi} |\sin\ x-ax| dx$を最小にする$a$の値を求めよ。
出典：2010年横浜国立大学 入試問題
この動画を見る
（1）
$0 \lt x \lt \pi$のとき
$\sin\ x-x\cos\ x \gt 0$を示せ
（2）
$0 \lt a \lt 1$
$I=\displaystyle \int_{0}^{\pi} |\sin\ x-ax| dx$を最小にする$a$の値を求めよ。
出典：2010年横浜国立大学 入試問題
大学入試問題#356「初手迷う」 関東学院大学(2019) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{2} \displaystyle \frac{5x^2+2}{x(x^2+1)} dx$
出典：2019年関東学院大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2} \displaystyle \frac{5x^2+2}{x(x^2+1)} dx$
出典：2019年関東学院大学 入試問題
大学入試問題#355「定番の定食」 山梨大学2019 #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#山梨大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} \sqrt{ 4-3x^2 }\ dx$
出典：2019年山梨大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \sqrt{ 4-3x^2 }\ dx$
出典：2019年山梨大学 入試問題
福田の数学〜杏林大学2022年医学部第２問〜定積分と関数の増減
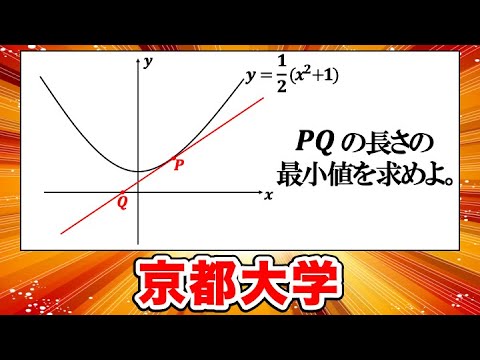
単元：
#大学入試過去問(数学)#微分とその応用#積分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
(1)Cを積分定数として、指数関数とたんっ公式の席の不定積分について、次式が成り立つ。
$\int xe^{-3x}dx = -(\frac{\boxed{ア}\ x+\boxed{イ}}{\boxed{ウ}})\ e^{-3x}+C$
$\int x^2e^{-3x}dx = -(\frac{\boxed{エ}\ x^2+\boxed{オ}\ x+\boxed{カ}}{\boxed{キク}})\ e^{-3x}+C$
また、定積分について、
$\int_0^1|(9x^2-1)e^{-3x}|dx=\frac{1}{\boxed{ケ}}(-1+\boxed{コ}\ e^{\boxed{サシ}}-\boxed{スセ}\ e^{-3})$
が成り立つ。
(2)p,q,rを実数の定数とする。関数$f(x)=(px^2+qx+r)e^{-3x}$が$x=0$で極大、
$x=1$で極小となるための必要十分条件は
$p=\boxed{ソタ}\ r,\ \ \ q=\boxed{チ}\ r,\ \ \ \boxed{ツ}$
である。さらに、$f(x)$の極小値が-1であるとすると、$f(x)$の極大値は$\frac{e^{\boxed{テ}}}{\boxed{ト }}$となる.
このとき、$\int_0^1f(x)dx=\frac{\boxed{ナ}}{\boxed{二}}$である。
$\boxed{ツ}$の解答群
$①\ r\gt 0\ \ \ \ ②\ r=0\ \ \ \ ③\ r \lt 0\ \ \ \ ④\ r \gt 1\ \ \ \ ⑤\ r=1$
$⑥\ r \lt 1\ \ \ \ ⑦\ r \gt \frac{1}{3}\ \ \ \ ⑧\ r =\frac{1}{3}\ \ \ \ ⑨r \lt \frac{1}{3}$
2022杏林大学医学部過去問
この動画を見る
(1)Cを積分定数として、指数関数とたんっ公式の席の不定積分について、次式が成り立つ。
$\int xe^{-3x}dx = -(\frac{\boxed{ア}\ x+\boxed{イ}}{\boxed{ウ}})\ e^{-3x}+C$
$\int x^2e^{-3x}dx = -(\frac{\boxed{エ}\ x^2+\boxed{オ}\ x+\boxed{カ}}{\boxed{キク}})\ e^{-3x}+C$
また、定積分について、
$\int_0^1|(9x^2-1)e^{-3x}|dx=\frac{1}{\boxed{ケ}}(-1+\boxed{コ}\ e^{\boxed{サシ}}-\boxed{スセ}\ e^{-3})$
が成り立つ。
(2)p,q,rを実数の定数とする。関数$f(x)=(px^2+qx+r)e^{-3x}$が$x=0$で極大、
$x=1$で極小となるための必要十分条件は
$p=\boxed{ソタ}\ r,\ \ \ q=\boxed{チ}\ r,\ \ \ \boxed{ツ}$
である。さらに、$f(x)$の極小値が-1であるとすると、$f(x)$の極大値は$\frac{e^{\boxed{テ}}}{\boxed{ト }}$となる.
このとき、$\int_0^1f(x)dx=\frac{\boxed{ナ}}{\boxed{二}}$である。
$\boxed{ツ}$の解答群
$①\ r\gt 0\ \ \ \ ②\ r=0\ \ \ \ ③\ r \lt 0\ \ \ \ ④\ r \gt 1\ \ \ \ ⑤\ r=1$
$⑥\ r \lt 1\ \ \ \ ⑦\ r \gt \frac{1}{3}\ \ \ \ ⑧\ r =\frac{1}{3}\ \ \ \ ⑨r \lt \frac{1}{3}$
2022杏林大学医学部過去問
大学入試問題#354「思った以上に大変でした・・・」 弘前大学 改 #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{log\ x} \displaystyle \frac{(e^x-1)(e^x-2)}{e^x+1} dx$
出典：広前大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{log\ x} \displaystyle \frac{(e^x-1)(e^x-2)}{e^x+1} dx$
出典：広前大学 入試問題