 数Ⅲ
数Ⅲ
 数Ⅲ
数Ⅲ
練習問題45 北海道大学 微分と積分 教員採用試験 数検準1級
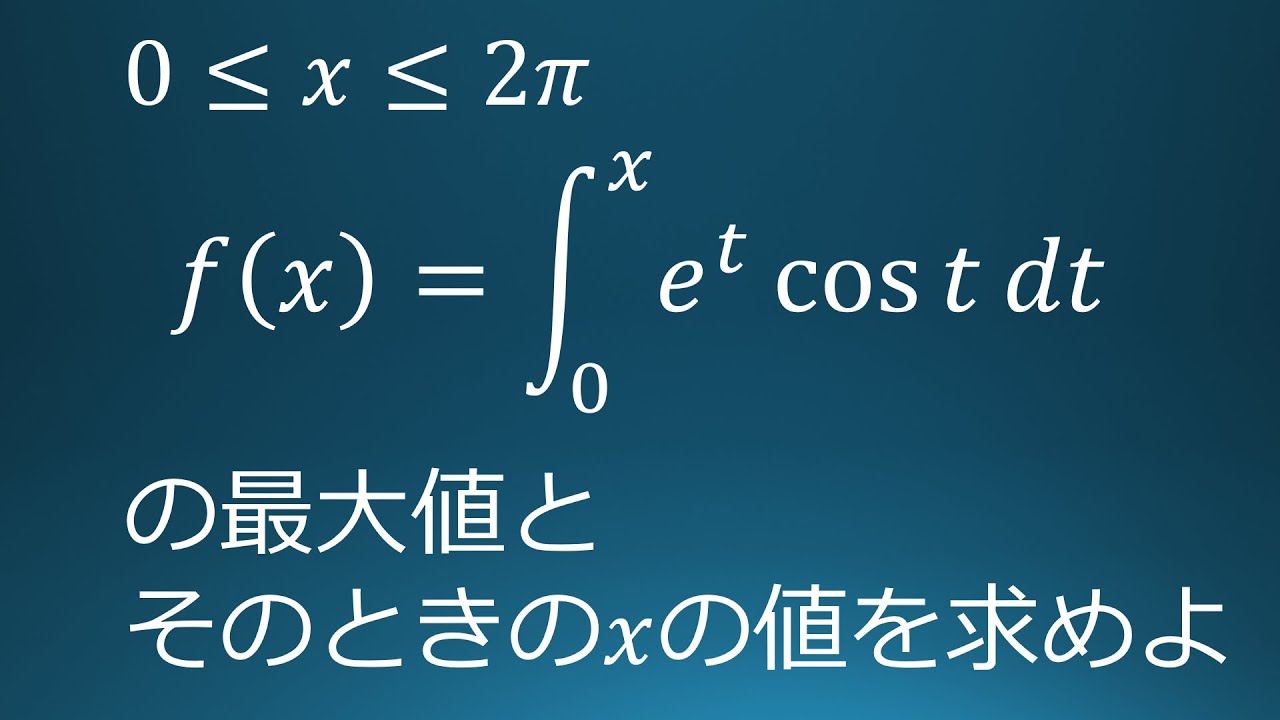
単元:
#大学入試過去問(数学)#数学検定・数学甲子園・数学オリンピック等#微分とその応用#積分とその応用#学校別大学入試過去問解説(数学)#その他#数学検定#数学検定準1級#数学(高校生)#北海道大学#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq x \leqq 2\pi$
関数
$f(x)=\displaystyle \int_{0}^{x}e^t\ cos\ t\ dt$の最大値とそのときの$x$の値を求めよ。
出典:北海道大学 教員採用試験
この動画を見る
$0 \leqq x \leqq 2\pi$
関数
$f(x)=\displaystyle \int_{0}^{x}e^t\ cos\ t\ dt$の最大値とそのときの$x$の値を求めよ。
出典:北海道大学 教員採用試験
数学「大学入試良問集」【19−5定積分で表された関数】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#神戸商船大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
(1)
次の定積分の値を求めよ。
(ⅰ)$\displaystyle \int_{0}^{\pi}\sin\ x\ dx$
(ⅱ)$\displaystyle \int_{0}^{\pi}e^{2x}\sin\ x\ dx$
(2)
次の等式をみたす$f(x)$を求めよ。
$f(x)=e^{2x}+\displaystyle \int_{0}^{\pi}f(t)\sin\ t\ dt$
この動画を見る
(1)
次の定積分の値を求めよ。
(ⅰ)$\displaystyle \int_{0}^{\pi}\sin\ x\ dx$
(ⅱ)$\displaystyle \int_{0}^{\pi}e^{2x}\sin\ x\ dx$
(2)
次の等式をみたす$f(x)$を求めよ。
$f(x)=e^{2x}+\displaystyle \int_{0}^{\pi}f(t)\sin\ t\ dt$
福田のわかった数学〜高校3年生理系063〜微分(8)多重因子(2)

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 微分(8) 多重因子(2)
$f(x)=ax^4+bx^3+cx^2+dx+e$ を
$(x-1)^3$で割った余りを$f(1),f'(1),f''(1)$を
用いて表せ。
この動画を見る
数学$\textrm{III}$ 微分(8) 多重因子(2)
$f(x)=ax^4+bx^3+cx^2+dx+e$ を
$(x-1)^3$で割った余りを$f(1),f'(1),f''(1)$を
用いて表せ。
練習問題44 東京工業大学 極限値 数検1級 教員採用試験(数学)

単元:
#数学検定・数学甲子園・数学オリンピック等#関数と極限#数列の極限#その他#数学検定#数学検定1級#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty }(\displaystyle \frac{{}_{ 3n } C_n}{{}_{ 2n } C_n})^\frac{1}{n}$の極限値を求めよ。
$\displaystyle \int_{0}^{1}f(x)dx=\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\displaystyle \sum_{k=1}^n f(\displaystyle \frac{k}{n})$
出典:東京工業大学 練習問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }(\displaystyle \frac{{}_{ 3n } C_n}{{}_{ 2n } C_n})^\frac{1}{n}$の極限値を求めよ。
$\displaystyle \int_{0}^{1}f(x)dx=\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\displaystyle \sum_{k=1}^n f(\displaystyle \frac{k}{n})$
出典:東京工業大学 練習問題
12東京都教員採用試験(数学:1-(5) 連続と微分)
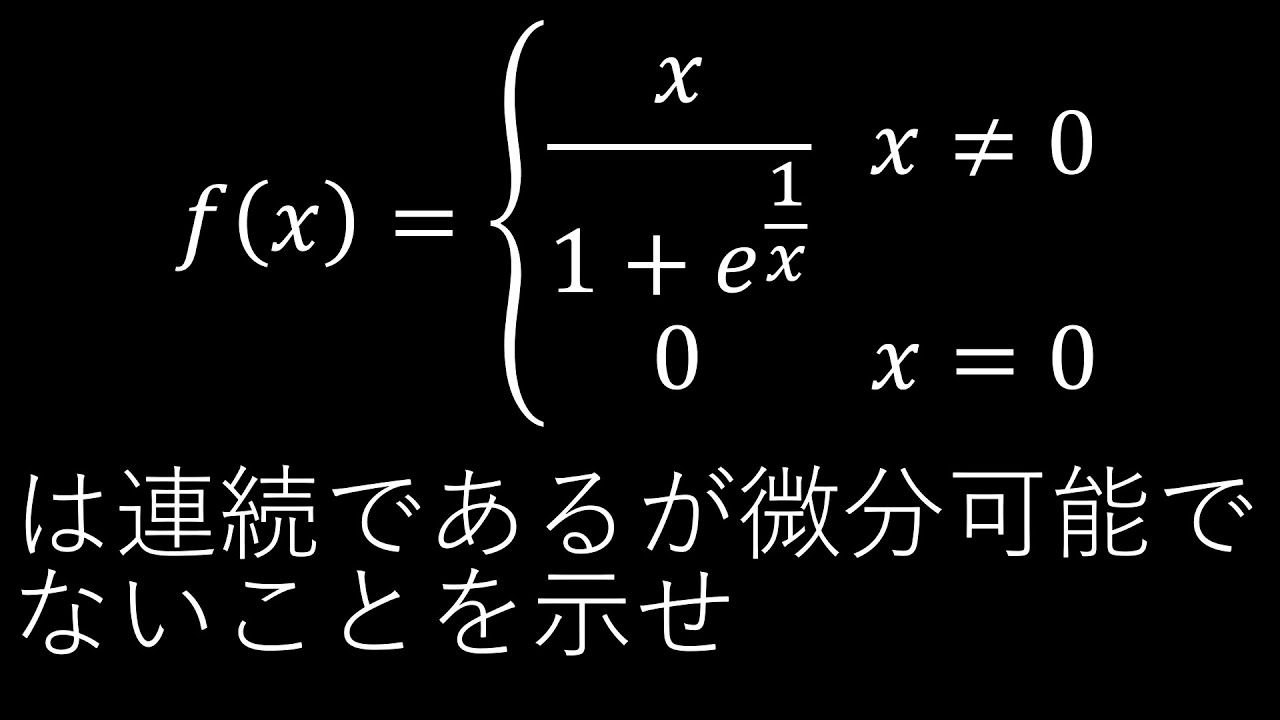
単元:
#微分とその応用#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{x}{1+e^{\frac{1}{x}}}(x \neq 0) \\
0(x=0)
\end{array}
\right.
\end{eqnarray}$ は連続であるが微分可能でないことを示せ
この動画を見る
$f(x)=\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{x}{1+e^{\frac{1}{x}}}(x \neq 0) \\
0(x=0)
\end{array}
\right.
\end{eqnarray}$ は連続であるが微分可能でないことを示せ
福田のわかった数学〜高校3年生理系062〜微分(7)多重因子(1)

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 微分(7) 多重因子(1)
整式$f(x)$が$(x-\alpha)^3$で割り切れる$\iff f(a)=f'(a)=f''(a)=0$
であることを示せ。
この動画を見る
数学$\textrm{III}$ 微分(7) 多重因子(1)
整式$f(x)$が$(x-\alpha)^3$で割り切れる$\iff f(a)=f'(a)=f''(a)=0$
であることを示せ。
練習問題43 区分求積法 数検1級1次 教員採用試験
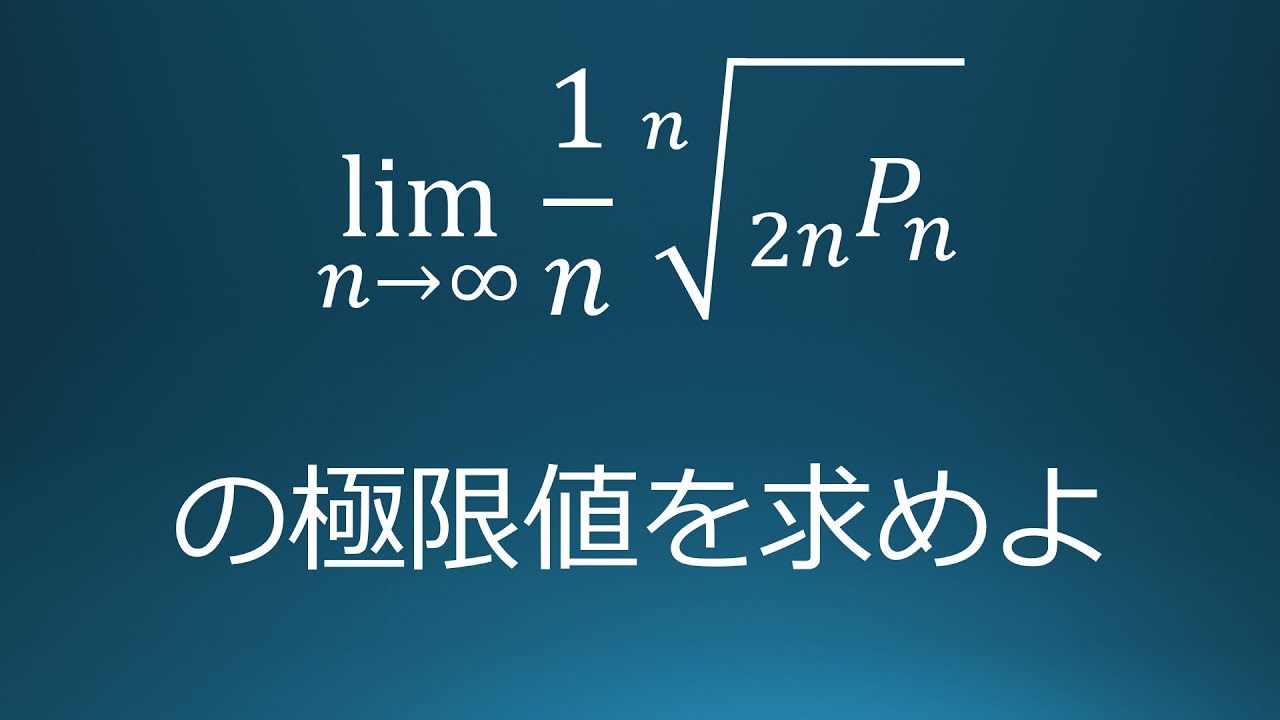
単元:
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#定積分#その他#数学検定#数学検定1級#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ {}_{ 2n } P_n }$の極限値を求めよ。
$\displaystyle \int_{0}^{1}f(x)dx=\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\displaystyle \sum_{k=1}^n f(\displaystyle \frac{k}{n})$
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ {}_{ 2n } P_n }$の極限値を求めよ。
$\displaystyle \int_{0}^{1}f(x)dx=\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\displaystyle \sum_{k=1}^n f(\displaystyle \frac{k}{n})$
練習問題42 早稲田大学 定積分 数学検定1級 教員採用試験
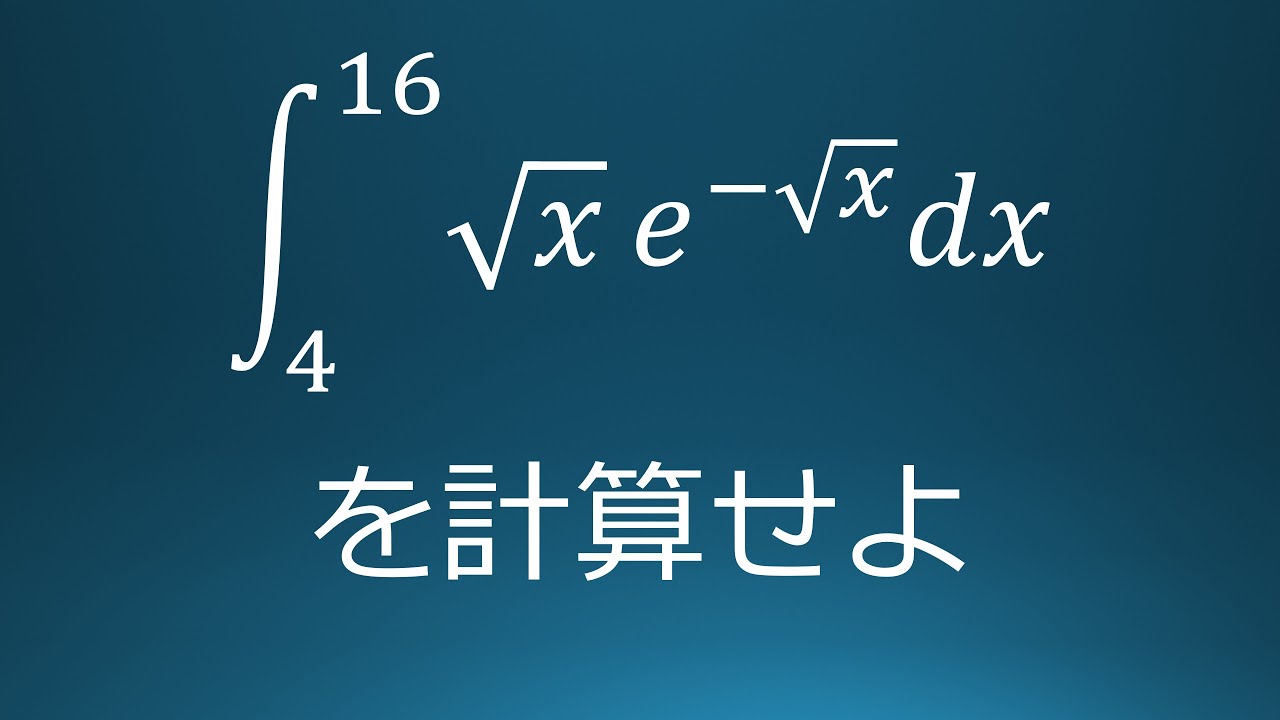
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#その他#早稲田大学#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{4}^{16}\sqrt{ x }\ e^{-\sqrt{ x }}\ dx$
出典:早稲田大学 教員採用試験
この動画を見る
$\displaystyle \int_{4}^{16}\sqrt{ x }\ e^{-\sqrt{ x }}\ dx$
出典:早稲田大学 教員採用試験
福田のわかった数学〜高校3年生理系061〜微分(6)高次導関数

単元:
#微分とその応用#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 微分(6) 高次導関数
$f(x)=\sin x$の第$n$次導関数は
$f^{(n)}(x)=\sin(x+\frac{n\pi}{2})$であることを示せ。
この動画を見る
数学$\textrm{III}$ 微分(6) 高次導関数
$f(x)=\sin x$の第$n$次導関数は
$f^{(n)}(x)=\sin(x+\frac{n\pi}{2})$であることを示せ。
高専数学 微積II #67 2変数関数の極限
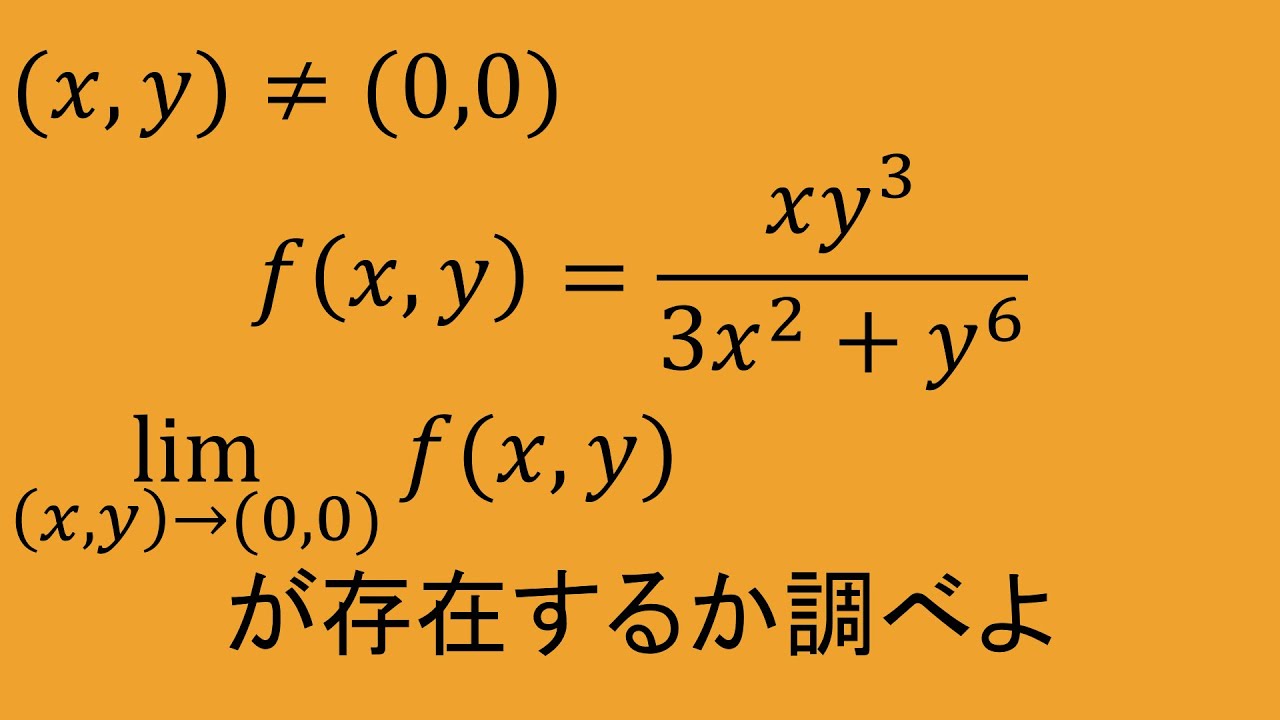
単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x,y)=\displaystyle \frac{xy^3}{3x^2+y^6}$
$(x,y) \neq (0,0)$において
$\displaystyle \lim_{ (x,y) \to (0,0) }f(x,y)$が存在するか調べよ。
この動画を見る
$f(x,y)=\displaystyle \frac{xy^3}{3x^2+y^6}$
$(x,y) \neq (0,0)$において
$\displaystyle \lim_{ (x,y) \to (0,0) }f(x,y)$が存在するか調べよ。
数学「大学入試良問集」【19−4 2曲線が接する条件】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
2曲線$y=\sqrt{ x },\ y=a\ log\ x$、が1点のみを共有するように正の数$a$を定め、このとき2曲線と$x$軸で囲まれる面積を求めよ。
ただし、必要なら$\displaystyle \lim_{ x \to \infty }\displaystyle \frac{log\ x}{x}=0$は用いてよい。
この動画を見る
2曲線$y=\sqrt{ x },\ y=a\ log\ x$、が1点のみを共有するように正の数$a$を定め、このとき2曲線と$x$軸で囲まれる面積を求めよ。
ただし、必要なら$\displaystyle \lim_{ x \to \infty }\displaystyle \frac{log\ x}{x}=0$は用いてよい。
福田のわかった数学〜高校3年生理系060〜微分(5)陰関数の微分(2)

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 微分(5) 陰関数の微分(2)
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ 上の点$(p,q)$での接線の方程式
は $\frac{px}{a^2}+\frac{qy}{b^2}=1$ であることを示せ。
この動画を見る
数学$\textrm{III}$ 微分(5) 陰関数の微分(2)
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ 上の点$(p,q)$での接線の方程式
は $\frac{px}{a^2}+\frac{qy}{b^2}=1$ であることを示せ。
【数学Ⅲ/微分】三角関数の微分②(積の微分、2倍角の公式など)

単元:
#三角関数#微分法#数学(高校生)#数Ⅲ
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の関数を微分せよ。
(1)
$y=\displaystyle \frac{1}{\sin^2x}$
(2)
$y=x\sin3x$
(3)
$y=\sin x\cos x$
この動画を見る
次の関数を微分せよ。
(1)
$y=\displaystyle \frac{1}{\sin^2x}$
(2)
$y=x\sin3x$
(3)
$y=\sin x\cos x$
【数学Ⅲ/微分】三角関数の微分①(合成関数の微分)

単元:
#微分法#数Ⅲ
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の関数を微分せよ。
(1)
$y=\sin x-\tan x$
(2)
$y=\cos(3x+1)$
(3)
$y=\cos x^2$
(4)
$y=\sin^3x$
この動画を見る
次の関数を微分せよ。
(1)
$y=\sin x-\tan x$
(2)
$y=\cos(3x+1)$
(3)
$y=\cos x^2$
(4)
$y=\sin^3x$
【数学Ⅲ/微分】逆関数の微分

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
逆関数の微分法の公式を用いて、次の関数を微分せよ。
$y=x^{\frac{1}{5}}$
この動画を見る
逆関数の微分法の公式を用いて、次の関数を微分せよ。
$y=x^{\frac{1}{5}}$
福田のわかった数学〜高校3年生理系059〜微分(4)陰関数の微分

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 微分(4) 陰関数の微分
$\frac{x^2}{4}-\frac{y^2}{9}=1$について$\frac{dy}{dx},\frac{d^2y}{dx^2}$を
$x$と$y$を用いて表せ。ただし、$y\neq 0$とする。
この動画を見る
数学$\textrm{III}$ 微分(4) 陰関数の微分
$\frac{x^2}{4}-\frac{y^2}{9}=1$について$\frac{dy}{dx},\frac{d^2y}{dx^2}$を
$x$と$y$を用いて表せ。ただし、$y\neq 0$とする。
練習問題41 微分方程式(数研1級1次 高専数学 教員採用試験)

単元:
#数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#その他#数学検定#数学検定1級#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$(1-x)y+(1+y)x\dfrac{dy}{dx}=0$の
一般解を求めよ.
この動画を見る
$(1-x)y+(1+y)x\dfrac{dy}{dx}=0$の
一般解を求めよ.
高専数学 微積II #61(1)(2) 合成関数の微分法
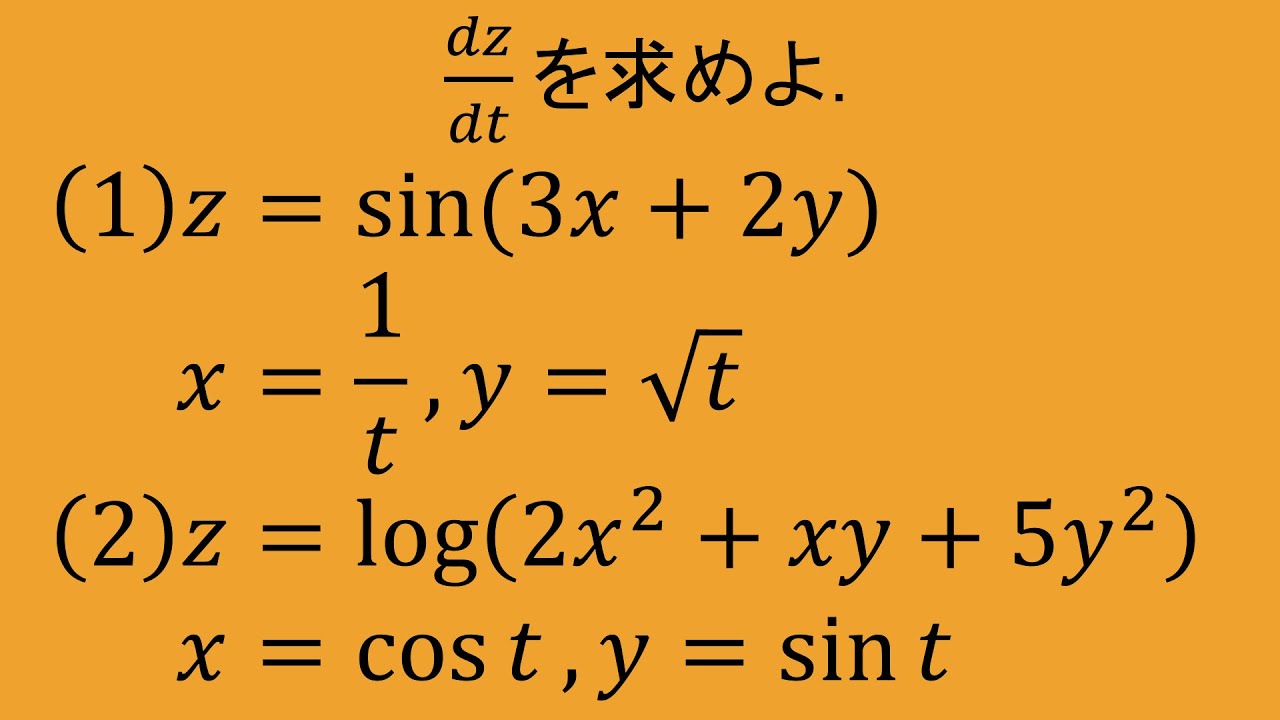
単元:
#数Ⅱ#微分法と積分法#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\dfrac{dz}{dt}$を求めよ.
(1)$z=\sin (3x+2y)$
$x=\dfrac{1}{t},y=\sqrt t$
(2)$z=\log(2x^2+xy+5y^2)$
$x=\cos t,y=\sin t$
この動画を見る
$\dfrac{dz}{dt}$を求めよ.
(1)$z=\sin (3x+2y)$
$x=\dfrac{1}{t},y=\sqrt t$
(2)$z=\log(2x^2+xy+5y^2)$
$x=\cos t,y=\sin t$
お茶の水女子大 3次関数と放物線

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$y=x^3+(k+1)x^2+kx$と$y=x^2q$とが全ての実数$q$において
共有点がただ1つである$k$の範囲を求めよ.
2021お茶の水女子大過去問
この動画を見る
$y=x^3+(k+1)x^2+kx$と$y=x^2q$とが全ての実数$q$において
共有点がただ1つである$k$の範囲を求めよ.
2021お茶の水女子大過去問
高専数学 微積II #53(3)(4) 合成関数の微分法

単元:
#数Ⅱ#微分法と積分法#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$z=f(x,y)$:全微分可能
$z_u,z_{\nu}$を,$u,\nu,z_x,z_y$で表せ.
(3)$x=\tan\dfrac{\nu}{u},y-\cos(u+\nu)$
(4)$x=u\log\nu,y=e^u \nu$
この動画を見る
$z=f(x,y)$:全微分可能
$z_u,z_{\nu}$を,$u,\nu,z_x,z_y$で表せ.
(3)$x=\tan\dfrac{\nu}{u},y-\cos(u+\nu)$
(4)$x=u\log\nu,y=e^u \nu$
福田のわかった数学〜高校3年生理系058〜微分(3)媒介変数表示の微分

単元:
#平面上の曲線#微分とその応用#色々な関数の導関数#媒介変数表示と極座標#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数列$\textrm{III}$ 微分(3) 媒介変数表示
$x=a(\theta-\sin\theta), y=a(1-\cos\theta)$のとき、$\frac{dy}{dx},\frac{d^2y}{dx^2}$を$\theta$で表せ。
この動画を見る
数列$\textrm{III}$ 微分(3) 媒介変数表示
$x=a(\theta-\sin\theta), y=a(1-\cos\theta)$のとき、$\frac{dy}{dx},\frac{d^2y}{dx^2}$を$\theta$で表せ。
高専数学 微積II #53(1)(2) 合成関数の微分法
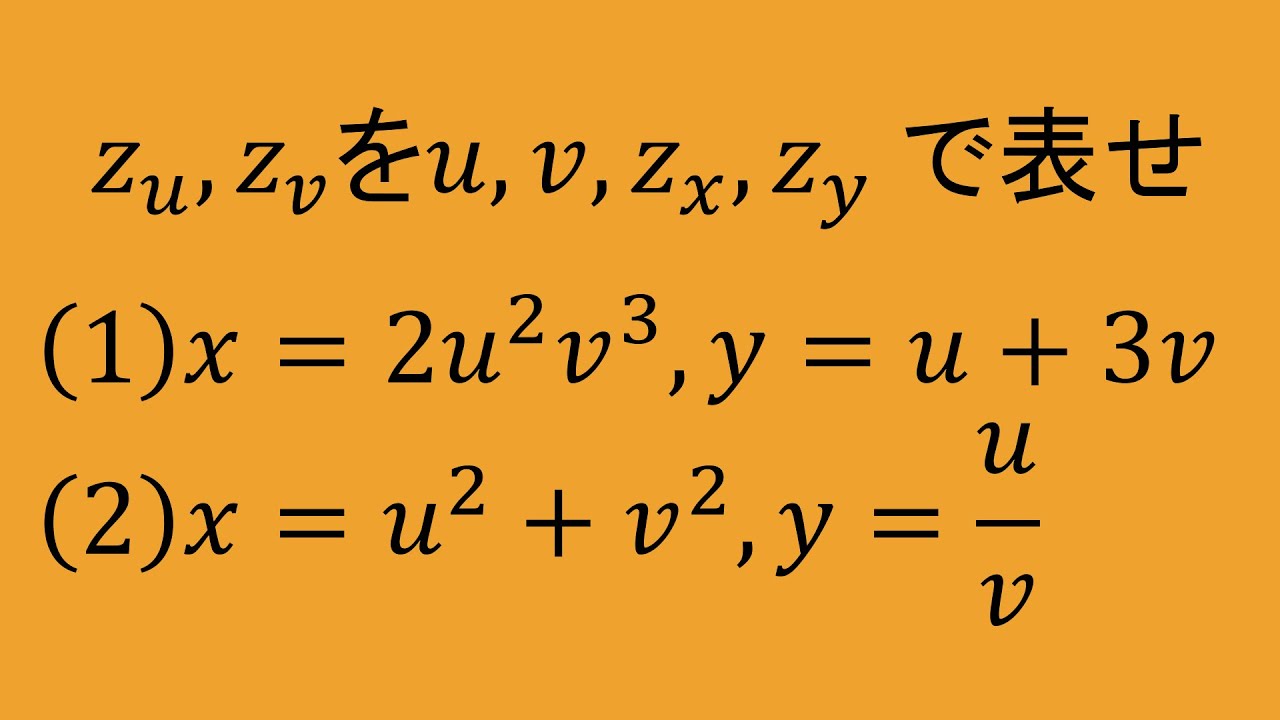
単元:
#数Ⅱ#微分法と積分法#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$z=f(x,y)$:全微分可能
$z_u,z_{\nu}$を$u,\nu,z_x,z_y$で表せ.
(1)$x=2u^2 \nu^3,y=u+3\nu$
(2)$x=u^2+\nu^2,y=\dfrac{u}{\nu}$
この動画を見る
$z=f(x,y)$:全微分可能
$z_u,z_{\nu}$を$u,\nu,z_x,z_y$で表せ.
(1)$x=2u^2 \nu^3,y=u+3\nu$
(2)$x=u^2+\nu^2,y=\dfrac{u}{\nu}$
高専数学 微積II #51(3)(4) 合成関数の微分法
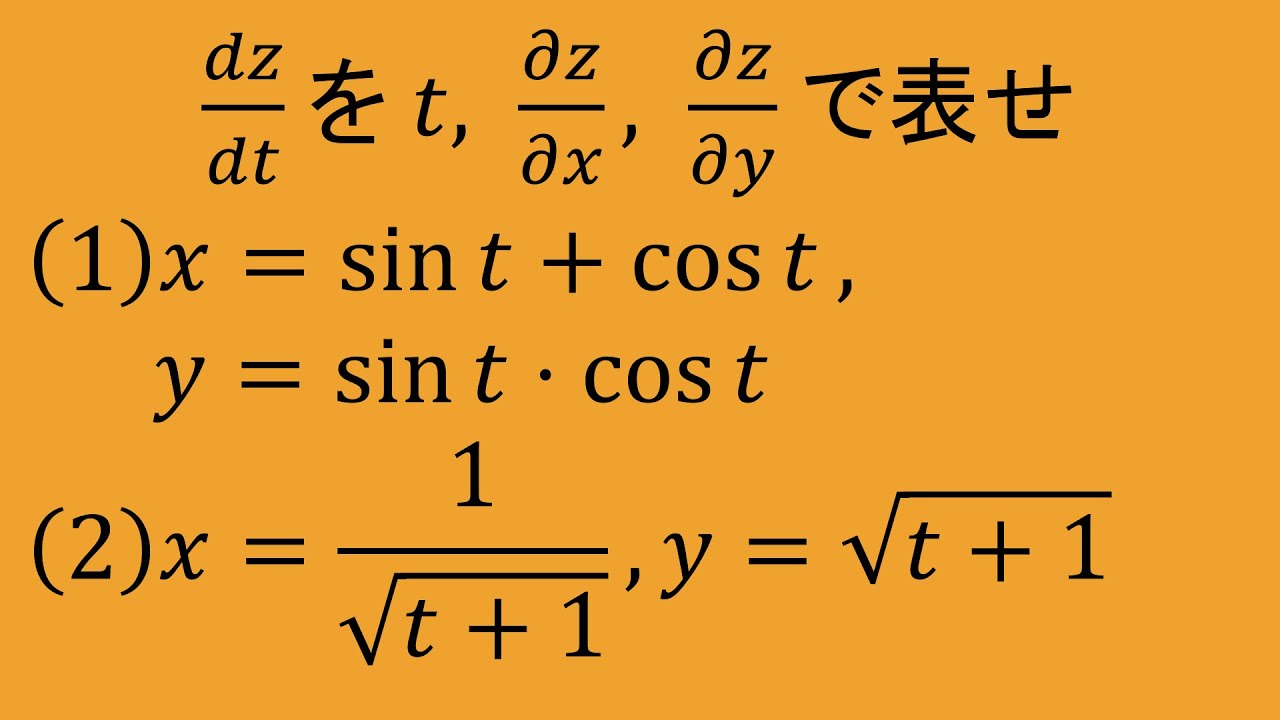
単元:
#数Ⅱ#微分法と積分法#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$z=f(x,y)$:全微分可能
$\dfrac{dz}{dt}$を$t,\dfrac{\alpha z}{\alpha x},\dfrac{\alpha z}{\alpha y}$で表せ.
(3)$x=\sin t+\cos t$
$y=\sin t \cos t$
(4)$x=\dfrac{1}{\sqrt{x+1}}$
$y=\sqrt{t+1}$
この動画を見る
$z=f(x,y)$:全微分可能
$\dfrac{dz}{dt}$を$t,\dfrac{\alpha z}{\alpha x},\dfrac{\alpha z}{\alpha y}$で表せ.
(3)$x=\sin t+\cos t$
$y=\sin t \cos t$
(4)$x=\dfrac{1}{\sqrt{x+1}}$
$y=\sqrt{t+1}$
数学「大学入試良問集」【19−3 f(sinx)と置換積分】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$f(x)$が$0 \leqq x \leqq 1$で連続な関数であるとき
$\displaystyle \int_{0}^{\pi}xf(\sin\ x)dx=\displaystyle \frac{\pi}{2}\displaystyle \int_{0}^{\pi}f(\sin\ x)dx$
が成立することを示し、これを用いて$\displaystyle \int_{0}^{\pi}\displaystyle \frac{x\ \sin\ x}{3+\sin^2x}dx$を求めよ。
この動画を見る
$f(x)$が$0 \leqq x \leqq 1$で連続な関数であるとき
$\displaystyle \int_{0}^{\pi}xf(\sin\ x)dx=\displaystyle \frac{\pi}{2}\displaystyle \int_{0}^{\pi}f(\sin\ x)dx$
が成立することを示し、これを用いて$\displaystyle \int_{0}^{\pi}\displaystyle \frac{x\ \sin\ x}{3+\sin^2x}dx$を求めよ。
福田のわかった数学〜高校3年生理系057〜微分(2)逆関数の微分

単元:
#微分とその応用#微分法#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 微分(2) 逆関数の微分
$y=\tan x (-\frac{\pi}{2} \lt x \lt \frac{\pi}{2})$
の逆関数の第2次導関数を求めよ。
この動画を見る
数学$\textrm{III}$ 微分(2) 逆関数の微分
$y=\tan x (-\frac{\pi}{2} \lt x \lt \frac{\pi}{2})$
の逆関数の第2次導関数を求めよ。
高専数学 微積II #51(1)(2) 合成関数の微分法

単元:
#数Ⅱ#微分法と積分法#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$z=f(x,y)$:全微分可能である.
$\dfrac{dz}{dt}$を$t,\dfrac{\delta z}{\delta x},\dfrac{\delta z}{\delta y}$で表せ.
(1)$x-te^t,y=\log t$
(2)$x=\dfrac{t}{2t+1},y=\dfrac{t+1}{2t+1}$
この動画を見る
$z=f(x,y)$:全微分可能である.
$\dfrac{dz}{dt}$を$t,\dfrac{\delta z}{\delta x},\dfrac{\delta z}{\delta y}$で表せ.
(1)$x-te^t,y=\log t$
(2)$x=\dfrac{t}{2t+1},y=\dfrac{t+1}{2t+1}$
福田のわかった数学〜高校3年生理系056〜微分(1)逆関数の微分

単元:
#微分とその応用#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 微分(1) 逆関数の微分
$y=\sin x (-\frac{\pi}{2} \lt x \lt \frac{\pi}{2})$
の逆関数の導関数を求めよ。
この動画を見る
数学$\textrm{III}$ 微分(1) 逆関数の微分
$y=\sin x (-\frac{\pi}{2} \lt x \lt \frac{\pi}{2})$
の逆関数の導関数を求めよ。
練習問題40 数研1級1次 高専数学 教採対応 微分方程式
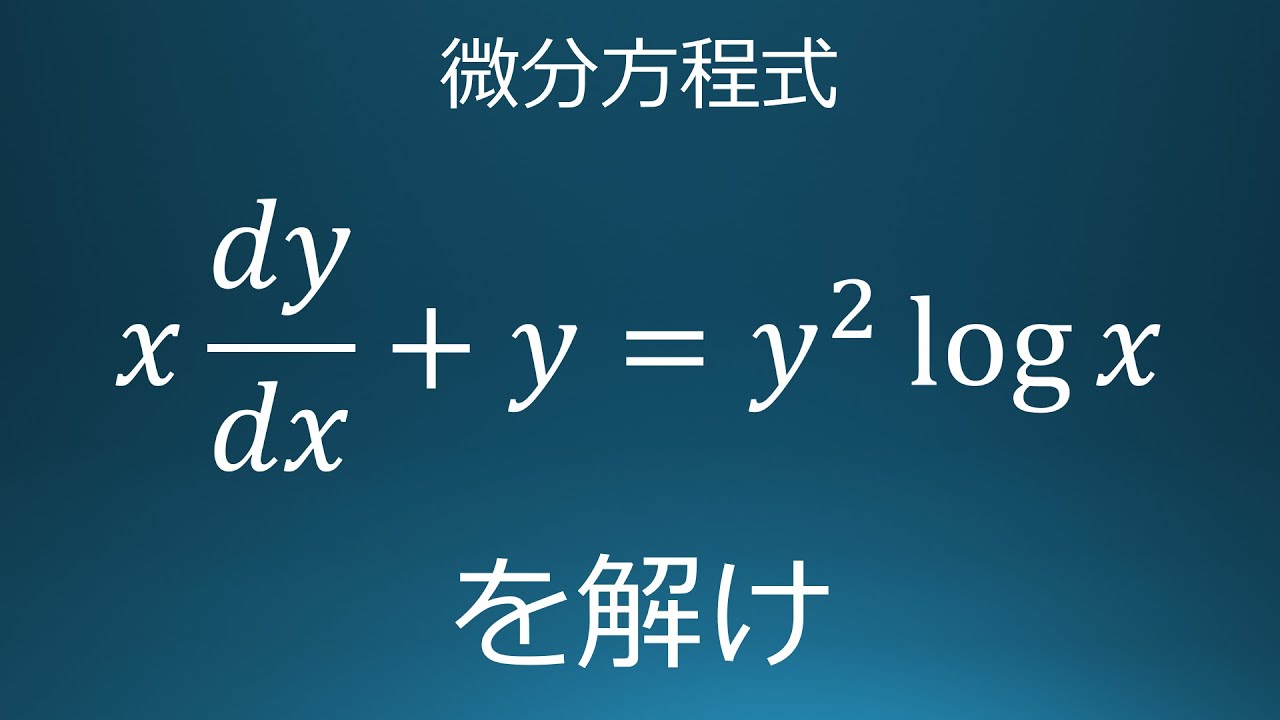
単元:
#数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x\dfrac{dy}{dx}+y=y^2\log x$の
一般解を求めよ.
この動画を見る
$x\dfrac{dy}{dx}+y=y^2\log x$の
一般解を求めよ.
福田のわかった数学〜高校3年生理系055〜格子点の個数と極限
単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
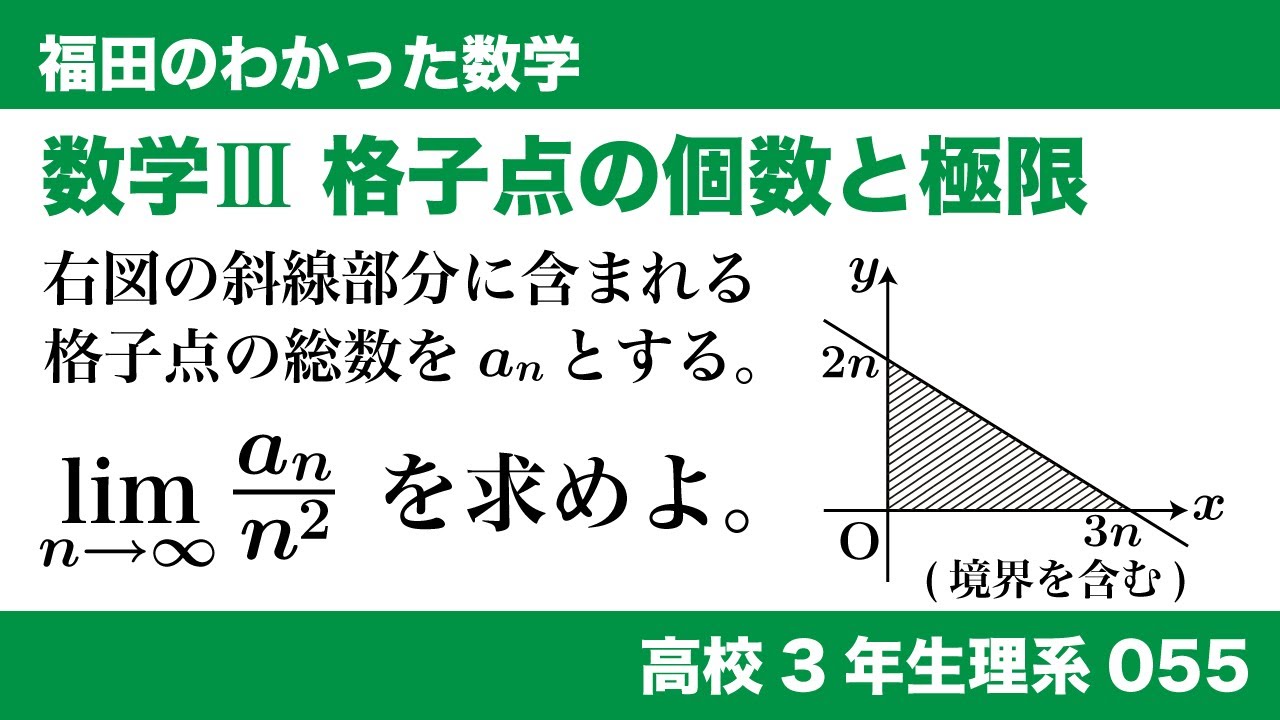
数学$\textrm{III}$ 格子点の個数と極限
右図の斜線部分(※動画参照)に含まれる
格子点の総数を$a_n$とする。
$\lim_{n \to \infty}\frac{a_n}{n^2}$を求めよ。
この動画を見る
数学$\textrm{III}$ 格子点の個数と極限
右図の斜線部分(※動画参照)に含まれる
格子点の総数を$a_n$とする。
$\lim_{n \to \infty}\frac{a_n}{n^2}$を求めよ。
数学「大学入試良問集」【19−2 三角関数の面積の二等分】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#京都府立医科大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の不等式が定める図形を$D$とする。
$0 \leqq x \leqq \displaystyle \frac{\pi}{2},0 \leqq y \leqq \sin2x$
(1)
曲線$y=a\ \sin\ x$と$y=\sin2x$が$0 \lt x \lt \displaystyle \frac{\pi}{2}$で交わるような定数$a$の範囲を求めよ。
(2)
曲線$y=a\ \sin\ x$が図形$D$を面積の等しい2つの部分に分けるような定数$a$を求めよ。
この動画を見る
次の不等式が定める図形を$D$とする。
$0 \leqq x \leqq \displaystyle \frac{\pi}{2},0 \leqq y \leqq \sin2x$
(1)
曲線$y=a\ \sin\ x$と$y=\sin2x$が$0 \lt x \lt \displaystyle \frac{\pi}{2}$で交わるような定数$a$の範囲を求めよ。
(2)
曲線$y=a\ \sin\ x$が図形$D$を面積の等しい2つの部分に分けるような定数$a$を求めよ。
