平面上のベクトルと内積
平面上のベクトルと内積
【数C】ベクトル平面ベクトル：ベクトルの基本③ 絶対値の最大最小は２乗で考えよ
単元：
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師：
理数個別チャンネル
問題文全文(内容文)：
tは実数とする。
aベクトル=(2,1), bベクトル=(3,4)に対して
｜a+tb｜はt=□のとき最小値□を取る
この動画を見る
tは実数とする。
aベクトル=(2,1), bベクトル=(3,4)に対して
｜a+tb｜はt=□のとき最小値□を取る
福田の数学〜筑波大学2022年理系第３問〜平行四辺形の中の平行四辺形
単元：
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数C
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$0 \lt t \lt 1$とする。平行四辺形ABCDにおいて、線分AB,BC,CD,DAを
$t:1-t$に内分する点をそれぞれ$A_1,B_1,C_1,D_1$とする。さらに$A_2,B_2,C_2,D_2$および$A_3,B_3,C_3,D_3$を次の条件を満たすように定める。
$(\ 条件\ )k=1,2$について、点$A_{k+1},B_{k+1},C_{k+1},D_{k+1}$はそれぞれ線分$A_kB_k$,
$B_kC_k,C_kD_k,D_kA_k$を$t:1-t$に内分する。
$\overrightarrow{ AB }=\overrightarrow{ a }, \overrightarrow{ AD }=\overrightarrow{ b }$とするとき、以下の問いに答えよ。
(1)$\overrightarrow{ A_1B_1 }=p\overrightarrow{ a }+q\overrightarrow{ b }, \overrightarrow{ A_1D_1 }=x\ \overrightarrow{ a }+y\ \overrightarrow{ b }$ を満たす実数p,q,x,yを
tを用いて表せ。
(2)四角形$A_1B_1C_1D_1$は平行四辺形であることを示せ。
(3)$\overrightarrow{ AD }$と$\overrightarrow{ A_3B_3 }$が平行となるようなtの値を求めよ。
2022筑波大学理系過去問
この動画を見る
$0 \lt t \lt 1$とする。平行四辺形ABCDにおいて、線分AB,BC,CD,DAを
$t:1-t$に内分する点をそれぞれ$A_1,B_1,C_1,D_1$とする。さらに$A_2,B_2,C_2,D_2$および$A_3,B_3,C_3,D_3$を次の条件を満たすように定める。
$(\ 条件\ )k=1,2$について、点$A_{k+1},B_{k+1},C_{k+1},D_{k+1}$はそれぞれ線分$A_kB_k$,
$B_kC_k,C_kD_k,D_kA_k$を$t:1-t$に内分する。
$\overrightarrow{ AB }=\overrightarrow{ a }, \overrightarrow{ AD }=\overrightarrow{ b }$とするとき、以下の問いに答えよ。
(1)$\overrightarrow{ A_1B_1 }=p\overrightarrow{ a }+q\overrightarrow{ b }, \overrightarrow{ A_1D_1 }=x\ \overrightarrow{ a }+y\ \overrightarrow{ b }$ を満たす実数p,q,x,yを
tを用いて表せ。
(2)四角形$A_1B_1C_1D_1$は平行四辺形であることを示せ。
(3)$\overrightarrow{ AD }$と$\overrightarrow{ A_3B_3 }$が平行となるようなtの値を求めよ。
2022筑波大学理系過去問
福田の数学〜東京医科歯科大学2022年理系第１問〜2つのベクトルで生成される異なる点の個数
単元：
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#平面上のベクトル#場合の数#三角関数#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京医科歯科大学
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
nを自然数とする。整数i,jに対し、xy平面上の点$P_{i,j}$の座標を
$(\cos\frac{2\pi}{n}i+\cos\frac{2\pi}{n}j, \sin\frac{2\pi}{n}i+\sin\frac{2\pi}{n}j)$
で与える。さらに、i,jを動かしたとき、$P_{i,j}$の取り得る異なる座標の
個数を$S_n$とする。このとき、以下の問いに答えよ。
(1)$n=3$のとき、$\triangle P_{0,0}P_{0,1}P_{0,2}$および$\triangle P_{1,0}P_{1,1}P_{1,2}$を同一平面上
に図示せよ。
(2)$S_4$を求めよ。
(3)平面上の異なる2点A,Bに対して、$AQ=BQ=1$であるような
同一平面上の点Qはいくつあるか。AB=dの値で場合分けして答えよ。
(4)$S_n$をnを用いて表せ。
2022東京医科歯科大学理系過去問
この動画を見る
nを自然数とする。整数i,jに対し、xy平面上の点$P_{i,j}$の座標を
$(\cos\frac{2\pi}{n}i+\cos\frac{2\pi}{n}j, \sin\frac{2\pi}{n}i+\sin\frac{2\pi}{n}j)$
で与える。さらに、i,jを動かしたとき、$P_{i,j}$の取り得る異なる座標の
個数を$S_n$とする。このとき、以下の問いに答えよ。
(1)$n=3$のとき、$\triangle P_{0,0}P_{0,1}P_{0,2}$および$\triangle P_{1,0}P_{1,1}P_{1,2}$を同一平面上
に図示せよ。
(2)$S_4$を求めよ。
(3)平面上の異なる2点A,Bに対して、$AQ=BQ=1$であるような
同一平面上の点Qはいくつあるか。AB=dの値で場合分けして答えよ。
(4)$S_n$をnを用いて表せ。
2022東京医科歯科大学理系過去問
【数B】平面ベクトル：ベクトルの基本② ベクトルの大きさ
【数C】ベクトル平面ベクトル：ベクトルの基本② ベクトルの大きさ
単元：
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師：
理数個別チャンネル
問題文全文(内容文)：
ベクトルの大きさの求め方
a=(3,4)の大きさを求めよ。
この動画を見る
ベクトルの大きさの求め方
a=(3,4)の大きさを求めよ。
【数B】平面ベクトル：ベクトルの基本① 基本的な考え方「終わり－始め」
単元：
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師：
理数個別チャンネル
問題文全文(内容文)：
ベクトルの基本的な考え方、ベクトルの和、始点の変更に関して解説していきます.
この動画を見る
ベクトルの基本的な考え方、ベクトルの和、始点の変更に関して解説していきます.
【数C】ベクトル平面ベクトル：ベクトルの基本① 基本的な考え方「終わり－始め」
福田の数学〜九州大学2022年文系第２問〜点と平面の距離と対称点
単元：
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
座標空間内の4点
$O(0,0,0),A(1,1,0),B(2,1,2),P(4,0,-1)$
を考える。3点O,A,Bを通る平面を$\alpha$とし、$\overrightarrow{ a }=\overrightarrow{ OA }$,
$\overrightarrow{ b }=\overrightarrow{ OB }$とおく。
以下の問いに答えよ。
(1)ベクトル$\overrightarrow{ a },\ \overrightarrow{ b }$の両方に垂直であり、x成分が正であるような、大きさが1
のベクトル$\overrightarrow{ n }$を求めよ。
(2)点Pから平面$\alpha$に垂線を下ろし、その交点をQとおく。
線分PQの長さを求めよ。
(3)平面$\alpha$に関して点Pと対称な点P'の座標を求めよ。
2022九州大学文系過去問
この動画を見る
座標空間内の4点
$O(0,0,0),A(1,1,0),B(2,1,2),P(4,0,-1)$
を考える。3点O,A,Bを通る平面を$\alpha$とし、$\overrightarrow{ a }=\overrightarrow{ OA }$,
$\overrightarrow{ b }=\overrightarrow{ OB }$とおく。
以下の問いに答えよ。
(1)ベクトル$\overrightarrow{ a },\ \overrightarrow{ b }$の両方に垂直であり、x成分が正であるような、大きさが1
のベクトル$\overrightarrow{ n }$を求めよ。
(2)点Pから平面$\alpha$に垂線を下ろし、その交点をQとおく。
線分PQの長さを求めよ。
(3)平面$\alpha$に関して点Pと対称な点P'の座標を求めよ。
2022九州大学文系過去問
【数学B/平面ベクトル】ベクトルの成分の成分計算
単元：
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師：
理科大卒の超絶わかりやすい数学・物理
問題文全文(内容文)：
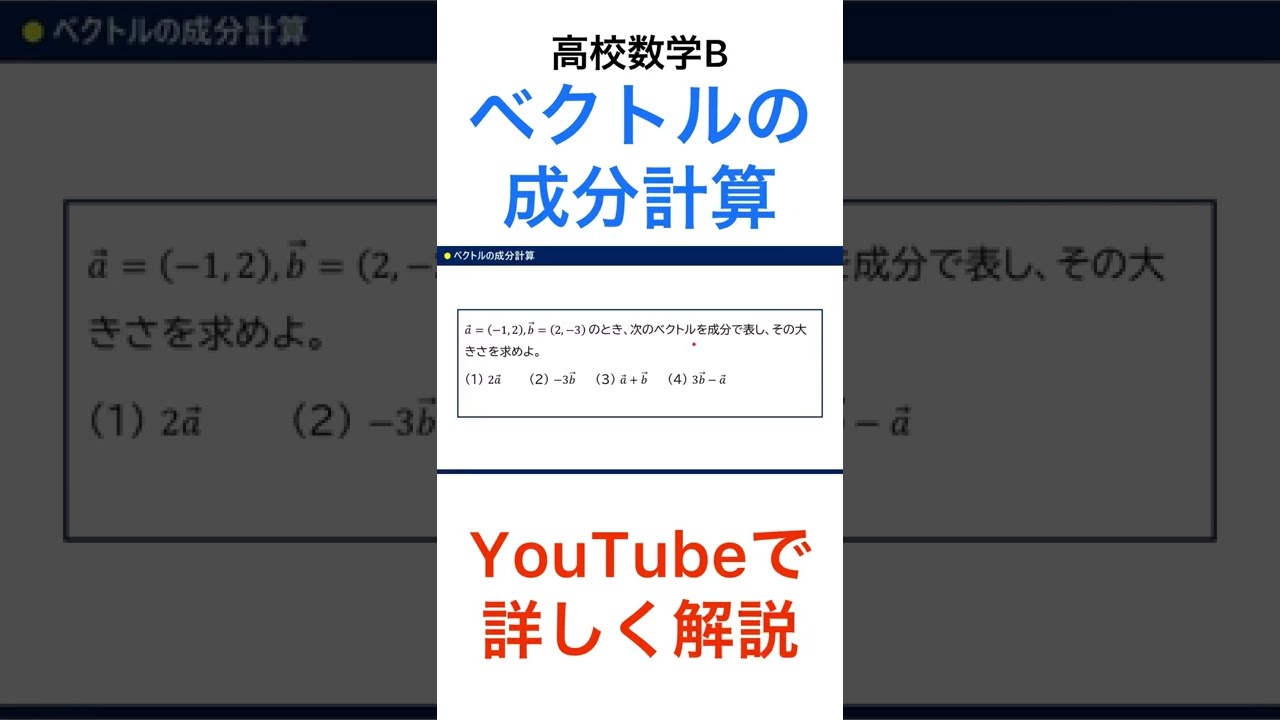
$\vec{ a }=(-1,2),\vec{ b }=(2,-3)$のとき、次のベクトルを成分で表し、その大きさを求めよ。
この動画を見る
$\vec{ a }=(-1,2),\vec{ b }=(2,-3)$のとき、次のベクトルを成分で表し、その大きさを求めよ。
【数学B/平面ベクトル】ベクトルの成分表示と大きさ
単元：
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師：
理科大卒の超絶わかりやすい数学・物理
問題文全文(内容文)：
動画内の図のベクトル$\vec{ a },\vec{ b },\vec{ c },\vec{ d },\vec{ e }$を成分で表し、それぞれ大きさを求めよ
この動画を見る
動画内の図のベクトル$\vec{ a },\vec{ b },\vec{ c },\vec{ d },\vec{ e }$を成分で表し、それぞれ大きさを求めよ
【わかりやすく】2点を結ぶベクトルの成分表示（高校数学B/C／平面ベクトル）
単元：
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師：
理科大卒の超絶わかりやすい数学・物理
問題文全文(内容文)：
4点$O(0,0),A(3,0),B(6,2),C(2,1)$について、次のベクトルを成分表示で表せ。
また、その大きさを求めよ。
（1）$\overrightarrow{ OC }$
（2）$\overrightarrow{ AB }$
（3）$\overrightarrow{ BC }$
（4）$\overrightarrow{ CO }$
この動画を見る
4点$O(0,0),A(3,0),B(6,2),C(2,1)$について、次のベクトルを成分表示で表せ。
また、その大きさを求めよ。
（1）$\overrightarrow{ OC }$
（2）$\overrightarrow{ AB }$
（3）$\overrightarrow{ BC }$
（4）$\overrightarrow{ CO }$
【わかりやすく解説】ベクトルの平行条件（数学B／平面ベクトル）
単元：
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師：
理科大卒の超絶わかりやすい数学・物理
問題文全文(内容文)：
ベクトル$\vec{ a }=(3,1),\vec{ b }=(5-4x,-3+x)$が平行になるように、$x$の値を求めよ。
この動画を見る
ベクトル$\vec{ a }=(3,1),\vec{ b }=(5-4x,-3+x)$が平行になるように、$x$の値を求めよ。
【わかりやすく】ベクトルの成分の成分計算（数学B／平面ベクトル）
単元：
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師：
理科大卒の超絶わかりやすい数学・物理
問題文全文(内容文)：
$\vec{ a }=(-1,2),\vec{ b }=(2,-3)$のとき、次のベクトルを成分で表し、その大きさを求めよ。
（1）$2\vec{ a }$
（2）$-3\vec{ b }$
（3）$\vec{ a }+\vec{ b }$
（4）$3\vec{ b }-\vec{ a }$
この動画を見る
$\vec{ a }=(-1,2),\vec{ b }=(2,-3)$のとき、次のベクトルを成分で表し、その大きさを求めよ。
（1）$2\vec{ a }$
（2）$-3\vec{ b }$
（3）$\vec{ a }+\vec{ b }$
（4）$3\vec{ b }-\vec{ a }$
【わかりやすく】ベクトルの成分表示と大きさ（数学B／平面ベクトル）
単元：
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師：
理科大卒の超絶わかりやすい数学・物理
問題文全文(内容文)：
図のベクトル$\vec{ a },\vec{ b },\vec{ c },\vec{ d },\vec{ e }$を成分で表し、それぞれの大きさを求めよ
この動画を見る
図のベクトル$\vec{ a },\vec{ b },\vec{ c },\vec{ d },\vec{ e }$を成分で表し、それぞれの大きさを求めよ
【基礎から解説】ベクトルをほかのベクトルで表す（高校数学B）
単元：
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師：
理科大卒の超絶わかりやすい数学・物理
問題文全文(内容文)：
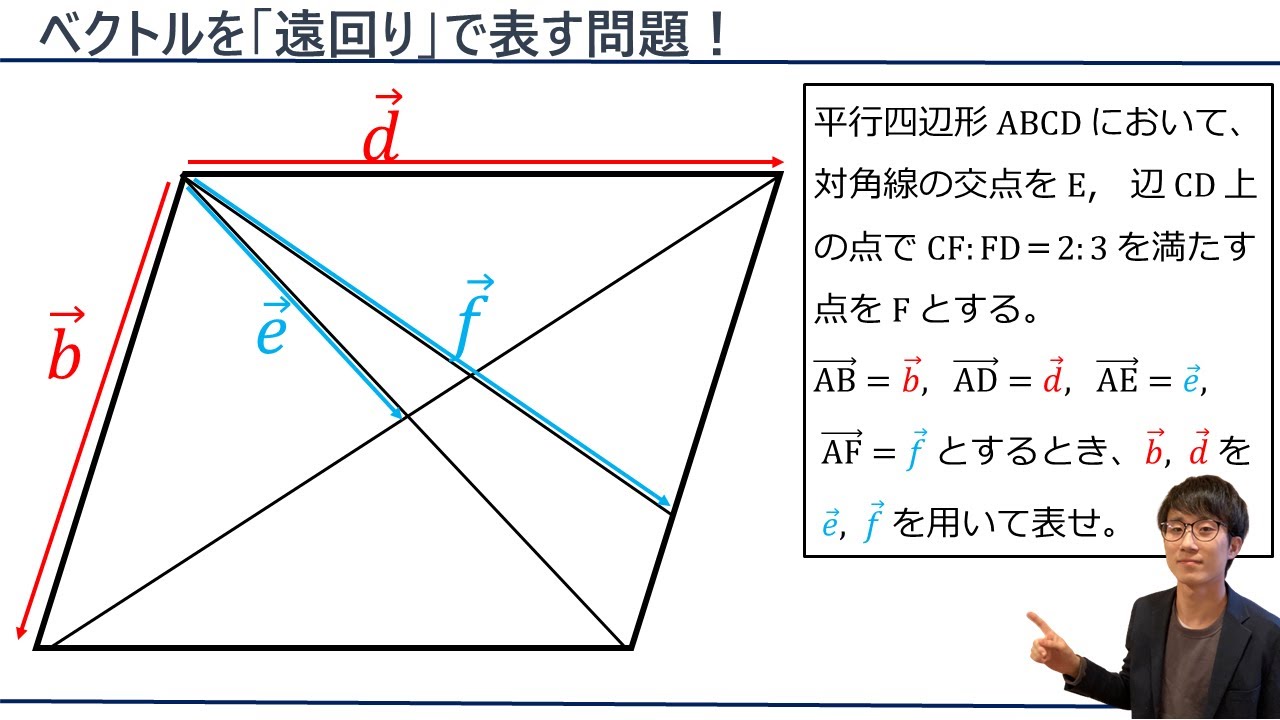
平行四辺形$ABCD$において、対角線の交点を$E$、辺$CD$上の点で$CF:FD=2:3$を満たす点を$F$とする。
$\overrightarrow{ AB }=\vec{ b },\overrightarrow{ AD }=\vec{ d },\overrightarrow{ AE }=\vec{ e },\overrightarrow{ AF }=\vec{ f }$とするとき、$\vec{ b },\vec{ d }$を$\vec{ e },\vec{ f }$を用いて表せ。
この動画を見る
平行四辺形$ABCD$において、対角線の交点を$E$、辺$CD$上の点で$CF:FD=2:3$を満たす点を$F$とする。
$\overrightarrow{ AB }=\vec{ b },\overrightarrow{ AD }=\vec{ d },\overrightarrow{ AE }=\vec{ e },\overrightarrow{ AF }=\vec{ f }$とするとき、$\vec{ b },\vec{ d }$を$\vec{ e },\vec{ f }$を用いて表せ。
ベクトルと図形のよくある問題の裏技を紹介!!#shorts
単元：
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師：
いつもの先生
問題文全文(内容文)：
ベクトルと図形のよくある問題の裏技を紹介します。
この動画を見る
ベクトルと図形のよくある問題の裏技を紹介します。
テストによく出る一問「ベクトルと図形」【高校数学B】
単元：
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師：
いつもの先生
問題文全文(内容文)：
$△ABC$において、辺$AB$を$1:2$に内分する点を$P$、
辺$AC$を$3:1$に内分する点を$E$とし、
線分$CD、BE$の交点を$P$とする。
$\overrightarrow{ AB }=\overrightarrow{b}$
$\overrightarrow{ AC }=\overrightarrow{c}$とするとき、
$\overrightarrow{ AP }$を$\overrightarrow{ b},\overrightarrow{c}$を用いて表せ。
＊図は動画内参照
この動画を見る
$△ABC$において、辺$AB$を$1:2$に内分する点を$P$、
辺$AC$を$3:1$に内分する点を$E$とし、
線分$CD、BE$の交点を$P$とする。
$\overrightarrow{ AB }=\overrightarrow{b}$
$\overrightarrow{ AC }=\overrightarrow{c}$とするとき、
$\overrightarrow{ AP }$を$\overrightarrow{ b},\overrightarrow{c}$を用いて表せ。
＊図は動画内参照
福田の入試問題解説〜北海道大学2022年理系第２問〜ベクトルと漸化式
単元：
#大学入試過去問(数学)#平面上のベクトル#数列#平面上のベクトルと内積#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数B#数C
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
aは$a\neq 1$を満たす正の実数とする。xy平面上の点$P_1,P_2,\ldots\ldots,P_n,\ldots\ldots$および
$Q_1,Q_2,\ldots\ldots,Q_n,\ldots\ldots$が、すべての自然数nについて
$\overrightarrow{ P_nP_{n+1} }=(1-a)\overrightarrow{ P_nQ_n }, \overrightarrow{ Q_nQ_{n+1} }=(0, \frac{a^{-n}}{1-a})$
を満たしているとする。また$P_n$の座標を$(x_n,y_n)$とする。
(1)$x_{n+2}$を$a, x_n, x_{n+1}$で表せ。
(2)$x_1=0, x_2=1$のとき、数列$\left\{x_n\right\}$の一般項を求めよ。
(3)$y_1=\frac{a}{(1-a)^2}, y_2-y_1=1$のとき数列$\left\{y_n\right\}$の一般項を求めよ。
2022北海道大学理系過去問
この動画を見る
aは$a\neq 1$を満たす正の実数とする。xy平面上の点$P_1,P_2,\ldots\ldots,P_n,\ldots\ldots$および
$Q_1,Q_2,\ldots\ldots,Q_n,\ldots\ldots$が、すべての自然数nについて
$\overrightarrow{ P_nP_{n+1} }=(1-a)\overrightarrow{ P_nQ_n }, \overrightarrow{ Q_nQ_{n+1} }=(0, \frac{a^{-n}}{1-a})$
を満たしているとする。また$P_n$の座標を$(x_n,y_n)$とする。
(1)$x_{n+2}$を$a, x_n, x_{n+1}$で表せ。
(2)$x_1=0, x_2=1$のとき、数列$\left\{x_n\right\}$の一般項を求めよ。
(3)$y_1=\frac{a}{(1-a)^2}, y_2-y_1=1$のとき数列$\left\{y_n\right\}$の一般項を求めよ。
2022北海道大学理系過去問
【数C】平面ベクトル：ベクトルの公式を基礎から
【数B】平面ベクトル：ベクトルの内積を基礎から
【数C】平面ベクトル：ベクトルの内積を基礎から
大学入試問題#104 一橋大学(2006) ベクトル
単元：
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$|\vec{ a }|=5,|\vec{ b }|=3,|\vec{ c }|=1$
$\vec{ Z }=\vec{ a }+\vec{ b }+\vec{ c }$
（1）$|\vec{ Z }|$の最大値、最小値
（2）$\vec{ a }・\vec{ Z }=20$
をみたすとき
$|\vec{ Z }|$の最大値、最小値を求めよ
出典：2006年一橋大学 入試問題
この動画を見る
$|\vec{ a }|=5,|\vec{ b }|=3,|\vec{ c }|=1$
$\vec{ Z }=\vec{ a }+\vec{ b }+\vec{ c }$
（1）$|\vec{ Z }|$の最大値、最小値
（2）$\vec{ a }・\vec{ Z }=20$
をみたすとき
$|\vec{ Z }|$の最大値、最小値を求めよ
出典：2006年一橋大学 入試問題
【数学B/平面ベクトル】内積を求める（大きさの式の変形方法）
単元：
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師：
理科大卒の超絶わかりやすい数学・物理
問題文全文(内容文)：
$|\vec{ a }|=2\sqrt{ 5 },|\vec{ b }|=\sqrt{ 5 },$ $|\vec{ a }+2\vec{ b }|=2\sqrt{ 5 }$のとき、ベクトル$\vec{ a },\vec{ b }$のなす角$\theta$を求めよ。
この動画を見る
$|\vec{ a }|=2\sqrt{ 5 },|\vec{ b }|=\sqrt{ 5 },$ $|\vec{ a }+2\vec{ b }|=2\sqrt{ 5 }$のとき、ベクトル$\vec{ a },\vec{ b }$のなす角$\theta$を求めよ。
【数学B/平面ベクトル】垂直なベクトル・単位ベクトル
単元：
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師：
理科大卒の超絶わかりやすい数学・物理
問題文全文(内容文)：
ベクトル$\vec{ a }=(\sqrt{ 3 },-1)$に垂直な単位ベクトル$\vec{ e }$を求めよ。
この動画を見る
ベクトル$\vec{ a }=(\sqrt{ 3 },-1)$に垂直な単位ベクトル$\vec{ e }$を求めよ。
【数学B/平面ベクトル】ベクトルの内積（成分表示の内積計算）
単元：
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師：
理科大卒の超絶わかりやすい数学・物理
問題文全文(内容文)：
2つのベクトル$\vec{ a },\vec{ b }$の内積と、そのなす角$\theta$を求めよ。
（1）$\vec{ a }=(4,2),\vec{ b }=(3,-6)$
（2）$\vec{ a }=(-1,1),\vec{ b }=(1-\sqrt{ 3 },1+\sqrt{ 3 })$
この動画を見る
2つのベクトル$\vec{ a },\vec{ b }$の内積と、そのなす角$\theta$を求めよ。
（1）$\vec{ a }=(4,2),\vec{ b }=(3,-6)$
（2）$\vec{ a }=(-1,1),\vec{ b }=(1-\sqrt{ 3 },1+\sqrt{ 3 })$
【数学B/平面ベクトル】ベクトルの内積（公式と使い方）
単元：
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師：
理科大卒の超絶わかりやすい数学・物理
問題文全文(内容文)：
2つのベクトル$\vec{ a },\vec{ b }$について、$\vec{ a }$と$\vec{ b }$の内積を求めよ。
（1）$|\vec{ a }|=2,|\vec{ b }|=3,\theta=45^{ \circ }$
（2）$|\vec{ a }|=1,|\vec{ b }|=4,\theta=150^{ \circ }$
この動画を見る
2つのベクトル$\vec{ a },\vec{ b }$について、$\vec{ a }$と$\vec{ b }$の内積を求めよ。
（1）$|\vec{ a }|=2,|\vec{ b }|=3,\theta=45^{ \circ }$
（2）$|\vec{ a }|=1,|\vec{ b }|=4,\theta=150^{ \circ }$
【数B】ベクトル：直線と平面のなす角
単元：
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師：
理数個別チャンネル
問題文全文(内容文)：
平面と直線のなす角を求めます！
この動画を見る
平面と直線のなす角を求めます！
数学「大学入試良問集」【14−3 垂直と平面ベクトルと正射影】を宇宙一わかりやすく
単元：
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数C
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
$\triangle OAB$において、辺$OA,$辺$OB$の長さをそれぞれ$a,b$とする。
また、$\angle AOB$は直角ではないとする。
2つのベクトル$\overrightarrow{ OA }$と$\overrightarrow{ OB }$の内積$\overrightarrow{ OA }・\overrightarrow{ OB }$を$k$とおく。
次の問いに答えよ。
（1）
直線$OA$上に点$C$を、$\overrightarrow{ BC }$が$\overrightarrow{ OA }$と垂直になるようにとる。
$\overrightarrow{ OC }$を$a,k,\overrightarrow{ OA }$を用いて表せ。
（2）
$a=\sqrt{ 2 },b=1$とする。
直線$BC$上に点$H$を、$\overrightarrow{ AH }$が$\overrightarrow{ OB }$と垂直になるようにとる。
$\overrightarrow{ OH }=u\overrightarrow{ OA }+v\overrightarrow{ OB }$とおくとき、$u$と$v$をそれぞれ$k$で表せ。
この動画を見る
$\triangle OAB$において、辺$OA,$辺$OB$の長さをそれぞれ$a,b$とする。
また、$\angle AOB$は直角ではないとする。
2つのベクトル$\overrightarrow{ OA }$と$\overrightarrow{ OB }$の内積$\overrightarrow{ OA }・\overrightarrow{ OB }$を$k$とおく。
次の問いに答えよ。
（1）
直線$OA$上に点$C$を、$\overrightarrow{ BC }$が$\overrightarrow{ OA }$と垂直になるようにとる。
$\overrightarrow{ OC }$を$a,k,\overrightarrow{ OA }$を用いて表せ。
（2）
$a=\sqrt{ 2 },b=1$とする。
直線$BC$上に点$H$を、$\overrightarrow{ AH }$が$\overrightarrow{ OB }$と垂直になるようにとる。
$\overrightarrow{ OH }=u\overrightarrow{ OA }+v\overrightarrow{ OB }$とおくとき、$u$と$v$をそれぞれ$k$で表せ。
福田の数学〜立教大学2021年理学部第１問(1)〜正六角形の対角線ベクトルの内積
単元：
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
${\Large\boxed{1}}$(1)1辺の長さが1の正六角形の頂点を反時計回りにA,B,C,D,E,Fとする。
このとき、2つのベクトル$\overrightarrow{ AC },\overrightarrow{ AD }$の内積$\overrightarrow{ AC }・\overrightarrow{ AD }$の値は$\boxed{\ \ ア\ \ }$である。
2021立教大学理学部過去問
この動画を見る
${\Large\boxed{1}}$(1)1辺の長さが1の正六角形の頂点を反時計回りにA,B,C,D,E,Fとする。
このとき、2つのベクトル$\overrightarrow{ AC },\overrightarrow{ AD }$の内積$\overrightarrow{ AC }・\overrightarrow{ AD }$の値は$\boxed{\ \ ア\ \ }$である。
2021立教大学理学部過去問
【数B】ベクトル：直線と平面の交点
単元：
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師：
理数個別チャンネル
問題文全文(内容文)：
直線$\dfrac{x-2}{4}=\dfrac{y-1}{-1}=z-3$と平面$x-4y+z=0$の交点を求めよ
この動画を見る
直線$\dfrac{x-2}{4}=\dfrac{y-1}{-1}=z-3$と平面$x-4y+z=0$の交点を求めよ