 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
福田の数学〜大阪大学2025文系第2問〜漸化式と数列の和

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
次の条件によって定められる数列$\{ a_n\}$がある。
$a_1=1,a_{n+1}=\dfrac{2n-1}{2n}a_n \quad (n=1,2,3,\cdots)$
(1)正の整数$k,\ell$に対して
$\dfrac{k}{k+\ell-1}a_{k+1}a_{\ell}+\dfrac{\ell}{k+\ell-1}a_ka_{\ell+1}=a_ka_{\ell}$
が成り立つことを示せ。
(2)正の整数$m$に対して
$\displaystyle \sum_{k=1}^{m} a_ka_{m-K+1}=1$
が成り立つことを示せ。
$2025$年大阪大学文系過去問題
この動画を見る
$\boxed{2}$
次の条件によって定められる数列$\{ a_n\}$がある。
$a_1=1,a_{n+1}=\dfrac{2n-1}{2n}a_n \quad (n=1,2,3,\cdots)$
(1)正の整数$k,\ell$に対して
$\dfrac{k}{k+\ell-1}a_{k+1}a_{\ell}+\dfrac{\ell}{k+\ell-1}a_ka_{\ell+1}=a_ka_{\ell}$
が成り立つことを示せ。
(2)正の整数$m$に対して
$\displaystyle \sum_{k=1}^{m} a_ka_{m-K+1}=1$
が成り立つことを示せ。
$2025$年大阪大学文系過去問題
福田のおもしろ数学530〜三角関数の最大値

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x_i \in R \ (i=1,2,\cdots,n)$
$n$は$2$以上の自然数
$\sin x_1 \cos x_2 +\sin x_2 \cos x_3+ \cdots + \sin x_n \cos x_1$
の最大値を求めよ。
この動画を見る
$x_i \in R \ (i=1,2,\cdots,n)$
$n$は$2$以上の自然数
$\sin x_1 \cos x_2 +\sin x_2 \cos x_3+ \cdots + \sin x_n \cos x_1$
の最大値を求めよ。
福田の数学〜大阪大学2025理系第5問〜確率漸化式

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{5}$
投げたときに表と裏の出る確率が
それぞれ$\dfrac{1}{2}$のコインがある。
$A,B,C$の$3$文字を$BAC$のように$1$個ずつ
すべて並べて得られる文字列に対して、
コインを投げて次の操作を行う。
・表がで出たら文字列の左から$1$文字目と
$2$文字目を入れかえる。
・裏がで出たら文字列の左から$2$文字目と
$3$文字目を入れかえる。
例えば、文字列が$BAC$であるときに、
$2$回続けてコインを投げて表、裏の順に出た
とすると、文字列は$BAC$から$ABC$を経て
$ACB$となる。
最初の文字列は$ABC$であるとする。
コインを$n$回続けて投げたあとの文字列が
$ABC$である確率を$p_n$とし、
$BCA$である確率を$q_n$とする。
(1)$k$を正の整数とするとき、
$p_{2k}-q_{2k}$を求めよ。
(2)$n$を正の整数とするとき、
$p_n$を求めよ。
$2025$年大阪大学理系過去問題
この動画を見る
$\boxed{5}$
投げたときに表と裏の出る確率が
それぞれ$\dfrac{1}{2}$のコインがある。
$A,B,C$の$3$文字を$BAC$のように$1$個ずつ
すべて並べて得られる文字列に対して、
コインを投げて次の操作を行う。
・表がで出たら文字列の左から$1$文字目と
$2$文字目を入れかえる。
・裏がで出たら文字列の左から$2$文字目と
$3$文字目を入れかえる。
例えば、文字列が$BAC$であるときに、
$2$回続けてコインを投げて表、裏の順に出た
とすると、文字列は$BAC$から$ABC$を経て
$ACB$となる。
最初の文字列は$ABC$であるとする。
コインを$n$回続けて投げたあとの文字列が
$ABC$である確率を$p_n$とし、
$BCA$である確率を$q_n$とする。
(1)$k$を正の整数とするとき、
$p_{2k}-q_{2k}$を求めよ。
(2)$n$を正の整数とするとき、
$p_n$を求めよ。
$2025$年大阪大学理系過去問題
【数Ⅲ】【関数と極限】nは自然数とし、h>0のとき、不等式(1+h)^n≧1+nh+n(n-1)/2・h²が成り立つ。このことを用いて、数列{n/3^n}の極限を求めよ。

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
nは自然数とし、h>0のとき、
不等式$(1+h)^n≧1+nh+\dfrac{n(n-1)}{2}・h²$が成り立つ。
このことを用いて、数列$\dfrac{n}{3^n}$の極限を求めよ。
この動画を見る
nは自然数とし、h>0のとき、
不等式$(1+h)^n≧1+nh+\dfrac{n(n-1)}{2}・h²$が成り立つ。
このことを用いて、数列$\dfrac{n}{3^n}$の極限を求めよ。
【数Ⅲ】【関数と極限】次の条件によって定められる数列{an}の極限を求めよ。a₁=0、a₂=1、3an+₂=an+₁+2an他

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の条件によって定められる数列$a_n$の極限を求めよ。
(1) $a₁=0$、$a₂=1$、$3a_{n+2}=a_{n+1}+2a_n$
(2) $a₁=0$、$a₂=1$、$a_{n+2}-7a_{n+1}+10a_n=0$
(3) $a₁=1$、$a₂=2$、$a_{n+2}-6a_{n+1}+9a_n=0$
この動画を見る
次の条件によって定められる数列$a_n$の極限を求めよ。
(1) $a₁=0$、$a₂=1$、$3a_{n+2}=a_{n+1}+2a_n$
(2) $a₁=0$、$a₂=1$、$a_{n+2}-7a_{n+1}+10a_n=0$
(3) $a₁=1$、$a₂=2$、$a_{n+2}-6a_{n+1}+9a_n=0$
福田の数学〜大阪大学2025理系第4問〜不等式の証明と関数の極限

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
次の問いに答えよ。
(1)$t\gt 0$のとき
$-\dfrac{1}{t}\lt \displaystyle \int_{t}^{2t} \dfrac{\sin x}{x^2}dx \lt \dfrac{1}{t}$
が成り立つことを示せ。
(2)$\displaystyle \lim_{t\to\infty}\displaystyle \dfrac{\cos x}{x}dx=0$を示せ。
(3)$f(x)=\sin\left(\dfrac{3x}{2}\right)\sin\left(\dfrac{x}{2}\right)$おく。
$\displaystyle \lim_{t\to\infty}\displaystyle \int_{1}^{t} \dfrac{f(x)}{x}dx=\dfrac{1}{2} \displaystyle \int_{1}^{2} \dfrac{\cos x}{x} dx$
を示せ。
$2025$年大阪大学理系過去問題
この動画を見る
$\boxed{4}$
次の問いに答えよ。
(1)$t\gt 0$のとき
$-\dfrac{1}{t}\lt \displaystyle \int_{t}^{2t} \dfrac{\sin x}{x^2}dx \lt \dfrac{1}{t}$
が成り立つことを示せ。
(2)$\displaystyle \lim_{t\to\infty}\displaystyle \dfrac{\cos x}{x}dx=0$を示せ。
(3)$f(x)=\sin\left(\dfrac{3x}{2}\right)\sin\left(\dfrac{x}{2}\right)$おく。
$\displaystyle \lim_{t\to\infty}\displaystyle \int_{1}^{t} \dfrac{f(x)}{x}dx=\dfrac{1}{2} \displaystyle \int_{1}^{2} \dfrac{\cos x}{x} dx$
を示せ。
$2025$年大阪大学理系過去問題
【カイホウの検討…!】整数:文教大学付属高等学校~全国入試問題解法

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
連続する4つの自然数がある。それぞれの数を2乗したものを足すと294になった。このとき4つの自然数の中で最も小さいものを答えなさい。
この動画を見る
連続する4つの自然数がある。それぞれの数を2乗したものを足すと294になった。このとき4つの自然数の中で最も小さいものを答えなさい。
【この一本でルートのルール全部確認!!】平方根の基礎全まとめ(平方根とは・有理化・乗法除法・加法減法 )〔現役講師解説、中学数学・高校数学〕

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
次の数の平方根は?
①$4$
②$0.01$
③$3$
④$0.2$
平方根を使わずに表しなさい。
①$\sqrt4$
②$-\sqrt{25}$
③$(\sqrt3)^2$
④$(-\sqrt5)^2$
次の計算をせよ。
①$\sqrt3\times \sqrt2$
②$\sqrt5 \times \sqrt7 $
③$\sqrt6 \div \sqrt3$
④$\sqrt{45} \div \sqrt5$
$a\sqrt b$の形にせよ。
①$\sqrt{20}$
②$\sqrt{48}$
有理化しなさい。
①$\dfrac{3}{7}$
②$\dfrac{1}{12}$
次の計算をしなさい。
①$2\sqrt2 +3\sqrt2$
②$4\sqrt3-2\sqrt3$
③$2\sqrt3+2\sqrt2+4\sqrt3-5\sqrt2$
④$\sqrt{28}-3\sqrt7$
⑤$\sqrt2+\sqrt8-6\sqrt2$
この動画を見る
次の数の平方根は?
①$4$
②$0.01$
③$3$
④$0.2$
平方根を使わずに表しなさい。
①$\sqrt4$
②$-\sqrt{25}$
③$(\sqrt3)^2$
④$(-\sqrt5)^2$
次の計算をせよ。
①$\sqrt3\times \sqrt2$
②$\sqrt5 \times \sqrt7 $
③$\sqrt6 \div \sqrt3$
④$\sqrt{45} \div \sqrt5$
$a\sqrt b$の形にせよ。
①$\sqrt{20}$
②$\sqrt{48}$
有理化しなさい。
①$\dfrac{3}{7}$
②$\dfrac{1}{12}$
次の計算をしなさい。
①$2\sqrt2 +3\sqrt2$
②$4\sqrt3-2\sqrt3$
③$2\sqrt3+2\sqrt2+4\sqrt3-5\sqrt2$
④$\sqrt{28}-3\sqrt7$
⑤$\sqrt2+\sqrt8-6\sqrt2$
福田のおもしろ数学528〜平面幾何の証明
単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
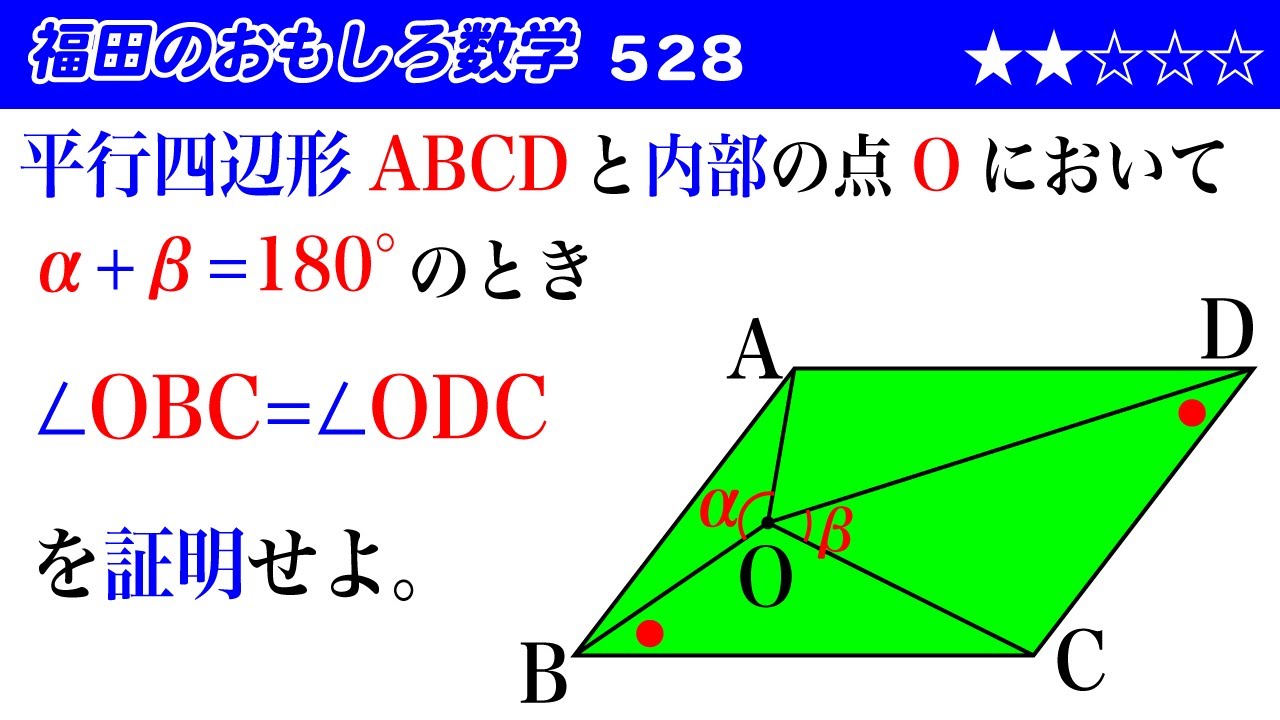
平行四辺形$ABCD$と内部の点$O$において
$\alpha+\beta=180°$のとき
$\angle OBC=\angle ODC$
を証明せよ。
図は動画内参照
この動画を見る
平行四辺形$ABCD$と内部の点$O$において
$\alpha+\beta=180°$のとき
$\angle OBC=\angle ODC$
を証明せよ。
図は動画内参照
福田の数学〜大阪大学2025理系第3問〜空間図形と最大最小の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#微分法と積分法#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
座標空間に$3$点$O(0,0,0),A(0,1,1),B(x,y,0)$がある。
$\angle OAP=30°$かつ$y\geqq 0$を満たすように
点$P$が動くとき、
$(x+1)(y+1)$の最大値と最小値を求めよ。
$2025$年大阪大学理系過去問題
この動画を見る
$\boxed{3}$
座標空間に$3$点$O(0,0,0),A(0,1,1),B(x,y,0)$がある。
$\angle OAP=30°$かつ$y\geqq 0$を満たすように
点$P$が動くとき、
$(x+1)(y+1)$の最大値と最小値を求めよ。
$2025$年大阪大学理系過去問題
【数Ⅲ】【積分とその応用】点Pの座標(x,y)が 3x=t³+6t², 3y=2t³-3t²(1)点Pが座標(27,9)を通るときの速度を求めよ(2)点Pが時刻0からaまでに通過する道のりLを求めよ。

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
点Pの座標(x,y)が、時刻の関数として次のように表されている。
3x=t³+6t², 3y=2t³-3t²
(1)点Pが座標(27,9)を通るときの速度を求めよ。
(2)点Pが時刻0からa(a>0)までに通過する道のりLを求めよ。
この動画を見る
点Pの座標(x,y)が、時刻の関数として次のように表されている。
3x=t³+6t², 3y=2t³-3t²
(1)点Pが座標(27,9)を通るときの速度を求めよ。
(2)点Pが時刻0からa(a>0)までに通過する道のりLを求めよ。
【数Ⅲ】【積分とその応用】t秒後の速度が v=30-10t(m/s)となるように地上から真上に投げ上げられた物体は、何秒後に何mの高さまで上がって落ち始めるか。

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
t秒後の速度が v=30-10t(m/s)となるように地上から真上に投げ上げられた物体は、何秒後に何mの高さまで上がって落ち始めるか。
この動画を見る
t秒後の速度が v=30-10t(m/s)となるように地上から真上に投げ上げられた物体は、何秒後に何mの高さまで上がって落ち始めるか。
【数Ⅲ】【積分とその応用】曲線x=θcosθ、y=θsinθ(0≦θ≦2π)の長さは、曲線y=x²/2(0≦θ≦2π)の長さに等しいことを示せ。

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
曲線x=θcosθ、y=θsinθ(0≦θ≦2π)の長さは、曲線y=x²/2(0≦θ≦2π)の長さに等しいことを示せ。
この動画を見る
曲線x=θcosθ、y=θsinθ(0≦θ≦2π)の長さは、曲線y=x²/2(0≦θ≦2π)の長さに等しいことを示せ。
【数Ⅲ】【積分とその応用】次の曲線の長さLを求めよ。ただし、θは媒介変数a,p,qは定数であり、a>0,0<q<π/2 を満たす。

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の曲線の長さLを求めよ。ただし、θは媒介変数a,p,qは定数であり、a>0,0<q<π/2 を満たす。
(1) x=a(cosθ+θsinθ)、y=a(sinθ-θcosθ) (0≦θ≦p)
(2) y=log(cosx) (0≦θ≦p)
この動画を見る
次の曲線の長さLを求めよ。ただし、θは媒介変数a,p,qは定数であり、a>0,0<q<π/2 を満たす。
(1) x=a(cosθ+θsinθ)、y=a(sinθ-θcosθ) (0≦θ≦p)
(2) y=log(cosx) (0≦θ≦p)
福田のおもしろ数学527〜最大公約数と最小公倍数からxとyの組の個数を求める

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$gcd(x,y)=5!$
$Icm(x,y)=50!$
$(x\leqq y)$
を満たす自然数の組
$(x,y)$は何組あるか?
この動画を見る
$gcd(x,y)=5!$
$Icm(x,y)=50!$
$(x\leqq y)$
を満たす自然数の組
$(x,y)$は何組あるか?
福田の数学〜大阪大学2025理系第2問〜3次関数の極値と変曲点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
$p$と$m$を実数とし、
関数$f(x)=x^3+3px^2+3mx$は
$x=\alpha$で極大値をとり、
$x=\beta$で極小値をとるとする。
(1)$f(\alpha)-f(\beta)$を$p$と$m$を用いて表せ。
(2)$p$と$m$が$f(\alpha)-f(\beta)=4$を
満たしながら動くとき、
曲線$y=f(x)$の変曲点の軌跡を求めよ。
$2025$年大阪大学理系過去問題
この動画を見る
$\boxed{2}$
$p$と$m$を実数とし、
関数$f(x)=x^3+3px^2+3mx$は
$x=\alpha$で極大値をとり、
$x=\beta$で極小値をとるとする。
(1)$f(\alpha)-f(\beta)$を$p$と$m$を用いて表せ。
(2)$p$と$m$が$f(\alpha)-f(\beta)=4$を
満たしながら動くとき、
曲線$y=f(x)$の変曲点の軌跡を求めよ。
$2025$年大阪大学理系過去問題
福田のおもしろ数学526〜数値評価
単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
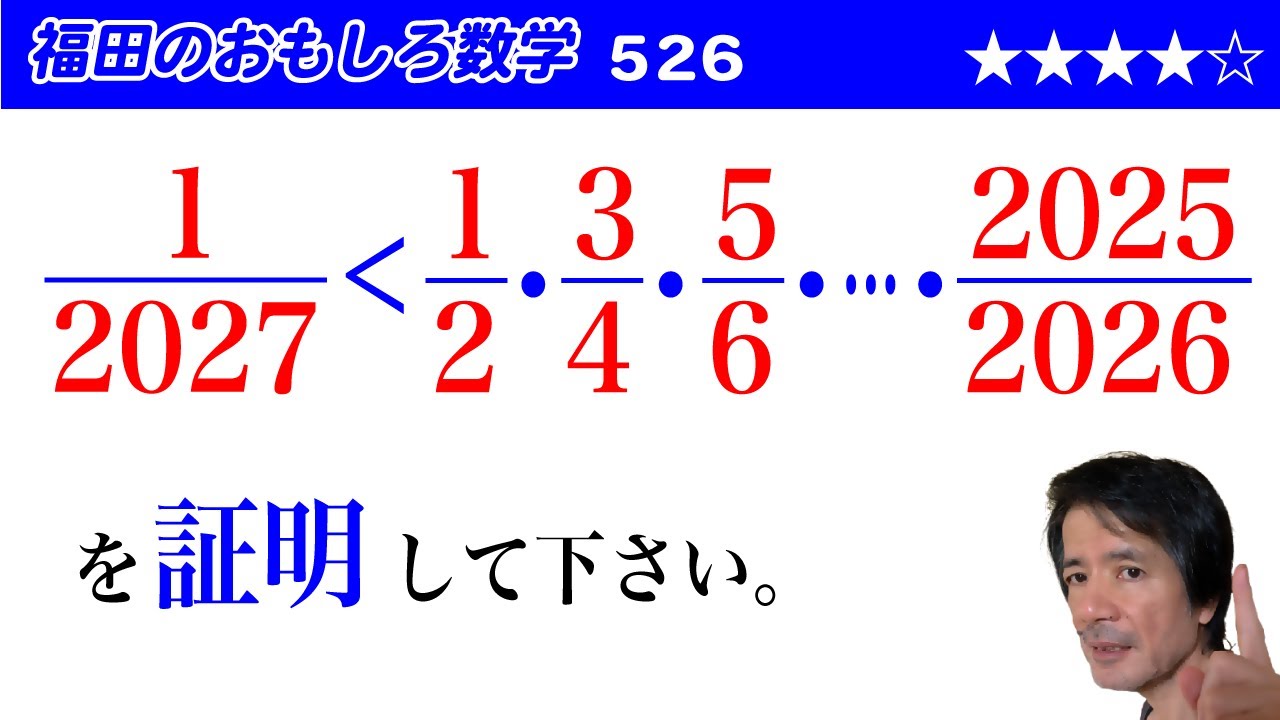
$\dfrac{1}{2027} \lt \dfrac{1}{2}・\dfrac{3}{4}・\dfrac{5}{6}・\cdots ・\dfrac{2025}{2026}$
を証明して下さい。
この動画を見る
$\dfrac{1}{2027} \lt \dfrac{1}{2}・\dfrac{3}{4}・\dfrac{5}{6}・\cdots ・\dfrac{2025}{2026}$
を証明して下さい。
福田の数学〜大阪大学2025理系第1問〜平面図形とベクトルの証明

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
平面上の三角形$OAB$を考える。
$\angle AOB$は鋭角、$OA=3,OB=t$とする。
また、点$A$から直線$OB$に下ろした垂線と
直線$OB$の交点を$C$とし、$OC=1$とする。
線分$AB$を$2:1$に内分する点を$P$、点$A$から
直線$OP$に下ろした垂線と直線$OB$との交点を
$R$とする。
(1)内積$\overrightarrow{OA}・\overrightarrow{OB}$を$t$を用いて表せ。
(2)線分$OR$の長さを$t$を用いて表せ。
(3)線分$OB$の中点を$M$とする。
点$R$が線分$MB$上にあるとき、
$t$のとりうる値の範囲を求めよ。
$2025$年大阪大学理系過去問題
この動画を見る
$\boxed{1}$
平面上の三角形$OAB$を考える。
$\angle AOB$は鋭角、$OA=3,OB=t$とする。
また、点$A$から直線$OB$に下ろした垂線と
直線$OB$の交点を$C$とし、$OC=1$とする。
線分$AB$を$2:1$に内分する点を$P$、点$A$から
直線$OP$に下ろした垂線と直線$OB$との交点を
$R$とする。
(1)内積$\overrightarrow{OA}・\overrightarrow{OB}$を$t$を用いて表せ。
(2)線分$OR$の長さを$t$を用いて表せ。
(3)線分$OB$の中点を$M$とする。
点$R$が線分$MB$上にあるとき、
$t$のとりうる値の範囲を求めよ。
$2025$年大阪大学理系過去問題
【数Ⅲ】【積分とその応用】半径がaである円Oの直径ABの両端AおよびBから出発して円Oの周上を同じ向きに動く2点P,QがPの速さはQの速さの2倍でAからBまで動くとき、△APQの面積の最大値を求めよ。

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
半径がaである円Oの直径ABの両端AおよびBから出発して円Oの周上を同じ向きにそれぞれ一定の速さで動く2点P,Qがある。Pの速さはQの速さの2倍で、PがAからBまで動くとき、△APQの面積の最大値を求めよ。また,その時の∠BOQの大きさを求めよ。
この動画を見る
半径がaである円Oの直径ABの両端AおよびBから出発して円Oの周上を同じ向きにそれぞれ一定の速さで動く2点P,Qがある。Pの速さはQの速さの2倍で、PがAからBまで動くとき、△APQの面積の最大値を求めよ。また,その時の∠BOQの大きさを求めよ。
【数Ⅲ】【積分とその応用】点Pが原点Oを中心とする半径rの円の周上を等速円運動OPが毎秒π/6ラジアンだけ回転するとき,点Pの速さと加速度の大きさを求めよ。

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
点Pが,原点Oを中心とする半径rの円の周上を,等速円運動。OPが毎秒π/6ラジアンだけ回転するとき,点Pの速さと加速度の大きさを求めよ。ただし,Pは円周上の点(r,0)から出発するものとする。
この動画を見る
点Pが,原点Oを中心とする半径rの円の周上を,等速円運動。OPが毎秒π/6ラジアンだけ回転するとき,点Pの速さと加速度の大きさを求めよ。ただし,Pは円周上の点(r,0)から出発するものとする。
【数Ⅲ】【積分とその応用】半径が10cm深さが20cmの直円錐形容器に毎秒3cm³の割合で静かに水を注ぐとき水の深さが6cmになった瞬間の水面の上昇する速さと水面の面積の増加する速さを求めよ。

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
上面の半径が10cm,深さが20cmの直円錐形の容器が,その軸を鉛直にして固定されている。この容器に毎秒3cm³の割合で静かに水を注ぐとき,水の深さが6cmになった瞬間の,水面の上昇する速さと,水面の面積の増加する速さを求めよ。
この動画を見る
上面の半径が10cm,深さが20cmの直円錐形の容器が,その軸を鉛直にして固定されている。この容器に毎秒3cm³の割合で静かに水を注ぐとき,水の深さが6cmになった瞬間の,水面の上昇する速さと,水面の面積の増加する速さを求めよ。
福田のおもしろ数学525〜数値評価
単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
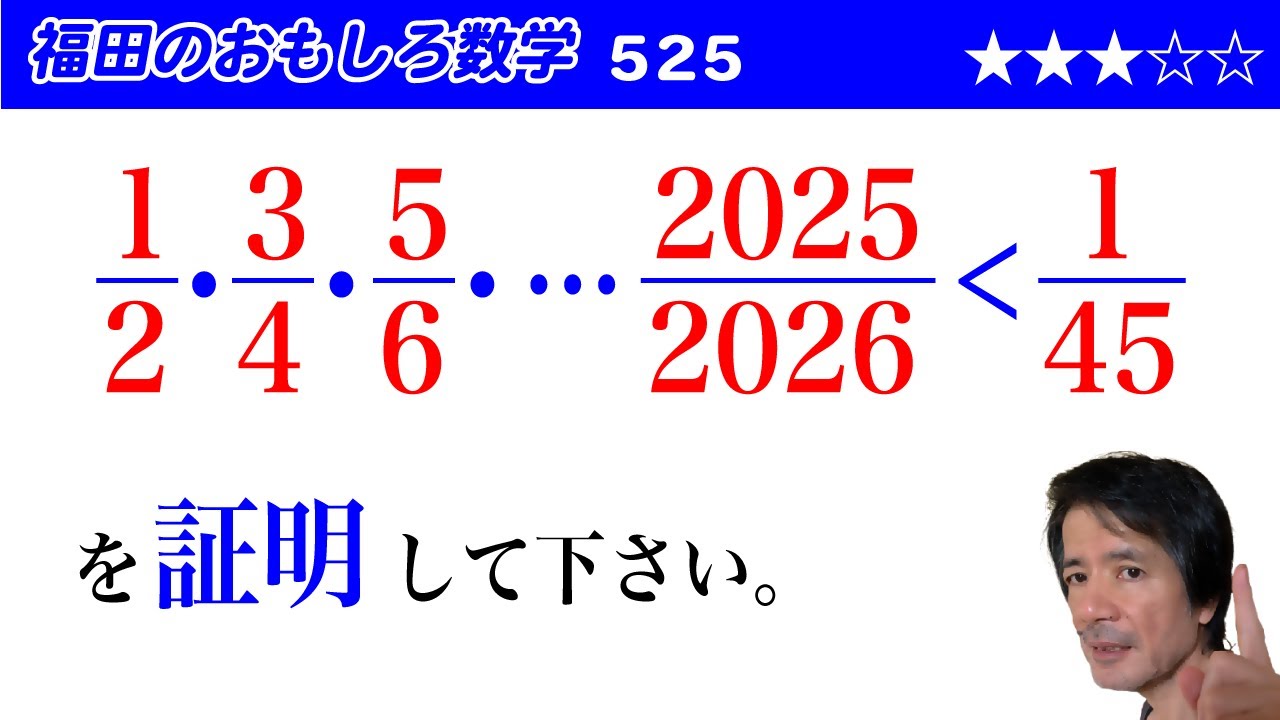
$\dfrac{1}{2}・\dfrac{3}{4}・\dfrac{5}{6}・\cdots \dfrac{2025}{2026}\lt \dfrac{1}{45}$
を証明して下さい。
この動画を見る
$\dfrac{1}{2}・\dfrac{3}{4}・\dfrac{5}{6}・\cdots \dfrac{2025}{2026}\lt \dfrac{1}{45}$
を証明して下さい。
福田の数学〜立教大学2025理学部第4問〜整式がある数の倍数であることの証明

単元:
#数Ⅰ#数A#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数学的帰納法#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$n$を$2$以上の自然数とする。次の問いに答えよ。
(1)$n^3-n$は$6$のばいすうであることを示せ。
(2)$n^4+2n^3-n^2-2n$は$24$の倍数であることを示せ。
(3)$n$に関する数学的帰納法を用いて、
$n^5+4n$は$5$の倍数であることを示せ。
(4)$n^9+2n^8-n^7-2n^6+4n^5+8n^4-4n^3-8n^2$は
$120$の倍数であることを示せ。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{4}$
$n$を$2$以上の自然数とする。次の問いに答えよ。
(1)$n^3-n$は$6$のばいすうであることを示せ。
(2)$n^4+2n^3-n^2-2n$は$24$の倍数であることを示せ。
(3)$n$に関する数学的帰納法を用いて、
$n^5+4n$は$5$の倍数であることを示せ。
(4)$n^9+2n^8-n^7-2n^6+4n^5+8n^4-4n^3-8n^2$は
$120$の倍数であることを示せ。
$2025$年立教大学理学部過去問題
equation : Shirotan's cute kawaii math show #数学 #小学生テスト #高校入試 #歌ってみた #高校受験 #占い

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
a¹⁰b⁸+a⁶b⁸-3a⁵b⁵=?
この動画を見る
a¹⁰b⁸+a⁶b⁸-3a⁵b⁵=?
福田のおもしろ数学524〜無限級数の和

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \sum_{k=1}^{\infty} \dfrac{k^2}{3^k}$を求めて下さい。
この動画を見る
$\displaystyle \sum_{k=1}^{\infty} \dfrac{k^2}{3^k}$を求めて下さい。
福田の数学〜立教大学2025理学部第3問〜指数関数と円でできる領域の面積

単元:
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$a,p$は正の実数とする。
座標平面上の曲線$C_1:y=e^x$と$C_1$上の点
$(p,e^p)$がある。
$P$における$C_1$の法線を$\ell,\ell$と$x$軸の
交点を$A(a,0)$、$A$を中心とする半径$r$の円を
$C_2$とする。
$P$が$C_1$と$C_2$のただ一つの共有点であるとき、
次の問いに答えよ。
(1)$\ell$の方程式を$p$を用いて表せ。
(2)$a$を$p$を用いて表せ。
(3)$r$を$p$を用いて表せ。
(4)$\angle OAP=\dfrac{\pi}{6}$のとき、$p$の値を求めよ。
(5)$p$を(4)で求めた値とするとき、
次の不等式の表す領域$D$の面積$S$を求めよ。
$-2 \leqq x \leqq p,\ y\geqq 0,\ y\leqq e^x,$
$(x-a)^2+y^2\geqq r^2$
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{3}$
$a,p$は正の実数とする。
座標平面上の曲線$C_1:y=e^x$と$C_1$上の点
$(p,e^p)$がある。
$P$における$C_1$の法線を$\ell,\ell$と$x$軸の
交点を$A(a,0)$、$A$を中心とする半径$r$の円を
$C_2$とする。
$P$が$C_1$と$C_2$のただ一つの共有点であるとき、
次の問いに答えよ。
(1)$\ell$の方程式を$p$を用いて表せ。
(2)$a$を$p$を用いて表せ。
(3)$r$を$p$を用いて表せ。
(4)$\angle OAP=\dfrac{\pi}{6}$のとき、$p$の値を求めよ。
(5)$p$を(4)で求めた値とするとき、
次の不等式の表す領域$D$の面積$S$を求めよ。
$-2 \leqq x \leqq p,\ y\geqq 0,\ y\leqq e^x,$
$(x-a)^2+y^2\geqq r^2$
$2025$年立教大学理学部過去問題
福田のおもしろ数学523〜命題の真偽の判定

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x+y$と$x+y^2$がともに有理数であるとき
$x$と$y$はともに有理数であると言えるか?
$x+y$と$x+y^2$と$x+y^3$がすべて
有理数であるとき
$x$と$y$はともに有理数であると言えるか?
この動画を見る
$x+y$と$x+y^2$がともに有理数であるとき
$x$と$y$はともに有理数であると言えるか?
$x+y$と$x+y^2$と$x+y^3$がすべて
有理数であるとき
$x$と$y$はともに有理数であると言えるか?
福田の数学〜立教大学2025理学部第2問〜三角関数の最大最小の定番

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
実数$x$に対し、関数$f(x)$を
$f(x)=\sin^3x+\cos^3x+4sin x \cos x$
により定める。
また、$t=\sin x+\cos x$とおく。次の問いに答えよ。
(1)$\sin x \cos x$を$t$を用いて表せ。
(2)$f(x)$を$t$を用いて表せ。
(3)$x$がすべてに実数を動くとき、
$t$のとりうる値の範囲を求めよ。
(4)$x$がすべてに実数を動くとき、
$f(x)$の最大値と最小値をそれぞれ求めよ。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{2}$
実数$x$に対し、関数$f(x)$を
$f(x)=\sin^3x+\cos^3x+4sin x \cos x$
により定める。
また、$t=\sin x+\cos x$とおく。次の問いに答えよ。
(1)$\sin x \cos x$を$t$を用いて表せ。
(2)$f(x)$を$t$を用いて表せ。
(3)$x$がすべてに実数を動くとき、
$t$のとりうる値の範囲を求めよ。
(4)$x$がすべてに実数を動くとき、
$f(x)$の最大値と最小値をそれぞれ求めよ。
$2025$年立教大学理学部過去問題
【数C】【平面上の曲線】中心の極座標が(a,0)で極Oを通る円をCとし、極Oを除くC上の動点をPとする。線分OPを1辺とする正方形OPQRを作るとき、点Qの軌跡の極方程式を求めよ。

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
aを正の定数とする。中心の極座標が(a,0)で極Oを通る円をCとし、極Oを除くC上の動点をPとする。線分OPを1辺とする正方形OPQRを作るとき、点Qの軌跡の極方程式を求めよ。
この動画を見る
aを正の定数とする。中心の極座標が(a,0)で極Oを通る円をCとし、極Oを除くC上の動点をPとする。線分OPを1辺とする正方形OPQRを作るとき、点Qの軌跡の極方程式を求めよ。
【数C】【平面上の曲線】極座標が(2,0)である点Aを通り始線OXに垂直な直線をlとし、極Oを端点とする半直線OP上に、OP・OQ=4を満たす点Qをとるとき、点Qの軌跡の極方程式を求めよ。

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
極座標が(2,0)である点Aを通り始線OXに垂直な直線をlとし、l上の動点をPとする。極Oを端点とする半直線OP上に、OP・OQ=4を満たす点Qをとるとき、点Qの軌跡の極方程式を求めよ。
この動画を見る
極座標が(2,0)である点Aを通り始線OXに垂直な直線をlとし、l上の動点をPとする。極Oを端点とする半直線OP上に、OP・OQ=4を満たす点Qをとるとき、点Qの軌跡の極方程式を求めよ。
