 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
福田の数学〜2023年共通テスト速報〜数学IIB第3問確率分布〜正規分布と二項分布

単元:
#大学入試過去問(数学)#確率分布と統計的な推測#確率分布#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト#数B
指導講師:
福田次郎
問題文全文(内容文):
第3問
以下の問題を解答するにあたっては、必要に応じて43ページの正規分布表を用いてもよい。
(1)ある生産地で生産されるピーマン全体を母集団とし、この母集団におけるピーマン1個の重さ(単位はg)を表す確率変数をXとする。mとσを正の実数とし、Xは正規分布N(m, $\sigma^2$)に従うとする。
(i)この母集団から1個のピーマンを無作為に抽出したとき、重さがm g以上である確率P(X≧m)は
P(X≧m)=P$\left(\frac{X-m}{\sigma}\geqq \boxed{\ \ ア\ \ }\right)$=$\frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }}$
である。
(ii)母集団から無作為に抽出された大きさnの標本$X_1$, $X_2$, ..., $X_n$の標本平均を$\bar{X}$とする。$\bar{X}$の平均(期待値)と標準偏差はそれぞれ
E($\bar{X}$)=$\boxed{\boxed{\ \ エ\ \ }}$, σ($\bar{X}$)=$\boxed{\boxed{\ \ オ\ \ }}$
となる。
n=400, 標本平均が30.0g, 標本の標準偏差が3.6gのとき、mの信頼度90%の信頼区間を次の方針で求めよう。
方針:Zを標準正規分布N(0,1)に従う確率変数として、P($-z_0 \leqq Z \leqq z_0$)=0.901 となる$z_0$を正規分布表から求める。この$z_0$を用いるとmの信頼度90.1%の信頼区間が求められるが、これを信頼度90%の信頼区間とみなして考える。
方針において、$z_0$=$\boxed{\ \ カ\ \ }$.$\boxed{\ \ キク\ \ }$である。
一般に、標本の大きさnが大きいときには、母標準偏差の代わりに、標本の標準偏差を用いてよいことが知られている。n=400は十分に大きいので、方針に基づくと、mの信頼度90%の信頼区間は$\boxed{\boxed{\ \ ケ\ \ }}$となる。
$\boxed{\boxed{\ \ エ\ \ }}, \boxed{\boxed{\ \ オ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪σ ①$\sigma^2$ ②$\frac{\sigma}{\sqrt n}$ ③$\frac{\sigma^2}{n}$
④m ⑤2m ⑥$m^2$ ⑦$\sqrt m$
⑧$\frac{\sigma}{n}$ ⑨$n\sigma $ⓐ$nm$ ⓑ$\frac{m}{n}$
$\boxed{\boxed{\ \ ケ\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪28.6≦m≦31.4 ①28.7≦m≦31.3 ②28.9≦m≦31.1
③29.6≦m≦30.4 ④29.7≦m≦30.3 ⑤29.9≦m≦30.1
(2)(1)の確率変数Xにおいて、m=30.0, σ=3.6とした母集団から無作為にピーマンを1個ずつ抽出し、ピーマン2個を1組にしたものを袋に入れていく。このようにしてピーマン2個を1組にしたものを25袋作る。その際、1袋ずつの重さの分数を小さくするために、次のピーマン分類法を考える。
ピーマン分類法:無作為に抽出したいくつかのピーマンについて、重さが30.0g以下のときをSサイズ、30.0gを超えるときはLサイズと分類する。そして、分類されたピーマンからSサイズとLサイズのピーマンを一つずつ選び、ピーマン2個を1組とした袋を作る。
(i)ピーマンを無作為に50個抽出した時、ピーマン分類法で25袋作ることができる確率$p_0$を考えよう。無作為に1個抽出したピーマンがSサイズである確率は$\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。ピーマンを無作為に50個抽出したときのSサイズのピーマンの個数を表す確率変数を$U_0$とすると、$U_0$は二項分布$B\left(50, \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)$に従うので
$p_0$=${}_{50}C_{\boxed{シス}}×\left(\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)^{\boxed{シス}}×\left(1-\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)^{50-\boxed{シス}}$
となる。
$p_0$を計算すると、$p_0$=0.1122...となることから、ピーマンを無作為に50個抽出したとき、25袋作ることができる確率は0.11程度とわかる。
(ii)ピーマン分類法で25袋作ることができる確率が0.95以上となるようなピーマンの個数を考えよう。
kを自然数とし、ピーマンを無作為に(50+k)個抽出したとき、Sサイズのピーマンの個数を表す確率変数を$U_k$とすると、$U_k$は二項分布$B\left(50+k, \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)$に従う。
(50+k)は十分に大きいので、$U_k$は近似的に正規分布$N\left(\boxed{\boxed{\ \ セ\ \ }}, \boxed{\boxed{\ \ ソ\ \ }}\right)$に従い、$Y=\frac{U_k-\boxed{\boxed{\ \ セ\ \ }}}{\sqrt{\boxed{\boxed{\ \ ソ\ \ }}}}$とすると、Yは近似的に標準正規分布N(0,1)に従う。
よって、ピーマン分類法で、25袋作ることができる確率を$p_k$とすると
$p_k$=$P(25 \leqq U_k \leqq 25+k)$=$P\left(-\frac{\boxed{\boxed{\ \ タ\ \ }}}{\sqrt{50+k}} \leqq Y \leqq \frac{\boxed{\boxed{\ \ タ\ \ }}}{\sqrt{50+k}}\right)$
となる。
$\boxed{\boxed{\ \ タ\ \ }}$=a, $\sqrt{50+k}$=$\beta$とおく。
$p_k$≧0.95になるような$\frac{\alpha}{\beta}$について、正規分布表から$\frac{\alpha}{\beta}$≧1.96を満たせばよいことが分かる。ここでは
$\frac{\alpha}{\beta}$≧2 ...①
を満たす自然数kを考えることとする。①の両辺は正であるから、$\alpha^2$≧4$\beta^2$を満たす最小のkを$k_0$とすると、$k_0$=$\boxed{\ \ チツ\ \ }$であることがわかる。ただし、$\boxed{\ \ チツ\ \ }$の計算においては、$\sqrt{51}=7.14$を用いてもよい。
したがって、少なくとも(50+$\boxed{\ \ チツ\ \ }$)個のピーマンを抽出しておけば、ピーマン分類法で25袋作ることができる確率は0.95以上となる。
$\boxed{\boxed{\ \ セ\ \ }}$~$\boxed{\boxed{\ \ タ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪k ①2k ②3k ③$\frac{50+k}{2}$
④$\frac{25+k}{2}$ ⑤25+k ⑥$\frac{\sqrt{50+k}}{2}$ ⑦$\frac{50+k}{4}$
2023共通テスト過去問
この動画を見る
第3問
以下の問題を解答するにあたっては、必要に応じて43ページの正規分布表を用いてもよい。
(1)ある生産地で生産されるピーマン全体を母集団とし、この母集団におけるピーマン1個の重さ(単位はg)を表す確率変数をXとする。mとσを正の実数とし、Xは正規分布N(m, $\sigma^2$)に従うとする。
(i)この母集団から1個のピーマンを無作為に抽出したとき、重さがm g以上である確率P(X≧m)は
P(X≧m)=P$\left(\frac{X-m}{\sigma}\geqq \boxed{\ \ ア\ \ }\right)$=$\frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }}$
である。
(ii)母集団から無作為に抽出された大きさnの標本$X_1$, $X_2$, ..., $X_n$の標本平均を$\bar{X}$とする。$\bar{X}$の平均(期待値)と標準偏差はそれぞれ
E($\bar{X}$)=$\boxed{\boxed{\ \ エ\ \ }}$, σ($\bar{X}$)=$\boxed{\boxed{\ \ オ\ \ }}$
となる。
n=400, 標本平均が30.0g, 標本の標準偏差が3.6gのとき、mの信頼度90%の信頼区間を次の方針で求めよう。
方針:Zを標準正規分布N(0,1)に従う確率変数として、P($-z_0 \leqq Z \leqq z_0$)=0.901 となる$z_0$を正規分布表から求める。この$z_0$を用いるとmの信頼度90.1%の信頼区間が求められるが、これを信頼度90%の信頼区間とみなして考える。
方針において、$z_0$=$\boxed{\ \ カ\ \ }$.$\boxed{\ \ キク\ \ }$である。
一般に、標本の大きさnが大きいときには、母標準偏差の代わりに、標本の標準偏差を用いてよいことが知られている。n=400は十分に大きいので、方針に基づくと、mの信頼度90%の信頼区間は$\boxed{\boxed{\ \ ケ\ \ }}$となる。
$\boxed{\boxed{\ \ エ\ \ }}, \boxed{\boxed{\ \ オ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪σ ①$\sigma^2$ ②$\frac{\sigma}{\sqrt n}$ ③$\frac{\sigma^2}{n}$
④m ⑤2m ⑥$m^2$ ⑦$\sqrt m$
⑧$\frac{\sigma}{n}$ ⑨$n\sigma $ⓐ$nm$ ⓑ$\frac{m}{n}$
$\boxed{\boxed{\ \ ケ\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪28.6≦m≦31.4 ①28.7≦m≦31.3 ②28.9≦m≦31.1
③29.6≦m≦30.4 ④29.7≦m≦30.3 ⑤29.9≦m≦30.1
(2)(1)の確率変数Xにおいて、m=30.0, σ=3.6とした母集団から無作為にピーマンを1個ずつ抽出し、ピーマン2個を1組にしたものを袋に入れていく。このようにしてピーマン2個を1組にしたものを25袋作る。その際、1袋ずつの重さの分数を小さくするために、次のピーマン分類法を考える。
ピーマン分類法:無作為に抽出したいくつかのピーマンについて、重さが30.0g以下のときをSサイズ、30.0gを超えるときはLサイズと分類する。そして、分類されたピーマンからSサイズとLサイズのピーマンを一つずつ選び、ピーマン2個を1組とした袋を作る。
(i)ピーマンを無作為に50個抽出した時、ピーマン分類法で25袋作ることができる確率$p_0$を考えよう。無作為に1個抽出したピーマンがSサイズである確率は$\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。ピーマンを無作為に50個抽出したときのSサイズのピーマンの個数を表す確率変数を$U_0$とすると、$U_0$は二項分布$B\left(50, \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)$に従うので
$p_0$=${}_{50}C_{\boxed{シス}}×\left(\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)^{\boxed{シス}}×\left(1-\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)^{50-\boxed{シス}}$
となる。
$p_0$を計算すると、$p_0$=0.1122...となることから、ピーマンを無作為に50個抽出したとき、25袋作ることができる確率は0.11程度とわかる。
(ii)ピーマン分類法で25袋作ることができる確率が0.95以上となるようなピーマンの個数を考えよう。
kを自然数とし、ピーマンを無作為に(50+k)個抽出したとき、Sサイズのピーマンの個数を表す確率変数を$U_k$とすると、$U_k$は二項分布$B\left(50+k, \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)$に従う。
(50+k)は十分に大きいので、$U_k$は近似的に正規分布$N\left(\boxed{\boxed{\ \ セ\ \ }}, \boxed{\boxed{\ \ ソ\ \ }}\right)$に従い、$Y=\frac{U_k-\boxed{\boxed{\ \ セ\ \ }}}{\sqrt{\boxed{\boxed{\ \ ソ\ \ }}}}$とすると、Yは近似的に標準正規分布N(0,1)に従う。
よって、ピーマン分類法で、25袋作ることができる確率を$p_k$とすると
$p_k$=$P(25 \leqq U_k \leqq 25+k)$=$P\left(-\frac{\boxed{\boxed{\ \ タ\ \ }}}{\sqrt{50+k}} \leqq Y \leqq \frac{\boxed{\boxed{\ \ タ\ \ }}}{\sqrt{50+k}}\right)$
となる。
$\boxed{\boxed{\ \ タ\ \ }}$=a, $\sqrt{50+k}$=$\beta$とおく。
$p_k$≧0.95になるような$\frac{\alpha}{\beta}$について、正規分布表から$\frac{\alpha}{\beta}$≧1.96を満たせばよいことが分かる。ここでは
$\frac{\alpha}{\beta}$≧2 ...①
を満たす自然数kを考えることとする。①の両辺は正であるから、$\alpha^2$≧4$\beta^2$を満たす最小のkを$k_0$とすると、$k_0$=$\boxed{\ \ チツ\ \ }$であることがわかる。ただし、$\boxed{\ \ チツ\ \ }$の計算においては、$\sqrt{51}=7.14$を用いてもよい。
したがって、少なくとも(50+$\boxed{\ \ チツ\ \ }$)個のピーマンを抽出しておけば、ピーマン分類法で25袋作ることができる確率は0.95以上となる。
$\boxed{\boxed{\ \ セ\ \ }}$~$\boxed{\boxed{\ \ タ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪k ①2k ②3k ③$\frac{50+k}{2}$
④$\frac{25+k}{2}$ ⑤25+k ⑥$\frac{\sqrt{50+k}}{2}$ ⑦$\frac{50+k}{4}$
2023共通テスト過去問
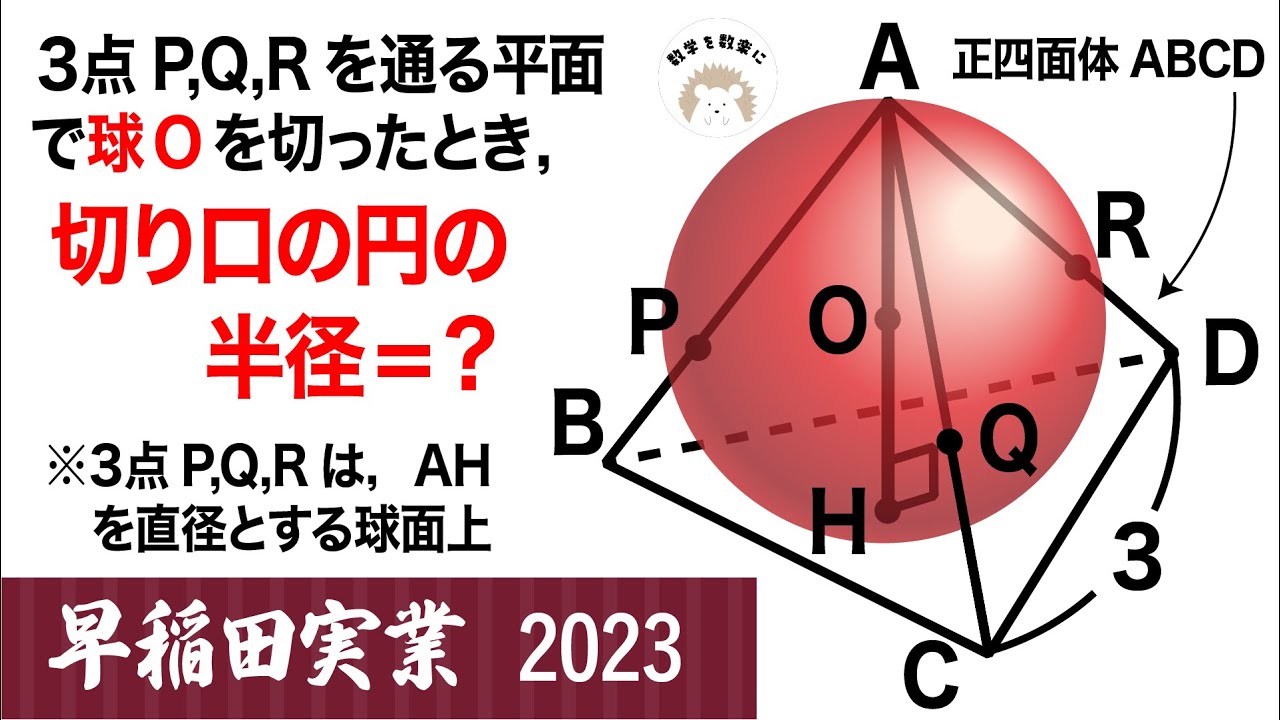
2023高校入試解説40問目 球の切り口 早稲田実業(改)
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
3点P,Q,Rを通る平面で球Oを切ったとき、切り口の円の半径=?
*3点P,Q,Rは、AHを直径とする球面上
*図は動画内参照
2023早稲田実業学校
この動画を見る
3点P,Q,Rを通る平面で球Oを切ったとき、切り口の円の半径=?
*3点P,Q,Rは、AHを直径とする球面上
*図は動画内参照
2023早稲田実業学校
大学入試問題#451「このタイプ、たまに出題される」 お茶の水女子大学1997 #不等式の応用

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#お茶の水女子大学
指導講師:
ますただ
問題文全文(内容文):
任意の正の数$x,y$に対して
$(x+y)^4 \leqq c^3(x^4+y^4)$が成り立つような$c$の値の範囲を求めよ。
出典:1997年お茶の水女子大学 入試問題
この動画を見る
任意の正の数$x,y$に対して
$(x+y)^4 \leqq c^3(x^4+y^4)$が成り立つような$c$の値の範囲を求めよ。
出典:1997年お茶の水女子大学 入試問題
昭和大(医学部)複素数の計算

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#昭和大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ Z=\cos\dfrac{2}{5}\pi+i\sin\dfrac{2}{5}\pi,w=Z+Z^3$とするとき,
①$w+\bar{w}$
②$w・\bar{w}$
の値を求めよ.
昭和大(医)過去問
この動画を見る
$ Z=\cos\dfrac{2}{5}\pi+i\sin\dfrac{2}{5}\pi,w=Z+Z^3$とするとき,
①$w+\bar{w}$
②$w・\bar{w}$
の値を求めよ.
昭和大(医)過去問
2023高校入試解説39問目 整数問題 早稲田実業

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
a,bは連続しない正の整数。
$(a-b)(a^2+b^2)=2023$を満たす
a,bの値=?
2023早稲田実業学校
この動画を見る
a,bは連続しない正の整数。
$(a-b)(a^2+b^2)=2023$を満たす
a,bの値=?
2023早稲田実業学校
2023高校入試解説38問目 中央値の値の範囲 早稲田実業

単元:
#数学(中学生)#数Ⅰ#データの分析#データの分析#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
29,10,23,16,34,30,12,a
中央値=26のときaの取り得る値の範囲は?
2023早稲田実業学校
この動画を見る
29,10,23,16,34,30,12,a
中央値=26のときaの取り得る値の範囲は?
2023早稲田実業学校
【一橋大学】合格勉強法!傾向と対策、おすすめ参考書・問題集と勉強法。

【2分でOK!まずはここから!】統計:明治学院高等学校~全国入試問題解法

単元:
#数学(中学生)#確率分布と統計的な推測#統計的な推測#高校入試過去問(数学)#数B
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の6つのデータの平均値は60であり,$ x:y=1:2 $である.
$ 75, 80, 60, x, 40, y$
このときの中央値を求めよ.
明治学院高校過去問
この動画を見る
次の6つのデータの平均値は60であり,$ x:y=1:2 $である.
$ 75, 80, 60, x, 40, y$
このときの中央値を求めよ.
明治学院高校過去問
2023高校入試解説36問目 正八角形の外接円の面積=❓ 中大杉並

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
正八角形の面積=?
円の面積=?
*図は動画内参照
2023中央大学杉並高等学校(改)
この動画を見る
正八角形の面積=?
円の面積=?
*図は動画内参照
2023中央大学杉並高等学校(改)
福田の1.5倍速演習〜合格する重要問題077〜東京大学2018年度理系第3問〜ベクトル方程式の表す点の存在範囲と面積

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#微分法と積分法#ベクトルと平面図形、ベクトル方程式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#面積、体積#東京大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
第3問
放物線y=$x^2$のうち-1≦x≦1を満たす部分をCとする。
座標平面上の原点Oと点A(1,0)を考える。k>0を実数とする。点PがC上を動き、点Qが線分OA上を動くとき
$\overrightarrow{OR}$=$\frac{1}{k}\overrightarrow{OP}$+$k\overrightarrow{OQ}$
を満たす点Rが動く領域の面積をS(k)とする。
S(k)および$\displaystyle\lim_{k \to +0}S(k)$, $\displaystyle\lim_{k \to \infty}S(k)$を求めよ。
2018東京大学理系過去問
この動画を見る
第3問
放物線y=$x^2$のうち-1≦x≦1を満たす部分をCとする。
座標平面上の原点Oと点A(1,0)を考える。k>0を実数とする。点PがC上を動き、点Qが線分OA上を動くとき
$\overrightarrow{OR}$=$\frac{1}{k}\overrightarrow{OP}$+$k\overrightarrow{OQ}$
を満たす点Rが動く領域の面積をS(k)とする。
S(k)および$\displaystyle\lim_{k \to +0}S(k)$, $\displaystyle\lim_{k \to \infty}S(k)$を求めよ。
2018東京大学理系過去問
2023高校入試解説34問目 知らないと損する2次方程式の偶数バージョン 中大杉並

単元:
#数学(中学生)#数Ⅰ#2次関数#2次方程式と2次不等式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-6x+4 = 0 $と$y^2 -14y +44 = 0$の解を適当に組み合わせてx-yの値を計算する。その値が有理数になるときx-yの値は?
2023中央大学杉並高等学校
この動画を見る
$x^2-6x+4 = 0 $と$y^2 -14y +44 = 0$の解を適当に組み合わせてx-yの値を計算する。その値が有理数になるときx-yの値は?
2023中央大学杉並高等学校
大学入試問題#450「計算の正確性のみを問う問題」 横浜国立大学(2006) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\pi} x^2\sin^3x\ dx$
出典:2006年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi} x^2\sin^3x\ dx$
出典:2006年横浜国立大学 入試問題
藤田医科大学 普通にやれば出るけどね

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\left(-\frac{\sqrt3-1-(\sqrt{3}+1)i}{1+\sqrt{3}i}\right)^5$
これを求めよ.
藤田医科大過去問
この動画を見る
$\left(-\frac{\sqrt3-1-(\sqrt{3}+1)i}{1+\sqrt{3}i}\right)^5$
これを求めよ.
藤田医科大過去問
2023高校入試解説32問目 3辺の長さがわかれば面積求まる 桃山学院

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABC=?
*図は動画内参照
2023桃山学院高等学校
この動画を見る
△ABC=?
*図は動画内参照
2023桃山学院高等学校
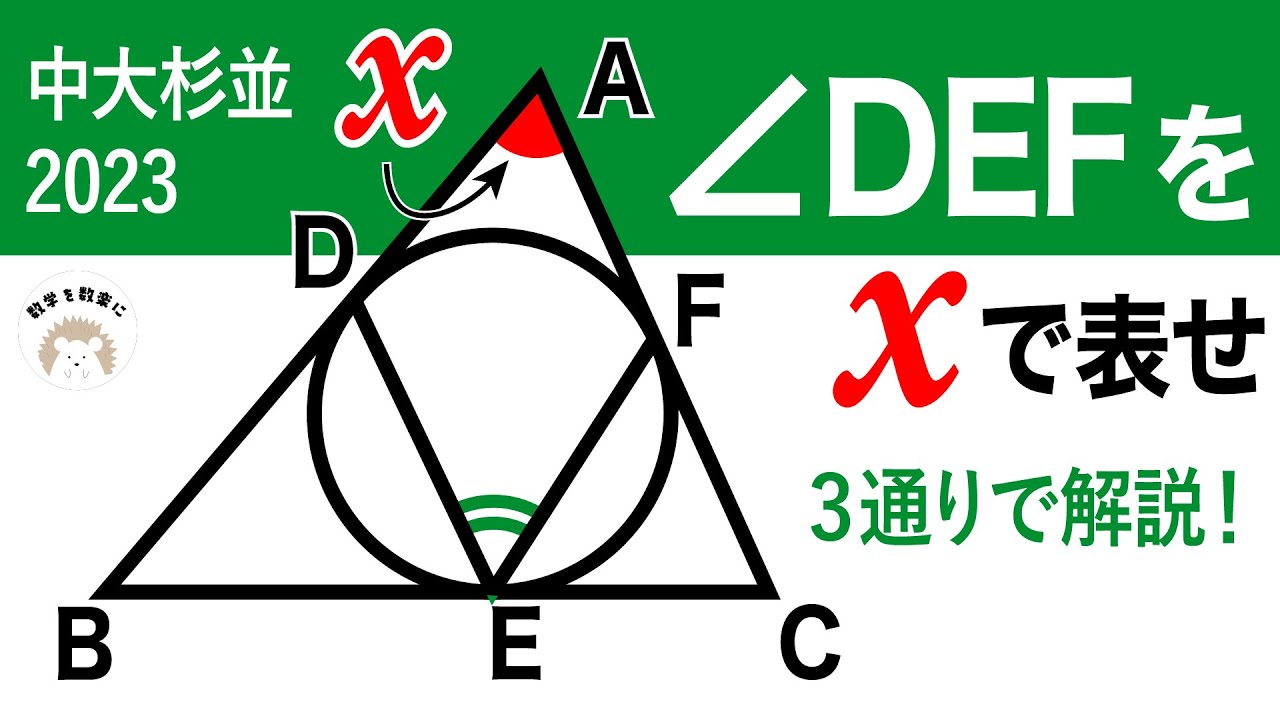
2023高校入試解説35問目 円と角度 中大杉並
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle DEF$をxで表せ
*図は動画内参照
2023中央大学杉並高等学校
この動画を見る
$\angle DEF$をxで表せ
*図は動画内参照
2023中央大学杉並高等学校
2023高校入試解説31問目 ルートが外れる問題 桃山学院

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{\frac{2023}{n}}$が自然数となるような自然数nをすべて求めよ。
2023桃山学院高等学校
この動画を見る
$\sqrt{\frac{2023}{n}}$が自然数となるような自然数nをすべて求めよ。
2023桃山学院高等学校
【数学雑学】無限に続く円周率。その羅列した数字の中には。。。 #shorts

単元:
#算数(中学受験)#その他#その他#その他#その他#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
円周率の中にある数学の不思議を解説していきます。
この動画を見る
円周率の中にある数学の不思議を解説していきます。
福田の1.5倍速演習〜合格する重要問題076〜東京大学2018年度理系第2問〜数列の項の大小とユークリッドの互除法

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
第2問
数列$a_1$, $a_2$, $\cdots$を
$a_n$=$\displaystyle\frac{{}_{2n+1}C_n}{n!}$ ($n$=1,2,...)
で定める。
(1)n≧2とする。$\frac{a_n}{a_{n-1}}$を既約分数$\frac{q_n}{p_n}$として表したときの分母$p_n$≧1と分子$q_n$を求めよ。
(2)$a_n$が整数となるn≧1をすべて求めよ。
2018東京大学理系過去問
この動画を見る
第2問
数列$a_1$, $a_2$, $\cdots$を
$a_n$=$\displaystyle\frac{{}_{2n+1}C_n}{n!}$ ($n$=1,2,...)
で定める。
(1)n≧2とする。$\frac{a_n}{a_{n-1}}$を既約分数$\frac{q_n}{p_n}$として表したときの分母$p_n$≧1と分子$q_n$を求めよ。
(2)$a_n$が整数となるn≧1をすべて求めよ。
2018東京大学理系過去問
2023高校入試解説29問目 整数問題その1 早稲田本庄

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$h(m,n) = \frac{1}{2}(m+n)(m+n-1)-m+1$と定める。(m,nは正の整数)
$h(3m,3m+4) = 1987$を満たすmをすべて求めよ。
2023早稲田大学 本庄高等学院
この動画を見る
$h(m,n) = \frac{1}{2}(m+n)(m+n-1)-m+1$と定める。(m,nは正の整数)
$h(3m,3m+4) = 1987$を満たすmをすべて求めよ。
2023早稲田大学 本庄高等学院
大学入試問題#449「やることは決まっているが、計算力のみが必要」 東京理科大学(2013) #区分求積法

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \sqrt[ n ]{ \displaystyle \frac{{}_{ 8n } P_{ 4n }}{{}_{ 6n } P_{ 4n }} }$
出典:2013年東京理科大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \sqrt[ n ]{ \displaystyle \frac{{}_{ 8n } P_{ 4n }}{{}_{ 6n } P_{ 4n }} }$
出典:2013年東京理科大学 入試問題
指数・対数連立不等式 京都府立大

単元:
#2次関数#2次方程式と2次不等式#2次関数とグラフ#指数関数と対数関数#指数関数#対数関数
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a>0,a \neq 1$とする.
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^{2x-4}-1<a^{x+1}-a^{x-5} \\
2\log_a(x-2)\geqq \log_a(x-2)+\log_a5
\end{array}
\right.
\end{eqnarray}$
連立不等式を解け.
この動画を見る
$a>0,a \neq 1$とする.
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^{2x-4}-1<a^{x+1}-a^{x-5} \\
2\log_a(x-2)\geqq \log_a(x-2)+\log_a5
\end{array}
\right.
\end{eqnarray}$
連立不等式を解け.
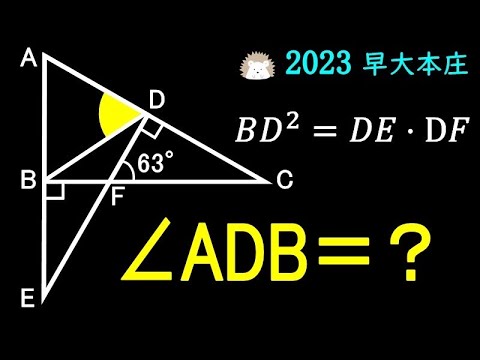
2023高校入試解説28問目 あの条件発動 早稲田本庄
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$BD^2 = DE・DF$
$\angle ADB = ?$
*図は動画内参照
2023早稲田大学 本庄高等学院
この動画を見る
$BD^2 = DE・DF$
$\angle ADB = ?$
*図は動画内参照
2023早稲田大学 本庄高等学院
2023高校入試解説27問目 √が入っている因数分解 早稲田本庄

単元:
#数学(中学生)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$3x^2+y^2+2 \sqrt{3}xy+7 \sqrt3x+7y -18$
2023早稲田大学 本庄高等学院
この動画を見る
因数分解せよ
$3x^2+y^2+2 \sqrt{3}xy+7 \sqrt3x+7y -18$
2023早稲田大学 本庄高等学院
2023高校入試解説26問目 √の計算 早稲田本庄最初の一問

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\{ \frac{\sqrt2 + \sqrt3 -\sqrt5}{\sqrt{18}(\sqrt2 -1)} \}^2 \div
\{ \frac{\sqrt2(\sqrt8 + 2 )}{\sqrt{2}+ \sqrt3 + \sqrt5)} \}^2$
2023早稲田大学 本庄高等学院
この動画を見る
$\{ \frac{\sqrt2 + \sqrt3 -\sqrt5}{\sqrt{18}(\sqrt2 -1)} \}^2 \div
\{ \frac{\sqrt2(\sqrt8 + 2 )}{\sqrt{2}+ \sqrt3 + \sqrt5)} \}^2$
2023早稲田大学 本庄高等学院
【ひらめきで解ける人もいるけれど…】整数:立命館高等学校~全国入試問題解法

単元:
#数学(中学生)#数A#整数の性質#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ ab=9991 $となる2以上の自然数$ a,b $の値をそれぞれ求めなさい.
※$ a\lt b $とします.
立命館高校過去問
この動画を見る
$ ab=9991 $となる2以上の自然数$ a,b $の値をそれぞれ求めなさい.
※$ a\lt b $とします.
立命館高校過去問
福田の1.5倍速演習〜合格する重要問題086〜慶應義塾大学2020年度医学部第1問(1)〜平面と平面のなす角

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)座標空間に3点O(0,0,0), A(1,0,a), B(0,1,b)をとり、O,A,Bによって定められる平面をαとする。ただし、a>0, b>0とする。平面αとxy平面との交線をlとすると、lはOを通り、ベクトル$\overrightarrow{u}$=(1, $\boxed{あ}$,0)に平行な直線である。また平面αとxy平面のなす角をθ(ただし0≦θ≦$\frac{\pi}{2}$)とすると、$\cos\theta$=$\boxed{\ \ い\ \ }$である。
2020慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{1}$ (1)座標空間に3点O(0,0,0), A(1,0,a), B(0,1,b)をとり、O,A,Bによって定められる平面をαとする。ただし、a>0, b>0とする。平面αとxy平面との交線をlとすると、lはOを通り、ベクトル$\overrightarrow{u}$=(1, $\boxed{あ}$,0)に平行な直線である。また平面αとxy平面のなす角をθ(ただし0≦θ≦$\frac{\pi}{2}$)とすると、$\cos\theta$=$\boxed{\ \ い\ \ }$である。
2020慶應義塾大学医学部過去問
大学入試問題#448「深夜24時動画ストック0との闘い!」 藤田医科大学(2023) #曲線の長さ

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq x \leqq \displaystyle \frac{5}{3}$において
曲線$y=2x\sqrt{ x }$の長さを求めよ。
出典:2023年藤田医科大学 入試問題
この動画を見る
$0 \leqq x \leqq \displaystyle \frac{5}{3}$において
曲線$y=2x\sqrt{ x }$の長さを求めよ。
出典:2023年藤田医科大学 入試問題
愛があれば解決する。愛はなくても問題ない

単元:
#数Ⅱ#式と証明#複素数と方程式#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+2\sqrt{3}y=\dfrac{x}{x^2+y^2} \\
2\sqrt{3}x-2y=\dfrac{y}{x^2+y^2}
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+2\sqrt{3}y=\dfrac{x}{x^2+y^2} \\
2\sqrt{3}x-2y=\dfrac{y}{x^2+y^2}
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け.
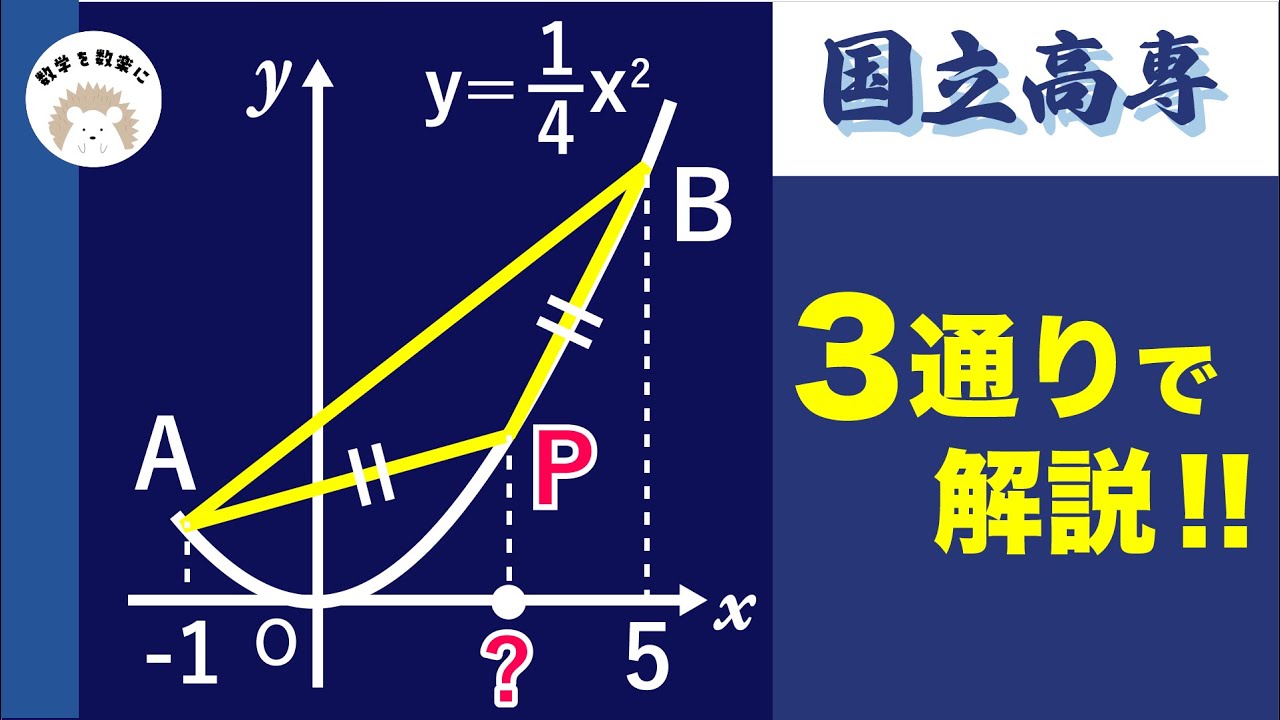
放物線と二等辺三角形 国立高専
単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$y=\frac{1}{4}x^2$
P=?
*図は動画内参照
国立高専
この動画を見る
$y=\frac{1}{4}x^2$
P=?
*図は動画内参照
国立高専
【東北大学】合格勉強法!傾向と対策、おすすめ教材と勉強法。

