 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
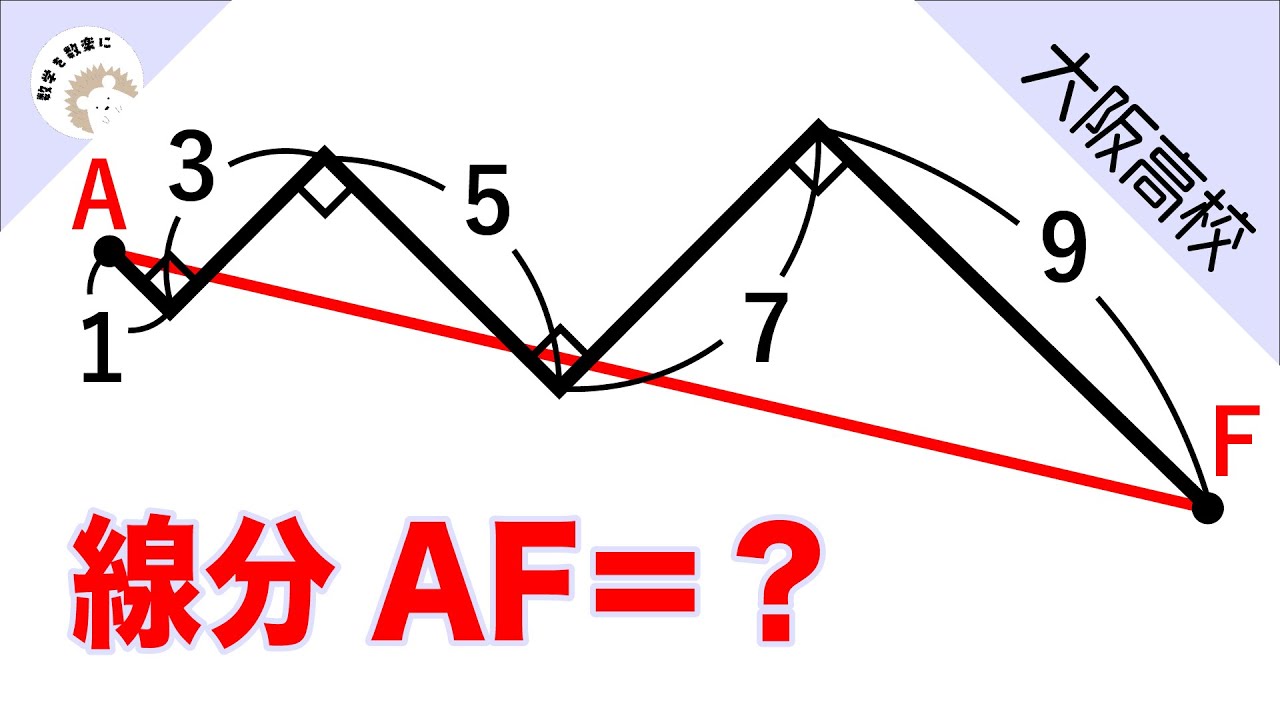
ジグザグ 大阪高校
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
線分AF=?
*図は動画内参照
大阪高等学校
この動画を見る
線分AF=?
*図は動画内参照
大阪高等学校
福田の数学〜東京理科大学2022年理工学部第2問〜位置ベクトルと面積比
単元:
#大学入試過去問(数学)#平面上のベクトル#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
平面上に三角形ABCと点Pがあり、点Pは、ある正の定数tに対して
$3t\overrightarrow{ AP }+t^2\overrightarrow{ BP }+4\overrightarrow{ CP }=\overrightarrow{ 0 }$
を満たすとする。
$\overrightarrow{ b } =\overrightarrow{ AB },\overrightarrow{ c } =\overrightarrow{ AC }$とおく。
(1)$\overrightarrow{ BP }$を、$\overrightarrow{ b }$と$\overrightarrow{ AP }$を用いて表せ。
(2)$\overrightarrow{ AP }=v\ \overrightarrow{ b }+w\ \overrightarrow{ c }$となる実数v,wを、tを用いて表せ。
(3)直線APと直線BCの交点をDとする。
$\overrightarrow{ AD }=x\ \overrightarrow{ b }+y\ \overrightarrow{ c }$となる実数x,yを、tを用いて表せ。
(4)$\frac{S_2}{S_1}$を、tを用いて表せ。
(5)tが正の実数全体を動くとき、$\frac{S_2}{S_1}$が最大となるtの値を求めよ。
2022東京理科大学理工学部過去問
この動画を見る
平面上に三角形ABCと点Pがあり、点Pは、ある正の定数tに対して
$3t\overrightarrow{ AP }+t^2\overrightarrow{ BP }+4\overrightarrow{ CP }=\overrightarrow{ 0 }$
を満たすとする。
$\overrightarrow{ b } =\overrightarrow{ AB },\overrightarrow{ c } =\overrightarrow{ AC }$とおく。
(1)$\overrightarrow{ BP }$を、$\overrightarrow{ b }$と$\overrightarrow{ AP }$を用いて表せ。
(2)$\overrightarrow{ AP }=v\ \overrightarrow{ b }+w\ \overrightarrow{ c }$となる実数v,wを、tを用いて表せ。
(3)直線APと直線BCの交点をDとする。
$\overrightarrow{ AD }=x\ \overrightarrow{ b }+y\ \overrightarrow{ c }$となる実数x,yを、tを用いて表せ。
(4)$\frac{S_2}{S_1}$を、tを用いて表せ。
(5)tが正の実数全体を動くとき、$\frac{S_2}{S_1}$が最大となるtの値を求めよ。
2022東京理科大学理工学部過去問
大学入試問題#367「これは、たぶん一撃で倒せる」 横浜国立大学2012 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{2+\sin\ x}{1+\cos\ x}dx$
出典:2012年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{2+\sin\ x}{1+\cos\ x}dx$
出典:2012年横浜国立大学 入試問題
奈良女子大 三次方程式の解

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#奈良女子大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3+mx^2+nx+1=0$は絶対値が1となる虚数解を持つ.
このとき整数(m,n)をすべて求めよ.
奈良女子大過去問
この動画を見る
$x^3+mx^2+nx+1=0$は絶対値が1となる虚数解を持つ.
このとき整数(m,n)をすべて求めよ.
奈良女子大過去問
福田の数学〜東京理科大学2022年理工学部第1問(3)〜2つの円の位置関係

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(3)座標平面上の3点(2,3),(-5,10),(-2,1)を通る円をC_1とする。この
とき、C_1の中心は$(-\boxed{ナ}, \boxed{ニ})$、半径は$\boxed{ヌ}$である。
$C_1$と点(2,3)で外接し、x軸とも接している円を$C_2$とする。このとき、
$C_2$の中心は$(\frac{\boxed{ネ}}{\boxed{ノ}},\frac{\boxed{ハヒ}}{\boxed{フ}})、半径は\frac{\boxed{ヘホ}}{\boxed{マ}}$である。
2022東京理科大学理工学部過去問
この動画を見る
(3)座標平面上の3点(2,3),(-5,10),(-2,1)を通る円をC_1とする。この
とき、C_1の中心は$(-\boxed{ナ}, \boxed{ニ})$、半径は$\boxed{ヌ}$である。
$C_1$と点(2,3)で外接し、x軸とも接している円を$C_2$とする。このとき、
$C_2$の中心は$(\frac{\boxed{ネ}}{\boxed{ノ}},\frac{\boxed{ハヒ}}{\boxed{フ}})、半径は\frac{\boxed{ヘホ}}{\boxed{マ}}$である。
2022東京理科大学理工学部過去問
数学で80点突破したい人は全員見てください【共通テスト】【勉強法】

大学入試問題#366「これは有名問題」 静岡大学2014 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#静岡大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\cos^3x}{\cos\ x+\sin\ x}dx$
出典:2014年静岡大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\cos^3x}{\cos\ x+\sin\ x}dx$
出典:2014年静岡大学 入試問題
ただの2次方程式⁉️ just a quadratic equation⁉️

福田の数学〜東京理科大学2022年理工学部第1問(2)〜三角方程式

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#円と方程式#加法定理とその応用#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)角θに関する方程式
$\cos 4θ=\cos θ(0\leqq θ\leqq \pi)$
について考える。①を満たすθは小さい方から順に
$θ=0,\frac{\boxed{キ}}{\boxed{ク}}\pi,\frac{\boxed{ケ}}{\boxed{コ}}\pi,\frac{\boxed{サ}}{\boxed{シ}}\pi$
の4つである。一方、θが①を満たすとき、$t=\cos θ$とおくとtは
$\boxed{ス}t^4 - \boxed{セ}t^2+\boxed{ソ}=t$
を満たす。$t=1,\cos \frac{\boxed{ケ}}{\boxed{コ}}\pi$は②の解なので、2次方程式
$\boxed{タ}t^2+\boxed{チ}t-1=0$
は$\cos \frac{\boxed{キ}}{\boxed{ク}}\pi,\cos \frac{\boxed{サ}}{\boxed{シ}}\pi$を解にもつ。これより、
$\cos \frac{\boxed{キ}}{\boxed{ク}}\pi=\frac{\sqrt{\boxed{ツ}}-\boxed{テ}}{\boxed{ト}},\cos \frac{\boxed{サ}}{\boxed{シ}}\pi=-\frac{\sqrt{\boxed{ツ}}+\boxed{テ}}{\boxed{ト}}$であることが分かる。
この動画を見る
(2)角θに関する方程式
$\cos 4θ=\cos θ(0\leqq θ\leqq \pi)$
について考える。①を満たすθは小さい方から順に
$θ=0,\frac{\boxed{キ}}{\boxed{ク}}\pi,\frac{\boxed{ケ}}{\boxed{コ}}\pi,\frac{\boxed{サ}}{\boxed{シ}}\pi$
の4つである。一方、θが①を満たすとき、$t=\cos θ$とおくとtは
$\boxed{ス}t^4 - \boxed{セ}t^2+\boxed{ソ}=t$
を満たす。$t=1,\cos \frac{\boxed{ケ}}{\boxed{コ}}\pi$は②の解なので、2次方程式
$\boxed{タ}t^2+\boxed{チ}t-1=0$
は$\cos \frac{\boxed{キ}}{\boxed{ク}}\pi,\cos \frac{\boxed{サ}}{\boxed{シ}}\pi$を解にもつ。これより、
$\cos \frac{\boxed{キ}}{\boxed{ク}}\pi=\frac{\sqrt{\boxed{ツ}}-\boxed{テ}}{\boxed{ト}},\cos \frac{\boxed{サ}}{\boxed{シ}}\pi=-\frac{\sqrt{\boxed{ツ}}+\boxed{テ}}{\boxed{ト}}$であることが分かる。
大学入試問題#365「さすがに小問」 旭川医科大学(2014) #定積分
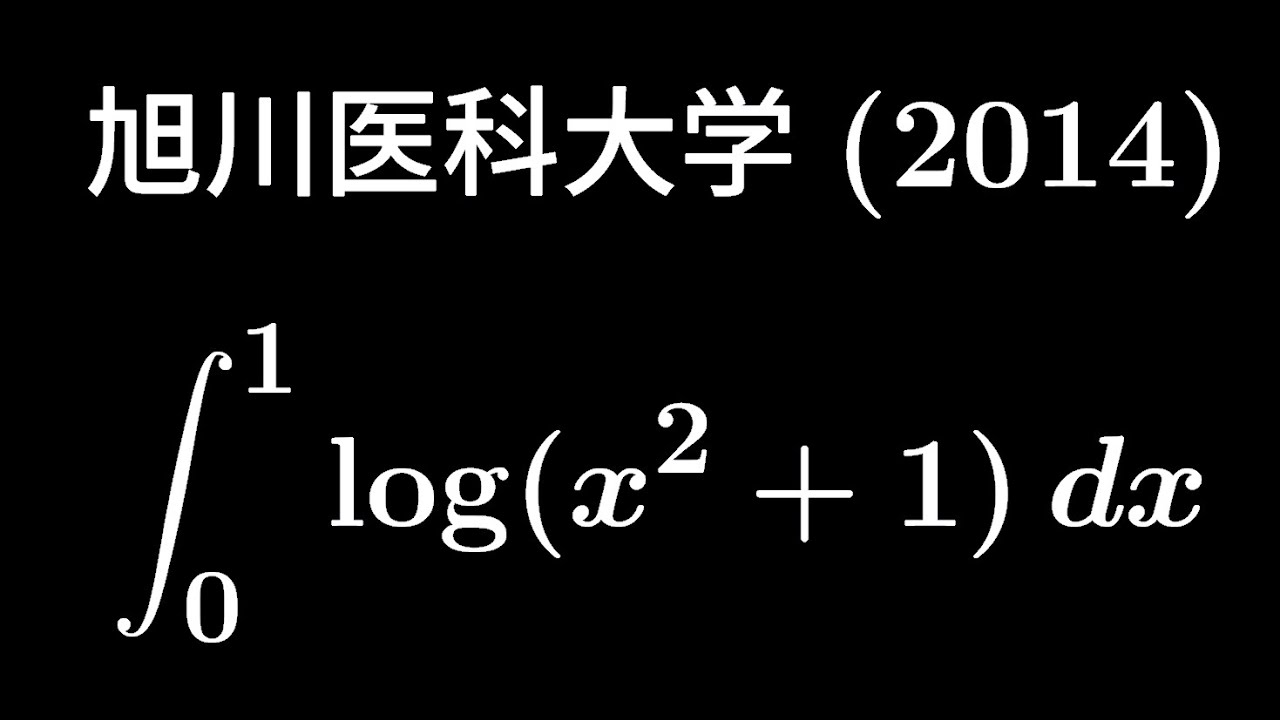
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#旭川医科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}log(x^2+1)dx$
出典:2014年旭川医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}log(x^2+1)dx$
出典:2014年旭川医科大学 入試問題
平方根の方程式

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt{x-4}+\sqrt{x+4}-2\sqrt{x^2-16}=2x-12$
これを解け.
この動画を見る
$ \sqrt{x-4}+\sqrt{x+4}-2\sqrt{x^2-16}=2x-12$
これを解け.
席替えで好きな人と隣になる確率は?

ベクトルの簡単すぎる京大の問題【京都大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$\triangle OAB$において$OA=3,OB=2,\angle AOB=90^{ \circ }$とする。$\triangle OAB$の垂心を$H$とするとき,$\overrightarrow{OH}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
京都大過去問
この動画を見る
$\triangle OAB$において$OA=3,OB=2,\angle AOB=90^{ \circ }$とする。$\triangle OAB$の垂心を$H$とするとき,$\overrightarrow{OH}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
京都大過去問
【条件から導き出されることは…!】整数:灘高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#整数の性質#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x$を$x-n+a$と表す.
$ x^2+a^2=8$のとき,$n=\Box,x=\Box$である.
灘高校過去問
この動画を見る
$x$を$x-n+a$と表す.
$ x^2+a^2=8$のとき,$n=\Box,x=\Box$である.
灘高校過去問
福田の数学〜東京理科大学2022年理工学部第1問(1)〜解と係数の関係と3次関数の最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#指数関数と対数関数#解と判別式・解と係数の関係#指数関数#接線と増減表・最大値・最小値#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(1)mを実数とする。xについての2次方程式$x^2-(m+3)x+m^2-9=0$の
二つの解を$α,β$とする。$α,β$が実数であるための必要十分条件は$- \boxed{ア} \leqq m \leqq \boxed{イ}$である。
mが$- \boxed{ア} \leqq m \leqq \boxed{イ}$の範囲を動くときの
$α^3+β^3$の最小値は$\boxed{ウ}$、最大値は$\boxed{エオカ}$である。
この動画を見る
(1)mを実数とする。xについての2次方程式$x^2-(m+3)x+m^2-9=0$の
二つの解を$α,β$とする。$α,β$が実数であるための必要十分条件は$- \boxed{ア} \leqq m \leqq \boxed{イ}$である。
mが$- \boxed{ア} \leqq m \leqq \boxed{イ}$の範囲を動くときの
$α^3+β^3$の最小値は$\boxed{ウ}$、最大値は$\boxed{エオカ}$である。
大学入試問題#364「計算が大変でした」 岩手大学2014 #不定積分
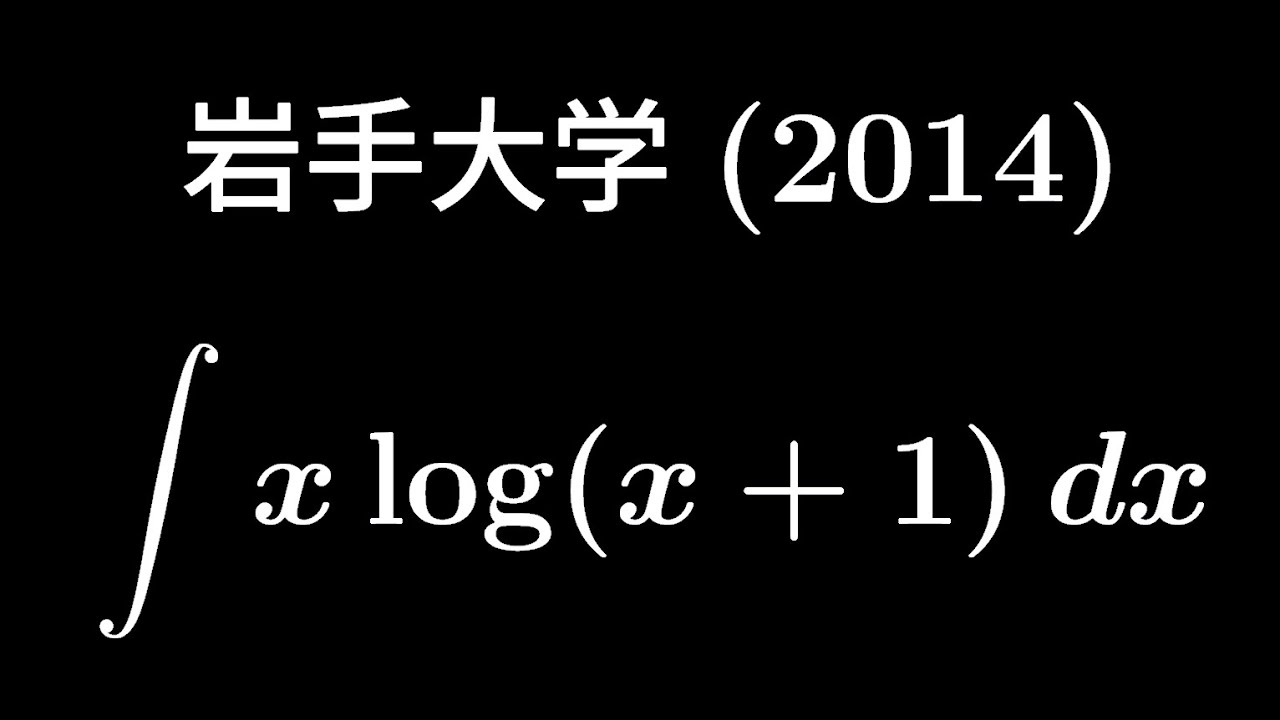
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int x\ log(x+1)dx$
出典:2014年岩手大学 入試問題
この動画を見る
$\displaystyle \int x\ log(x+1)dx$
出典:2014年岩手大学 入試問題
ナイスな整数問題

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a^2+b^2-a^2b^2+10ab-16$が素数となるような整数(a.b)をすべて求めよ.
この動画を見る
$ a^2+b^2-a^2b^2+10ab-16$が素数となるような整数(a.b)をすべて求めよ.
角の和 茨城県 動画内に誘導あり 茨城県
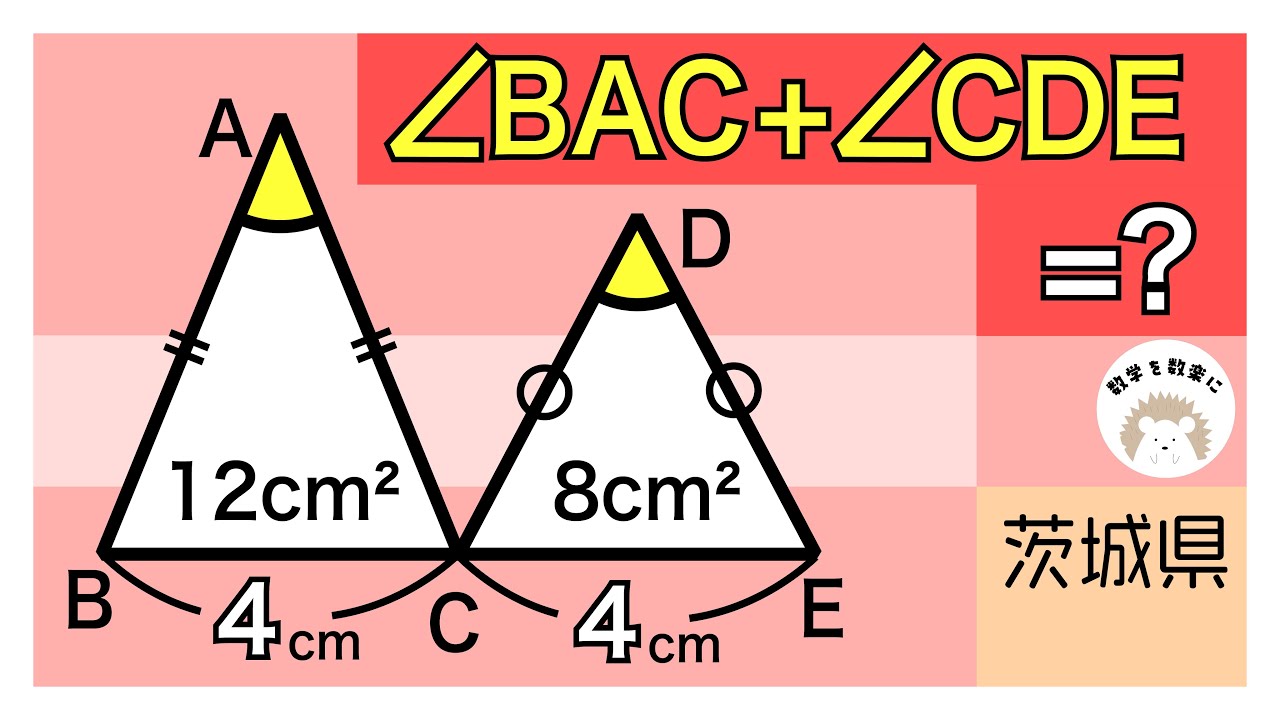
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle BAC + \angle CDE$=?
*図は動画内参照
茨城県
この動画を見る
$\angle BAC + \angle CDE$=?
*図は動画内参照
茨城県
福田の数学〜中央大学2022年経済学部第3問〜下一桁が一致する整数と下二桁が一致する整数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正の整数xについて、以下の設問に答えよ。
なお、ここでxの下一桁とはxを10で割った余りであり、
xの下二桁とはxを100で割った余りであるとする。
(1)$10 \leqq x \leqq 40$の範囲で、xn下一桁と$x^2$の下一桁が一致するようなxの個数を求めよ。
(2)$10 \leqq x \leqq 99$の範囲で、$x^2$の下一桁と$x^4$の下一桁が一致するxをすべて足した数を
Yとする。整数Yの下一桁を求めよ。
(3)$10 \leqq x \leqq 99$の範囲で、$x^2$の下二桁がxと等しいものをすべて求めよ。
この動画を見る
正の整数xについて、以下の設問に答えよ。
なお、ここでxの下一桁とはxを10で割った余りであり、
xの下二桁とはxを100で割った余りであるとする。
(1)$10 \leqq x \leqq 40$の範囲で、xn下一桁と$x^2$の下一桁が一致するようなxの個数を求めよ。
(2)$10 \leqq x \leqq 99$の範囲で、$x^2$の下一桁と$x^4$の下一桁が一致するxをすべて足した数を
Yとする。整数Yの下一桁を求めよ。
(3)$10 \leqq x \leqq 99$の範囲で、$x^2$の下二桁がxと等しいものをすべて求めよ。
大学入試問題#363「置換からの部分積分?」 横浜国立大学(2014) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\sqrt{ \frac{\pi}{2} }}x^3\cos(x^2)dx$
出典:2014年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\sqrt{ \frac{\pi}{2} }}x^3\cos(x^2)dx$
出典:2014年横浜国立大学 入試問題
どっちがでかい?かなりの大差じゃね?

円と台形
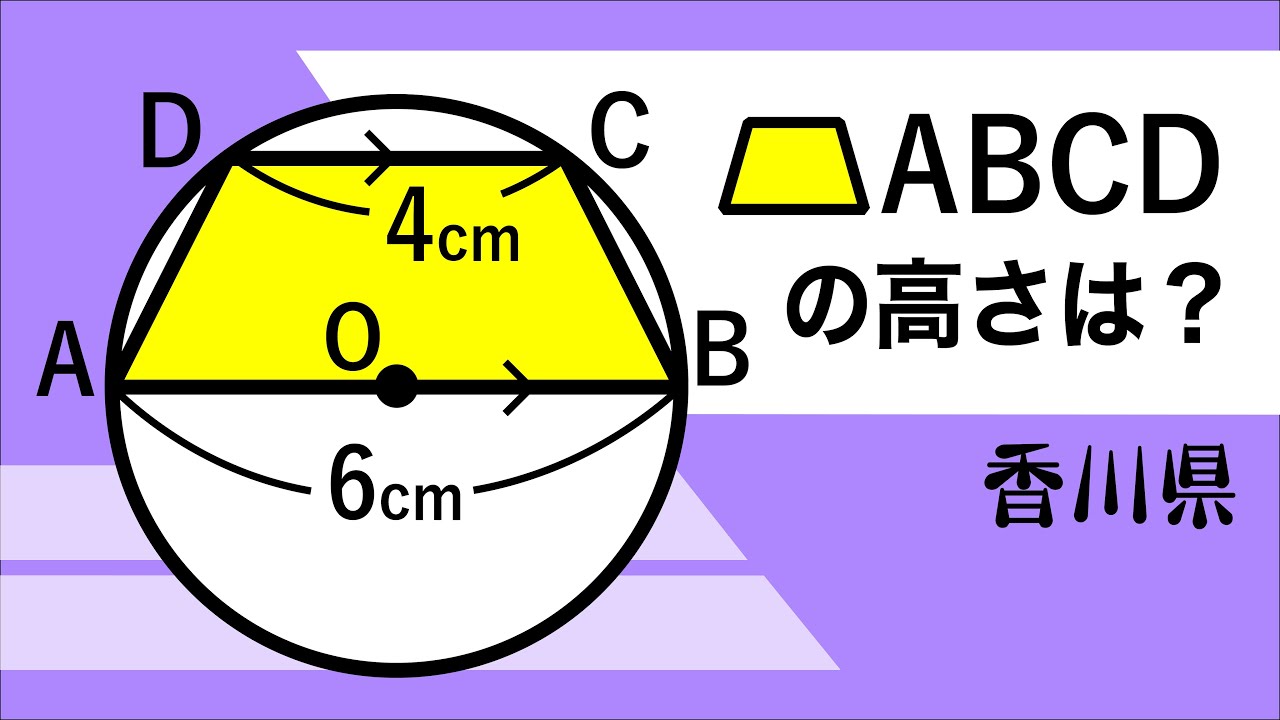
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
台形ABCDの高さは?
*図は動画内参照
香川県
この動画を見る
台形ABCDの高さは?
*図は動画内参照
香川県
福田の数学〜中央大学2022年経済学部第2問〜ベクトルの内積と三角形の面積

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\triangle ABC$において、ベクトルの内積が
$\overrightarrow{ CA }・\overrightarrow{ AB }=-2,\ \ \overrightarrow{ AB }・\overrightarrow{ BC }=-4,\ \ \ \overrightarrow{ BC }・\overrightarrow{ CA }=-5$
であるとき、以下の設問に答えよ。
(1)3辺AB,BC,CAの長さを求めよ。
(2)\triangle ABCの面積を求めよ。
2022中央大学経済学部過去問
この動画を見る
$\triangle ABC$において、ベクトルの内積が
$\overrightarrow{ CA }・\overrightarrow{ AB }=-2,\ \ \overrightarrow{ AB }・\overrightarrow{ BC }=-4,\ \ \ \overrightarrow{ BC }・\overrightarrow{ CA }=-5$
であるとき、以下の設問に答えよ。
(1)3辺AB,BC,CAの長さを求めよ。
(2)\triangle ABCの面積を求めよ。
2022中央大学経済学部過去問
大学入試問題#362「頻出問題ではないでしょうか?」 福島大学 改 2014 #定積分 #極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ a \to \infty } \displaystyle \int_{-a}^{a}\displaystyle \frac{dx}{(e^x+e^{-x})^2}$
出典:2014年福島大学 入試問題
この動画を見る
$\displaystyle \lim_{ a \to \infty } \displaystyle \int_{-a}^{a}\displaystyle \frac{dx}{(e^x+e^{-x})^2}$
出典:2014年福島大学 入試問題
整数問題(類・東工大)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
nを自然数とする.
$a_n=19^n+(-1)^{n-1}・3^{6n-5}$
すべての$a_n$を割り切る素数をすべて求めよ.
東工大(類)過去問
この動画を見る
nを自然数とする.
$a_n=19^n+(-1)^{n-1}・3^{6n-5}$
すべての$a_n$を割り切る素数をすべて求めよ.
東工大(類)過去問
約数4個の数 渋谷教育学園幕張

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
自然数nはちょうど4つの約数を持ちそのうち2つは素数である。
これら4つの約数の和が24であるような自然数nをすべて求めよ。
渋谷教育学園幕張高等学校
この動画を見る
自然数nはちょうど4つの約数を持ちそのうち2つは素数である。
これら4つの約数の和が24であるような自然数nをすべて求めよ。
渋谷教育学園幕張高等学校
福田の数学〜中央大学2022年経済学部第1問(6)〜放物線と直線で囲まれた面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(6)放物線$y=x^2-4x+3$と直線$y=2x-2$で囲まれた図形の面積を求めよ。
2022中央大学経済学部過去問
この動画を見る
(6)放物線$y=x^2-4x+3$と直線$y=2x-2$で囲まれた図形の面積を求めよ。
2022中央大学経済学部過去問
大学入試問題#361「作成時間がありませんでした。」 横浜国立大学(2014) #定積分
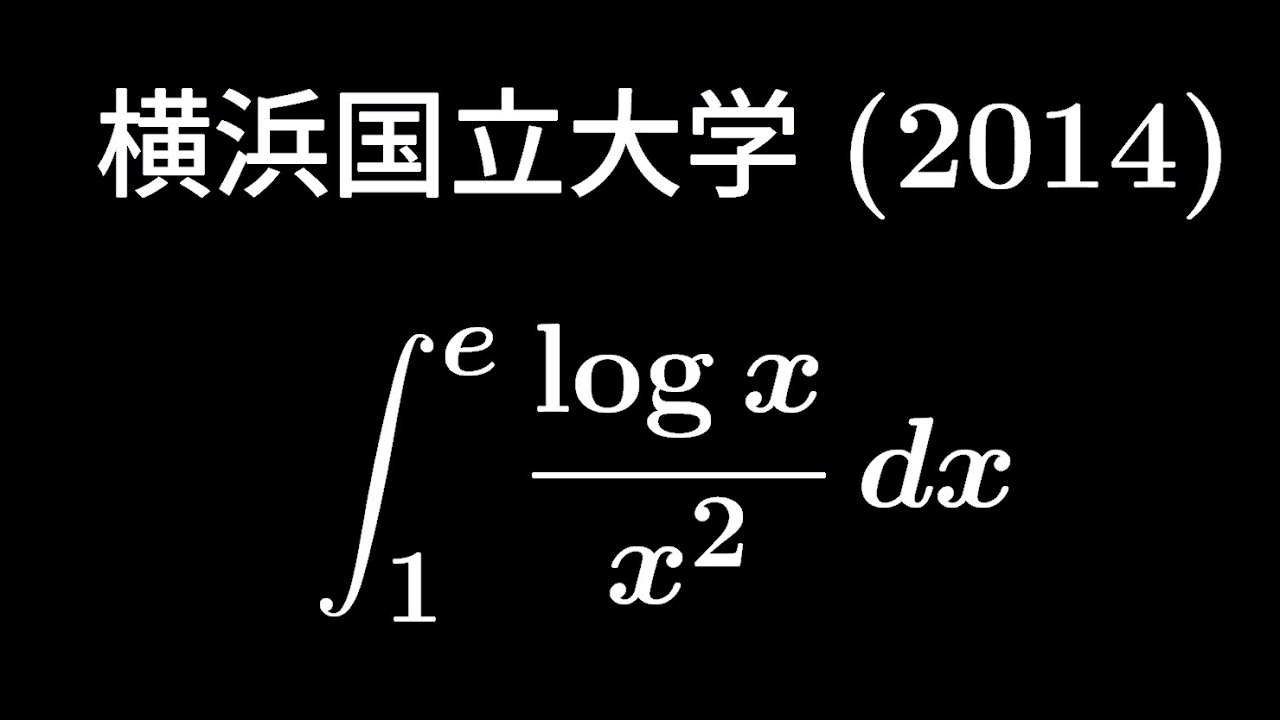
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e}\displaystyle \frac{log\ x}{x^2}dx$
出典:2014年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e}\displaystyle \frac{log\ x}{x^2}dx$
出典:2014年横浜国立大学 入試問題
指数方程式

n進法の理解が深まる問題!2通りで解説!【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
10進法で表された数6.75を二進法で表せ。また,この数と2進法で表された数101.0101の積として与えられる数を2進法および4進法で表せ。
この動画を見る
10進法で表された数6.75を二進法で表せ。また,この数と2進法で表された数101.0101の積として与えられる数を2進法および4進法で表せ。
