 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
指数方程式 解はアレだけじゃないよ

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$5^x・16^{\frac{x-1}{x}}=100$
この動画を見る
これを解け.
$5^x・16^{\frac{x-1}{x}}=100$
大学入試問題#101 東海大学医学部(2017) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東海大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}x^3(1-x^2)^8dx$を計算せよ。
出典:2017年東海大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}x^3(1-x^2)^8dx$を計算せよ。
出典:2017年東海大学医学部 入試問題
2022近畿大(医)場合の数

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$人を区別のある 部屋に入れます。
0人部屋はダメ
(1)2部屋 (2)3部屋 (3)4部屋
何通りか求めよ。
2022年 近畿大学医学部 過去問
この動画を見る
$n$人を区別のある 部屋に入れます。
0人部屋はダメ
(1)2部屋 (2)3部屋 (3)4部屋
何通りか求めよ。
2022年 近畿大学医学部 過去問
【数学B/平面ベクトル】点Pの存在範囲(2)

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$\triangle OAB$に対して、点$P$が次の条件を満たしながら動くとき、点$P$の存在範囲を図示せよ。
$\overrightarrow{ OP }=s\overrightarrow{ OA }+t\overrightarrow{ OB },$ $2 \leqq s+t \leqq 3,$ $s \geqq 0,$ $t \geqq 0$
この動画を見る
$\triangle OAB$に対して、点$P$が次の条件を満たしながら動くとき、点$P$の存在範囲を図示せよ。
$\overrightarrow{ OP }=s\overrightarrow{ OA }+t\overrightarrow{ OB },$ $2 \leqq s+t \leqq 3,$ $s \geqq 0,$ $t \geqq 0$
Σ
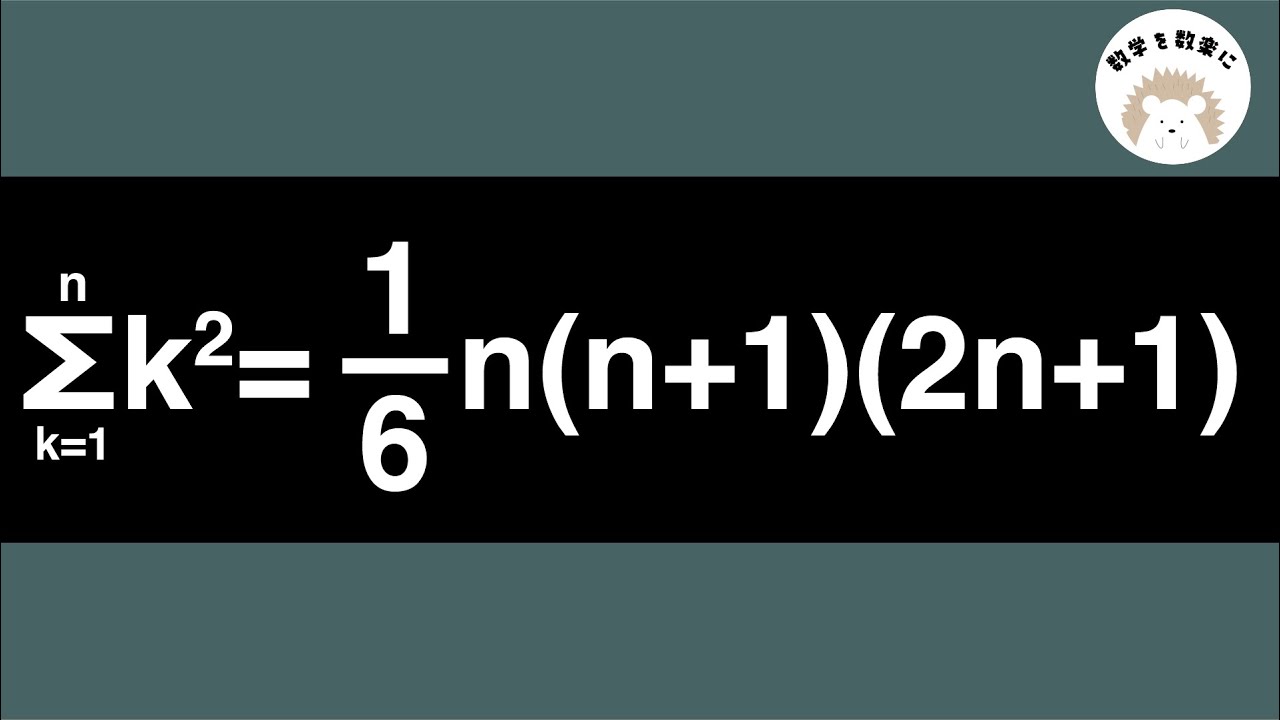
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$\displaystyle \sum_{k=1}^n k^2 = \frac{1}{6}n(n+1)(2n+1)$
この動画を見る
$\displaystyle \sum_{k=1}^n k^2 = \frac{1}{6}n(n+1)(2n+1)$
大学入試問題#100 東京大学(1954) 軌跡・領域

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
点($x,y$)が原点を中心とする半径1の円の内部を動くとき
点($x+y,xy$)の動く範囲を図示せよ。
出典:1954年東京大学 入試問題
この動画を見る
点($x,y$)が原点を中心とする半径1の円の内部を動くとき
点($x+y,xy$)の動く範囲を図示せよ。
出典:1954年東京大学 入試問題
2022藤田医科大 出題意図は「瞬殺せよ」なのかな?

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=5,$
$a_{n+1}=3a_n+2$
$\displaystyle \frac{a_{16}-a_{13}}{a_{12}-a_9}$
の値を求めよ。
2022年藤田医科大学 過去問
この動画を見る
$a_1=5,$
$a_{n+1}=3a_n+2$
$\displaystyle \frac{a_{16}-a_{13}}{a_{12}-a_9}$
の値を求めよ。
2022年藤田医科大学 過去問
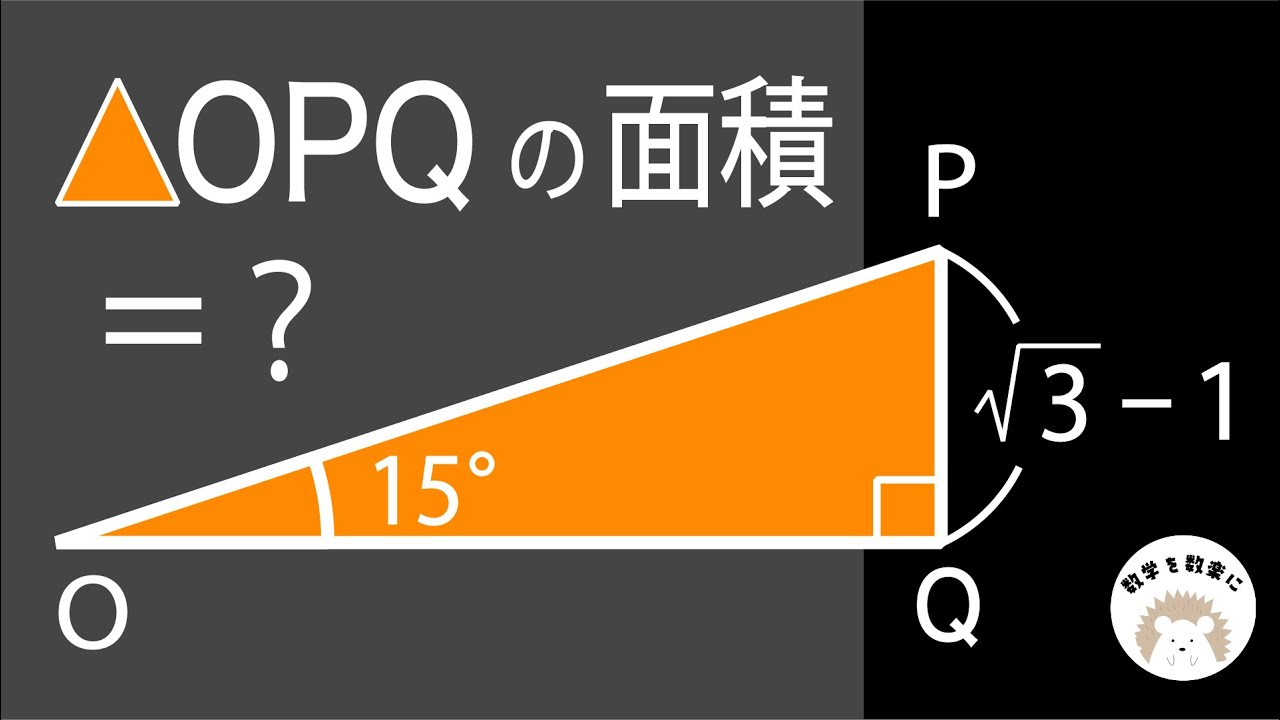
15度75度90度の直角三角形の面積を求める
【数学B/平面ベクトル】点Pの存在範囲(1)

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$\triangle OAB$に対して、点$P$が次の条件を満たしながら動くとき、点$P$の存在範囲を図示せよ。
$\overrightarrow{ OP }=s\overrightarrow{ OA }+t\overrightarrow{ OB },$ $1 \leqq s \leqq 2,$ $0 \leqq t \leqq 1$
この動画を見る
$\triangle OAB$に対して、点$P$が次の条件を満たしながら動くとき、点$P$の存在範囲を図示せよ。
$\overrightarrow{ OP }=s\overrightarrow{ OA }+t\overrightarrow{ OB },$ $1 \leqq s \leqq 2,$ $0 \leqq t \leqq 1$
大学入試問題#99 慶應義塾大学2004 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x^2+y^2 \lt 9$
$x^2 \leqq y^2$をみたす整数の組$x,y$の個数を求めよ。
出典:2004年慶應義塾大学 入試問題
この動画を見る
$x^2+y^2 \lt 9$
$x^2 \leqq y^2$をみたす整数の組$x,y$の個数を求めよ。
出典:2004年慶應義塾大学 入試問題
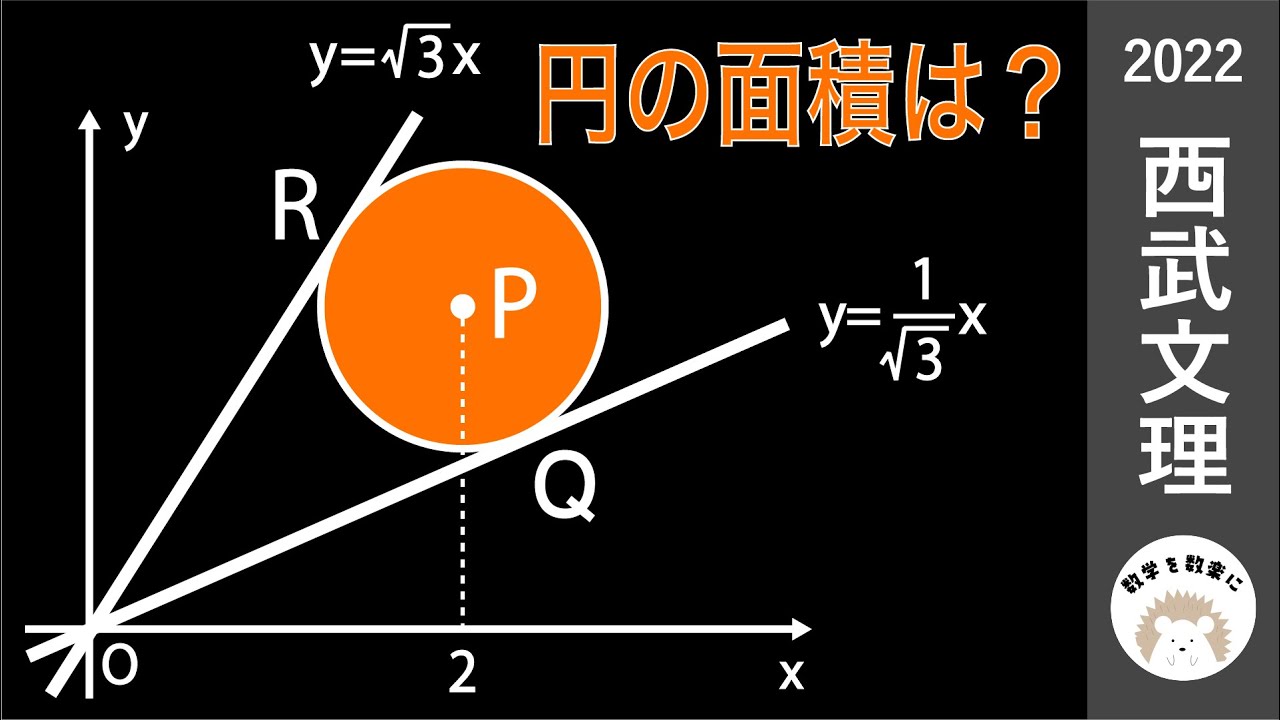
2つの接線に囲まれた円の面積 西武文理 2022入試問題解説 20問目
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円の面積は?
*図は動画内参照
2022西武学園文理高等学校
この動画を見る
円の面積は?
*図は動画内参照
2022西武学園文理高等学校
図形的イメージ
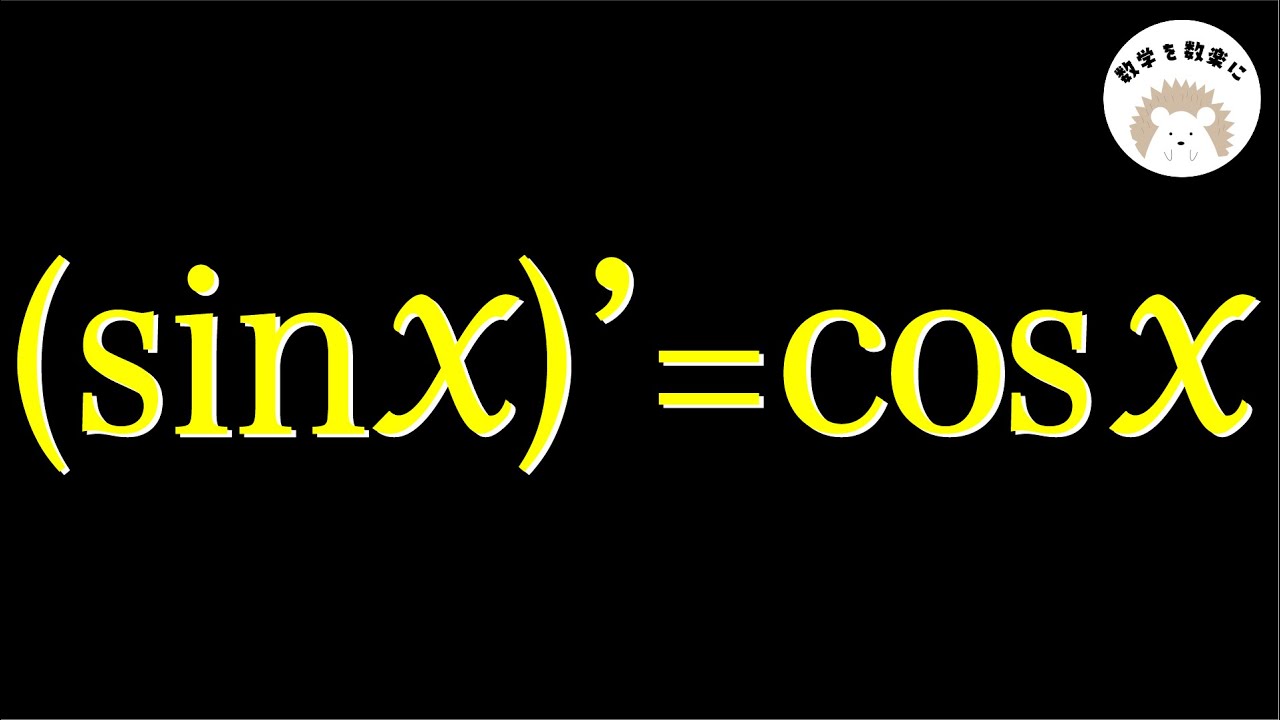
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(sinx)' = cosx
この動画を見る
(sinx)' = cosx
大学入試問題#98 千葉大学医学部(2018) 積分・極限
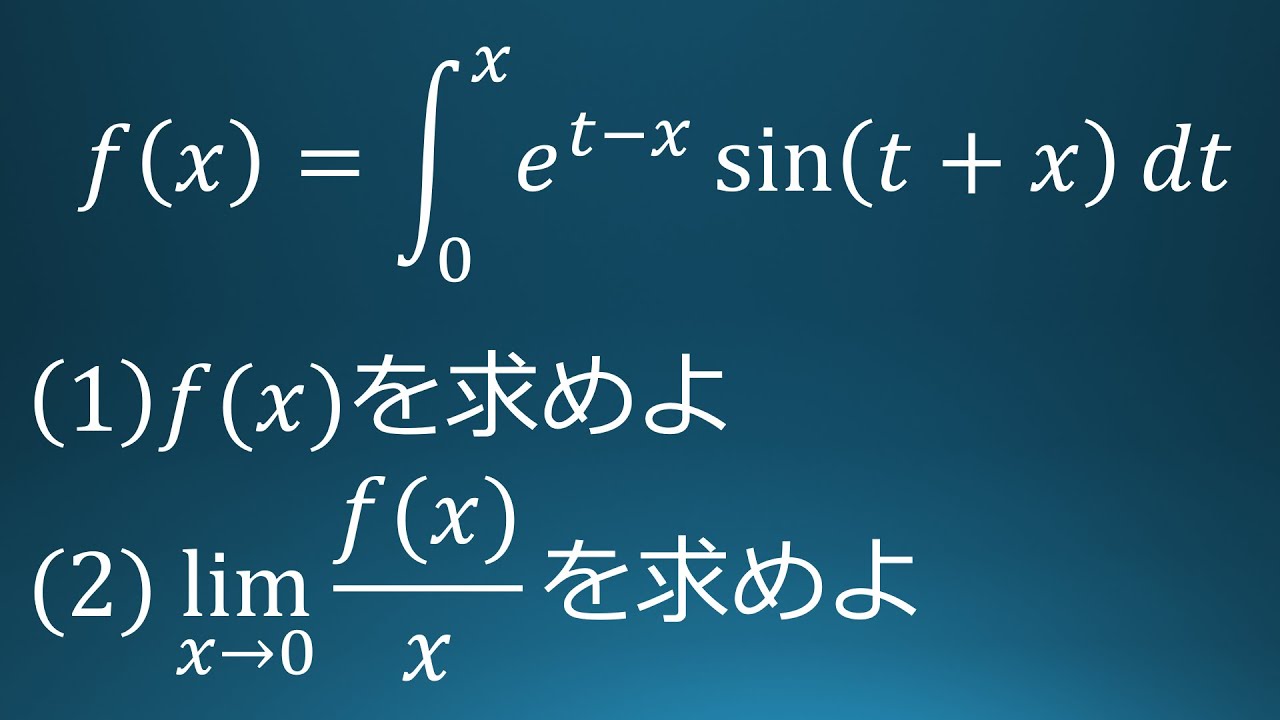
単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#不定積分#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$f(x)=\displaystyle \int_{0}^{x}e^{t-x}\sin(t+x)dt$を求めよ。
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{f(x)}{x}$を求めよ。
出典:2018年千葉大学 入試問題
この動画を見る
(1)
$f(x)=\displaystyle \int_{0}^{x}e^{t-x}\sin(t+x)dt$を求めよ。
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{f(x)}{x}$を求めよ。
出典:2018年千葉大学 入試問題
2022東北医科薬科大(医)微分・積分の基本問題

単元:
#数学(中学生)#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^4-4x^3$上の$(P,f(P))$における接線を$\ell $とする.
(1)$f(x)$と$\ell$の共有点が接線のみである$P$の範囲を求めよ.
(2)$P$が最小値のとき,$f(x)$と$\ell$で囲まれる面積を求めよ.
東北医科薬科大(医)過去問
この動画を見る
$f(x)=x^4-4x^3$上の$(P,f(P))$における接線を$\ell $とする.
(1)$f(x)$と$\ell$の共有点が接線のみである$P$の範囲を求めよ.
(2)$P$が最小値のとき,$f(x)$と$\ell$で囲まれる面積を求めよ.
東北医科薬科大(医)過去問
球 中央大学附属(推薦)2022入試問題解説18問目

単元:
#数学(中学生)#数A#図形の性質#方べきの定理と2つの円の関係#立体図形#体積・表面積・回転体・水量・変化のグラフ#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
半径の差が1
表面積の和が34π
2つの球の体積の和は?
2022中央大学附属高等学校(推薦)
この動画を見る
半径の差が1
表面積の和が34π
2つの球の体積の和は?
2022中央大学附属高等学校(推薦)
【数Ⅱ】虚数を解に持つ3次方程式【3次方程式の解と係数の関係】

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ 3次方程式x^3-4x^2+ax+b=0の解の1つが3+iであるとき,
実際の定数a,bを求めよ.$
この動画を見る
$ 3次方程式x^3-4x^2+ax+b=0の解の1つが3+iであるとき,
実際の定数a,bを求めよ.$
大学入試問題#97 学習院大学(2003) 整数問題 帰納法

単元:
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#数B#学習院大学
指導講師:
ますただ
問題文全文(内容文):
$n$:自然数
$11^{n+1}+12^{2n-1}$は$19$で割り切れることを示せ
出典:2003年学習院大学 入試問題
この動画を見る
$n$:自然数
$11^{n+1}+12^{2n-1}$は$19$で割り切れることを示せ
出典:2003年学習院大学 入試問題
2022年藤田医科大 確率 超基本問題

福田の共通テスト直前演習〜2021年共通テスト数学ⅡB問題5。ベクトルの問題。

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#センター試験・共通テスト関連#共通テスト#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
平面上の点Oを中心とする半径1の円周上に、3点A,B,Cがあり、
$\overrightarrow{ OA }・\overrightarrow{ OB }=-\frac{2}{3}および\overrightarrow{ OC }=-\overrightarrow{ OA }$を満たすとする。tを$0 \lt t \lt 1$を満たす
実数とし、線分ABを$t:(1-t)$に内分する点をPとする。
また、直線OP上に点Qをとる。
(1)$\cos\angle AOB=\frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウ\ \ }}$ である。
また、実数$k$を用いて、$\overrightarrow{ OQ }=k\overrightarrow{ OP }$と表せる。したがって
$\overrightarrow{ OQ }=\boxed{\ \ エ\ \ }\ \overrightarrow{ OA }+\boxed{\ \ オ\ \ }\ \overrightarrow{ OB } \ldots\ldots\ldots\ldots①$
$\overrightarrow{ CQ }=\boxed{\ \ カ\ \ }\ \overrightarrow{ OA }+\boxed{\ \ キ\ \ }\ \overrightarrow{ OB }$
となる。
$\overrightarrow{ OA }$と$\overrightarrow{ OP }$が垂直となるのは、$t=\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }}$ のときである。
$\boxed{\ \ エ\ \ } ~ \boxed{\ \ キ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
⓪$kt$ ①$(k-kt)$ ②$(kt+1)$
③$(kt-1)$ ④$(k-kt+1)$ ⑤$(k-kt-1)$
以下、$t \neq \frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }}$とし、$\angle OCQ$が直角であるとする。
(2)$\angle OCQ$が直角であることにより、(1)のkは
$k=\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }\ t-\boxed{\ \ シ\ \ }} \ldots②$
となることがわかる。
平面から直線OAを除いた部分は、直線OAを境に二つの部分に分けられる。
そのうち、点Bを含む部分を$D_1$、含まない部分を$D_2$とする。また、平面
から直線OBを除いた部分は、直線OBを境に二つの部分に分けられる。
そのうち、点Aを含む部分を$E_1$、含まない部分を$E_2$とする。
・$0 \lt t \lt \frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }}$ならば、点Qは$\boxed{\ \ ス\ \ }$。
・$\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }} \lt t \lt 1$ならば、点Qは$\boxed{\ \ セ\ \ }$。
$\boxed{\ \ ス\ \ }、\boxed{\ \ セ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
⓪$D_1$に含まれ、かつ$E_1$に含まれる
①$D_1$に含まれ、かつ$E_2$に含まれる
②$D_2$に含まれ、かつ$E_1$に含まれる
③$D_2$に含まれ、かつ$E_2$に含まれる
(3)太郎さんと花子さんは、点Pの位置と$|\overrightarrow{ OQ }|$の関係について考えている。
$t=\frac{1}{2}$のとき、①と②により、$|\overrightarrow{ OQ }|=\sqrt{\boxed{\ \ ソ\ \ }}$とわかる。
太郎:$t\neq \frac{1}{2}$のときにも、$|\overrightarrow{ OQ }|=\sqrt{\boxed{\ \ ソ\ \ }}$となる場合があるかな。
花子:$|\overrightarrow{ OQ }|$を$t$を用いて表して、$|\overrightarrow{ OQ }|=\sqrt{\boxed{\ \ ソ\ \ }}$
を満たすtの値について考えればいいと思うよ。
太郎:計算が大変そうだね。
花子:直線OAに関して、$t=\frac{1}{2}$のときの点Qと対称な点をRとしたら
$|\overrightarrow{ OR }|=\sqrt{\boxed{\ \ ソ\ \ }}$となるよ。
太郎:$\overrightarrow{ OR }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$を用いて表すことができれば、
tの値が求められそうだね。
直線OAに関して、$t=\frac{1}{2}$のときの点Qと対称な点をRとすると
$\overrightarrow{ CR }=\boxed{\ \ タ\ \ }\ \overrightarrow{ CQ }$
$=\boxed{\ \ チ\ \ }\ \overrightarrow{ OA }+\boxed{\ \ ツ\ \ }\ \overrightarrow{ OB }$
となる。
$t\neq \frac{1}{2}$のとき、$|\overrightarrow{ OQ }|=\sqrt{\boxed{\ \ ソ\ \ }}$となるtの値は$\frac{\boxed{\ \ テ\ \ }}{\boxed{\ \ ト\ \ }}$である。
2021共通テスト数学過去問
この動画を見る
平面上の点Oを中心とする半径1の円周上に、3点A,B,Cがあり、
$\overrightarrow{ OA }・\overrightarrow{ OB }=-\frac{2}{3}および\overrightarrow{ OC }=-\overrightarrow{ OA }$を満たすとする。tを$0 \lt t \lt 1$を満たす
実数とし、線分ABを$t:(1-t)$に内分する点をPとする。
また、直線OP上に点Qをとる。
(1)$\cos\angle AOB=\frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウ\ \ }}$ である。
また、実数$k$を用いて、$\overrightarrow{ OQ }=k\overrightarrow{ OP }$と表せる。したがって
$\overrightarrow{ OQ }=\boxed{\ \ エ\ \ }\ \overrightarrow{ OA }+\boxed{\ \ オ\ \ }\ \overrightarrow{ OB } \ldots\ldots\ldots\ldots①$
$\overrightarrow{ CQ }=\boxed{\ \ カ\ \ }\ \overrightarrow{ OA }+\boxed{\ \ キ\ \ }\ \overrightarrow{ OB }$
となる。
$\overrightarrow{ OA }$と$\overrightarrow{ OP }$が垂直となるのは、$t=\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }}$ のときである。
$\boxed{\ \ エ\ \ } ~ \boxed{\ \ キ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
⓪$kt$ ①$(k-kt)$ ②$(kt+1)$
③$(kt-1)$ ④$(k-kt+1)$ ⑤$(k-kt-1)$
以下、$t \neq \frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }}$とし、$\angle OCQ$が直角であるとする。
(2)$\angle OCQ$が直角であることにより、(1)のkは
$k=\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }\ t-\boxed{\ \ シ\ \ }} \ldots②$
となることがわかる。
平面から直線OAを除いた部分は、直線OAを境に二つの部分に分けられる。
そのうち、点Bを含む部分を$D_1$、含まない部分を$D_2$とする。また、平面
から直線OBを除いた部分は、直線OBを境に二つの部分に分けられる。
そのうち、点Aを含む部分を$E_1$、含まない部分を$E_2$とする。
・$0 \lt t \lt \frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }}$ならば、点Qは$\boxed{\ \ ス\ \ }$。
・$\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }} \lt t \lt 1$ならば、点Qは$\boxed{\ \ セ\ \ }$。
$\boxed{\ \ ス\ \ }、\boxed{\ \ セ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
⓪$D_1$に含まれ、かつ$E_1$に含まれる
①$D_1$に含まれ、かつ$E_2$に含まれる
②$D_2$に含まれ、かつ$E_1$に含まれる
③$D_2$に含まれ、かつ$E_2$に含まれる
(3)太郎さんと花子さんは、点Pの位置と$|\overrightarrow{ OQ }|$の関係について考えている。
$t=\frac{1}{2}$のとき、①と②により、$|\overrightarrow{ OQ }|=\sqrt{\boxed{\ \ ソ\ \ }}$とわかる。
太郎:$t\neq \frac{1}{2}$のときにも、$|\overrightarrow{ OQ }|=\sqrt{\boxed{\ \ ソ\ \ }}$となる場合があるかな。
花子:$|\overrightarrow{ OQ }|$を$t$を用いて表して、$|\overrightarrow{ OQ }|=\sqrt{\boxed{\ \ ソ\ \ }}$
を満たすtの値について考えればいいと思うよ。
太郎:計算が大変そうだね。
花子:直線OAに関して、$t=\frac{1}{2}$のときの点Qと対称な点をRとしたら
$|\overrightarrow{ OR }|=\sqrt{\boxed{\ \ ソ\ \ }}$となるよ。
太郎:$\overrightarrow{ OR }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$を用いて表すことができれば、
tの値が求められそうだね。
直線OAに関して、$t=\frac{1}{2}$のときの点Qと対称な点をRとすると
$\overrightarrow{ CR }=\boxed{\ \ タ\ \ }\ \overrightarrow{ CQ }$
$=\boxed{\ \ チ\ \ }\ \overrightarrow{ OA }+\boxed{\ \ ツ\ \ }\ \overrightarrow{ OB }$
となる。
$t\neq \frac{1}{2}$のとき、$|\overrightarrow{ OQ }|=\sqrt{\boxed{\ \ ソ\ \ }}$となるtの値は$\frac{\boxed{\ \ テ\ \ }}{\boxed{\ \ ト\ \ }}$である。
2021共通テスト数学過去問
大学入試問題#96 横浜国立大学(2015) 定積分
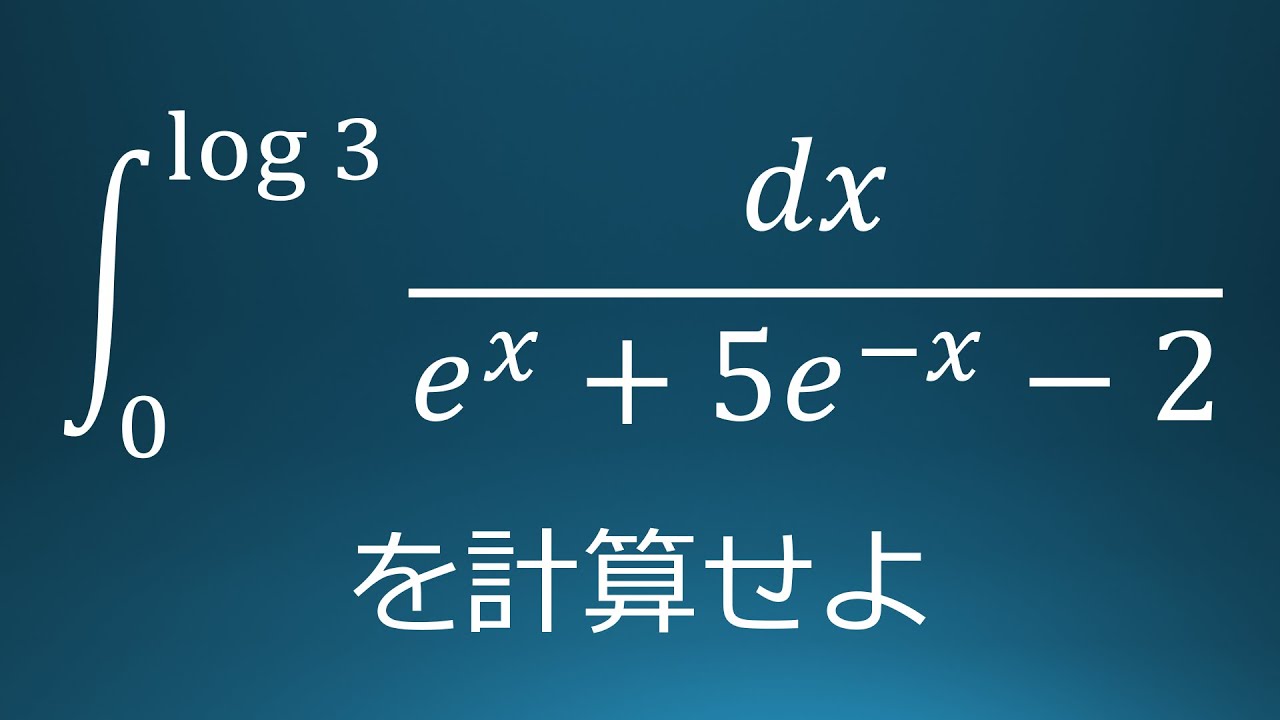
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{log\ 3}\displaystyle \frac{dx}{e^x+5e^{-x}-2}$を求めよ。
出典:2015横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{log\ 3}\displaystyle \frac{dx}{e^x+5e^{-x}-2}$を求めよ。
出典:2015横浜国立大学 入試問題
福田の共通テスト直前演習〜2021年共通テスト数学ⅡB問題3。確率分布、統計の問題。

単元:
#大学入試過去問(数学)#確率分布と統計的な推測#確率分布#統計的な推測#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
(1)A地区で保護されるジャガイモには1個の重さが200gを超えるものが
25%含まれることが経験的にわかっている。花子さんはA地区で収穫された
ジャガイモから400個を無作為に抽出し、重さを計測した。そのうち、重さが
200gを超えるジャガイモの個数を表す確率変数をZとする。このときZは
二項分布B($400,0,\boxed{\ \ アイ\ \ }$)に従うから、Zの平均(期待値)は$\boxed{\ \ ウエオ\ \ }$である。
(2)Zを(1)の確率変数とし、A地区で収穫されたジャガイモ400個からなる標本において
重さが200gを超えていたジャガイモの標本における比率を
$R=\frac{Z}{400}$とする。このとき、Rの標準偏差は$\sigma(R)=\boxed{\ \ カ\ \ }$である。
標本の大きさ400は十分に大きいので、Rは近似的に正規分布
$N(0,\boxed{\ \ アイ\ \ },(\boxed{\ \ カ\ \ })^2)$に従う。
したがって、$P(R \geqq x)=0.0465$となるようなxの値は$\boxed{\ \ キ\ \ }$となる。
ただし、$\boxed{\ \ キ\ \ }$の計算においては$\sqrt3=1.73$とする。
$\boxed{\ \ カ\ \ }$の解答群
⓪$\frac{3}{6400}$ ①$\frac{\sqrt3}{4}$ ②$\frac{\sqrt3}{80}$ ③$\frac{3}{40}$
$\boxed{\ \ キ\ \ }$については、最も適当なものを、次の⓪~③のうちから一つ選べ。
⓪0.209 ①0.251 ②0.286 ③0.395
(3)B地区で収穫され、出荷される予定のジャガイモ1個の重さは100gから
300gの間に分布している。B地区で収穫され、出荷される予定のジャガイモ
1個の重さを表す確率変数をXとするとき、Xは連続型確率変数であり、X
の取り得る値xの範囲は$100 \leqq x \leqq 300$である。
花子さんは、B地区で収穫され、出荷される予定の全てのジャガイモのうち、
重さが200g以上のものの割合を見積もりたいと考えた。そのために花子さんは
Xの確率密度関数f(x)として適当な関数を定め、それを用いて割合を
見積もるという方針を立てた。
B地区で収穫され、出荷される予定のジャガイモから206個を無作為に抽出
したところ、重さの標本平均は180gであった。
図1(※動画参照)はこの標本のヒストグラムである。
花子さんは図1のヒストグラムにおいて、重さxの増加とともに度数がほぼ
一定の割合で減少している傾向に着目し、Xの確率密度関数f(x)として、1次関数
$f(x)=ax+b (100 \leqq x \leqq 300)$
を考えることにした。ただし、$100 \leqq x \leqq 300$の範囲で$f(x) \geqq 0$とする。
このとき、$P(100 \leqq X \leqq 300)=\boxed{\ \ ク\ \ }$であることから
$\boxed{\ \ ケ\ \ }・10^4a+\boxed{\ \ コ\ \ }・10^2b=\boxed{\ \ ク\ \ } \ldots①$
である。
花子さんは、Xの平均(期待値)が重さの標本平均180gと等しくなるように
確率密度関数を定める方法を用いることにした。
連続型確率変数Xの取り得る値xの範囲が$100 \leqq x \leqq 300$で、その
確率密度関数がf(x)のとき、Xの平均(期待値)mは
$m=\int_{100}^{300}xf(x)dx$
で定義される。この定義と花子さんの採用した方法から
$m=\frac{26}{3}・10^5a+4・10^4b=180 \ldots②$
となる。①と②により、確率密度関数は
$f(x)=-\ \boxed{\ \ サ\ \ }・10^{-5}x+\boxed{\ \ シス\ \ }・10^{-3} \ldots③$
と得られる。このようにして得られた③のf(x)は、$100 \leqq x \leqq 300$の範囲で
$f(x) \geqq 0$を満たしており、確かに確率密度関数として適当である。
したがって、この花子さんお方針に基づくと、B地区で収穫され、出荷される
予定の全てのジャガイモのうち、重さが200g以上のものは$\boxed{\ \ セ\ \ }%$
あると見積もることができる。
$\boxed{\ \ セ\ \ }$については、最も適当なものを、次の⓪~③のうちから一つ選べ。
⓪33 ①34 ②35 ③36
2022共通テスト数学過去問
この動画を見る
(1)A地区で保護されるジャガイモには1個の重さが200gを超えるものが
25%含まれることが経験的にわかっている。花子さんはA地区で収穫された
ジャガイモから400個を無作為に抽出し、重さを計測した。そのうち、重さが
200gを超えるジャガイモの個数を表す確率変数をZとする。このときZは
二項分布B($400,0,\boxed{\ \ アイ\ \ }$)に従うから、Zの平均(期待値)は$\boxed{\ \ ウエオ\ \ }$である。
(2)Zを(1)の確率変数とし、A地区で収穫されたジャガイモ400個からなる標本において
重さが200gを超えていたジャガイモの標本における比率を
$R=\frac{Z}{400}$とする。このとき、Rの標準偏差は$\sigma(R)=\boxed{\ \ カ\ \ }$である。
標本の大きさ400は十分に大きいので、Rは近似的に正規分布
$N(0,\boxed{\ \ アイ\ \ },(\boxed{\ \ カ\ \ })^2)$に従う。
したがって、$P(R \geqq x)=0.0465$となるようなxの値は$\boxed{\ \ キ\ \ }$となる。
ただし、$\boxed{\ \ キ\ \ }$の計算においては$\sqrt3=1.73$とする。
$\boxed{\ \ カ\ \ }$の解答群
⓪$\frac{3}{6400}$ ①$\frac{\sqrt3}{4}$ ②$\frac{\sqrt3}{80}$ ③$\frac{3}{40}$
$\boxed{\ \ キ\ \ }$については、最も適当なものを、次の⓪~③のうちから一つ選べ。
⓪0.209 ①0.251 ②0.286 ③0.395
(3)B地区で収穫され、出荷される予定のジャガイモ1個の重さは100gから
300gの間に分布している。B地区で収穫され、出荷される予定のジャガイモ
1個の重さを表す確率変数をXとするとき、Xは連続型確率変数であり、X
の取り得る値xの範囲は$100 \leqq x \leqq 300$である。
花子さんは、B地区で収穫され、出荷される予定の全てのジャガイモのうち、
重さが200g以上のものの割合を見積もりたいと考えた。そのために花子さんは
Xの確率密度関数f(x)として適当な関数を定め、それを用いて割合を
見積もるという方針を立てた。
B地区で収穫され、出荷される予定のジャガイモから206個を無作為に抽出
したところ、重さの標本平均は180gであった。
図1(※動画参照)はこの標本のヒストグラムである。
花子さんは図1のヒストグラムにおいて、重さxの増加とともに度数がほぼ
一定の割合で減少している傾向に着目し、Xの確率密度関数f(x)として、1次関数
$f(x)=ax+b (100 \leqq x \leqq 300)$
を考えることにした。ただし、$100 \leqq x \leqq 300$の範囲で$f(x) \geqq 0$とする。
このとき、$P(100 \leqq X \leqq 300)=\boxed{\ \ ク\ \ }$であることから
$\boxed{\ \ ケ\ \ }・10^4a+\boxed{\ \ コ\ \ }・10^2b=\boxed{\ \ ク\ \ } \ldots①$
である。
花子さんは、Xの平均(期待値)が重さの標本平均180gと等しくなるように
確率密度関数を定める方法を用いることにした。
連続型確率変数Xの取り得る値xの範囲が$100 \leqq x \leqq 300$で、その
確率密度関数がf(x)のとき、Xの平均(期待値)mは
$m=\int_{100}^{300}xf(x)dx$
で定義される。この定義と花子さんの採用した方法から
$m=\frac{26}{3}・10^5a+4・10^4b=180 \ldots②$
となる。①と②により、確率密度関数は
$f(x)=-\ \boxed{\ \ サ\ \ }・10^{-5}x+\boxed{\ \ シス\ \ }・10^{-3} \ldots③$
と得られる。このようにして得られた③のf(x)は、$100 \leqq x \leqq 300$の範囲で
$f(x) \geqq 0$を満たしており、確かに確率密度関数として適当である。
したがって、この花子さんお方針に基づくと、B地区で収穫され、出荷される
予定の全てのジャガイモのうち、重さが200g以上のものは$\boxed{\ \ セ\ \ }%$
あると見積もることができる。
$\boxed{\ \ セ\ \ }$については、最も適当なものを、次の⓪~③のうちから一つ選べ。
⓪33 ①34 ②35 ③36
2022共通テスト数学過去問
福田の共通テスト直前演習〜2021年共通テスト数学ⅡB問題4。数列の問題。

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
以下のように、歩行者と自転車が自宅を出発して移動と停止を繰り返してい
る。歩行者と自転車の動きについて、数学的に考えてみよう。
自宅を原点とする数直線を考え、歩行者と自転車をその数直線上を動く点とみ
なす。数直線上の点の座標がyであるとき、その点は位置にあるということに
する。また、歩行者が自宅を出発してからx分経過した時点を時刻xと表す。歩
行者は時刻0に自宅を出発し、正の向きに毎分1の速さで歩き始める。自転車は
時刻2に自宅を出発し、毎分2の速さで歩行者を追いかける。自転車が歩行者に
追いつくと、歩行者と自転車はともに1分だけ停止する。その後、歩行者は再び
正の向きに毎分1の速さで歩き出し、自転車は毎分2の速さで自宅に戻る。自転
車は自宅に到着すると、1分だけ停止した後、再び毎分2の速さで歩行者を追い
かける。これを繰り返し、自転車は自宅と歩行者の間を往復する。
$x=a_n$を自転車がn回目に自宅を出発する時刻とし、$y=b_n$をそのときの歩
行者の位置とする。
(1) 花子さんと太郎さんは、数列$\left\{a_n\right\}, \left\{b_n\right\}$の一般項を求めるために、歩行者
と自転車について、時刻において位置yにいることをOを原点とする座標
平面上の点(x,y)で表すことにした。
$a_1=2,b_1=2$により、自転車が最初に自宅を出発するときの時刻と自転
車の位置を表す点の座標は(2,0)であり、その時の時刻と歩行者の位置を
表す点の座標は(2,2)である。また、自転車が最初に歩行者に追いつくとき
の時刻と位置を表す点の座標は$(\boxed{\ \ ア\ \ },\boxed{\ \ ア\ \ })$である。よって
$a_2=\boxed{\ \ イ\ \ }, b_2=\boxed{\ \ ウ\ \ }$
である。
花子:数列$\left\{a_n\right\}, \left\{b_n\right\}$の一般項について考える前に、
$(\boxed{\ \ ア\ \ },\boxed{\ \ ア\ \ })$の求め方について整理してみようか。
太郎:花子さんはどうやって求めたの?
花子:自転車が歩行者を追いかけるときに、間隔が1分間に1ずつ縮まっていくこと
を利用したよ。
太郎:歩行者と自転車の動きをそれぞれ直線の方程式で表して、交点を
計算して求めることもできるね。
自転車がn回目に自宅を出発するときの時刻と自転車の位置を表す点の座標
は$(a_n,0)$であり、そのときの時刻と歩行者の位置を表す点の座標は
$(a_n,b_n)$である。よって、n回目に自宅を出発した自転車が次に歩行者に
追いつくときの時刻と位置を表す点の座標は、$a_n,b_n$を用いて、
$(\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ })$と表せる。
$\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
⓪$a_n$ ①$b_n$ ②$2a_n$
③$a_n+b_n$ ④$2b_n$ ⑤$3a_n$
⑥$2a_n+b_n$ ⑦$a_n+2b_n$ ⑧$3b_n$
以上から、数列$\left\{a_n\right\}, \left\{b_n\right\}$について、自然数nに対して、関係式
$a_{n+1}=a_n+\boxed{\ \ カ\ \ }\ b_n+\boxed{\ \ キ\ \ } \ldots①$
$b_{n+1}=3b_n+\boxed{\ \ ク\ \ } \ldots②$
が成り立つことが分かる。まず、$b_1=2$と②から
$b_n=\boxed{\ \ ケ\ \ } (n=1,2,3,\ldots)$
を得る。この結果と、$a_1=2$および1から
$a_n=\boxed{\ \ コ\ \ } (n=1,2,3,\ldots)$
がわかる。
$\boxed{\ \ ケ\ \ }, \boxed{\ \ コ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
⓪$3^{n-1}+1$ ①$\frac{1}{2}・3^n+\frac{1}{2}$
②$3^{n-1}+n$ ③$\frac{1}{2}・3^n+n-\frac{1}{2}$
④$3^{n-1}+n^2$ ⑤$\frac{1}{2}・3^n+n^2-\frac{1}{2}$
⑥$2・3^{n-1}$ ⑦$\frac{5}{2}・3^{n-1}-\frac{1}{2}$
⑧$2・3^{n-1}+n-1$ ⑨$\frac{5}{2}・3^{n-1}+n-\frac{3}{2}$
ⓐ$2・3^{n-1}+n^2-1$ ⓑ$\frac{5}{2}・3^{n-1}+n^2-\frac{3}{2}$
(2)歩行者が$y=300$の位置に到着するときまでに、自転車が装甲車に追いつく
回数は$\boxed{\ \ サ\ \ }$回である。また、$\boxed{\ \ サ\ \ }$回目に自転車が歩行者に追いつく
時刻は、$x=\boxed{\ \ シスセ\ \ }$である。
2022共通テスト数学過去問
この動画を見る
以下のように、歩行者と自転車が自宅を出発して移動と停止を繰り返してい
る。歩行者と自転車の動きについて、数学的に考えてみよう。
自宅を原点とする数直線を考え、歩行者と自転車をその数直線上を動く点とみ
なす。数直線上の点の座標がyであるとき、その点は位置にあるということに
する。また、歩行者が自宅を出発してからx分経過した時点を時刻xと表す。歩
行者は時刻0に自宅を出発し、正の向きに毎分1の速さで歩き始める。自転車は
時刻2に自宅を出発し、毎分2の速さで歩行者を追いかける。自転車が歩行者に
追いつくと、歩行者と自転車はともに1分だけ停止する。その後、歩行者は再び
正の向きに毎分1の速さで歩き出し、自転車は毎分2の速さで自宅に戻る。自転
車は自宅に到着すると、1分だけ停止した後、再び毎分2の速さで歩行者を追い
かける。これを繰り返し、自転車は自宅と歩行者の間を往復する。
$x=a_n$を自転車がn回目に自宅を出発する時刻とし、$y=b_n$をそのときの歩
行者の位置とする。
(1) 花子さんと太郎さんは、数列$\left\{a_n\right\}, \left\{b_n\right\}$の一般項を求めるために、歩行者
と自転車について、時刻において位置yにいることをOを原点とする座標
平面上の点(x,y)で表すことにした。
$a_1=2,b_1=2$により、自転車が最初に自宅を出発するときの時刻と自転
車の位置を表す点の座標は(2,0)であり、その時の時刻と歩行者の位置を
表す点の座標は(2,2)である。また、自転車が最初に歩行者に追いつくとき
の時刻と位置を表す点の座標は$(\boxed{\ \ ア\ \ },\boxed{\ \ ア\ \ })$である。よって
$a_2=\boxed{\ \ イ\ \ }, b_2=\boxed{\ \ ウ\ \ }$
である。
花子:数列$\left\{a_n\right\}, \left\{b_n\right\}$の一般項について考える前に、
$(\boxed{\ \ ア\ \ },\boxed{\ \ ア\ \ })$の求め方について整理してみようか。
太郎:花子さんはどうやって求めたの?
花子:自転車が歩行者を追いかけるときに、間隔が1分間に1ずつ縮まっていくこと
を利用したよ。
太郎:歩行者と自転車の動きをそれぞれ直線の方程式で表して、交点を
計算して求めることもできるね。
自転車がn回目に自宅を出発するときの時刻と自転車の位置を表す点の座標
は$(a_n,0)$であり、そのときの時刻と歩行者の位置を表す点の座標は
$(a_n,b_n)$である。よって、n回目に自宅を出発した自転車が次に歩行者に
追いつくときの時刻と位置を表す点の座標は、$a_n,b_n$を用いて、
$(\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ })$と表せる。
$\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
⓪$a_n$ ①$b_n$ ②$2a_n$
③$a_n+b_n$ ④$2b_n$ ⑤$3a_n$
⑥$2a_n+b_n$ ⑦$a_n+2b_n$ ⑧$3b_n$
以上から、数列$\left\{a_n\right\}, \left\{b_n\right\}$について、自然数nに対して、関係式
$a_{n+1}=a_n+\boxed{\ \ カ\ \ }\ b_n+\boxed{\ \ キ\ \ } \ldots①$
$b_{n+1}=3b_n+\boxed{\ \ ク\ \ } \ldots②$
が成り立つことが分かる。まず、$b_1=2$と②から
$b_n=\boxed{\ \ ケ\ \ } (n=1,2,3,\ldots)$
を得る。この結果と、$a_1=2$および1から
$a_n=\boxed{\ \ コ\ \ } (n=1,2,3,\ldots)$
がわかる。
$\boxed{\ \ ケ\ \ }, \boxed{\ \ コ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
⓪$3^{n-1}+1$ ①$\frac{1}{2}・3^n+\frac{1}{2}$
②$3^{n-1}+n$ ③$\frac{1}{2}・3^n+n-\frac{1}{2}$
④$3^{n-1}+n^2$ ⑤$\frac{1}{2}・3^n+n^2-\frac{1}{2}$
⑥$2・3^{n-1}$ ⑦$\frac{5}{2}・3^{n-1}-\frac{1}{2}$
⑧$2・3^{n-1}+n-1$ ⑨$\frac{5}{2}・3^{n-1}+n-\frac{3}{2}$
ⓐ$2・3^{n-1}+n^2-1$ ⓑ$\frac{5}{2}・3^{n-1}+n^2-\frac{3}{2}$
(2)歩行者が$y=300$の位置に到着するときまでに、自転車が装甲車に追いつく
回数は$\boxed{\ \ サ\ \ }$回である。また、$\boxed{\ \ サ\ \ }$回目に自転車が歩行者に追いつく
時刻は、$x=\boxed{\ \ シスセ\ \ }$である。
2022共通テスト数学過去問
🟨にあてはまる数は? 連分数 渋谷教育学園幕張 2022入試問題解説14問目
単元:
#数学(中学生)#数Ⅱ#式と証明#整式の除法・分数式・二項定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
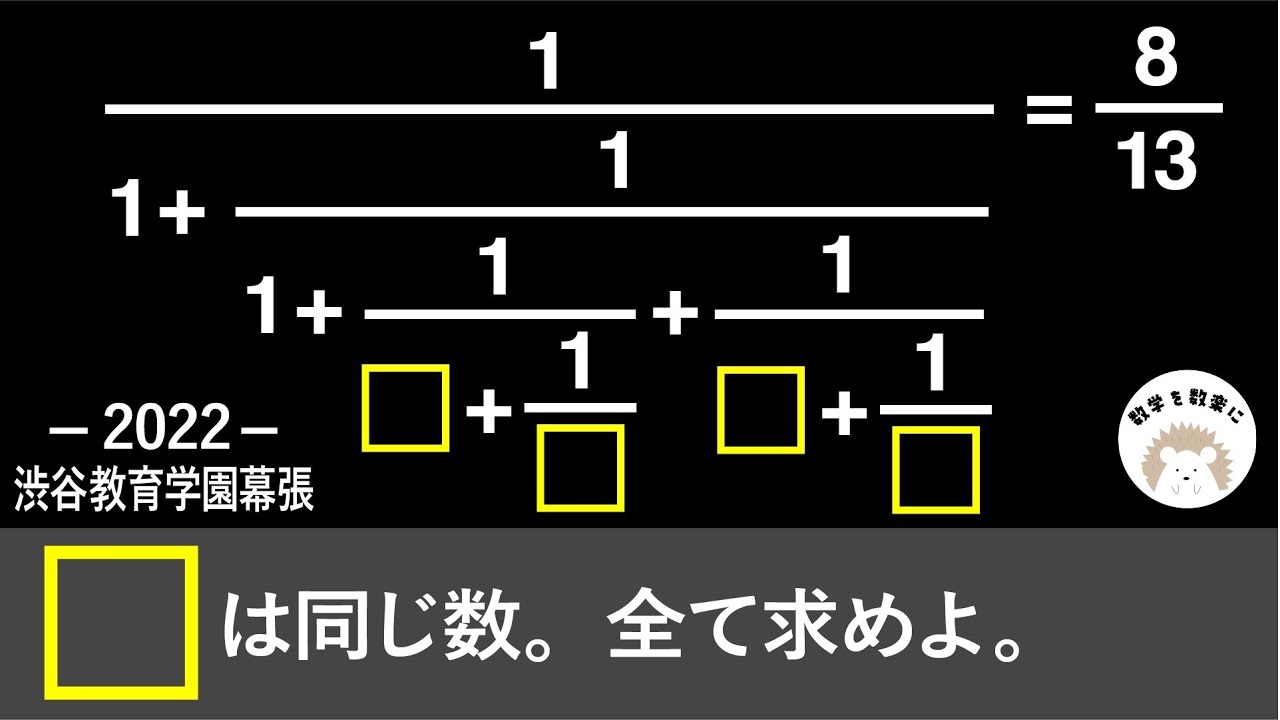
$\frac{1}{1+\frac{1}{1+\frac{1}{▢+\frac{1}{▢}}+\frac{1}{▢+\frac{1}{▢}}}}$=$\frac{8}{13}$
▢は同じ数。全て求めよ。
2022渋谷教育学園幕張
この動画を見る
$\frac{1}{1+\frac{1}{1+\frac{1}{▢+\frac{1}{▢}}+\frac{1}{▢+\frac{1}{▢}}}}$=$\frac{8}{13}$
▢は同じ数。全て求めよ。
2022渋谷教育学園幕張
大学入試問題#95 横浜市立大学医学部(2013) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#横浜市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\sqrt{ 2 }}{\sin\ x+\cos\ x}\ dx$を求めよ。
出典:2013年横浜市立大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\sqrt{ 2 }}{\sin\ x+\cos\ x}\ dx$を求めよ。
出典:2013年横浜市立大学医学部 入試問題
無題
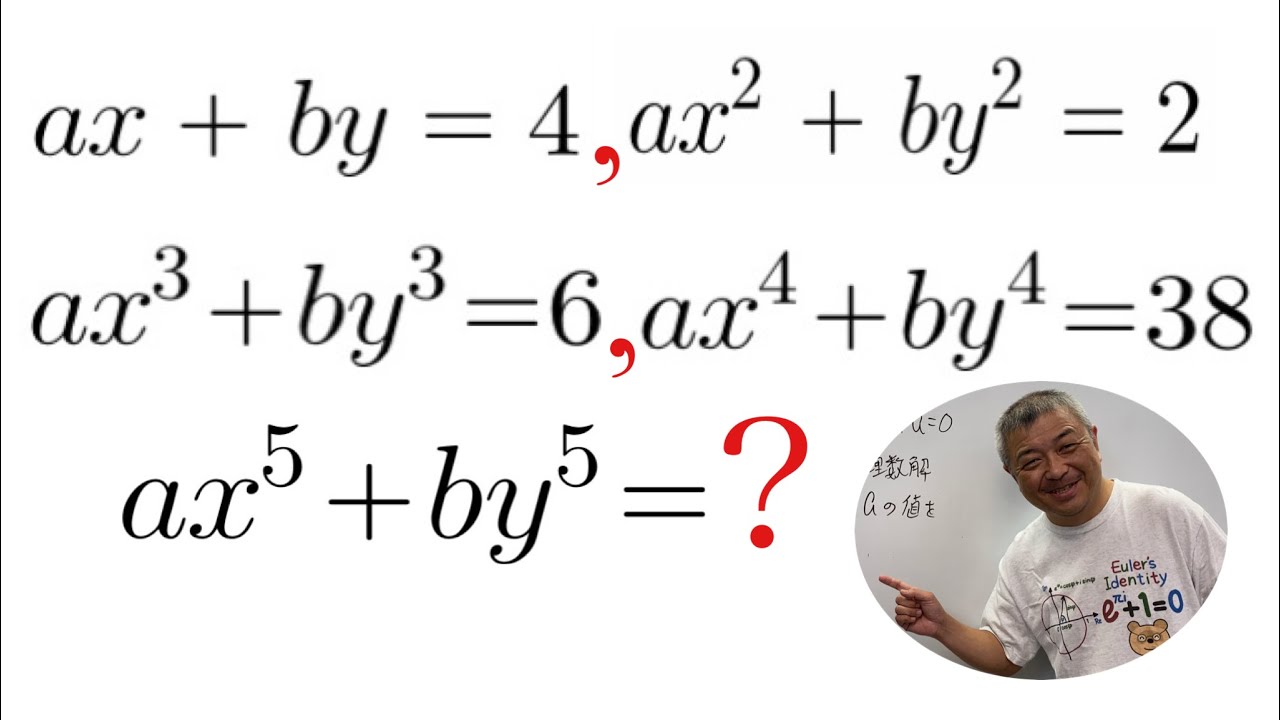
単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ax+by=4$
$ax^2+by^2=2$
$ax^3+by^3=6$
$ax^4+by^4=38$
$ax^5+by^5=\Box$
これを解け.
この動画を見る
$ax+by=4$
$ax^2+by^2=2$
$ax^3+by^3=6$
$ax^4+by^4=38$
$ax^5+by^5=\Box$
これを解け.
福田の共通テスト直前演習〜2021年共通テスト数学ⅡB問題2。微分積分の問題。

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#センター試験・共通テスト関連#共通テスト#面積、体積#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
[1]aを実数とし、$f(x)=x^3-6ax+16$
(1)$y=f(x)$のグラフの概形は
$a=0$のとき、$\boxed{\ \ ア\ \ }$
$a \gt 0$のとき、$\boxed{\ \ イ\ \ }$
である.
$\boxed{\ \ ア\ \ },\boxed{\ \ イ\ \ }$については、最も適当なものを、次の⓪~⑤のうちから
1つずつ選べ。ただし、同じものを繰り返し選んでもよい。
(※選択肢は動画参照)
(2)$a \gt 0$とし、pを実数とする。座標平面上の曲線$y=f(x)$と直線$y=p$
が3個の共有点をもつようなpの値の範囲は$\boxed{\ \ ウ\ \ } \lt p \lt \boxed{\ \ エ\ \ }$
である。
$p=\boxed{\ \ ウ\ \ }$のとき、曲線$y=f(x)$と直線$y=p$は2個の共有点をもつ。
それらのx座標を$q,r(q \lt r)$とする。曲線$y=f(x)$と直線$y=p$
が点(r,p)で接することに注意すると
$q=\boxed{\ \ オカ\ \ }\sqrt{\boxed{\ \ キ\ \ }}\ a^{\frac{1}{2}}, r=\sqrt{\boxed{\ \ ク\ \ }}\ a^{\frac{1}{2}}$
と表せる。
$\boxed{\ \ ウ\ \ }, \boxed{\ \ エ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
⓪$2\sqrt2a^{\frac{3}{2}}+16$ ①$-2\sqrt2a^{\frac{3}{2}}+16$
②$4\sqrt2a^{\frac{3}{2}}+16$ ③$-4\sqrt2a^{\frac{3}{2}}+16$
④$8\sqrt2a^{\frac{3}{2}}+16$ ⑤$-8\sqrt2a^{\frac{3}{2}}+16$
(3)方程式$f(x)=0$の異なる実数解の個数をnとする。次の⓪~⑤のうち、
正しいものは$\boxed{\ \ ケ\ \ }$と$\boxed{\ \ コ\ \ }$である。
$\boxed{\ \ ケ\ \ }, \boxed{\ \ コ\ \ }$の解答群(解答の順序は問わない。)
$⓪n=1ならばa \lt 0 ①a \lt 0ならばn=1$
$②n=2ならばa \lt 0 ③a \lt 0ならばn=2$
$④n=2ならばa \gt 0 ⑤a \gt 0ならばn=3$
[2]$b \gt 0$とし、$g(x)=x^3-3bx+3b^2, h(x)=x^3-x^2+b^2$とおく。
座標平面上の曲線$y=g(x)$を$C_1$, 曲線$y=h(x)$を$C_2$とする。
$C_1$と$C_2$は2点で交わる。これらの交点のx座標をそれぞれ$\alpha,\beta$
$(\alpha \lt \beta)$とすると、$\alpha=\boxed{\ \ サ\ \ }, \beta=\boxed{\ \ シス\ \ }$である。
$\alpha \leqq x \leqq \beta$の範囲で$C_1$と$C_2$で囲まれた図形の面積をSとする。また、
$t \gt \beta$とし、$\beta \leqq x \leqq t$の範囲で$C_1$と$C_2$および直線$x=t$で囲まれた図形の
面積をTとする。
このとき
$S=\int_{\alpha}^{\beta}\boxed{\ \ セ\ \ }dx$
$T=\int_{\beta}^{t}\boxed{\ \ ソ\ \ }dx$
$S-T=\int_{\alpha}^{t}\boxed{\ \ タ\ \ }dx$
であるので
$S-T=\frac{\boxed{\ \ チツ\ \ }}{\boxed{\ \ テ\ \ }}(2t^3-\ \boxed{\ \ ト\ \ }bt^2+\boxed{\ \ ナニ\ \ }b^2t-\ \boxed{\ \ ヌ\ \ }b^3)$
が得られる。
したがって、$S=T$となるのは$t=\frac{\boxed{\ \ ネ\ \ }}{\boxed{\ \ ノ\ \ }}\ b$のときである。
$\boxed{\ \ セ\ \ }~\boxed{\ \ タ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
$⓪\left\{g(x)+h(x)\right\} ①\left\{g(x)-h(x)\right\}$
$②\left\{h(x)-g(x)\right\} ③\left\{2g(x)+2h(x)\right\}$
$④\left\{2g(x)-2h(x)\right\} ⑤\left\{2h(x)-2g(x)\right\}$
$⑥2g(x) ⑦2h(x)$
2022共通テスト数学過去問
この動画を見る
[1]aを実数とし、$f(x)=x^3-6ax+16$
(1)$y=f(x)$のグラフの概形は
$a=0$のとき、$\boxed{\ \ ア\ \ }$
$a \gt 0$のとき、$\boxed{\ \ イ\ \ }$
である.
$\boxed{\ \ ア\ \ },\boxed{\ \ イ\ \ }$については、最も適当なものを、次の⓪~⑤のうちから
1つずつ選べ。ただし、同じものを繰り返し選んでもよい。
(※選択肢は動画参照)
(2)$a \gt 0$とし、pを実数とする。座標平面上の曲線$y=f(x)$と直線$y=p$
が3個の共有点をもつようなpの値の範囲は$\boxed{\ \ ウ\ \ } \lt p \lt \boxed{\ \ エ\ \ }$
である。
$p=\boxed{\ \ ウ\ \ }$のとき、曲線$y=f(x)$と直線$y=p$は2個の共有点をもつ。
それらのx座標を$q,r(q \lt r)$とする。曲線$y=f(x)$と直線$y=p$
が点(r,p)で接することに注意すると
$q=\boxed{\ \ オカ\ \ }\sqrt{\boxed{\ \ キ\ \ }}\ a^{\frac{1}{2}}, r=\sqrt{\boxed{\ \ ク\ \ }}\ a^{\frac{1}{2}}$
と表せる。
$\boxed{\ \ ウ\ \ }, \boxed{\ \ エ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
⓪$2\sqrt2a^{\frac{3}{2}}+16$ ①$-2\sqrt2a^{\frac{3}{2}}+16$
②$4\sqrt2a^{\frac{3}{2}}+16$ ③$-4\sqrt2a^{\frac{3}{2}}+16$
④$8\sqrt2a^{\frac{3}{2}}+16$ ⑤$-8\sqrt2a^{\frac{3}{2}}+16$
(3)方程式$f(x)=0$の異なる実数解の個数をnとする。次の⓪~⑤のうち、
正しいものは$\boxed{\ \ ケ\ \ }$と$\boxed{\ \ コ\ \ }$である。
$\boxed{\ \ ケ\ \ }, \boxed{\ \ コ\ \ }$の解答群(解答の順序は問わない。)
$⓪n=1ならばa \lt 0 ①a \lt 0ならばn=1$
$②n=2ならばa \lt 0 ③a \lt 0ならばn=2$
$④n=2ならばa \gt 0 ⑤a \gt 0ならばn=3$
[2]$b \gt 0$とし、$g(x)=x^3-3bx+3b^2, h(x)=x^3-x^2+b^2$とおく。
座標平面上の曲線$y=g(x)$を$C_1$, 曲線$y=h(x)$を$C_2$とする。
$C_1$と$C_2$は2点で交わる。これらの交点のx座標をそれぞれ$\alpha,\beta$
$(\alpha \lt \beta)$とすると、$\alpha=\boxed{\ \ サ\ \ }, \beta=\boxed{\ \ シス\ \ }$である。
$\alpha \leqq x \leqq \beta$の範囲で$C_1$と$C_2$で囲まれた図形の面積をSとする。また、
$t \gt \beta$とし、$\beta \leqq x \leqq t$の範囲で$C_1$と$C_2$および直線$x=t$で囲まれた図形の
面積をTとする。
このとき
$S=\int_{\alpha}^{\beta}\boxed{\ \ セ\ \ }dx$
$T=\int_{\beta}^{t}\boxed{\ \ ソ\ \ }dx$
$S-T=\int_{\alpha}^{t}\boxed{\ \ タ\ \ }dx$
であるので
$S-T=\frac{\boxed{\ \ チツ\ \ }}{\boxed{\ \ テ\ \ }}(2t^3-\ \boxed{\ \ ト\ \ }bt^2+\boxed{\ \ ナニ\ \ }b^2t-\ \boxed{\ \ ヌ\ \ }b^3)$
が得られる。
したがって、$S=T$となるのは$t=\frac{\boxed{\ \ ネ\ \ }}{\boxed{\ \ ノ\ \ }}\ b$のときである。
$\boxed{\ \ セ\ \ }~\boxed{\ \ タ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
$⓪\left\{g(x)+h(x)\right\} ①\left\{g(x)-h(x)\right\}$
$②\left\{h(x)-g(x)\right\} ③\left\{2g(x)+2h(x)\right\}$
$④\left\{2g(x)-2h(x)\right\} ⑤\left\{2h(x)-2g(x)\right\}$
$⑥2g(x) ⑦2h(x)$
2022共通テスト数学過去問
これできる?

平均値=中央値 昭和学院秀英 2022入試問題解説13問目

単元:
#数学(中学生)#数Ⅰ#データの分析#データの分析#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
x点 2点 4点 8点 3点 3点 7点 7点
この得点の平均値と中央値が一致したとき
x=?(*$x \geqq 0$)
2022昭和学院秀英高等学校
この動画を見る
x点 2点 4点 8点 3点 3点 7点 7点
この得点の平均値と中央値が一致したとき
x=?(*$x \geqq 0$)
2022昭和学院秀英高等学校
【数学B/平面ベクトル】ベクトル方程式の総まとめ

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
(1)
点$A(2,4),\vec{ d }=(1,3)$のとき、点$A$を通り、$\vec{ d }$が方向ベクトルである直線の媒介変数表示を、媒介変数を$t$として求めよ。
また、$t$を消去した式で表せ。
(2)
2点$A(-1,2),$ $B(3,5)$を通る直線の媒介変数表示を、媒介変数を$t$として求めよ。
(3)
点$A(-1,2),\vec{ n }=(3,4)$のとき、点$A$を通り、$\vec{ n }$が法線ベクトルである直線の方程式を求めよ。
(4)
点$A(1,2)$を中心とし、半径が$3$である円の方程式を、ベクトルを利用して求めよ。
この動画を見る
(1)
点$A(2,4),\vec{ d }=(1,3)$のとき、点$A$を通り、$\vec{ d }$が方向ベクトルである直線の媒介変数表示を、媒介変数を$t$として求めよ。
また、$t$を消去した式で表せ。
(2)
2点$A(-1,2),$ $B(3,5)$を通る直線の媒介変数表示を、媒介変数を$t$として求めよ。
(3)
点$A(-1,2),\vec{ n }=(3,4)$のとき、点$A$を通り、$\vec{ n }$が法線ベクトルである直線の方程式を求めよ。
(4)
点$A(1,2)$を中心とし、半径が$3$である円の方程式を、ベクトルを利用して求めよ。
大学入試問題#94 横浜国立大学(2007) 定積分
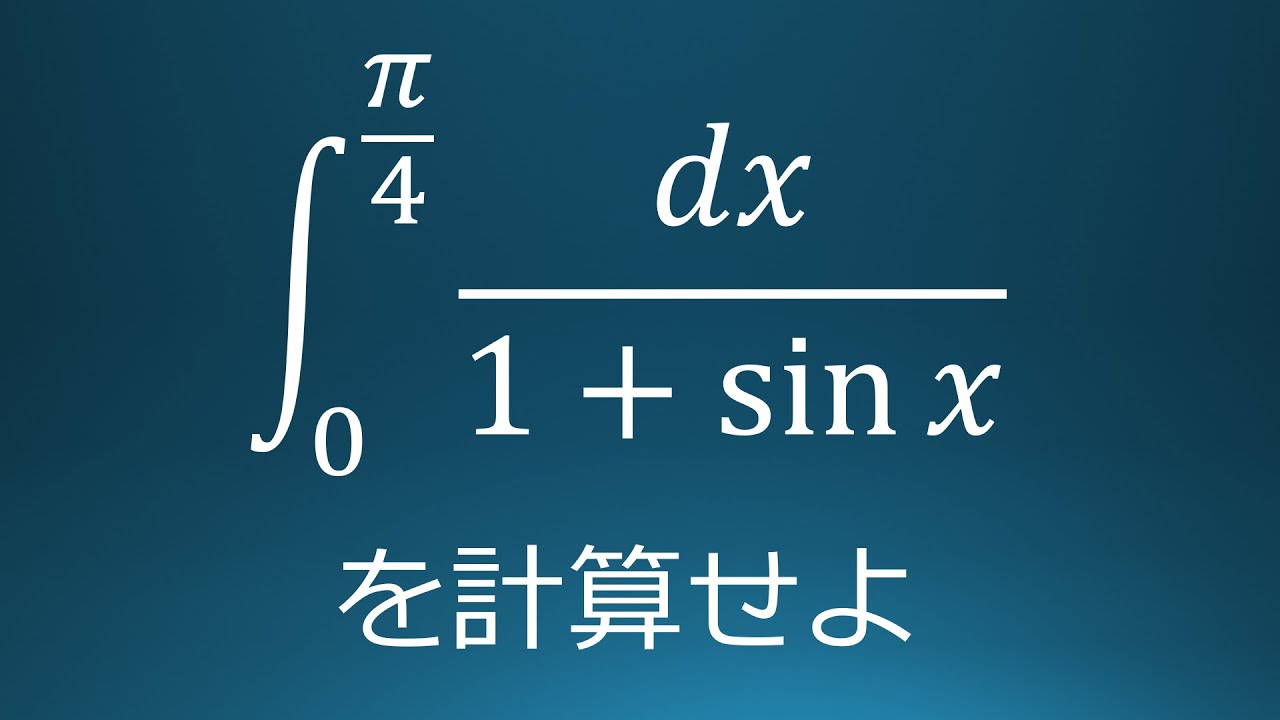
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{dx}{1+\sin\ x}$を計算せよ。
出典:2007年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{dx}{1+\sin\ x}$を計算せよ。
出典:2007年横浜国立大学 入試問題
