数学(高校生)
数学(高校生)
二次関数とて侮ることなかれ。難問です【京都大学】【数学 入試問題】
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
aを正の定数とする。次の関数の最大値を求めよ。
f(x)=|x²-(ax+3a²/4)|+ax+3a²/4 (-1<=x<=1)
この動画を見る
aを正の定数とする。次の関数の最大値を求めよ。
f(x)=|x²-(ax+3a²/4)|+ax+3a²/4 (-1<=x<=1)
福田のおもしろ数学345〜複雑な2重根号の式が整数となる条件
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\sqrt{ \mathstrut \frac{25}{2} +\sqrt{ \mathstrut \frac{625}{4} -n}}$+$\sqrt{ \mathstrut \frac{25}{2} -\sqrt{ \mathstrut \frac{625}{4} -n}}$が整数となるような整数$n$をすべて求めよ。
この動画を見る
$\sqrt{ \mathstrut \frac{25}{2} +\sqrt{ \mathstrut \frac{625}{4} -n}}$+$\sqrt{ \mathstrut \frac{25}{2} -\sqrt{ \mathstrut \frac{625}{4} -n}}$が整数となるような整数$n$をすべて求めよ。
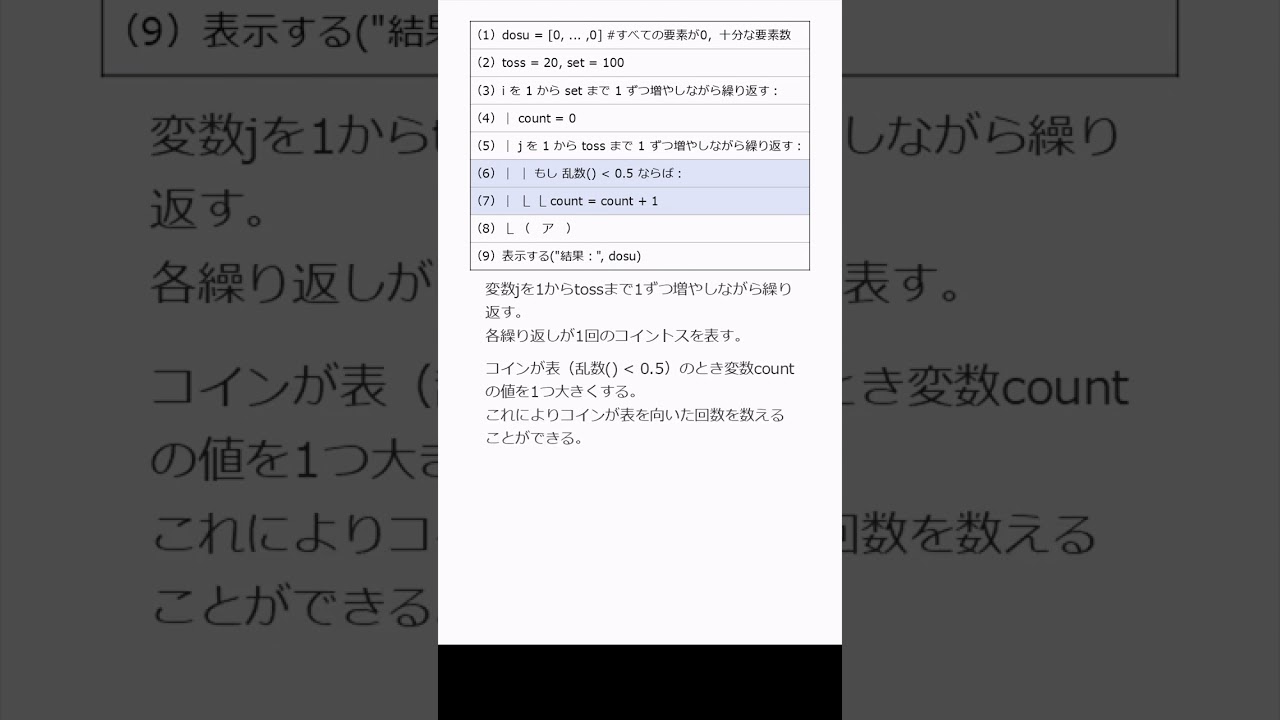
324 コイン投げの結果を度数分布表にまとめる：ばらつきを可視化しよう！
【数Ⅲ】【微分とその応用】微分計算の基本1 ※問題文は概要欄
単元：
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
微分しなさい
$y=(x+2)(x-1)(x-5)$
$y=(x^3-x)(x^2+1)(x-1)$
$ y= \dfrac{x}{(1+x^3)^2}$
$y= \dfrac{1}{x\sqrt[ 4 ]{ x }}$
$y=x \sqrt{x^2+2}$
$y= \dfrac{x}{\sqrt{1-x^2}}$
$f(x) = \dfrac{1}{x^3+1}$の逆関数$f^{-1}(x)$ の $x=\dfrac{1}{9}$における微分係数を求めよ。
この動画を見る
微分しなさい
$y=(x+2)(x-1)(x-5)$
$y=(x^3-x)(x^2+1)(x-1)$
$ y= \dfrac{x}{(1+x^3)^2}$
$y= \dfrac{1}{x\sqrt[ 4 ]{ x }}$
$y=x \sqrt{x^2+2}$
$y= \dfrac{x}{\sqrt{1-x^2}}$
$f(x) = \dfrac{1}{x^3+1}$の逆関数$f^{-1}(x)$ の $x=\dfrac{1}{9}$における微分係数を求めよ。
30秒で解ける！？早稲田の入試問題！ #Shorts #ずんだもん #勉強 #数学
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
x>0のとき、3x+(1/x³)の最小値は？
この動画を見る
x>0のとき、3x+(1/x³)の最小値は？
整数問題の良問！どうやって解く？ #Shorts #ずんだもん #勉強 #数学
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
直角三角形の３辺の長さがすべて整数のとき、面積は２の整数倍であることを示せ。
この動画を見る
直角三角形の３辺の長さがすべて整数のとき、面積は２の整数倍であることを示せ。
福田のおもしろ数学344〜条件付き最小値問題と絶対値の処理
単元：
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\log_{ 4 }( x+2y)+\log_{ 4 } (x-2y)=1$のとき、$|x|ー|y|$の最小値を求めよ。
この動画を見る
$\log_{ 4 }( x+2y)+\log_{ 4 } (x-2y)=1$のとき、$|x|ー|y|$の最小値を求めよ。
疲労を求める？京大数学を２通りで解説！【京都大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
Aが毎時akmの一定の速さで、ある地点から出発し、lkm進んだのち、Bが同一地点を出発し、同一の路をへて一定の速さでAを追う。BがAに追いつくまでの疲労を最小にするには、どんな速さで進めばよいか。ただし、疲労は速さの二乗と時間とに比例するものとする。
この動画を見る
Aが毎時akmの一定の速さで、ある地点から出発し、lkm進んだのち、Bが同一地点を出発し、同一の路をへて一定の速さでAを追う。BがAに追いつくまでの疲労を最小にするには、どんな速さで進めばよいか。ただし、疲労は速さの二乗と時間とに比例するものとする。
福田のおもしろ数学343〜3次方程式の解の存在範囲
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$1 \geq a \geq b \geq c >0$ のとき $x^3+a x^2+bx+c=0$ の1つの解を $\alpha$ とする。
$|a| \leq 1$ を証明してください。
この動画を見る
$1 \geq a \geq b \geq c >0$ のとき $x^3+a x^2+bx+c=0$ の1つの解を $\alpha$ とする。
$|a| \leq 1$ を証明してください。
東大数学！巨大数を扱う問題！ #Shorts #ずんだもん #勉強 #数学
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
10^210/10^10 +3の1の位の数字を求めよ。ただし、3^21＝10460353203を用いてよい。
この動画を見る
10^210/10^10 +3の1の位の数字を求めよ。ただし、3^21＝10460353203を用いてよい。
このイラストは何の公式？
【手と思考を止めるな…！】整数：法政大学第二高等学校～全国入試問題解法
単元：
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)#法政大学第二高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$2^nを19で割ったときの余りが9となる最小の自然数nを求めなさい。$
この動画を見る
$2^nを19で割ったときの余りが9となる最小の自然数nを求めなさい。$
京大の不等式の証明問題！３通りで解いてみました【京都大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
0<x(1-x²)√x/2が成り立つことを証明せよ。
この動画を見る
0<x(1-x²)√x/2が成り立つことを証明せよ。
シンプルで難しい整数問題 #Shorts #ずんだもん #勉強 #数学
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
連立方程式
x²=yz+7
y²=zx+7
z²=xy+7
を満たす整数の組(x,y,z)でx<=y<=zとなるものを求めよ。
この動画を見る
連立方程式
x²=yz+7
y²=zx+7
z²=xy+7
を満たす整数の組(x,y,z)でx<=y<=zとなるものを求めよ。
福田のおもしろ数学342〜複素数に関する三角不等式と等号成立条件
単元：
#複素数平面#複素数平面#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
複素数$z_1,z_2$に対して、$|z_1+z_2|\leqq |z_1|+|z_2|が成り立つことを証明してください。$
この動画を見る
複素数$z_1,z_2$に対して、$|z_1+z_2|\leqq |z_1|+|z_2|が成り立つことを証明してください。$
福田のおもしろ数学341〜関数方程式を解く
単元：
#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
実数から実数への関数$f(x)$が$f(x+y)=f(x)f(y)f(xy)$を満たしている。このような$f(x)$をすべて求めて下さい。
この動画を見る
実数から実数への関数$f(x)$が$f(x+y)=f(x)f(y)f(xy)$を満たしている。このような$f(x)$をすべて求めて下さい。
【数Ⅰ】【2次関数】絶対値を含む関数のグラフ ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の関数のグラフをかけ。
(1)y=|2x+1|
(2)y=|x²+x|
(3)y=|x²-3x-4|
次の関数のグラフをかけ。
(1)y=x²-4|x|
(2)y=|x+1|(x-3)
次の関数のグラフをかけ。
(1)y=|x|+|x-1|
(2)y=|x+1|-|x-2|
この動画を見る
次の関数のグラフをかけ。
(1)y=|2x+1|
(2)y=|x²+x|
(3)y=|x²-3x-4|
次の関数のグラフをかけ。
(1)y=x²-4|x|
(2)y=|x+1|(x-3)
次の関数のグラフをかけ。
(1)y=|x|+|x-1|
(2)y=|x+1|-|x-2|
【数Ⅰ】【2次関数】2次不等式応用4 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2次関数y=x²+mx+2が次の条件を満たすように、定数mの値の範囲を定めよ。
(1)この2次関数のグラフとx軸の正の部分が異なる2点で交わる。
(2)この2次関数のグラフとx軸のx＜-1の部分が異なる2点で交わる。
放物線y=x²+2(m-1)x+5-m²がx軸の正の部分と負の部分のそれぞれと交わるように、定数mの値の範囲を定めよ。
2次方程式x²+2mx+2m+3=0が次のような実数解をもつように、定数mの値の範囲を定めよ。
(1)異なる2つの負の解
(2)-4より大きい異なる2つの解
この動画を見る
2次関数y=x²+mx+2が次の条件を満たすように、定数mの値の範囲を定めよ。
(1)この2次関数のグラフとx軸の正の部分が異なる2点で交わる。
(2)この2次関数のグラフとx軸のx＜-1の部分が異なる2点で交わる。
放物線y=x²+2(m-1)x+5-m²がx軸の正の部分と負の部分のそれぞれと交わるように、定数mの値の範囲を定めよ。
2次方程式x²+2mx+2m+3=0が次のような実数解をもつように、定数mの値の範囲を定めよ。
(1)異なる2つの負の解
(2)-4より大きい異なる2つの解
【数Ⅰ】【2次関数】2次不等式応用3 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の$x$についての不等式を解け。
(1)$x^2-(a+2)x+2a\lt 0$
(2)$x^2-(a-1)x-a\gt 0$
(3)$x^2-ax-2a^2\leqq 0$
不等式$x^2-(a+1)x+a\lt 0$を満たす整数$x$がちょうど2個だけ存在するように、定数$a$の値の範囲を定めよ。
この動画を見る
次の$x$についての不等式を解け。
(1)$x^2-(a+2)x+2a\lt 0$
(2)$x^2-(a-1)x-a\gt 0$
(3)$x^2-ax-2a^2\leqq 0$
不等式$x^2-(a+1)x+a\lt 0$を満たす整数$x$がちょうど2個だけ存在するように、定数$a$の値の範囲を定めよ。
【数Ⅰ】【2次関数】2次不等式応用2 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2つの放物線$y=x^2+mx+3m,y=x^2-mx+m^2-3$が、いずれも$x$軸と共有点をもたないとき、定数$m$の値の範囲を求めよ。
2つの2次方程式$x^2+mx+m=0$・・・・・・①、$x^2-2mx+m+6=0$・・・・・・②がある。次の条件を満たすように、定数$m$の値の範囲を定めよ。
(1)①、②がともに異なる2つの実数解をもつ。
(2)①、②がともに実数解をもたない。
(3)①、②の少なくとも一方が実数解をもつ。
(4) ①、②のうち一方だけが、異なる2つの実数解をもつ。
この動画を見る
2つの放物線$y=x^2+mx+3m,y=x^2-mx+m^2-3$が、いずれも$x$軸と共有点をもたないとき、定数$m$の値の範囲を求めよ。
2つの2次方程式$x^2+mx+m=0$・・・・・・①、$x^2-2mx+m+6=0$・・・・・・②がある。次の条件を満たすように、定数$m$の値の範囲を定めよ。
(1)①、②がともに異なる2つの実数解をもつ。
(2)①、②がともに実数解をもたない。
(3)①、②の少なくとも一方が実数解をもつ。
(4) ①、②のうち一方だけが、異なる2つの実数解をもつ。
福田のおもしろ数学340〜三角関数の最大値
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$-\dfrac{5}{12}\pi \leqq x \leqq -\dfrac{\pi}{3}$のとき
$y=\tan(x+\dfrac23\pi)-\tan(x+\dfrac\pi6)+\cos(x+\dfrac\pi6)$
の最大値を求めて下さい。
この動画を見る
$-\dfrac{5}{12}\pi \leqq x \leqq -\dfrac{\pi}{3}$のとき
$y=\tan(x+\dfrac23\pi)-\tan(x+\dfrac\pi6)+\cos(x+\dfrac\pi6)$
の最大値を求めて下さい。
【素早く解くには…！】文字式：青雲高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#高校入試過去問(数学)#数学(高校生)#青雲高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$x=\dfrac{3\sqrt{2}+2\sqrt{3}}{3},y=\dfrac{3\sqrt{2}-2\sqrt{3}}{2}のとき、$
$9x^2-4y^2の値を求めよ。$
この動画を見る
$x=\dfrac{3\sqrt{2}+2\sqrt{3}}{3},y=\dfrac{3\sqrt{2}-2\sqrt{3}}{2}のとき、$
$9x^2-4y^2の値を求めよ。$
気付けば一瞬！内心が絡んだ京大のベクトル！【京都大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
⊿ABCの内心をPとする。PA＋PB＋PC＝0が成り立っているとき、この三角形は正三角形であることを示せ。
この動画を見る
⊿ABCの内心をPとする。PA＋PB＋PC＝0が成り立っているとき、この三角形は正三角形であることを示せ。
最小値？「あれ」を使いそうな東大の入試問題 #Shorts #ずんだもん #勉強 #数学
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
kを正の実数とし、2次方程式 x²+x-k=0の二つの実数解をα、βとする。kがk>2の範囲を動くとき、α³/(1-β) + β³/(1-α)の最小値を求めよ。
この動画を見る
kを正の実数とし、2次方程式 x²+x-k=0の二つの実数解をα、βとする。kがk>2の範囲を動くとき、α³/(1-β) + β³/(1-α)の最小値を求めよ。
福田のおもしろ数学339〜自然数の列から平方数を除いてできる列の第2024項の値
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
自然数の列$1,2,3,\cdots$から平方数を除いてできる列を$a_1,a_2,a_3,\cdots$とする。$a_{2024}$を求めて下さい。
この動画を見る
自然数の列$1,2,3,\cdots$から平方数を除いてできる列を$a_1,a_2,a_3,\cdots$とする。$a_{2024}$を求めて下さい。
落とせないベクトル！京大でもびびる必要なし！【京都大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
三角形ABCと点Pに対して、次の二つの条件は同値であることを証明せよ。
(i) 点Pは三角形ABCの内部(周は除く)にある
(ii)正の数a,b,cがあって、aPA+bPB+cPC=0が成り立つ。
この動画を見る
三角形ABCと点Pに対して、次の二つの条件は同値であることを証明せよ。
(i) 点Pは三角形ABCの内部(周は除く)にある
(ii)正の数a,b,cがあって、aPA+bPB+cPC=0が成り立つ。
これ解けたら自信持っていい！整数問題の難問 #Shorts #ずんだもん #勉強 #数学
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
pを素数、kを自然数とする。
12p²+12p+1=k²を満たすようなpの値を求めよ。
この動画を見る
pを素数、kを自然数とする。
12p²+12p+1=k²を満たすようなpの値を求めよ。
福田のおもしろ数学338〜不定方程式の整数解
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a^2+b=b^{2025}$を満たす整数$a,b$を求めて下さい。
この動画を見る
$a^2+b=b^{2025}$を満たす整数$a,b$を求めて下さい。
【数Ⅰ】【2次関数】2次不等式応用1 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2次不等式$ax^2+x+b\gt 0$の解が$x\lt -3,2\lt x$であるとき、定数$a,b$の値を求めよ。
$a,b$は定数とする。2次不等式$4x^2+ax+b\lt 0$の解が$1\lt x\lt \dfrac{5}{4}$であるとき、2次不等式$bx^2+ax+4\geqq 0$の解を求めよ。
この動画を見る
2次不等式$ax^2+x+b\gt 0$の解が$x\lt -3,2\lt x$であるとき、定数$a,b$の値を求めよ。
$a,b$は定数とする。2次不等式$4x^2+ax+b\lt 0$の解が$1\lt x\lt \dfrac{5}{4}$であるとき、2次不等式$bx^2+ax+4\geqq 0$の解を求めよ。
【初見では固まる…！】平方根：慶応義塾高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#高校入試過去問(数学)#数学(高校生)#慶應義塾高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$次の式を計算せよ。$
$\dfrac{1}{(1+\sqrt{2}+\sqrt{3})^2}+\dfrac{1}{(1+\sqrt{2}-\sqrt{3})^2}$
この動画を見る
$次の式を計算せよ。$
$\dfrac{1}{(1+\sqrt{2}+\sqrt{3})^2}+\dfrac{1}{(1+\sqrt{2}-\sqrt{3})^2}$