 高校入試過去問(数学)
高校入試過去問(数学)
 高校入試過去問(数学)
高校入試過去問(数学)
これが高校受験!?整数問題 巣鴨

単元:
#計算と数の性質#数学(中学生)#約数・倍数を利用する問題#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
3x+4yが表せない自然数は全部で何個?(x,y:自然数)
巣鴨高等学校
この動画を見る
3x+4yが表せない自然数は全部で何個?(x,y:自然数)
巣鴨高等学校
【2分で今後、役に立つ知識を得る!】二次関数:東京都立産業技術高等専門学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#東京都立産業技術高等専門学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立産業技術高等専門学校
次の等式が成り立つように、 $\fbox{ ① }$、$\fbox{ ② }$に当てはまる数を求めよ。
$x^2-4x=(x-\fbox{ ① })^2-\fbox{ ② }$
この動画を見る
入試問題 東京都立産業技術高等専門学校
次の等式が成り立つように、 $\fbox{ ① }$、$\fbox{ ② }$に当てはまる数を求めよ。
$x^2-4x=(x-\fbox{ ① })^2-\fbox{ ② }$
2通りで解説!!式の値 日本女子大附属

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{x} - \frac{1}{y} = -5$
$\frac{(x-1)(y+1)+1}{xy} = ?$
日本女子大学附属高等学校
この動画を見る
$\frac{1}{x} - \frac{1}{y} = -5$
$\frac{(x-1)(y+1)+1}{xy} = ?$
日本女子大学附属高等学校
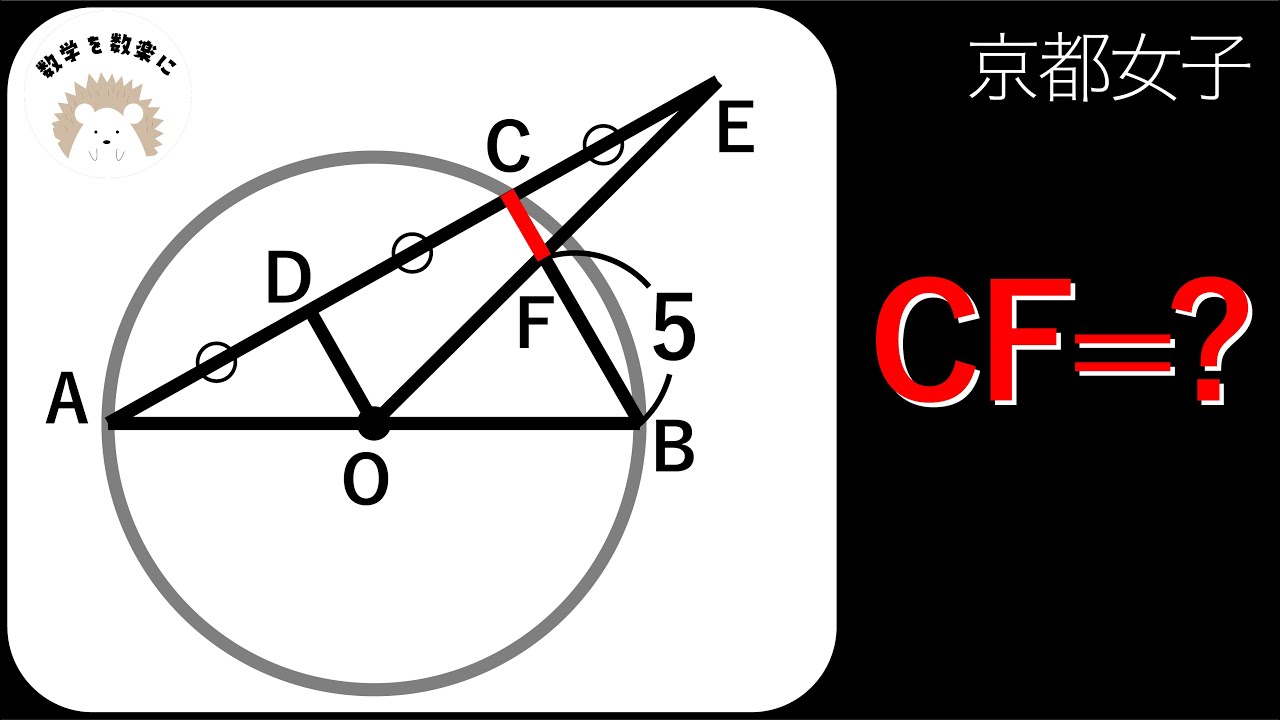
2通りで解説!!京都女子
単元:
#数学(中学生)#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
CF=?
*図は動画内参照
京都女子高等学校
この動画を見る
CF=?
*図は動画内参照
京都女子高等学校
ルートがらみの連立方程式。明大明治

単元:
#数学(中学生)#中2数学#中3数学#連立方程式#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{2021}x + \sqrt{2019}y = 2$
$\sqrt{2019}x + \sqrt{2021}y = 1$
$x^2 - y^2 =?$
明治大学付属明治高等学校
この動画を見る
$\sqrt{2021}x + \sqrt{2019}y = 2$
$\sqrt{2019}x + \sqrt{2021}y = 1$
$x^2 - y^2 =?$
明治大学付属明治高等学校
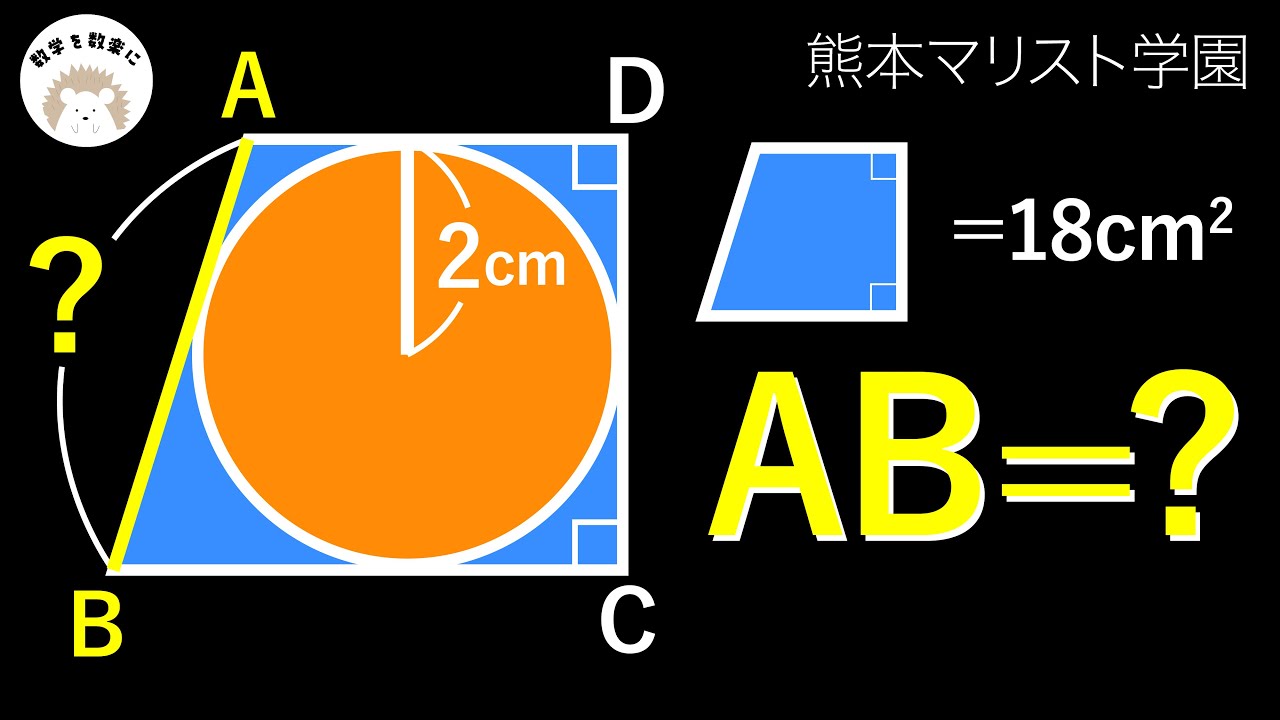
円と台形 熊本マリスト学園
単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
四角形ABCD=18㎠
AB=?
*図は動画内参照
熊本マリスト学園高等学校
この動画を見る
四角形ABCD=18㎠
AB=?
*図は動画内参照
熊本マリスト学園高等学校
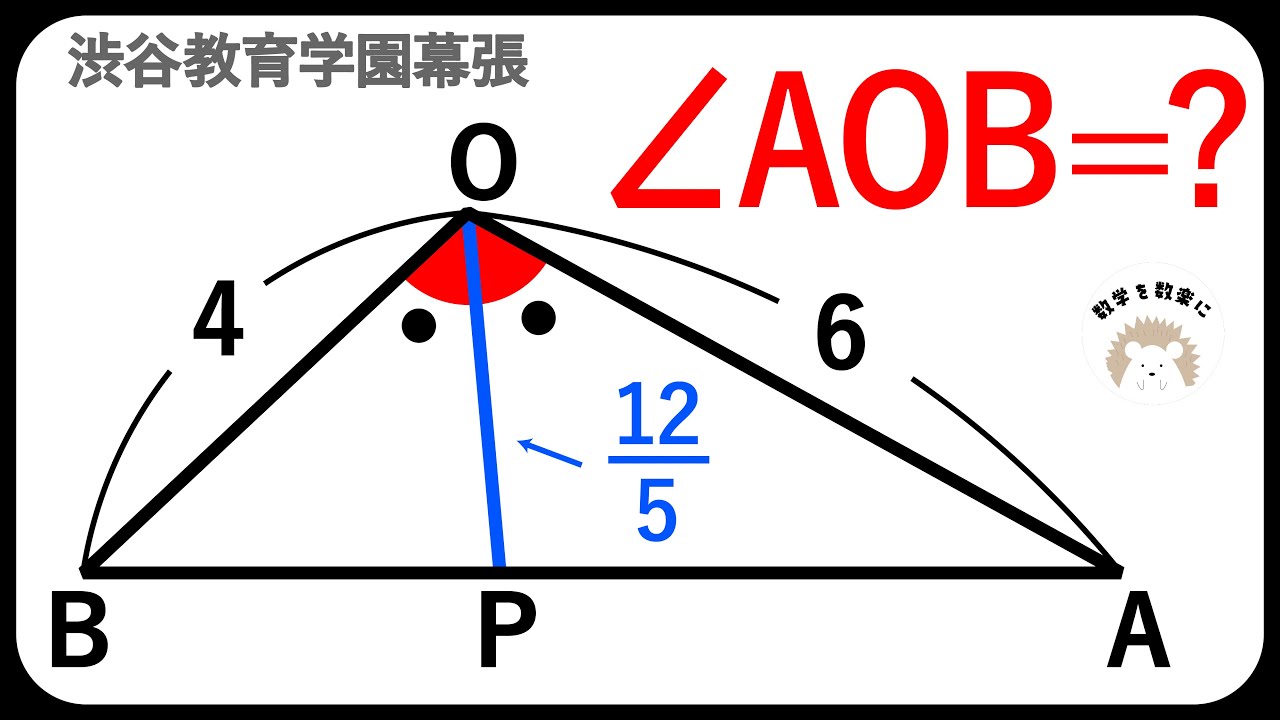
角度が出てないのに角度が出る問題 渋谷教育学園幕張高校
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle AOB =?$
*図は動画内参照
渋谷教育学園幕張高校
この動画を見る
$\angle AOB =?$
*図は動画内参照
渋谷教育学園幕張高校
【中学数学】証明の入試問題演習【高校受験】

高校生は解けるが中学生にはきつい

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$- \frac{1}{2}x^2+\frac{1}{2}x+3 = -\frac{1}{2}(x+▢)(x-▢) = -\frac{1}{2}(x-▢)^2+▢$
慶應義塾高等学校
この動画を見る
$- \frac{1}{2}x^2+\frac{1}{2}x+3 = -\frac{1}{2}(x+▢)(x-▢) = -\frac{1}{2}(x-▢)^2+▢$
慶應義塾高等学校
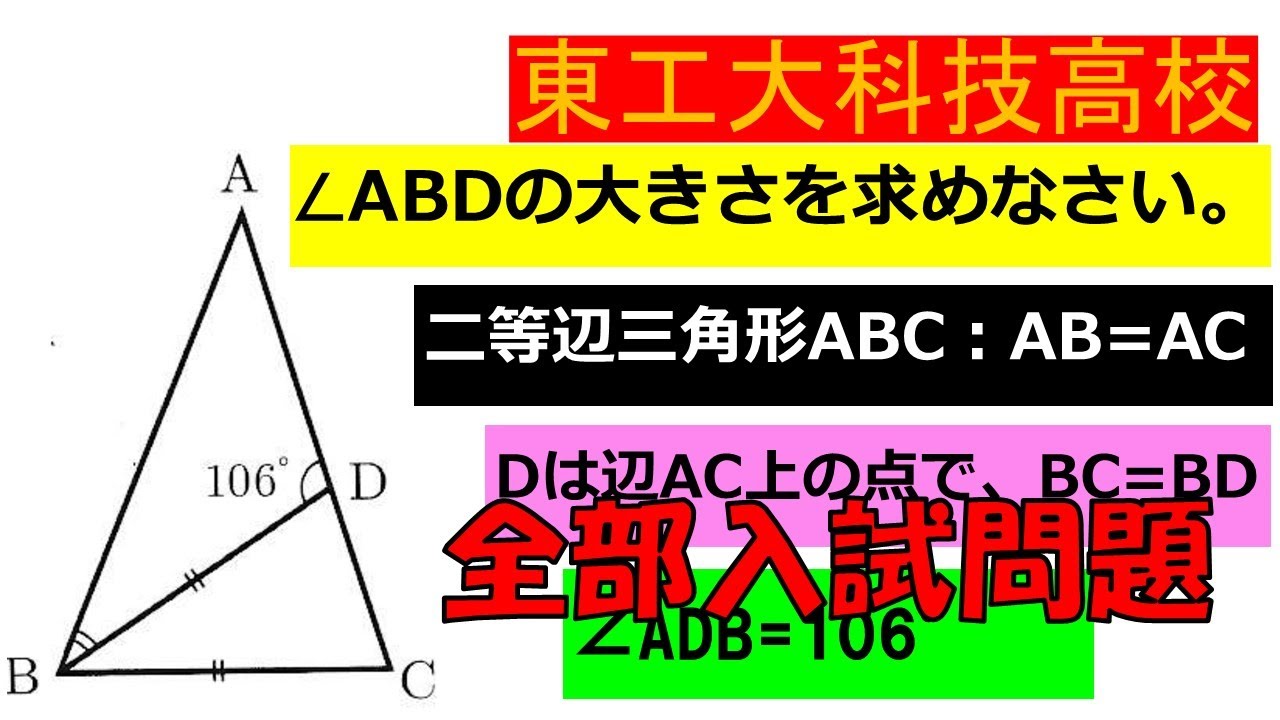
【1分で知る図形の本質!】図形:東京工業大学附属科学技術高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#東京工業大学附属科学技術高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京工業大学附属科学技術高等学校
$\angle ABD$の大きさを求めなさい。
二等辺三角形ABC:AB=AC
Dは辺AC上の点で、BC=BD
$\angle ADB=106°$
この動画を見る
入試問題 東京工業大学附属科学技術高等学校
$\angle ABD$の大きさを求めなさい。
二等辺三角形ABC:AB=AC
Dは辺AC上の点で、BC=BD
$\angle ADB=106°$
【中学の計算をまとめる3分間】平方根:東京学芸大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#東京学芸大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京学芸大学附属高等学校
$(\sqrt{ 2^2 }+\sqrt{ 3 }-\sqrt{ 2 }+\sqrt{ 1^2 })\{ \sqrt{ -(2)^2 } +\sqrt{ 3 } + \sqrt{ 2 }+ \sqrt{ -(1)^2 } \}$
を求めよ。
この動画を見る
入試問題 東京学芸大学附属高等学校
$(\sqrt{ 2^2 }+\sqrt{ 3 }-\sqrt{ 2 }+\sqrt{ 1^2 })\{ \sqrt{ -(2)^2 } +\sqrt{ 3 } + \sqrt{ 2 }+ \sqrt{ -(1)^2 } \}$
を求めよ。
整数問題 愛知高校

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1から9までの自然数から異なる2つを選びa,bとする。(a<b)
$\frac{1}{a} - \frac{1}{b}$の値が最も小さくなるa,bを求めよ。
愛知高等学校
この動画を見る
1から9までの自然数から異なる2つを選びa,bとする。(a<b)
$\frac{1}{a} - \frac{1}{b}$の値が最も小さくなるa,bを求めよ。
愛知高等学校
三乗−三乗の因数分解の公式知らなくても解けるよ。慶應義塾高校の小問。
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
a-b=3 \\
b= \frac{6}{a}
\end{array}
\right.
\end{eqnarray}
$
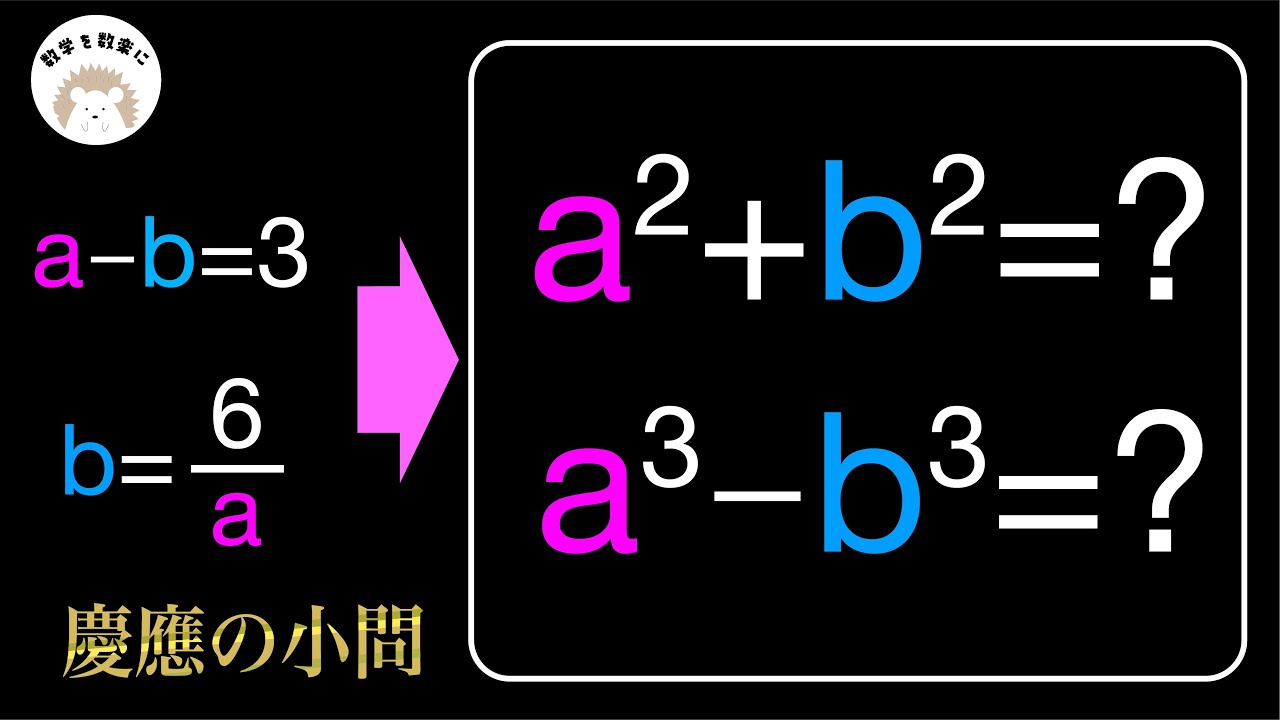
のとき$a^2+b^2=?$ $\quad$ $a^3-b^3=?$
慶應義塾高等学校
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
a-b=3 \\
b= \frac{6}{a}
\end{array}
\right.
\end{eqnarray}
$
のとき$a^2+b^2=?$ $\quad$ $a^3-b^3=?$
慶應義塾高等学校
2通りで解説!!注意点あり!

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$(a-b)^2+(b-a)-6$
関西大学第一高等学校
この動画を見る
因数分解せよ
$(a-b)^2+(b-a)-6$
関西大学第一高等学校
【1分で知る計算の世界!】因数分解:東京工業大学附属科学技術高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#東京工業大学附属科学技術高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京工業大学附属科学技術高等学校
次の式を因数分解しなさい。
$3x^2y-6xy-105y$
この動画を見る
入試問題 東京工業大学附属科学技術高等学校
次の式を因数分解しなさい。
$3x^2y-6xy-105y$
【1分で解く?本質を理解して解く!】整数:大阪教育大学附属高等学校平野校舎~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#大阪教育大学附属高等学校平野校舎
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 阪教育大学附属高等学校平野校舎
連続する4つの自然数があり、
小さい2数の和と大きい2数の 和の積が2021になるとき、
この4つの自然数を求めなさい。
※小さい2数とは、最も小さい数と2番目に小さい数のことであり、
大きい2数とは、最も大きい数と2番目に大きい数のことである。
この動画を見る
入試問題 阪教育大学附属高等学校平野校舎
連続する4つの自然数があり、
小さい2数の和と大きい2数の 和の積が2021になるとき、
この4つの自然数を求めなさい。
※小さい2数とは、最も小さい数と2番目に小さい数のことであり、
大きい2数とは、最も大きい数と2番目に大きい数のことである。
綺麗に解けます。 明大明治
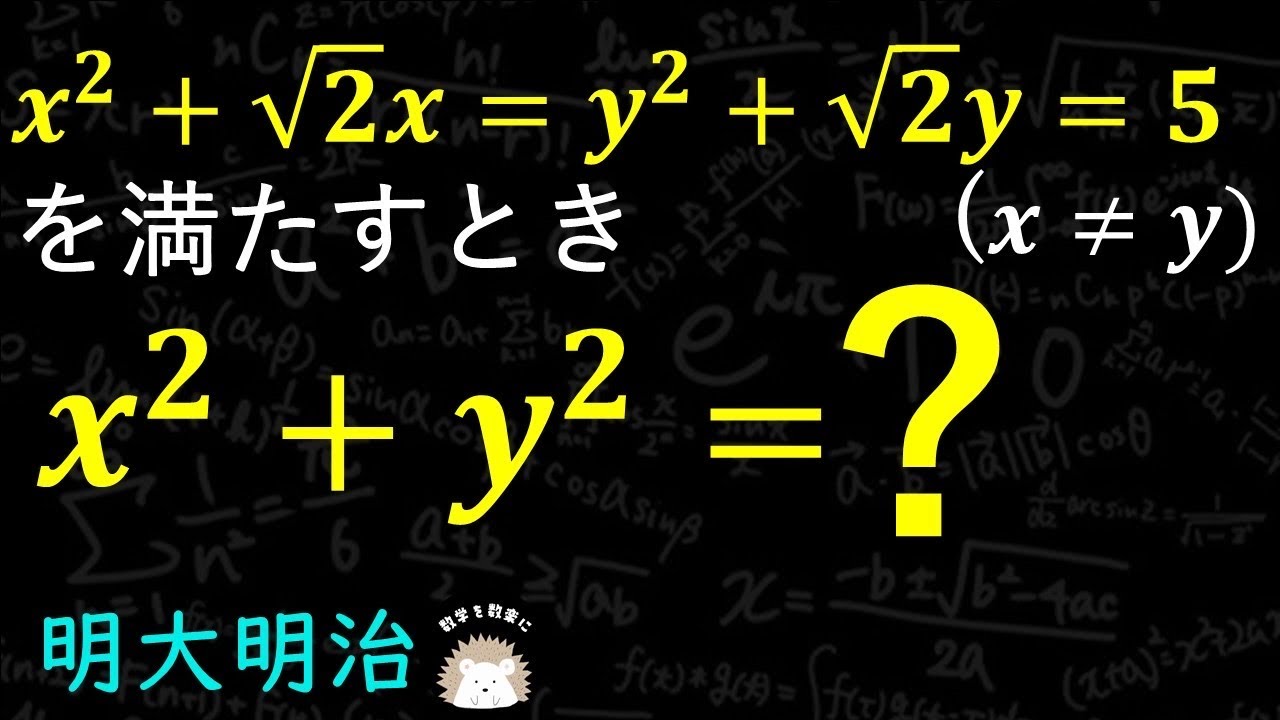
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2+\sqrt 2x = y^2+ \sqrt 2 y = 5(x \neq y)$を満たすとき
$x^2+y^2 =?$
明治大学付属明治高等学校
この動画を見る
$x^2+\sqrt 2x = y^2+ \sqrt 2 y = 5(x \neq y)$を満たすとき
$x^2+y^2 =?$
明治大学付属明治高等学校
【3分でOK!文字式が得意になる!】文字式:大阪教育大学附属高等学校池田校舎~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#大阪教育大学附属高等学校池田校舎
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 大阪教育大学附属高等学校池田校舎
$\displaystyle \frac{1}{a}-\displaystyle \frac{1}{b}=3$
のとき
$\displaystyle \frac{a+4ab-b}{3a-3b}$
の値を求めなさい。
この動画を見る
入試問題 大阪教育大学附属高等学校池田校舎
$\displaystyle \frac{1}{a}-\displaystyle \frac{1}{b}=3$
のとき
$\displaystyle \frac{a+4ab-b}{3a-3b}$
の値を求めなさい。
灘高校に受かるのは難だけど、この問題は難てこともない問題
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
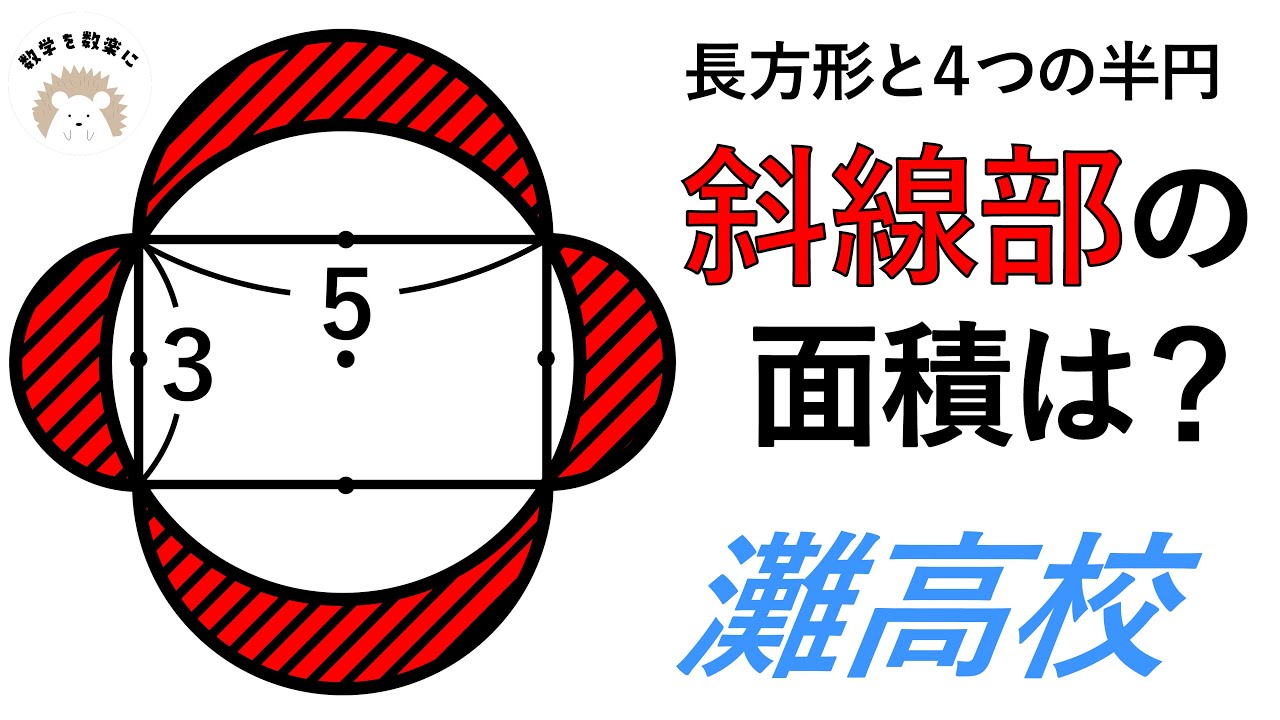
長方形と4つの半円
斜線部の面積は?
*図は動画内参照
灘高等学校
この動画を見る
長方形と4つの半円
斜線部の面積は?
*図は動画内参照
灘高等学校
【要領よく正解しよう!】整数:お茶の水女子大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#お茶の水女子大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 お茶の水女子大学附属高等学校
3以上の奇数はとなりあう自然数の平方の差で表すことができる。
(例)$7=4^2-3^2$
①奇数11を(例)のように表しなさい。
②3以上の奇数をp、となりあう自然数のうち大きい方をmとしたとき、 mをpの式で表しなさい。
③111を(例)のようにとなりあう自然数の平方の差で表しなさい。
この動画を見る
入試問題 お茶の水女子大学附属高等学校
3以上の奇数はとなりあう自然数の平方の差で表すことができる。
(例)$7=4^2-3^2$
①奇数11を(例)のように表しなさい。
②3以上の奇数をp、となりあう自然数のうち大きい方をmとしたとき、 mをpの式で表しなさい。
③111を(例)のようにとなりあう自然数の平方の差で表しなさい。
実はこの問題、瞬殺できます 大阪星光学院

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-5x+1=0$
$x^2+ \frac{1}{x^2}=?$
大阪星光学院高等学校
この動画を見る
$x^2-5x+1=0$
$x^2+ \frac{1}{x^2}=?$
大阪星光学院高等学校
【3分でOK!】因数分解:青雲高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#青雲高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 青雲高等学校
因数分解せよ。
$(x^2-2x-3)^2+13(x^2-2x-3)-90$
この動画を見る
入試問題 青雲高等学校
因数分解せよ。
$(x^2-2x-3)^2+13(x^2-2x-3)-90$
【3分で見えてくる。正解の道筋!】図形:石川県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#石川県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
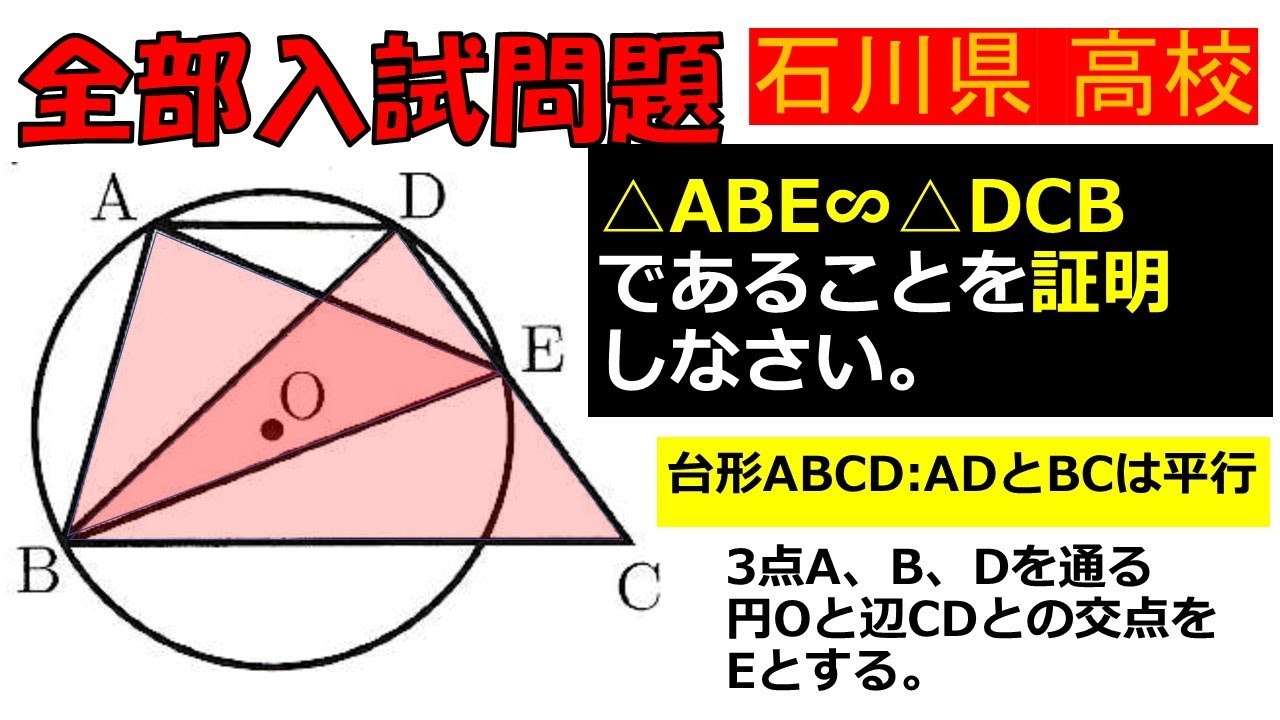
入試問題 石川県の公立高等学校
△ABE∞△DCB
であることを証明しなさい。
台形ABCD:ADとBCは平行
3点A、B、Dを通る
円Oと辺CDとの交点を Eとする。
この動画を見る
入試問題 石川県の公立高等学校
△ABE∞△DCB
であることを証明しなさい。
台形ABCD:ADとBCは平行
3点A、B、Dを通る
円Oと辺CDとの交点を Eとする。
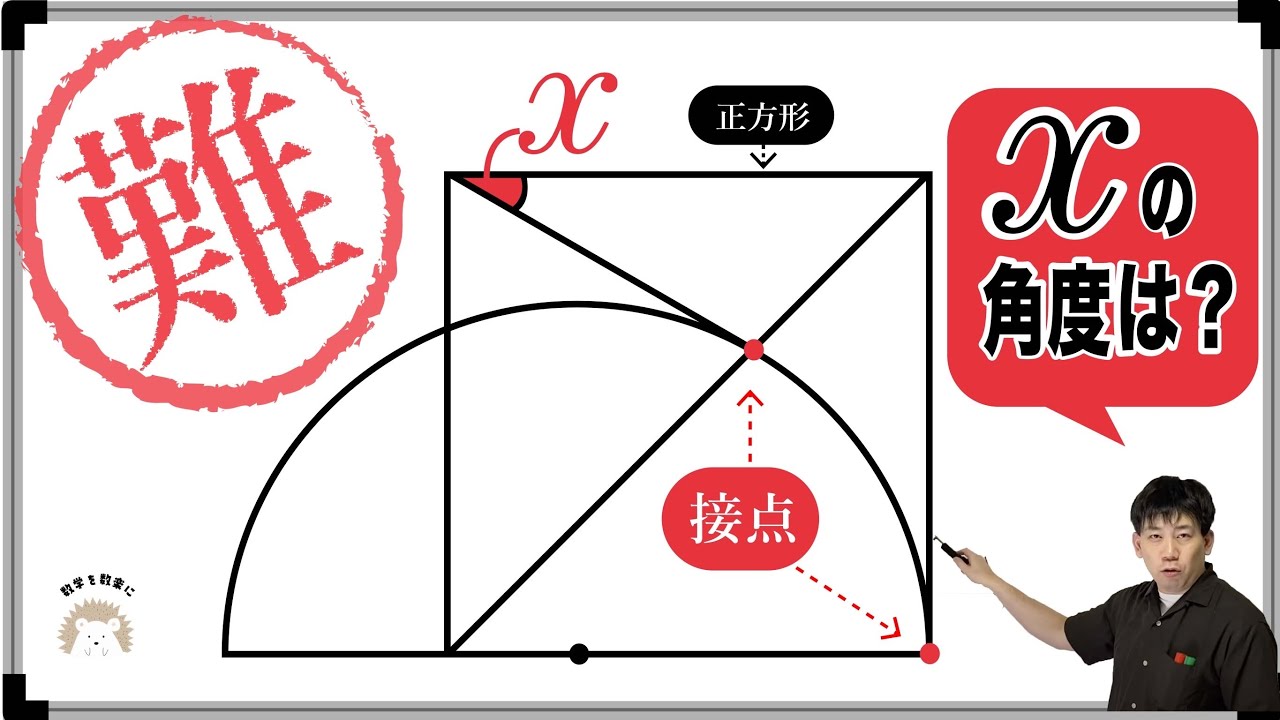
半円と正方形 難です。
単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x =?$
*図は動画内参照
灘高等学校
この動画を見る
$\angle x =?$
*図は動画内参照
灘高等学校
気付けば一瞬!!の確率の問題 東奥義塾

単元:
#数学(中学生)#数A#場合の数と確率#確率#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1⃣ 2⃣ 3⃣ 4⃣ 5⃣
の5枚のカードから3枚のカードを並べてできる3ケタの整数で
奇数となる確率は?
東奥義塾高等学校
この動画を見る
1⃣ 2⃣ 3⃣ 4⃣ 5⃣
の5枚のカードから3枚のカードを並べてできる3ケタの整数で
奇数となる確率は?
東奥義塾高等学校
【奇問認定!?】関数:立命館高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#立命館高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
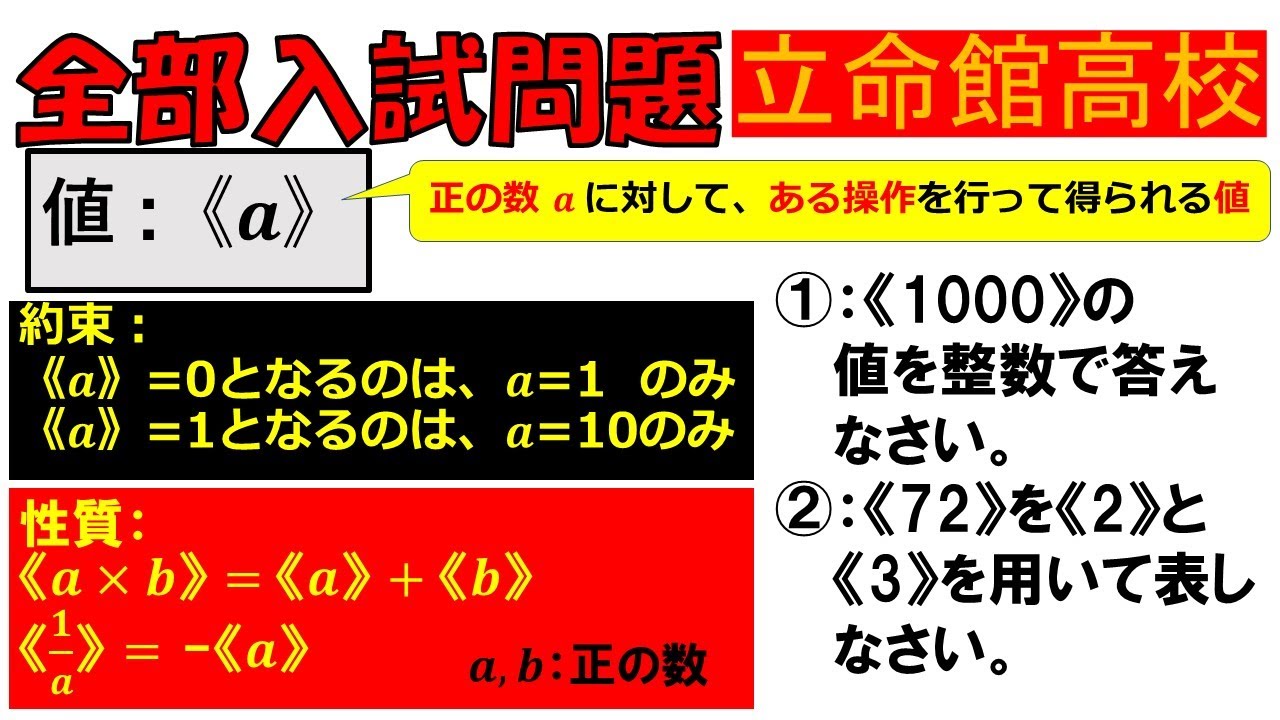
入試問題 立命館高等学校
値:《a》
正の数に対して、ある操作を行って得られる値
【約束:】
《a》=0となるのは、a=1 のみ
《a》 =1となるのは、a=10のみ
【性質:】
《a×b》 = 《a》+ 《b》 《$\displaystyle \frac{1}{a}$》 = -《a》
a, b: 正の数
①:《1000》の 値を整数で答えなさい。
②: 《72》を《2》と《3》を用いて表し なさい
この動画を見る
入試問題 立命館高等学校
値:《a》
正の数に対して、ある操作を行って得られる値
【約束:】
《a》=0となるのは、a=1 のみ
《a》 =1となるのは、a=10のみ
【性質:】
《a×b》 = 《a》+ 《b》 《$\displaystyle \frac{1}{a}$》 = -《a》
a, b: 正の数
①:《1000》の 値を整数で答えなさい。
②: 《72》を《2》と《3》を用いて表し なさい
【3分で見方が変わる!】図形:長野県 公立高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#長野県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
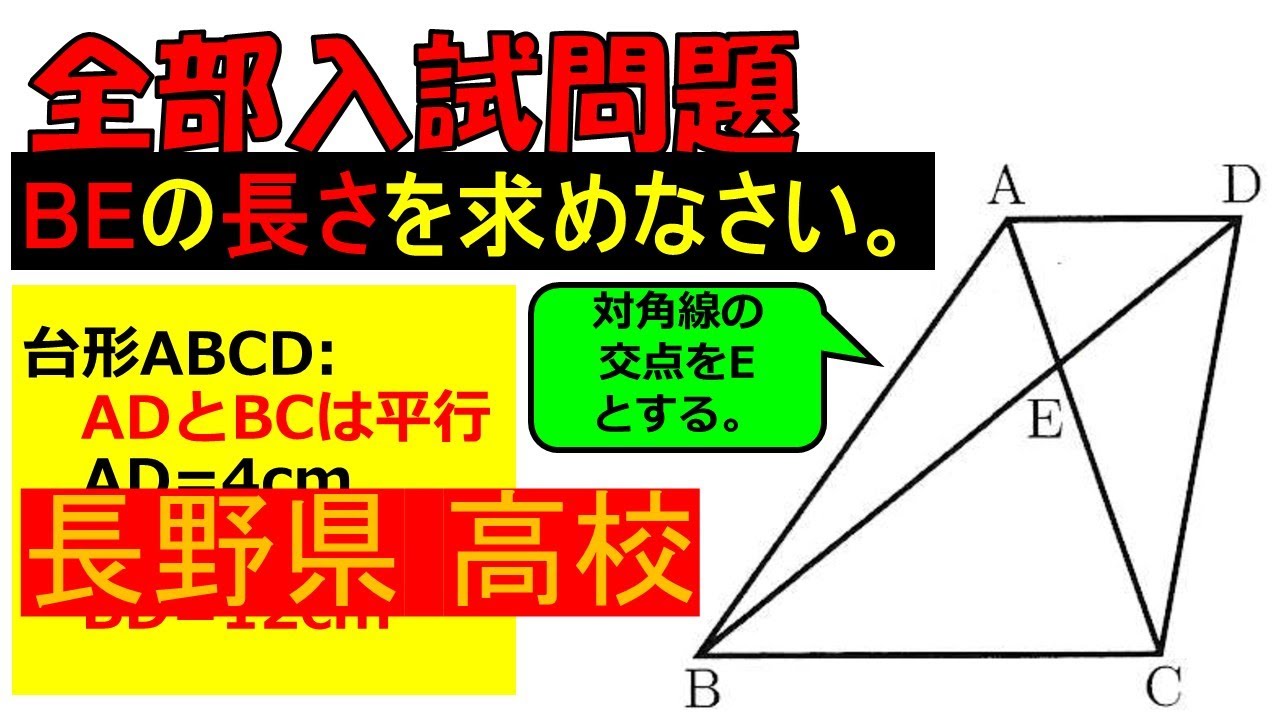
入試問題 長野県の公立高等学校
BEの長さを求めなさい。
台形ABCD:
ADとBCは平行
AD=4cm
BC=8cm
BD=12cm
【対角線の 交点をE とする。】
※図は動画内参照
この動画を見る
入試問題 長野県の公立高等学校
BEの長さを求めなさい。
台形ABCD:
ADとBCは平行
AD=4cm
BC=8cm
BD=12cm
【対角線の 交点をE とする。】
※図は動画内参照
初見で解けたら認めよう。2通りで解説。
単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#方べきの定理と2つの円の関係#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
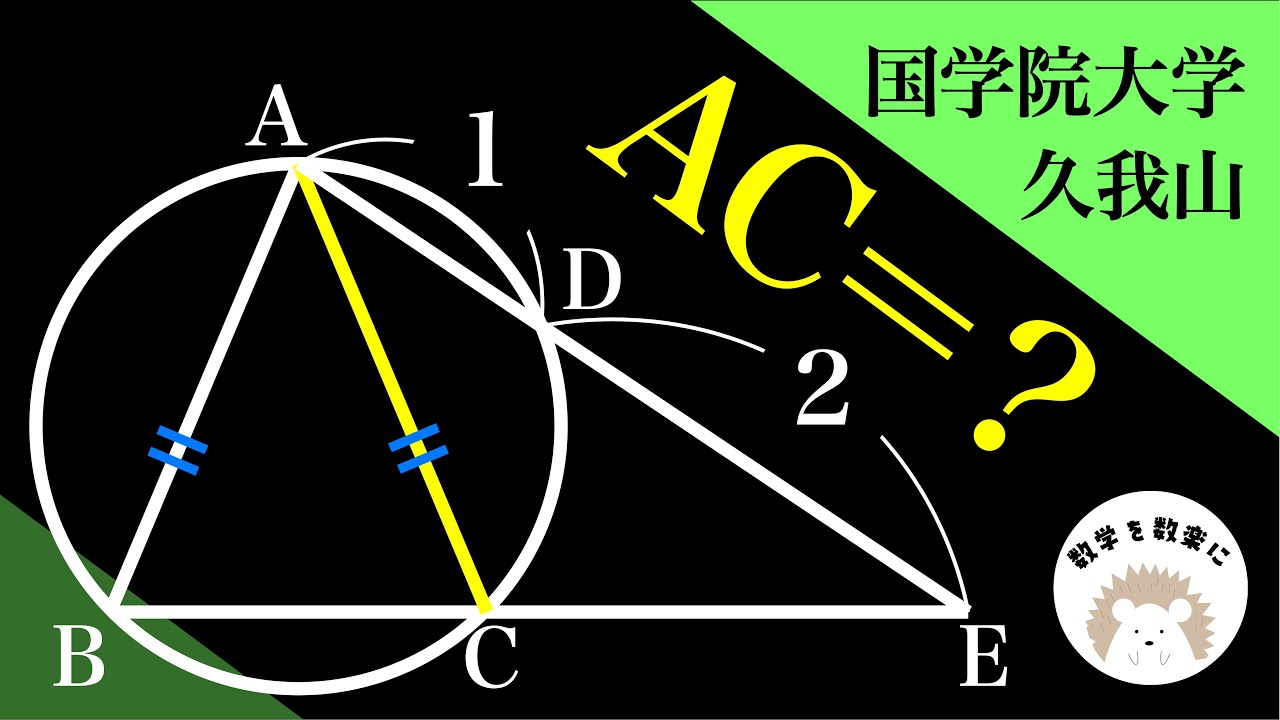
問題文全文(内容文):
AC=?
*図は動画内参照
國學院大學久我山高等学校
この動画を見る
AC=?
*図は動画内参照
國學院大學久我山高等学校
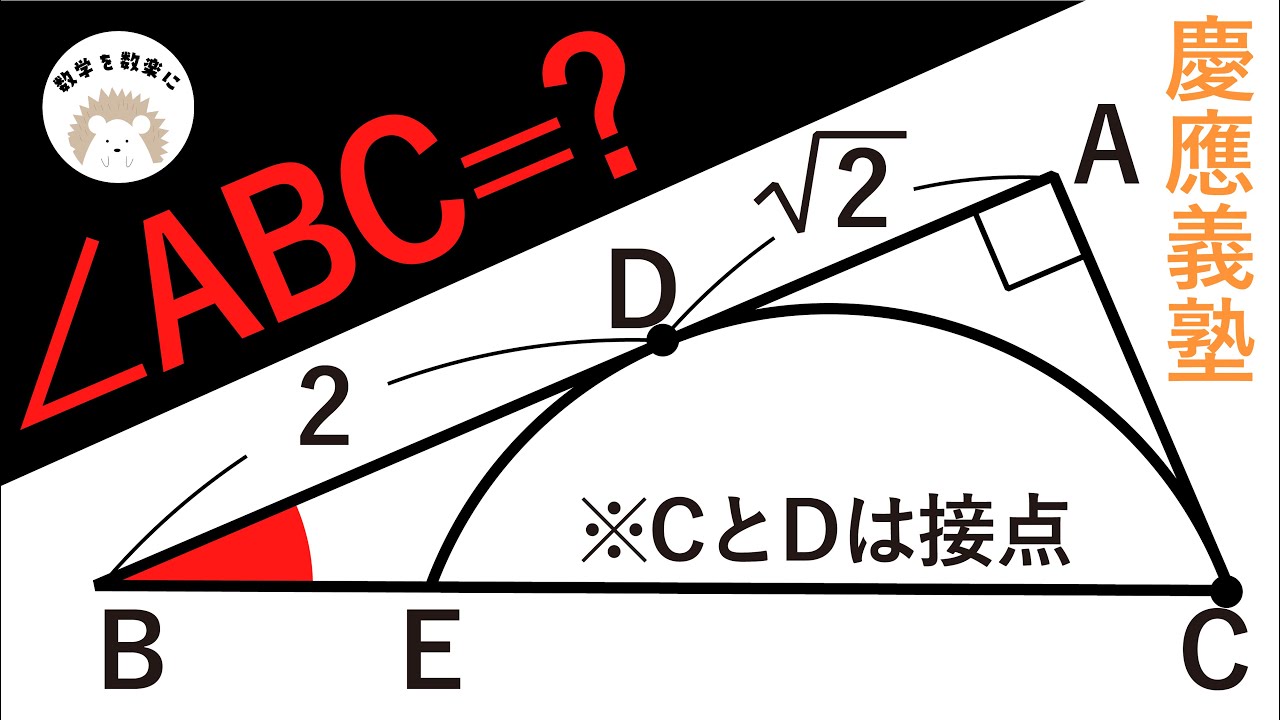
円と接線と角度 慶應義塾高校
単元:
#数学(中学生)#中3数学#数A#図形の性質#円#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点Cと点Dは接点
$\angle ABC=?$
*図は動画内参照
慶應義塾高等学校
この動画を見る
点Cと点Dは接点
$\angle ABC=?$
*図は動画内参照
慶應義塾高等学校
大学入試じゃないよ 高校入試だよ 3通りで解説 成城学園

単元:
#数学(中学生)#数Ⅱ#指数関数と対数関数#指数関数#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^{56}と5^{24}$はどっちが大きい?
成城学園高等学校
この動画を見る
$2^{56}と5^{24}$はどっちが大きい?
成城学園高等学校
