 高校入試過去問(数学)
高校入試過去問(数学)
 高校入試過去問(数学)
高校入試過去問(数学)
【まず3分!身に付く解法!】平方根:福岡大学附属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#平方根#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 福岡大学附属大濠高等学校
$\{ (2+\sqrt{ 5 })^2+(2-\sqrt{ 5 })^2\}^2-\{ (2+\sqrt{ 5 })^2-(2-\sqrt{ 5 })^2\}^2$
を計算し、簡単にすると▬である。
この動画を見る
入試問題 福岡大学附属大濠高等学校
$\{ (2+\sqrt{ 5 })^2+(2-\sqrt{ 5 })^2\}^2-\{ (2+\sqrt{ 5 })^2-(2-\sqrt{ 5 })^2\}^2$
を計算し、簡単にすると▬である。
平方根の計算 洛星高校

【3分で基礎力アップ!】平方根:福岡大学附属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#平方根#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 福岡大学附属大濠高等学校
$\displaystyle \frac{(\sqrt{ 3 }+2)(3+\sqrt{ 3 })(9-5\sqrt{ 3 })}{\sqrt{ 3 }}$
を計算し、簡単にすると▬である。
この動画を見る
入試問題 福岡大学附属大濠高等学校
$\displaystyle \frac{(\sqrt{ 3 }+2)(3+\sqrt{ 3 })(9-5\sqrt{ 3 })}{\sqrt{ 3 }}$
を計算し、簡単にすると▬である。
【図形の見方が変わる!】図形:明治学院高等学校~全国入試問題解法
単元:
#数学(中学生)#平面図形#高校入試過去問(数学)#明治学院高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治学院高等学校
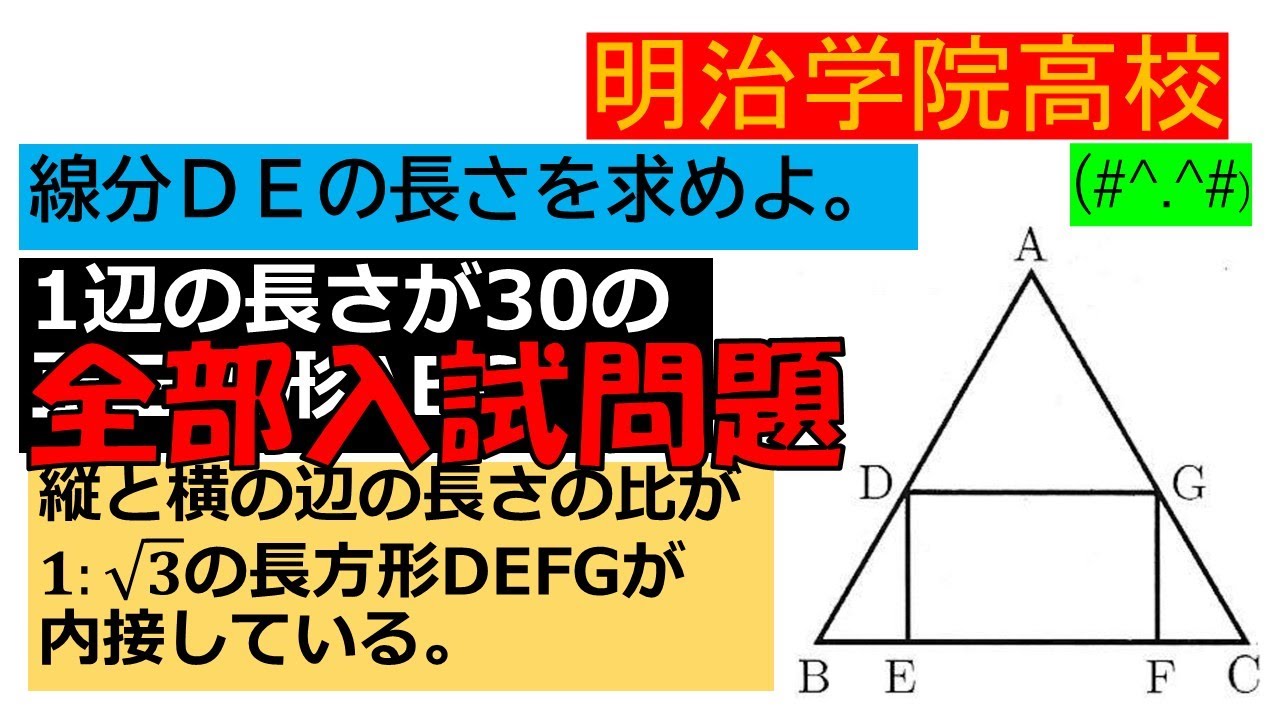
線分$DE$の長さを求めよ。
1辺の長さが30の正三角形$ABC$
縦と横の辺の長さの比が
$1:\sqrt{ 3 }$の長方形$DEFG$が
内接している。
※図は動画内参照
この動画を見る
入試問題 明治学院高等学校
線分$DE$の長さを求めよ。
1辺の長さが30の正三角形$ABC$
縦と横の辺の長さの比が
$1:\sqrt{ 3 }$の長方形$DEFG$が
内接している。
※図は動画内参照
【まず4分間!理解できる!】二次方程式:明治大学附属中野高等学校~全国入試問題解法

単元:
#数学(中学生)#2次方程式#高校入試過去問(数学)#明治大学付属中野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治大学附属中野高等学校
$X$についての2次方程式
$x^2 - (2k + 1)x + 4 = 0$
の1つの解が$x = k$のとき、 $k$の値を求めなさい。
この動画を見る
入試問題 明治大学附属中野高等学校
$X$についての2次方程式
$x^2 - (2k + 1)x + 4 = 0$
の1つの解が$x = k$のとき、 $k$の値を求めなさい。
【5分で身に付く整理する力!】文章題:明治大学附属中野高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#明治大学付属中野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治大学附属中野高等学校
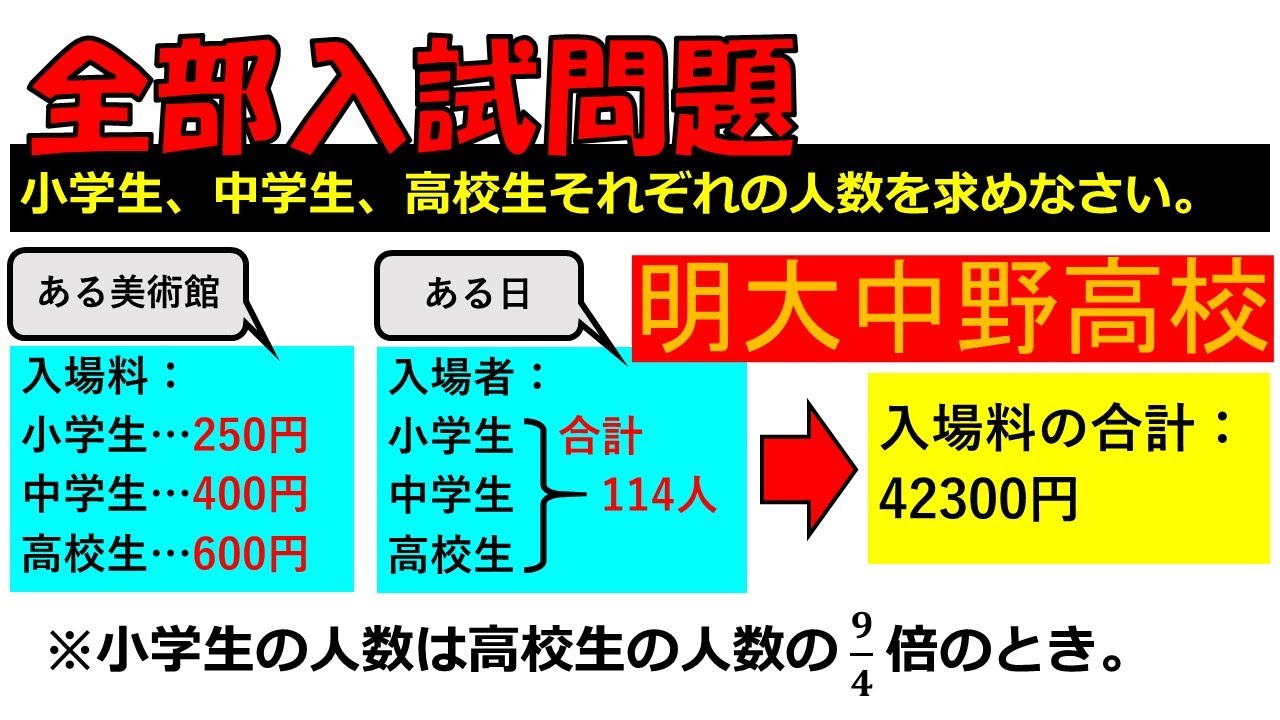
ある美術館
入場料:
小学生・・・250円
中学生・・・400円
高校生・・・600円
ある日
入場者:
小学生
中学生
高校生
合計114人
入場料の合計:42300円
※小学生の人数は高校生の人数の$\displaystyle \frac{9}{4}$倍のとき。
この動画を見る
入試問題 明治大学附属中野高等学校
ある美術館
入場料:
小学生・・・250円
中学生・・・400円
高校生・・・600円
ある日
入場者:
小学生
中学生
高校生
合計114人
入場料の合計:42300円
※小学生の人数は高校生の人数の$\displaystyle \frac{9}{4}$倍のとき。
【3分で統計の基礎力アップ!】統計:鹿児島県公立高校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#鹿児島県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 鹿児島県の公立高校
平均を求めよ。
ヒストグラムを選べ。
※資料の整理と活用標本調査
※表は動画内参照
この動画を見る
入試問題 鹿児島県の公立高校
平均を求めよ。
ヒストグラムを選べ。
※資料の整理と活用標本調査
※表は動画内参照
【式をたてる力!5分でつかめ!】文章題:法政大学第二高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#法政大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 法政大学第二高等学校
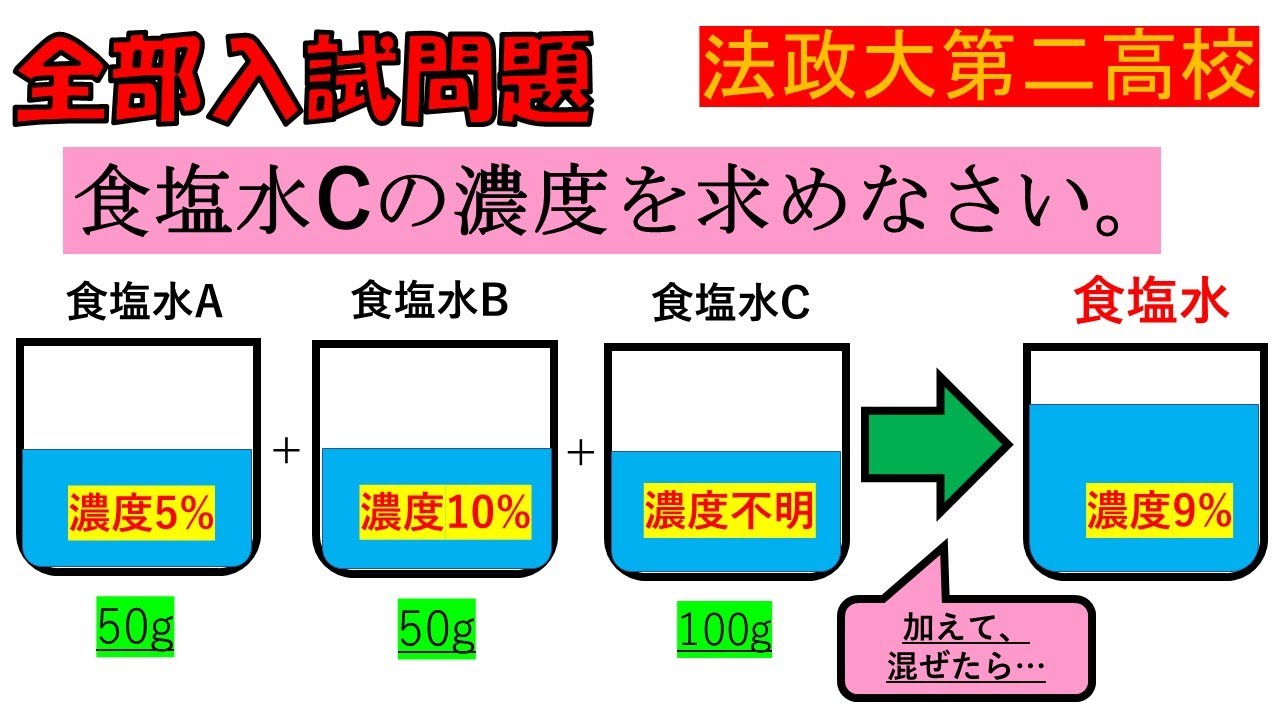
食塩水Cの濃度を求めなさい。
※図は動画内参照
この動画を見る
入試問題 法政大学第二高等学校
食塩水Cの濃度を求めなさい。
※図は動画内参照
円周角の定理の利用 お茶の水女子

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle BAC =?$
*図は動画内参照
お茶の水女子大学附属高等学校
この動画を見る
$\angle BAC =?$
*図は動画内参照
お茶の水女子大学附属高等学校
【覚えるのは数式じゃない。方法だ!】公式:二次関数の変化の割合~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
全国入試問題
覚えたら3秒で正解!?
$y=ax^2$に対して、変化の割合は
$a(x_1+x_2)$
$A:(x_1,y_1)$
$B:(x_2,y_2)$
この動画を見る
全国入試問題
覚えたら3秒で正解!?
$y=ax^2$に対して、変化の割合は
$a(x_1+x_2)$
$A:(x_1,y_1)$
$B:(x_2,y_2)$
【3分で身に付く整数問題の対処法!】整数:明治学院高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#明治学院高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治学院高等学校
$m$、$n$を1桁の自然数とする。
$(m + 3)(n-2)$
が素数となる$(m, n)$の組は いくつあるか求めよ。
この動画を見る
入試問題 明治学院高等学校
$m$、$n$を1桁の自然数とする。
$(m + 3)(n-2)$
が素数となる$(m, n)$の組は いくつあるか求めよ。
割って余る問題 整数問題 日大習志野

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
200より大きい自然数を17で割った。
商と余りが等しくなる自然数は全部で何コ?
日本大学習志野高等学校
この動画を見る
200より大きい自然数を17で割った。
商と余りが等しくなる自然数は全部で何コ?
日本大学習志野高等学校
【5分で学ぶ~表/裏ルート!】二次方程式:法政大学第二高等学校~全国入試問題解法

単元:
#数学(中学生)#2次方程式#高校入試過去問(数学)#法政大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 法政大学第二高等学校
【2次方程式】
$(x + 2)(x - 2) + 2x = 0$
を解の公式を使わずに解きなさい。
この動画を見る
入試問題 法政大学第二高等学校
【2次方程式】
$(x + 2)(x - 2) + 2x = 0$
を解の公式を使わずに解きなさい。
【5分間の格闘技!素早さを取るか、確実さを取るか!】二次方程式:函館ラ・サール高等学校~全国入試問題解法

単元:
#数学(中学生)#2次方程式#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 函館ラ・サール高等学校
【$x,t$の2次方程式】
$x^2 + ax + b = 0$
の解が$-3$と$2$のとき、
$t^2 + bt + a = −4$
を解きなさい。
この動画を見る
入試問題 函館ラ・サール高等学校
【$x,t$の2次方程式】
$x^2 + ax + b = 0$
の解が$-3$と$2$のとき、
$t^2 + bt + a = −4$
を解きなさい。
二次方程式 整数問題 都立自校作成

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式
$x^2+(a-2)x-6b = 0$の解の1つが-3のときa=? b=?
(a,bは自然数でa<b)
東京都立自校作成
この動画を見る
2次方程式
$x^2+(a-2)x-6b = 0$の解の1つが-3のときa=? b=?
(a,bは自然数でa<b)
東京都立自校作成
【瞬殺?基本方針を身に付けよう!】因数分解:函館ラ・サール高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 函館ラ・サール高等学校
因数分解しなさい。
$xy + 1 − x – y$
この動画を見る
入試問題 函館ラ・サール高等学校
因数分解しなさい。
$xy + 1 − x – y$
5人でじゃんけんの確率

【5分間冷静に対応すればいい!】二次関数:日本大学第二高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#日本大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 日本大学第二高等学校
$k$の値を求めよ。
関数$y = x^2$について、
$x$の値が、
”$k$から$k+2$まで増加する
ときの変化の割合が、
$k^2+2k-2$であった。
この動画を見る
入試問題 日本大学第二高等学校
$k$の値を求めよ。
関数$y = x^2$について、
$x$の値が、
”$k$から$k+2$まで増加する
ときの変化の割合が、
$k^2+2k-2$であった。
整数問題 筑波大学附属

単元:
#計算と数の性質#数学(中学生)#約数・倍数を利用する問題#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
素数a,bについて積abの正の約数の和が112のときab=?
筑波大学附属高等学校
この動画を見る
素数a,bについて積abの正の約数の和が112のときab=?
筑波大学附属高等学校
平方根の計算 工夫せよ 久留米大附設

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\sqrt {33} + \sqrt {21})(\sqrt {77} - 7)=$
久留米大附設高等学校
この動画を見る
$(\sqrt {33} + \sqrt {21})(\sqrt {77} - 7)=$
久留米大附設高等学校
平方完成

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-4x = (x-\boxed{ 1 })^2 - \boxed{ 2 }$
東京都立産業技術高等専門学校
この動画を見る
$x^2-4x = (x-\boxed{ 1 })^2 - \boxed{ 2 }$
東京都立産業技術高等専門学校
【その解法だけでいいのか!中学から高校へ。】二次方程式:日本大学習志野高等学校~全国入試問題解法

単元:
#数学(中学生)#2次方程式#高校入試過去問(数学)#日本大学習志野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 日本大学習志野高等学校
次の□を求めなさい。
$(2x-1)^2-2(2x-1)=15$
の2つの解の差の
2乗は$\boxed{ ァ}\boxed{ ィ}$である。
この動画を見る
入試問題 日本大学習志野高等学校
次の□を求めなさい。
$(2x-1)^2-2(2x-1)=15$
の2つの解の差の
2乗は$\boxed{ ァ}\boxed{ ィ}$である。
どうか筆算しないで。。。
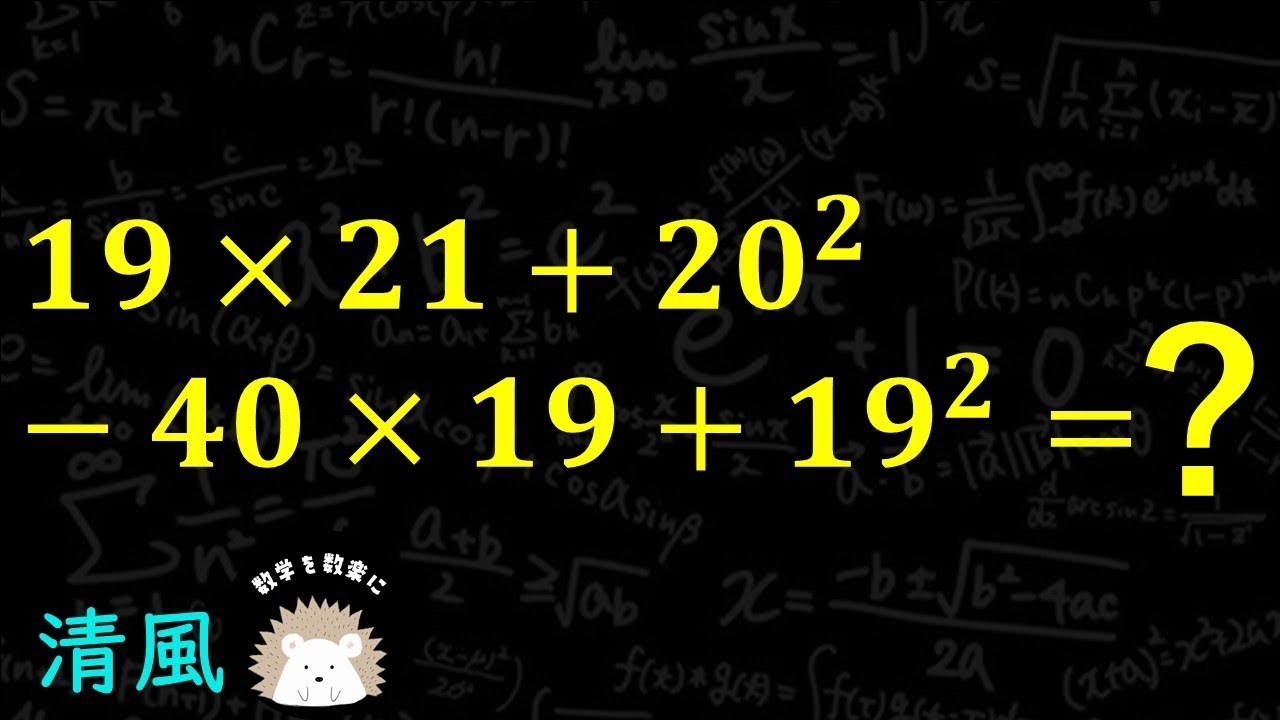
単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$19 \times 21 + 20^2 - 40 \times 19 +19^2$
清風高等学校
この動画を見る
$19 \times 21 + 20^2 - 40 \times 19 +19^2$
清風高等学校
自然数の和 日大習志野

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1からnまでの自然数の和=210
n=?(n:自然数)
日本大学習志野高等学校
この動画を見る
1からnまでの自然数の和=210
n=?(n:自然数)
日本大学習志野高等学校
どう解く? 小数を含む2次方程式の計算 桐光学園

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
(0.2x+0.3)(x-0.5) = 1.05
桐光学園高等学校
この動画を見る
2次方程式を解け
(0.2x+0.3)(x-0.5) = 1.05
桐光学園高等学校
灘高校 数学
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
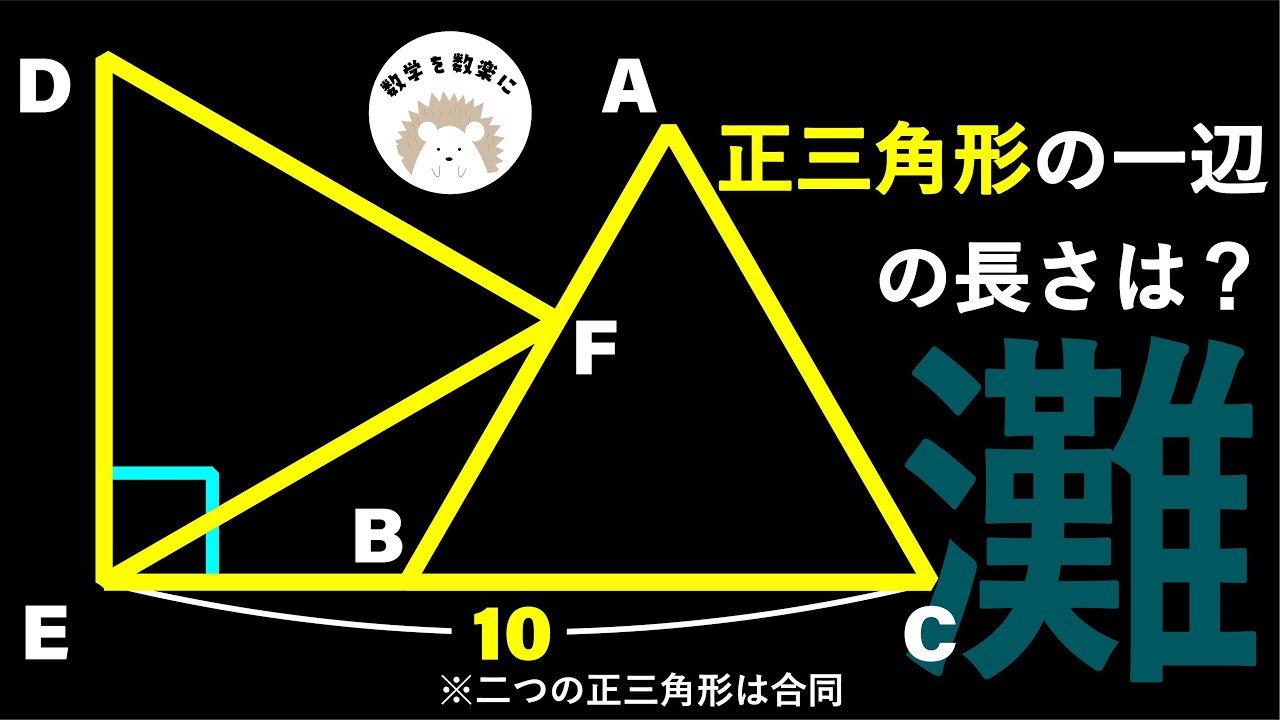
△ABCと△DEFは合同な正三角形
正三角形の1辺の長さ=?
*図は動画内参照
灘高等学校
この動画を見る
△ABCと△DEFは合同な正三角形
正三角形の1辺の長さ=?
*図は動画内参照
灘高等学校
【3分で身に付く考える力!】文字式:日本大学第三高等学校~全国入試問題解法

単元:
#数学(中学生)#文字と式#高校入試過去問(数学)#日本大学第三高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 日本大学第三高等学校
$(x+y)^2=\displaystyle \frac{51+10\sqrt{ 2 }}{5}$
のとき
$x-y=\displaystyle \frac{1-5\sqrt{ 2 }}{\sqrt{ 5 }}$
のとき
$4xy$の値を求めなさい。
この動画を見る
入試問題 日本大学第三高等学校
$(x+y)^2=\displaystyle \frac{51+10\sqrt{ 2 }}{5}$
のとき
$x-y=\displaystyle \frac{1-5\sqrt{ 2 }}{\sqrt{ 5 }}$
のとき
$4xy$の値を求めなさい。
複雑にみえる連立方程式 慶應義塾
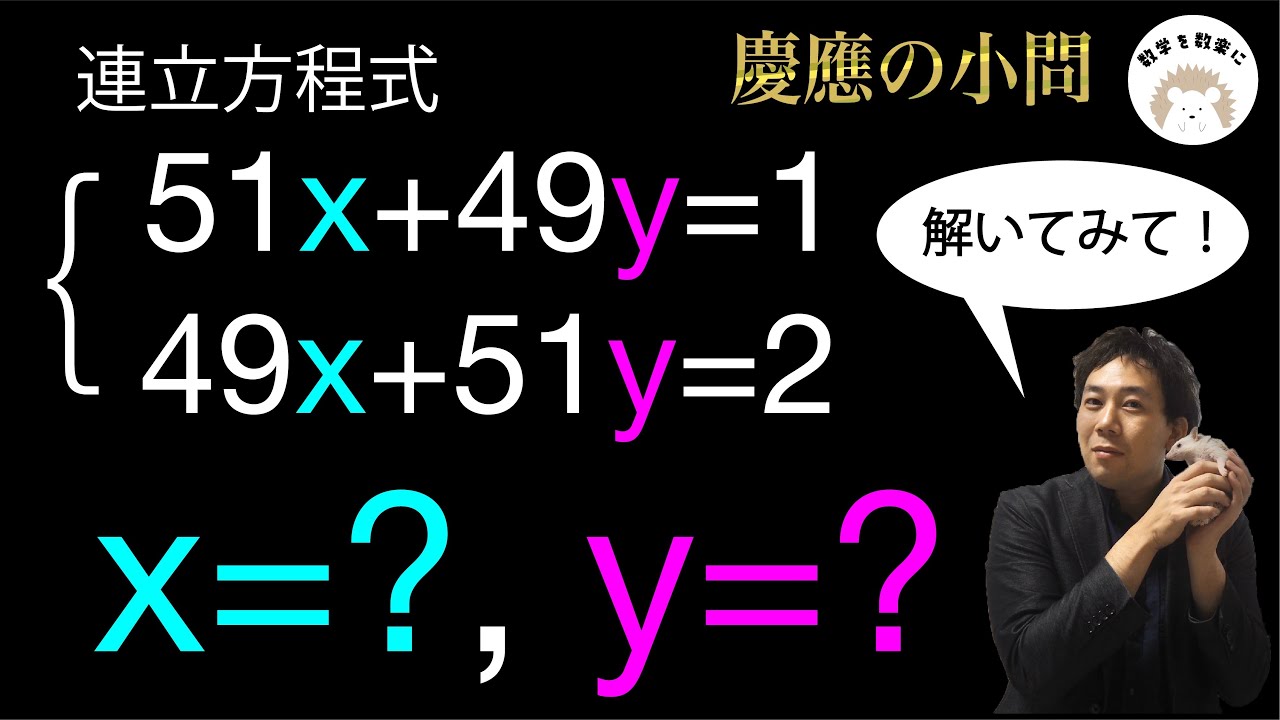
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
51x + 49y = 1 \\
49x + 51y = 2
\end{array}
\right.
\end{eqnarray}
$
慶應義塾高等学校
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
51x + 49y = 1 \\
49x + 51y = 2
\end{array}
\right.
\end{eqnarray}
$
慶應義塾高等学校
【3分でサイコロ問題が得意に!】確率:日本大学第二高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#日本大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 日本大学第二高等学校
さいころ 大 さいころ 小
を同時に投げ、
出目の数の和が 10以上となる
確率を求めよ。
この動画を見る
入試問題 日本大学第二高等学校
さいころ 大 さいころ 小
を同時に投げ、
出目の数の和が 10以上となる
確率を求めよ。
複雑にみえる二次方程式 桐光学園

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$\sqrt 5 x^2+x+2 = x^2 + \sqrt 5 x+ 2 \sqrt 5$
桐光学園高等学校
この動画を見る
2次方程式を解け
$\sqrt 5 x^2+x+2 = x^2 + \sqrt 5 x+ 2 \sqrt 5$
桐光学園高等学校
