 中2数学
中2数学
 中2数学
中2数学
発想の転換な動体視力と数学~全国入試問題解法 #Shorts
単元:
#数学(中学生)#中2数学#1次関数
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
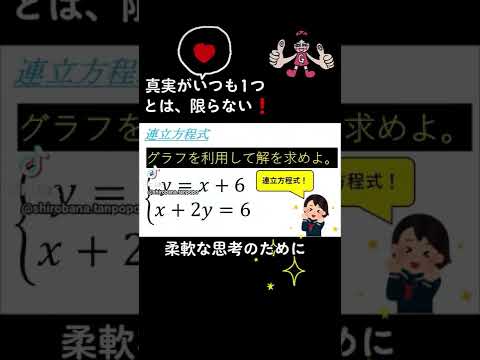
グラフを利用して解を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
y=x+6 \\
x+2y=6
\end{array}
\right.
\end{eqnarray}$
青森県高校過去問
この動画を見る
グラフを利用して解を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
y=x+6 \\
x+2y=6
\end{array}
\right.
\end{eqnarray}$
青森県高校過去問
ロニー先生の問題

和と差の積は二乗の差

0乗 −乗

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^3=$
$2^2=$
$2^1=$
$2^0=$
$2^{-1}=$
この動画を見る
$2^3=$
$2^2=$
$2^1=$
$2^0=$
$2^{-1}=$
正負の数 四則混合

単元:
#数学(中学生)#中1数学#中2数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)
指導講師:
数学を数楽に
問題文全文(内容文):
$9-3 \div \frac{1}{3} + 1$を計算しなさい
この動画を見る
$9-3 \div \frac{1}{3} + 1$を計算しなさい
文字4つの連立方程式 國學院久我山

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式
$
\begin{eqnarray}
\left\{
\begin{array}{l}
w+x + 2y+z = 1 \\
w-2x + y -z= -2
\end{array}
\right.
\end{eqnarray}
$
w,x,y,zのうち0でないものは1つだけであるときw,x,y,zを求めよ
この動画を見る
連立方程式
$
\begin{eqnarray}
\left\{
\begin{array}{l}
w+x + 2y+z = 1 \\
w-2x + y -z= -2
\end{array}
\right.
\end{eqnarray}
$
w,x,y,zのうち0でないものは1つだけであるときw,x,y,zを求めよ
みんなが間違う?コイントスの確率

単元:
#数学(中学生)#中2数学#数A#場合の数と確率#確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
コイントスの確率
コインを10回投げて表がぴったり5回出る確率を求めよ
この動画を見る
コイントスの確率
コインを10回投げて表がぴったり5回出る確率を求めよ
これ解ける?

単元:
#数学(中学生)#中2数学#数A#場合の数と確率#確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
コインを10回投げて表がぴったり5回出る確率は?
この動画を見る
コインを10回投げて表がぴったり5回出る確率は?
1分で学ぶ確率(変化球version)~全国入試問題解法 #Shorts
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
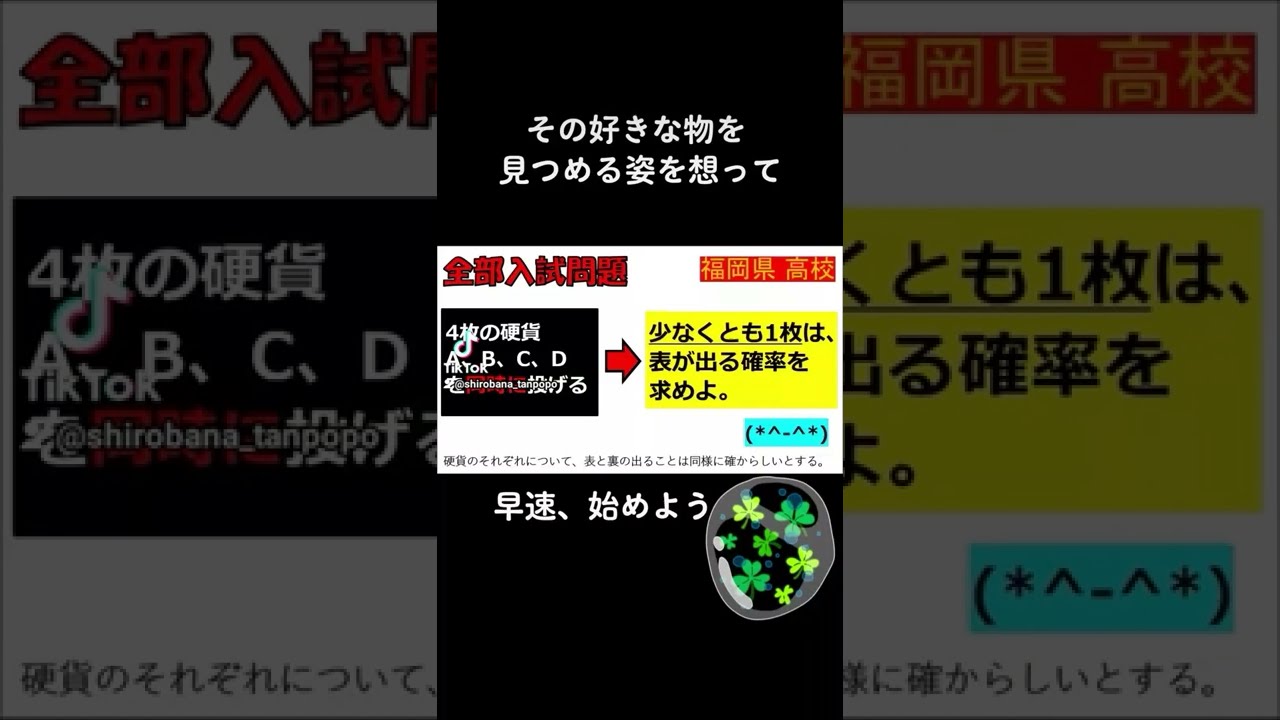
$4$枚の硬貨$A,B,C,D$を同時に投げる.
少なくとも1枚は表が出る確率を求めよ.
福岡県高校過去問
この動画を見る
$4$枚の硬貨$A,B,C,D$を同時に投げる.
少なくとも1枚は表が出る確率を求めよ.
福岡県高校過去問
これ2通りで解ける?

城北 令和4年度 2022 入試問題100題解説95問目!
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
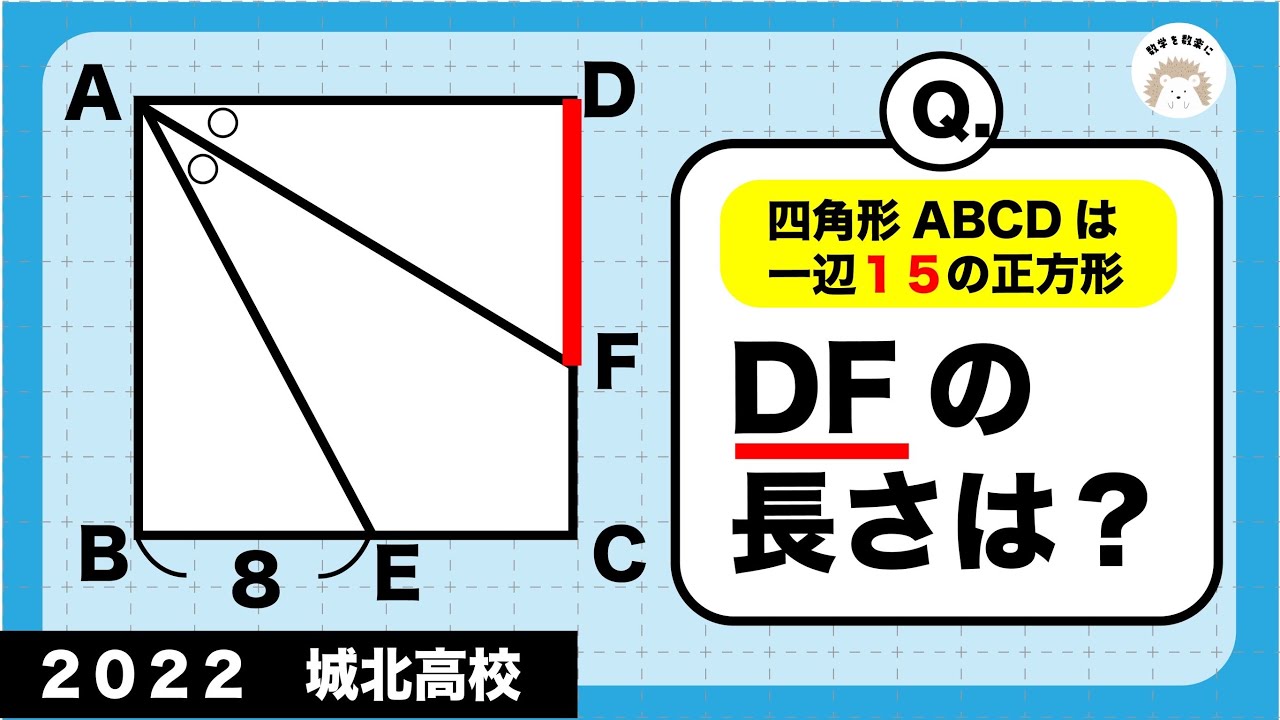
四角形ABCDは一辺15の正方形
DFの長さは?
*図は動画内参照
2022城北高等学校
この動画を見る
四角形ABCDは一辺15の正方形
DFの長さは?
*図は動画内参照
2022城北高等学校
正負の数 四則演算 福岡県最初の一問 令和4年度 2022 入試問題100題解説90問目!

平面図形は公立が面白い 愛知県(改) 令和4年度 2022 入試問題100題解説89問目!
単元:
#数学(中学生)#中1数学#中2数学#平面図形#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
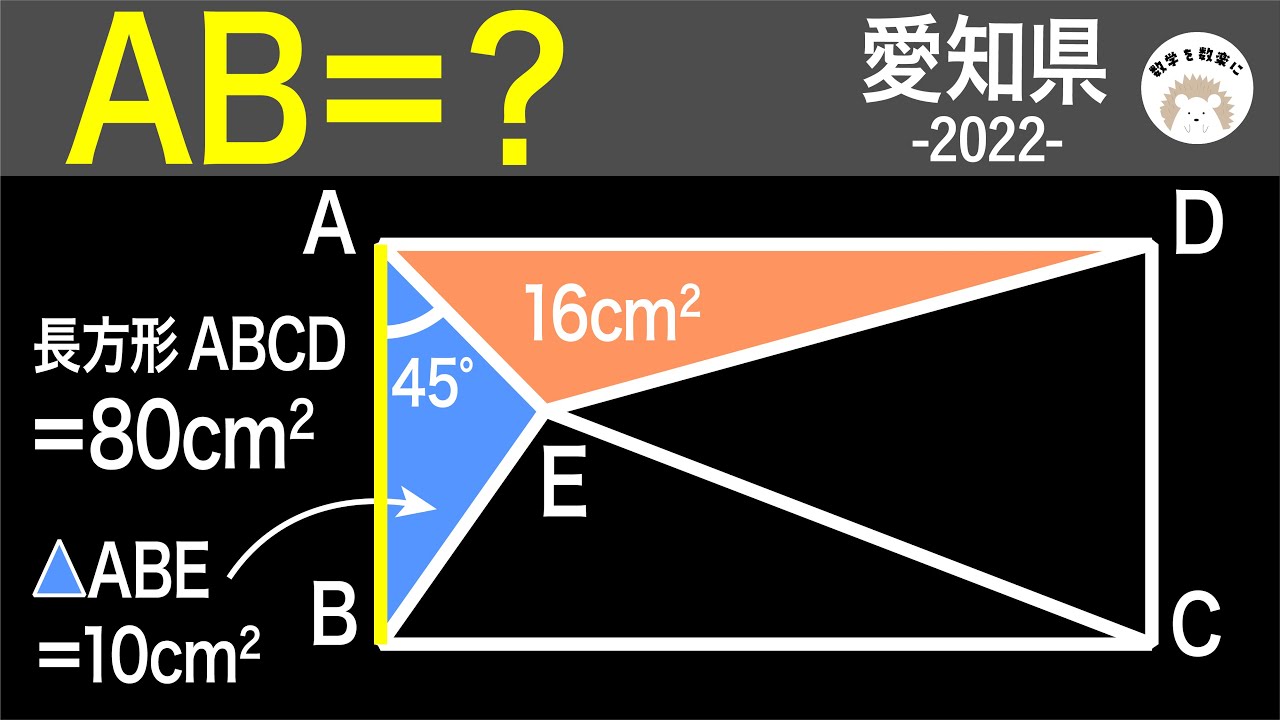
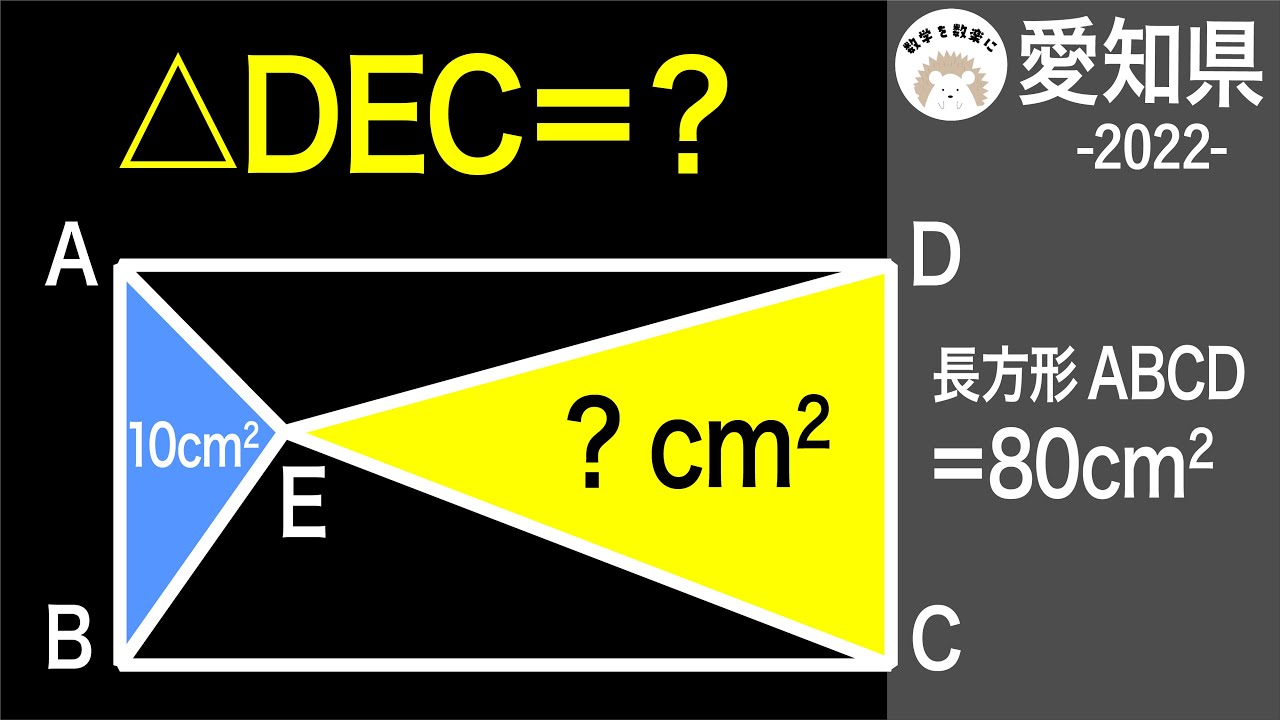
長方形ABCD=80㎠
△ABE=10㎠
AB=?
*図は動画内参照
2022愛知県
この動画を見る
長方形ABCD=80㎠
△ABE=10㎠
AB=?
*図は動画内参照
2022愛知県
【中学数学】カードの確率まとめ~樹形図と裏技~【中2数学】

単元:
#数学(中学生)#中2数学#確率
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
1から4までの数を書いたカードがある。
2回連続で引くとき、2回とも奇数になる確率を求めよ。
引いたカードはもとに戻さない。
2⃣
1から5までのカードが1枚ずつある。
同時に3枚のカードを取り出すとき、その3枚のカードに書かれている数のうち、
2番目に大きい数が偶数である確率を求めよ。
この動画を見る
1⃣
1から4までの数を書いたカードがある。
2回連続で引くとき、2回とも奇数になる確率を求めよ。
引いたカードはもとに戻さない。
2⃣
1から5までのカードが1枚ずつある。
同時に3枚のカードを取り出すとき、その3枚のカードに書かれている数のうち、
2番目に大きい数が偶数である確率を求めよ。
長方形の分割 愛知県(改) 令和4年度 2022 入試問題100題解説88問目!
動体視力と数学を鍛えるハスキー女子~全国入試問題解法 #Shorts

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
5本のうち2枚の当たりくじがあるくじを,$A,B$の2人がこの順に1本ずつ引く.
少なくとも1人は,あたりくじを引く確率を求めなさい.
*ひいたくじは,元に戻さないことにする.
青森県高校過去問
この動画を見る
5本のうち2枚の当たりくじがあるくじを,$A,B$の2人がこの順に1本ずつ引く.
少なくとも1人は,あたりくじを引く確率を求めなさい.
*ひいたくじは,元に戻さないことにする.
青森県高校過去問
明治学院 令和4年度 2022 入試問題100題解説84問目!
単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
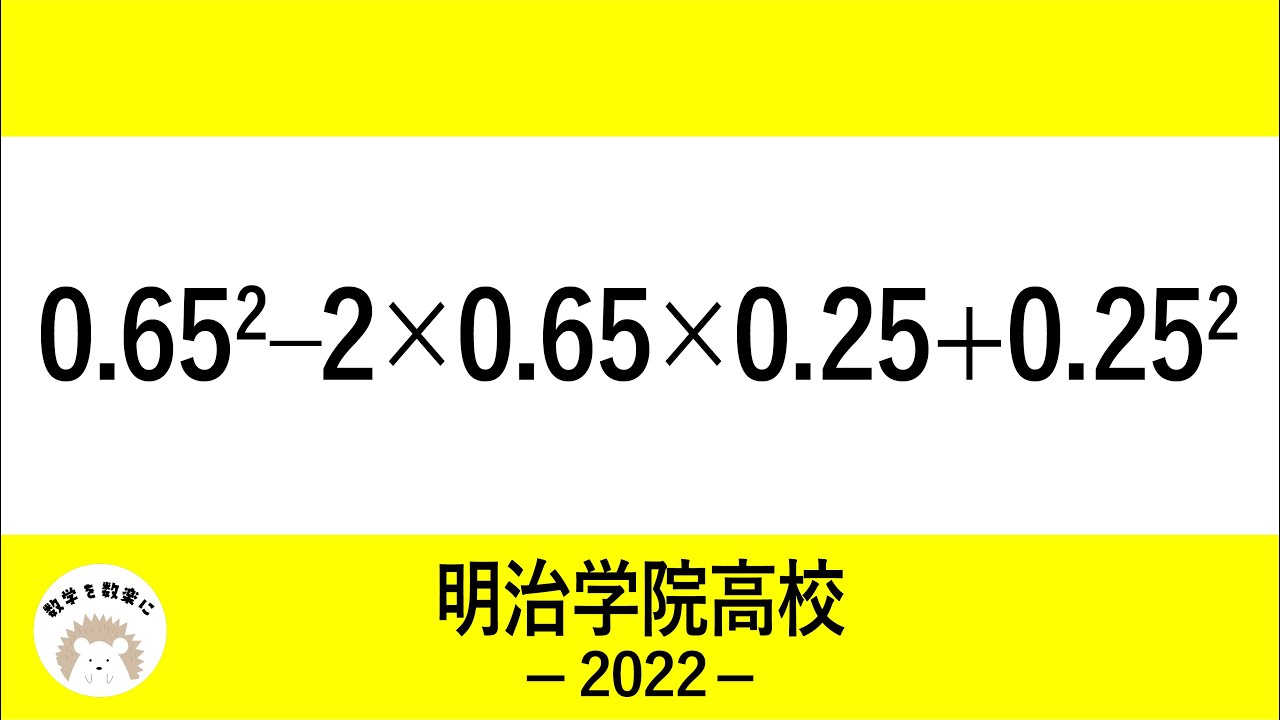
$0.65^2-2 \times 0.65 \times 0.25 + 0.25^2$
2022明治学院高等学校
この動画を見る
$0.65^2-2 \times 0.65 \times 0.25 + 0.25^2$
2022明治学院高等学校
【典型問題は、「手」で考える!】確率:平安女学院高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
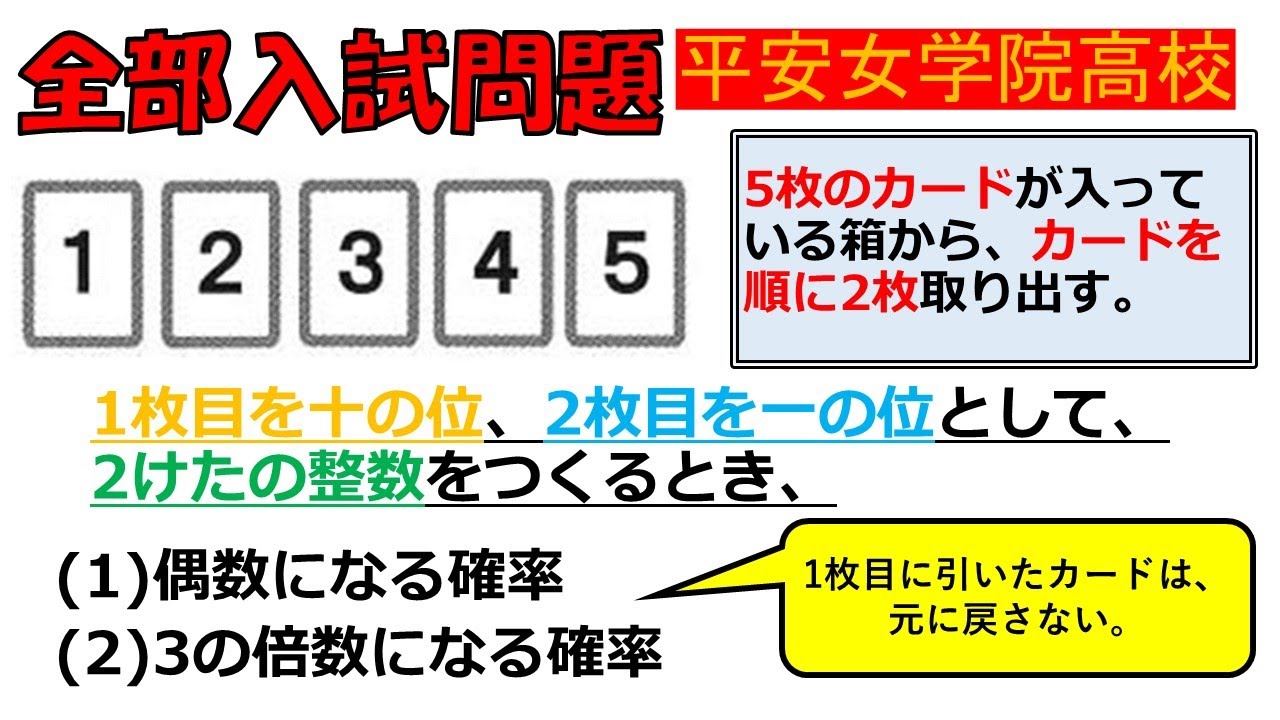
5枚のカードが入っている箱から,カードを順に2枚取り出す.
1枚を十の位,2枚目を一の位として,2けたの整数をつくるとき,
(1)偶数になる確率を求めよ.
(2)3の倍数になる確率を求めよ.
平安女学院高等学校過去問
この動画を見る
5枚のカードが入っている箱から,カードを順に2枚取り出す.
1枚を十の位,2枚目を一の位として,2けたの整数をつくるとき,
(1)偶数になる確率を求めよ.
(2)3の倍数になる確率を求めよ.
平安女学院高等学校過去問
みんな騙されるくない?

単元:
#数学(中学生)#中2数学#数A#場合の数と確率#確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\displaystyle \frac{1}{100}$の確率でレアが当たる。
100回引く。
レアは絶対当たる?
この動画を見る
$\displaystyle \frac{1}{100}$の確率でレアが当たる。
100回引く。
レアは絶対当たる?
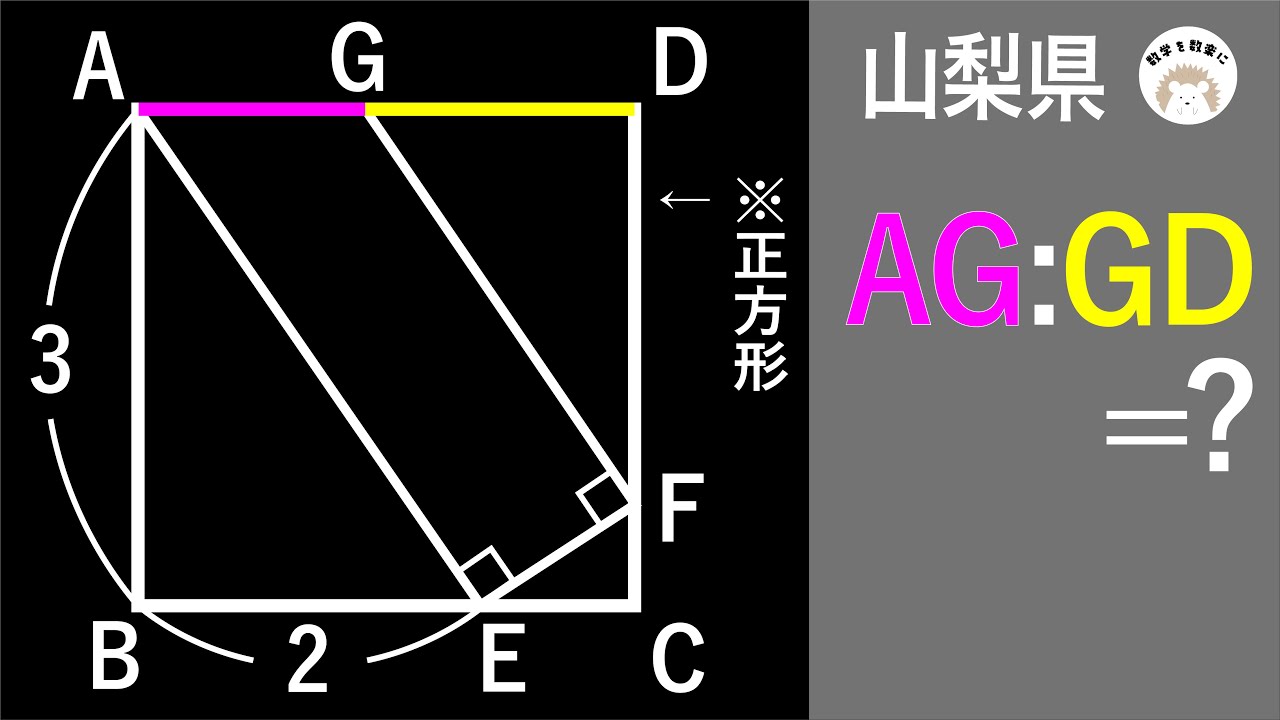
正方形 令和4年度 山梨県 2022 入試問題100題解説82問目!
おうぎ形と正方形 2通りで解説!令和4年度 茨城県 数学 2022 入試問題100題解説81問目!
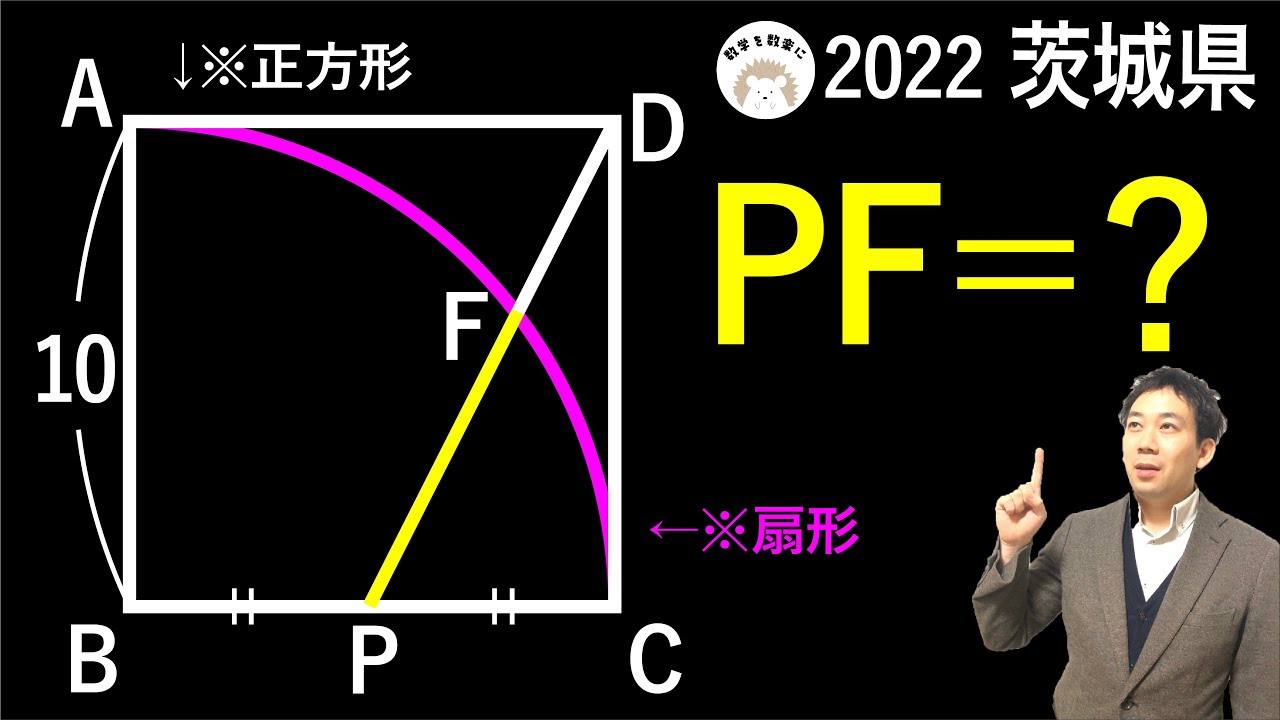
単元:
#数学(中学生)#中2数学#数Ⅰ#数A#図形の性質#図形と計量#三角形と四角形#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点PはBCの中点
PF=?
*図は動画内参照
2022茨城県
この動画を見る
点PはBCの中点
PF=?
*図は動画内参照
2022茨城県
サイコロの確率 立川高校 令和4年度 数学 2022 入試問題100題解説79問目!

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
サイコロを2回投げる
1回目に出た目→a、2回目に出た目→b
$337(a+b)$が2022の約数となる確率は?
2022立川高等学校
この動画を見る
サイコロを2回投げる
1回目に出た目→a、2回目に出た目→b
$337(a+b)$が2022の約数となる確率は?
2022立川高等学校
みんなできた?

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
鉛筆と消しゴムの値段の合計は110円、鉛筆は消しゴムより100円高い
消しゴムの値段は?
この動画を見る
鉛筆と消しゴムの値段の合計は110円、鉛筆は消しゴムより100円高い
消しゴムの値段は?
福田の数学〜慶應義塾大学2022年薬学部第1問(6)〜三角関数の連立方程式

単元:
#連立方程式#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(6)$0 \leqq x \leqq \pi, 0 \leqq y \leqq \pi$を満たすx,yに対して、等式$2\sin x+\sin y=1$が
成り立つとする。
$(\textrm{i})$この等式を満たすxの範囲は$\boxed{\ \ コ\ \ }$である。
$(\textrm{ii})x,y$が$2\cos x+\cos y=2\sqrt2$を満たすとき、$\sin(x+y)$の値を求めると
$\boxed{\ \ サ\ \ }$である。
2022慶應義塾大学薬学部過去問
この動画を見る
(6)$0 \leqq x \leqq \pi, 0 \leqq y \leqq \pi$を満たすx,yに対して、等式$2\sin x+\sin y=1$が
成り立つとする。
$(\textrm{i})$この等式を満たすxの範囲は$\boxed{\ \ コ\ \ }$である。
$(\textrm{ii})x,y$が$2\cos x+\cos y=2\sqrt2$を満たすとき、$\sin(x+y)$の値を求めると
$\boxed{\ \ サ\ \ }$である。
2022慶應義塾大学薬学部過去問
【中学数学】袋から玉の取り出し方の違い~確率の面白さ~【中2数学】

単元:
#数学(中学生)#中2数学#確率
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1)赤玉2個と白玉3個が入っている袋がある。この袋から玉を1個とり出して色を調べ、次にまた玉を1個取り出すとき、どちらも赤玉が出る確率を求めよ。ただし、1度取り出した玉はもとに戻さないものとする。
(2)赤玉2個と白玉3個が入っている袋がある。この袋から同時に2個玉を取り出すときどちらも赤玉が出る確率を求めよ。
(3)赤玉2個と白玉3個が入っている袋がある。この袋から玉を1個とり出して色を調べ、玉を戻す。次にまた玉を一個取り出すとき、どちらも赤玉が出る確率を求めよ。
この動画を見る
(1)赤玉2個と白玉3個が入っている袋がある。この袋から玉を1個とり出して色を調べ、次にまた玉を1個取り出すとき、どちらも赤玉が出る確率を求めよ。ただし、1度取り出した玉はもとに戻さないものとする。
(2)赤玉2個と白玉3個が入っている袋がある。この袋から同時に2個玉を取り出すときどちらも赤玉が出る確率を求めよ。
(3)赤玉2個と白玉3個が入っている袋がある。この袋から玉を1個とり出して色を調べ、玉を戻す。次にまた玉を一個取り出すとき、どちらも赤玉が出る確率を求めよ。
動体視力と数学を同時に鍛える動画~全国入試問題解法 #Shorts

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
大中小3つのさいころを同時に投げる.
さいころの大の出た目を$a$とし,中の出た目を$b$,小の出た目を$c$とする.
$(a-b)(b-c)=0$となる確率を求めよ.
早稲田実業高等部過去問
この動画を見る
大中小3つのさいころを同時に投げる.
さいころの大の出た目を$a$とし,中の出た目を$b$,小の出た目を$c$とする.
$(a-b)(b-c)=0$となる確率を求めよ.
早稲田実業高等部過去問
ガチャでレアが出ないのはこういうこと

単元:
#数学(中学生)#中2数学#確率
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\displaystyle \frac{1}{100}$の確率で当たる。
100回引いたら絶対当たる 確率問題解説動画です
この動画を見る
$\displaystyle \frac{1}{100}$の確率で当たる。
100回引いたら絶対当たる 確率問題解説動画です
気付けば一瞬! 正方形の折り返し 八王子東 2022 入試問題100題解説70問目!!
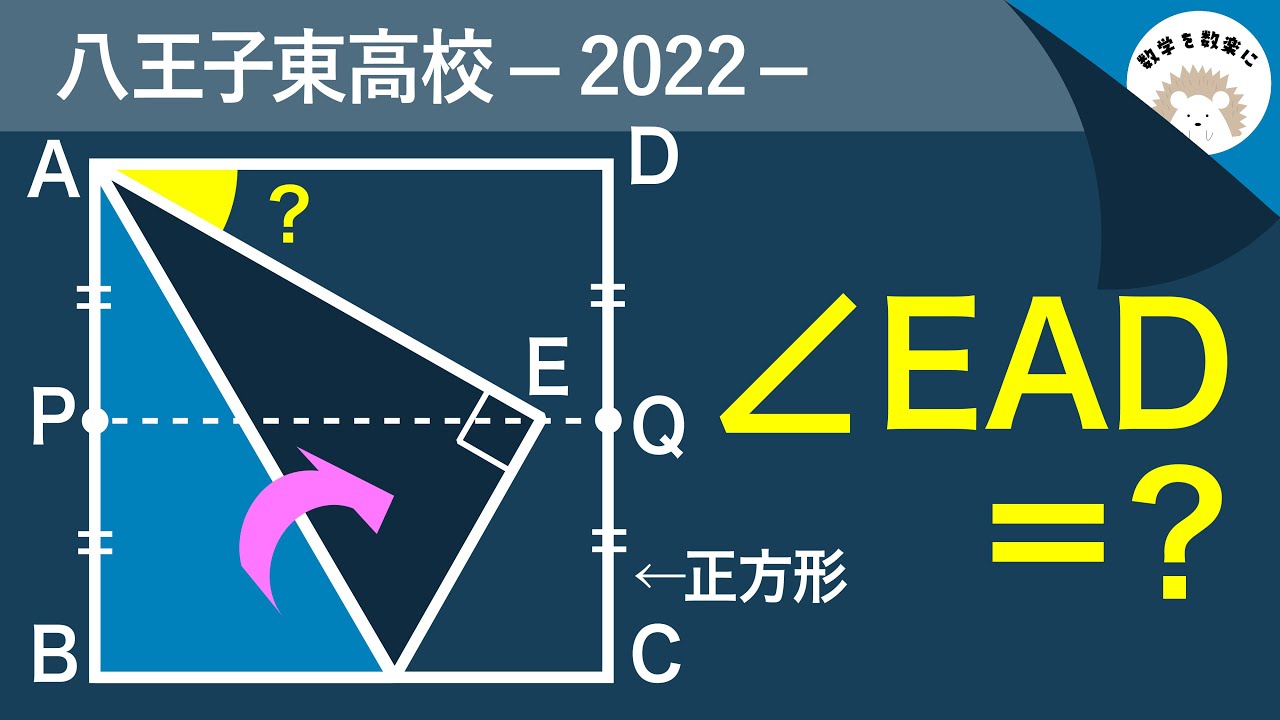
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle EAD =?$
*図は動画内参照
2022八王子東高等学校
この動画を見る
$\angle EAD =?$
*図は動画内参照
2022八王子東高等学校
【中学数学】平行四辺形の証明~中点が与えられてる問題~【中2数学】
なんとなくの雰囲気で変域の問題を解くと間違える 日比谷高校 2022入試問題100題解説67問目!! オープニング失敗!

単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
1次関数$y=ax+4$においてxの変域が$-3 \leqq x \leqq 6$のとき
yの変域が$2 \leqq y \leqq 5$である。
定数aの値を求めよ。
2022日比谷高等学校
この動画を見る
1次関数$y=ax+4$においてxの変域が$-3 \leqq x \leqq 6$のとき
yの変域が$2 \leqq y \leqq 5$である。
定数aの値を求めよ。
2022日比谷高等学校
