 中2数学
中2数学
 中2数学
中2数学
equation : Shirotan's cute kawaii math show #数学 #京大数学 #高校入試 #小学生テスト
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
Let's enjoy oriental mathematics for just a little while.
You will discover a cute world from mathematics.
Everyone in the world should love and be good at mathematics.
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
この動画を見る
Let's enjoy oriental mathematics for just a little while.
You will discover a cute world from mathematics.
Everyone in the world should love and be good at mathematics.
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
福田のおもしろ数学474〜3変数の関係からa+b+cの値を求める

単元:
#連立方程式#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
実数$a,b,c$が次の条件を満たしている。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^2+b^2+c^2=1 \\
a^3+b^3+c^3=1
\end{array}
\right.
\end{eqnarray}$
$a+b+c$の値を求めよ。
この動画を見る
実数$a,b,c$が次の条件を満たしている。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^2+b^2+c^2=1 \\
a^3+b^3+c^3=1
\end{array}
\right.
\end{eqnarray}$
$a+b+c$の値を求めよ。
福田のおもしろ数学473〜難しい連立方程式を解くための飛び道具

単元:
#連立方程式#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
5\left(x+\dfrac{1}{x}\right)=12\left(y+\dfrac{1}{y}\right)=13\left(z+\dfrac{1}{z}\right) \\
xy+yz+zx=1
\end{array}
\right.
\end{eqnarray}$
を満たす実数$x,y,z$をすべて求めよ。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
5\left(x+\dfrac{1}{x}\right)=12\left(y+\dfrac{1}{y}\right)=13\left(z+\dfrac{1}{z}\right) \\
xy+yz+zx=1
\end{array}
\right.
\end{eqnarray}$
を満たす実数$x,y,z$をすべて求めよ。
integer problems : Shirotan's cute kawaii math show #数学 #高校入試 #京大数学 #小学生テスト

単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
Let's enjoy oriental mathematics for just a little while.
You will discover a cute world from mathematics.
Everyone in the world should love and be good at mathematics.
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
この動画を見る
Let's enjoy oriental mathematics for just a little while.
You will discover a cute world from mathematics.
Everyone in the world should love and be good at mathematics.
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
福田のおもしろ数学468〜4変数の連立方程式

単元:
#連立方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
実数$x,y,z,w$の連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y + z + w =5 \\
xy+yz+zw+wx=4 \\\
xyz+yzw+zwx+wxy3 \\\
xyzw=-1
\end{array}
\right.
\end{eqnarray}$
を解いて下さい。
この動画を見る
実数$x,y,z,w$の連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y + z + w =5 \\
xy+yz+zw+wx=4 \\\
xyz+yzw+zwx+wxy3 \\\
xyzw=-1
\end{array}
\right.
\end{eqnarray}$
を解いて下さい。
福田のおもしろ数学456〜5変数の連立方程式

単元:
#連立方程式#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
実数$x,y,z,w,t$に対して次の連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
\hspace{ 2pt } x^5=y+y^5= \cdots ① \\
\hspace{ 2pt }y^5=z+z^5=\cdots ② \\\
\hspace{ 0.1pt }z^5=w+w^5=\cdots ③ \\\
\hspace{ 0.2pt }w^5=t+t^5=\cdots ④ \\\
\hspace{ 1pt }t^5=x+x^5= \cdots ⑤
\end{array}
\right.
\end{eqnarray}$
この動画を見る
実数$x,y,z,w,t$に対して次の連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
\hspace{ 2pt } x^5=y+y^5= \cdots ① \\
\hspace{ 2pt }y^5=z+z^5=\cdots ② \\\
\hspace{ 0.1pt }z^5=w+w^5=\cdots ③ \\\
\hspace{ 0.2pt }w^5=t+t^5=\cdots ④ \\\
\hspace{ 1pt }t^5=x+x^5= \cdots ⑤
\end{array}
\right.
\end{eqnarray}$
shape problems : Shirotan's cute kawaii math show #数学 #高校入試 #勉強 #サイ数学

福田の数学〜東京大学2025文系第4問〜放物線で囲まれた面積の最大値

単元:
#連立方程式#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$a$は実数とする。
座標平面において、次の連立不等式の表す領域の
面積を$S(a)$とする。
$\begin{eqnarray}
\left\{
\begin{array}{l}
y \leqq -\dfrac{1}{2}x^2+2 \\
y \geqq \vert x^2+a \vert \\\
-1 \leqq x \leqq 1
\end{array}
\right.
\end{eqnarray}$
$a$が$ 2\leqq a \leqq 2$の範囲を動くとき、
$S(a)$の最大値を求めよ。
$2025$年東京大学文系過去問
この動画を見る
$\boxed{4}$
$a$は実数とする。
座標平面において、次の連立不等式の表す領域の
面積を$S(a)$とする。
$\begin{eqnarray}
\left\{
\begin{array}{l}
y \leqq -\dfrac{1}{2}x^2+2 \\
y \geqq \vert x^2+a \vert \\\
-1 \leqq x \leqq 1
\end{array}
\right.
\end{eqnarray}$
$a$が$ 2\leqq a \leqq 2$の範囲を動くとき、
$S(a)$の最大値を求めよ。
$2025$年東京大学文系過去問
【中学数学】箱ひげ図の問題~2024年度北海道公立高校入試大問1~【高校受験】
単元:
#数学(中学生)#中1数学#中2数学#中3数学#高校入試過去問(数学)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
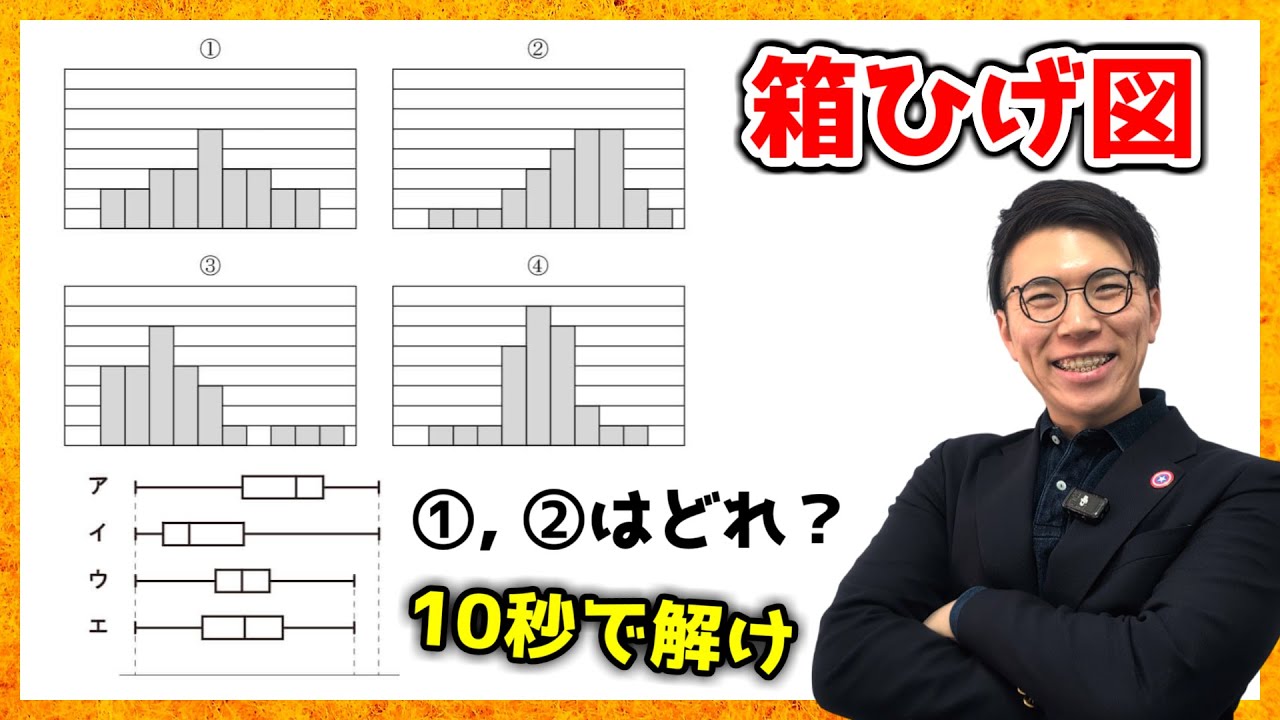
【中学数学】箱ひげ図の問題~2024年度北海道公立高校入試大問1~【高校受験】①~④のヒストグラムは、それぞれア~エのいずれかの箱ひげ図と同じデータを使ってまとめたものです。①、②のヒストグラムは、どの箱ひげ図と同じデータを使ってまとめたものですか。最も適当なものを、それぞれア~エから選びなさい。
この動画を見る
【中学数学】箱ひげ図の問題~2024年度北海道公立高校入試大問1~【高校受験】①~④のヒストグラムは、それぞれア~エのいずれかの箱ひげ図と同じデータを使ってまとめたものです。①、②のヒストグラムは、どの箱ひげ図と同じデータを使ってまとめたものですか。最も適当なものを、それぞれア~エから選びなさい。
福田のおもしろ数学408〜変数が素数である連立方程式

単元:
#連立方程式#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
pq=r+1 \\
2(p^2+q^2)=r^2+1
\end{array}
\right.
\end{eqnarray}$
を満たす素数$p,q,r$を求めて下さい。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
pq=r+1 \\
2(p^2+q^2)=r^2+1
\end{array}
\right.
\end{eqnarray}$
を満たす素数$p,q,r$を求めて下さい。
2つの二次方程式 2025立教新座

単元:
#算数(中学受験)#数学(中学生)#中2数学#中3数学#連立方程式#2次方程式#過去問解説(学校別)#立教新座中学
指導講師:
数学を数楽に
問題文全文(内容文):
2つの2次方程式
$x^2-kx-10=0$
$x^2+5x+2k=0$
が共通解を1つだけ持つ。この共有解と定数$k$の値を求めよ。
ただし$k≠5$
この動画を見る
2つの2次方程式
$x^2-kx-10=0$
$x^2+5x+2k=0$
が共通解を1つだけ持つ。この共有解と定数$k$の値を求めよ。
ただし$k≠5$
式の値 X求めなくていい
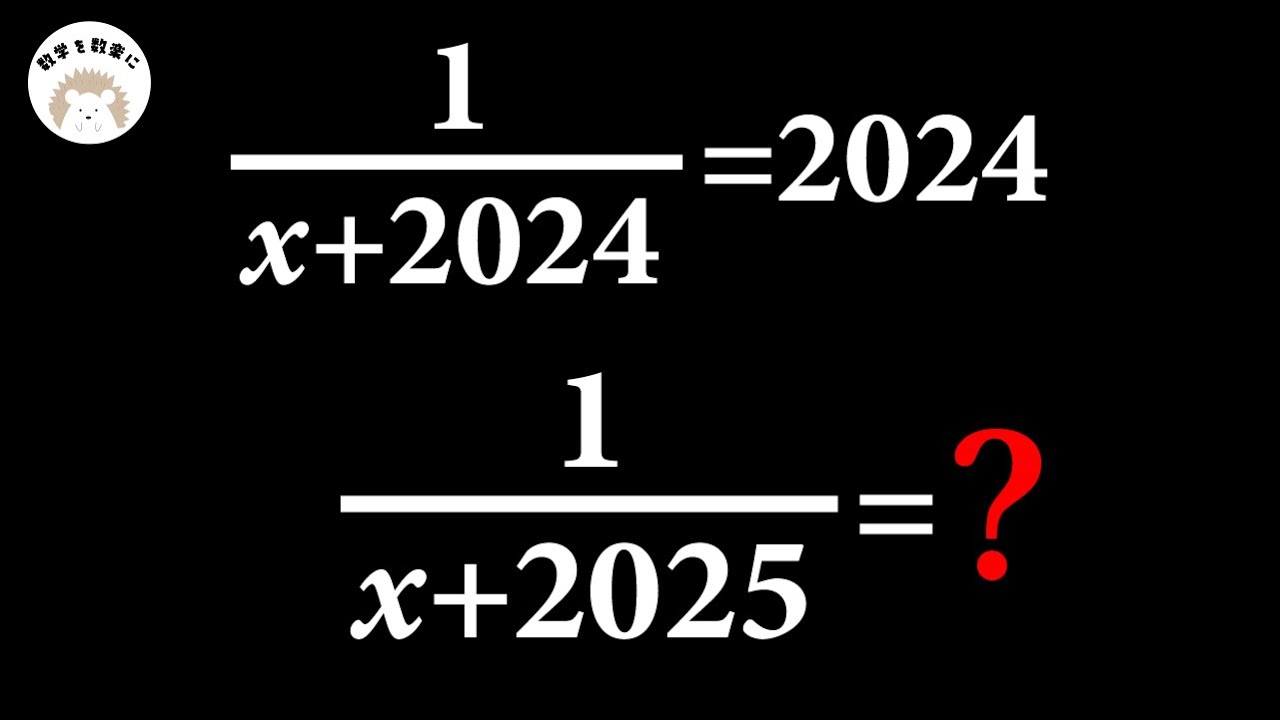
単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
数学を数楽に
問題文全文(内容文):
$\dfrac{1}{x+2024}=2024$
$\dfrac{1}{x+2025}= ?$
この動画を見る
$\dfrac{1}{x+2024}=2024$
$\dfrac{1}{x+2025}= ?$
ガウス記号 2025渋谷幕張

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)#渋谷教育学園幕張高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
正の数$x$に対して、$x$以下の最大の整数を$[x]$と表す。
\begin{eqnarray}
\left\{
\begin{array}{l}
[x] + [2x] = 7 \\
3x^2 - 4[2x]x + 16[x] = 0
\end{array}
\right.
\end{eqnarray}
$[x]$=? $x$=?
この動画を見る
正の数$x$に対して、$x$以下の最大の整数を$[x]$と表す。
\begin{eqnarray}
\left\{
\begin{array}{l}
[x] + [2x] = 7 \\
3x^2 - 4[2x]x + 16[x] = 0
\end{array}
\right.
\end{eqnarray}
$[x]$=? $x$=?
これが入試問題の現実か。。。連立方程式 渋谷幕張2025
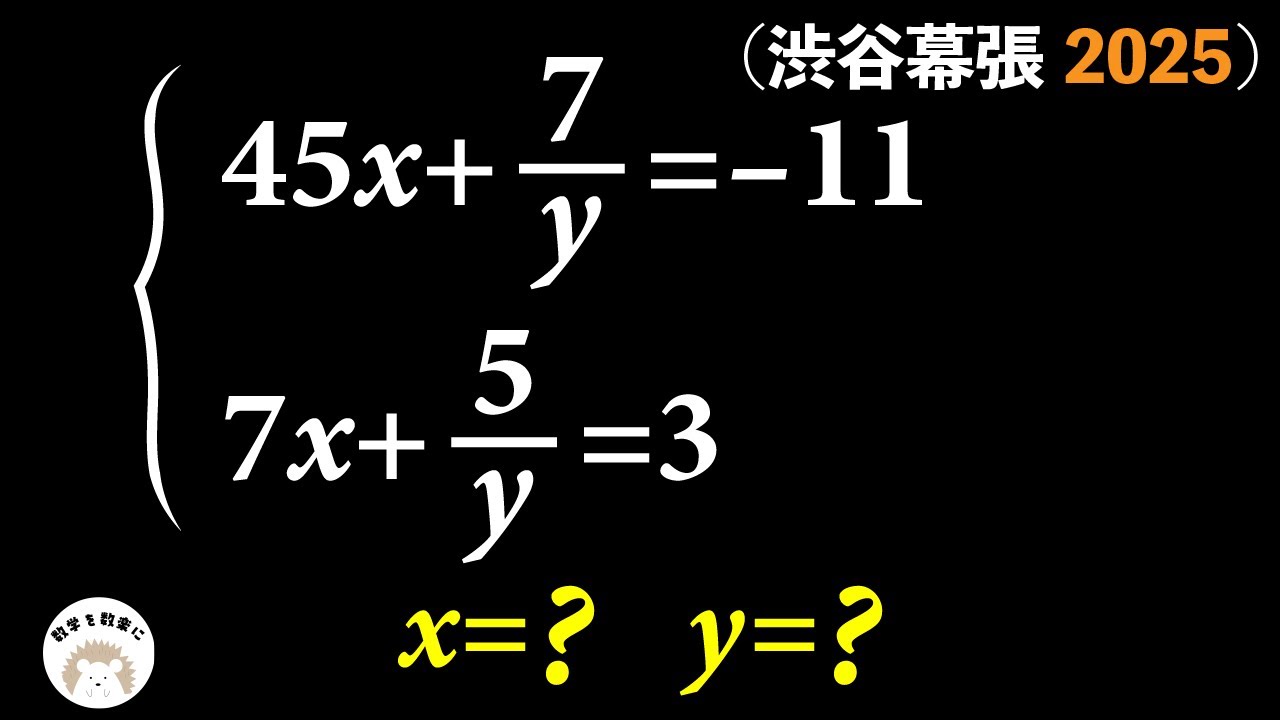
福田のおもしろ数学389〜三角関数を含んだ連立方程式

単元:
#数学(中学生)#中2数学#連立方程式#三角関数
指導講師:
福田次郎
問題文全文(内容文):
連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
\sin x = y \\
\sin y = x
\end{array}
\right.
\end{eqnarray}$
を解いて下さい。
この動画を見る
連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
\sin x = y \\
\sin y = x
\end{array}
\right.
\end{eqnarray}$
を解いて下さい。
これが入試問題の現実か。。。連立方程式 渋谷幕張2025
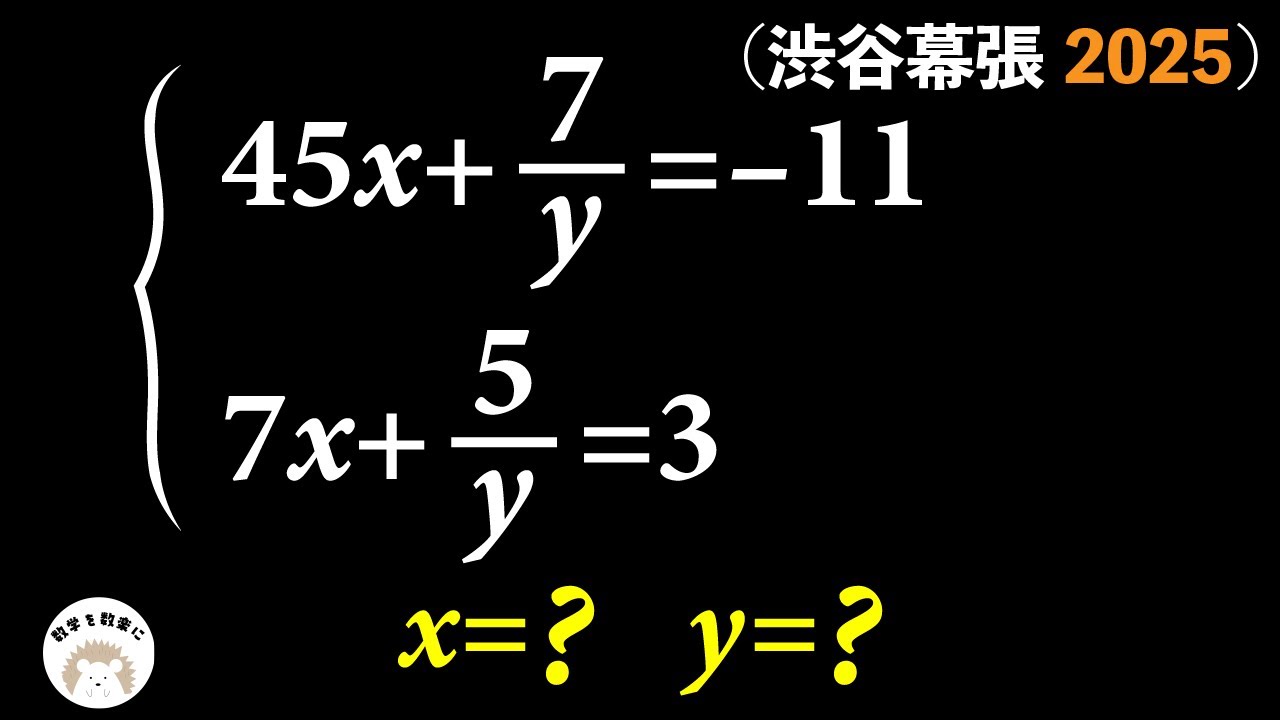
単元:
#数学(中学生)#中2数学#連立方程式#1次関数#高校入試過去問(数学)#渋谷教育学園幕張高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
45x + \displaystyle \frac{7}{y} = -11 \\
7x + \displaystyle \frac{5}{y} = 3
\end{array}
\right.
\end{eqnarray}
$x$=? $y$=?
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
45x + \displaystyle \frac{7}{y} = -11 \\
7x + \displaystyle \frac{5}{y} = 3
\end{array}
\right.
\end{eqnarray}
$x$=? $y$=?
福田のおもしろ数学387〜連立方程式を解こう

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
福田次郎
問題文全文(内容文):
$x,y,z$は正の実数とする。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x - y + \dfrac{1}{z}=2025 \\
y - z + \dfrac{1}{x}=2025 \\\
z - x + \dfrac{1}{y}=2025
\end{array}
\right.
\end{eqnarray}$
を解いて下さい。
この動画を見る
$x,y,z$は正の実数とする。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x - y + \dfrac{1}{z}=2025 \\
y - z + \dfrac{1}{x}=2025 \\\
z - x + \dfrac{1}{y}=2025
\end{array}
\right.
\end{eqnarray}$
を解いて下さい。
2025年浦和明の星女子中算数大問1(1)~(3)中学受験指導歴20年以上のプロ解説

単元:
#数学(中学生)#中1数学#中2数学#方程式#式の計算(単項式・多項式・式の四則計算)
指導講師:
重吉
問題文全文(内容文):
(12-9/2+1.25)+17.5*8/3-6/5*(3-2.88)+3/10
計算問題の宿題がでました。明子さんは1日目に全体の1/3と4問、2日目に残りの半分と2問、3日目には12問解いて、宿題をすべて終えました。問題は全部で何問ありましたか。
濃さの違う3つの食塩水A,B,Cがあり、それぞれの濃さは9%、12%、18%です。AとBの食塩水を2:1の重さの比で混ぜた後、Cの食塩水を加えて、合計240gの食塩水を作りました。その後、できた食塩水から水をすべて蒸発させたところ、残った食塩の重さは36gでした。混ぜたAの食塩水の重さは何gであったか答えなさい。
この動画を見る
(12-9/2+1.25)+17.5*8/3-6/5*(3-2.88)+3/10
計算問題の宿題がでました。明子さんは1日目に全体の1/3と4問、2日目に残りの半分と2問、3日目には12問解いて、宿題をすべて終えました。問題は全部で何問ありましたか。
濃さの違う3つの食塩水A,B,Cがあり、それぞれの濃さは9%、12%、18%です。AとBの食塩水を2:1の重さの比で混ぜた後、Cの食塩水を加えて、合計240gの食塩水を作りました。その後、できた食塩水から水をすべて蒸発させたところ、残った食塩の重さは36gでした。混ぜたAの食塩水の重さは何gであったか答えなさい。
4分の1円の中の面積 2025早稲田佐賀
単元:
#数学(中学生)#中2数学#平行と合同#高校入試過去問(数学)#早稲田大学系属早稲田佐賀高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
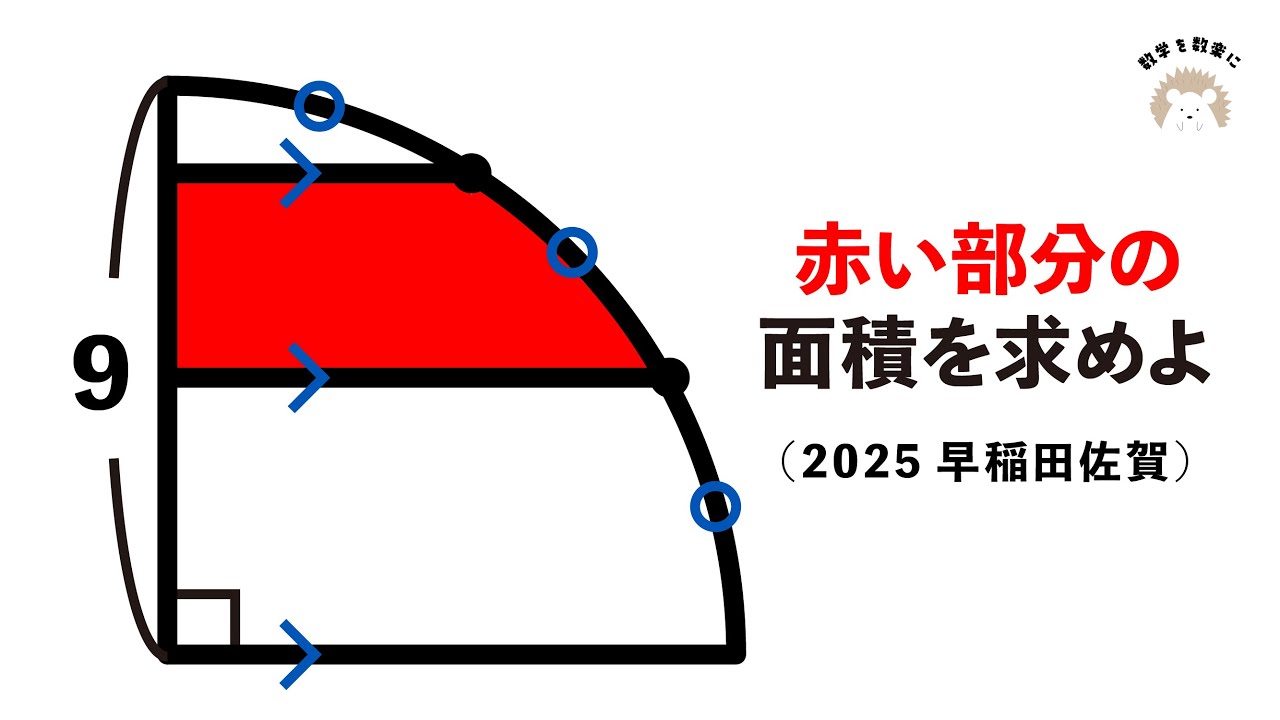
図の赤い部分の面積を求めよ(図は動画参照)
この動画を見る
図の赤い部分の面積を求めよ(図は動画参照)
【正解を導くことが第一…!】連立方程式:東京都立新宿高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学
指導講師:
問題文全文(内容文):
連立方程式
\begin{align}
\left\{
\begin{array}{l}
0.25x + y = 0.75 \\
\displaystyle\frac{x - 2y}{5} = \frac{21}{25}
\end{array}
\right.
\end{align}
この動画を見る
連立方程式
\begin{align}
\left\{
\begin{array}{l}
0.25x + y = 0.75 \\
\displaystyle\frac{x - 2y}{5} = \frac{21}{25}
\end{array}
\right.
\end{align}
【話題】三角形の面積を求めよ

単元:
#数学(中学生)#中1数学#中2数学#中3数学#その他#その他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
辺BCの長さは12㎝です。
三角形ABCの面積は?
この動画を見る
辺BCの長さは12㎝です。
三角形ABCの面積は?
【別解も好手…!】連立方程式:東京都立産業技術高等専門学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#東京都立産業技術高等専門学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$連立方程式$
\begin{eqnarray}
\left\{
\begin{array}{l}
2(x+\dfrac{1}{2}) - (y-\dfrac{1}{2}) = 8 \\
3(x+\dfrac{1}{2}) + 2(y-\dfrac{1}{2}) = 5
\end{array}
\right.
\end{eqnarray}
$を解け。$
この動画を見る
$連立方程式$
\begin{eqnarray}
\left\{
\begin{array}{l}
2(x+\dfrac{1}{2}) - (y-\dfrac{1}{2}) = 8 \\
3(x+\dfrac{1}{2}) + 2(y-\dfrac{1}{2}) = 5
\end{array}
\right.
\end{eqnarray}
$を解け。$
【効率…良く…!】文字式:立教新座高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#中3数学#連立方程式#平方根#高校入試過去問(数学)#立教新座高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
2\sqrt{3}a+\sqrt{3}b=5\\
\sqrt{3}a+2\sqrt{3}b=-3
\end{array}
\right.
\end{eqnarray}\;$のとき、
$a+b$の値を求めなさい。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
2\sqrt{3}a+\sqrt{3}b=5\\
\sqrt{3}a+2\sqrt{3}b=-3
\end{array}
\right.
\end{eqnarray}\;$のとき、
$a+b$の値を求めなさい。
【見た目より難しい…!】連立方程式:福岡大学附属大濠高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+4y=23\\
2x-6y=-15
\end{array}
\right.
\end{eqnarray}\;$を解け。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+4y=23\\
2x-6y=-15
\end{array}
\right.
\end{eqnarray}\;$を解け。
【最初からこうすれば良かった!】3元1次連立方程式②:中学からの連立方程式~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の3元1次連立方程式を解け.
$ x+y-z=-1 $
$ x-y+z=3 $
$ -x+y+z=7 $
この動画を見る
次の3元1次連立方程式を解け.
$ x+y-z=-1 $
$ x-y+z=3 $
$ -x+y+z=7 $
【スッキリと「分かる」…!】連立方程式:早稲田大学系属早稲田実業学校高等部~全国入試問題解法
単元:
#数学(中学生)#中2数学#中3数学#連立方程式#式の計算(展開、因数分解)#高校入試過去問(数学)#早稲田大学系属早稲田実業学校高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x \gt 0,\;\;y \gt 0\;$のとき連立方程式を解け。
\begin{eqnarray}
\left\{
\begin{array}{l}
\left(x+y\right)^2+x^2+y^2+\left(x-y\right)^2=2019\\
\left(x+y\right)\left(x-y\right)=385
\end{array}
\right.
\end{eqnarray}
この動画を見る
$x \gt 0,\;\;y \gt 0\;$のとき連立方程式を解け。
\begin{eqnarray}
\left\{
\begin{array}{l}
\left(x+y\right)^2+x^2+y^2+\left(x-y\right)^2=2019\\
\left(x+y\right)\left(x-y\right)=385
\end{array}
\right.
\end{eqnarray}
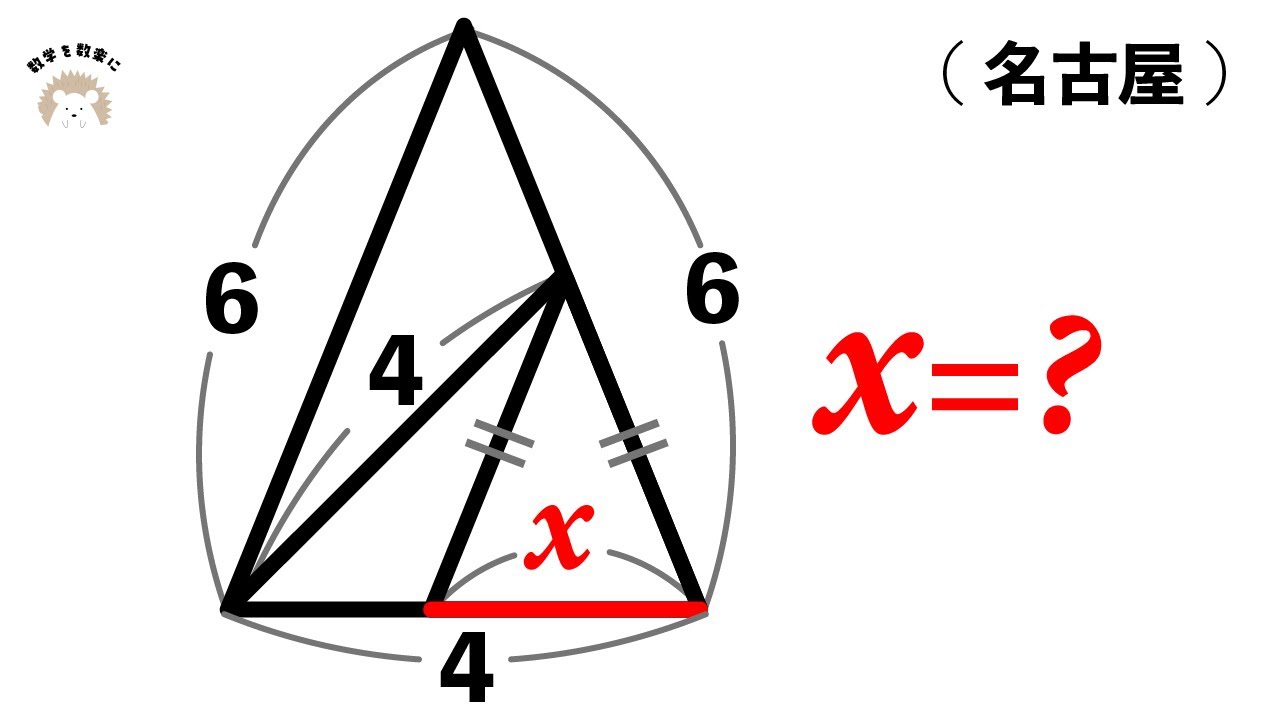
3つの二等辺三角形 名古屋高校
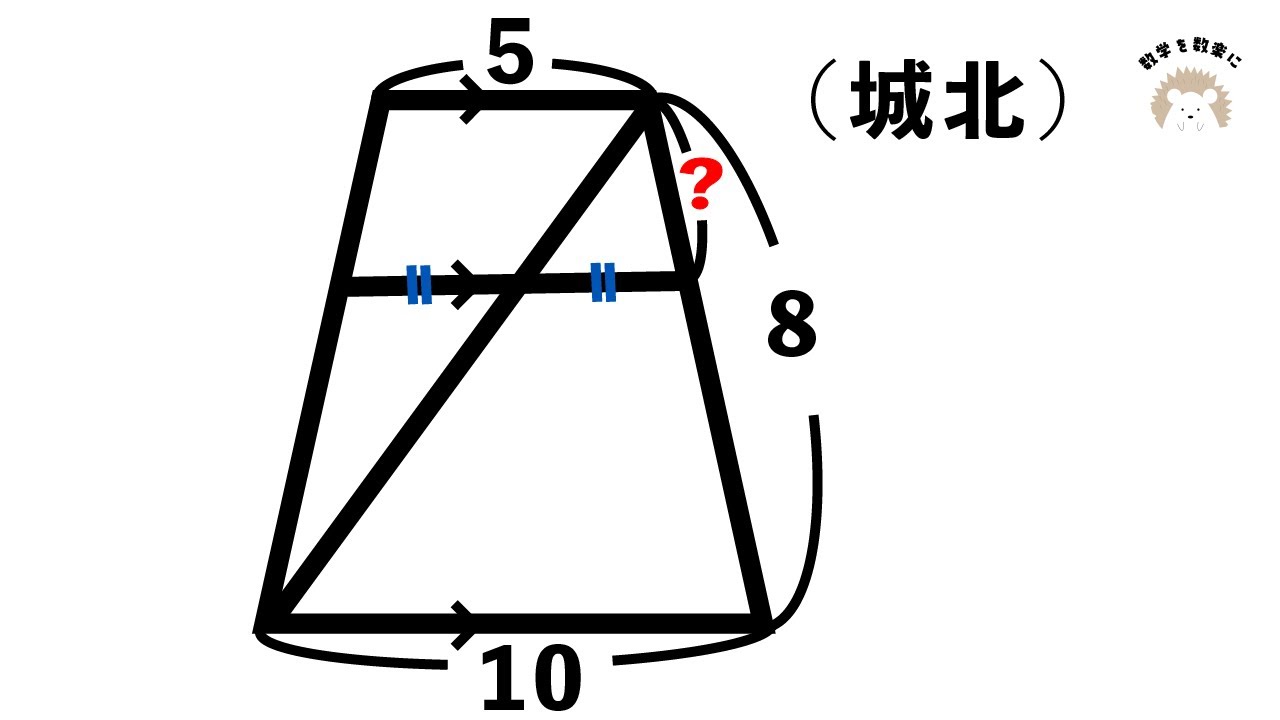
台形 城北高校
【中学数学】平行線と線分の比~分かりやすく~ 5-5 【中3数学】

単元:
#数学(中学生)#中2数学#平行と合同
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
図中の$x$の長さを求めなさい。
※図は動画内参照
また、平行線上における線分の比が等しくなる理由について解説します。
この動画を見る
図中の$x$の長さを求めなさい。
※図は動画内参照
また、平行線上における線分の比が等しくなる理由について解説します。
大谷翔平選手の凄さを計算しました

