 中2数学
中2数学
 中2数学
中2数学
【高校数学】定期テスト直前対策!個別指導プロ講師が厳選したプレテスト〜多項式の展開、因数分解〜【数学のコツ】

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
個別指導プロ講師が厳選したプレテスト〜多項式の展開、因数分解を解説していきます.
この動画を見る
個別指導プロ講師が厳選したプレテスト〜多項式の展開、因数分解を解説していきます.
連立方程式の基本的な考え方

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
連立方程式の基本的な考え方について説明動画です
$\begin{cases}
x+2y=5 \\
5x+4y=13
\end{cases}$
この動画を見る
連立方程式の基本的な考え方について説明動画です
$\begin{cases}
x+2y=5 \\
5x+4y=13
\end{cases}$
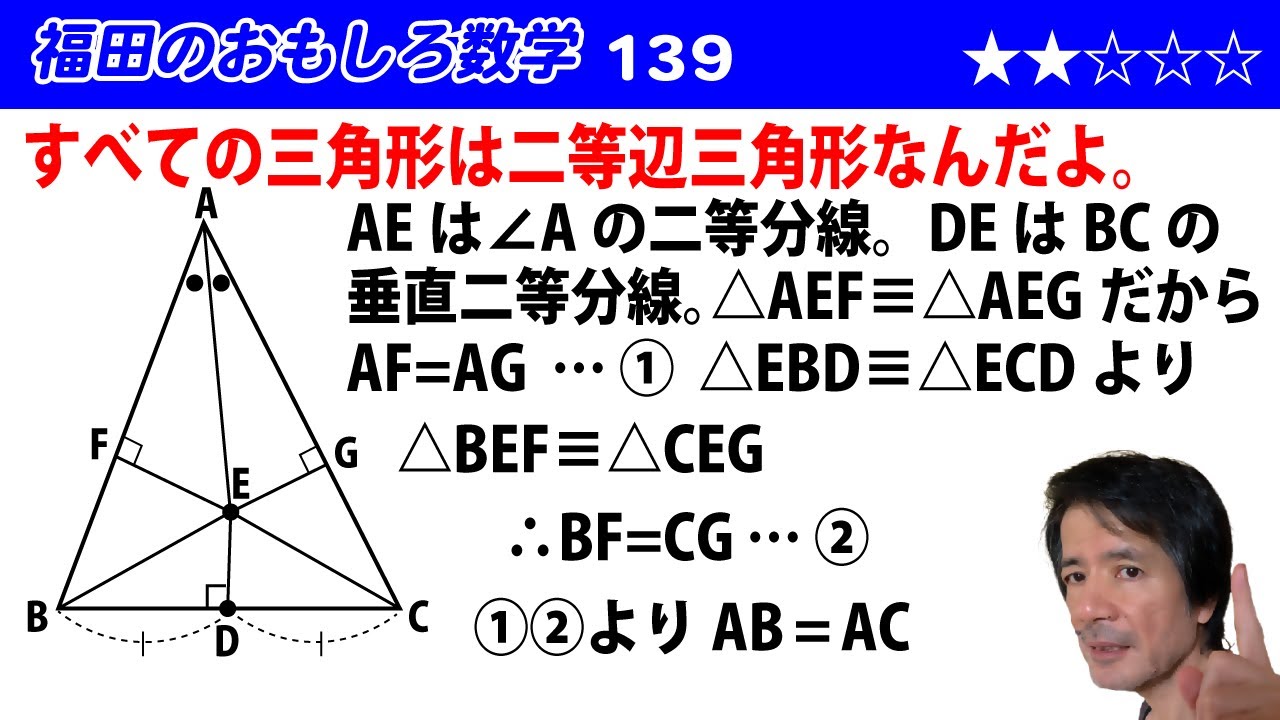
福田のおもしろ数学139〜全ての三角形は二等辺三角形である証明
複雑な連立方程式 久留米大附設

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{1}{x-1} + y = -1 \\
\frac{2}{x-1} + \frac{y}{2} = 4
\end{array}
\right.
\end{eqnarray}
久留米大学附設高等学校
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{1}{x-1} + y = -1 \\
\frac{2}{x-1} + \frac{y}{2} = 4
\end{array}
\right.
\end{eqnarray}
久留米大学附設高等学校
【整数の表し方一覧】式の活用[現役講師解説、中学2年、数学〕

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
3rd School
問題文全文(内容文):
$n$を整数としたとき、文字で表すときにどうするべきか解説動画です
偶数=
奇数=
3の倍数=
3で割って1余る数=
連続する2つの整数=
連続する2つの偶数=
連続する2つの奇数=
異なる2つの偶数=
異なる2つの奇数=
($m,n$は整数)
2桁の自然数=
($x,y$は整数)
この動画を見る
$n$を整数としたとき、文字で表すときにどうするべきか解説動画です
偶数=
奇数=
3の倍数=
3で割って1余る数=
連続する2つの整数=
連続する2つの偶数=
連続する2つの奇数=
異なる2つの偶数=
異なる2つの奇数=
($m,n$は整数)
2桁の自然数=
($x,y$は整数)
福田のおもしろ数学135〜ガウス記号のついた方程式の解

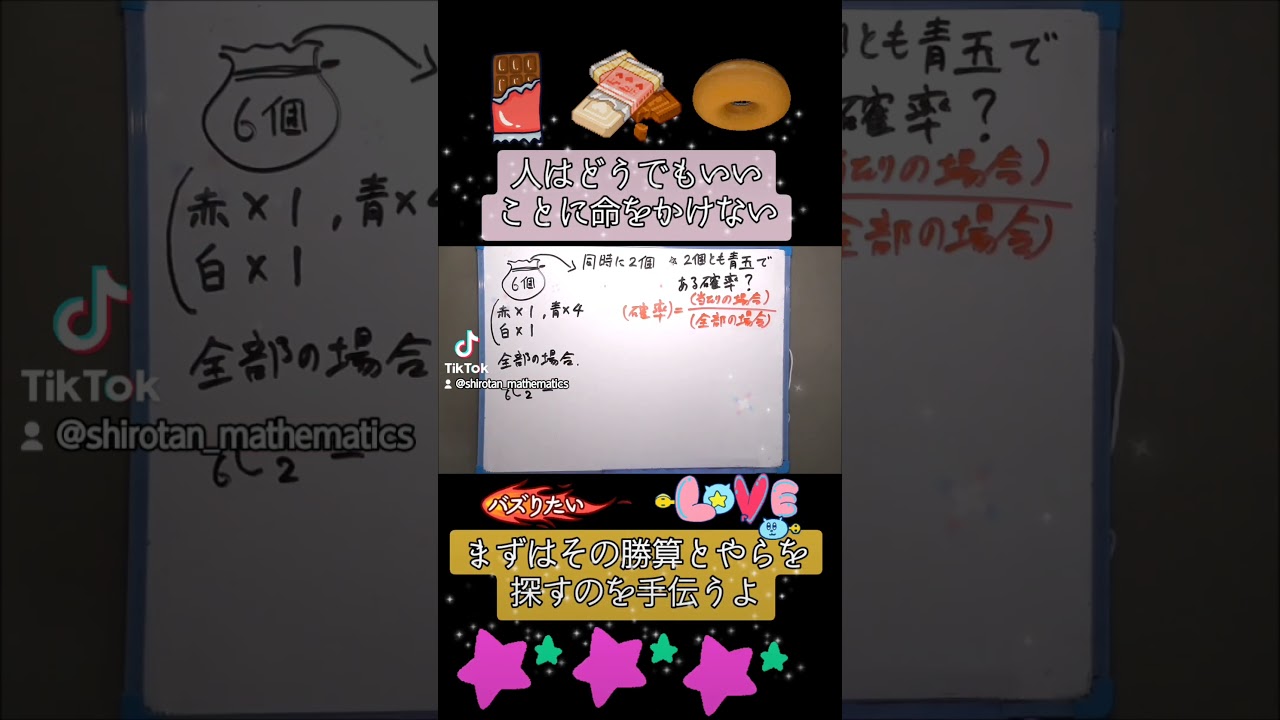
確率なんてジャンジャンバリバリですよ~全国入試問題解法 #shorts #数学 #高校入試 #頭の体操 #確率
単元:
#数学(中学生)#中2数学#確率
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
袋の中には6個の玉があり,この袋の中から同時に2個の玉を取り出す.
2個とも青玉である確率は$ \Box $である.
*どの玉が取り出されることも同様に確からしいものとする.
全国入試過去問題
この動画を見る
袋の中には6個の玉があり,この袋の中から同時に2個の玉を取り出す.
2個とも青玉である確率は$ \Box $である.
*どの玉が取り出されることも同様に確からしいものとする.
全国入試過去問題
#63 #数検1級1次過去問 #連立方程式

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
ますただ
問題文全文(内容文):
$xy \neq 0$のとき、次の連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x+y)(x^2+y^2)=\displaystyle \frac{40}{3}xy \\
(x^2+y^2)(x^4-y^4)=\displaystyle \frac{800}{9}x^2y^2
\end{array}
\right.
\end{eqnarray}$
出典:数検1級1次
この動画を見る
$xy \neq 0$のとき、次の連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x+y)(x^2+y^2)=\displaystyle \frac{40}{3}xy \\
(x^2+y^2)(x^4-y^4)=\displaystyle \frac{800}{9}x^2y^2
\end{array}
\right.
\end{eqnarray}$
出典:数検1級1次
クラス替えで好きな人と同じになる確率

高校入試でも何でも計算は工夫をしたい動画~全国入試問題解法 #数学, #高校入試, #偏差値アップ

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の計算をし,$ \Box $に当てはまる数を答えなさい.
$ 340^2-337^2-3^2=\Box $
大教大付属高校過去問
この動画を見る
次の計算をし,$ \Box $に当てはまる数を答えなさい.
$ 340^2-337^2-3^2=\Box $
大教大付属高校過去問
気付けば一瞬!!平行四辺形
小学生でも解ける高校入試の数学…!~全国入試問題解法 #shorts, #数学, #高校入試 , #頭の体操

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ 2021\times 2020-2020\times2019+2021\times2022-2022\times2023 $
を計算しなさい.
中大杉並高校過去問
この動画を見る
$ 2021\times 2020-2020\times2019+2021\times2022-2022\times2023 $
を計算しなさい.
中大杉並高校過去問
それぞれの角は出ていないけど和は求まります!

単元:
#数学(中学生)#中1数学#中2数学#平面図形#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x+\angle y+\angle z=$
*図は動画内参照
この動画を見る
$\angle x+\angle y+\angle z=$
*図は動画内参照
連立方程式 法政一

単元:
#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
1042x + 347y = 2 \\
1652x + 551y = -2
\end{array}
\right.
\end{eqnarray}
法政大学第一高等学校
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
1042x + 347y = 2 \\
1652x + 551y = -2
\end{array}
\right.
\end{eqnarray}
法政大学第一高等学校
定規で7cmを3等分する方法とは?

補助線引けるかな?
分数式の計算
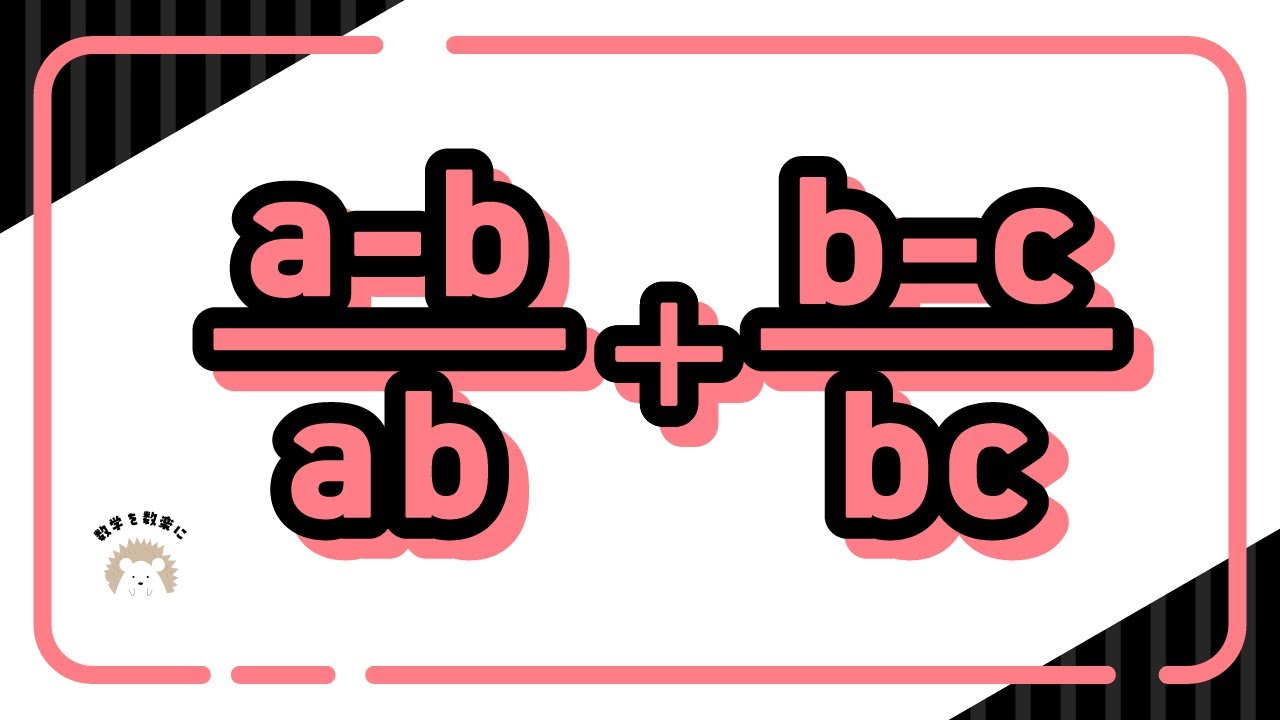
単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{a-b}{ab}$+$\frac{b-c}{bc}$
この動画を見る
$\frac{a-b}{ab}$+$\frac{b-c}{bc}$
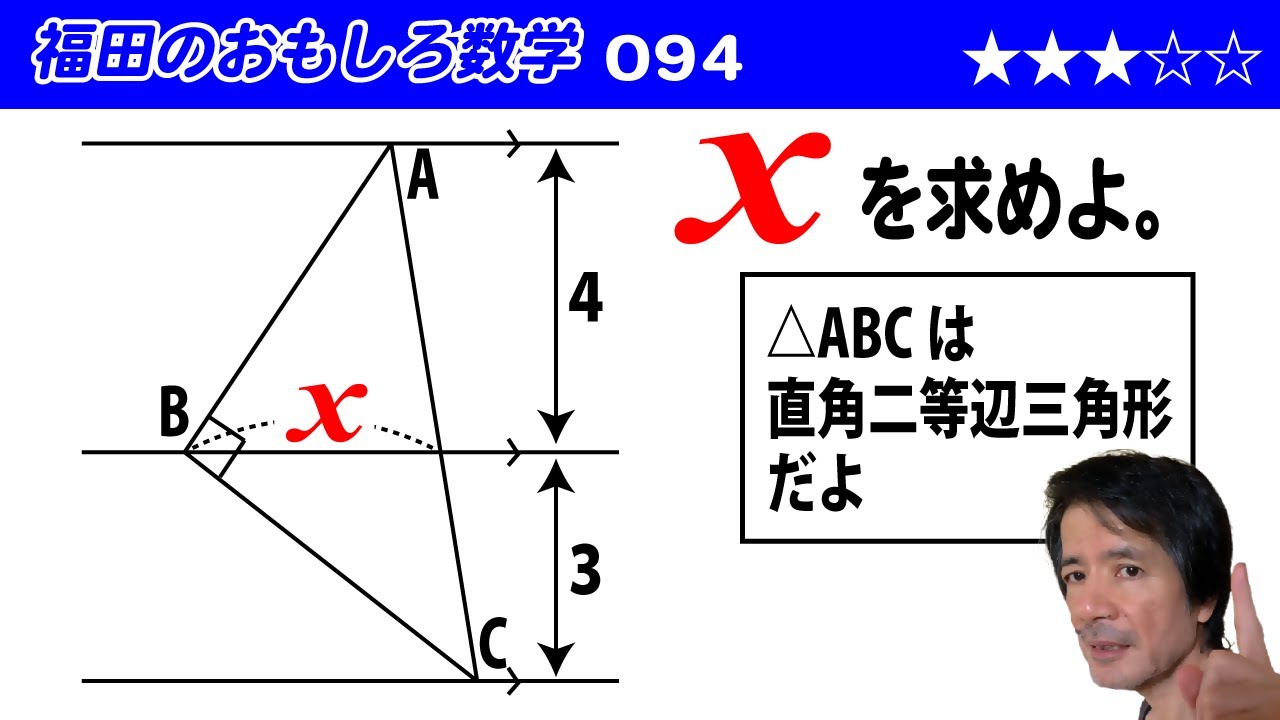
福田のおもしろ数学094〜平行線と直角二等辺三角形
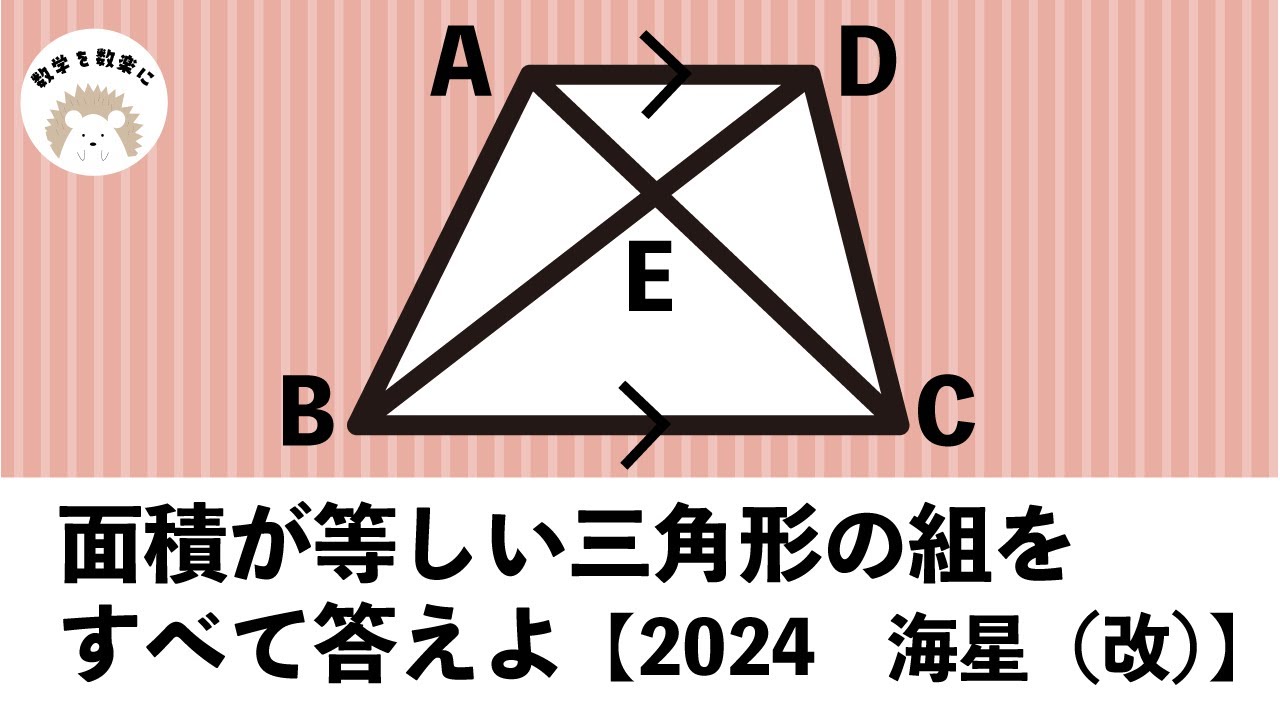
面積の等しい三角形
単元:
#数学(中学生)#中2数学#平行と合同#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
面積が等しい三角形の組をすべて答えよ
*図は動画内参照
2024海星高等学校
この動画を見る
面積が等しい三角形の組をすべて答えよ
*図は動画内参照
2024海星高等学校
グラフを描く

大学入試の連立方程式 東北学院大

単元:
#連立方程式#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
x(y+z)=5 \\
y(z+x)=8 \\
z(x+y)=9
\end{array}
\right.
\end{eqnarray}
東北学院大学
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
x(y+z)=5 \\
y(z+x)=8 \\
z(x+y)=9
\end{array}
\right.
\end{eqnarray}
東北学院大学
「席替えで好きな人と隣になる確率」をおかじゅんに授業してみた

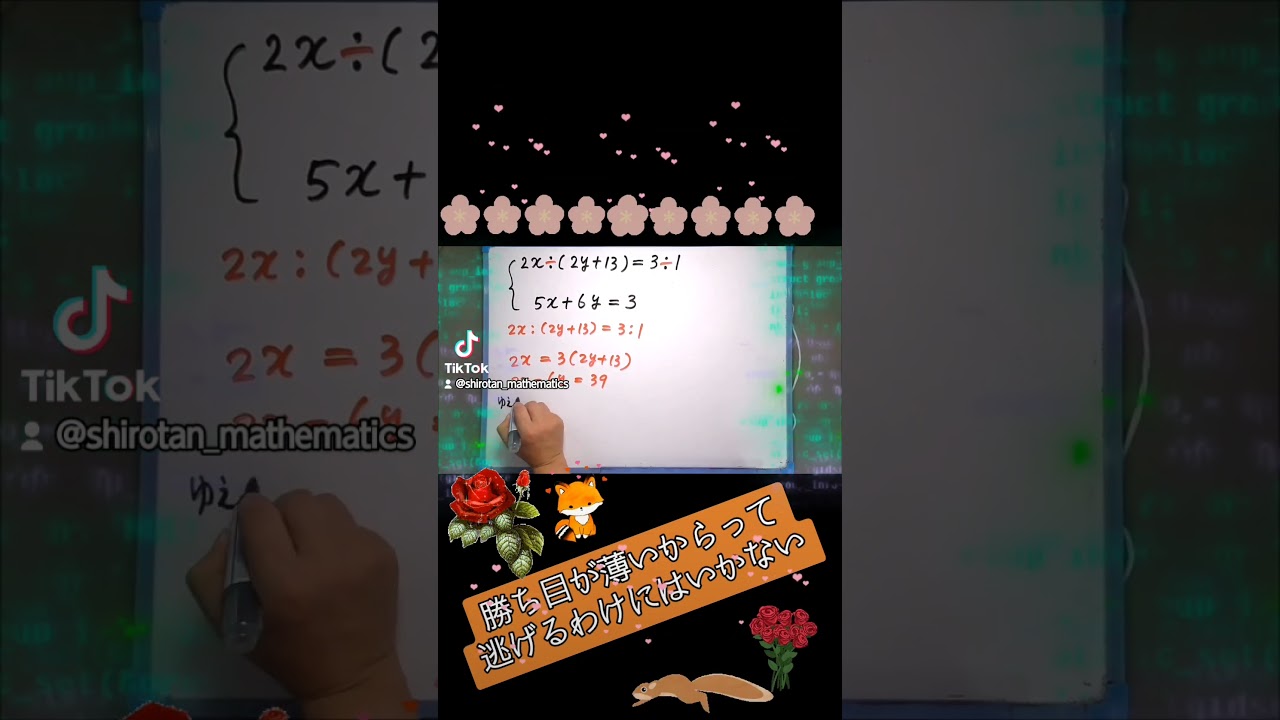
連立方程式は知ってるカタチに直せ…!~全国入試問題解法 #shorts, #数学, #高校入試, #頭の体操, #連立方程式,
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x\div(2y+13)=3:1 \\
5x+6y=3
\end{array}
\right.
\end{eqnarray}$
次の連立方程式を解きなさい.
広大付属高校過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x\div(2y+13)=3:1 \\
5x+6y=3
\end{array}
\right.
\end{eqnarray}$
次の連立方程式を解きなさい.
広大付属高校過去問
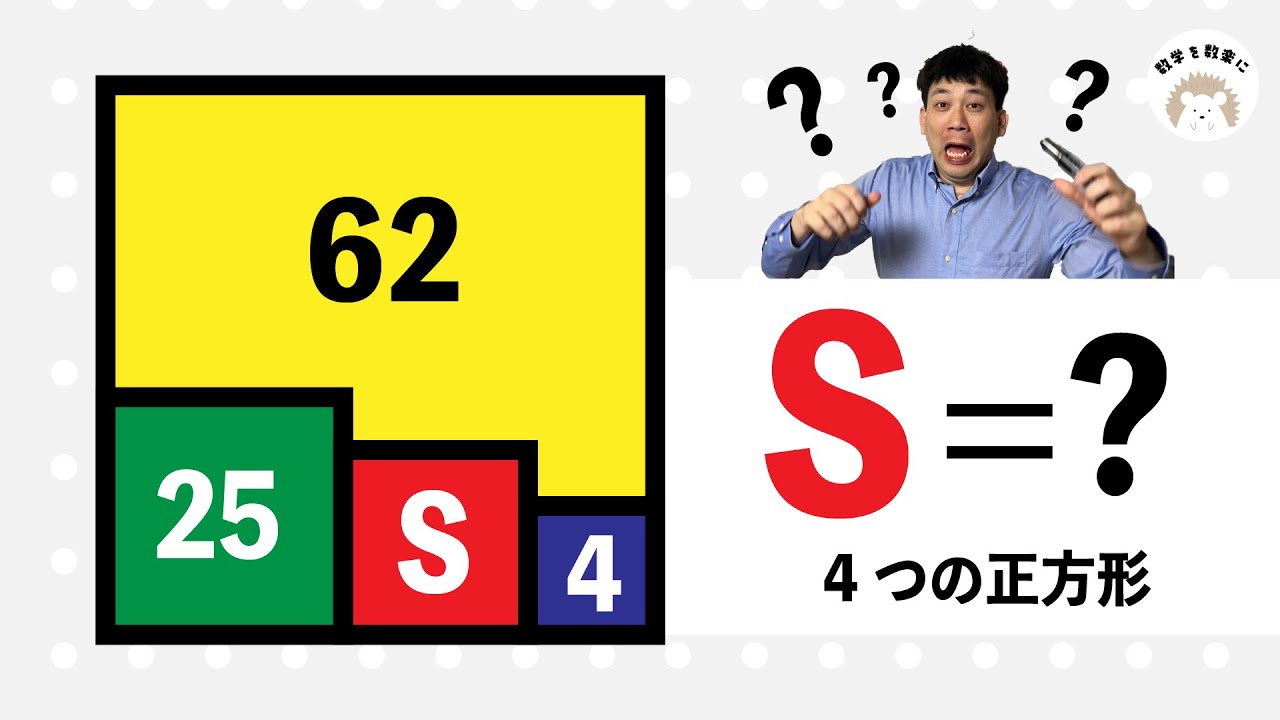
4つの正方形
式の値 2通りで解説
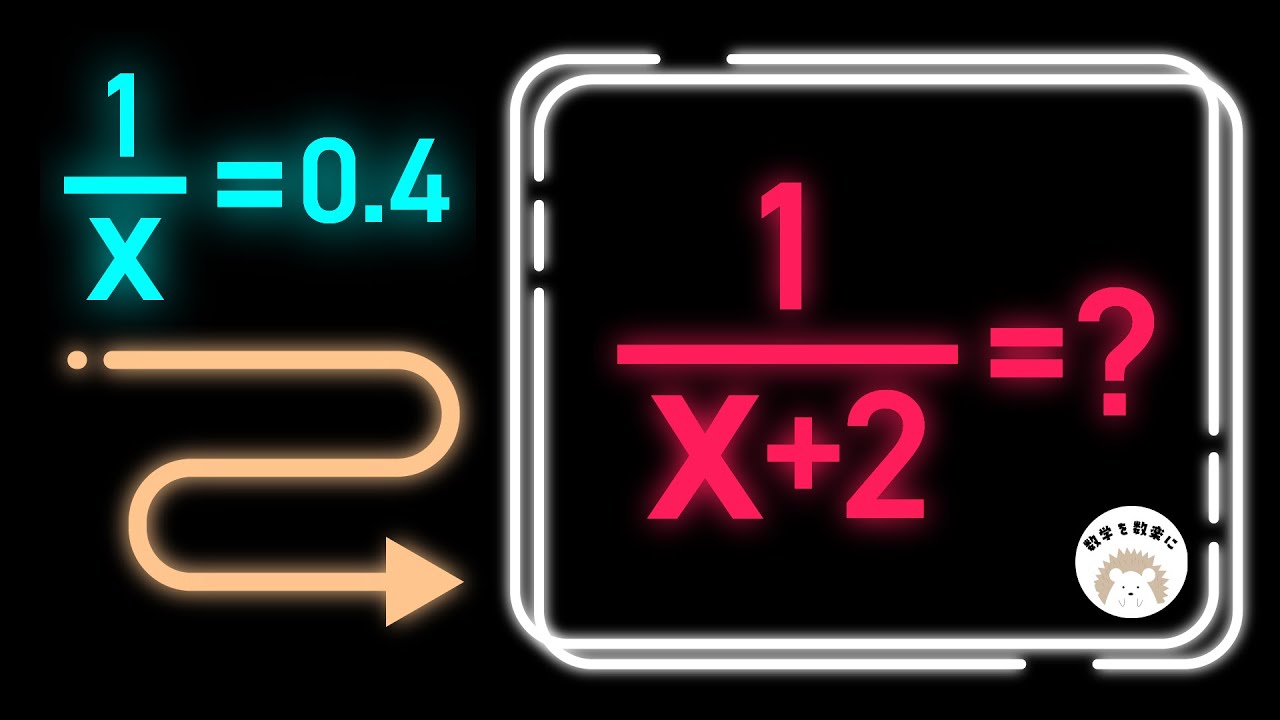
単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{x}=0.4$のとき$\frac{1}{x+2}=$
この動画を見る
$\frac{1}{x}=0.4$のとき$\frac{1}{x+2}=$
【条件をフル活用…!】図形:兵庫県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)#兵庫県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
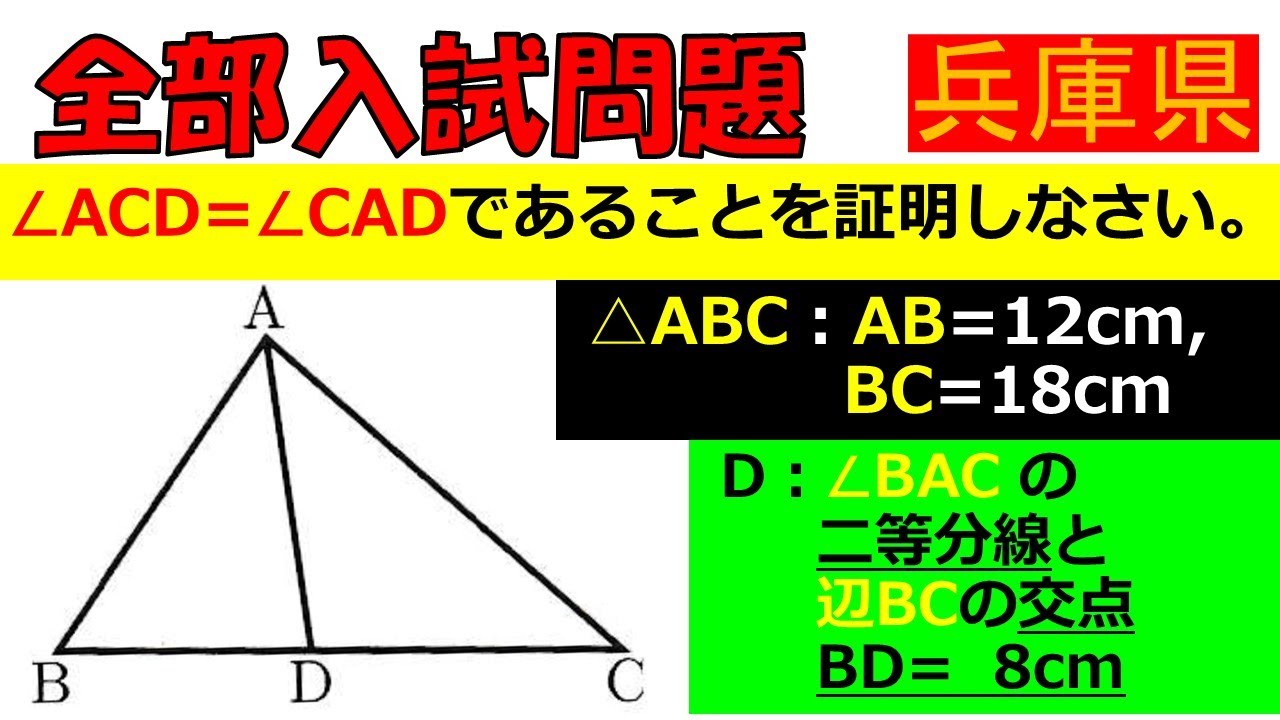
$ \triangle ABC $の$ AB$は12cmであり,$ BC $は18cmである.
$ D $は$ \angle BAC $の二等分線と辺$ BC $の交点である.
$ \angle ACD=\angle CAD $であることを証明しなさい.
兵庫県公立高等学校過去問
この動画を見る
$ \triangle ABC $の$ AB$は12cmであり,$ BC $は18cmである.
$ D $は$ \angle BAC $の二等分線と辺$ BC $の交点である.
$ \angle ACD=\angle CAD $であることを証明しなさい.
兵庫県公立高等学校過去問
証明がわからない人へ

単元:
#数学(中学生)#中2数学#平行と合同
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
三角形の合同の証明の動画です
$AB=AD,\angle ABC= \angle ADE$ならば$\triangle ABC \equiv \triangle ADE$となることを証明してください
この動画を見る
三角形の合同の証明の動画です
$AB=AD,\angle ABC= \angle ADE$ならば$\triangle ABC \equiv \triangle ADE$となることを証明してください
こんな学校知ってる?

【学んだことを活かせ…!】連立方程式:明治大学付属中野高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#明治大学付属中野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x,y $についての連立方程式 $ \begin{eqnarray}
\left\{
\begin{array}{l}
4x+3y=11 \\
x-ky=-\dfrac{1}{2}k
\end{array}
\right.
\end{eqnarray}$ の解が $\begin{eqnarray}
\left\{
\begin{array}{l}
x=p \\
y=q
\end{array}
\right.
\end{eqnarray}$ であり,
$ p+q=3 $が成り立つ.$ k $の値を求めなさい.
明治大学付属中野高等学校過去問
この動画を見る
$ x,y $についての連立方程式 $ \begin{eqnarray}
\left\{
\begin{array}{l}
4x+3y=11 \\
x-ky=-\dfrac{1}{2}k
\end{array}
\right.
\end{eqnarray}$ の解が $\begin{eqnarray}
\left\{
\begin{array}{l}
x=p \\
y=q
\end{array}
\right.
\end{eqnarray}$ であり,
$ p+q=3 $が成り立つ.$ k $の値を求めなさい.
明治大学付属中野高等学校過去問
【案外戸惑う…!】整数:福岡大学付属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
直線$ y=-\dfrac{1}{2}x+10 $上の点で
$ x $座標も$ y $座標も正の整数である点は全部で$ \Box $個ある.
福岡大学付属大濠高等学校過去問
この動画を見る
直線$ y=-\dfrac{1}{2}x+10 $上の点で
$ x $座標も$ y $座標も正の整数である点は全部で$ \Box $個ある.
福岡大学付属大濠高等学校過去問
