 2次方程式
2次方程式
 2次方程式
2次方程式
【高校受験対策/数学】死守83

単元:
#数学(中学生)#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#平方根#2次方程式#比例・反比例#空間図形#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守83
①$-1-5$を計算しなさい。
②$(-3)^2+4×(-2)$を計算しなさい。
③$10xy^2÷ (-5y)×3x$を計算しなさい。
④$2x-y-\frac{5x+y}{3}$を計算しなさい。
⑤$(\sqrt{5}+3)(\sqrt{5}-2)$を計算しなさい。
⑥次の方程式を解きなさい。
$x^2=9x$
⑦$l=2\pi r$を$r$について解きなさい。
⑧正$n$角形の1つの内角が$140°$であるとき、$n$の値を求めなさい。
⑨$y$は$x$に比例し、$x=-3$のとき、$y=18$である。
$x=\frac{1}{2}$のときの$y$の値を求めなさい。
➉空間内の平面について述べた文として適切でないものを、次のア~エの中から1つ選びその記号を書きなさい。
ア 一直線上にある3点をふくむ平面は1つに決まる。
イ 交わる2直線をふくむ平面は1つに決まる。
ウ 平行な2直線をふくむ平面は1つに決まる。
エ 1つの直線とその直線上にない1点をふくむ平面は1つに決まる。
この動画を見る
高校受験対策・死守83
①$-1-5$を計算しなさい。
②$(-3)^2+4×(-2)$を計算しなさい。
③$10xy^2÷ (-5y)×3x$を計算しなさい。
④$2x-y-\frac{5x+y}{3}$を計算しなさい。
⑤$(\sqrt{5}+3)(\sqrt{5}-2)$を計算しなさい。
⑥次の方程式を解きなさい。
$x^2=9x$
⑦$l=2\pi r$を$r$について解きなさい。
⑧正$n$角形の1つの内角が$140°$であるとき、$n$の値を求めなさい。
⑨$y$は$x$に比例し、$x=-3$のとき、$y=18$である。
$x=\frac{1}{2}$のときの$y$の値を求めなさい。
➉空間内の平面について述べた文として適切でないものを、次のア~エの中から1つ選びその記号を書きなさい。
ア 一直線上にある3点をふくむ平面は1つに決まる。
イ 交わる2直線をふくむ平面は1つに決まる。
ウ 平行な2直線をふくむ平面は1つに決まる。
エ 1つの直線とその直線上にない1点をふくむ平面は1つに決まる。
【中学数学】2次方程式の演習~2021年度成城学園高等学校~【高校受験】

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\displaystyle \frac{(x + 7) ^ 2 - (x - 7) ^ 2}{12} = \displaystyle \frac{1}{4}x^ 2 +\displaystyle \frac{1}{3}x+4$
この動画を見る
$\displaystyle \frac{(x + 7) ^ 2 - (x - 7) ^ 2}{12} = \displaystyle \frac{1}{4}x^ 2 +\displaystyle \frac{1}{3}x+4$
超気持ちいい!!気付けば一瞬!!帝京大学高校

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-2x-1 = 0$のとき
$x^2(x-1)^2(x-2)^2$ =
帝京大学高等学校
この動画を見る
$x^2-2x-1 = 0$のとき
$x^2(x-1)^2(x-2)^2$ =
帝京大学高等学校
2次方程式と式の値 本郷高校
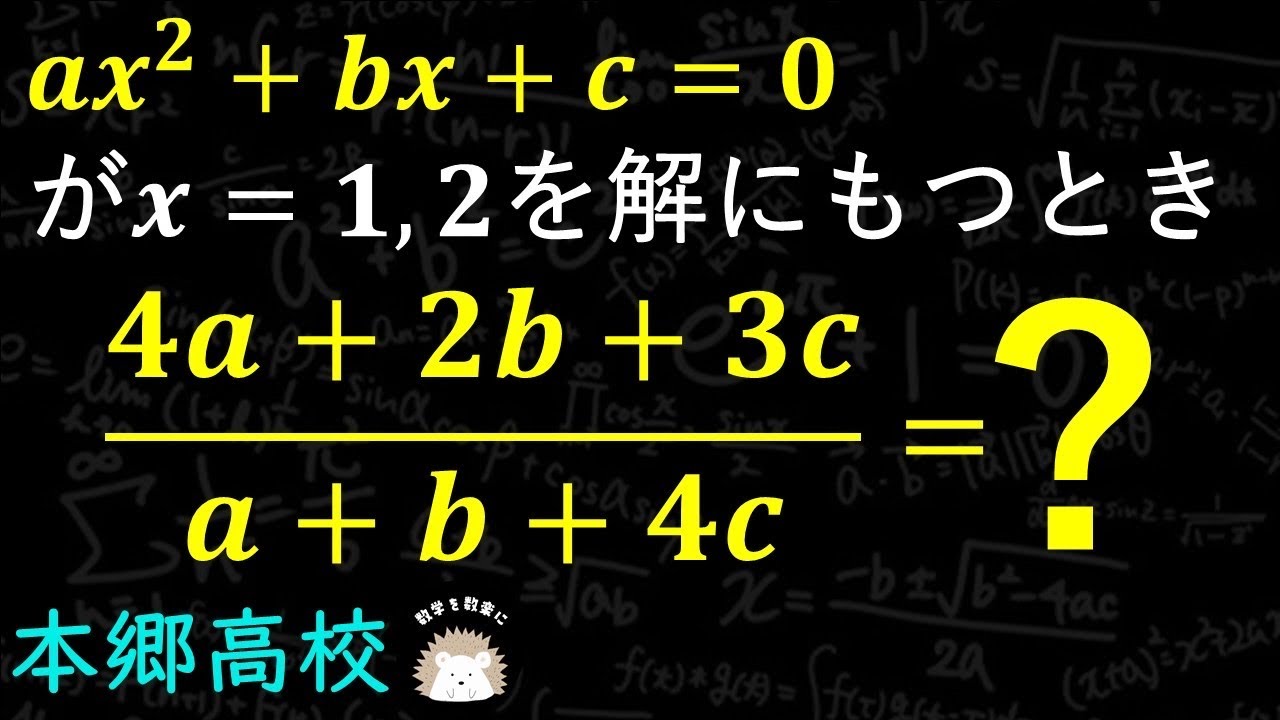
単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$ax^2+bx+c=0$がx=1,2を解にもつ
$\frac{4a+2b+3c}{a+b+4c}$
本郷高等学校
この動画を見る
$ax^2+bx+c=0$がx=1,2を解にもつ
$\frac{4a+2b+3c}{a+b+4c}$
本郷高等学校
【高校受験対策/数学】死守-80

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#2次方程式#空間図形#1次関数#確率#2次関数#文字と式#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守80
①$-3+(-4)×5$を計算しなさい。
②$4xy÷8x×6y$を計算しなさい。
③$\frac{4x-y}{2}-(2x-3y)$を計算しなさい。
④連立方程式を解きなさい。
$5x-4y=9$
$2x-3y=5$
③下の図で、$\angle x$の大きさを求めなさい。
④地球の直径は約$12700km$です。
有効数字が$1,2,7$であるとして、この距離を整数部分が1けたの数と、10の何乗かの積の形で表すと右のようになります。
アとイにあてはまる数を書きなさい。
⑦半径が$2cm$の球の体積と表面積を求めなさい。ただし円周率は$\pi$とする。
⑧赤玉3個と白玉2個が入っている袋があります。
この袋から玉を1個取り出して色を確認して、それを袋に戻してから、もう一度玉を1個取り出して色を確認します。
このとき、2回とも同じ色の玉が出る確率を求めなさい。
ただし、袋の中は見えないものとし、どの玉が出ることも同様に確からしいものとする。
⑨関数$y=ax^2$について、$x$の変域が$-2 \leqq x \leqq 3$のとき、$y$の変域は$-3b \leqq y \leqq 0$となりました。
このとき$a$の値を求めなさい。
この動画を見る
高校受験対策・死守80
①$-3+(-4)×5$を計算しなさい。
②$4xy÷8x×6y$を計算しなさい。
③$\frac{4x-y}{2}-(2x-3y)$を計算しなさい。
④連立方程式を解きなさい。
$5x-4y=9$
$2x-3y=5$
③下の図で、$\angle x$の大きさを求めなさい。
④地球の直径は約$12700km$です。
有効数字が$1,2,7$であるとして、この距離を整数部分が1けたの数と、10の何乗かの積の形で表すと右のようになります。
アとイにあてはまる数を書きなさい。
⑦半径が$2cm$の球の体積と表面積を求めなさい。ただし円周率は$\pi$とする。
⑧赤玉3個と白玉2個が入っている袋があります。
この袋から玉を1個取り出して色を確認して、それを袋に戻してから、もう一度玉を1個取り出して色を確認します。
このとき、2回とも同じ色の玉が出る確率を求めなさい。
ただし、袋の中は見えないものとし、どの玉が出ることも同様に確からしいものとする。
⑨関数$y=ax^2$について、$x$の変域が$-2 \leqq x \leqq 3$のとき、$y$の変域は$-3b \leqq y \leqq 0$となりました。
このとき$a$の値を求めなさい。
【高校受験対策/数学】死守-79

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#2次方程式#文字と式#平面図形#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守79
①$-3-(-7)$を計算しなさい。
②$8a^3b^5÷4a^2b^3$を計算しなさい。
③$x^2-8x+16$を因数分解しなさい。
④$a=\frac{2b-c}{5}$を$c$について解きなさい。
⑤二次方程式$x^2+5x+2=0$を解きなさい。
⑥$a=2$、$b=-3$のとき、$a+b^2$の値を求めなさい。
⑦次の文の( )に当てはまる条件として最も適切なものを、ア~エから1つ選んで記号で答えなさい。
平行四辺形$ABCD$に、( )の条件が加わると、平行四辺形$ABCD$は長方形になる。
ア $AB=BC$
イ $AC\perp BD$
ウ $AC=BD$
エ $\angle ABD=\angle CBD$
⑧$A$地点から$B$地点まで、初めは毎分$60m$で$am$歩き、途中から毎分$100m$で$bm$走ったところ、$20$分以内で$B$地点に到着した。この数量の関係を不等式で表しなさい。
⑨次のア~エのうちから、内容が正しいものを1つ選んで記号で答えなさい。
ア $9$の平方根は$3$と$-3$である。
イ $\sqrt{16}$を根号を使わずに表すと$\pm 4$である。
ウ $\sqrt{5}+\sqrt{7}$と$\sqrt{5+7}$は同じ値である。
エ $(\sqrt{2}+\sqrt{6})^2$と$(\sqrt{2})^2+(\sqrt{6})^2$は同じ値である。
この動画を見る
高校受験対策・死守79
①$-3-(-7)$を計算しなさい。
②$8a^3b^5÷4a^2b^3$を計算しなさい。
③$x^2-8x+16$を因数分解しなさい。
④$a=\frac{2b-c}{5}$を$c$について解きなさい。
⑤二次方程式$x^2+5x+2=0$を解きなさい。
⑥$a=2$、$b=-3$のとき、$a+b^2$の値を求めなさい。
⑦次の文の( )に当てはまる条件として最も適切なものを、ア~エから1つ選んで記号で答えなさい。
平行四辺形$ABCD$に、( )の条件が加わると、平行四辺形$ABCD$は長方形になる。
ア $AB=BC$
イ $AC\perp BD$
ウ $AC=BD$
エ $\angle ABD=\angle CBD$
⑧$A$地点から$B$地点まで、初めは毎分$60m$で$am$歩き、途中から毎分$100m$で$bm$走ったところ、$20$分以内で$B$地点に到着した。この数量の関係を不等式で表しなさい。
⑨次のア~エのうちから、内容が正しいものを1つ選んで記号で答えなさい。
ア $9$の平方根は$3$と$-3$である。
イ $\sqrt{16}$を根号を使わずに表すと$\pm 4$である。
ウ $\sqrt{5}+\sqrt{7}$と$\sqrt{5+7}$は同じ値である。
エ $(\sqrt{2}+\sqrt{6})^2$と$(\sqrt{2})^2+(\sqrt{6})^2$は同じ値である。
【高校受験対策/数学】死守-78

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#平方根#2次方程式#比例・反比例#1次関数#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守78
①下の図のように、長方形$ABCD$の中に 1辺の長さが$\sqrt{5}cm$と$\sqrt{10}cm$の正方形がある。
このとき、斜線部分の長方形の間の長さを求めなさい。
②葉一くんは、下の図の平行四辺形$ABCD$の面積を求めるために、辺$BC$を底辺とみて、高さを測ろうと考えた。
点を$P$下の図のようにとるとき、線分$PH$が高さとなるような点$H$を作図によって求めなさい。
③1000円で、1個$a$円のクリームパン5個と1個$b$円のジャムパン3個を買うことができる。
ただし消費税は考えないものとする。
この数量の関係を表した不等式としてもっとも適切なものを、次の ア~エの中から一つ選んで、その記号を書きなさい。
ア $1000-(5a+3b) \lt 0$
イ $5a+3b \lt 1000$
ウ $1000-(5a+3b) \geqq 0$
エ $(5a+3b) \geqq 1000$
④ 右の図で、点$A$は関数$y=\frac{2}{x }$と関数$y=ax^2$のグラフの交点である。
点$B$は点$A$を$y$軸を対称の軸として対称移動させたものであり、$x$座標は$-1$である。
このことから、$a$の値はアであり、関数$y=ax^2$について、 $x$の値が1から3まで増加するときの変化の割合はイであることがわ かる。
このとき上のア・イに当てはまる数をそれぞれ書きなさい。
この動画を見る
高校受験対策・死守78
①下の図のように、長方形$ABCD$の中に 1辺の長さが$\sqrt{5}cm$と$\sqrt{10}cm$の正方形がある。
このとき、斜線部分の長方形の間の長さを求めなさい。
②葉一くんは、下の図の平行四辺形$ABCD$の面積を求めるために、辺$BC$を底辺とみて、高さを測ろうと考えた。
点を$P$下の図のようにとるとき、線分$PH$が高さとなるような点$H$を作図によって求めなさい。
③1000円で、1個$a$円のクリームパン5個と1個$b$円のジャムパン3個を買うことができる。
ただし消費税は考えないものとする。
この数量の関係を表した不等式としてもっとも適切なものを、次の ア~エの中から一つ選んで、その記号を書きなさい。
ア $1000-(5a+3b) \lt 0$
イ $5a+3b \lt 1000$
ウ $1000-(5a+3b) \geqq 0$
エ $(5a+3b) \geqq 1000$
④ 右の図で、点$A$は関数$y=\frac{2}{x }$と関数$y=ax^2$のグラフの交点である。
点$B$は点$A$を$y$軸を対称の軸として対称移動させたものであり、$x$座標は$-1$である。
このことから、$a$の値はアであり、関数$y=ax^2$について、 $x$の値が1から3まで増加するときの変化の割合はイであることがわ かる。
このとき上のア・イに当てはまる数をそれぞれ書きなさい。
これ思いつくのすごい

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$x=2-\sqrt{ 3 }$のとき、$x^2-4x-1$の値を求めよ
この動画を見る
$x=2-\sqrt{ 3 }$のとき、$x^2-4x-1$の値を求めよ
【中学数学】2次方程式の演習~解が1つ分かってる問題~ 3-5.5【中3数学】

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
2次方程式$x^²+ax-15=0$の解の1つが3であるとき、aともう1つの解の値を答えよ。
この動画を見る
2次方程式$x^²+ax-15=0$の解の1つが3であるとき、aともう1つの解の値を答えよ。
【高校受験対策/数学】死守77

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#1次関数#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守77
①$-3+(-2)$を計算しなさい。
➁$8-4÷(-2)^2$を計算しなさい。
③$5×(-5a)$を計算しなさい。
④$\frac{1}{2}x^2y÷\frac{1}{4}xy$を計算しなさい。
⑤$\sqrt{48}-\sqrt{3}$を計算しなさい。
⑥$(2a-b)^2$を展開しなさい。
⑦$x^2-x-42$を因数分解しなさい。
⑧半径が$6cm$で中心角が$45°$のおうぎ形の面積を求めなさい。
ただし、円周率は$\pi$とする。
⑨解が$-5,1$の2つの数となる、$x$についての2次方程式を1つ作りなさい。
⑩次のア~エのうち、数の集合と四則との関係について述べた文として正しいものをすべて選び、記号で答えなさい。
ア 自然数と自然数の加法の結果は、いつでも自然数となる。
イ 自然数と自然数の減法の結果は、いつでも整数となる。
ウ 自然数と自然数の乗法の結果は、いつでも自然数となる。
エ 自然数と自然数の除法の結果は、いつでも整数となる。
この動画を見る
高校受験対策・死守77
①$-3+(-2)$を計算しなさい。
➁$8-4÷(-2)^2$を計算しなさい。
③$5×(-5a)$を計算しなさい。
④$\frac{1}{2}x^2y÷\frac{1}{4}xy$を計算しなさい。
⑤$\sqrt{48}-\sqrt{3}$を計算しなさい。
⑥$(2a-b)^2$を展開しなさい。
⑦$x^2-x-42$を因数分解しなさい。
⑧半径が$6cm$で中心角が$45°$のおうぎ形の面積を求めなさい。
ただし、円周率は$\pi$とする。
⑨解が$-5,1$の2つの数となる、$x$についての2次方程式を1つ作りなさい。
⑩次のア~エのうち、数の集合と四則との関係について述べた文として正しいものをすべて選び、記号で答えなさい。
ア 自然数と自然数の加法の結果は、いつでも自然数となる。
イ 自然数と自然数の減法の結果は、いつでも整数となる。
ウ 自然数と自然数の乗法の結果は、いつでも自然数となる。
エ 自然数と自然数の除法の結果は、いつでも整数となる。
これ解ける?

単元:
#中3数学#2次方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\sqrt{ 3 \sqrt{ 3 } \sqrt{ 3 } \sqrt{ 3 } \sqrt{ 3… } }$
解き方解説動画です
この動画を見る
$\sqrt{ 3 \sqrt{ 3 } \sqrt{ 3 } \sqrt{ 3 } \sqrt{ 3… } }$
解き方解説動画です
【一歩先行く3分間!】二次方程式:東大寺学園高等学校~全国入試問題解法

単元:
#数学(中学生)#2次方程式#高校入試過去問(数学)#数学
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東大寺学園高等学校
aの値とpの値を求めよ。
【$x$の二次方程式】
$\sqrt{ 5x^2 }+ax+4\sqrt{ 5 }=0$
の解の1つが
$\sqrt{ 15x }+ax+2\sqrt{ 3 }=0$
の解である。
もう一つの解を pとする。
この動画を見る
入試問題 東大寺学園高等学校
aの値とpの値を求めよ。
【$x$の二次方程式】
$\sqrt{ 5x^2 }+ax+4\sqrt{ 5 }=0$
の解の1つが
$\sqrt{ 15x }+ax+2\sqrt{ 3 }=0$
の解である。
もう一つの解を pとする。
【高校受験対策/数学】死守75

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#2次方程式#1次関数#平行と合同#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守75
①$-8+5$を計算しなさい。
②$1+3×-(\frac{2}{7})$を計算しなさい。
③$2(a+4b)+3(a-2b)$を計算しなさい。
④$\sqrt{27}-\frac{6}{\sqrt{3}}$を計算しなさい。
⑤$(x+1)^2+(x-4)(x+2)$を計算しなさい。
⑥次の式を因数分解しなさい。
$9x^2-4y^2$
⑦右の図のように、長方形$ABCD$を対角線$AC$を折り目として折り返し、
頂点$B$が移った点を$E$とする。
$\angle ACE=20°$のとき、$\angle x$の大きさを求めなさい。
⑧右の図のように、2点$A(2,6)$、$B(8,2)$がある。
次の文中の(ア)、(イ)にあてはまる数を求めなさい。
直線$y=ax$のグラフが、線分$AB$上の点を通るとき、$a$の値の範囲は、(ア) $ \leqq a\leqq$ (イ)である。
この動画を見る
高校受験対策・死守75
①$-8+5$を計算しなさい。
②$1+3×-(\frac{2}{7})$を計算しなさい。
③$2(a+4b)+3(a-2b)$を計算しなさい。
④$\sqrt{27}-\frac{6}{\sqrt{3}}$を計算しなさい。
⑤$(x+1)^2+(x-4)(x+2)$を計算しなさい。
⑥次の式を因数分解しなさい。
$9x^2-4y^2$
⑦右の図のように、長方形$ABCD$を対角線$AC$を折り目として折り返し、
頂点$B$が移った点を$E$とする。
$\angle ACE=20°$のとき、$\angle x$の大きさを求めなさい。
⑧右の図のように、2点$A(2,6)$、$B(8,2)$がある。
次の文中の(ア)、(イ)にあてはまる数を求めなさい。
直線$y=ax$のグラフが、線分$AB$上の点を通るとき、$a$の値の範囲は、(ア) $ \leqq a\leqq$ (イ)である。
【中学数学】意外と間違える2次方程式の問題 3-5.5【中3数学】

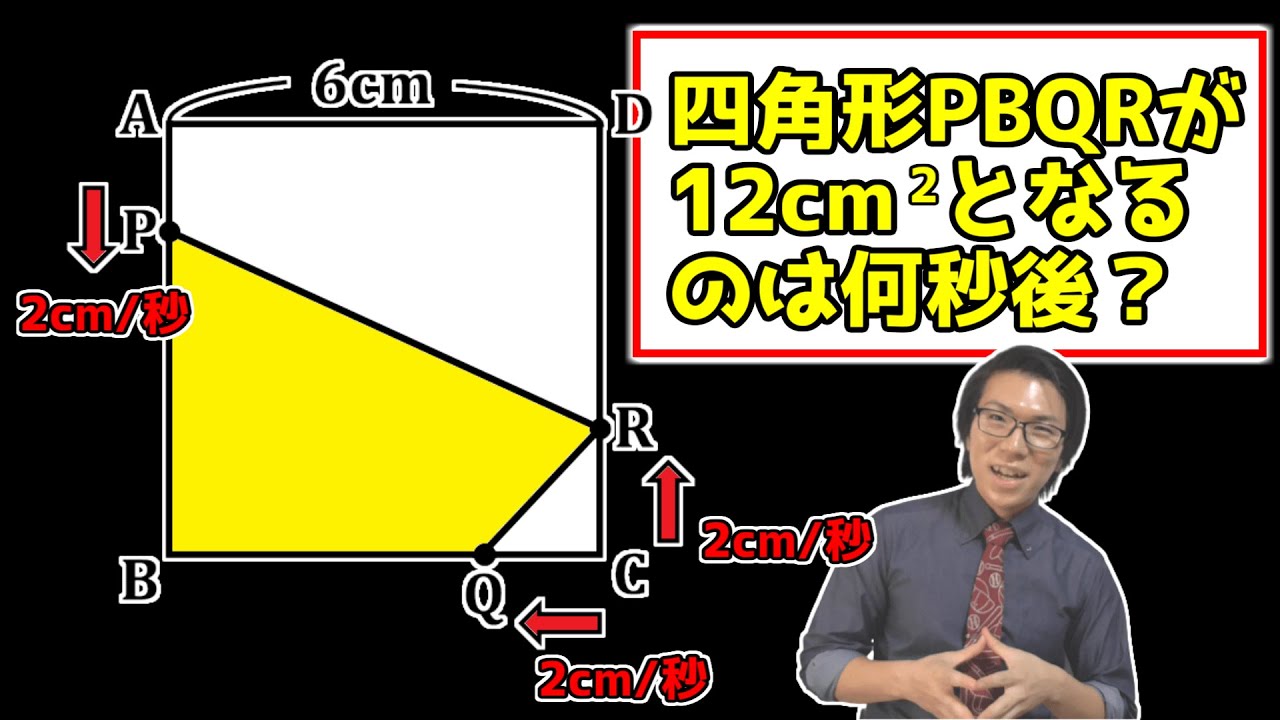
【中学数学】2次方程式の利用~動く点Pの問題~ 3-5【中3数学】
単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
動画内の図のような正方形ABCDで点Pは辺AB上を秒速2cmでAからBまで動く。
また、点Qは点PがAを出発するのと同時にCを出発し、辺BC上を点Pと同じ速さでBまで動く。
点Rは点PがAを出発するのと同時にCを出発し、辺CD上を点Pと同じ速さでDまで動く。
四角形PBQRの面積が12cm²になるのは点PがAを出発してから何秒後か。
この動画を見る
動画内の図のような正方形ABCDで点Pは辺AB上を秒速2cmでAからBまで動く。
また、点Qは点PがAを出発するのと同時にCを出発し、辺BC上を点Pと同じ速さでBまで動く。
点Rは点PがAを出発するのと同時にCを出発し、辺CD上を点Pと同じ速さでDまで動く。
四角形PBQRの面積が12cm²になるのは点PがAを出発してから何秒後か。
【高校受験対策/数学】死守73

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#確率#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守73
①$-9+(-8)$を計算しなさい。
②$\frac{3}{4}÷-(\frac{5}{6})$を計算しなさい。
③$2(a+46)-(-3a+7b) を計算しなさい。
④$\sqrt{12}×\sqrt{2}÷\sqrt{6}$を計算しなさい。
⑤二次方程式$3x^2-x-1=0$を解きなさい。
⑥連立方程式を解きなさい。
$2x+3y=20$
$4y=x+1$
⑦2つのさいころを同時に投げるとき、出る目の和が8に ならない確率を求めなさい。
ただし、どの目が出ることも同様に確からしいとする。
⑧右の図のように、線分$OA$、$OB$がある。
$\angle AOB$の二等分線上にあり、2点$O,B$から等しい距離にある点$P$を、コンパスと定規を使って作図しなさい。
この動画を見る
高校受験対策・死守73
①$-9+(-8)$を計算しなさい。
②$\frac{3}{4}÷-(\frac{5}{6})$を計算しなさい。
③$2(a+46)-(-3a+7b) を計算しなさい。
④$\sqrt{12}×\sqrt{2}÷\sqrt{6}$を計算しなさい。
⑤二次方程式$3x^2-x-1=0$を解きなさい。
⑥連立方程式を解きなさい。
$2x+3y=20$
$4y=x+1$
⑦2つのさいころを同時に投げるとき、出る目の和が8に ならない確率を求めなさい。
ただし、どの目が出ることも同様に確からしいとする。
⑧右の図のように、線分$OA$、$OB$がある。
$\angle AOB$の二等分線上にあり、2点$O,B$から等しい距離にある点$P$を、コンパスと定規を使って作図しなさい。
【高校受験対策/数学】死守72

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#2次方程式#空間図形#平行と合同#確率#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守72
①$2-6$を計算しなさい。
➁$-3×(-2^2)$を計算しなさい。
③$\frac{2a+b}{ 3 }+\frac{a-b}{ 2 }$を計算しなさい。
④$xy^2×x^2÷xy$を計算しなさい。
⑤$\frac{6}{\sqrt{3}}+\sqrt{15}×\sqrt{5}$を計算しなさい。
⑥2次方程式$x^2+7x-18=0$ を解きなさい。
⑦$a=\sqrt{5}+3$のとき、$a^2-6a+9$の値を求めなさい。
⑧500円、100円、50円の硬貨が1枚ずつある。
この3枚を同時に1回投げるとき、表が出た硬貨の合計金額が500円以下になる確率を求めなさい。
ただし3枚の硬貨のそれぞれについて、表と裏の出方は同様に確からしいとする。
⑨右の図は底面の半径が$3cm$、側面になるおうぎ形の半径が$5cm$の円錐の展開図である。
これを組み立ててできる円錐の体積を求めなさい。
この動画を見る
高校受験対策・死守72
①$2-6$を計算しなさい。
➁$-3×(-2^2)$を計算しなさい。
③$\frac{2a+b}{ 3 }+\frac{a-b}{ 2 }$を計算しなさい。
④$xy^2×x^2÷xy$を計算しなさい。
⑤$\frac{6}{\sqrt{3}}+\sqrt{15}×\sqrt{5}$を計算しなさい。
⑥2次方程式$x^2+7x-18=0$ を解きなさい。
⑦$a=\sqrt{5}+3$のとき、$a^2-6a+9$の値を求めなさい。
⑧500円、100円、50円の硬貨が1枚ずつある。
この3枚を同時に1回投げるとき、表が出た硬貨の合計金額が500円以下になる確率を求めなさい。
ただし3枚の硬貨のそれぞれについて、表と裏の出方は同様に確からしいとする。
⑨右の図は底面の半径が$3cm$、側面になるおうぎ形の半径が$5cm$の円錐の展開図である。
これを組み立ててできる円錐の体積を求めなさい。
2次方程式の難問 早稲田実業

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-px+q^2=0$は異なる2つの整数解をもつ。
p=? q=?(p,qは素数)
早稲田実業学校
この動画を見る
$x^2-px+q^2=0$は異なる2つの整数解をもつ。
p=? q=?(p,qは素数)
早稲田実業学校
【中学数学】2次方程式の解の公式・改~得意な人にはおすすめ~ 3-2.5【中3数学】

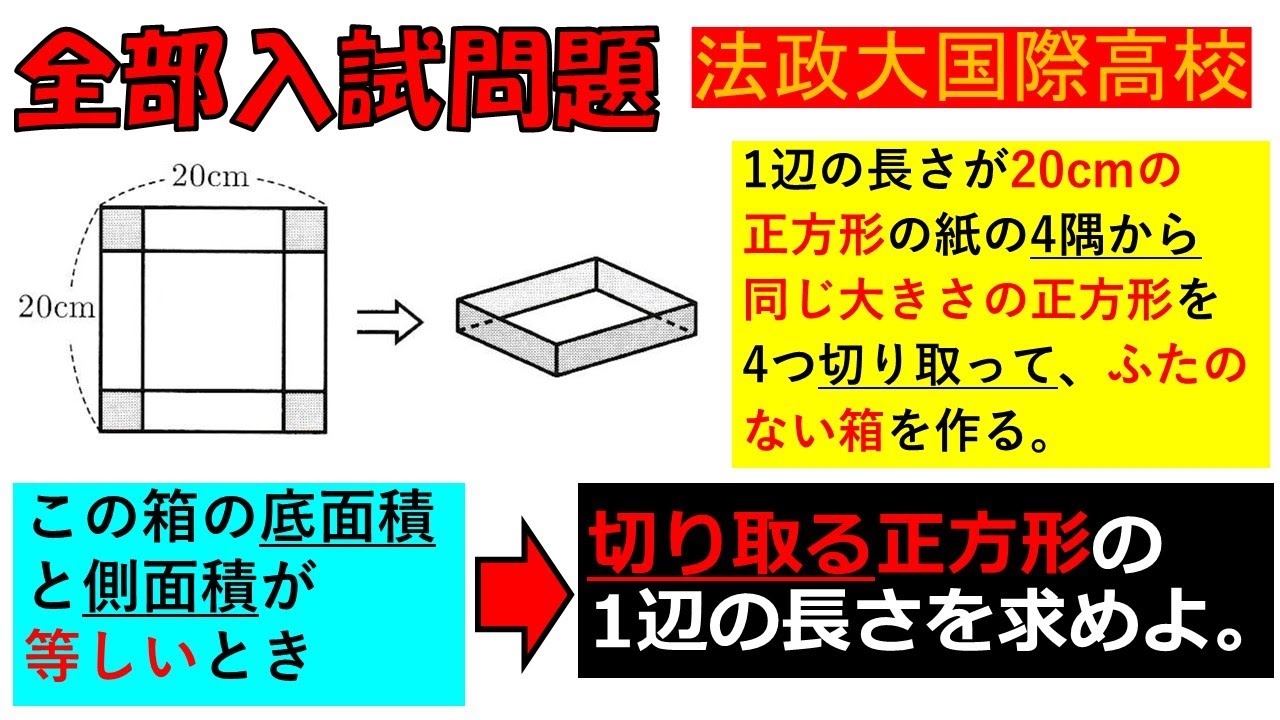
【類題ザクザク⁈まず3分で本質をつかもう。】文章題:法政大学国際高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#法政大学国際高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 法政大学国際高等学校
1辺の長さが20cmの正方形の紙の4隅から 同じ大きさの正方形を 4つ切り取って、ふたのない箱を作る。
この箱の底面積と側面積が等しいとき
↓
切り取る正方形の 1辺の長さを求めよ。
この動画を見る
入試問題 法政大学国際高等学校
1辺の長さが20cmの正方形の紙の4隅から 同じ大きさの正方形を 4つ切り取って、ふたのない箱を作る。
この箱の底面積と側面積が等しいとき
↓
切り取る正方形の 1辺の長さを求めよ。
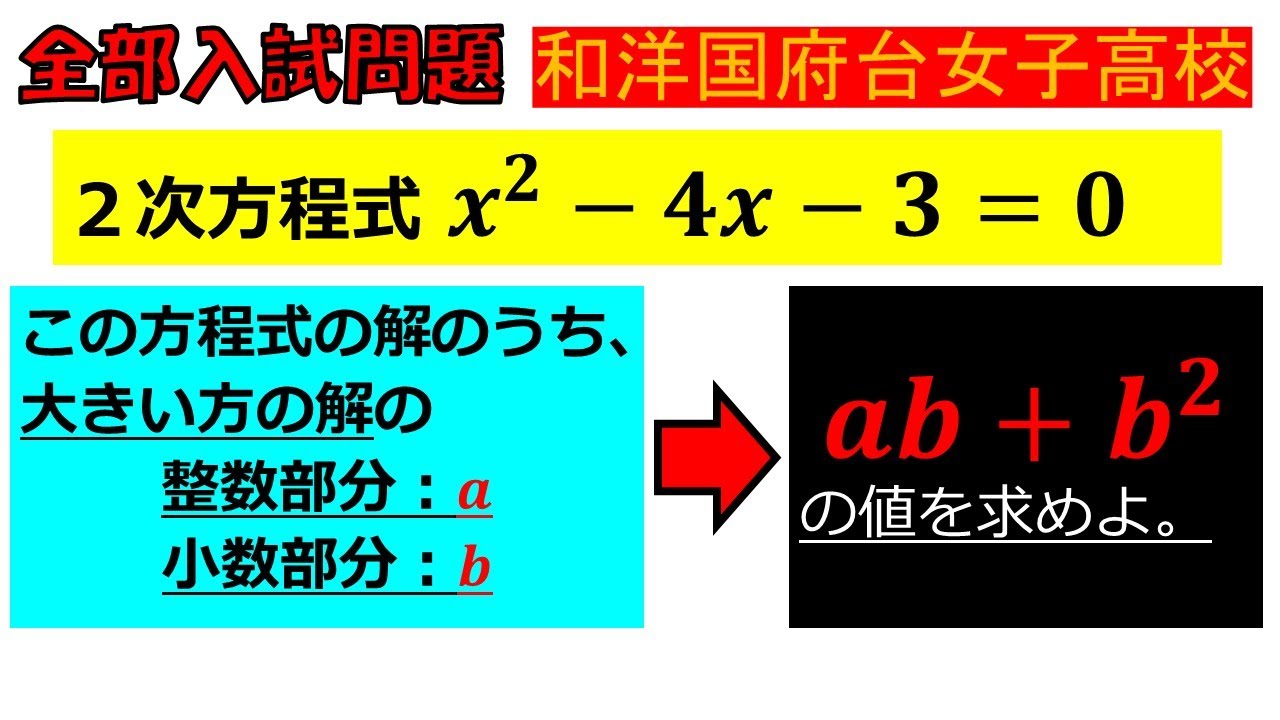
【総合力が試される5分間!】二次方程式:和洋国府台女子高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#和洋国府台女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 和洋国府台女子高等学校
【二次方程式】
$x^2-4x-3=0$
この方程式の解のうち、 大きい方の解の
整数部分:a
小数部分:b
↓
$ab+b^2$
の値を求めよ。
この動画を見る
入試問題 和洋国府台女子高等学校
【二次方程式】
$x^2-4x-3=0$
この方程式の解のうち、 大きい方の解の
整数部分:a
小数部分:b
↓
$ab+b^2$
の値を求めよ。
【中学数学】2次方程式の基礎を学ぼう~数学苦手な人は見てね~ 3-1【中3数学】

【まず4分間!理解できる!】二次方程式:明治大学附属中野高等学校~全国入試問題解法

単元:
#数学(中学生)#2次方程式#高校入試過去問(数学)#明治大学付属中野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治大学附属中野高等学校
$X$についての2次方程式
$x^2 - (2k + 1)x + 4 = 0$
の1つの解が$x = k$のとき、 $k$の値を求めなさい。
この動画を見る
入試問題 明治大学附属中野高等学校
$X$についての2次方程式
$x^2 - (2k + 1)x + 4 = 0$
の1つの解が$x = k$のとき、 $k$の値を求めなさい。
【5分で学ぶ~表/裏ルート!】二次方程式:法政大学第二高等学校~全国入試問題解法

単元:
#数学(中学生)#2次方程式#高校入試過去問(数学)#法政大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 法政大学第二高等学校
【2次方程式】
$(x + 2)(x - 2) + 2x = 0$
を解の公式を使わずに解きなさい。
この動画を見る
入試問題 法政大学第二高等学校
【2次方程式】
$(x + 2)(x - 2) + 2x = 0$
を解の公式を使わずに解きなさい。
【5分間の格闘技!素早さを取るか、確実さを取るか!】二次方程式:函館ラ・サール高等学校~全国入試問題解法

単元:
#数学(中学生)#2次方程式#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 函館ラ・サール高等学校
【$x,t$の2次方程式】
$x^2 + ax + b = 0$
の解が$-3$と$2$のとき、
$t^2 + bt + a = −4$
を解きなさい。
この動画を見る
入試問題 函館ラ・サール高等学校
【$x,t$の2次方程式】
$x^2 + ax + b = 0$
の解が$-3$と$2$のとき、
$t^2 + bt + a = −4$
を解きなさい。
二次方程式 整数問題 都立自校作成

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式
$x^2+(a-2)x-6b = 0$の解の1つが-3のときa=? b=?
(a,bは自然数でa<b)
東京都立自校作成
この動画を見る
2次方程式
$x^2+(a-2)x-6b = 0$の解の1つが-3のときa=? b=?
(a,bは自然数でa<b)
東京都立自校作成
【その解法だけでいいのか!中学から高校へ。】二次方程式:日本大学習志野高等学校~全国入試問題解法

単元:
#数学(中学生)#2次方程式#高校入試過去問(数学)#日本大学習志野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 日本大学習志野高等学校
次の□を求めなさい。
$(2x-1)^2-2(2x-1)=15$
の2つの解の差の
2乗は$\boxed{ ァ}\boxed{ ィ}$である。
この動画を見る
入試問題 日本大学習志野高等学校
次の□を求めなさい。
$(2x-1)^2-2(2x-1)=15$
の2つの解の差の
2乗は$\boxed{ ァ}\boxed{ ィ}$である。
どう解く? 小数を含む2次方程式の計算 桐光学園

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
(0.2x+0.3)(x-0.5) = 1.05
桐光学園高等学校
この動画を見る
2次方程式を解け
(0.2x+0.3)(x-0.5) = 1.05
桐光学園高等学校
複雑にみえる二次方程式 桐光学園

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$\sqrt 5 x^2+x+2 = x^2 + \sqrt 5 x+ 2 \sqrt 5$
桐光学園高等学校
この動画を見る
2次方程式を解け
$\sqrt 5 x^2+x+2 = x^2 + \sqrt 5 x+ 2 \sqrt 5$
桐光学園高等学校
【5分で基礎から応用へ!】二次方程式:法政大学高等学校~全国入試問題解法【裏ワザ付き!】

単元:
#数学(中学生)#2次方程式#高校入試過去問(数学)#法政大学高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 法政大学高等学校
$x^2-ax+6=0$
の解の1つが$\sqrt{ 3 }$であるとき、
もう1つの解を求めなさい。
この動画を見る
入試問題 法政大学高等学校
$x^2-ax+6=0$
の解の1つが$\sqrt{ 3 }$であるとき、
もう1つの解を求めなさい。
