2次関数
2次関数
【中学数学】関数y=ax²：2次関数y=ax²の変化の割合を素早く求める方法！学校では教えてくれない必殺技！！
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$y=\dfrac{1}{2}x^2$で、xの値が2から4まで増加するときの変化の割合を求めましょう。
この動画を見る
$y=\dfrac{1}{2}x^2$で、xの値が2から4まで増加するときの変化の割合を求めましょう。
【中学数学】関数：比例、反比例、1次関数、2次関数のそれぞれの特徴とポイントをわかりやすく解説！！
単元：
#数学(中学生)#中１数学#中２数学#中３数学#比例・反比例#1次関数#2次関数
指導講師：
理数個別チャンネル
問題文全文(内容文)：
比例、反比例、1次関数、2次関数のそれぞれの特徴とポイントをわかりやすく解説します！！
この動画を見る
比例、反比例、1次関数、2次関数のそれぞれの特徴とポイントをわかりやすく解説します！！
【高校受験対策/数学/関数46】ひし形の面積を二等分せよ。
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・関数46
Q
右の図において、①は関数$y=x^2$、②は関数$y=ax^2$のグラフであり、$a \lt 0$である。
点A,Bは①のグラフ上にあり、点Aの$x$座標は$2$で、点Aと点Bの$y$座標は等しい。
点Cを$y$軸上にとり、点Oと点A、点Oと点B、点AとC、点Bと点Cをそれぞれ結んで、ひし形OACBをつくる。
また、②のグラフ上に点Aと$x$座標が等しい点Dをとる。
このとき次の各問いに答えなさい。
問1
2点O,Bを通る直線の式を求めよ。
問2
点Cの座標を求めよ。
問3
$x$軸上に点$(3,0)$をとる。
点$(3,0)$を通り、ひし形OACBの面積を2等分する直線の式を求めよ。
問4
点Oと点Dを結んだ線分ODを1辺とする正方形をつくる。
この正方形とひし形OACBの面積の比が$25:64$であるとき、$a$の値を求めよ。
この動画を見る
高校受験対策・関数46
Q
右の図において、①は関数$y=x^2$、②は関数$y=ax^2$のグラフであり、$a \lt 0$である。
点A,Bは①のグラフ上にあり、点Aの$x$座標は$2$で、点Aと点Bの$y$座標は等しい。
点Cを$y$軸上にとり、点Oと点A、点Oと点B、点AとC、点Bと点Cをそれぞれ結んで、ひし形OACBをつくる。
また、②のグラフ上に点Aと$x$座標が等しい点Dをとる。
このとき次の各問いに答えなさい。
問1
2点O,Bを通る直線の式を求めよ。
問2
点Cの座標を求めよ。
問3
$x$軸上に点$(3,0)$をとる。
点$(3,0)$を通り、ひし形OACBの面積を2等分する直線の式を求めよ。
問4
点Oと点Dを結んだ線分ODを1辺とする正方形をつくる。
この正方形とひし形OACBの面積の比が$25:64$であるとき、$a$の値を求めよ。
【高校受験対策】数学-関数43
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・関数43
Q.
右の図において、曲線アは関数$y=\frac{1}{2}x^2$のグラフである。
曲線ア上の点で$x$座標が$4$である点を$A$、$y$軸上の点で$y$座標が$10,6$である点をそれぞれ$B,C$とし、線分$OB$の中点を$D$とする。
また、線分$OA$上に点$E$をとる。ただし$O$は原点とする。
①2点$A,D$を通る直線の式を求めなさい。
②$△OAB$の面積を求めなさい。
③四角形$ABCE$の面積が$△OAB$の面積の$\frac{1}{2}$であるとき、 点$E$の座標を求めなさい。
この動画を見る
高校受験対策・関数43
Q.
右の図において、曲線アは関数$y=\frac{1}{2}x^2$のグラフである。
曲線ア上の点で$x$座標が$4$である点を$A$、$y$軸上の点で$y$座標が$10,6$である点をそれぞれ$B,C$とし、線分$OB$の中点を$D$とする。
また、線分$OA$上に点$E$をとる。ただし$O$は原点とする。
①2点$A,D$を通る直線の式を求めなさい。
②$△OAB$の面積を求めなさい。
③四角形$ABCE$の面積が$△OAB$の面積の$\frac{1}{2}$であるとき、 点$E$の座標を求めなさい。
【高校受験対策】数学-死守38
単元：
#数学(中学生)#中１数学#中２数学#中３数学#方程式#連立方程式#２次方程式#1次関数#確率#2次関数#円
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・死守38
①$-7+5$を計算しなさい。
➁$\frac{3x-2}{5} \times10$を計算しなさい。
③$5ab^2 \div\frac{a}{3}$を計算しなさい。
④$(x+8)(x-6)$を計算しなさい。
⑤$25$の平方根を求めなさい。
⑥関数$y=\frac{a}{x}$のグラフが点$(6,-2)$を通るとき、$a$の値をを求めなさい。
⑦連立方程式を解きなさい。
$3x+y=-5$
$2x+3y=6$
⑧二次方程式を解きなさい。
$x^2+7x+1=0$
⑨右の図1で$\angle x$大きさを求めなさい。
⑩大小2つのさいころを同時に投げるとき、 2つとも同じ目が出る確率を求めなさい。
⑪右の図2において、点$A,B,C$は円$O$の周上の点である。
$\angle x$の大きさを求めなさい。
⑫左の図3のように、$y=ax^2(a\gt0)$のグラフ上 に2点$A,B$があり、$x$座標はそれぞれ$-6,4$である。
直線$AB$の傾きがであるとき、$a$の値を求めなさい。
この動画を見る
高校受験対策・死守38
①$-7+5$を計算しなさい。
➁$\frac{3x-2}{5} \times10$を計算しなさい。
③$5ab^2 \div\frac{a}{3}$を計算しなさい。
④$(x+8)(x-6)$を計算しなさい。
⑤$25$の平方根を求めなさい。
⑥関数$y=\frac{a}{x}$のグラフが点$(6,-2)$を通るとき、$a$の値をを求めなさい。
⑦連立方程式を解きなさい。
$3x+y=-5$
$2x+3y=6$
⑧二次方程式を解きなさい。
$x^2+7x+1=0$
⑨右の図1で$\angle x$大きさを求めなさい。
⑩大小2つのさいころを同時に投げるとき、 2つとも同じ目が出る確率を求めなさい。
⑪右の図2において、点$A,B,C$は円$O$の周上の点である。
$\angle x$の大きさを求めなさい。
⑫左の図3のように、$y=ax^2(a\gt0)$のグラフ上 に2点$A,B$があり、$x$座標はそれぞれ$-6,4$である。
直線$AB$の傾きがであるとき、$a$の値を求めなさい。
【高校受験対策】数学-関数41
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のように、関数$y=\frac{1}{2}x^2$のグラフ上に2点$A$・$B$があり、点$A$の$x$座標は$-3$、点$B$は点$A$と$y$軸について対称である。
このとき次の問いに答えなさい。
問1
関数$y=\frac{1}{2}x^2$について、$x$の変域が$-3 \leqq x \leqq 4$のときの$y$の変域を求めなさい。
問2
$y$軸上に点$C$を、四角形$OBCA$がひし形となるようにとる。
このとき次の問いに答えなさい。
(1) 直線$AC$の式を求めなさい。
(2) 線分$AC$上に点$D$をとる。$△ODA$と四角形$OBCA$の面積比が$1:4$となるとき、点$D$の座標を求 めなさい。
この動画を見る
右の図のように、関数$y=\frac{1}{2}x^2$のグラフ上に2点$A$・$B$があり、点$A$の$x$座標は$-3$、点$B$は点$A$と$y$軸について対称である。
このとき次の問いに答えなさい。
問1
関数$y=\frac{1}{2}x^2$について、$x$の変域が$-3 \leqq x \leqq 4$のときの$y$の変域を求めなさい。
問2
$y$軸上に点$C$を、四角形$OBCA$がひし形となるようにとる。
このとき次の問いに答えなさい。
(1) 直線$AC$の式を求めなさい。
(2) 線分$AC$上に点$D$をとる。$△ODA$と四角形$OBCA$の面積比が$1:4$となるとき、点$D$の座標を求 めなさい。
【高校受験対策】数学-関数40
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
下の図のように、関数$y=\frac{1}{3}x^2$のグラフ上に2点$A$、$B$がある。
点Ａの$x$座標は$-6$、点$B$の$x$座標は$3$であり、2点$A$、$B$を通る直線と$x$軸との交点を$C$とする。
このとき、次の間1~問6に答えなさい。
問1 点$B$の$y$座標を求めなさい。
問2 関数$y=\frac{1}{3}x^2$について、 $x$の変域が$-6 \leqq x \leqq 3$のときの$y$の変域を求めなさい。
問3 2点$A$、$B$を通る直線の式を求めなさい。
問4 点$C$の座標を求めなさい。
問5 $△OAB$の面積を求めなさい。
問6 $y=\frac{1}{3}x^2$のグラフ上に点$P$にある。$△POC$の面積が$△OAB$の面積と等しくなるような点$P$の$x$座標をすべて求めなさい。
この動画を見る
下の図のように、関数$y=\frac{1}{3}x^2$のグラフ上に2点$A$、$B$がある。
点Ａの$x$座標は$-6$、点$B$の$x$座標は$3$であり、2点$A$、$B$を通る直線と$x$軸との交点を$C$とする。
このとき、次の間1~問6に答えなさい。
問1 点$B$の$y$座標を求めなさい。
問2 関数$y=\frac{1}{3}x^2$について、 $x$の変域が$-6 \leqq x \leqq 3$のときの$y$の変域を求めなさい。
問3 2点$A$、$B$を通る直線の式を求めなさい。
問4 点$C$の座標を求めなさい。
問5 $△OAB$の面積を求めなさい。
問6 $y=\frac{1}{3}x^2$のグラフ上に点$P$にある。$△POC$の面積が$△OAB$の面積と等しくなるような点$P$の$x$座標をすべて求めなさい。
【1/3】中３冬特訓１０日目
単元：
#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
Q.
右の図で、点A・Bは関数$y=x^2$のグラフ上の点、点Cは関数$y=\frac{1}{4}x^2$のグラフ上の点である。また、AC・BCはそれぞれ$x$軸、$y$軸に平行である。
次の問いに答えなさい。ただし3点、A・B・Cは$x \gt 0$にあるものとする。
①点Aの座標が$(2,4)$のとき、点Bの座標を求めよ。
②AC=BCのとき、点Aの座標を求めよ。
この動画を見る
Q.
右の図で、点A・Bは関数$y=x^2$のグラフ上の点、点Cは関数$y=\frac{1}{4}x^2$のグラフ上の点である。また、AC・BCはそれぞれ$x$軸、$y$軸に平行である。
次の問いに答えなさい。ただし3点、A・B・Cは$x \gt 0$にあるものとする。
①点Aの座標が$(2,4)$のとき、点Bの座標を求めよ。
②AC=BCのとき、点Aの座標を求めよ。
【12/28】中３冬特訓４日目
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#平方根#２次方程式#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$x^3+x^2-x-1$を因数分解しなさい。
➁関数$y=ax^2$は$x$の変域が$-4 \leqq x \leqq3$のとき、$y$の変域が$0 \leqq y \leqq8$である。
$x$の値が1から5まで増加するとき、この関数の変化の割合を求めよ。
③二次方程式$x^2-ax-5=0$の解の１つが$x=5$のとき、$a$の値ともう一つの解を求めよ。
④$\sqrt{6a}$を小数第一位で四捨五入すると2になるような整数$a$を求めよ。
この動画を見る
①$x^3+x^2-x-1$を因数分解しなさい。
➁関数$y=ax^2$は$x$の変域が$-4 \leqq x \leqq3$のとき、$y$の変域が$0 \leqq y \leqq8$である。
$x$の値が1から5まで増加するとき、この関数の変化の割合を求めよ。
③二次方程式$x^2-ax-5=0$の解の１つが$x=5$のとき、$a$の値ともう一つの解を求めよ。
④$\sqrt{6a}$を小数第一位で四捨五入すると2になるような整数$a$を求めよ。
【高校受験対策】数学-死守34
単元：
#数学(中学生)#中１数学#中２数学#中３数学#正の数・負の数#式の計算（単項式・多項式・式の四則計算）#式の計算（展開、因数分解）#平方根#２次方程式#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・死守34
①$(-8)+(-4)$
②$-\frac{5}{7}+\frac{2}{3}$
③$65a^2b \div5a$
④$\frac{18}{\sqrt{2}}-\sqrt{98}$
⑤$(x+9)^2-(x-3)(x-7)$
⑥$(x+4)^2-2(x+4)-24$を因数分解しなさい。
⑦2次方程式$6x^2-2x-1=0$を解きなさい。
⑧関数$y=ax^2$について、$x$の値が$2$から$5$まで増加するときの変化の割合が$ー4$であった。このときの$a$の値を求めなさい。
④1本$a$円のえんぴつを9本と1個100円の消しゴムを1個買って1000円を支払い、おつりを受け取った。
このときの数量の関係を不等式で表しなさい。ただし、右辺は1000だけとする。
⑩$\sqrt{53-2n}$が整数となるような正の整数$n$をすべて書きなさい。
⑪
Aさんの家からバス停までの道のりは$a$km、バス停から駅までの道のりは$b$kmである。Aさんが、Aさんの家からバス停までは時速4kmで歩き、バス停から駅までは時速30kmで走るバスに乗ったところ、 Aさんの家から駅まで$t$時間かかった。
このとき、$t$を$a$と$b$を使った式で表しなさい。 ただし、バス停でバスを待つ時間は考えないものとする。
⑫
右の度数分布表は、あるクラスの生徒20人のハンドボール投げの記録をまとめたものである。この度数分布表から求められる記録の平均値を求めなさい。
この動画を見る
高校受験対策・死守34
①$(-8)+(-4)$
②$-\frac{5}{7}+\frac{2}{3}$
③$65a^2b \div5a$
④$\frac{18}{\sqrt{2}}-\sqrt{98}$
⑤$(x+9)^2-(x-3)(x-7)$
⑥$(x+4)^2-2(x+4)-24$を因数分解しなさい。
⑦2次方程式$6x^2-2x-1=0$を解きなさい。
⑧関数$y=ax^2$について、$x$の値が$2$から$5$まで増加するときの変化の割合が$ー4$であった。このときの$a$の値を求めなさい。
④1本$a$円のえんぴつを9本と1個100円の消しゴムを1個買って1000円を支払い、おつりを受け取った。
このときの数量の関係を不等式で表しなさい。ただし、右辺は1000だけとする。
⑩$\sqrt{53-2n}$が整数となるような正の整数$n$をすべて書きなさい。
⑪
Aさんの家からバス停までの道のりは$a$km、バス停から駅までの道のりは$b$kmである。Aさんが、Aさんの家からバス停までは時速4kmで歩き、バス停から駅までは時速30kmで走るバスに乗ったところ、 Aさんの家から駅まで$t$時間かかった。
このとき、$t$を$a$と$b$を使った式で表しなさい。 ただし、バス停でバスを待つ時間は考えないものとする。
⑫
右の度数分布表は、あるクラスの生徒20人のハンドボール投げの記録をまとめたものである。この度数分布表から求められる記録の平均値を求めなさい。
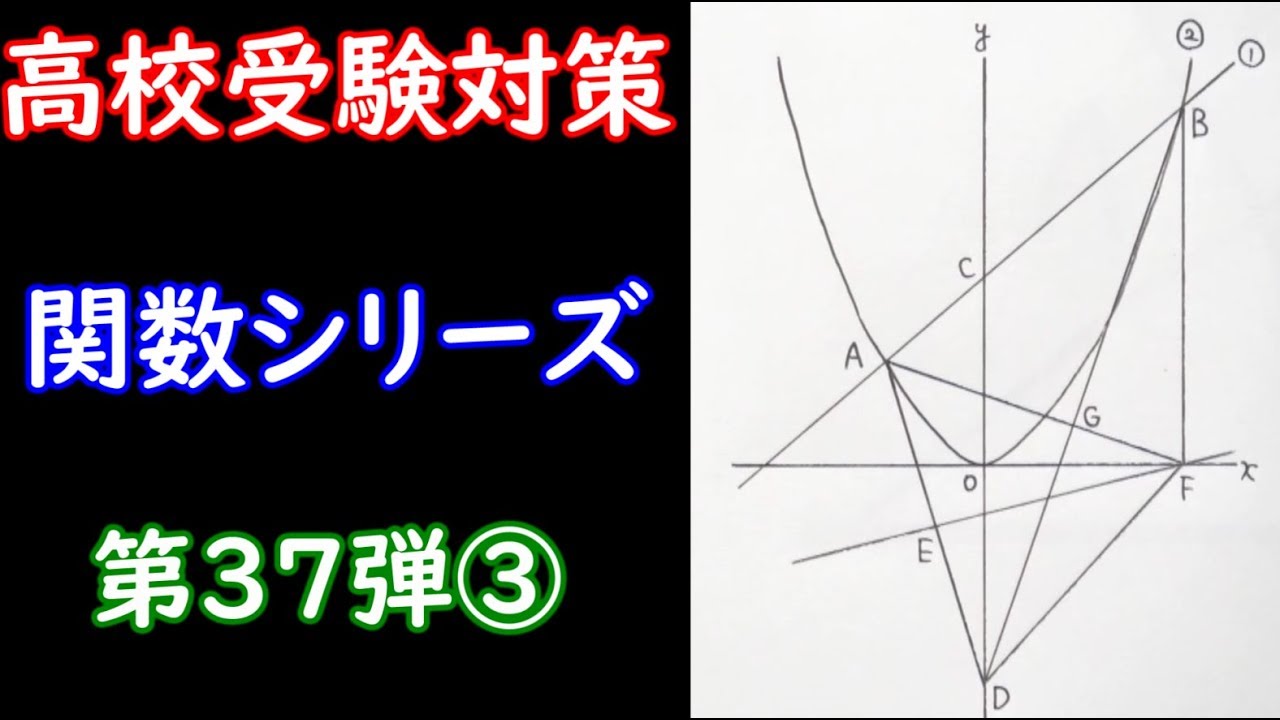
【高校受験対策】数学-関数37(③)
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・関数37
Q.
右の図において、直線①は関数$y=x+6$のグラフであり、曲線②は関数$y=ax^2$のグラフである。 2点、A・Bはともに直線①と曲線②との交点で、点Aの$x$座標は$-3$、 点Bの$x$座標は$6$であり、点Cは直線①と$y$軸との交点である。
また、原点を$o$とするとき、点Dは$y$軸上の点で$CO:OD=6:7$であり、 その$y$座標は負である。
点Eは線分AD上の点でAE=EDである。 さらに点Fは$x$軸上の点で、線分BFは$y$軸に平行である。 このとき次の問いに答えなさい。
①曲線②の式$y=ax^2$の$a$の値を求めなさい。
➁直線EFの式を求めなさい。
③線分AFと線分BOとの交点をGとするとき、三角形AGBと三角形DFGの曲積の比を最も簡単な整数の比で表しなさい。
この動画を見る
高校受験対策・関数37
Q.
右の図において、直線①は関数$y=x+6$のグラフであり、曲線②は関数$y=ax^2$のグラフである。 2点、A・Bはともに直線①と曲線②との交点で、点Aの$x$座標は$-3$、 点Bの$x$座標は$6$であり、点Cは直線①と$y$軸との交点である。
また、原点を$o$とするとき、点Dは$y$軸上の点で$CO:OD=6:7$であり、 その$y$座標は負である。
点Eは線分AD上の点でAE=EDである。 さらに点Fは$x$軸上の点で、線分BFは$y$軸に平行である。 このとき次の問いに答えなさい。
①曲線②の式$y=ax^2$の$a$の値を求めなさい。
➁直線EFの式を求めなさい。
③線分AFと線分BOとの交点をGとするとき、三角形AGBと三角形DFGの曲積の比を最も簡単な整数の比で表しなさい。
【高校受験対策】数学-関数36
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・関数36
Q.
右の図で曲線は関数$y=x^2$のグラフです。2点A・Bは、$x>0$の部分にあり、 それぞれの$y$座標は$1,16$です。また、点Pは$y$軸上の$1 \lt y \lt 16$の部分にあります。
次の各問に答えなさい。
①2点A、Bの座標をそれぞれ求めなさい。
②関数$y=x^2$で、$x$の変域が$-3 \leqq x \leqq 2$のとき、$y$の変域を求めなさい。
③△ABPの面積が$14cm^2$のとき、点Pの座標を求めなさい。
ただし、座標軸の単位の長さを$1cm$とします。
この動画を見る
高校受験対策・関数36
Q.
右の図で曲線は関数$y=x^2$のグラフです。2点A・Bは、$x>0$の部分にあり、 それぞれの$y$座標は$1,16$です。また、点Pは$y$軸上の$1 \lt y \lt 16$の部分にあります。
次の各問に答えなさい。
①2点A、Bの座標をそれぞれ求めなさい。
②関数$y=x^2$で、$x$の変域が$-3 \leqq x \leqq 2$のとき、$y$の変域を求めなさい。
③△ABPの面積が$14cm^2$のとき、点Pの座標を求めなさい。
ただし、座標軸の単位の長さを$1cm$とします。
【テスト対策 中3】7章-4
単元：
#数学(中学生)#中３数学#2次関数#三平方の定理
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のように、2つの関数$y =\dfrac{1}{4}x^2$と、$y=\dfrac{1}{2}x+6$が
2点$A、B$で交わっている。
原点$O$から$y=\dfrac{1}{2}x+6$に垂線$OH$をひく。
点$A$の$x$座標が$-4$のとき、次の問いに答えなさい。
①点$A$の座標を求めなさい。
②点$B$の座標を求めなさい。
③線分$AB$の長さを求めなさい。
④線分$OH$の長さを求めなさい。
図は動画内参照
この動画を見る
右の図のように、2つの関数$y =\dfrac{1}{4}x^2$と、$y=\dfrac{1}{2}x+6$が
2点$A、B$で交わっている。
原点$O$から$y=\dfrac{1}{2}x+6$に垂線$OH$をひく。
点$A$の$x$座標が$-4$のとき、次の問いに答えなさい。
①点$A$の座標を求めなさい。
②点$B$の座標を求めなさい。
③線分$AB$の長さを求めなさい。
④線分$OH$の長さを求めなさい。
図は動画内参照
【高校受験対策】数学-関数15
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図で、曲線は関数$y = \dfrac{1}{2}x^2$のグラフです。
次の各問に答えなさい。
①点$P$は曲線上の$x \gt 0$の部分にあります。
点$P$の$x$座標が4のとき、点$P$の座標を求めなさい。
②点$Q$は曲線上の$x\lt 0$の部分にあります。
点$Q$の$y$座標が18 のとき、点$Q$の座標を求めなさい。
③ 四角形$ABCD$は、辺$AD$と辺$BC$がともに$y$軸と平行な台形で、
点$A$と点$B$は曲線上の$x \gt 0$の部分に、点$C$と点$D$は$x$軸上にあります。
点$D$は、点$C$の右側にあり、$CD = 2cm $です。
四角形$ABCD$の面積が$17cm^2$のとき、
点$A$の座標を求めなさい。
ただし、座標軸の単位の長さを$1cm$とします。
図は動画内参照
この動画を見る
右の図で、曲線は関数$y = \dfrac{1}{2}x^2$のグラフです。
次の各問に答えなさい。
①点$P$は曲線上の$x \gt 0$の部分にあります。
点$P$の$x$座標が4のとき、点$P$の座標を求めなさい。
②点$Q$は曲線上の$x\lt 0$の部分にあります。
点$Q$の$y$座標が18 のとき、点$Q$の座標を求めなさい。
③ 四角形$ABCD$は、辺$AD$と辺$BC$がともに$y$軸と平行な台形で、
点$A$と点$B$は曲線上の$x \gt 0$の部分に、点$C$と点$D$は$x$軸上にあります。
点$D$は、点$C$の右側にあり、$CD = 2cm $です。
四角形$ABCD$の面積が$17cm^2$のとき、
点$A$の座標を求めなさい。
ただし、座標軸の単位の長さを$1cm$とします。
図は動画内参照
【高校受験対策】数学-関数31
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のように、関数$y = x ^ 2$のグラフ上に2点$A、B$がある。
四角形$AOCB$は長方形であり、点$A$の$x$座標は$-\dfrac{1}{2}$である。
2点$A、C$から$x$軸に垂線$AP、CQ$をそれぞれひくとき、次の問いに答えなさい。
①$△APO$の面積を求めなさい。
②$△APO∞△OQC$である。
このことを用いて、直線$OC$の傾きを求めなさい。
③直線$AB$上に点$M$があり、関数$y = x ^ 2$のグラフ上に点$N(t、t^2)$がある。
点$M$と点$N$の$x$座標が等しいとき、点$M$の座標を$t$を用いて表しなさい。
④点$B$の座標を求めなさい。
⑤$△OQC$の面積を求めなさい。
図は動画内参照
この動画を見る
右の図のように、関数$y = x ^ 2$のグラフ上に2点$A、B$がある。
四角形$AOCB$は長方形であり、点$A$の$x$座標は$-\dfrac{1}{2}$である。
2点$A、C$から$x$軸に垂線$AP、CQ$をそれぞれひくとき、次の問いに答えなさい。
①$△APO$の面積を求めなさい。
②$△APO∞△OQC$である。
このことを用いて、直線$OC$の傾きを求めなさい。
③直線$AB$上に点$M$があり、関数$y = x ^ 2$のグラフ上に点$N(t、t^2)$がある。
点$M$と点$N$の$x$座標が等しいとき、点$M$の座標を$t$を用いて表しなさい。
④点$B$の座標を求めなさい。
⑤$△OQC$の面積を求めなさい。
図は動画内参照
【高校受験対策】数学-死守31
単元：
#数学(中学生)#中１数学#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#平方根#２次方程式#確率#2次関数#表とグラフ#表とグラフ・集合
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$13 + 3\times (- 6)$を計算せよ。
②$3(2a + 3) - 2(5a + 4)$ を計算せよ。
③$a = - 3 , b = 4$とき、$3a^2-5b$の値を求めよ。
④$\dfrac{30}{\sqrt5}+\sqrt{20}$を計算せよ。
⑤ 1次方程式$3x-8=7x+16$を解け。
⑥2次方程式$(x + 1) ^ 2 = x + 13$を解け。
⑦関数$y =\dfrac{2}{3}x^2$について、
$x$の変域が$-1\leqq x \leqq 3$のときの$y$の変域を求めよ。
⑧$\boxed{1},\boxed{3},\boxed{5},\boxed{7},\boxed{9}$のカードが1枚ずつある。
この5枚のカードから、同時に2枚のカードを取り出すとき、
その2枚のカードにかかれている数の和が10以上になる確率を求めよ。
ただし、どのカードを取り出すことも同様に確からしいものとする。
⑨右の表は、A中学校とB中学校の生徒を対象に、
携帯電話やスマートフォンの1日あたりの使用時間を調査し、
その結果を度数分布表に整理したものである。
この表をもとに、A中学校とB中学校の「0時間以上1時間未満」の階級の相対度数のうち、
大きい方の相対度数を四捨五入して小数第2位まで求めよ。
図は動画内参照
この動画を見る
①$13 + 3\times (- 6)$を計算せよ。
②$3(2a + 3) - 2(5a + 4)$ を計算せよ。
③$a = - 3 , b = 4$とき、$3a^2-5b$の値を求めよ。
④$\dfrac{30}{\sqrt5}+\sqrt{20}$を計算せよ。
⑤ 1次方程式$3x-8=7x+16$を解け。
⑥2次方程式$(x + 1) ^ 2 = x + 13$を解け。
⑦関数$y =\dfrac{2}{3}x^2$について、
$x$の変域が$-1\leqq x \leqq 3$のときの$y$の変域を求めよ。
⑧$\boxed{1},\boxed{3},\boxed{5},\boxed{7},\boxed{9}$のカードが1枚ずつある。
この5枚のカードから、同時に2枚のカードを取り出すとき、
その2枚のカードにかかれている数の和が10以上になる確率を求めよ。
ただし、どのカードを取り出すことも同様に確からしいものとする。
⑨右の表は、A中学校とB中学校の生徒を対象に、
携帯電話やスマートフォンの1日あたりの使用時間を調査し、
その結果を度数分布表に整理したものである。
この表をもとに、A中学校とB中学校の「0時間以上1時間未満」の階級の相対度数のうち、
大きい方の相対度数を四捨五入して小数第2位まで求めよ。
図は動画内参照
【高校受験対策】数学-死守29
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#２次方程式#1次関数#2次関数#円#立体図形#立体切断#立体図形その他
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$16a \div (- 8)$を計算しなさい。
②$-12 + 2\times (- 5)$を計算しなさい。
③$\sqrt{50} - 2\sqrt{2}$を計算しなさい。
④$18ab \div \dfrac{3}{8}a \times b$を計算しなさい。
⑤$x = sqrt3 - 3$のとき、$x ^ 2 + 6x$の値を求めなさい。
⑥2次方程式$x ^ 2 + 3x = 8x - 2$を解きなさい。
⑦$\sqrt7 = 2.646$として、$\sqrt{0.07} $の値を求めなさい。
⑧右の図1は、立方体の展開図である。 この展開図を組み立てて作られる立方体について、
辺$AB$と垂直な面をア~カのなかからすべて選び、符号で書きなさい。
⑨その値が正の値をとらない関数を、次のア~エから1つ選び、符号で書きなさい。
ア→$y= -\dfrac{x}{2}$
イ→$y = -\dfrac{2}{x}$
ウ→$y = -2x + 3$
エ→$y = - 2x ^ 2$
⑩右の図2は、円錐の展開図である。
側面になるおうぎ形の半径が8cm、 底面になる円の半径が3cmのとき、
おうぎ形の面積を求めなさい。 ただし、円周率は$\pi$とする。
図は動画内参照
この動画を見る
①$16a \div (- 8)$を計算しなさい。
②$-12 + 2\times (- 5)$を計算しなさい。
③$\sqrt{50} - 2\sqrt{2}$を計算しなさい。
④$18ab \div \dfrac{3}{8}a \times b$を計算しなさい。
⑤$x = sqrt3 - 3$のとき、$x ^ 2 + 6x$の値を求めなさい。
⑥2次方程式$x ^ 2 + 3x = 8x - 2$を解きなさい。
⑦$\sqrt7 = 2.646$として、$\sqrt{0.07} $の値を求めなさい。
⑧右の図1は、立方体の展開図である。 この展開図を組み立てて作られる立方体について、
辺$AB$と垂直な面をア~カのなかからすべて選び、符号で書きなさい。
⑨その値が正の値をとらない関数を、次のア~エから1つ選び、符号で書きなさい。
ア→$y= -\dfrac{x}{2}$
イ→$y = -\dfrac{2}{x}$
ウ→$y = -2x + 3$
エ→$y = - 2x ^ 2$
⑩右の図2は、円錐の展開図である。
側面になるおうぎ形の半径が8cm、 底面になる円の半径が3cmのとき、
おうぎ形の面積を求めなさい。 ただし、円周率は$\pi$とする。
図は動画内参照
【高校受験対策】数学-死守28
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#連立方程式#式の計算（展開、因数分解）#平方根#２次方程式#確率#2次関数#相似な図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$(- 4) + 3\times (- 3)$を計算しなさい。
②$\dfrac{2x - 1}{3} - \dfrac{3x + 1}{5}$を計算しなさい。
③$(\sqrt{12} + \sqrt{18})(\sqrt3 - \sqrt2)$を計算しなさい。
④$(x - 4)^ 2 + 2(x - 2) - 3$を因数分解しなさい。
⑤方程式$(x + 3)(x - 5) = 5x - 24$を解きなさい。
⑥次の連立方程式を解きなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x+5=3y-2 \\
3x+2y=16
\end{array}
\right.
\end{eqnarray}$
⑦関数$y=-3x^2$について、
$x$の値が1から3まで増加するときの変化の割合を求めなさい。
⑧1つのさいころを2回投げるとき、1回目に出た目の数が、
2回目に出た目の数の倍数となる確率を求めなさい。
⑨男子20人、好16人のクラスでテストを行ったところ、 男子の平均点が$x$点で、
女子の平均点が$y$点であった。このクラスのテストの合計点は何点か、
$y$を使った式で表しなさい。
⑩三角柱と三角すいがあり、底面は相似な三角形で高さが等しい。
三角柱の底面と三角すいの底面の相似比が$1:2$であるとき、
三角柱の体積は三角すいの体積の何倍か、求めなさい。
この動画を見る
①$(- 4) + 3\times (- 3)$を計算しなさい。
②$\dfrac{2x - 1}{3} - \dfrac{3x + 1}{5}$を計算しなさい。
③$(\sqrt{12} + \sqrt{18})(\sqrt3 - \sqrt2)$を計算しなさい。
④$(x - 4)^ 2 + 2(x - 2) - 3$を因数分解しなさい。
⑤方程式$(x + 3)(x - 5) = 5x - 24$を解きなさい。
⑥次の連立方程式を解きなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x+5=3y-2 \\
3x+2y=16
\end{array}
\right.
\end{eqnarray}$
⑦関数$y=-3x^2$について、
$x$の値が1から3まで増加するときの変化の割合を求めなさい。
⑧1つのさいころを2回投げるとき、1回目に出た目の数が、
2回目に出た目の数の倍数となる確率を求めなさい。
⑨男子20人、好16人のクラスでテストを行ったところ、 男子の平均点が$x$点で、
女子の平均点が$y$点であった。このクラスのテストの合計点は何点か、
$y$を使った式で表しなさい。
⑩三角柱と三角すいがあり、底面は相似な三角形で高さが等しい。
三角柱の底面と三角すいの底面の相似比が$1:2$であるとき、
三角柱の体積は三角すいの体積の何倍か、求めなさい。
【高校受験対策】関数-30
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図で、曲線は関数$y = \dfrac{1}{2}x^2$のグラフです。
2点$A、B$は曲線上の点で、点$A$の座標は(-4,8)、点$B$の座標は(2,2)です。
曲線上の$x \lt 0$の部分に点C、曲線上の$x \gt 0$の部分に点Dを、
$CD//AB$となるようにとり、線分 $CD$と$y$軸との交点を$E$とします。
このとき、次の各問に答えなさい。
①2点$A、B$を通る直線の式を求めなさい。
②関数$y=\dfrac{1}{2}x^2$で、$x$の変域が$-4 \leqq x \leqq 2$のとき、
その変域を求めなさい。
③$△ACE$と$△BDE$の面積の比が8:5のとき、点$c$の$x$座標を求めなさい。
図は動画内参照
この動画を見る
右の図で、曲線は関数$y = \dfrac{1}{2}x^2$のグラフです。
2点$A、B$は曲線上の点で、点$A$の座標は(-4,8)、点$B$の座標は(2,2)です。
曲線上の$x \lt 0$の部分に点C、曲線上の$x \gt 0$の部分に点Dを、
$CD//AB$となるようにとり、線分 $CD$と$y$軸との交点を$E$とします。
このとき、次の各問に答えなさい。
①2点$A、B$を通る直線の式を求めなさい。
②関数$y=\dfrac{1}{2}x^2$で、$x$の変域が$-4 \leqq x \leqq 2$のとき、
その変域を求めなさい。
③$△ACE$と$△BDE$の面積の比が8:5のとき、点$c$の$x$座標を求めなさい。
図は動画内参照
【テスト対策・中３】４章－８
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のように、放物線$y=ax^2$と直線が点$A(4,-8)$と点$B$で交わり、
点$B$の$y$座標は-2である。
$y$軸上に点$P(0,P)$があるとき、次の問いに答えなさい。
ただし、$P \lt 0$とする。
①$a$の値を求めなさい。
②直線$AB$の式を求めなさい。
③$△OAB$と$△ABP$の面積比が$1:3$となるとき、
$P$の値を求めなさい。
④$△OAB$と$△ABP$の面積比が$2:5$となるとき、
$P$の値を求めなさい。
図は動画内参照
この動画を見る
右の図のように、放物線$y=ax^2$と直線が点$A(4,-8)$と点$B$で交わり、
点$B$の$y$座標は-2である。
$y$軸上に点$P(0,P)$があるとき、次の問いに答えなさい。
ただし、$P \lt 0$とする。
①$a$の値を求めなさい。
②直線$AB$の式を求めなさい。
③$△OAB$と$△ABP$の面積比が$1:3$となるとき、
$P$の値を求めなさい。
④$△OAB$と$△ABP$の面積比が$2:5$となるとき、
$P$の値を求めなさい。
図は動画内参照
【テスト対策・中３】４章－７
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のように、関数$y=\dfrac{1}{2}x^2$のグラフ上に2点$A,B$があり、
それぞれの$x$座標は$-2,4$である。
直線$AB$と$y$軸との交点を$C$とするとき、次の問いに答えなさい。
①$△AOB$の面積を求めなさい。
②原点$O$を通り、$△AOB$の面積を2等分する直線の式を求めなさい。
③点$A$を通り、$△AOB$の面積を2等分する直線の式を求めなさい。
図は動画内参照
この動画を見る
右の図のように、関数$y=\dfrac{1}{2}x^2$のグラフ上に2点$A,B$があり、
それぞれの$x$座標は$-2,4$である。
直線$AB$と$y$軸との交点を$C$とするとき、次の問いに答えなさい。
①$△AOB$の面積を求めなさい。
②原点$O$を通り、$△AOB$の面積を2等分する直線の式を求めなさい。
③点$A$を通り、$△AOB$の面積を2等分する直線の式を求めなさい。
図は動画内参照
【テスト対策・中３】４章－６
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右図のように、関数$y=x^2$のグラフ上に3点$A、B、C$があり、
$y$軸上に点$D$がある。
四角形$ABCD$が平行四辺形となるとき、次の問いに答えなさい。
①$A(- 1, 1), B(2, 4), D(0, 6)$のとき、点$c$の座標を求めなさい。
②$A(- 1, 1), D(0, 8)$のとき、四角形$ABCD$の面積を求めなさい。
図は動画内参照
この動画を見る
右図のように、関数$y=x^2$のグラフ上に3点$A、B、C$があり、
$y$軸上に点$D$がある。
四角形$ABCD$が平行四辺形となるとき、次の問いに答えなさい。
①$A(- 1, 1), B(2, 4), D(0, 6)$のとき、点$c$の座標を求めなさい。
②$A(- 1, 1), D(0, 8)$のとき、四角形$ABCD$の面積を求めなさい。
図は動画内参照
【テスト対策・中３】４章－５
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右図のように、関数$ y=\dfrac{1}{2}x^2$のグラフ上に2点$A(0,18),B(2,2)$がある。
次の問いに答えなさい。ただし、$ a \lt 0$とする。
①$a$の値を求めなさい。
②直線$AB$の式を求めなさい。
③$△OAB$の面積を求めなさい。
④$x$軸上に点$Q$をとる。
$AQ+BQ$の長さが最短となるときの点$Q$の座標を求めなさい。
図は動画内参照
この動画を見る
右図のように、関数$ y=\dfrac{1}{2}x^2$のグラフ上に2点$A(0,18),B(2,2)$がある。
次の問いに答えなさい。ただし、$ a \lt 0$とする。
①$a$の値を求めなさい。
②直線$AB$の式を求めなさい。
③$△OAB$の面積を求めなさい。
④$x$軸上に点$Q$をとる。
$AQ+BQ$の長さが最短となるときの点$Q$の座標を求めなさい。
図は動画内参照
【テスト対策・中３】４章－４
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
点$(-2,-2)$を通り、傾き2の直線を$\ell$とし、
$\ell$が関数$y = x ^ 2$と交わる2点を$P、Q$とする。
右の図のように、$P、Q$から$x$軸に下ろした垂線をそれぞれ$PA、QB$とするとき、
次の問いに答えなさい。
①直線の式を求めなさい。
②線分$AB$の長さを求めなさい。
③四角形$ABQP$の面積を求めなさい。
図は動画内参照
この動画を見る
点$(-2,-2)$を通り、傾き2の直線を$\ell$とし、
$\ell$が関数$y = x ^ 2$と交わる2点を$P、Q$とする。
右の図のように、$P、Q$から$x$軸に下ろした垂線をそれぞれ$PA、QB$とするとき、
次の問いに答えなさい。
①直線の式を求めなさい。
②線分$AB$の長さを求めなさい。
③四角形$ABQP$の面積を求めなさい。
図は動画内参照
【テスト対策・中３】４章－３
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①関数$y=ax^2$について、$x$の変域が$-3≦x≦2$のとき、
$y$の変域は$0\leqq y \leqq 6$である。 このとき、$a$の値を求めなさい。
②関数$y=\dfrac{1}{3}x^2$で、$x$の変域を$a≦x≦3$とすると、
その変域は$b\leqq y\leqq 12$となる。$a、b$の値を求めなさい。
③関数$y=-\dfrac{1}{4}x^2$について、$x$の変域が$a≦y≦a+5$であるとき、
$y$の変域が$-4≦y\leqq 0$となるような$a$の値をすべて求めなさい。
この動画を見る
①関数$y=ax^2$について、$x$の変域が$-3≦x≦2$のとき、
$y$の変域は$0\leqq y \leqq 6$である。 このとき、$a$の値を求めなさい。
②関数$y=\dfrac{1}{3}x^2$で、$x$の変域を$a≦x≦3$とすると、
その変域は$b\leqq y\leqq 12$となる。$a、b$の値を求めなさい。
③関数$y=-\dfrac{1}{4}x^2$について、$x$の変域が$a≦y≦a+5$であるとき、
$y$の変域が$-4≦y\leqq 0$となるような$a$の値をすべて求めなさい。
【テスト対策・中３】４章－２
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右のア～エの関数について、下の問いに記号で答えなさい。
①$y$の値が、$x=0$のとき最大になるものをすべて選びなさい。
②$x\geqq 0$の範囲で、$x$の値が増加するにつれて、
$y$の値が減少するものをすべて選びなさい。
ア.$y=-3x^2$
イ.$y=x^2$
ウ.$y=4x^2$
エ.$y=-\dfrac{2}{3}x^2$
③$x$の変域を$-2\leqq x \leqq 1$とするとき、
関数$y-3x^2$と$y$の変域が同じになる関数を
次のア～エから一つ選び、記号で答えなさい。
ア.$y=-4x+8$
イ.$y=-3x^2$
ウ.$y=4x+8$
エ.$y=3x-3$
この動画を見る
右のア～エの関数について、下の問いに記号で答えなさい。
①$y$の値が、$x=0$のとき最大になるものをすべて選びなさい。
②$x\geqq 0$の範囲で、$x$の値が増加するにつれて、
$y$の値が減少するものをすべて選びなさい。
ア.$y=-3x^2$
イ.$y=x^2$
ウ.$y=4x^2$
エ.$y=-\dfrac{2}{3}x^2$
③$x$の変域を$-2\leqq x \leqq 1$とするとき、
関数$y-3x^2$と$y$の変域が同じになる関数を
次のア～エから一つ選び、記号で答えなさい。
ア.$y=-4x+8$
イ.$y=-3x^2$
ウ.$y=4x+8$
エ.$y=3x-3$
【テスト対策・中３】４章－１
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$y=ax^2$について、$ x = 2$のとき$y=-3$である。
このとき、$a$の値を求めなさい。
②$y$は$x$の2乗に比例し、$x=-6$のとき$y = 9$である。
$x = 12$のときの$y$の値を求めなさい。
③右図において、$m$は$y=ax^2$($a$は定数)のグラフで、
$A(3,-4)$は$m$上にある。
このとき、$a$の値を求めなさい。
図は動画内参照
この動画を見る
①$y=ax^2$について、$ x = 2$のとき$y=-3$である。
このとき、$a$の値を求めなさい。
②$y$は$x$の2乗に比例し、$x=-6$のとき$y = 9$である。
$x = 12$のときの$y$の値を求めなさい。
③右図において、$m$は$y=ax^2$($a$は定数)のグラフで、
$A(3,-4)$は$m$上にある。
このとき、$a$の値を求めなさい。
図は動画内参照
【高校受験対策】数学－関数２９
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
図1のように,関数$y = ax^2$のグラフ上に2点$A,B$があり,
$A$の座標は$(-4,-8)$である.
線分$AB$は$x$軸に平行で,この線分と$y$軸との交点を$C$とする.
また,点$P$は線分$OC$上の点である.次の各問いに答えなさい.
①$a$の値を求めなさい.
②$\angle APB = 60°$であるとき,線分$BP$の長さを求めなさい.
③$P$の$y$座標が-4のとき,直線$AP$と$x$軸との交点を$Q$とする.
このとき,$Q$を通り,$△ABQ$の面積を2等分する直線の式を求めなさい.
④図2のように,$P$の座標が-6のとき,
$x$軸上に,点$R(6,0)$をとり, $△BRP$をつくる.
$B$から辺$PR$に垂線をひき、辺$PR$との交点を$H$とするとき,
線分$BH$の長さを求めなさい.
図は動画内参照
この動画を見る
図1のように,関数$y = ax^2$のグラフ上に2点$A,B$があり,
$A$の座標は$(-4,-8)$である.
線分$AB$は$x$軸に平行で,この線分と$y$軸との交点を$C$とする.
また,点$P$は線分$OC$上の点である.次の各問いに答えなさい.
①$a$の値を求めなさい.
②$\angle APB = 60°$であるとき,線分$BP$の長さを求めなさい.
③$P$の$y$座標が-4のとき,直線$AP$と$x$軸との交点を$Q$とする.
このとき,$Q$を通り,$△ABQ$の面積を2等分する直線の式を求めなさい.
④図2のように,$P$の座標が-6のとき,
$x$軸上に,点$R(6,0)$をとり, $△BRP$をつくる.
$B$から辺$PR$に垂線をひき、辺$PR$との交点を$H$とするとき,
線分$BH$の長さを求めなさい.
図は動画内参照
【高校受験対策】数学－関数２８
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
図1のように,
$y=ax^2...①$
$y=\dfrac{10}{x}\quad (x \gt 0)･･･②$のグラフがある.
また,①のグラフ上に点$B(2.5)$がある.
$A$を通り,$x$軸に平行な直線と,
①との交点のうち,$A$以外の点を$C$とする.
このとき,次の各問いに答えなさい.
問1
$a$の値を求めなさい.
問2
3点$A,B,C$を通る円の半径を求めなさい.
問3
②のグラフ上に点$P$をとり,
$△ACP$の面積が12となるとき, 点$P$の座標を求めなさい.
問4
図2のように,直線$AB$と$y$軸との交点を$D$,
直線$OB$と直線$AC$との交点を$E$とするとき,
$△BDE$の面積は,$△OAB$の面積の何倍になるか,求めなさい.
図は動画内参照
この動画を見る
図1のように,
$y=ax^2...①$
$y=\dfrac{10}{x}\quad (x \gt 0)･･･②$のグラフがある.
また,①のグラフ上に点$B(2.5)$がある.
$A$を通り,$x$軸に平行な直線と,
①との交点のうち,$A$以外の点を$C$とする.
このとき,次の各問いに答えなさい.
問1
$a$の値を求めなさい.
問2
3点$A,B,C$を通る円の半径を求めなさい.
問3
②のグラフ上に点$P$をとり,
$△ACP$の面積が12となるとき, 点$P$の座標を求めなさい.
問4
図2のように,直線$AB$と$y$軸との交点を$D$,
直線$OB$と直線$AC$との交点を$E$とするとき,
$△BDE$の面積は,$△OAB$の面積の何倍になるか,求めなさい.
図は動画内参照
【高校受験対策】数学－関数２７
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図1のように,関数$y = \dfrac{1}{4} x ^ 2$のグラフ上に点$A$がある.
$y$軸上に点$A$と$y$座標が等しい点$B$をとり,
$y=\dfrac{1}{4}x^2$のグラフ上に$AC = BC$となる点$C$をとる.
このとき,次の各問いに答えなさい.
ただし,原点0から点$(1,0)$までの距離及び
原点0から点$(0,1)$までの距離をそれぞれ$1cm$とする.
①点$A$の$x$座標が6のとき,点$B$の座標を求めなさい.
②点$A$の$y$座標が4のとき,$△ABC$の面積を求めなさい.
③点$A$を$y=\dfrac{1}{4}x^2$のグラフ上で動かしたところ,
右の図2のように $\triangle ABC$が直角二等辺三角形となった.
このとき,点$A$の座標を求めなさい.
ただし,点$A$の$x$座標は正とする.
図は動画内参照
この動画を見る
右の図1のように,関数$y = \dfrac{1}{4} x ^ 2$のグラフ上に点$A$がある.
$y$軸上に点$A$と$y$座標が等しい点$B$をとり,
$y=\dfrac{1}{4}x^2$のグラフ上に$AC = BC$となる点$C$をとる.
このとき,次の各問いに答えなさい.
ただし,原点0から点$(1,0)$までの距離及び
原点0から点$(0,1)$までの距離をそれぞれ$1cm$とする.
①点$A$の$x$座標が6のとき,点$B$の座標を求めなさい.
②点$A$の$y$座標が4のとき,$△ABC$の面積を求めなさい.
③点$A$を$y=\dfrac{1}{4}x^2$のグラフ上で動かしたところ,
右の図2のように $\triangle ABC$が直角二等辺三角形となった.
このとき,点$A$の座標を求めなさい.
ただし,点$A$の$x$座標は正とする.
図は動画内参照