相似な図形
相似な図形
 相似な図形
相似な図形
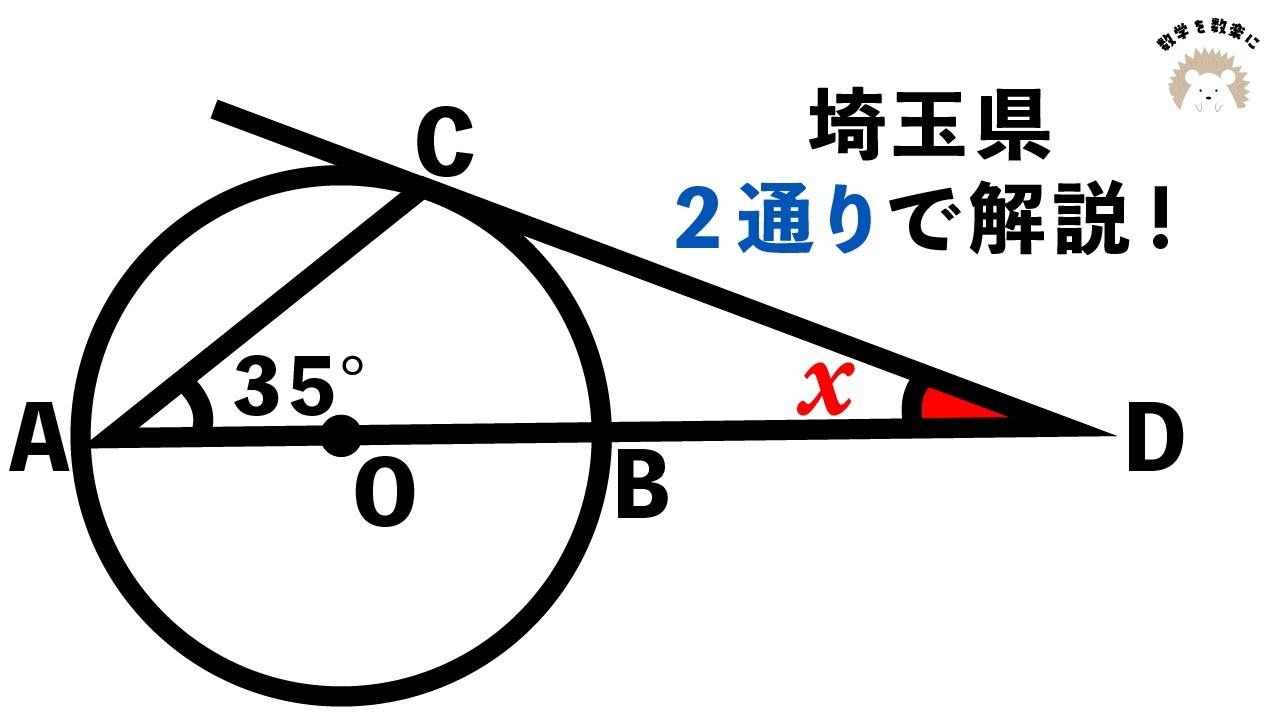
円と接線 2通りで解説
【一撃で処理…!】図形:長野県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#長野県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
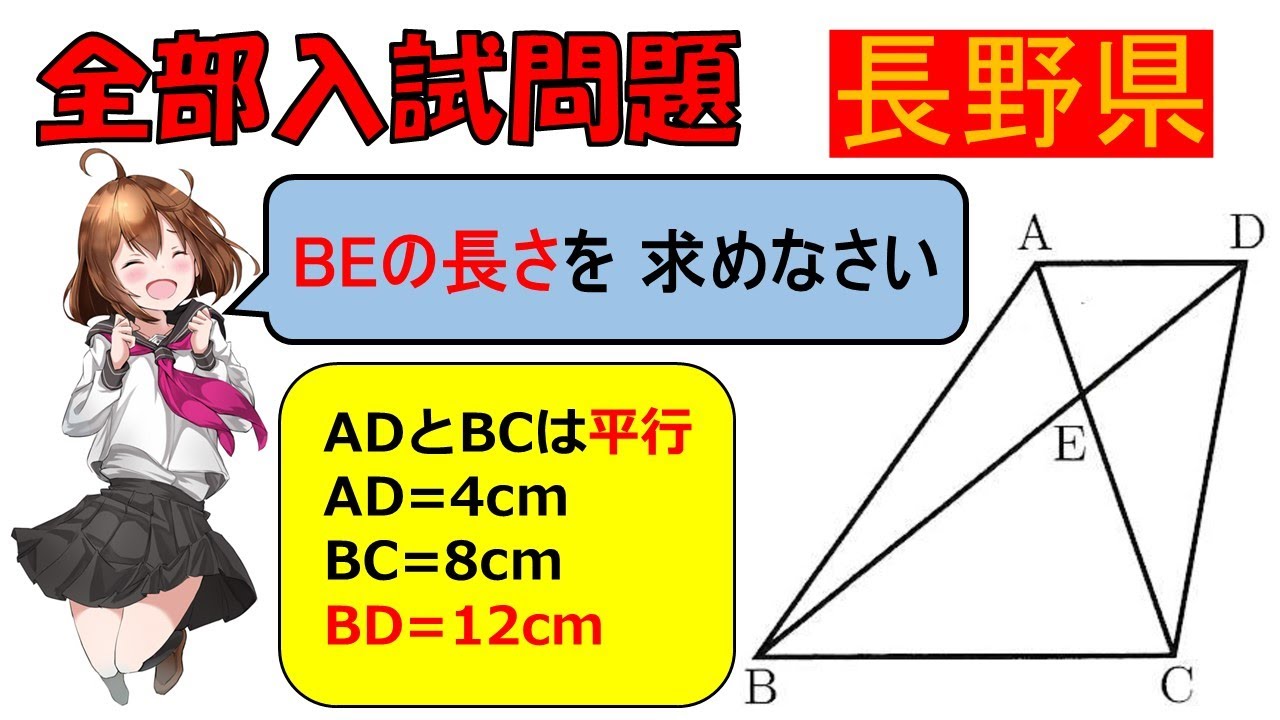
台形ABCDについて(※図は動画内参照)AD=4cm,BC=8cm,BD=12cmのときBEの長さを求めなさい。
この動画を見る
台形ABCDについて(※図は動画内参照)AD=4cm,BC=8cm,BD=12cmのときBEの長さを求めなさい。
factorization : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study

単元:
#数学(中学生)#相似な図形#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x^2-\boxed{ }x+14$が$(x-a)(x-b)$の形に因数分解できる。
$\boxed{ }$に当てはまる自然数を二つ書け。
この動画を見る
$x^2-\boxed{ }x+14$が$(x-a)(x-b)$の形に因数分解できる。
$\boxed{ }$に当てはまる自然数を二つ書け。
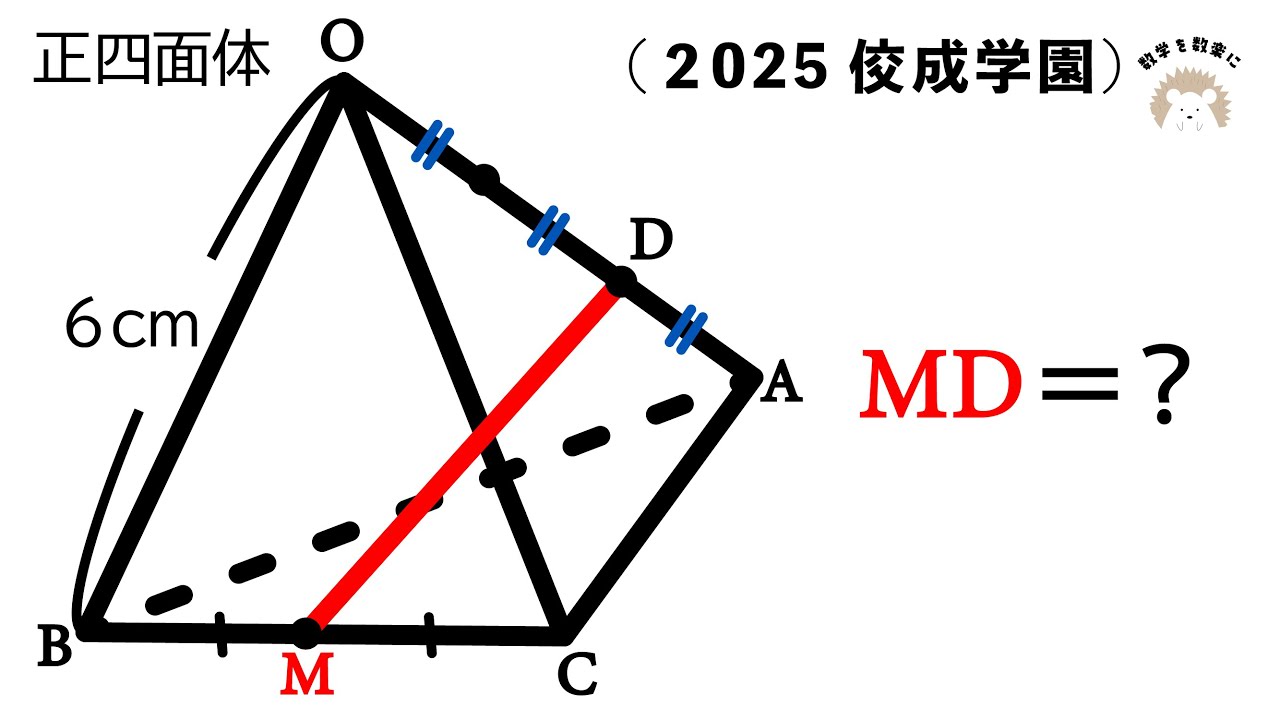
正四面体上の2点間の距離 2025佼成学園
【重要な図形…!】図形:岐阜県~全国入試問題解法
単元:
#数学(中学生)#中1数学#中3数学#相似な図形#平面図形#高校入試過去問(数学)#岐阜県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
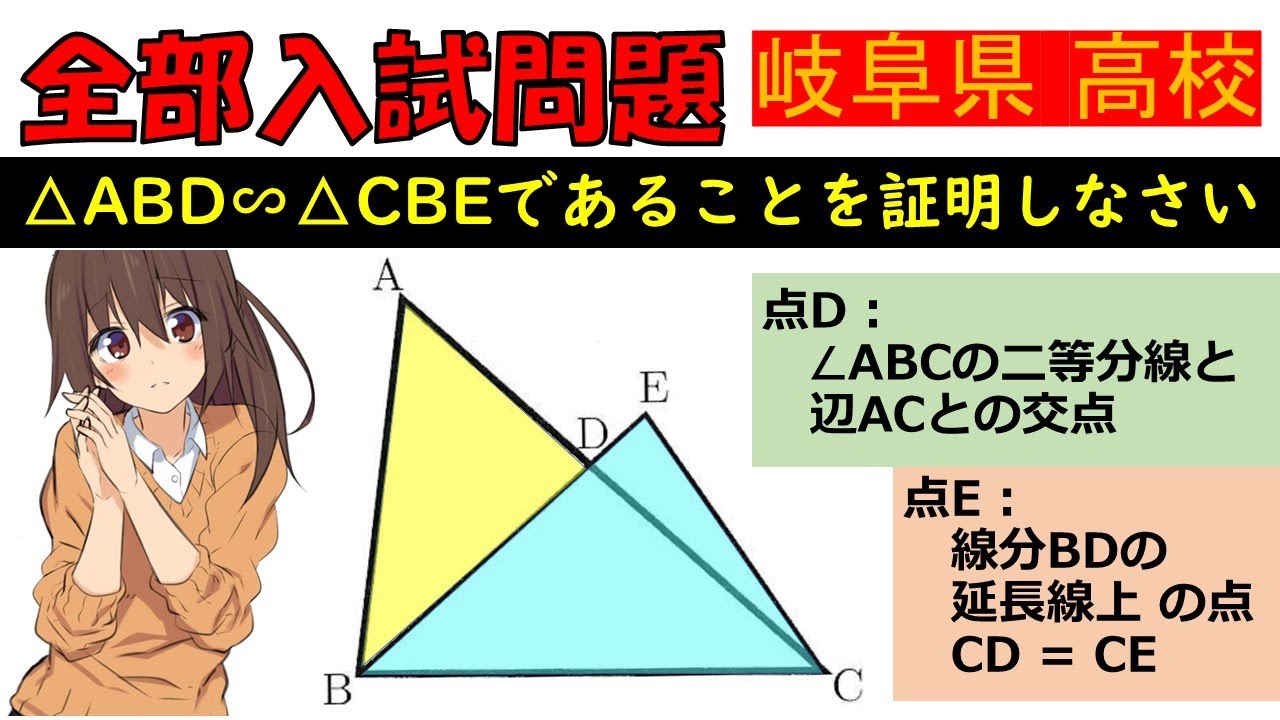
$\triangle ABD \backsim \triangle CBE であることを証明しなさい$
$点D : \angle ABCの二等分線と辺ACとの交点$
$点E : 線分BDの延長線上の点CD =CE$
この動画を見る
$\triangle ABD \backsim \triangle CBE であることを証明しなさい$
$点D : \angle ABCの二等分線と辺ACとの交点$
$点E : 線分BDの延長線上の点CD =CE$
【ひらめきと経験と…!】図形:慶応義塾高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\triangle ABCにおいて、AB=AC,BC=2,\angle BAC=36^{ \circ }$
$のとき、ABの長さを求めよ。$
この動画を見る
$\triangle ABCにおいて、AB=AC,BC=2,\angle BAC=36^{ \circ }$
$のとき、ABの長さを求めよ。$
【中学数学】相似な図形の面積比と体積比~分かりやすく~【中3数学】

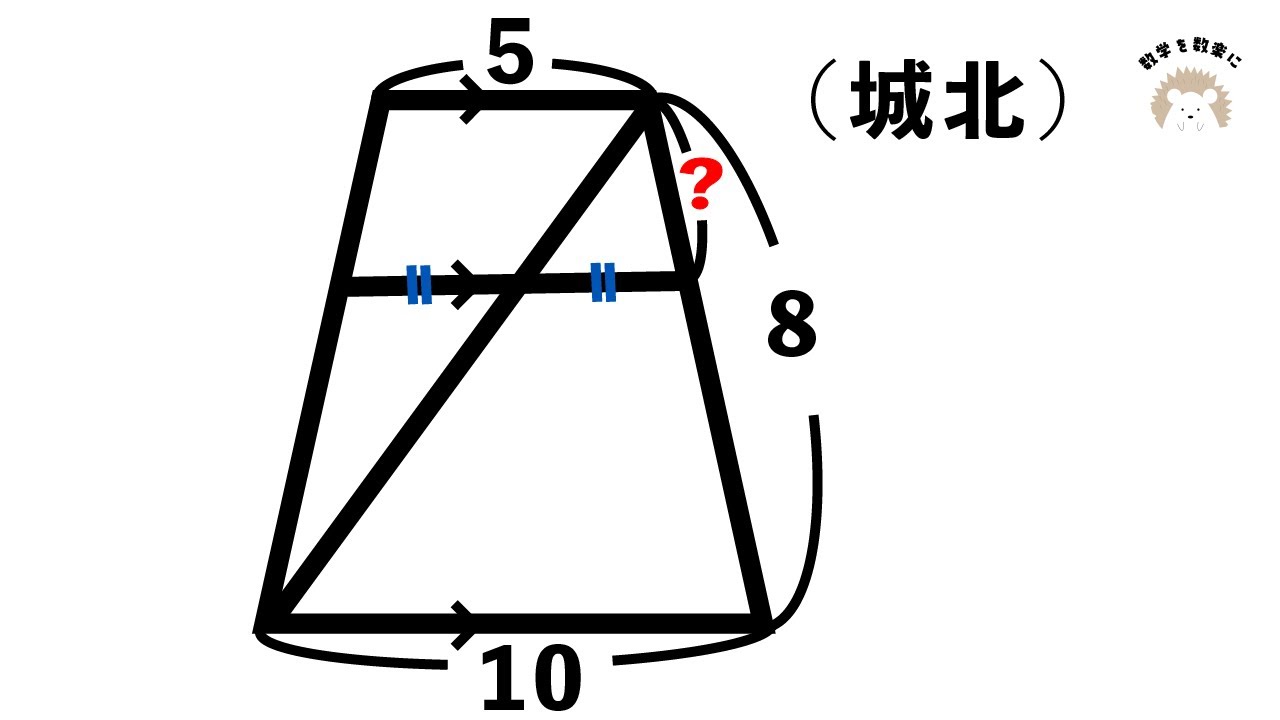
台形 城北高校
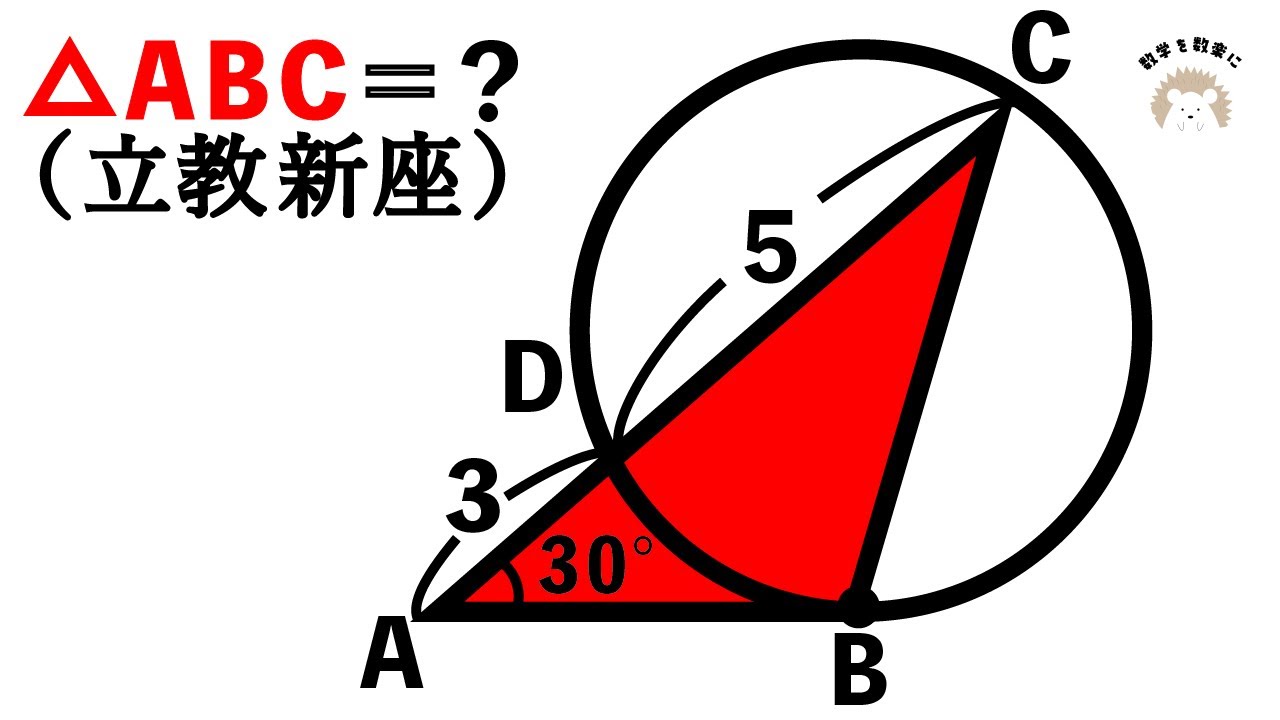
円と接線と三角形 立教新座
円と接線 2通りで解説 埼玉県

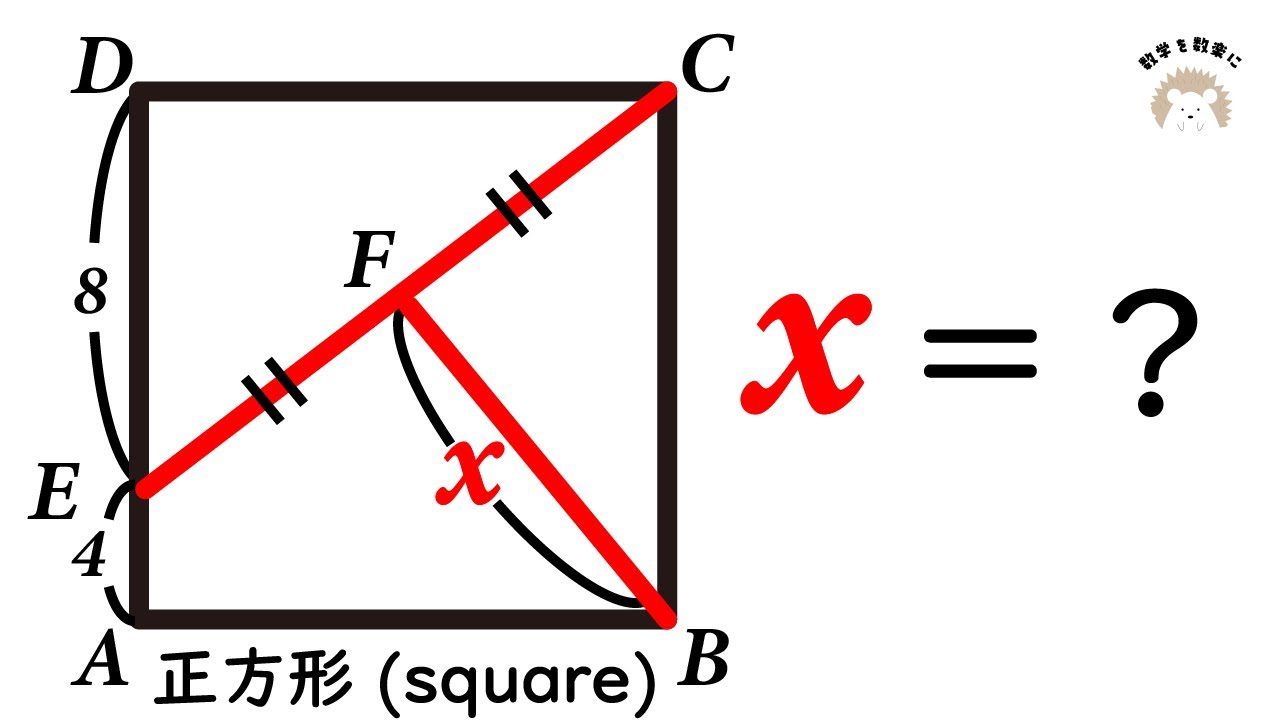
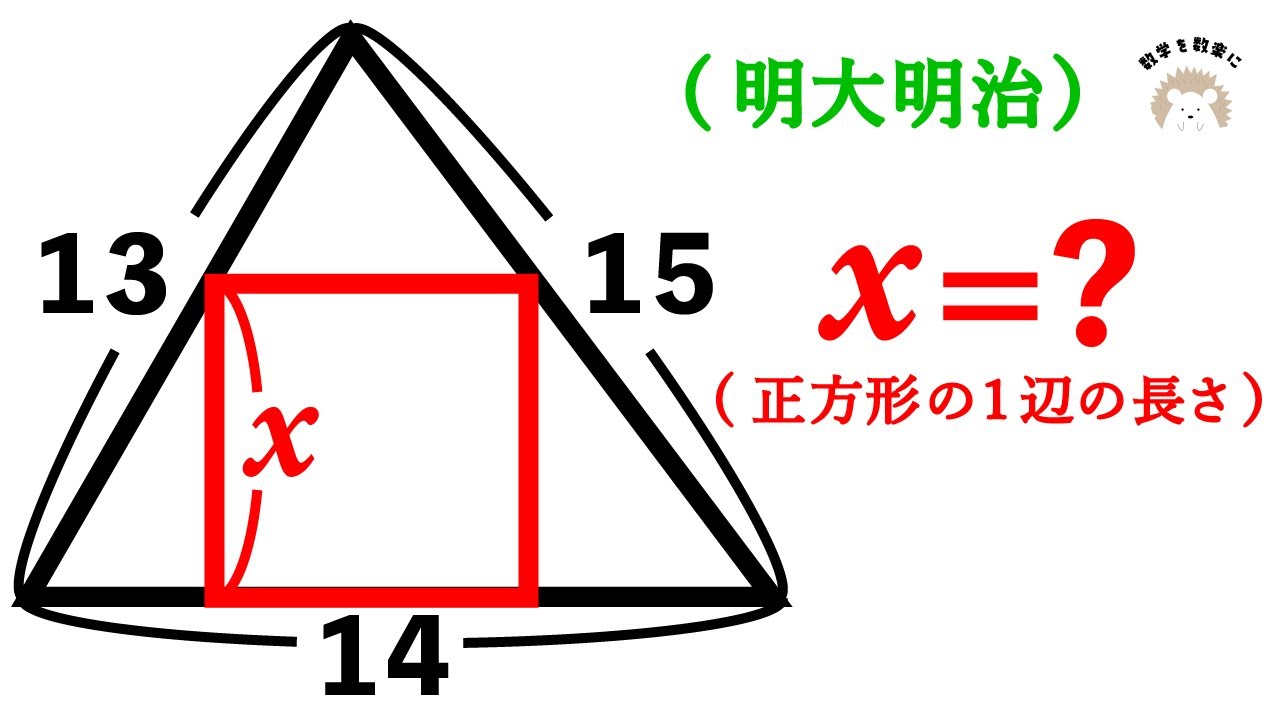
三角形に内接する正方形 明大明治
単元:
#数学(中学生)#中1数学#中2数学#中3数学#相似な図形#平面図形#三角形と四角形#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
x=?(正方形の1辺の長さ)
この動画を見る
x=?(正方形の1辺の長さ)
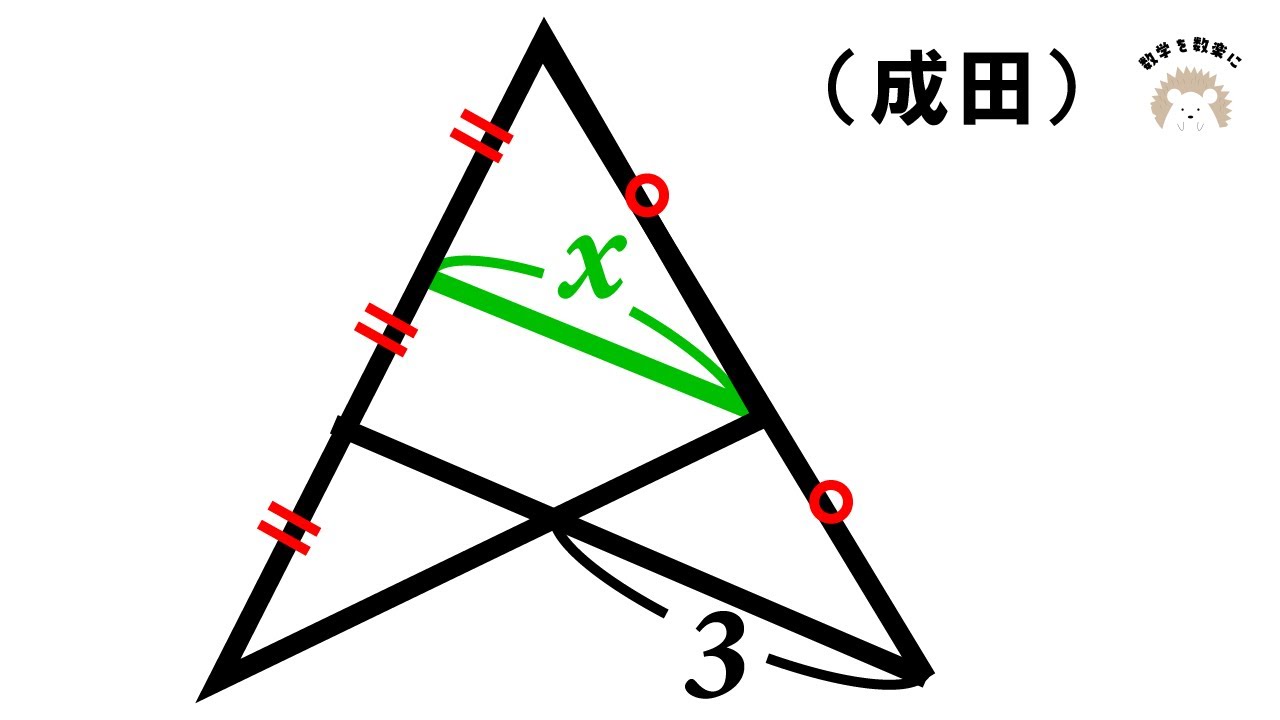
平面図形 成田高校
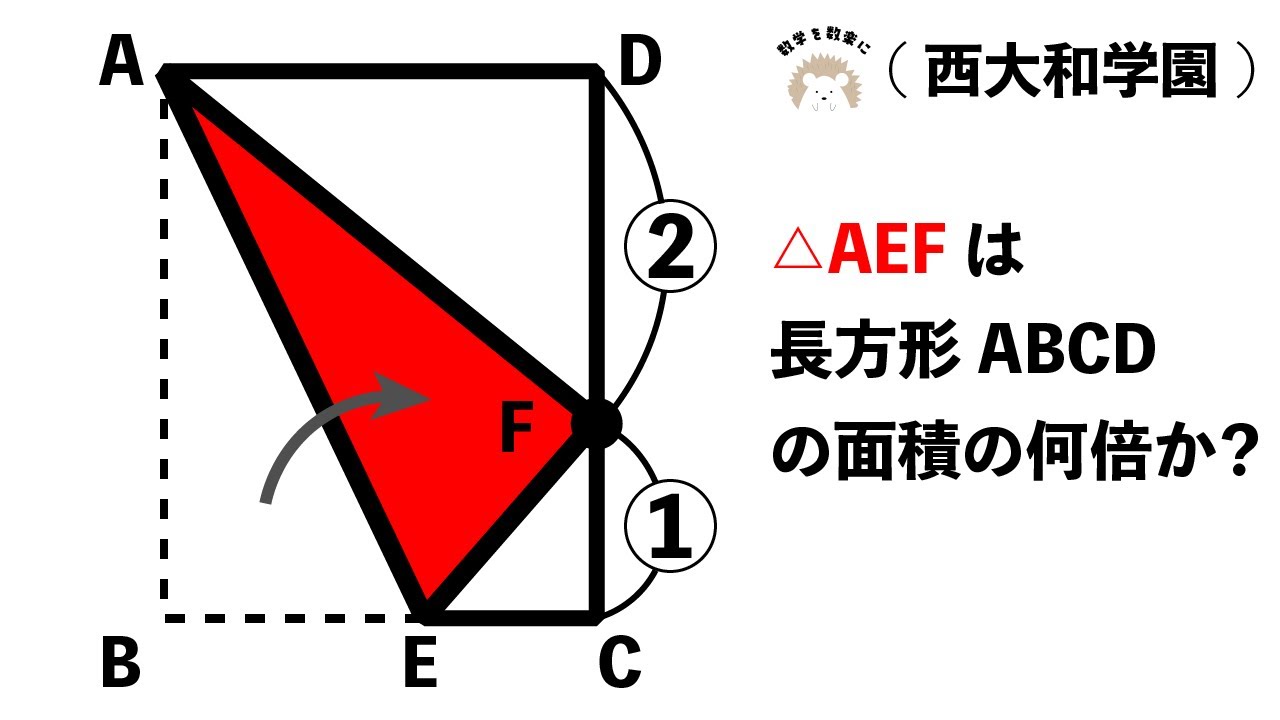
長方形の折り返し 西大和学園
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#西大和学園高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
$△AEFは長方形ABCDの面積の何倍か?$
この動画を見る
$△AEFは長方形ABCDの面積の何倍か?$
平行四辺形の中にある〇〇
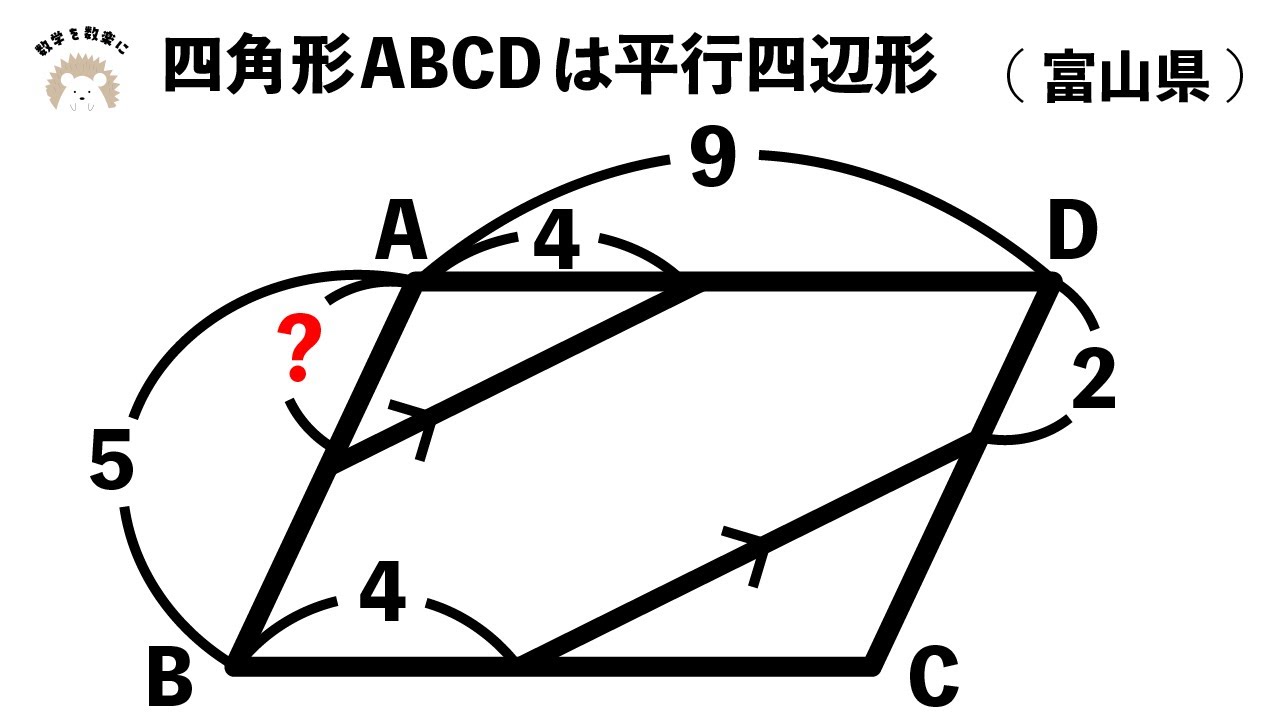
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#富山県公立高校入試
指導講師:
数学を数楽に
問題文全文(内容文):
次の図の?に当てはまる長さを求めよ(図は動画参照)
この動画を見る
次の図の?に当てはまる長さを求めよ(図は動画参照)
三角形の相似 日大二
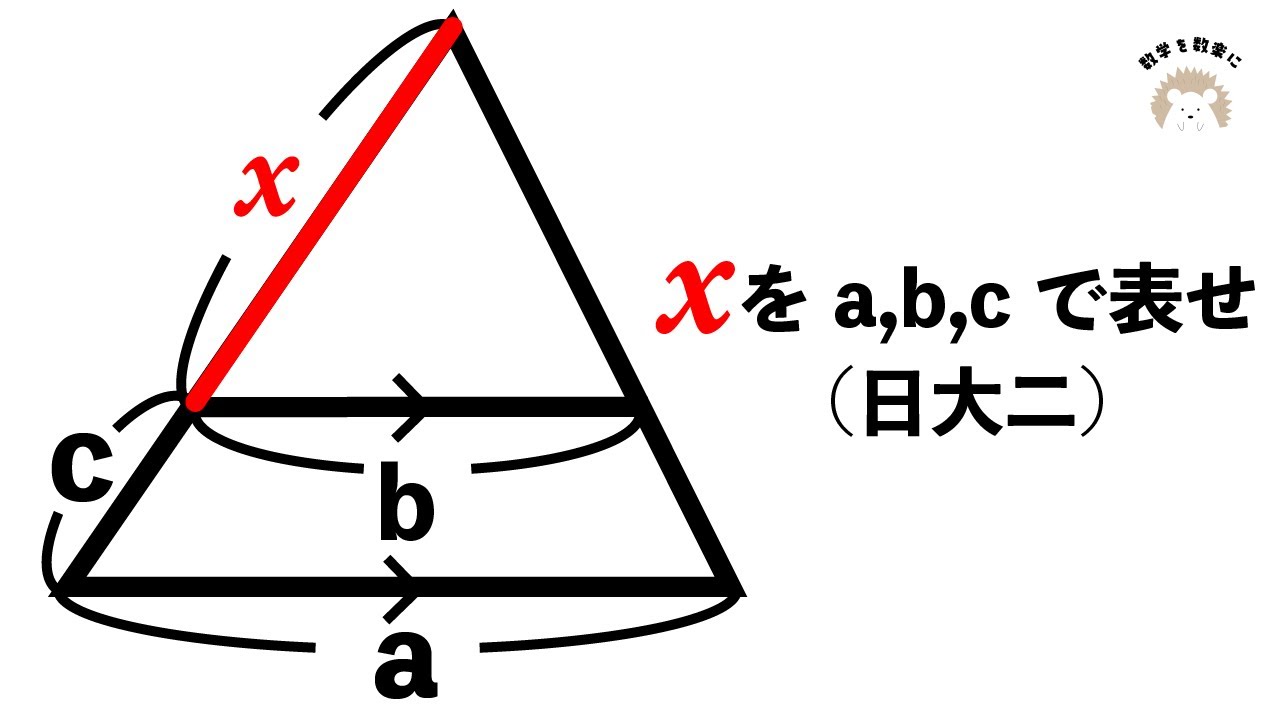
空間上の線分の長さ 昭和学院秀英
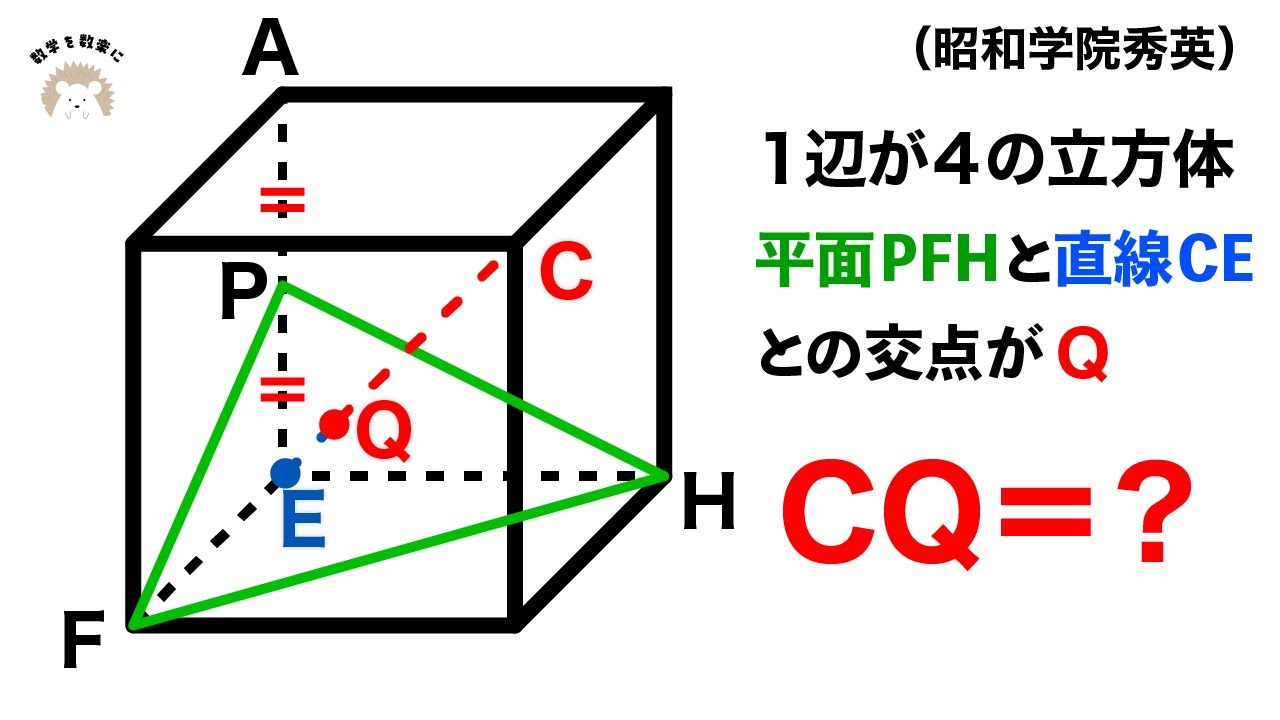
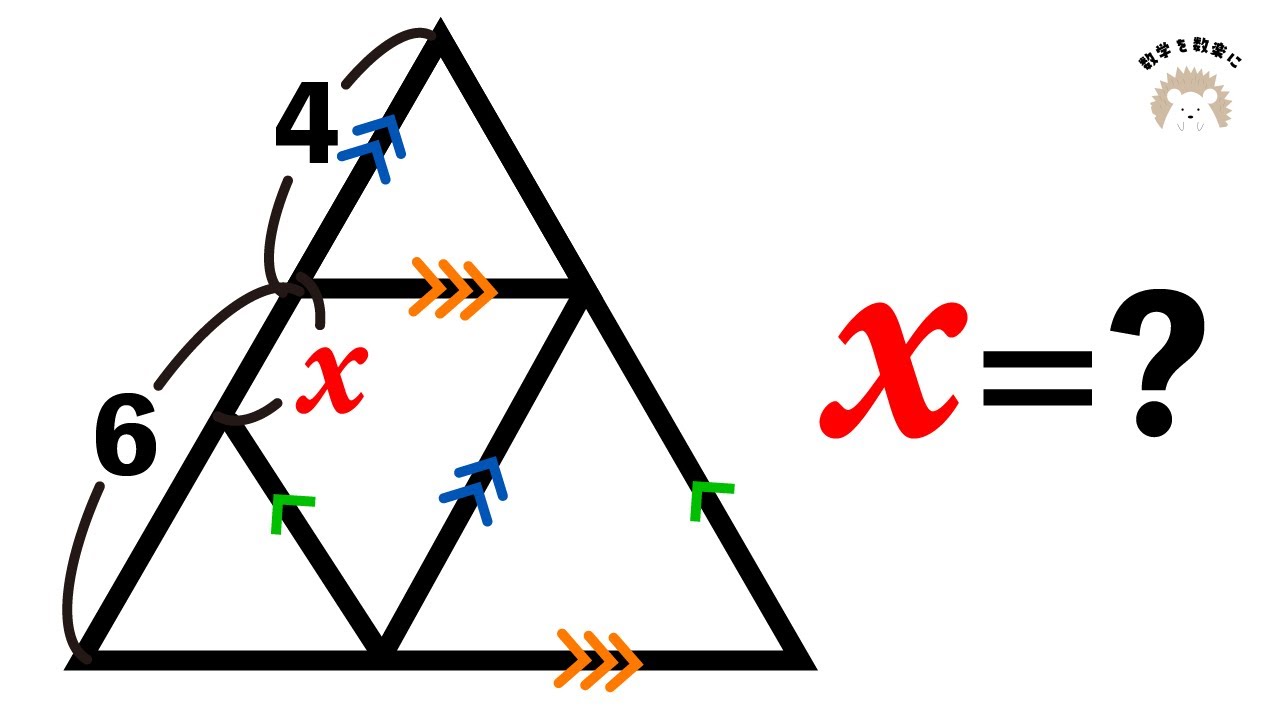
正三角形の中にある60度
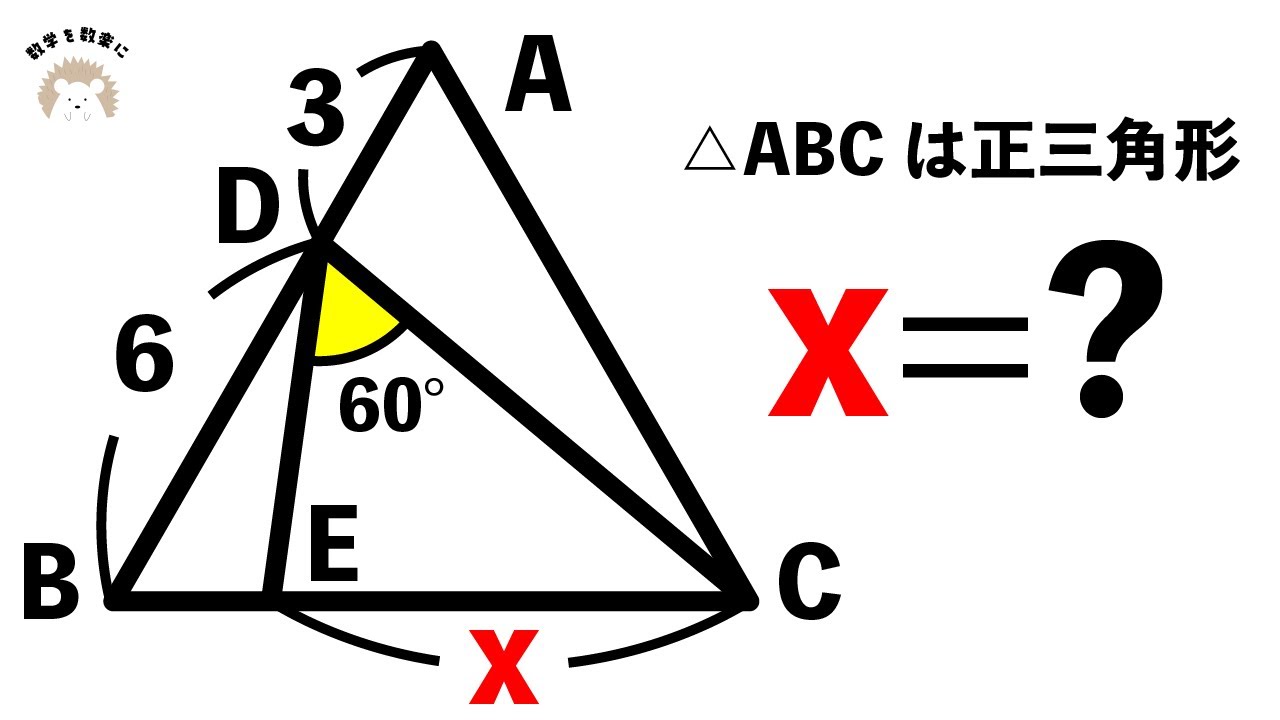
長方形の面積🟰❓
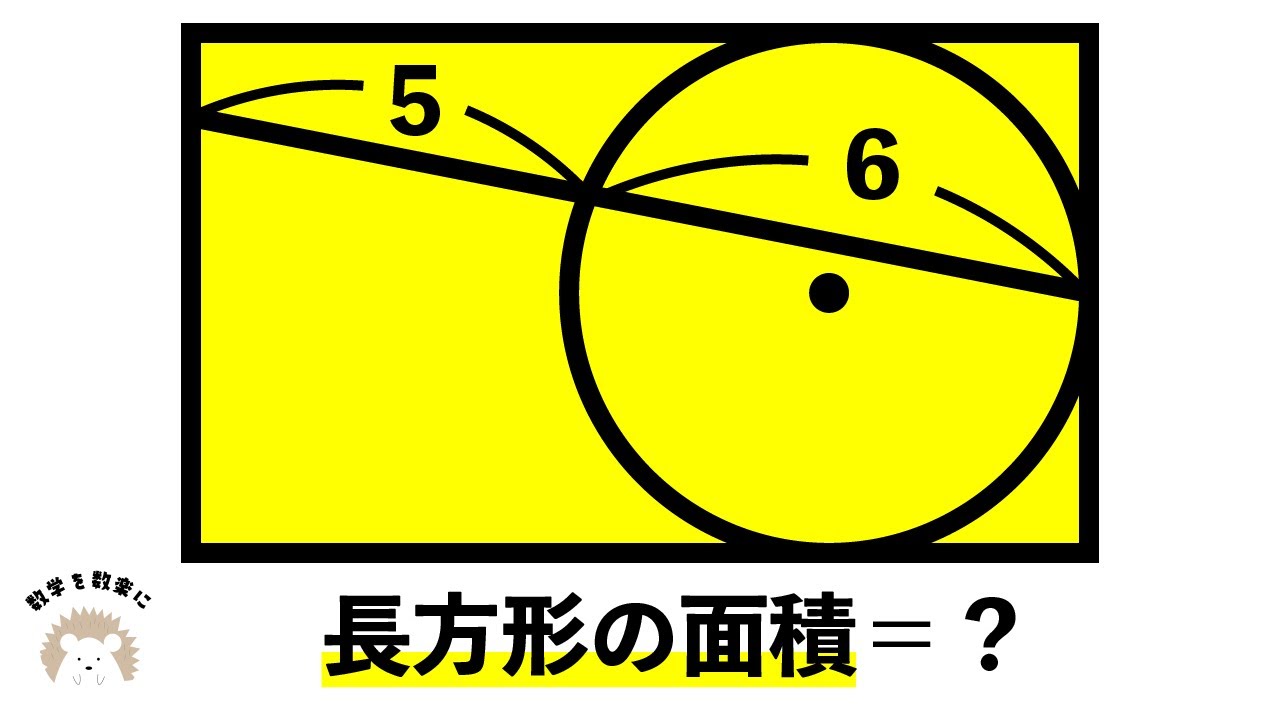
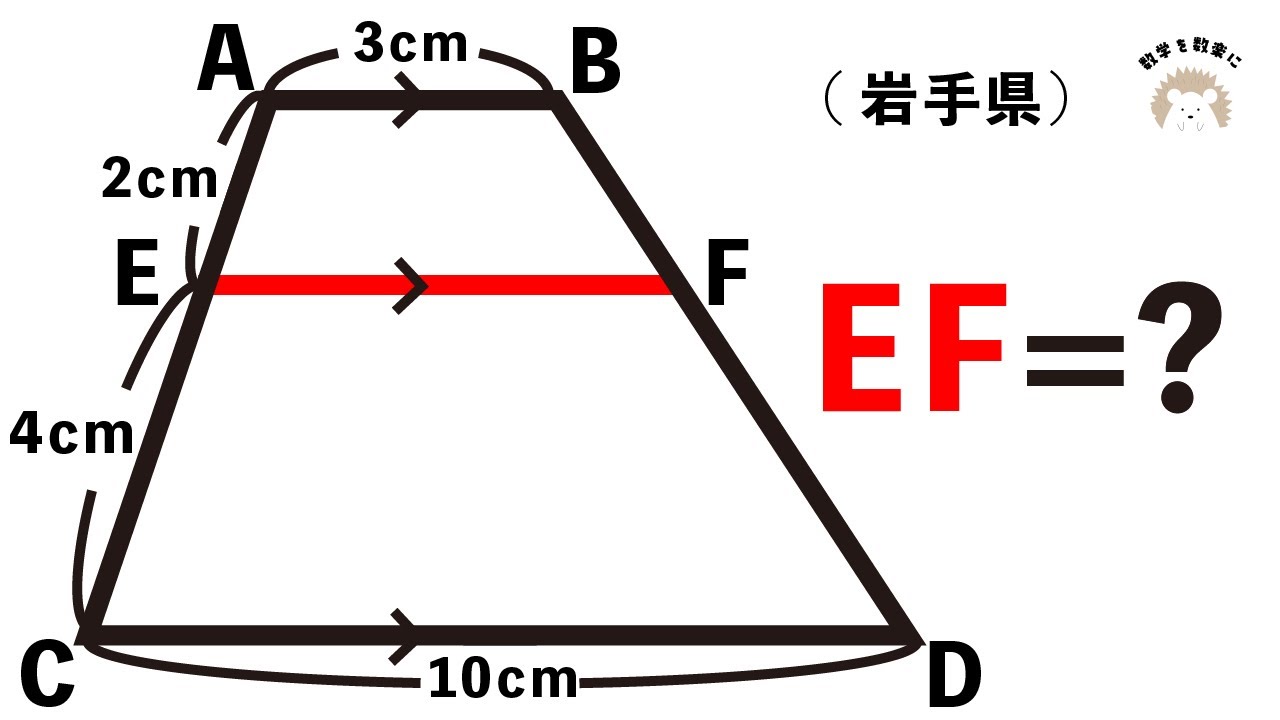
台形の中の線分 岩手県
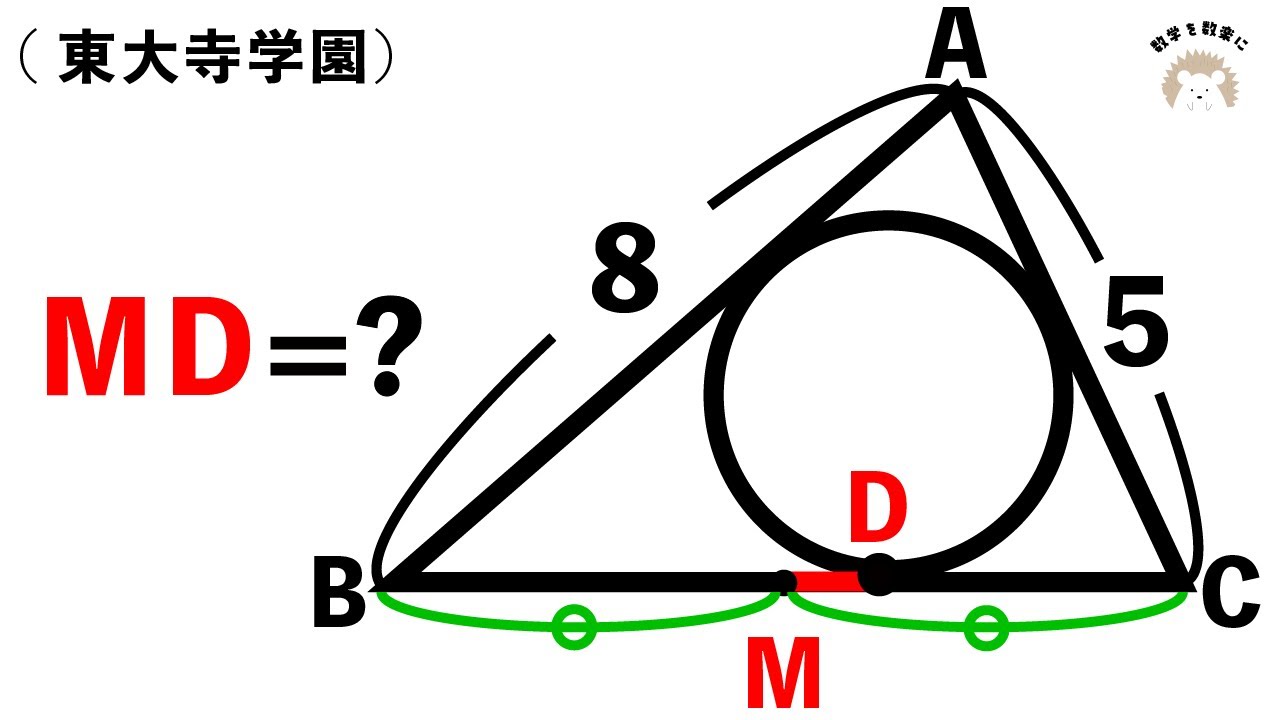
三角形と内接円 東大寺学園
中学受験解き方は高校受験の解き方より難しい
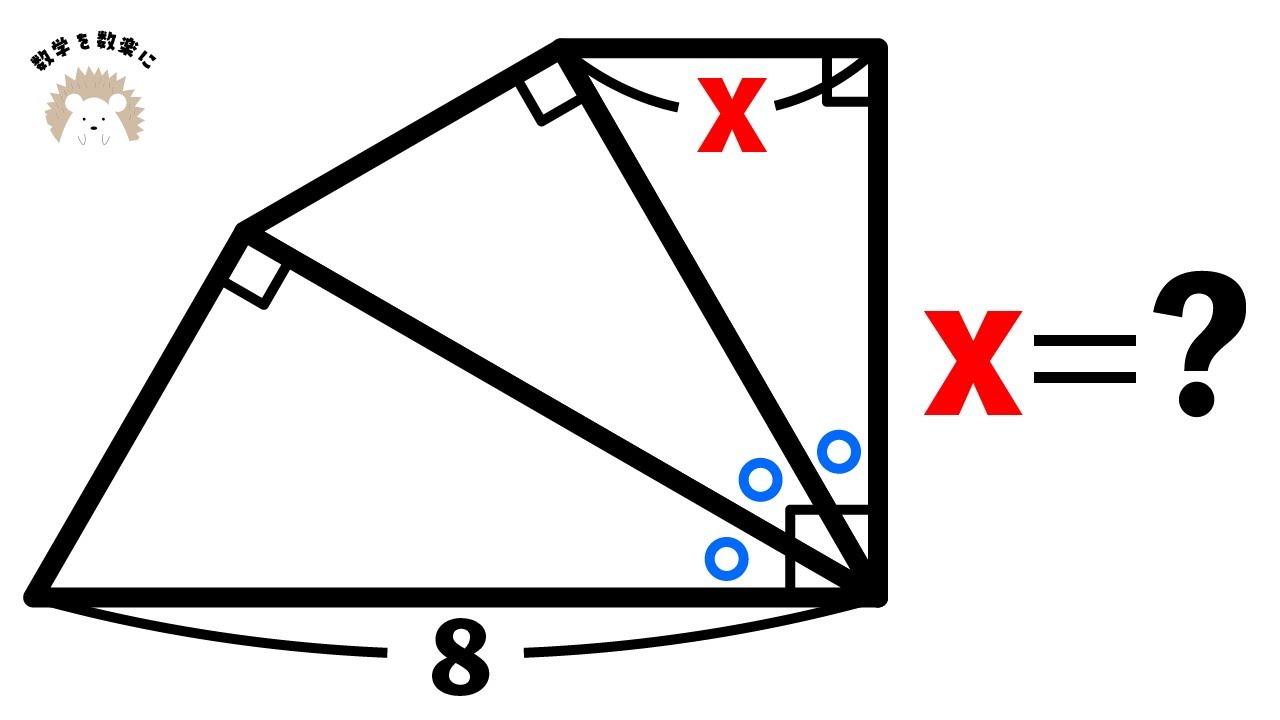
平行線と比
解けると気持ちいい!2通りで解説!!半円と長方形
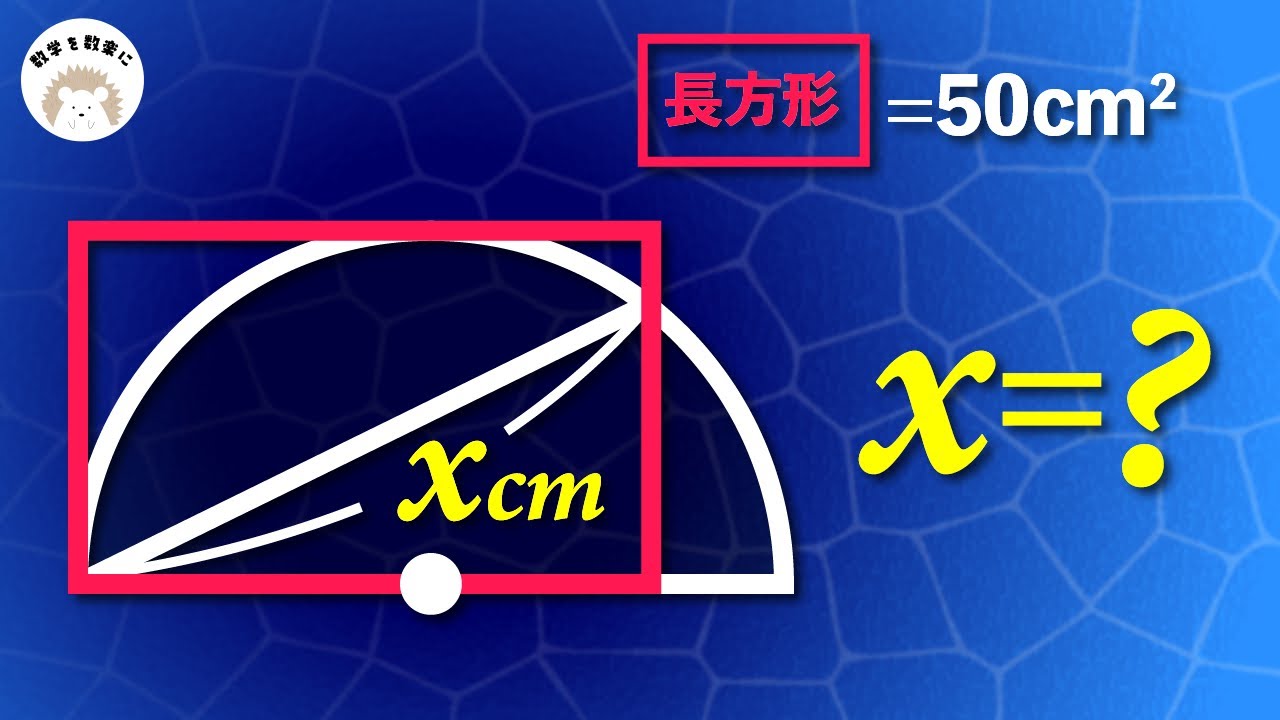
解けると気持ちいい!2通りで解説!!半円と長方形

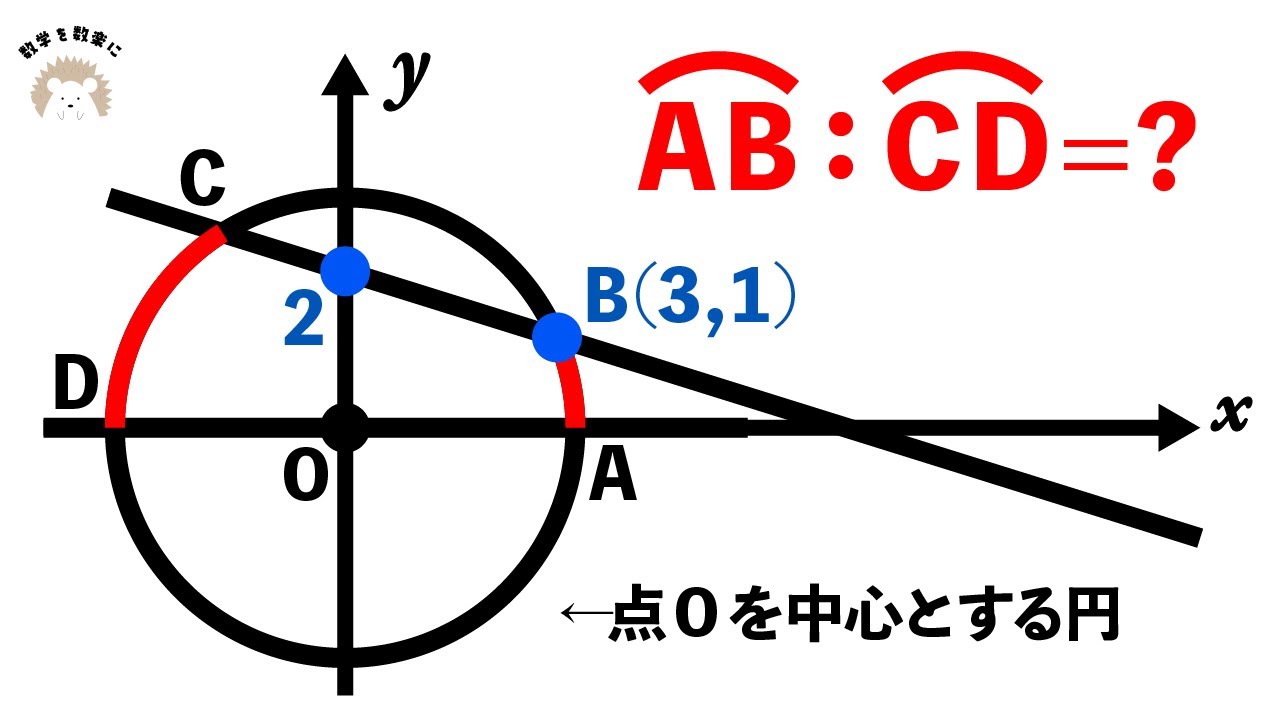
座標平面上の円
単元:
#数学(中学生)#中1数学#中3数学#相似な図形#平面図形
指導講師:
数学を数楽に
問題文全文(内容文):
$\stackrel{\huge\frown}{AB}:\stackrel{\huge\frown}{CD}=?$
この動画を見る
$\stackrel{\huge\frown}{AB}:\stackrel{\huge\frown}{CD}=?$
【情報を合わせて…!】図形:活水高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#平行と合同#相似な図形#三角形と四角形#高校入試過去問(数学)#活水高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
lとmが平行であり、AB=BC であるとき、xの角度を求めよ
この動画を見る
lとmが平行であり、AB=BC であるとき、xの角度を求めよ
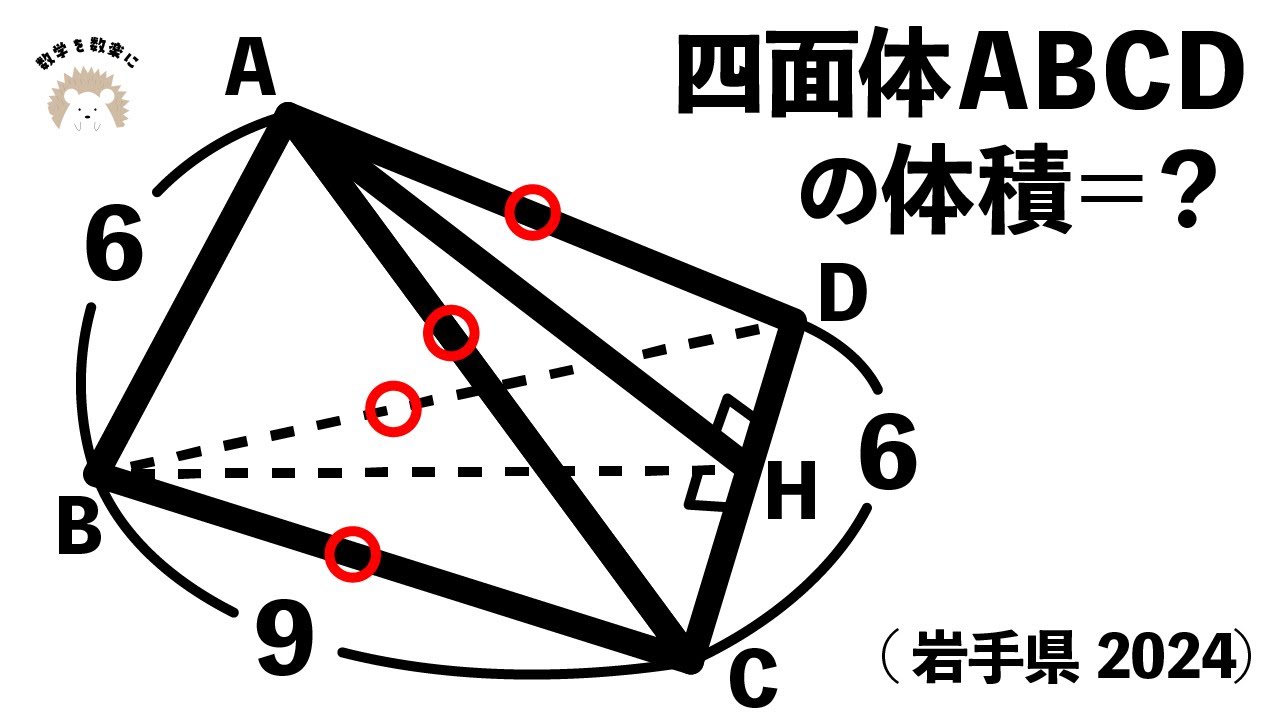
2024年岩手県のラスボス 四面体の体積
斜めの正方形

実は半分しか入ってないって信じれる?

単元:
#数学(中学生)#中3数学#相似な図形#その他#その他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
実は半分しか入ってないって信じれる?
※問題は動画内参照
この動画を見る
実は半分しか入ってないって信じれる?
※問題は動画内参照
図形の問題に見えて〇〇の問題 2通りで解説 正方形