 中3数学
中3数学
 中3数学
中3数学
最後まで〇〇するなよ因数分解 明大中野2022入試問題解説100問解説!!54問目

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$(x^2+x)^2-x(x+1)-2$
2022明治大学付属中野高等学校
この動画を見る
因数分解せよ
$(x^2+x)^2-x(x+1)-2$
2022明治大学付属中野高等学校
平方根の計算 城北高校 2022年入試問題解説52問目

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{2023 \times 2021 - 4044 +2}$
2022城北高等学校
この動画を見る
$\sqrt{2023 \times 2021 - 4044 +2}$
2022城北高等学校
三平方の定理 高校数学不要

開成高校 令和四年度最初の一問 2022年入試問題解説50問目

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式$7x^2-4\sqrt 2x+1=0$($\sqrt 2$の近似値=1.414)
2つの解を求めよ。
また、2つの解のうち$\frac{2}{5}$に近い方を、小数第4位を四捨五入し小数第3位まで求めよ。
2022開成高等学校
この動画を見る
2次方程式$7x^2-4\sqrt 2x+1=0$($\sqrt 2$の近似値=1.414)
2つの解を求めよ。
また、2つの解のうち$\frac{2}{5}$に近い方を、小数第4位を四捨五入し小数第3位まで求めよ。
2022開成高等学校
令和4年度 灘高校の最初の一問 2022年入試問題解説47問目

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\sqrt {2022} + \sqrt {77})^2
-2(\sqrt {2022} + \sqrt {77})(\sqrt {2022} - 1)
+2(\sqrt {2022} - \sqrt {77})(\sqrt {2022} - 1)
-(\sqrt {2022} - \sqrt {77})^2
$
2022灘高等学校
この動画を見る
$(\sqrt {2022} + \sqrt {77})^2
-2(\sqrt {2022} + \sqrt {77})(\sqrt {2022} - 1)
+2(\sqrt {2022} - \sqrt {77})(\sqrt {2022} - 1)
-(\sqrt {2022} - \sqrt {77})^2
$
2022灘高等学校
【中学数学】2次方程式の解き方まとめ 3-6【中3数学】

令和4年度 中央大杉並の最初の一問 2022入試問題解説43問目

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(x^2+2022)^2 - 4092529x^2$
因数分解せよ
$83521=17^4$を用いて良い
2022中央大学杉並高等学校
この動画を見る
$(x^2+2022)^2 - 4092529x^2$
因数分解せよ
$83521=17^4$を用いて良い
2022中央大学杉並高等学校
令和4年度 中央大杉並の最初の一問 2022入試問題解説42問目

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x+y+z=7,xyz=7$
$\frac{1}{x}+\frac{1}{y}+\frac{1}{z} = \frac{13}{7}$
$(1+ \frac{1}{x})(1+ \frac{1}{y})(1+ \frac{1}{z}) = ?$
2022中央大学杉並高等学校
この動画を見る
$x+y+z=7,xyz=7$
$\frac{1}{x}+\frac{1}{y}+\frac{1}{z} = \frac{13}{7}$
$(1+ \frac{1}{x})(1+ \frac{1}{y})(1+ \frac{1}{z}) = ?$
2022中央大学杉並高等学校
早稲田本庄 因数分解2022 入試問題解説38問目

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(x+y)xy - (y+z)yz$
因数分解せよ
2022早稲田大学本庄高等学院
この動画を見る
$(x+y)xy - (y+z)yz$
因数分解せよ
2022早稲田大学本庄高等学院
【自力本願⁈ 神のお告げ待ち⁈】因数分解:中央大学附属高等学校~全部入試問題

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$S$を因数分解しなさい.
$S=n^4-5n^3-10n^2+35n+49$
中央大附属高校過去問
この動画を見る
$S$を因数分解しなさい.
$S=n^4-5n^3-10n^2+35n+49$
中央大附属高校過去問
高等学校入学試験問題予想:法政大学第二高等学校~全部入試問題

単元:
#数学(中学生)#中2数学#中3数学#式の計算(展開、因数分解)#2次方程式#確率#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\boxed{1}$
因数分解せよ.
(1)$(x-2y)^2+(x+y)(x-5y)+y^2$
(2)$a=\dfrac{1}{\sqrt5+1},b=\dfrac{1}{\sqrt5-1}$のとき,$(a-4b)(b-4a)=?$
$\boxed{2}$
1~5までの数字が書かれたカードが2枚ずつ合計10枚ある.
(1)これらのカードを袋に入れてその中から同時に2枚取り出すとき,カードの数字の積が偶数となる確率は?
(2)$n$の3以上の自然数$\dfrac{4}{\sqrt n-\sqrt2}$の整数部分が2であるとき,
$n$として考えられる値を全て求めよ.
$\boxed{3}$
$PQ$と$D$の交点を$R$とする.
点$P,Q$の$x$座標を$p,q$とする.
直線$PQ$の傾きが,$C,D$の比例定数$a$と等しく,$R$が線分$PQ$の中点となる.
(1)点$A$の座標を$a$で表せ.
(2)$p+q=?$
(3)点$R$の座標を$a$で表せ.
(4)$p.q$の値
法政第二高校過去問
この動画を見る
$\boxed{1}$
因数分解せよ.
(1)$(x-2y)^2+(x+y)(x-5y)+y^2$
(2)$a=\dfrac{1}{\sqrt5+1},b=\dfrac{1}{\sqrt5-1}$のとき,$(a-4b)(b-4a)=?$
$\boxed{2}$
1~5までの数字が書かれたカードが2枚ずつ合計10枚ある.
(1)これらのカードを袋に入れてその中から同時に2枚取り出すとき,カードの数字の積が偶数となる確率は?
(2)$n$の3以上の自然数$\dfrac{4}{\sqrt n-\sqrt2}$の整数部分が2であるとき,
$n$として考えられる値を全て求めよ.
$\boxed{3}$
$PQ$と$D$の交点を$R$とする.
点$P,Q$の$x$座標を$p,q$とする.
直線$PQ$の傾きが,$C,D$の比例定数$a$と等しく,$R$が線分$PQ$の中点となる.
(1)点$A$の座標を$a$で表せ.
(2)$p+q=?$
(3)点$R$の座標を$a$で表せ.
(4)$p.q$の値
法政第二高校過去問
サクッと解こう!高校入試レベル
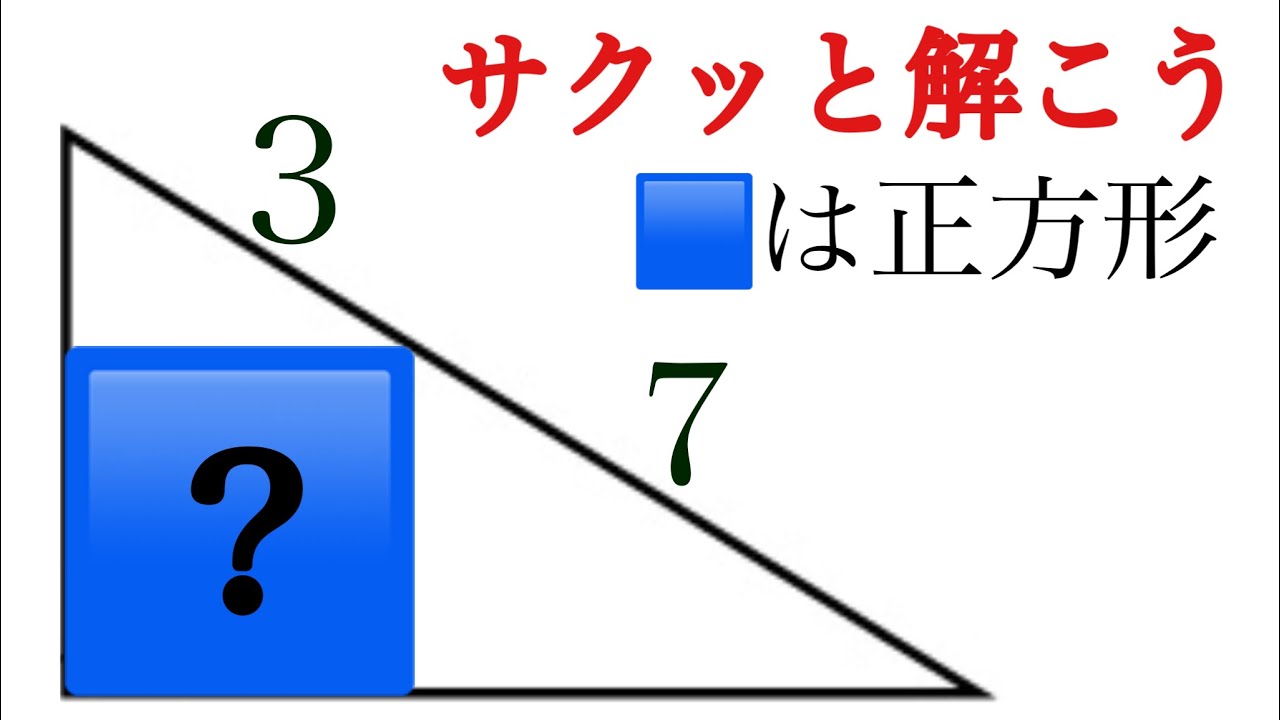
【裏技】これ知ってる?

【中学数学】円周角の定理のまとめ~基礎固め~【中3数学】

単元:
#数学(中学生)#中3数学#円
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1つの弧に対する円周角は中心角の半分の大きさ $\angle APB=\frac{1}{2}2\angle AOB~\angle AOB=2\angle APB$
1つの弧に対する円周角の大きさは等しい$\angle APB=\angle AQB$
弧の長さが等しい⇔円周角が等しい$\stackrel{\frown}{AB}=\stackrel{\frown}{AB}~\angle APB=\angle CQD$
線分$AB$が直径$\angle APB=90°$
この動画を見る
1つの弧に対する円周角は中心角の半分の大きさ $\angle APB=\frac{1}{2}2\angle AOB~\angle AOB=2\angle APB$
1つの弧に対する円周角の大きさは等しい$\angle APB=\angle AQB$
弧の長さが等しい⇔円周角が等しい$\stackrel{\frown}{AB}=\stackrel{\frown}{AB}~\angle APB=\angle CQD$
線分$AB$が直径$\angle APB=90°$
【中学数学】因数分解のテクニックまとめ 3-4【中3数学】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\displaystyle
(1)\,6x^2y-15xy^2+27xy$
$\displaystyle
(2)\,x^2+x-56$
$\displaystyle
(3)\,x^2-18x+81$
$\displaystyle
(4)\,4x^2+20x+25$
$\displaystyle
(5)\,4x^2-81$
$\displaystyle
(6)\,9(a+B)^2-30(a+b)+16$
$\displaystyle
(7)\,6x^2+12x-48$
$\displaystyle
(8)\,ax+ay-5x-5y$
$\displaystyle
(9)\,x^2+6xy+9y^2-4a^2$
$\displaystyle
(10)\,1-x^2+8xy-16y^2$
この動画を見る
$\displaystyle
(1)\,6x^2y-15xy^2+27xy$
$\displaystyle
(2)\,x^2+x-56$
$\displaystyle
(3)\,x^2-18x+81$
$\displaystyle
(4)\,4x^2+20x+25$
$\displaystyle
(5)\,4x^2-81$
$\displaystyle
(6)\,9(a+B)^2-30(a+b)+16$
$\displaystyle
(7)\,6x^2+12x-48$
$\displaystyle
(8)\,ax+ay-5x-5y$
$\displaystyle
(9)\,x^2+6xy+9y^2-4a^2$
$\displaystyle
(10)\,1-x^2+8xy-16y^2$
2次方程式の応用 明大明治 2022入試問題解説 25問目

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
xについての2次方程式
$x^2-K^2x + 2(K^2 -2 )= 0$(K> 0)
一方の解がもう一方の解の2倍になる時、
Kの値を全て求めよ
2022明治大学付属明治高等学校
この動画を見る
xについての2次方程式
$x^2-K^2x + 2(K^2 -2 )= 0$(K> 0)
一方の解がもう一方の解の2倍になる時、
Kの値を全て求めよ
2022明治大学付属明治高等学校
【中学数学】相似な図形:線分比と面積比の巧みな利用
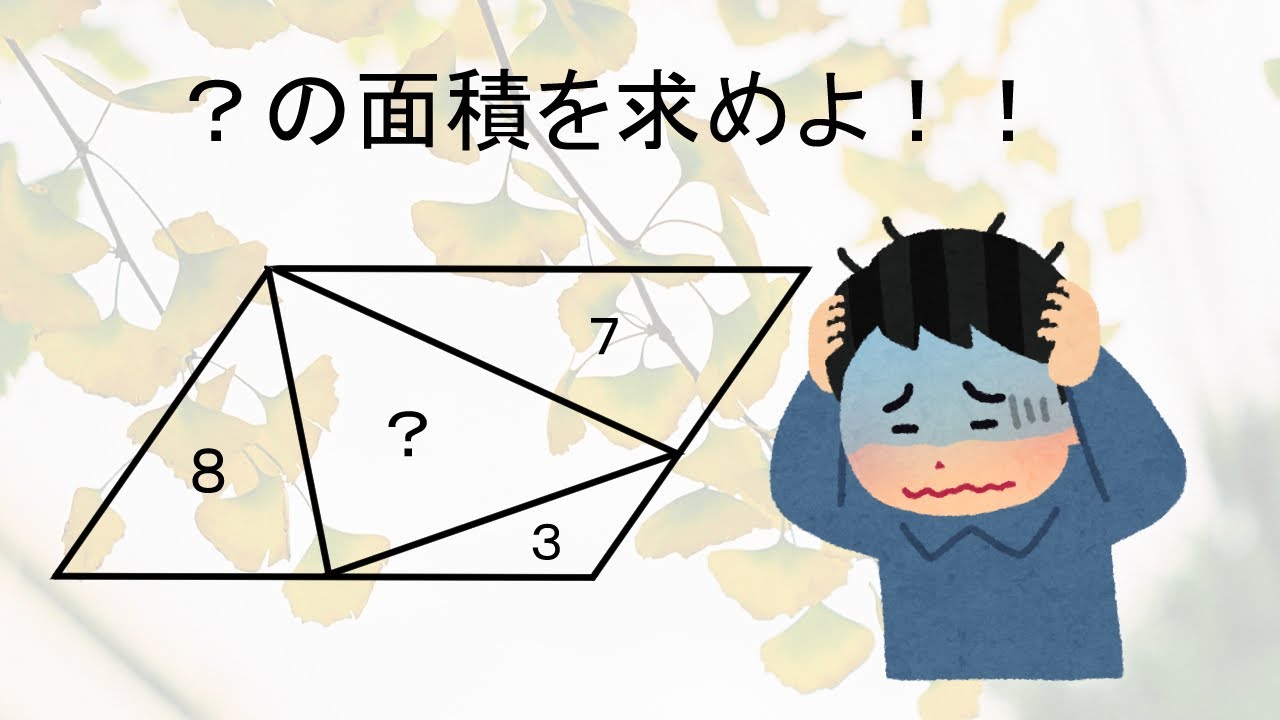
単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
【中学数学 相似な図形】
平行四辺形ABCDにおいて、△ABE=8、△ADF=7、△CEF=3のとき、△AEFの面積を求めよ。
この動画を見る
【中学数学 相似な図形】
平行四辺形ABCDにおいて、△ABE=8、△ADF=7、△CEF=3のとき、△AEFの面積を求めよ。
高校入試レベルだよ
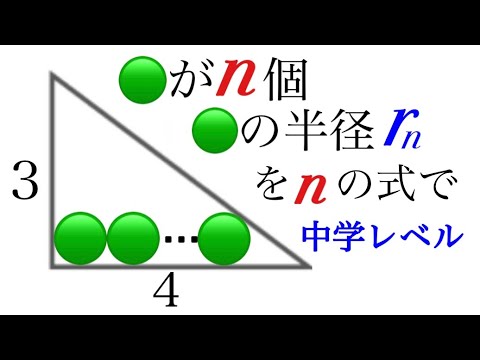
平方根の計算 香川誠陵 2022入試問題解説 22問目

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
計算せよ
$(\frac{2}{\sqrt 2} + \frac{3}{\sqrt 3}) \times (\sqrt {18} - \sqrt {12})$
2022香川誠陵高等学校
この動画を見る
計算せよ
$(\frac{2}{\sqrt 2} + \frac{3}{\sqrt 3}) \times (\sqrt {18} - \sqrt {12})$
2022香川誠陵高等学校
【裏技】三平方の定理の規則

ルートの傾き 西武文理 2022入試問題解説19問目
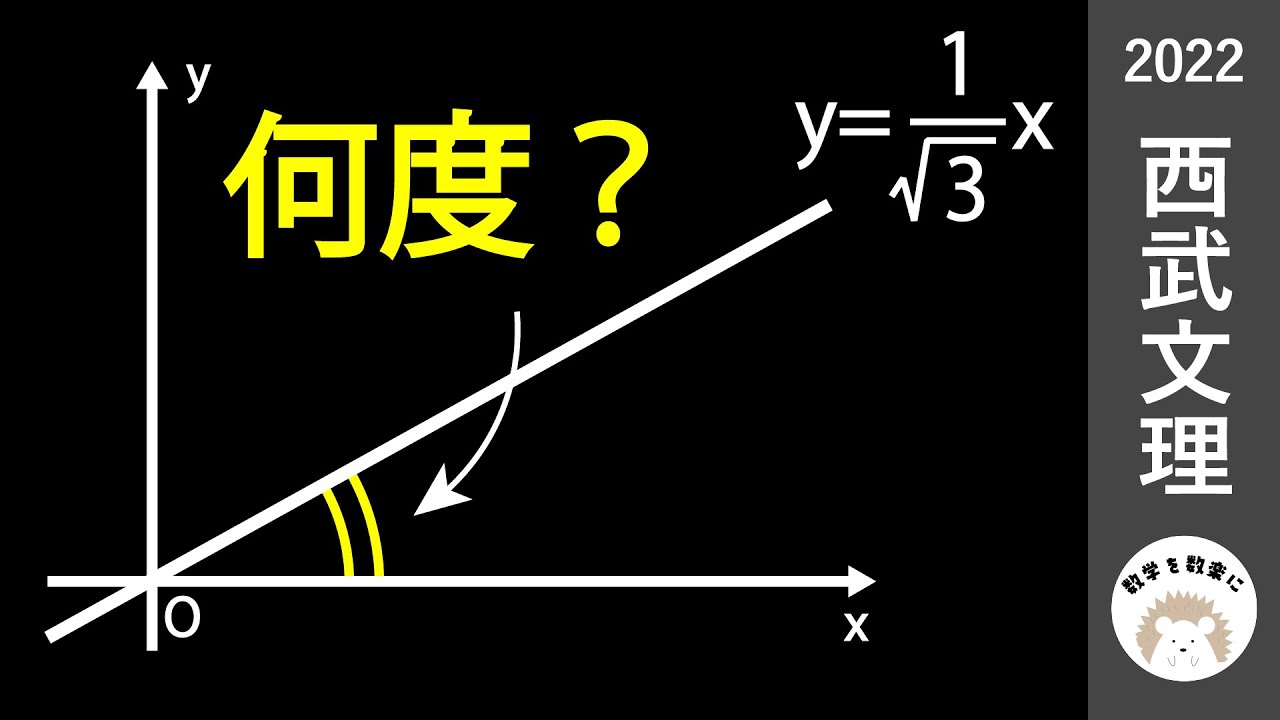
三平方の定理のこれ知ってる?

色々解き方あると思いますが僕はこう解きました 2次方程式と比 専修大学松戸 2022入試問題解説16問目

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式
$ax^2-2ax-b=0$
1つの解が$x=1+ \sqrt {10}$
a:b=?
2022専修大学松戸高等学校
この動画を見る
2次方程式
$ax^2-2ax-b=0$
1つの解が$x=1+ \sqrt {10}$
a:b=?
2022専修大学松戸高等学校
【中学数学】苦手かどうか分かる問題~相似の問題演習~【中3数学】
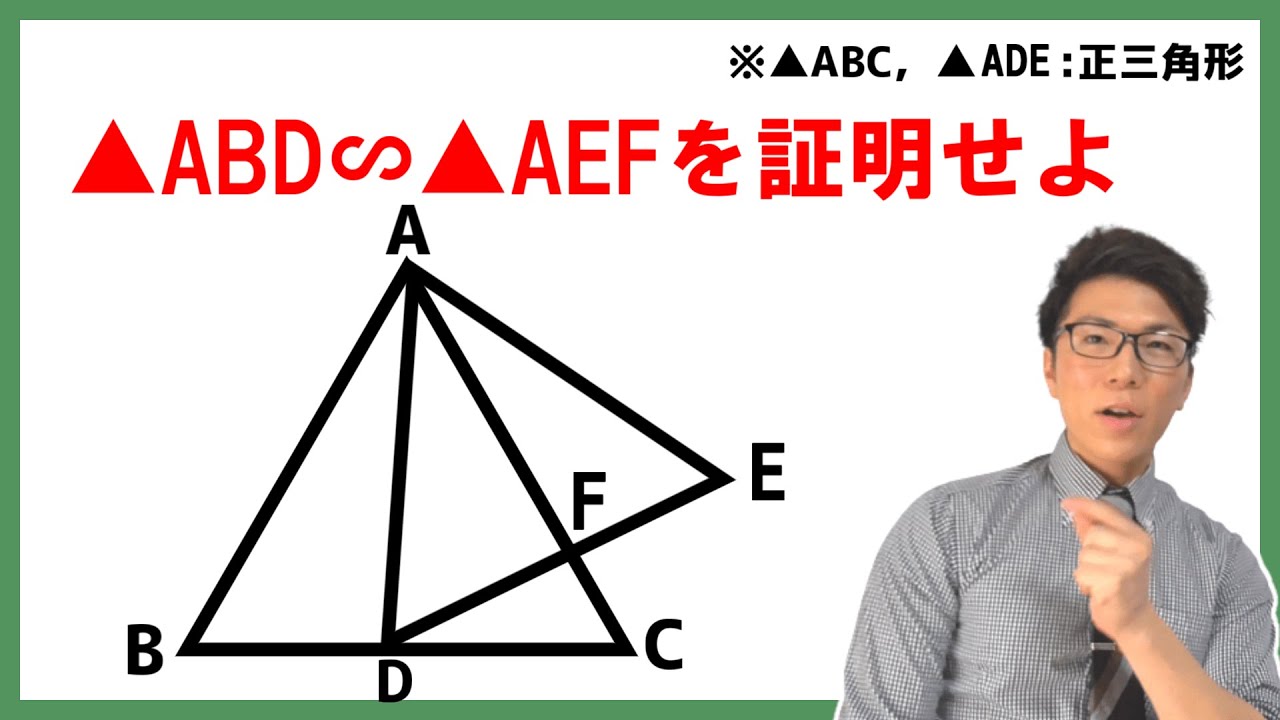
単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\triangle ABC$と$\triangle ADE$はともに正三角形である。この時$\triangle ABC$ ∽ $\triangle AEF$を証明せよ。
(図は動画参照)
この動画を見る
$\triangle ABC$と$\triangle ADE$はともに正三角形である。この時$\triangle ABC$ ∽ $\triangle AEF$を証明せよ。
(図は動画参照)
2022年市川高校 ヒントがなければ超難問

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$a,b$を正の数とする.
$a^2+4b^2=4$のとき,$ab$の最大値を求めよ.
図を参考にしても良い.
市川高校過去問
この動画を見る
$a,b$を正の数とする.
$a^2+4b^2=4$のとき,$ab$の最大値を求めよ.
図を参考にしても良い.
市川高校過去問
四乗の和 渋谷教育学園幕張の最初の一題 動画内に続きの問題あり 2022入試問題解説15問目

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
A=x+y
B=xy
$x^4+y^4=?$
A,Bを用いて表せ
2022渋谷教育学園幕張
この動画を見る
A=x+y
B=xy
$x^4+y^4=?$
A,Bを用いて表せ
2022渋谷教育学園幕張
因数分解 中学生の解き方 高校生の解き方 昭和学院秀英 2022入試問題解説11問目

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$ax^2-(a^2+a-2)x-2(a+1)$を因数分解せよ
2022昭和学院秀英高等学校
この動画を見る
$ax^2-(a^2+a-2)x-2(a+1)$を因数分解せよ
2022昭和学院秀英高等学校
時が止まった。。。日大習志野 2022入試問題解説8問目

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=2-3 \sqrt 2 $
$x^2 -4x-15 = ?$
2022日本大学習志野高等学校
この動画を見る
$x=2-3 \sqrt 2 $
$x^2 -4x-15 = ?$
2022日本大学習志野高等学校
2次方程式 〇〇するな! 青雲 2022入試問題解説5問目

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$\frac{1}{2}(\sqrt 2x-1)^2 -1 = 0$
2022青雲高等学校
この動画を見る
2次方程式を解け
$\frac{1}{2}(\sqrt 2x-1)^2 -1 = 0$
2022青雲高等学校
【裏技】三平方の定理

