数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
【高校受験対策/数学/関数46】ひし形の面積を二等分せよ。

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数46
Q
右の図において、①は関数$y=x^2$、②は関数$y=ax^2$のグラフであり、$a \lt 0$である。
点A,Bは①のグラフ上にあり、点Aの$x$座標は$2$で、点Aと点Bの$y$座標は等しい。
点Cを$y$軸上にとり、点Oと点A、点Oと点B、点AとC、点Bと点Cをそれぞれ結んで、ひし形OACBをつくる。
また、②のグラフ上に点Aと$x$座標が等しい点Dをとる。
このとき次の各問いに答えなさい。
問1
2点O,Bを通る直線の式を求めよ。
問2
点Cの座標を求めよ。
問3
$x$軸上に点$(3,0)$をとる。
点$(3,0)$を通り、ひし形OACBの面積を2等分する直線の式を求めよ。
問4
点Oと点Dを結んだ線分ODを1辺とする正方形をつくる。
この正方形とひし形OACBの面積の比が$25:64$であるとき、$a$の値を求めよ。
この動画を見る
高校受験対策・関数46
Q
右の図において、①は関数$y=x^2$、②は関数$y=ax^2$のグラフであり、$a \lt 0$である。
点A,Bは①のグラフ上にあり、点Aの$x$座標は$2$で、点Aと点Bの$y$座標は等しい。
点Cを$y$軸上にとり、点Oと点A、点Oと点B、点AとC、点Bと点Cをそれぞれ結んで、ひし形OACBをつくる。
また、②のグラフ上に点Aと$x$座標が等しい点Dをとる。
このとき次の各問いに答えなさい。
問1
2点O,Bを通る直線の式を求めよ。
問2
点Cの座標を求めよ。
問3
$x$軸上に点$(3,0)$をとる。
点$(3,0)$を通り、ひし形OACBの面積を2等分する直線の式を求めよ。
問4
点Oと点Dを結んだ線分ODを1辺とする正方形をつくる。
この正方形とひし形OACBの面積の比が$25:64$であるとき、$a$の値を求めよ。
傍接円に関する問題
単元:
#数学(中学生)#中3数学#高校入試過去問(数学)#青雲高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
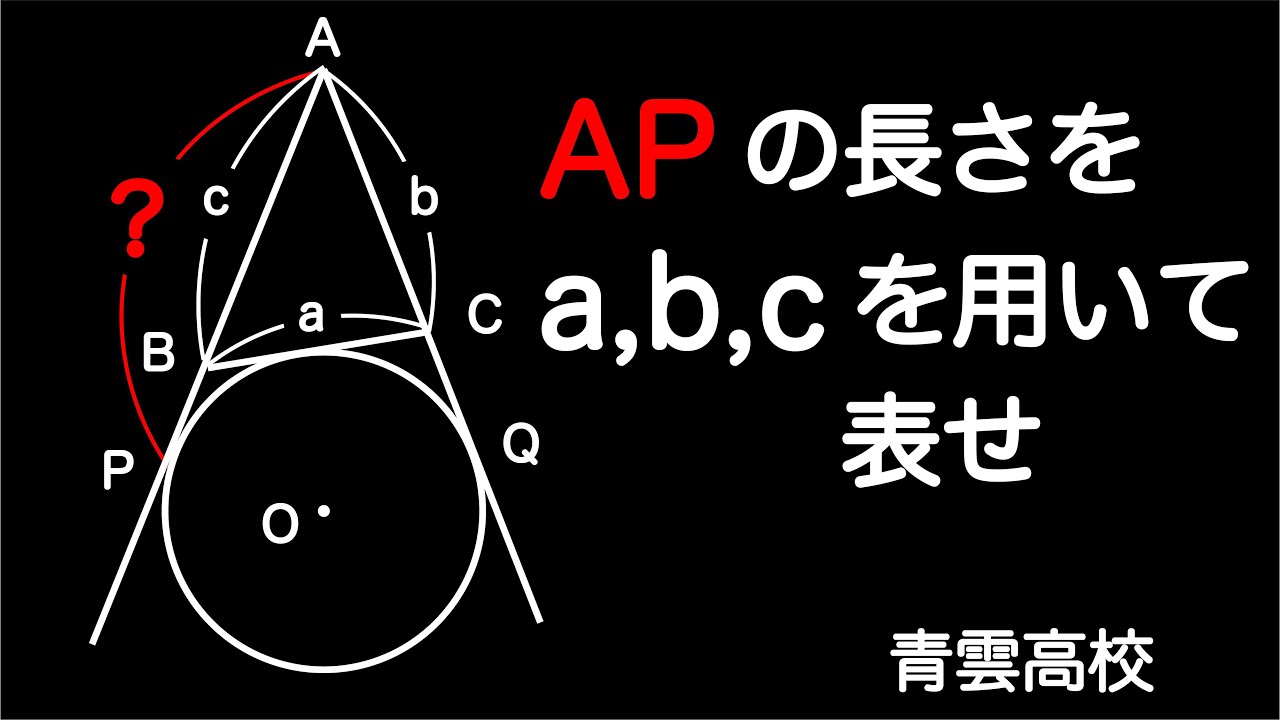
動画内の図を参照し、$\textrm{AP}$の長さを$a,b,c$で表せ。
出典:2002年青雲高等学校 高校入試
この動画を見る
動画内の図を参照し、$\textrm{AP}$の長さを$a,b,c$で表せ。
出典:2002年青雲高等学校 高校入試
【高校受験対策/数学/確率6】「難しそうに見せているだけ」という気持ちを持って欲しい

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・確率6
Q
下の図のように、さいころの1から6までの目が1つずつ表示された6つの箱がある。
それぞれの箱の中には、表示されたさいころの目と同じ数の玉が入っている。
大小2つのさいころを同時に1回投げ、それぞれのさいころの出た目の数によって、 箱の中の玉を移動させる。
このとき下の問1、問2に答えなさい。
ただし、さいころはどの目が出ることも同様に確からしいものとする。
問1
大きいさいころの出た目と同じ目が表示された箱から玉を1個だけ取り出す。
その取り出した1個の玉を、小さいさいころの出た目と同じ目が表示された箱に入れる。
このとき次の(1)、(2)の問いに答えよ。
(1) 空の箱ができる確率を求めよ。
(2) 6つの箱のうち、入っている玉の数が同じ箱が3つできる確率を求めよ。
問2
大きいさいころの出た目と同じ目が表示された箱から玉をすべて取り出す。
その取り出したすべての玉を、小さいさいころの出た目と同じ目が表示された箱に入れる。
このとき、6つの箱のうち入っている玉の数が同じ箱が2つできる確率を求めよ。
この動画を見る
高校受験対策・確率6
Q
下の図のように、さいころの1から6までの目が1つずつ表示された6つの箱がある。
それぞれの箱の中には、表示されたさいころの目と同じ数の玉が入っている。
大小2つのさいころを同時に1回投げ、それぞれのさいころの出た目の数によって、 箱の中の玉を移動させる。
このとき下の問1、問2に答えなさい。
ただし、さいころはどの目が出ることも同様に確からしいものとする。
問1
大きいさいころの出た目と同じ目が表示された箱から玉を1個だけ取り出す。
その取り出した1個の玉を、小さいさいころの出た目と同じ目が表示された箱に入れる。
このとき次の(1)、(2)の問いに答えよ。
(1) 空の箱ができる確率を求めよ。
(2) 6つの箱のうち、入っている玉の数が同じ箱が3つできる確率を求めよ。
問2
大きいさいころの出た目と同じ目が表示された箱から玉をすべて取り出す。
その取り出したすべての玉を、小さいさいころの出た目と同じ目が表示された箱に入れる。
このとき、6つの箱のうち入っている玉の数が同じ箱が2つできる確率を求めよ。
傾きについて!(高校入試数学)

【高校受験対策/数学】図形32

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形32
Q
右の図のような、$∠ACB=90°$の直角三角形がある。
$∠ABC$の二等分線と辺$AC$との交点を$D$とする。
点$C$から辺$AB$に垂線をひき、その交点を$E$とし、線分$CE$と線$BD$との交点を$F$とする。
また点から辺$BC$に垂線をひき、その交点を$G$とし、線分$EG$と線分$BD$との交点を$H$とする。
このとき、次の各問いに答えなさい。
①$\triangle BEH \backsim \triangle BAD$であることを証明せよ。
②点$E$から線分$HF$に垂線をひき、その交点を$I$とし、 直線$EI$と辺$BC$との交点を$J$とする。
このとき$EH=FJ$であることを証明せよ。
この動画を見る
高校受験対策・図形32
Q
右の図のような、$∠ACB=90°$の直角三角形がある。
$∠ABC$の二等分線と辺$AC$との交点を$D$とする。
点$C$から辺$AB$に垂線をひき、その交点を$E$とし、線分$CE$と線$BD$との交点を$F$とする。
また点から辺$BC$に垂線をひき、その交点を$G$とし、線分$EG$と線分$BD$との交点を$H$とする。
このとき、次の各問いに答えなさい。
①$\triangle BEH \backsim \triangle BAD$であることを証明せよ。
②点$E$から線分$HF$に垂線をひき、その交点を$I$とし、 直線$EI$と辺$BC$との交点を$J$とする。
このとき$EH=FJ$であることを証明せよ。
立方体に内部にできる三角形の面積
単元:
#数学(中学生)#中1数学#空間図形
指導講師:
数学を数楽に
問題文全文(内容文):
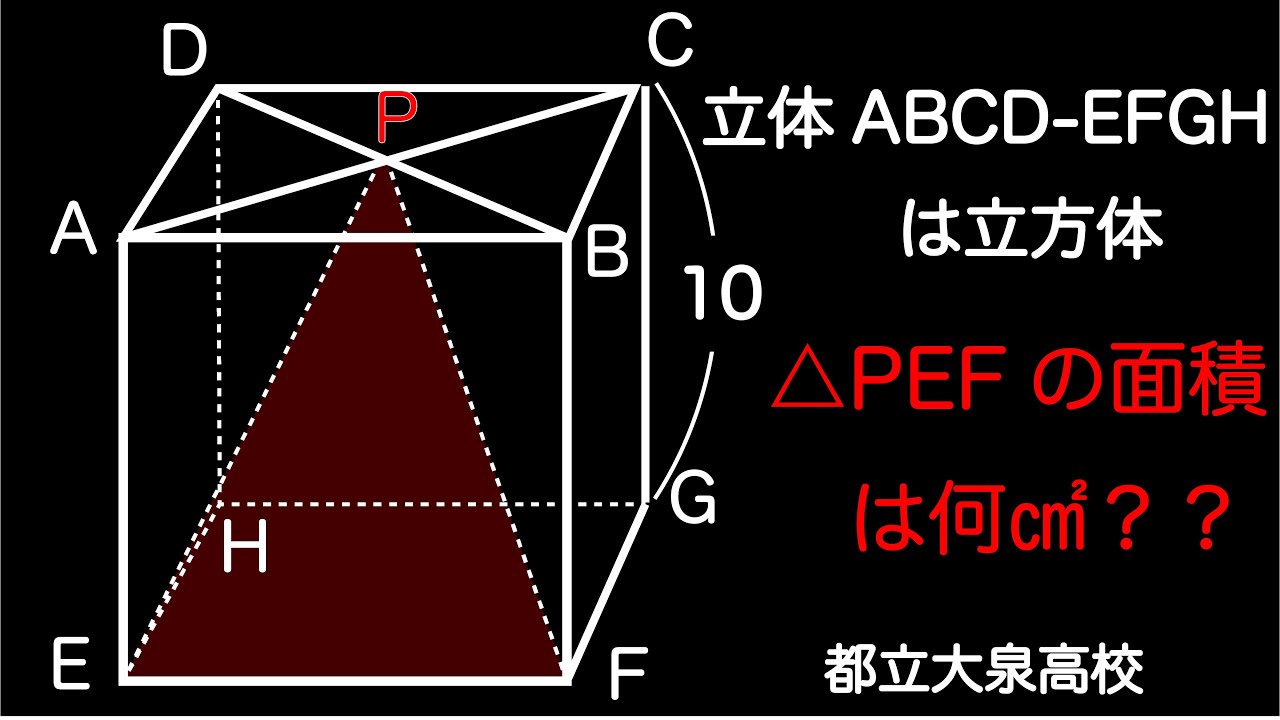
立体$ABCD-DFGH$は立方体
$\triangle PEF$の面積は何$cm^2$??
出典:東京都立大泉高等学校
この動画を見る
立体$ABCD-DFGH$は立方体
$\triangle PEF$の面積は何$cm^2$??
出典:東京都立大泉高等学校
二つの円と三平方!!(都立西)

【高校受験対策】数学-死守48

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策 数学・死守48
①$-7+3-4$を計算しなさい。
➁$\frac{1}{3} \div(-\frac{1}{6})$を計算しなさい。
③$\frac{3}{\sqrt{3}}+4\sqrt{3}-\sqrt{27}$を計算しなさい。
④$4(2x-1)-3(2x-3)$を計算しなさい。
⑤$(-xy)^2 \times 10xy^2 \div 5x^2$を計算しなさい。
⑥$(3x-1)(4x+3)$を展開しなさい。
⑦$x^2-4x+3$を因数分解しなさい。
⑧$a=-3$のとき、$a^2-2a$の値を求めなさい。
⑨等式を$V=\pi r^2h$$h$について解きなさい。
➉二次方程式$sx^2+3x-1=0$を解きなさい。
⑪
右の図1において、3点A,B,Cは点Oを中心とする円の周上の点である。
このとき、$∠x$の大きさを求めなさい。
⑫
右の図2のように、直線$l$上に2点O,Aがあり、OA=1とする。
このとき$OP=\sqrt{2}$となる点Pを、以下の指示に従って作図しなさい。
指示
・点Pは点Oよりも右側にとりなさい。
・作図に用いた線は消さずに残しておきなさい。
・作図した点Pには記号を書き入れなさい。
この動画を見る
高校受験対策 数学・死守48
①$-7+3-4$を計算しなさい。
➁$\frac{1}{3} \div(-\frac{1}{6})$を計算しなさい。
③$\frac{3}{\sqrt{3}}+4\sqrt{3}-\sqrt{27}$を計算しなさい。
④$4(2x-1)-3(2x-3)$を計算しなさい。
⑤$(-xy)^2 \times 10xy^2 \div 5x^2$を計算しなさい。
⑥$(3x-1)(4x+3)$を展開しなさい。
⑦$x^2-4x+3$を因数分解しなさい。
⑧$a=-3$のとき、$a^2-2a$の値を求めなさい。
⑨等式を$V=\pi r^2h$$h$について解きなさい。
➉二次方程式$sx^2+3x-1=0$を解きなさい。
⑪
右の図1において、3点A,B,Cは点Oを中心とする円の周上の点である。
このとき、$∠x$の大きさを求めなさい。
⑫
右の図2のように、直線$l$上に2点O,Aがあり、OA=1とする。
このとき$OP=\sqrt{2}$となる点Pを、以下の指示に従って作図しなさい。
指示
・点Pは点Oよりも右側にとりなさい。
・作図に用いた線は消さずに残しておきなさい。
・作図した点Pには記号を書き入れなさい。
日比谷高校の角度を求める問題!!
単元:
#数学(中学生)#高校入試過去問(数学)#東京都立日比谷高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
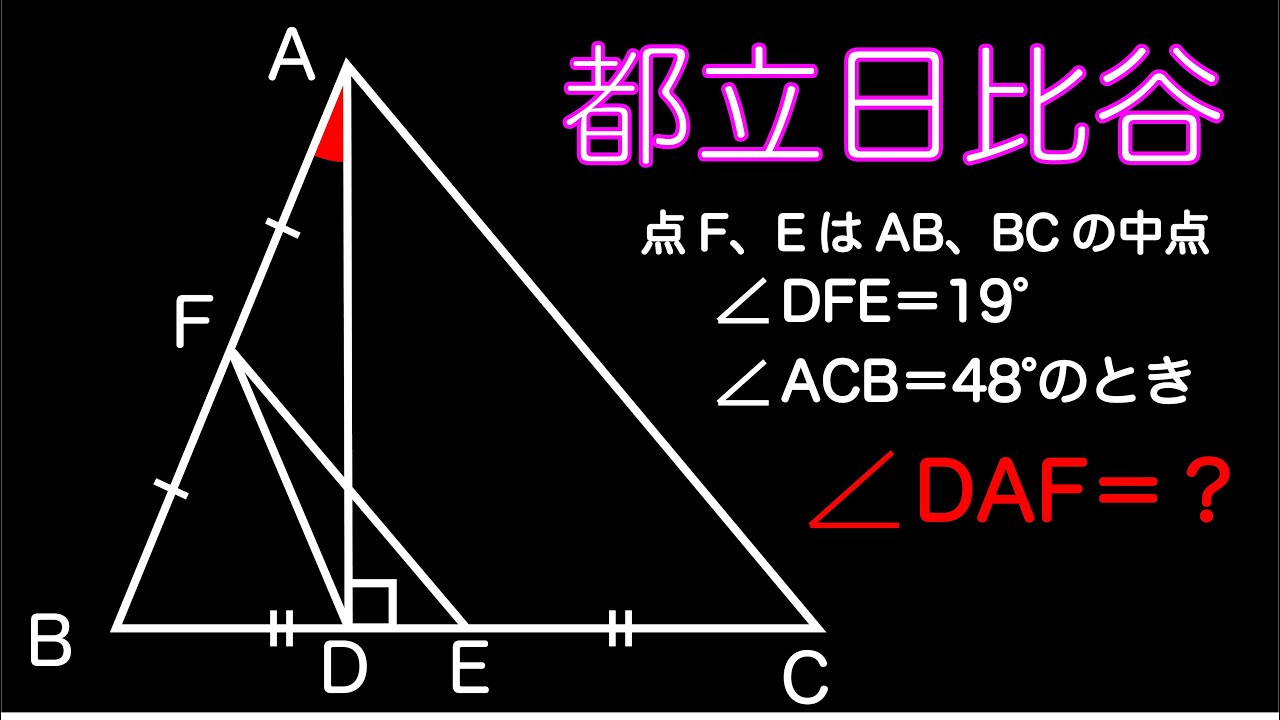
点$F,E$は$AB,BC$の中点
$\angle DFE=19^{ \circ }$
$\angle ACB=48^{ \circ }$のとき
$\angle DAF=??$
出典:東京都立日比谷高等学校
この動画を見る
点$F,E$は$AB,BC$の中点
$\angle DFE=19^{ \circ }$
$\angle ACB=48^{ \circ }$のとき
$\angle DAF=??$
出典:東京都立日比谷高等学校
【高校受験対策】数学-関数45

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数45
Q
右の図において、直線$y=x-1$と$x$軸との交点をA、直線$y=\frac{1}{3}x+3$と$y$軸との交点をBとする。
また、この2つの直線の交点をPとする。このとき次の各問いに答えなさい。
①点Aの$x$座標を求めなさい。
②点Pの座標を求めなさい。
③線分ABの長さを求めなさい。
④$\angle ABP=90°$であることを次のように証明した。
右の証明のⅠ~Ⅱにあてはまる数や関係を表す式を入れて、この証明を完成しなさい。
⑤3点、A,B,Pを通る円と$x$軸との交点のうち、点Aと異なる点をCとする。
また、この円における点Pを含まない弧ACと弦ACとで囲まれてできる図形をSとする。
この図形Sを、直線$y=x-1$を回転の軸として1回転させてできる立体の体積を求めなさい。
この動画を見る
高校受験対策・関数45
Q
右の図において、直線$y=x-1$と$x$軸との交点をA、直線$y=\frac{1}{3}x+3$と$y$軸との交点をBとする。
また、この2つの直線の交点をPとする。このとき次の各問いに答えなさい。
①点Aの$x$座標を求めなさい。
②点Pの座標を求めなさい。
③線分ABの長さを求めなさい。
④$\angle ABP=90°$であることを次のように証明した。
右の証明のⅠ~Ⅱにあてはまる数や関係を表す式を入れて、この証明を完成しなさい。
⑤3点、A,B,Pを通る円と$x$軸との交点のうち、点Aと異なる点をCとする。
また、この円における点Pを含まない弧ACと弦ACとで囲まれてできる図形をSとする。
この図形Sを、直線$y=x-1$を回転の軸として1回転させてできる立体の体積を求めなさい。
筆算したら負けですよ🤗慶應女子

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#高校入試過去問(数学)#慶應義塾女子高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
$\displaystyle \frac{86^2-2\times86\times77+77^2}{15^2}+\displaystyle \frac{15^2+2\times15\times13+13^2}{35^2}$
出典:慶應義塾女子
この動画を見る
$\displaystyle \frac{86^2-2\times86\times77+77^2}{15^2}+\displaystyle \frac{15^2+2\times15\times13+13^2}{35^2}$
出典:慶應義塾女子
普通に計算したら面白くないですよ

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\{3^3\div(-7)^3\}\times\{7^2\div(-3)^2\}+(\displaystyle \frac{7}{3}-\displaystyle \frac{3}{7})\div(\displaystyle \frac{3}{7}-\displaystyle \frac{7}{3})$
出典:都立両国高校
この動画を見る
$\{3^3\div(-7)^3\}\times\{7^2\div(-3)^2\}+(\displaystyle \frac{7}{3}-\displaystyle \frac{3}{7})\div(\displaystyle \frac{3}{7}-\displaystyle \frac{7}{3})$
出典:都立両国高校
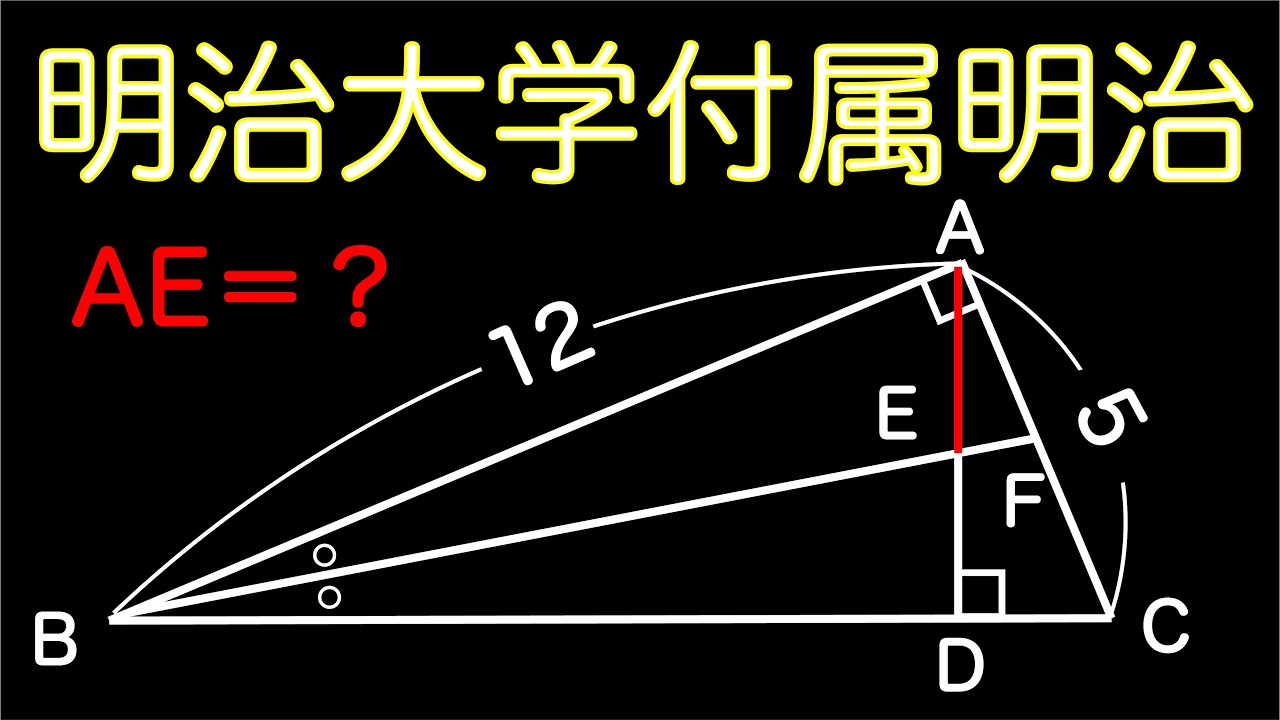
2012明大明治の問題!
単元:
#数学(中学生)#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図を参照し、AEの長さを求めよ。
出典:2012年明治大学付属明治高等学校
この動画を見る
動画内の図を参照し、AEの長さを求めよ。
出典:2012年明治大学付属明治高等学校
【高校受験対策】数学-関数44

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数44
Q
右の図で、点Oは原点であり、放物線①は関数$y=x^2$のグラフ で、直線②は関数$y=x-1$のグラフである。
点Aは直線②上の点で、その$x$座標は$-2$であり、点Pは放物線①上の点で、その$x$座標は正の数である。
点Pを通り$y$軸に平行な直線をひき、直線②との交点をQとする。
また、点Aを通り$x$軸に平行な直線をひき、直線PQとの 交点をRとする。
これについて、次の(1)、(2)の問いに答えよ。
(1)関数$y=x^2$で、$x$の変域が$-1 \leqq x \leqq 3$のとき、$y$の変域を求めよ。
(2)線分PQの長さと、線分QRの長さが等しになるとき、点Pの$x$座標はいくつか求めよ。
この動画を見る
高校受験対策・関数44
Q
右の図で、点Oは原点であり、放物線①は関数$y=x^2$のグラフ で、直線②は関数$y=x-1$のグラフである。
点Aは直線②上の点で、その$x$座標は$-2$であり、点Pは放物線①上の点で、その$x$座標は正の数である。
点Pを通り$y$軸に平行な直線をひき、直線②との交点をQとする。
また、点Aを通り$x$軸に平行な直線をひき、直線PQとの 交点をRとする。
これについて、次の(1)、(2)の問いに答えよ。
(1)関数$y=x^2$で、$x$の変域が$-1 \leqq x \leqq 3$のとき、$y$の変域を求めよ。
(2)線分PQの長さと、線分QRの長さが等しになるとき、点Pの$x$座標はいくつか求めよ。
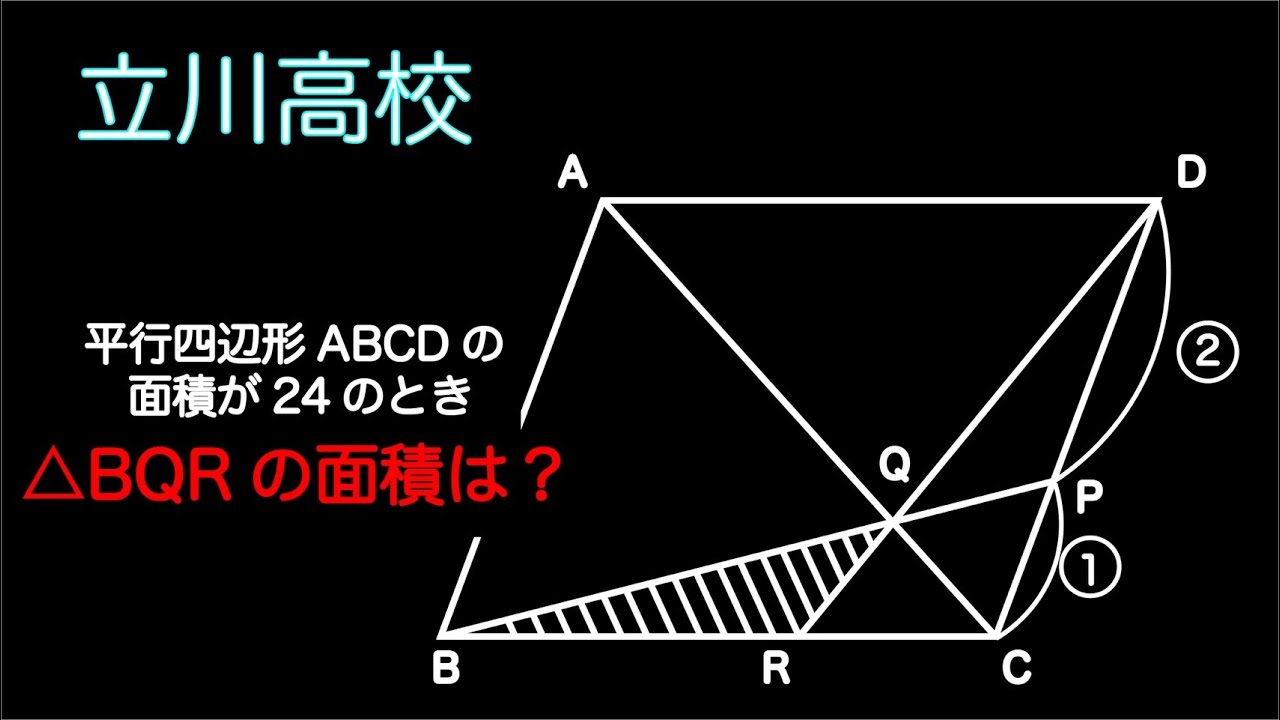
面積比!!
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#東京都立立川高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図の斜線部分の面積を求めよ
出典:2004年都立立川高校
この動画を見る
動画内の図の斜線部分の面積を求めよ
出典:2004年都立立川高校
【高校受験対策】数学-図形31

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形31
Q.
下の図のように、AB=6cm、 BC=8cm、CA=3cm、BE=12cmの三角柱ABC-DEFがある。
点Pは、点Bを出発して辺BE上を毎秒1cmの速さで動き、点で停止する。
点Qは、点Cを出 発して辺CF上を毎秒2cmの速さで動き、点Fで折り返して点Cに戻ったところで停止する。
2点P、Qが同時に出発し、出発してからの時間を$x$秒$(0 \leqq x \leqq 12)$とする。
このことについて、次の問いに答えなさい。
①$0 \leqq x \leqq 6$のとき、四角形PBCQの面積を$x$を使って表せ。
②$6 \leqq x \leqq 12$のとき、四角形PBCQの面積を$x$を使って表せ。
③線分PQが長方形BCFEの面積を2等分するときの$x$の値をすべて求めよ。
④三角DPQがDP=DQの二等辺三角形となるとき、線分PQの長さを求めよ。
この動画を見る
高校受験対策・図形31
Q.
下の図のように、AB=6cm、 BC=8cm、CA=3cm、BE=12cmの三角柱ABC-DEFがある。
点Pは、点Bを出発して辺BE上を毎秒1cmの速さで動き、点で停止する。
点Qは、点Cを出 発して辺CF上を毎秒2cmの速さで動き、点Fで折り返して点Cに戻ったところで停止する。
2点P、Qが同時に出発し、出発してからの時間を$x$秒$(0 \leqq x \leqq 12)$とする。
このことについて、次の問いに答えなさい。
①$0 \leqq x \leqq 6$のとき、四角形PBCQの面積を$x$を使って表せ。
②$6 \leqq x \leqq 12$のとき、四角形PBCQの面積を$x$を使って表せ。
③線分PQが長方形BCFEの面積を2等分するときの$x$の値をすべて求めよ。
④三角DPQがDP=DQの二等辺三角形となるとき、線分PQの長さを求めよ。
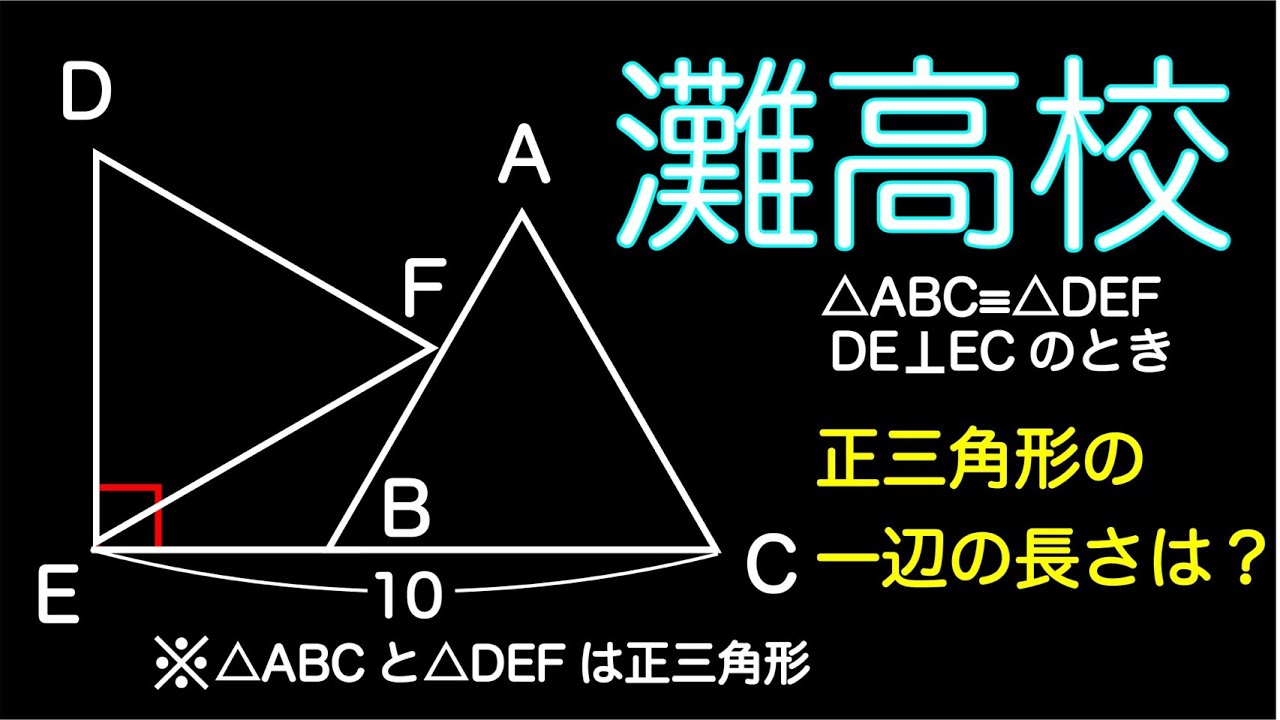
灘高校の小問 その3
単元:
#数学(中学生)#中2数学#平行と合同#高校入試過去問(数学)#灘高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
$\triangle \textrm{ABC} \equiv \triangle \textrm{FDE}$
正三角形の一辺の長さは?
この動画を見る
$\triangle \textrm{ABC} \equiv \triangle \textrm{FDE}$
正三角形の一辺の長さは?
【高校受験対策】数学-死守47

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守47
①$2-9-(-4)$を計算せよ。
➁$\frac{7x+2}{3}+x-3$を計算せよ。
③$8a \div(-4a^2b)\times ab^2$を計算せよ。
④$4\sqrt{3} \div \sqrt{2}+\sqrt{54}$を計算せよ。
⑤$\frac{9}{2}\lt \sqrt{n} \lt 5$となるような自然数$n$の個数を求めよ。
⑥$y$は$x$に反比例し、$x=-3$のとき$y=8$である。
$x=6$のときの$y$の値を求めよ。
⑦面積が$15 cm^2$の三角の底辺の長さを$a$cm、高さを$b$cmとする。
このとき、$b$を$a$の式で表せ。
⑧2次方程式$x^2-ax-12=0$の解の1つが2のとき、$a$の値ともう1つの 解を求めよ。
⑨関数$y=x^2$について、$x$の変域が$a \leqq x \leqq 2$のとき、$y$の変域は$0 \leqq y \leqq 9$である。
このときの$a$の値を求めよ。
⑩ある中学校の3年生70人について、夏休みに読み終えた本の冊数を調べた。
この3年生70人が読み終えた本の冊数の中央値は6.5冊であった。
この結果から必ずいえることについて通べた文として正しいものを、次のア~エから1つ選なさい。
ア 3年生70人が読み終えた本の冊数の平均は、6.5冊である。
イ 3年生70人が読み終えた本の冊数を多い順に並べたとき、多いほうから数えて35番目と36番目の冊数の平均は、6.5冊である。
ウ 3年生70人が読み終えた本の冊数のうち、最も多い冊数と最も少ない冊数の平均は6.5冊である。
エ 3年生70人が読み終えた本の冊数を度数分布表に整理すると、 6.5冊を含む階級の度数が最も多い。
この動画を見る
高校受験対策・死守47
①$2-9-(-4)$を計算せよ。
➁$\frac{7x+2}{3}+x-3$を計算せよ。
③$8a \div(-4a^2b)\times ab^2$を計算せよ。
④$4\sqrt{3} \div \sqrt{2}+\sqrt{54}$を計算せよ。
⑤$\frac{9}{2}\lt \sqrt{n} \lt 5$となるような自然数$n$の個数を求めよ。
⑥$y$は$x$に反比例し、$x=-3$のとき$y=8$である。
$x=6$のときの$y$の値を求めよ。
⑦面積が$15 cm^2$の三角の底辺の長さを$a$cm、高さを$b$cmとする。
このとき、$b$を$a$の式で表せ。
⑧2次方程式$x^2-ax-12=0$の解の1つが2のとき、$a$の値ともう1つの 解を求めよ。
⑨関数$y=x^2$について、$x$の変域が$a \leqq x \leqq 2$のとき、$y$の変域は$0 \leqq y \leqq 9$である。
このときの$a$の値を求めよ。
⑩ある中学校の3年生70人について、夏休みに読み終えた本の冊数を調べた。
この3年生70人が読み終えた本の冊数の中央値は6.5冊であった。
この結果から必ずいえることについて通べた文として正しいものを、次のア~エから1つ選なさい。
ア 3年生70人が読み終えた本の冊数の平均は、6.5冊である。
イ 3年生70人が読み終えた本の冊数を多い順に並べたとき、多いほうから数えて35番目と36番目の冊数の平均は、6.5冊である。
ウ 3年生70人が読み終えた本の冊数のうち、最も多い冊数と最も少ない冊数の平均は6.5冊である。
エ 3年生70人が読み終えた本の冊数を度数分布表に整理すると、 6.5冊を含む階級の度数が最も多い。
【高校受験対策】数学-死守46

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守46
①$4-3 \times (-1)$を計算せよ。
➁$(\frac{3}{4}-2)\div\frac{5}{6}$を計算せよ。
③$3a^2b \times 4ab \div (-2b)$を計算せよ。
④$\sqrt{12}+\sqrt{3}(\sqrt{3}-6)$を計算せよ。
⑤$2x^2-20x+50$を因数分解せよ。
⑥2次方程式$(x-2)(x+4)-6$を解け。
⑦$a$個のりんごを10人の生徒に$b$個ずつ配ったら、5個余った。
この数量の関係を等式で表せ。
⑧のア~エの関数のうち、そのグラフが点$(-2,1)$を通っているものはどれか。
正しいものを2つ選んでその記号を書け。
ア $y=2x$
イ $y=-\frac{2}{x}$
ウ $y=x-3$
エ $y=\frac{1}{4}x^2$
⑨右の図のような、線分$AB$を直径とする半円$o$が ある。
$\stackrel{\huge\frown}{AB}$上に2点、$A,B$と異なる点$C$をとる。
$\stackrel{\huge\frown}{AC}$上に$\stackrel{\huge\frown}{AD}$=$\stackrel{\huge\frown}{DC}$となるように点$D$をとり、 点$D$と点$A$、点$D$と点$C$をそれぞれ結ぶ。
$\angle ABD=35°$のとき、$\angle BAC$の大きさは何度か。
➉右の図のような直方体があり、$AB=BC$である。
点$A$と点$F$、点$B$と、点$D$をそれぞれ 結ぶ。
$AF=3cm$、$BD=2cm$であるとき、この直方体の体積が何$cm^3$か求めよ。
この動画を見る
高校受験対策・死守46
①$4-3 \times (-1)$を計算せよ。
➁$(\frac{3}{4}-2)\div\frac{5}{6}$を計算せよ。
③$3a^2b \times 4ab \div (-2b)$を計算せよ。
④$\sqrt{12}+\sqrt{3}(\sqrt{3}-6)$を計算せよ。
⑤$2x^2-20x+50$を因数分解せよ。
⑥2次方程式$(x-2)(x+4)-6$を解け。
⑦$a$個のりんごを10人の生徒に$b$個ずつ配ったら、5個余った。
この数量の関係を等式で表せ。
⑧のア~エの関数のうち、そのグラフが点$(-2,1)$を通っているものはどれか。
正しいものを2つ選んでその記号を書け。
ア $y=2x$
イ $y=-\frac{2}{x}$
ウ $y=x-3$
エ $y=\frac{1}{4}x^2$
⑨右の図のような、線分$AB$を直径とする半円$o$が ある。
$\stackrel{\huge\frown}{AB}$上に2点、$A,B$と異なる点$C$をとる。
$\stackrel{\huge\frown}{AC}$上に$\stackrel{\huge\frown}{AD}$=$\stackrel{\huge\frown}{DC}$となるように点$D$をとり、 点$D$と点$A$、点$D$と点$C$をそれぞれ結ぶ。
$\angle ABD=35°$のとき、$\angle BAC$の大きさは何度か。
➉右の図のような直方体があり、$AB=BC$である。
点$A$と点$F$、点$B$と、点$D$をそれぞれ 結ぶ。
$AF=3cm$、$BD=2cm$であるとき、この直方体の体積が何$cm^3$か求めよ。
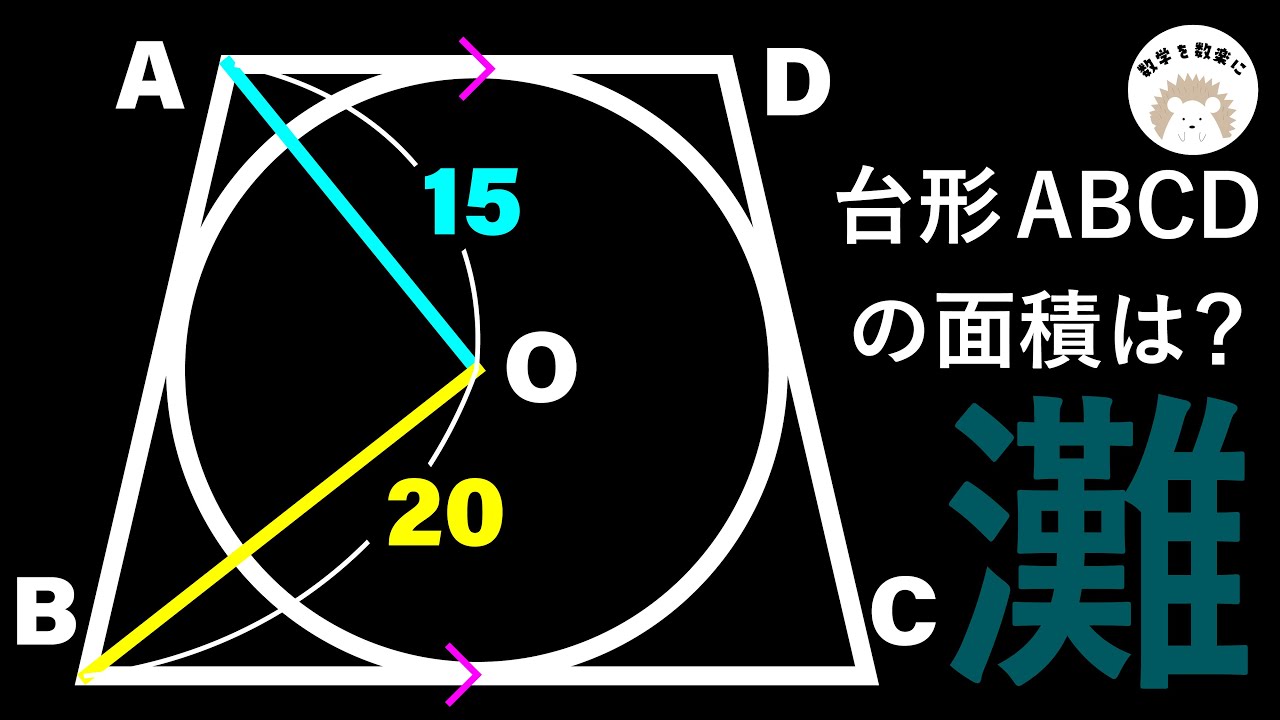
円と台形 灘高校の小問
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#灘高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
円と台形からできる相似
台形$\textrm{ABCD}$の面積を求めよ。
出典:2012年灘高等学校
この動画を見る
円と台形からできる相似
台形$\textrm{ABCD}$の面積を求めよ。
出典:2012年灘高等学校
直角三角形と内接円の問題
単元:
#数学(中学生)#中3数学#円#三平方の定理#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
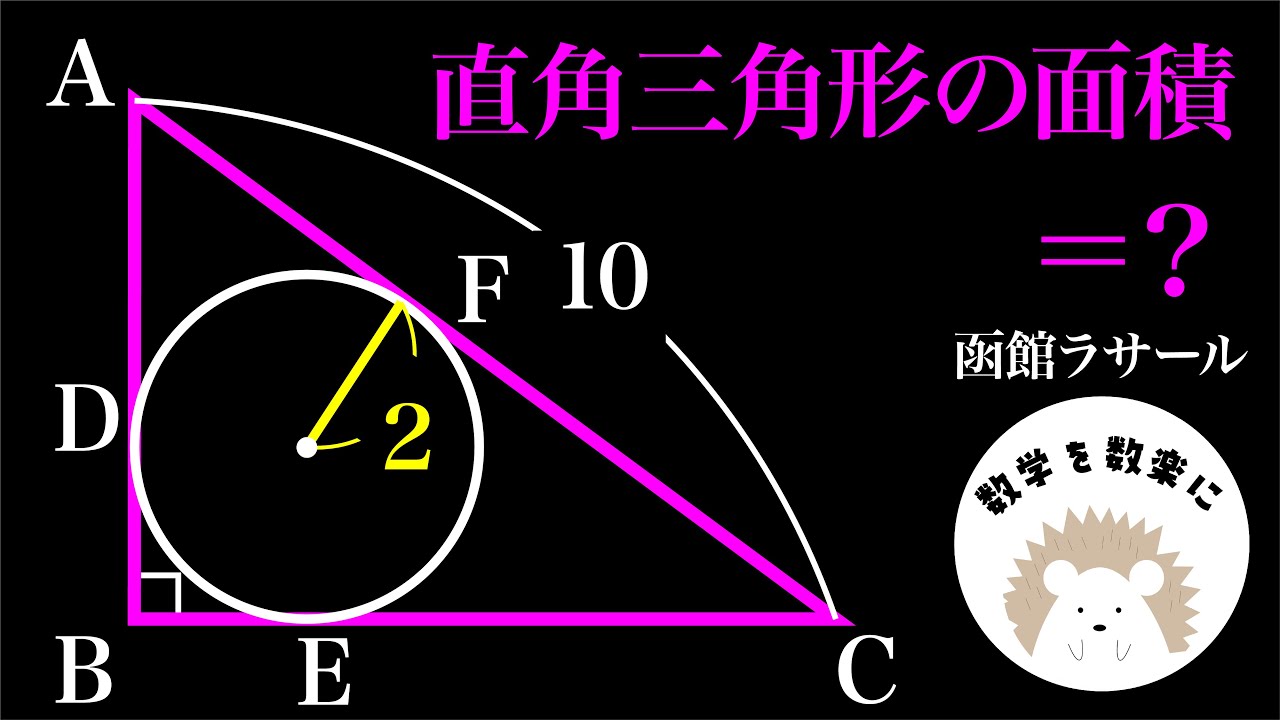
動画内の図を参照し、直角三角形ABCの面積を求めよ。
出典:2017年函館ラサール
この動画を見る
動画内の図を参照し、直角三角形ABCの面積を求めよ。
出典:2017年函館ラサール
角の二等分線+平行、垂直=?
単元:
#数学(中学生)#中2数学#平行と合同#三角形と四角形#高校入試過去問(数学)#江戸川学園取手高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
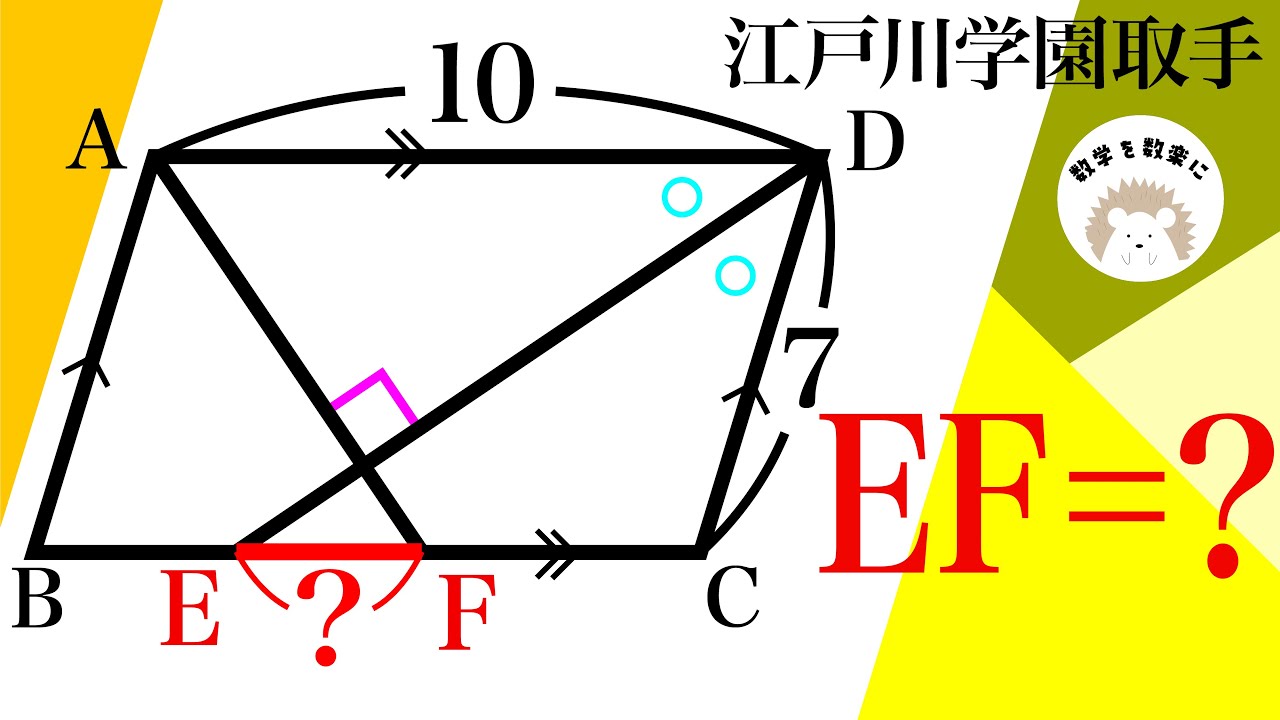
動画内の図を参照し、$\textrm{EF}$の長さを求めよ。
出典:2017年江戸川学園取手
この動画を見る
動画内の図を参照し、$\textrm{EF}$の長さを求めよ。
出典:2017年江戸川学園取手
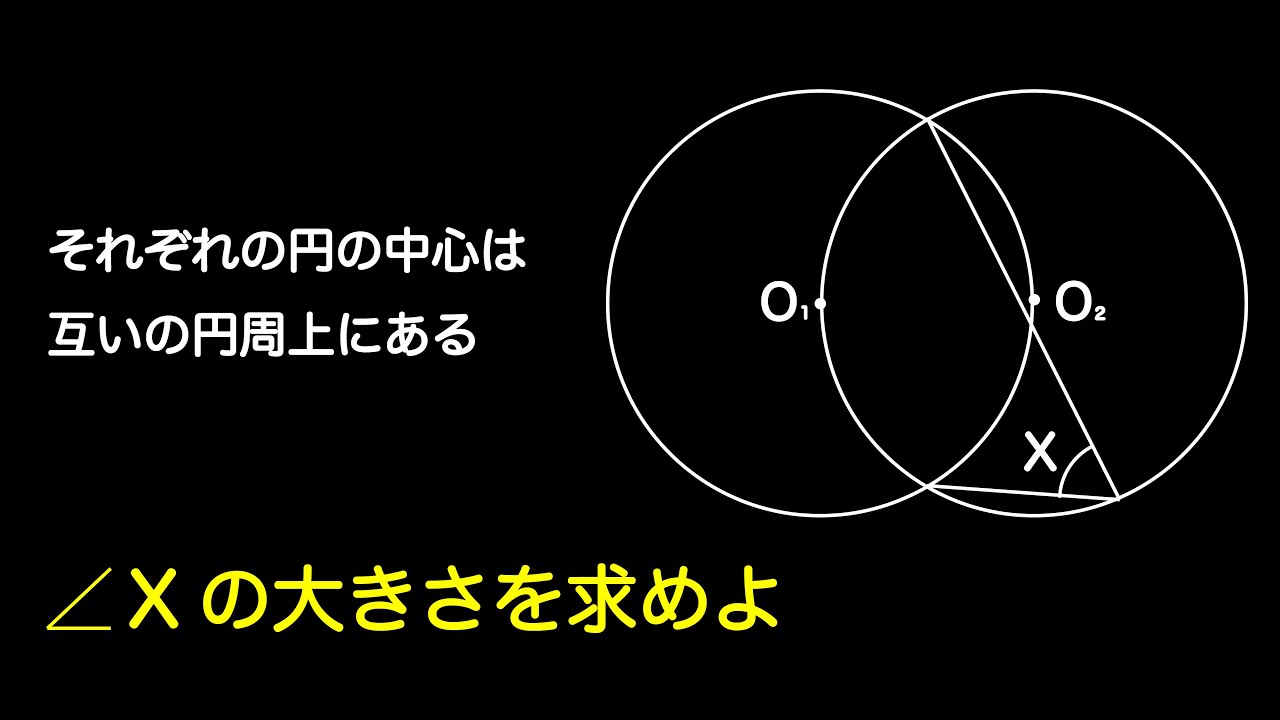
円周角と中心角の問題(高校受験数学)
約束記号(高校受験数学)

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$a☆b=2ab-a-b$のとき方程式$x☆(x-2)=0$を解け。
出典:2017年智辯学園和歌山高等学校 受験数学
この動画を見る
$a☆b=2ab-a-b$のとき方程式$x☆(x-2)=0$を解け。
出典:2017年智辯学園和歌山高等学校 受験数学
三平方の定理のポイントをまとめてみました。

単元:
#数学(中学生)#三平方の定理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
冬休み前に三平方の定理を習わなかった方は
過去問などを始める前に、この動画でポイントを押さえてください。
この動画を見る
冬休み前に三平方の定理を習わなかった方は
過去問などを始める前に、この動画でポイントを押さえてください。
3直線で三角形ができない時の条件とは?

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
数学を数楽に
問題文全文(内容文):
直線$y=x,y=3x,y=ax+(a+2)$がある。
3つの直線で三角形ができないとき$a=?$
この動画を見る
直線$y=x,y=3x,y=ax+(a+2)$がある。
3つの直線で三角形ができないとき$a=?$
日比谷高校の計算問題(2003)

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#東京都立日比谷高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
$(\displaystyle \frac{\sqrt{ 6 }+\sqrt{ 5 }}{\sqrt{ 2 }})^2-(\sqrt{ 6 }+\sqrt{ 5 })(\sqrt{ 6 }-\sqrt{ 5 })+(\displaystyle \frac{\sqrt{ 6 }-\sqrt{ 5 }}{\sqrt{ 2 }})^2$
出典:2003年東京都立日比谷高等学校
この動画を見る
$(\displaystyle \frac{\sqrt{ 6 }+\sqrt{ 5 }}{\sqrt{ 2 }})^2-(\sqrt{ 6 }+\sqrt{ 5 })(\sqrt{ 6 }-\sqrt{ 5 })+(\displaystyle \frac{\sqrt{ 6 }-\sqrt{ 5 }}{\sqrt{ 2 }})^2$
出典:2003年東京都立日比谷高等学校
【高校受験対策】数学-図形30

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形30
Q
図1のように、$AB=AC$である二等辺三角形$ABC$があります。
次の各問いに答えなさい。
①
図2のように、$AB=9$、$BC=6$のとき、辺$AB$上に$BE=3$となるとなる点$E$をとり、
辺$BC$上に$\angle BAC=\angle BDE$となる点$D$をとります。
このとき線分$BD$の長さを求めなさい。
②辺$BC$に平行な直線と辺$AB$、$AC$の交点を$F$、$G$とするとき、 $△AFG$の面積が$△ABC$の面積の半分になるような点$F$および点$G$を、コンパスと定規を使って作図しなさい。
ただし作図に使った線は消さないこと。
この動画を見る
高校受験対策・図形30
Q
図1のように、$AB=AC$である二等辺三角形$ABC$があります。
次の各問いに答えなさい。
①
図2のように、$AB=9$、$BC=6$のとき、辺$AB$上に$BE=3$となるとなる点$E$をとり、
辺$BC$上に$\angle BAC=\angle BDE$となる点$D$をとります。
このとき線分$BD$の長さを求めなさい。
②辺$BC$に平行な直線と辺$AB$、$AC$の交点を$F$、$G$とするとき、 $△AFG$の面積が$△ABC$の面積の半分になるような点$F$および点$G$を、コンパスと定規を使って作図しなさい。
ただし作図に使った線は消さないこと。
傾きの範囲(応用)

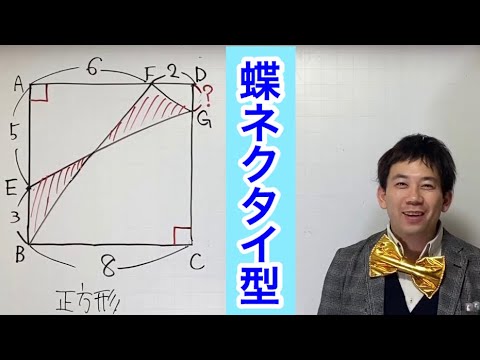
蝶ネクタイの左と右が等しいとき