 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
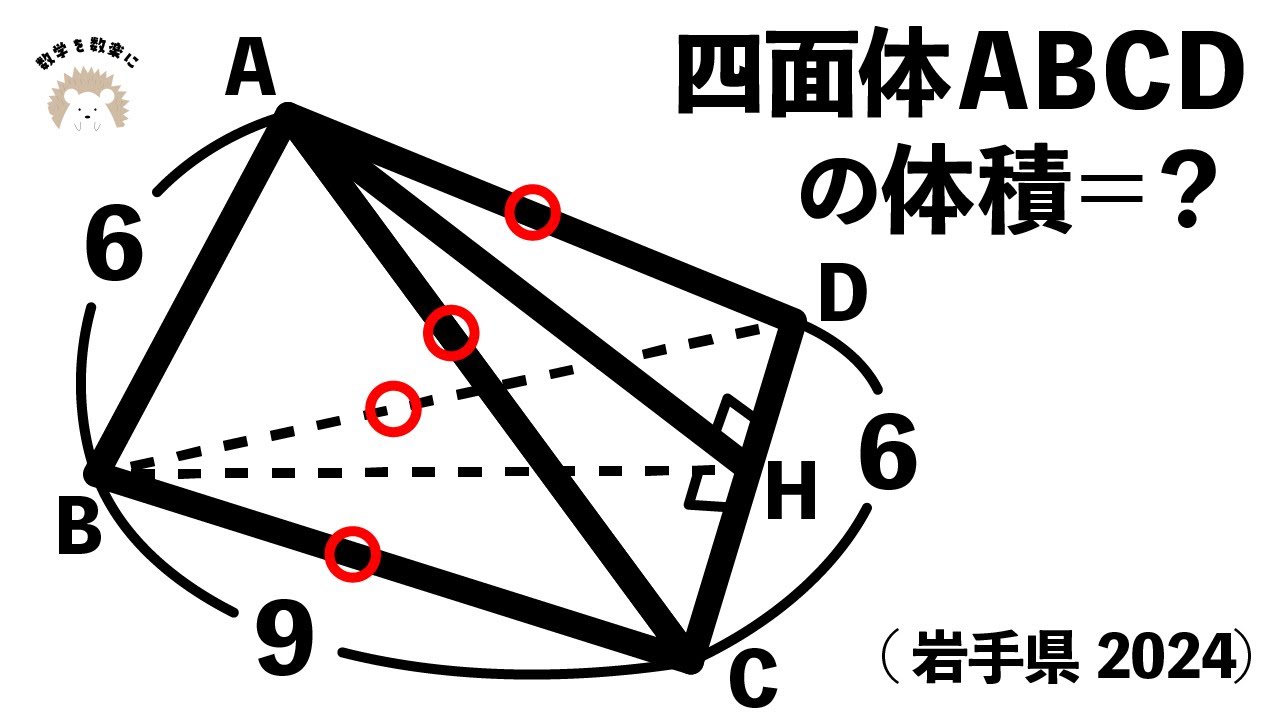
2024年岩手県のラスボス 四面体の体積
【ほら、例の方法が…!】計算:東京都立青山高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#東京都立青山高等学校
指導講師:
問題文全文(内容文):
$11^2-33^2-44^2+55^2を計算せよ。$
この動画を見る
$11^2-33^2-44^2+55^2を計算せよ。$
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 放物線と直線の交点の距離

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の放物線と直線は異なる2点で交わる。その交点をそれぞれA, Bとするとき、線分ABの長さを求めなさい。
(1)$y=x^2$, $y=x+2$
(2)$y=-\displaystyle \frac{x^2}{2}$, $y=-x-4$
この動画を見る
次の放物線と直線は異なる2点で交わる。その交点をそれぞれA, Bとするとき、線分ABの長さを求めなさい。
(1)$y=x^2$, $y=x+2$
(2)$y=-\displaystyle \frac{x^2}{2}$, $y=-x-4$
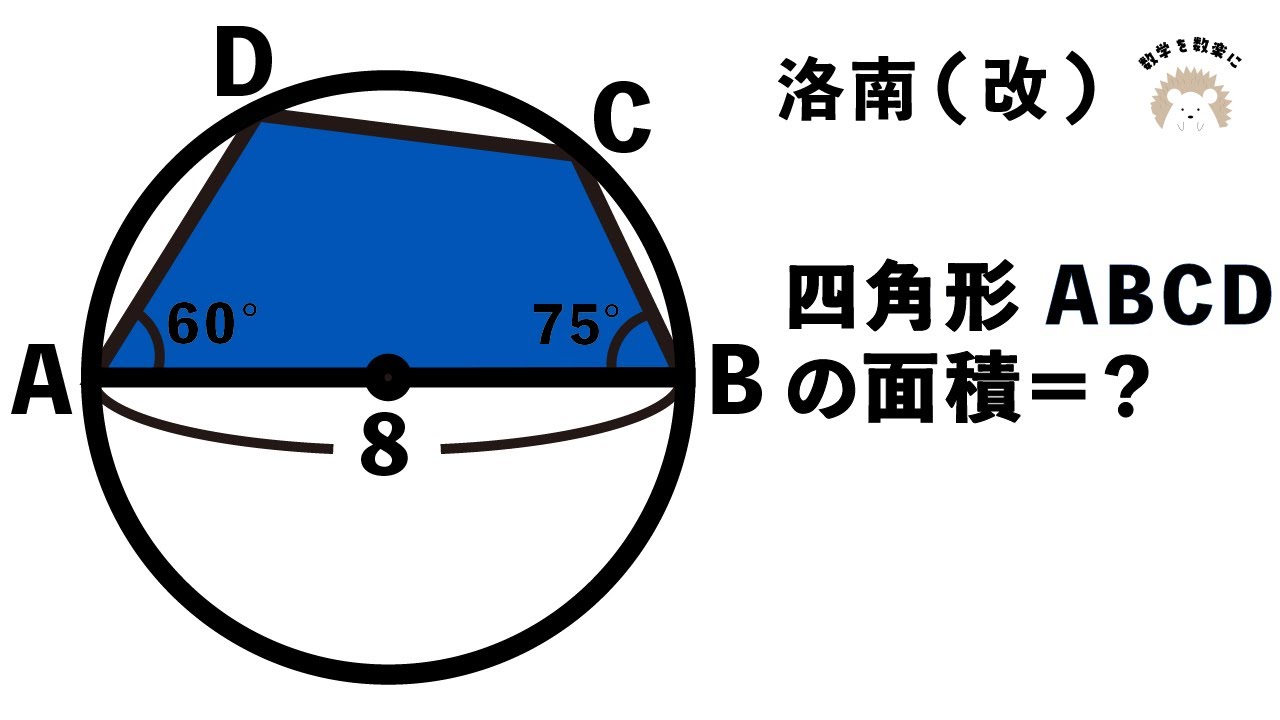
四角形の面積を求めよ!
斜めの正方形

実は半分しか入ってないって信じれる?

単元:
#数学(中学生)#中3数学#相似な図形#その他#その他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
実は半分しか入ってないって信じれる?
※問題は動画内参照
この動画を見る
実は半分しか入ってないって信じれる?
※問題は動画内参照
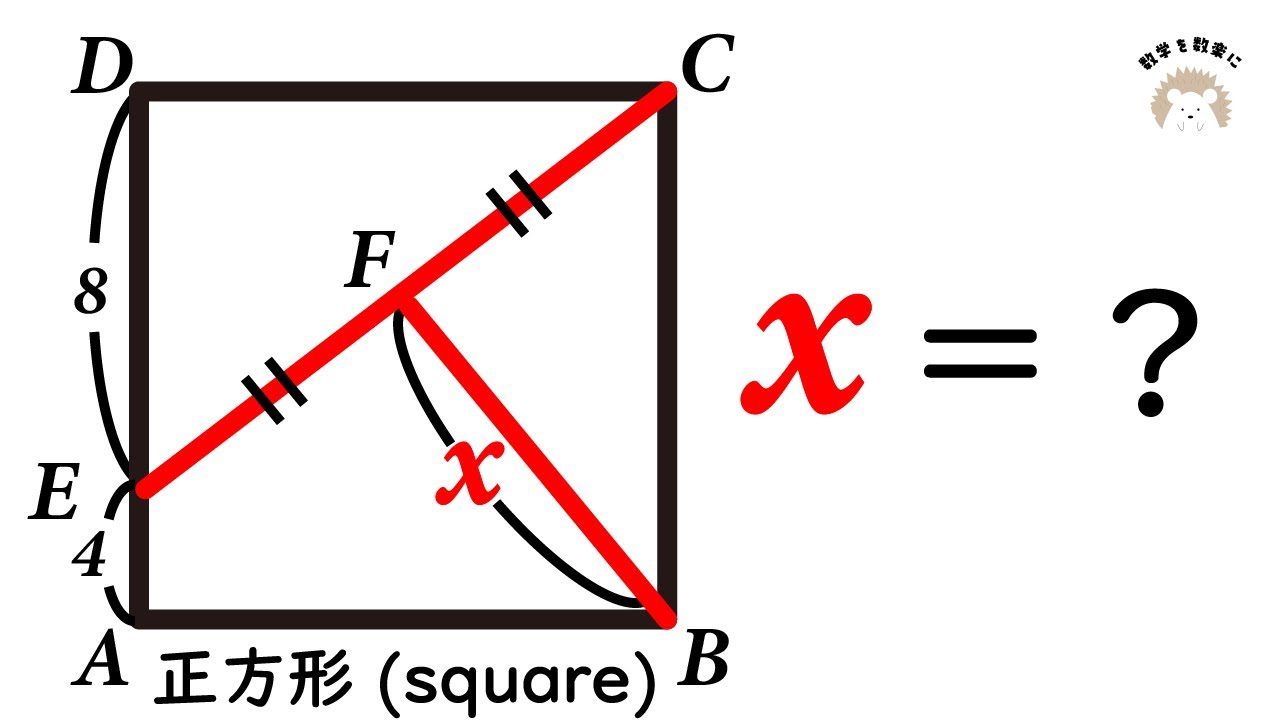
図形の問題に見えて〇〇の問題 2通りで解説 正方形
斜めの正方形

図形の問題に見えて〇〇の問題 2通りで解説 正方形

【より高度な考え方…!?】整数:桃山学院高等学校~全国入試問題解法
単元:
#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x + y + z = 9$を満たす自然数$x,y,z$の組は何通りあるか。ただし、$ z \leq x$とする。
この動画を見る
$x + y + z = 9$を満たす自然数$x,y,z$の組は何通りあるか。ただし、$ z \leq x$とする。
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 垂線の長さ

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の2点A,Bを通る直線に原点O(0,0)から引いた垂線OHの長さを求めなさい。
(1)$A(2,0)$, $B(0,6)$
(2)$A(\dfrac{25}{3},0)$, $B(0,\dfrac{25}{4})$
この動画を見る
次の2点A,Bを通る直線に原点O(0,0)から引いた垂線OHの長さを求めなさい。
(1)$A(2,0)$, $B(0,6)$
(2)$A(\dfrac{25}{3},0)$, $B(0,\dfrac{25}{4})$
二乗せよ

単元:
#数学(中学生)#中3数学#平方根
指導講師:
数学を数楽に
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^2=2+\sqrt{3} \\
b^2=2-\sqrt{3}
\end{array}
\right.
\end{eqnarray}
$
$(a\gt b\gt 0)$
のとき、
$ab=?$
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^2=2+\sqrt{3} \\
b^2=2-\sqrt{3}
\end{array}
\right.
\end{eqnarray}
$
$(a\gt b\gt 0)$
のとき、
$ab=?$
ごめんなさい

単元:
#数学(中学生)#中3数学#平方根#2次方程式#高校入試過去問(数学)#江戸川学園取手高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
a^2=2+√3
b^2=2+√3
b>a>0
abの値を求めよ
a-bの値を求めよ
この動画を見る
a^2=2+√3
b^2=2+√3
b>a>0
abの値を求めよ
a-bの値を求めよ
【中学校数学と言えば…!】図形:平安女学院高等学校~全国入試問題解法
単元:
#高校入試過去問(数学)#平安女学院高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
長さ10cmの線分ABを直径とする半円がある。弧AB上にあり$\angle ABC = 12^\circ$となるように点C、弧CBを2 : 1に分けるように点Dをとる。弧CDの長さを求めよ.
この動画を見る
長さ10cmの線分ABを直径とする半円がある。弧AB上にあり$\angle ABC = 12^\circ$となるように点C、弧CBを2 : 1に分けるように点Dをとる。弧CDの長さを求めよ.
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 長方形の回転

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
AB=4cm, BC=6cmの長方形ABCDがある。直線L上において、この長方形を右の図のように、点Bが再び直線L上にくるまですべることなく転がす。
(1)点Bの軌跡の長さを求めなさい。
(2)長方形ABCDの対角線の交点をOとするとき、点Oの軌跡の長さを求めなさい。
この動画を見る
AB=4cm, BC=6cmの長方形ABCDがある。直線L上において、この長方形を右の図のように、点Bが再び直線L上にくるまですべることなく転がす。
(1)点Bの軌跡の長さを求めなさい。
(2)長方形ABCDの対角線の交点をOとするとき、点Oの軌跡の長さを求めなさい。
factorization : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#江戸川学園取手高等学校
指導講師:
問題文全文(内容文):
$x^2-6xy+9y^2+3x-9y+2$
因数分解しなさい。
この動画を見る
$x^2-6xy+9y^2+3x-9y+2$
因数分解しなさい。
factorization : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元:
#数学(中学生)#高校入試過去問(数学)#江戸川学園取手高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x^2-6xy+9y^2+3x-9y+2$を因数分解しなさい。
この動画を見る
$x^2-6xy+9y^2+3x-9y+2$を因数分解しなさい。
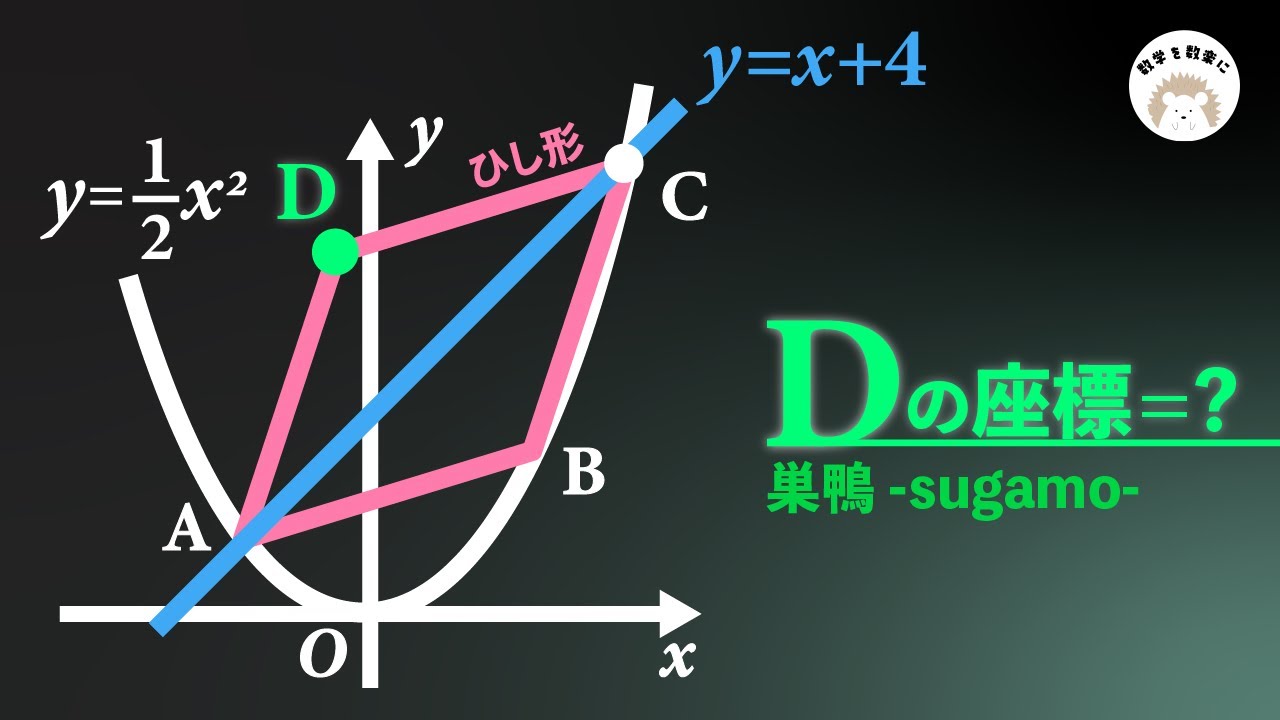
バリバリの高校入試問題 巣鴨高校 座標平面上のひし形
バリバリの高校入試問題 巣鴨高校 座標平面上のひし形

【ひるまず進め…!】文字式:東大寺学園高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#東大寺学園高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x=\frac{3+\sqrt5}{2}, y=\frac{-1+\sqrt5}{2}$のとき$x^2-xy-3$の値を求めよ。
この動画を見る
$x=\frac{3+\sqrt5}{2}, y=\frac{-1+\sqrt5}{2}$のとき$x^2-xy-3$の値を求めよ。
【ひるまず進め…!】文字式:東大寺学園高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#高校入試過去問(数学)#東大寺学園高等学校
指導講師:
問題文全文(内容文):
$x= {3+\sqrt{5}\over2} , y={-1+\sqrt{5}\over2}$ のとき
$x^2-xy-3$ の値を求めよ。
この動画を見る
$x= {3+\sqrt{5}\over2} , y={-1+\sqrt{5}\over2}$ のとき
$x^2-xy-3$ の値を求めよ。
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 直角三角形の回転

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように、AB=$1+\sqrt{3}$ cm、∠90°の直角二等辺三角形OABを、Oを中心として、時計の針の回転と同じ向きに30°だけ回転した図形を△OCDとする。AOとCDの交点をPとするとき、△PDOの面積を求めなさい。
この動画を見る
右の図のように、AB=$1+\sqrt{3}$ cm、∠90°の直角二等辺三角形OABを、Oを中心として、時計の針の回転と同じ向きに30°だけ回転した図形を△OCDとする。AOとCDの交点をPとするとき、△PDOの面積を求めなさい。
shape problems : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元:
#数学(中学生)#平面図形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
半径が1cm, 2cm, 3cmの同心円において、半径3cmの円の弦と半径1cmの円と点Rで接する。このときPQの長さを求めよ。
この動画を見る
半径が1cm, 2cm, 3cmの同心円において、半径3cmの円の弦と半径1cmの円と点Rで接する。このときPQの長さを求めよ。
三角形の重心 一点で交わるのはなぜ?

三角形の重心 一点で交わるのはなぜ?

【簡単な条件なのに…!】図形:愛知県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#愛知県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$AB=6$cm, $AC=5$cm, 辺$AB$上に$\angle DBC=\angle ACD$となるように点Dをとる。このとき、線分$AD$の長さは何cmか。
この動画を見る
$AB=6$cm, $AC=5$cm, 辺$AB$上に$\angle DBC=\angle ACD$となるように点Dをとる。このとき、線分$AD$の長さは何cmか。
内心 内角の二等分線が一点で交わるのはなぜ?
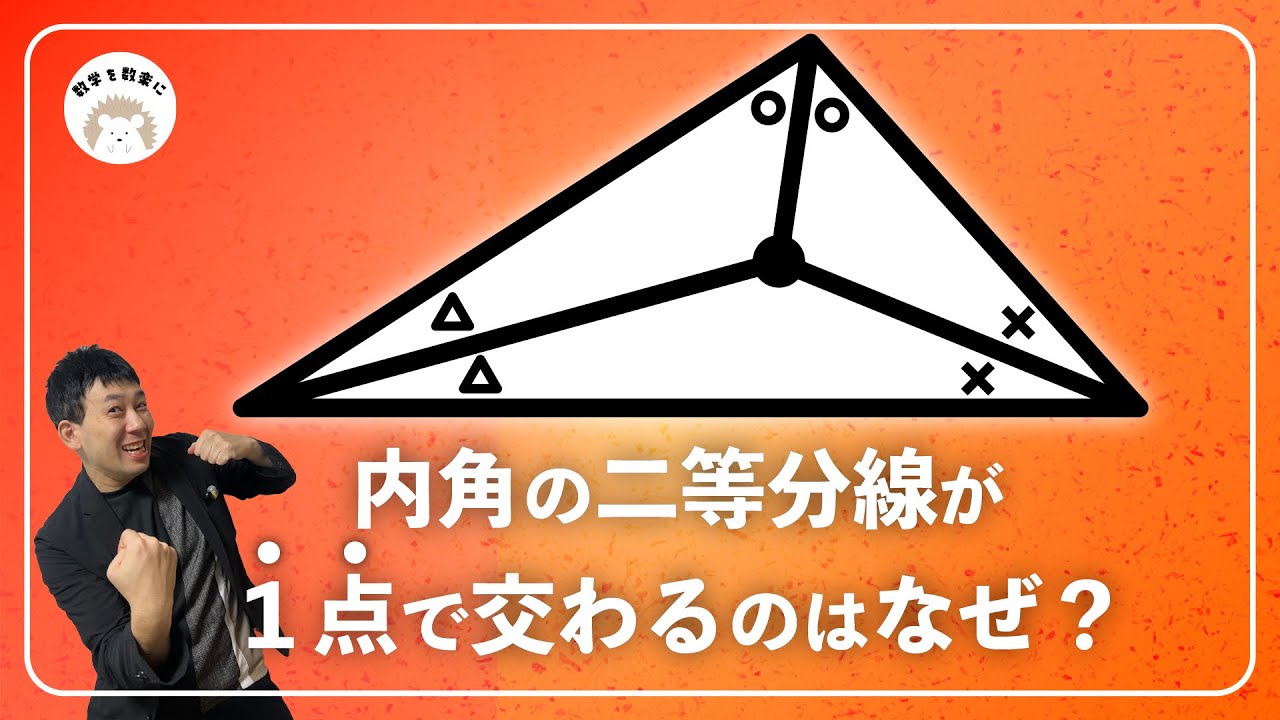
内心 内角の二等分線が一点で交わるのはなぜ?

【用語を理解して…!】文字式:鹿屋中央高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#鹿屋中央高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
3つの数$a,a+18,3a-7$の平均は$b$である。$a$を$b$の式で表せ。
この動画を見る
3つの数$a,a+18,3a-7$の平均は$b$である。$a$を$b$の式で表せ。
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 合同の利用

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図において、四角形の頂点A,B,C,DはBDを直径とする円Oの周上にあり、Eは直線BAとCDの交点で、辺DAは∠BDEを2等分している。DC=3cm、BD=6cmであるとき、辺DAの長さを求めなさい。
この動画を見る
右の図において、四角形の頂点A,B,C,DはBDを直径とする円Oの周上にあり、Eは直線BAとCDの交点で、辺DAは∠BDEを2等分している。DC=3cm、BD=6cmであるとき、辺DAの長さを求めなさい。
