 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
🎍西暦"2023"を含む入試予想問題(考察編)~全国入試問題解法
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の入試問題を導け.
$ 2023=?$
この動画を見る
次の入試問題を導け.
$ 2023=?$
知ってなきゃ解けない? 分母の有理化 開成高校 今年の反省 来年の抱負

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
分母を有理化せよ
$\frac{1}{1+\sqrt 2 + \sqrt 3}$
開成高等学校
この動画を見る
分母を有理化せよ
$\frac{1}{1+\sqrt 2 + \sqrt 3}$
開成高等学校
球が出てきただけでビビるなよ。海城高校
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
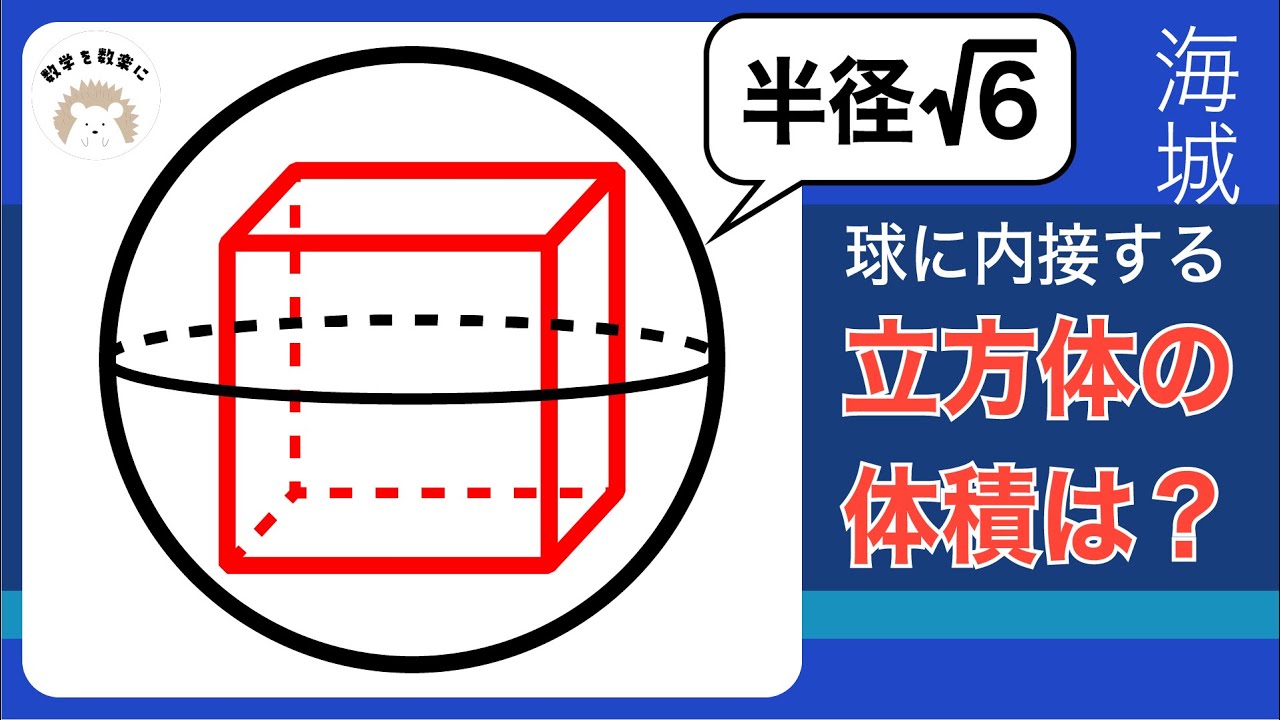
半径$\sqrt 6$の球に内接する立方体の体積=?
*図は動画内参照
海城高等学校
この動画を見る
半径$\sqrt 6$の球に内接する立方体の体積=?
*図は動画内参照
海城高等学校
【「式の形」が見えればOK!】平方根:東京都立国立高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \left(\dfrac{\sqrt5+\sqrt3}{\sqrt2}\right)^2+ \left(\dfrac{\sqrt5+\sqrt3}{\sqrt2}\right) \left(\dfrac{\sqrt5-\sqrt3}{\sqrt2}\right)-\left(\dfrac{\sqrt5-\sqrt3}{\sqrt2}\right)^2$を計算せよ.
都立国立高校過去問
この動画を見る
$ \left(\dfrac{\sqrt5+\sqrt3}{\sqrt2}\right)^2+ \left(\dfrac{\sqrt5+\sqrt3}{\sqrt2}\right) \left(\dfrac{\sqrt5-\sqrt3}{\sqrt2}\right)-\left(\dfrac{\sqrt5-\sqrt3}{\sqrt2}\right)^2$を計算せよ.
都立国立高校過去問
√の中に√入れたくないよね。式の値 巣鴨高校
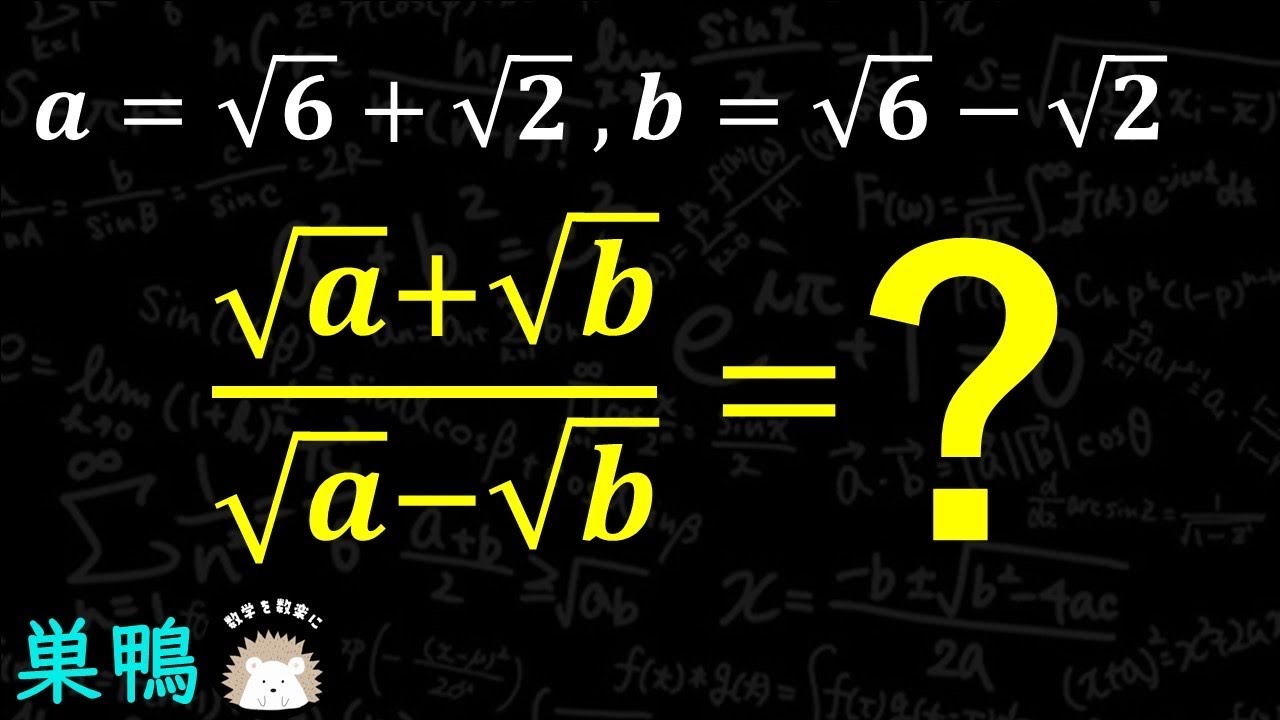
単元:
#数学(中学生)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a=\sqrt 6 +\sqrt 2,b=\sqrt 6 - \sqrt 2$
$\frac{\sqrt a +\sqrt b}{\sqrt a - \sqrt b} = ?$
巣鴨高等学校
この動画を見る
$a=\sqrt 6 +\sqrt 2,b=\sqrt 6 - \sqrt 2$
$\frac{\sqrt a +\sqrt b}{\sqrt a - \sqrt b} = ?$
巣鴨高等学校
斜線部分の面積を求めよ 洛南高校
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
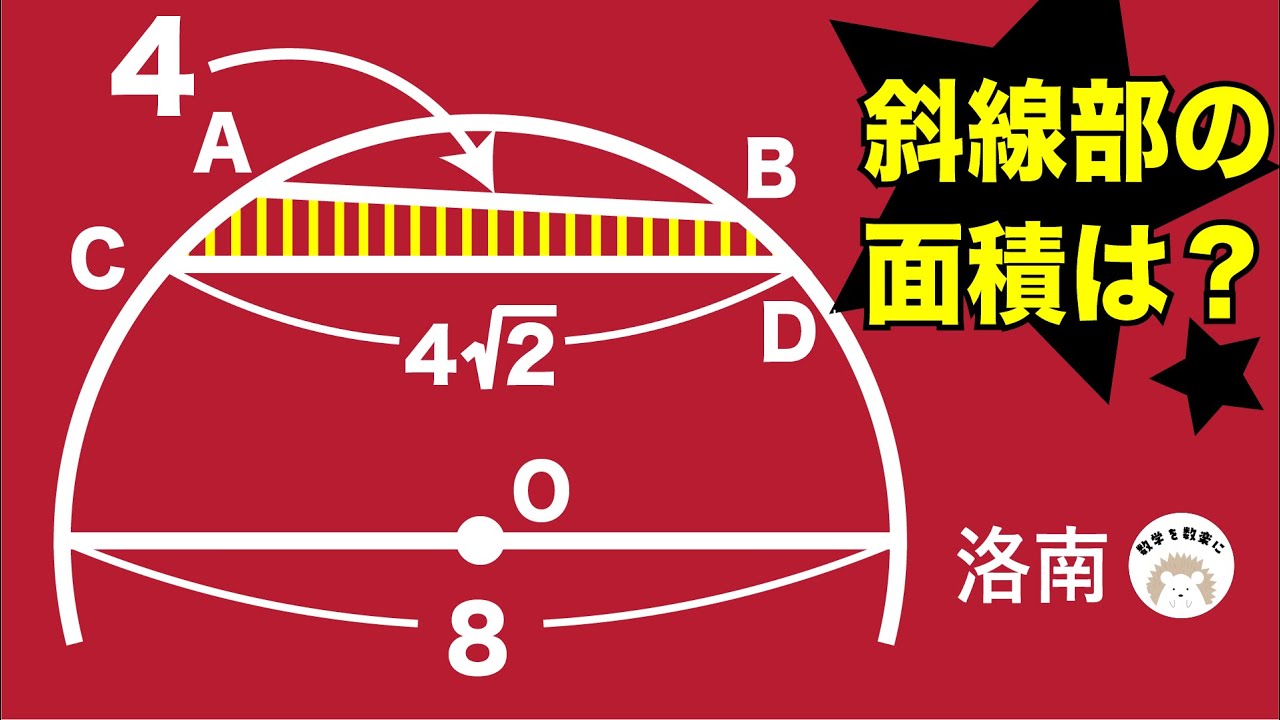
斜線部の面積を求めよ。
洛南高等学校
この動画を見る
斜線部の面積を求めよ。
洛南高等学校
【最初の2分間が全て!今年の的中問題】図形:高知県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#中2数学#平面図形#三角形と四角形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
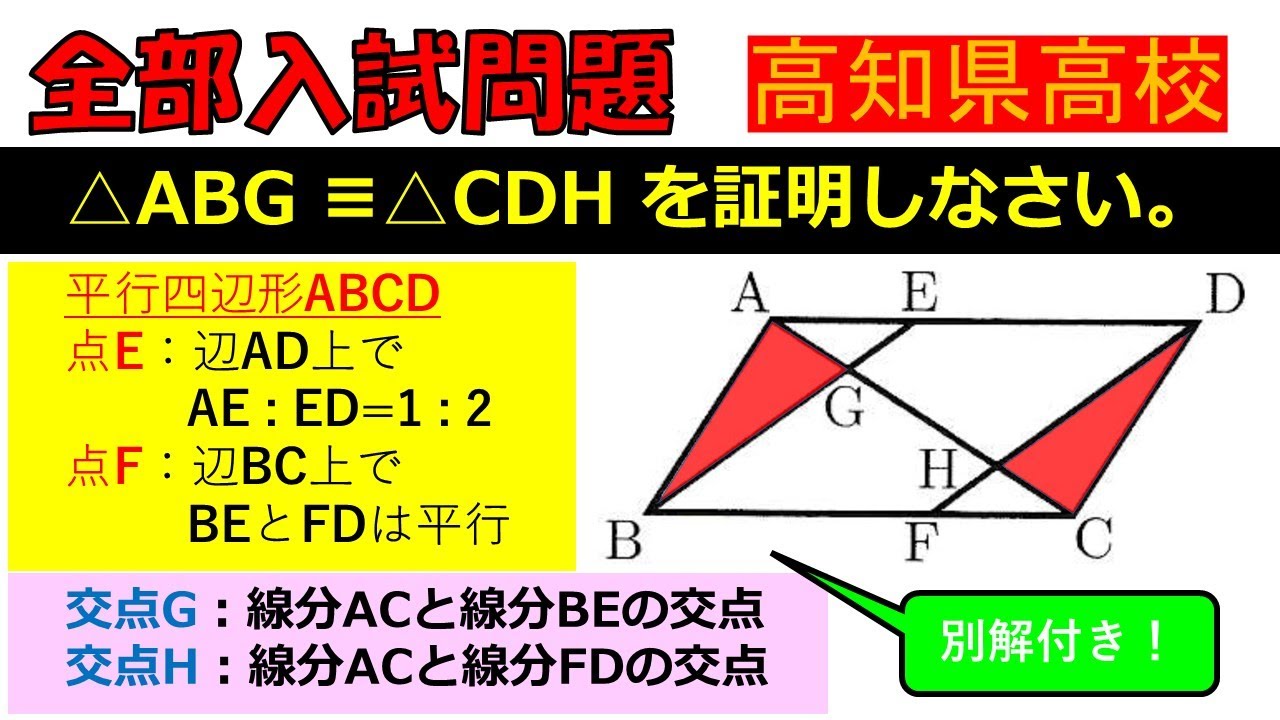
平行四辺形$ABCD$の点$E$は辺$AD$上で$AE:ED=1:2$である.
点$F$は辺$BC$上で$BE$と$FD$は平行である.
交点$G$は線分$AC$と線分$BE$の交点であり,交点$H$は線分$AC$と線分$FD$の交点である.
$ \triangle ABG \equiv CDH$を証明しなさい.
高知県高校過去問
この動画を見る
平行四辺形$ABCD$の点$E$は辺$AD$上で$AE:ED=1:2$である.
点$F$は辺$BC$上で$BE$と$FD$は平行である.
交点$G$は線分$AC$と線分$BE$の交点であり,交点$H$は線分$AC$と線分$FD$の交点である.
$ \triangle ABG \equiv CDH$を証明しなさい.
高知県高校過去問
ビビへの伏線がやばい

単元:
#算数(中学受験)#数学(中学生)#中1数学#比例・反比例#単位・比と割合・比例・反比例
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
ビビの視力ってどれくらい?
この動画を見る
下記質問の解説動画です
ビビの視力ってどれくらい?
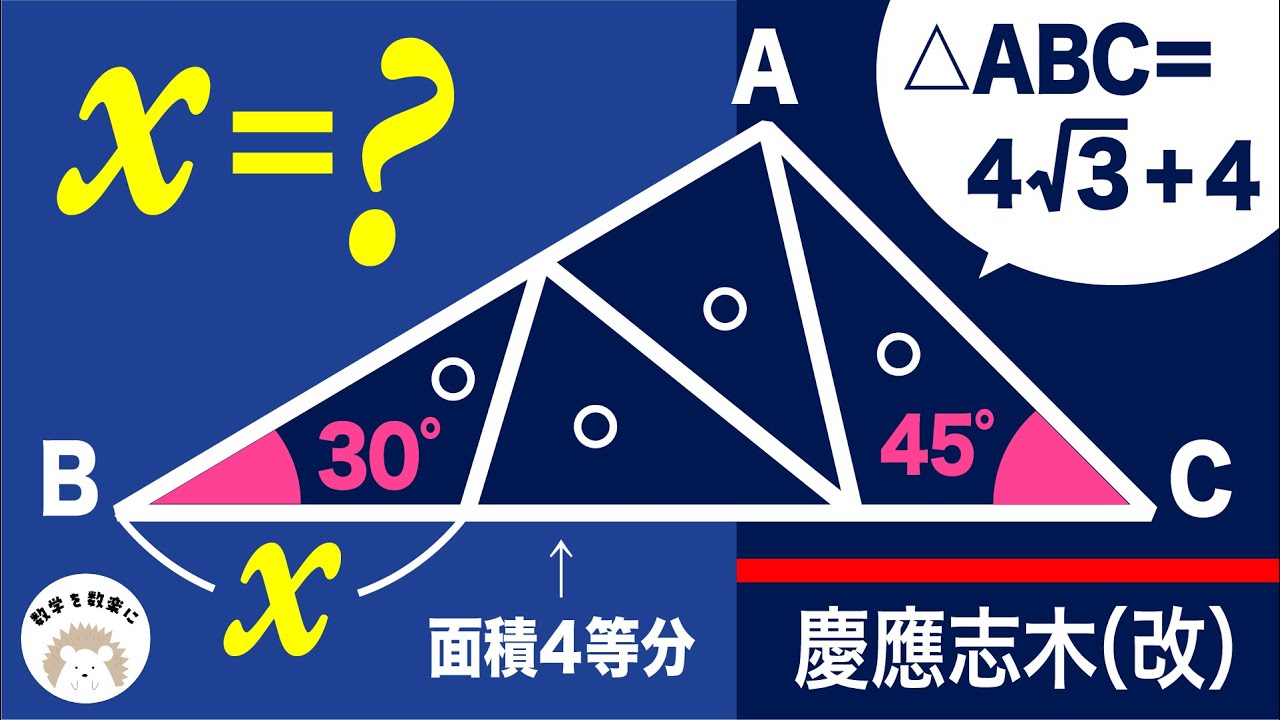
面積比やら三平方の定理やら。。良問!!慶應志木
単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
面積4等分
$△ABC=4 \sqrt 3 +4$
x=?
*図は動画内参照
慶應義塾志木高等学校(改)
この動画を見る
面積4等分
$△ABC=4 \sqrt 3 +4$
x=?
*図は動画内参照
慶應義塾志木高等学校(改)
🎄【メイン・テーマは番外編で…】二次方程式:開成高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$ 7x^2-4\sqrt2x+1=0$を考える.
2つの解を求めよ.
開成高校過去問
この動画を見る
2次方程式$ 7x^2-4\sqrt2x+1=0$を考える.
2つの解を求めよ.
開成高校過去問
式の値 灘高校
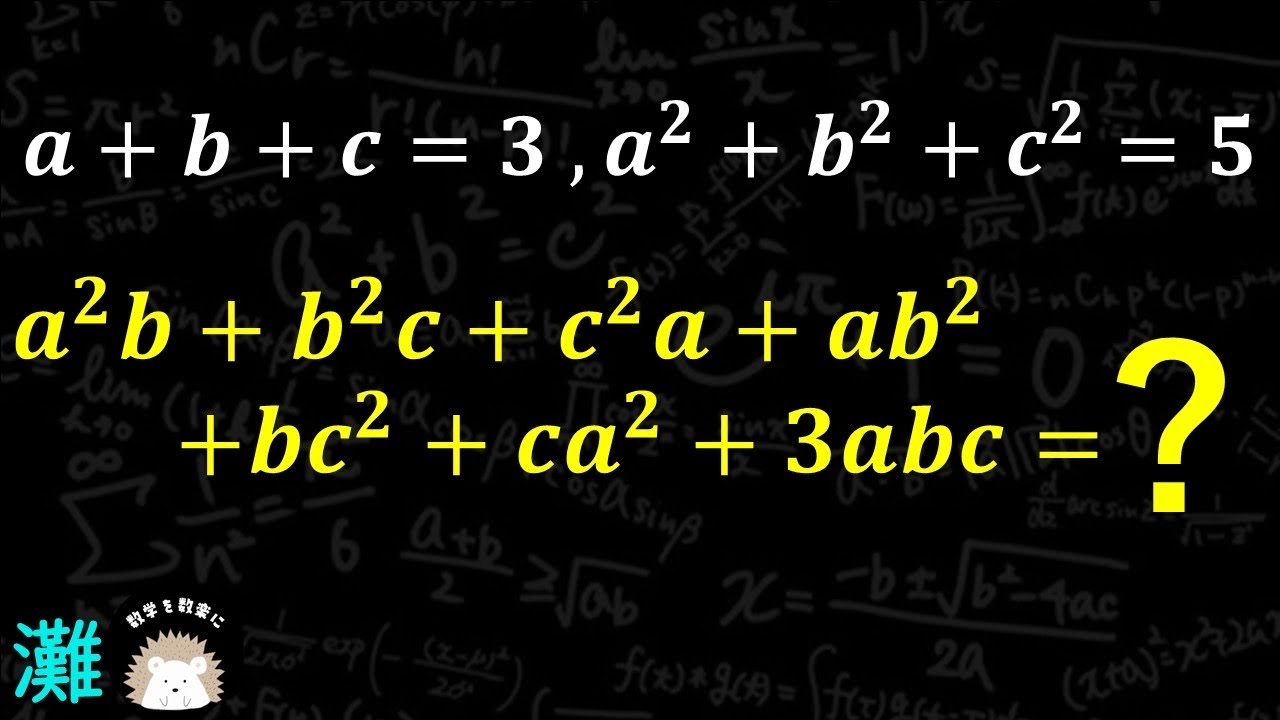
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$a+b+c=3,a^2+b^2+c^2 = 5$
$a^2+b^2c+c^2a+ab^2+bc^2+ca^2+3abc = ?$
灘高等学校
この動画を見る
$a+b+c=3,a^2+b^2+c^2 = 5$
$a^2+b^2c+c^2a+ab^2+bc^2+ca^2+3abc = ?$
灘高等学校
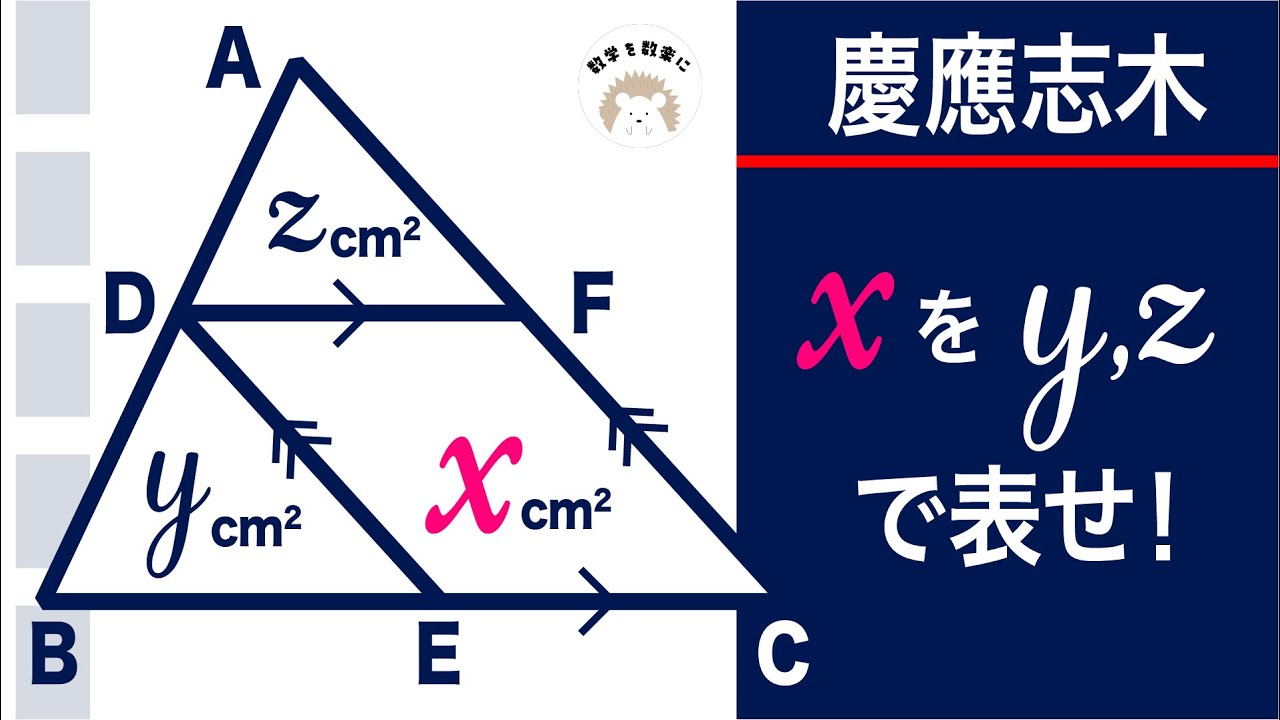
面積から辺への引越し 慶應志木
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
xをy,zで表せ
*図は動画内参照
慶應義塾志木高等学校
この動画を見る
xをy,zで表せ
*図は動画内参照
慶應義塾志木高等学校
【裏技】座標上の三角形の面積

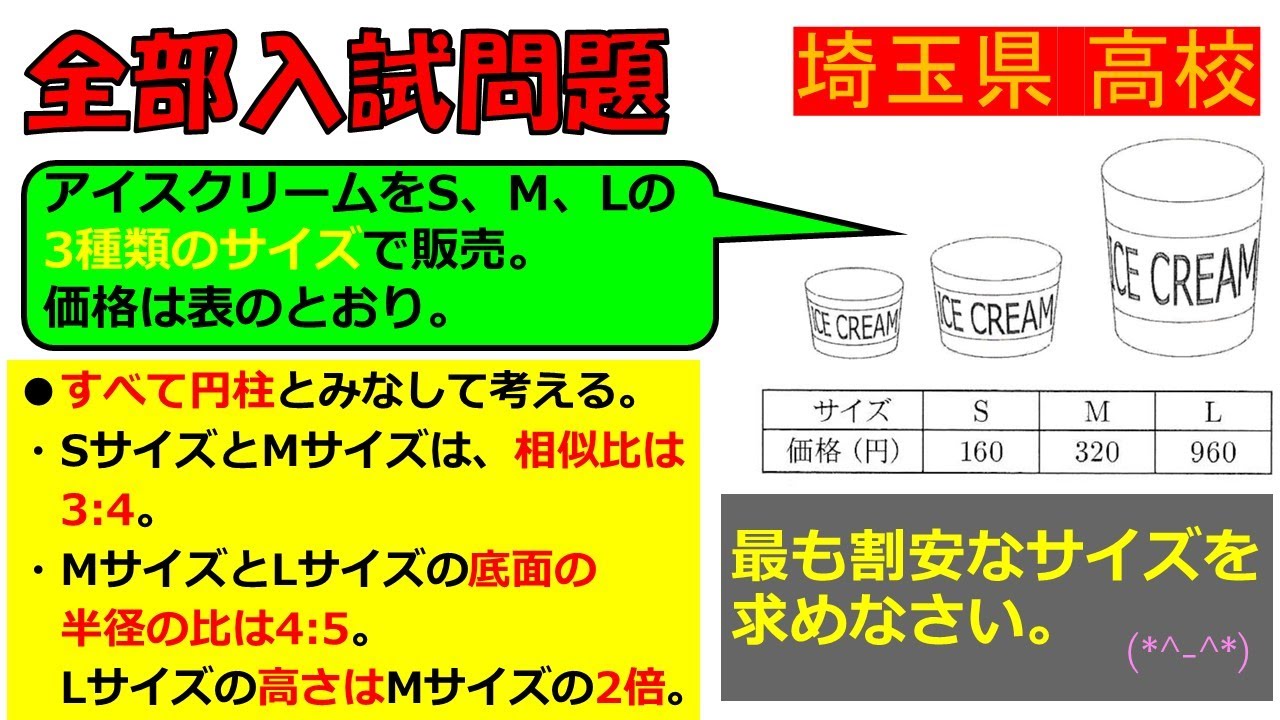
【これぞ、数学の「応用」…!】文章題:埼玉県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#比例・反比例#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
アイスクリームをS,M,Lの3種類のサイズで販売している.
最も割安なサイズを求めなさい.
埼玉県高校過去問
この動画を見る
アイスクリームをS,M,Lの3種類のサイズで販売している.
最も割安なサイズを求めなさい.
埼玉県高校過去問
【2つの解法!2分で?4分30秒で?】二次関数:宮城県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
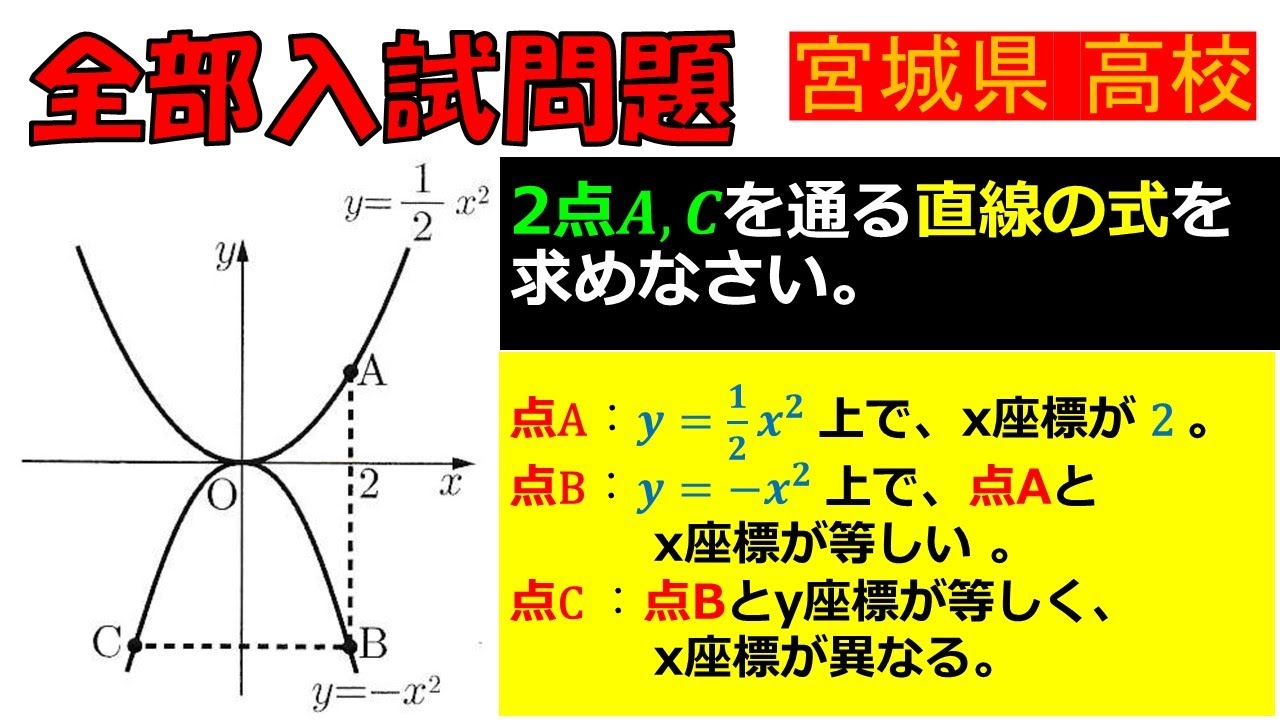
2点$A,C$を通る直線の式を求めなさい.
宮城県高校過去問
この動画を見る
2点$A,C$を通る直線の式を求めなさい.
宮城県高校過去問
中学入試でも二つの円!!開成中
二次方程式

単元:
#数学(中学生)#中3数学#2次方程式#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\dfrac{1}{2}x^2-4×10×82×6562=\dfrac{1}{2}$
この動画を見る
これを解け.
$\dfrac{1}{2}x^2-4×10×82×6562=\dfrac{1}{2}$
文字があると中学生は困ってしまうよね。二次方程式の応用。 2通りで解説 芝浦工大柏

単元:
#数学(中学生)#数Ⅰ#2次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a>0とする。
xについての二次方程式
$x^2+2ax-a^2=0$の解が$x= - a ± 10 \sqrt 2$のときa=?
芝浦工業大学柏高等学校
この動画を見る
a>0とする。
xについての二次方程式
$x^2+2ax-a^2=0$の解が$x= - a ± 10 \sqrt 2$のときa=?
芝浦工業大学柏高等学校
【初めが肝心!】整数:秋田県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#正の数・負の数
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2つの整数$148,245$を自然数$n$で割ったとき,余りがそれぞれ$4,5$となる.
自然数$n$は全部で何個あるか.
秋田県高校過去問
この動画を見る
2つの整数$148,245$を自然数$n$で割ったとき,余りがそれぞれ$4,5$となる.
自然数$n$は全部で何個あるか.
秋田県高校過去問
いろいろな四角形 暁

単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
四角形の性質について正しいものを1つ選べ。
⓪4つの角がすべて等しい四角形は正方形である。
①対角線が垂直に交わる四角形は長方形である。
②対角線の長さが等しい四角形は長方形である。
③対角線がそれぞれの中点で交わる四角形は平行四辺形である。
暁高等学校
この動画を見る
四角形の性質について正しいものを1つ選べ。
⓪4つの角がすべて等しい四角形は正方形である。
①対角線が垂直に交わる四角形は長方形である。
②対角線の長さが等しい四角形は長方形である。
③対角線がそれぞれの中点で交わる四角形は平行四辺形である。
暁高等学校
大学入試じゃね? 灘高校 小数部分

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正の数xの小数部分を
$(x - \langle x \rangle)^2 + (3 \langle x \rangle -1)^2 = 6$のとき
$x - \langle x \rangle = ? ,x=?$
灘高等学校
この動画を見る
正の数xの小数部分を
$(x - \langle x \rangle)^2 + (3 \langle x \rangle -1)^2 = 6$のとき
$x - \langle x \rangle = ? ,x=?$
灘高等学校
【さらに学べば見方も変わる!】二次方程式:成蹊高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
方程式$ 3\left(x-\dfrac{1}{2}\right)^2=3x+\dfrac{7}{4}$を解け.
成蹊高校過去問
この動画を見る
方程式$ 3\left(x-\dfrac{1}{2}\right)^2=3x+\dfrac{7}{4}$を解け.
成蹊高校過去問
【そして経験したことを思い出して】図形:国立高等専門学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#角度と面積#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
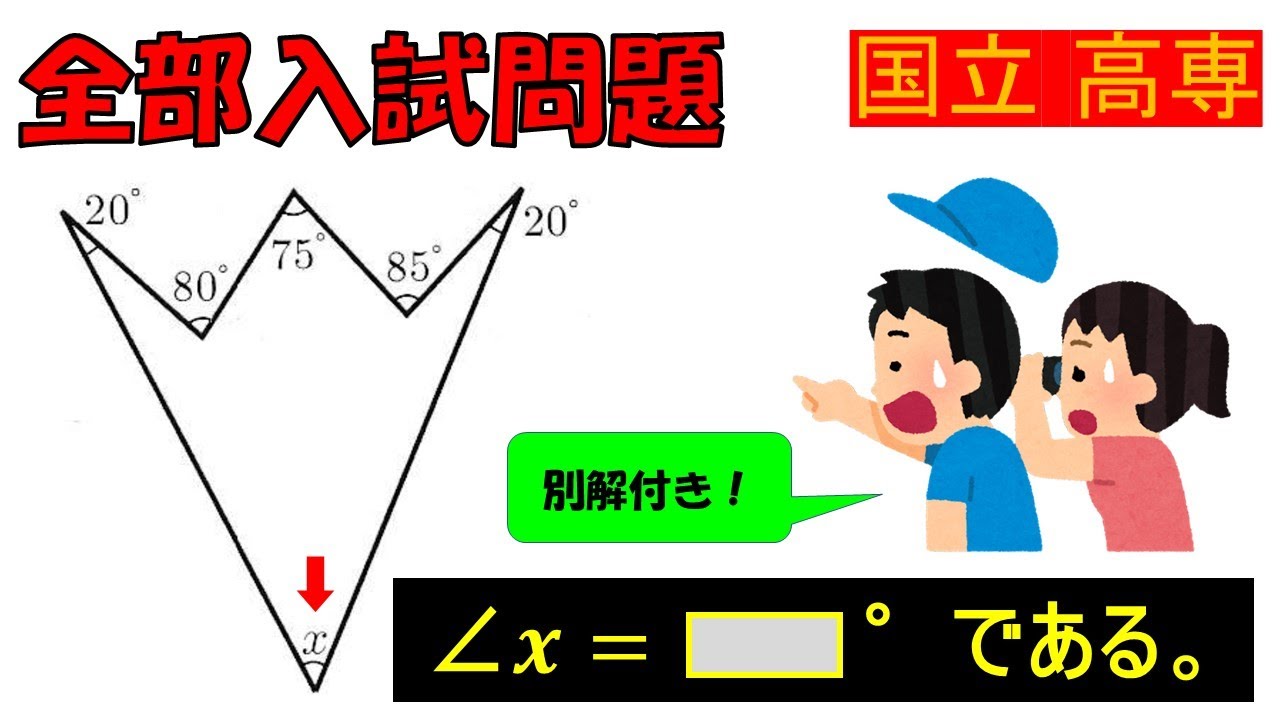
$ \angle x$は$\Box$である.
この動画を見る
$ \angle x$は$\Box$である.
知っていれば一瞬。傍接円と三角形の周の長さ 清風南海高校
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
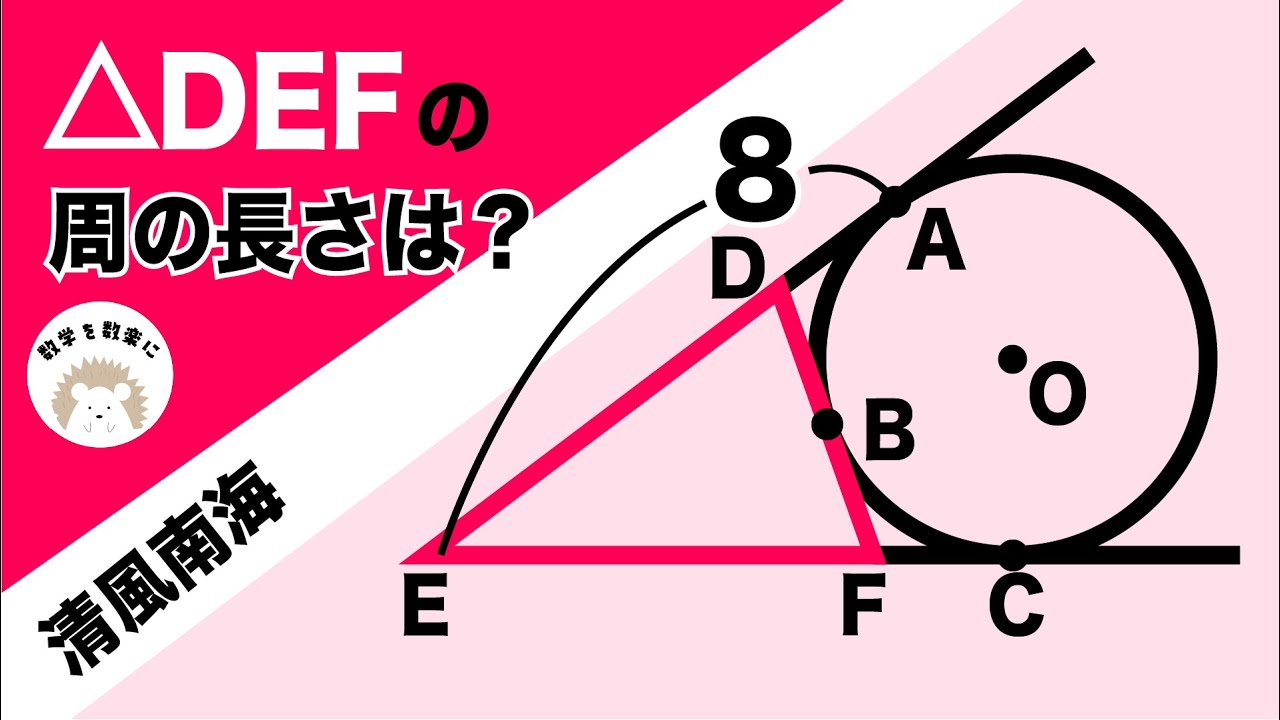
△DEFの周の長さは?
*図は動画内参照
清風南海高等学校
この動画を見る
△DEFの周の長さは?
*図は動画内参照
清風南海高等学校
眠れない夜に学ぶ数学~全国入試問題解法 #shorts #数学 #sound

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x-\dfrac{\sqrt2-2}{2}$のとき,$x^2+2x+\dfrac{1}{x+1}+1$の値を求めなさい.
立命館高校過去問
この動画を見る
$ x-\dfrac{\sqrt2-2}{2}$のとき,$x^2+2x+\dfrac{1}{x+1}+1$の値を求めなさい.
立命館高校過去問
書き出す訳にはいかないんだ。そんな時間ないんだ。ではどうする? 白陵高校

単元:
#数学(中学生)#数A#場合の数と確率#場合の数#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
異なる12冊の本から2冊以上の本を選びたい。
選ぶ方法は何通り?
白陵高等学校
この動画を見る
異なる12冊の本から2冊以上の本を選びたい。
選ぶ方法は何通り?
白陵高等学校
【よく出題される形式!4問分の解説】平方根:群馬県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
数について述べた次のア~エのうち,正しいものをすべて選びなさい.
ア すべての自然数は,その逆数も自然数となる.
イ 異なる2つの整数について,大きい方から小さい方をひいた差は,いつでも自然数となる.
ウ すべての2次方程式の解は,無理数となる.
エ すべての有理数や無理数は,数直線上に対応する点がある.
群馬県高校過去問
この動画を見る
数について述べた次のア~エのうち,正しいものをすべて選びなさい.
ア すべての自然数は,その逆数も自然数となる.
イ 異なる2つの整数について,大きい方から小さい方をひいた差は,いつでも自然数となる.
ウ すべての2次方程式の解は,無理数となる.
エ すべての有理数や無理数は,数直線上に対応する点がある.
群馬県高校過去問
【一本道が見えますか】連立方程式:巣鴨高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2つの連立方程式
$ \begin{eqnarray}
\left\{
\begin{array}{l}
3x + 2y = 14 \\
ax + by = 3
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
bx -ay = -5 \\
4x-5y = 11
\end{array}
\right.
\end{eqnarray}$
の解が一致するとき$a,b$の値をそれぞれ求めなさい.
巣鴨高校過去問
この動画を見る
2つの連立方程式
$ \begin{eqnarray}
\left\{
\begin{array}{l}
3x + 2y = 14 \\
ax + by = 3
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
bx -ay = -5 \\
4x-5y = 11
\end{array}
\right.
\end{eqnarray}$
の解が一致するとき$a,b$の値をそれぞれ求めなさい.
巣鴨高校過去問
x=❓
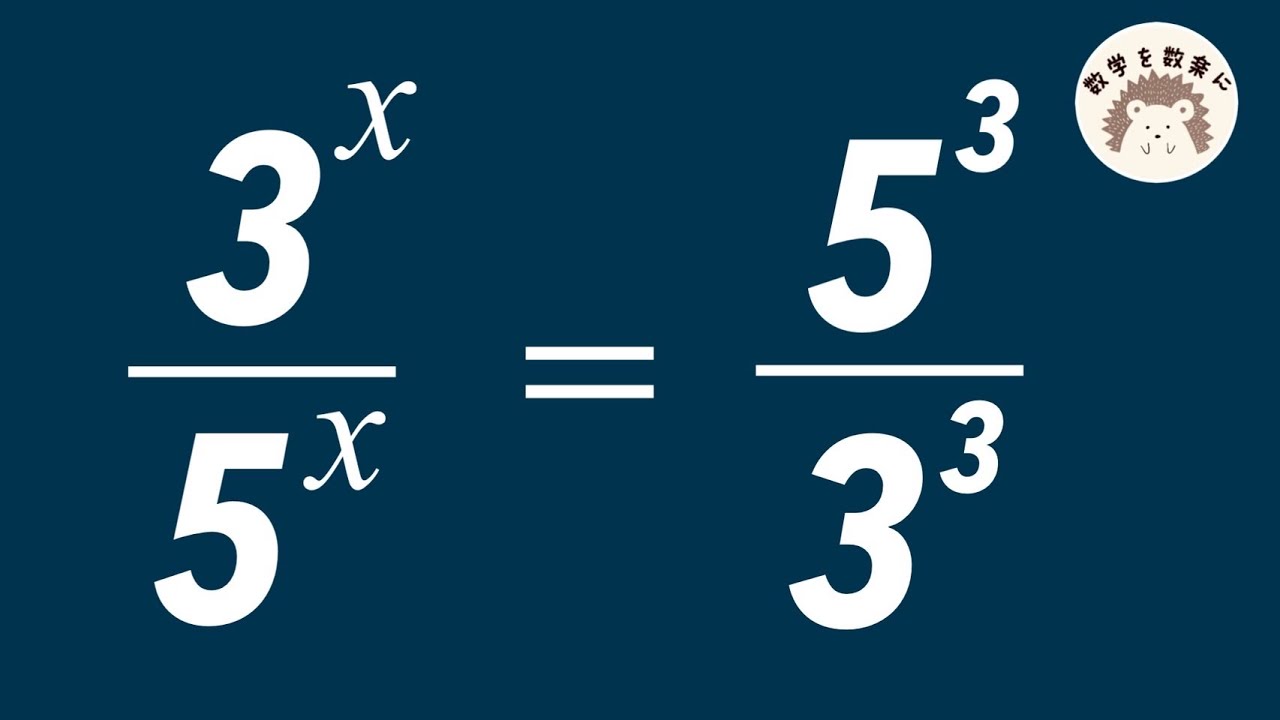
【数学】有理化がなぜ必要なのか?解説してみた!

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
有理化って何のためにしてるか知っていますか??
この動画を見る
有理化って何のためにしてるか知っていますか??
