数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
平方根の計算 城北高校 2022年入試問題解説52問目

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{2023 \times 2021 - 4044 +2}$
2022城北高等学校
この動画を見る
$\sqrt{2023 \times 2021 - 4044 +2}$
2022城北高等学校
三平方の定理 高校数学不要

連立方程式 法政ニ 2022年入試問題解説51問目

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式
$
\begin{eqnarray}
\left\{
\begin{array}{l}
37x - 53y = 2 \\
17x + 19y = 1
\end{array}
\right.
\end{eqnarray}
$
$x:y=?$
2022法政大学第二高等学校
この動画を見る
連立方程式
$
\begin{eqnarray}
\left\{
\begin{array}{l}
37x - 53y = 2 \\
17x + 19y = 1
\end{array}
\right.
\end{eqnarray}
$
$x:y=?$
2022法政大学第二高等学校
【中学数学】確率の裏技~取り扱い注意ね~【中2数学】

単元:
#数学(中学生)#中2数学#確率
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1) 袋の中に赤玉が2個、白玉が1個、青玉が1個入っている。この袋から同時に2個取り出すとき、2個とも赤玉である確率を求めよ。
(2) 袋の中に赤玉が4個、白玉が2個入っている。この袋から同時に2個取り出すとき、赤玉と白玉が1つずつ取り出される確率を求めよ。
(3) 袋の中に赤、白、青の玉がそれぞれ2個入っている。1回取り出した玉を袋に戻して、2回目を取り出すとき、取り出した2つの玉がどちらも青である確率を求めよ。
(4) 袋の中に赤玉4個、白玉2個が入っている。この袋から2個同時に取り出すとき、少なくとも1個は白玉が取り出される確率を求めよ。
この動画を見る
(1) 袋の中に赤玉が2個、白玉が1個、青玉が1個入っている。この袋から同時に2個取り出すとき、2個とも赤玉である確率を求めよ。
(2) 袋の中に赤玉が4個、白玉が2個入っている。この袋から同時に2個取り出すとき、赤玉と白玉が1つずつ取り出される確率を求めよ。
(3) 袋の中に赤、白、青の玉がそれぞれ2個入っている。1回取り出した玉を袋に戻して、2回目を取り出すとき、取り出した2つの玉がどちらも青である確率を求めよ。
(4) 袋の中に赤玉4個、白玉2個が入っている。この袋から2個同時に取り出すとき、少なくとも1個は白玉が取り出される確率を求めよ。
開成高校 令和四年度最初の一問 2022年入試問題解説50問目

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式$7x^2-4\sqrt 2x+1=0$($\sqrt 2$の近似値=1.414)
2つの解を求めよ。
また、2つの解のうち$\frac{2}{5}$に近い方を、小数第4位を四捨五入し小数第3位まで求めよ。
2022開成高等学校
この動画を見る
2次方程式$7x^2-4\sqrt 2x+1=0$($\sqrt 2$の近似値=1.414)
2つの解を求めよ。
また、2つの解のうち$\frac{2}{5}$に近い方を、小数第4位を四捨五入し小数第3位まで求めよ。
2022開成高等学校
【3分で理解!5分で発展的学習!】二次方程式:山口県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
差が1である大小2つの正の数がある.
これらの積が3であるとき,2つの数のうち,大きい方の数を求めなさい.
山口県高校過去問
この動画を見る
差が1である大小2つの正の数がある.
これらの積が3であるとき,2つの数のうち,大きい方の数を求めなさい.
山口県高校過去問
2022年の整数問題!この問題好きです❤️ 早稲田大学高等学院2022年入試問題解説49問目
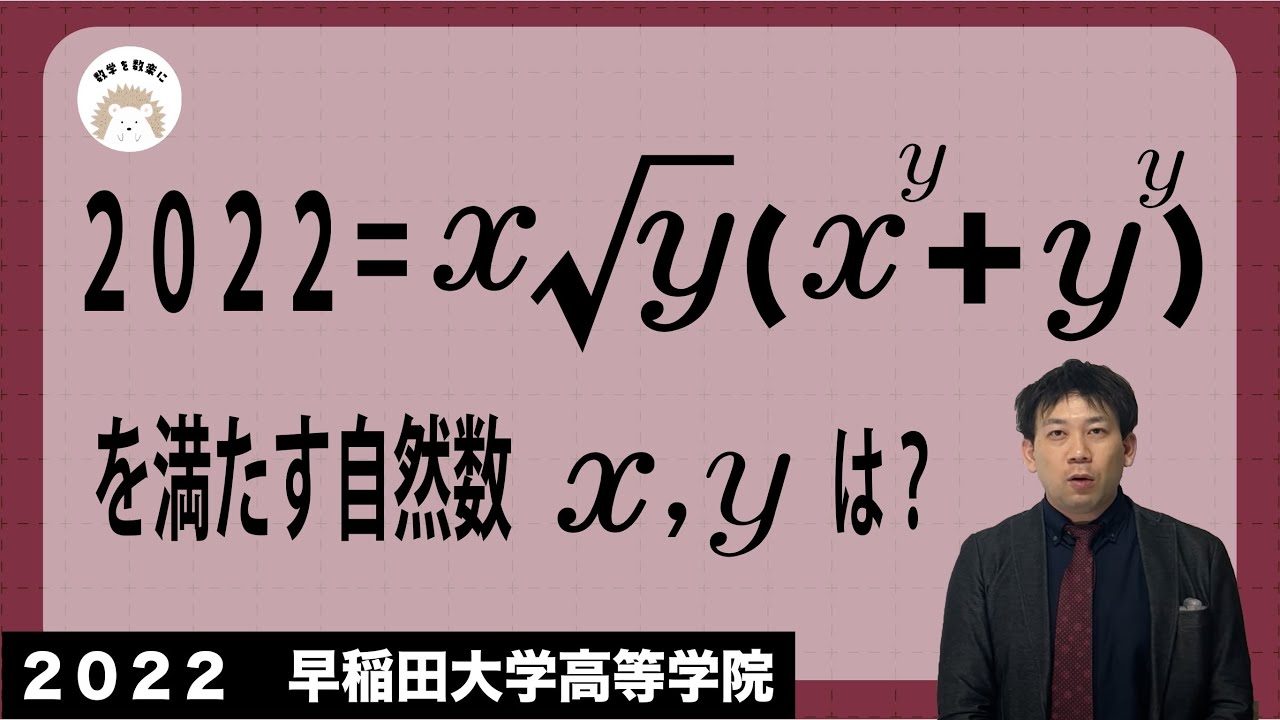
単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2022=x \sqrt y (x^y+y^y)$
を満たす自然数x,yは?
2022早稲田大学高等学院
この動画を見る
$2022=x \sqrt y (x^y+y^y)$
を満たす自然数x,yは?
2022早稲田大学高等学院
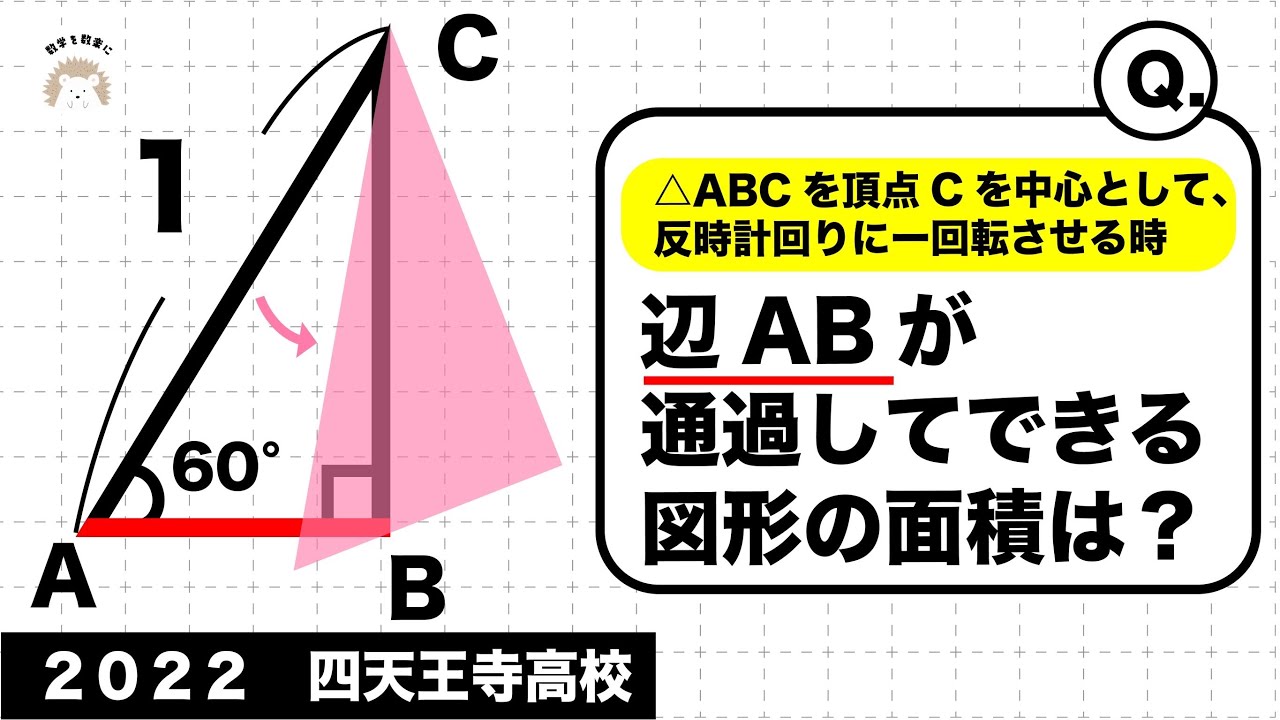
三角形の回転 四天王寺高校2022年入試問題解説48問目
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABCを頂点Cを中心として、反時計回りに一回点させる時
辺ABが通過してできる図形の面積は?
*図は動画内参照
2022四天王寺高等学校
この動画を見る
△ABCを頂点Cを中心として、反時計回りに一回点させる時
辺ABが通過してできる図形の面積は?
*図は動画内参照
2022四天王寺高等学校
令和4年度 灘高校の最初の一問 2022年入試問題解説47問目

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\sqrt {2022} + \sqrt {77})^2
-2(\sqrt {2022} + \sqrt {77})(\sqrt {2022} - 1)
+2(\sqrt {2022} - \sqrt {77})(\sqrt {2022} - 1)
-(\sqrt {2022} - \sqrt {77})^2
$
2022灘高等学校
この動画を見る
$(\sqrt {2022} + \sqrt {77})^2
-2(\sqrt {2022} + \sqrt {77})(\sqrt {2022} - 1)
+2(\sqrt {2022} - \sqrt {77})(\sqrt {2022} - 1)
-(\sqrt {2022} - \sqrt {77})^2
$
2022灘高等学校
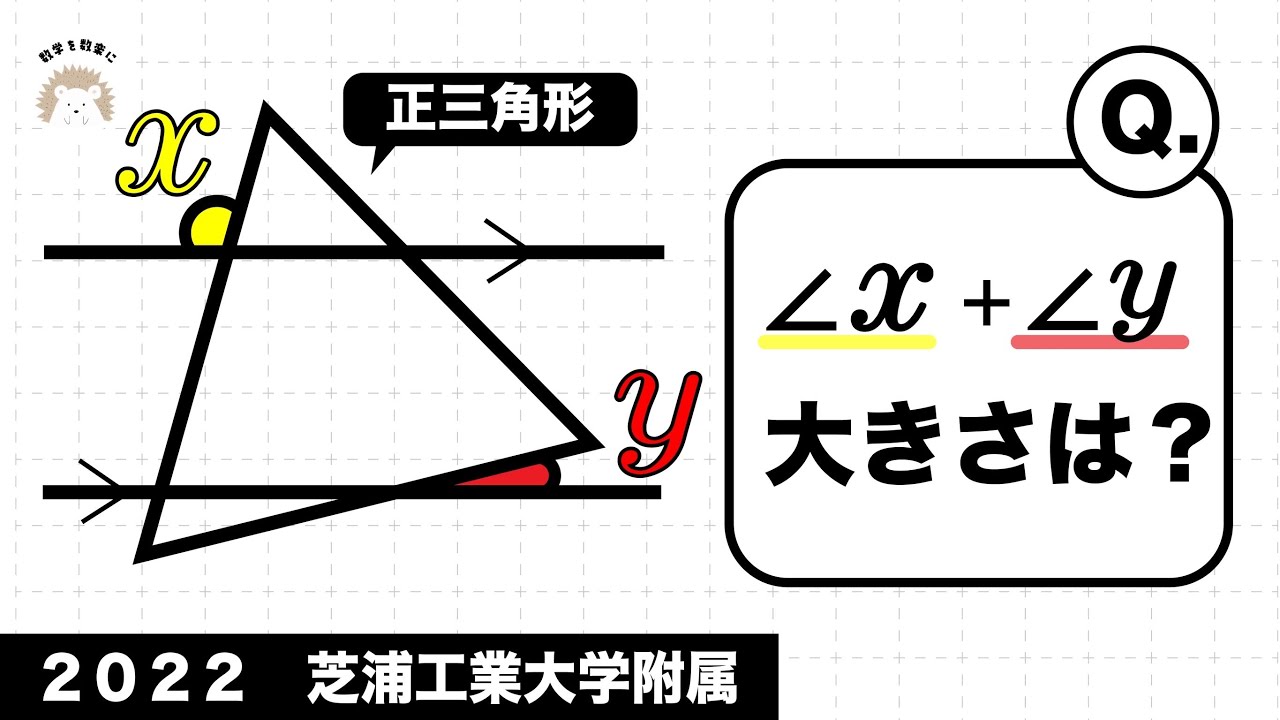
平行線と角の和 芝浦工大附属 2022年入試問題解説46問目
単元:
#数学(中学生)#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x+ \angle y$=?
*図は動画内参照
2022芝浦工業大学附属高等学校
この動画を見る
$\angle x+ \angle y$=?
*図は動画内参照
2022芝浦工業大学附属高等学校
令和4年度 慶應女子 2022年入試問題解説45問目

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$2044^2 + 1956^2 + 4022^2 + 3978^2$
2022慶應義塾女子高等学校
この動画を見る
$2044^2 + 1956^2 + 4022^2 + 3978^2$
2022慶應義塾女子高等学校
【中学数学】2次方程式の解き方まとめ 3-6【中3数学】

令和4年度 慶應女子の最初の一問 2022年入試問題解説44問目

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$2022^2+1978^2$
計算せよ
2022慶應義塾女子高等学校
この動画を見る
$2022^2+1978^2$
計算せよ
2022慶應義塾女子高等学校
箱ヒゲ図を基本から解説!! 早稲田実業 2022 入試問題解説41問目

単元:
#数学(中学生)#数Ⅰ#データの分析#データの分析#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
箱ひげ図を書け
*図は動画内参照
2022早稲田実業学校
この動画を見る
箱ひげ図を書け
*図は動画内参照
2022早稲田実業学校
令和4年度 中央大杉並の最初の一問 2022入試問題解説43問目

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(x^2+2022)^2 - 4092529x^2$
因数分解せよ
$83521=17^4$を用いて良い
2022中央大学杉並高等学校
この動画を見る
$(x^2+2022)^2 - 4092529x^2$
因数分解せよ
$83521=17^4$を用いて良い
2022中央大学杉並高等学校
令和4年度 中央大杉並の最初の一問 2022入試問題解説42問目

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x+y+z=7,xyz=7$
$\frac{1}{x}+\frac{1}{y}+\frac{1}{z} = \frac{13}{7}$
$(1+ \frac{1}{x})(1+ \frac{1}{y})(1+ \frac{1}{z}) = ?$
2022中央大学杉並高等学校
この動画を見る
$x+y+z=7,xyz=7$
$\frac{1}{x}+\frac{1}{y}+\frac{1}{z} = \frac{13}{7}$
$(1+ \frac{1}{x})(1+ \frac{1}{y})(1+ \frac{1}{z}) = ?$
2022中央大学杉並高等学校
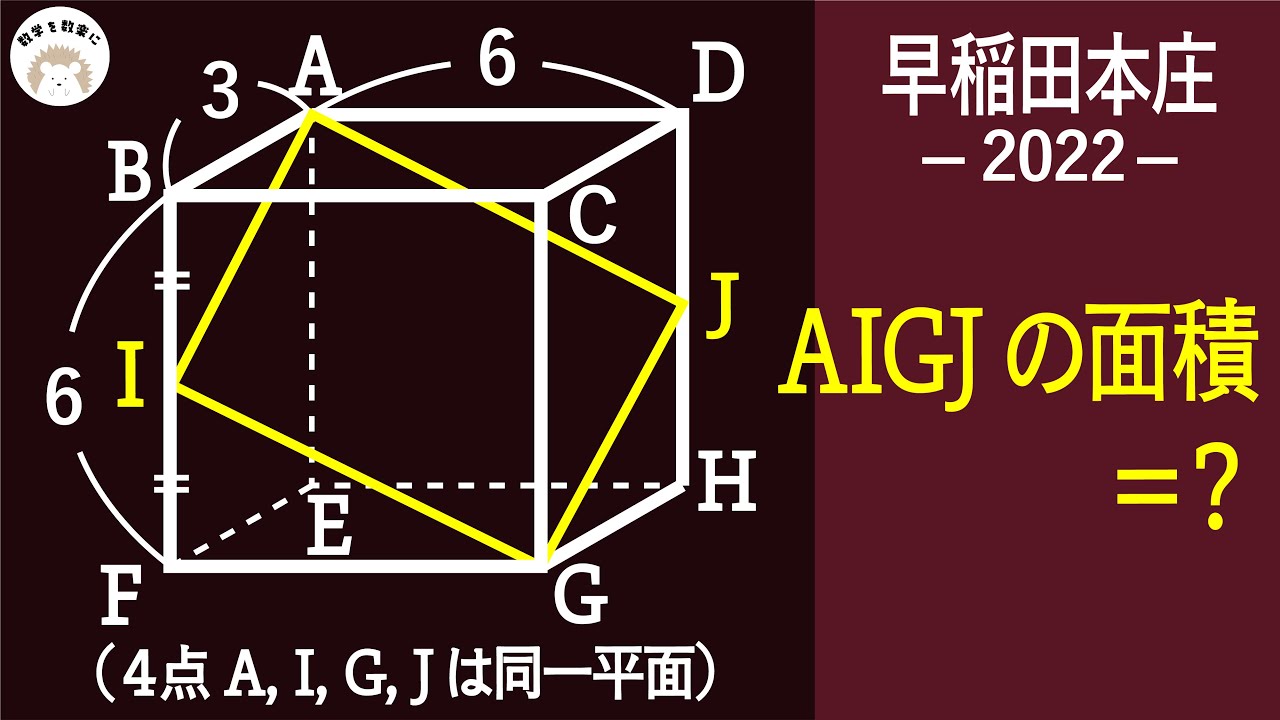
見た目に騙されるな 早稲田本庄 2022 入試問題解説40問目
単元:
#数学(中学生)#中1数学#空間図形#立体図形#体積・表面積・回転体・水量・変化のグラフ#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
四角形AIGJの面積=?
(4点A,I,G,Jは同一平面)
*図は動画内参照
2022早稲田大学 本庄高等学院
この動画を見る
四角形AIGJの面積=?
(4点A,I,G,Jは同一平面)
*図は動画内参照
2022早稲田大学 本庄高等学院
解ける?

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
233x+267y=400 \\
267x+233y=100
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
233x+267y=400 \\
267x+233y=100
\end{array}
\right.
\end{eqnarray}$
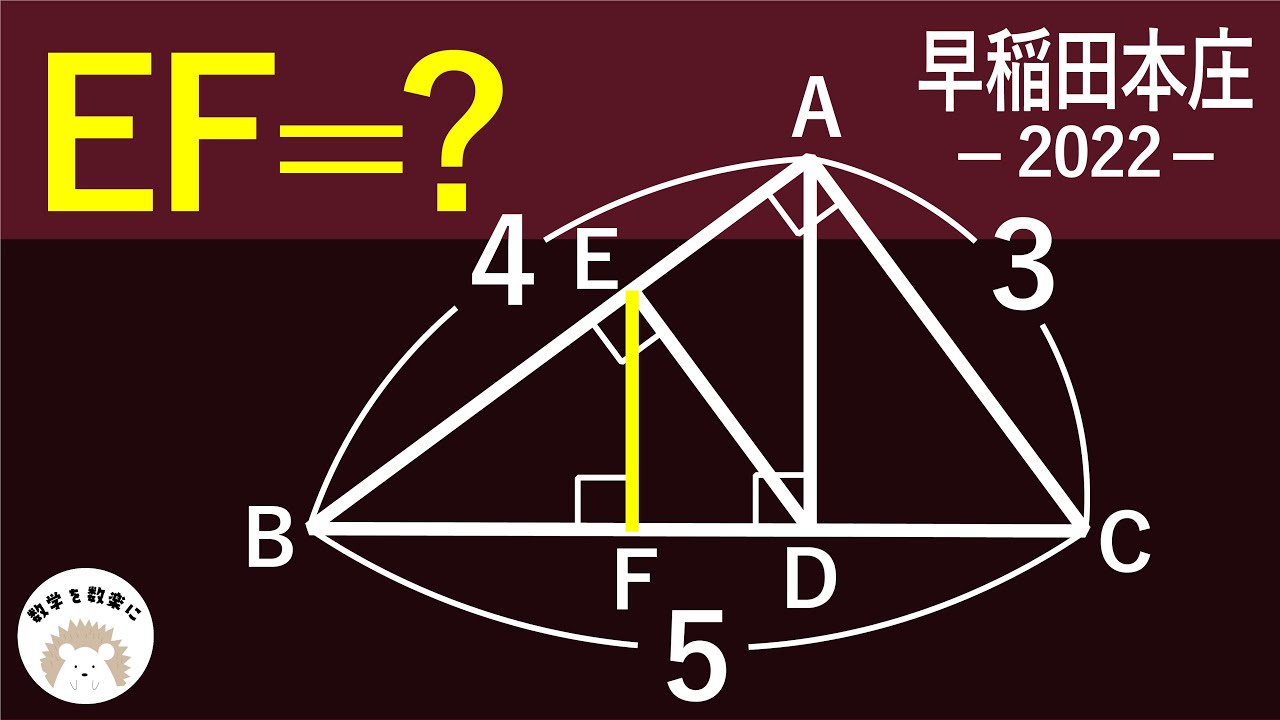
直角三角形たくさん! 早稲田本庄 2022 入試問題解説39問目
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
EF=?
*図は動画内参照
2022早稲田大学本庄高等学院
この動画を見る
EF=?
*図は動画内参照
2022早稲田大学本庄高等学院
早稲田本庄 因数分解2022 入試問題解説38問目

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(x+y)xy - (y+z)yz$
因数分解せよ
2022早稲田大学本庄高等学院
この動画を見る
$(x+y)xy - (y+z)yz$
因数分解せよ
2022早稲田大学本庄高等学院
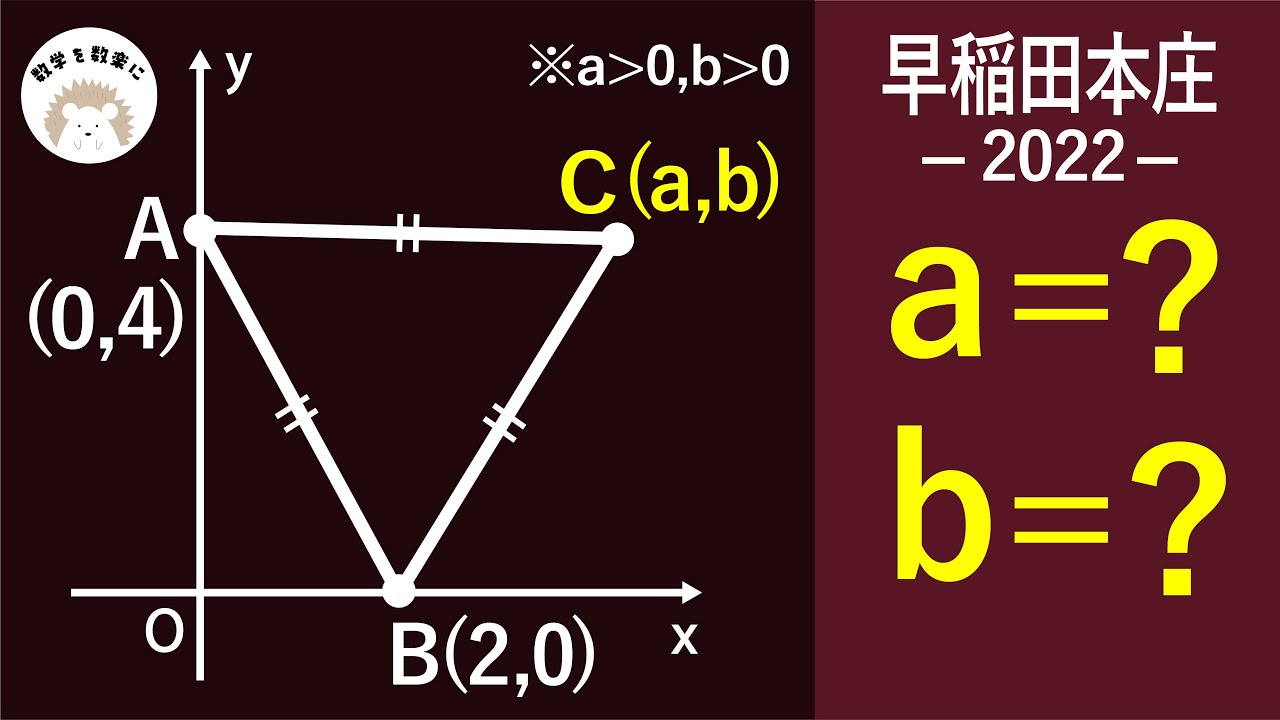
2022年2月9日 早稲田本庄 2022 入試問題解説37問目
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a=?
b=?
(a>0,b>0)
*図は動画内参照
2022早稲田大学本庄高等学院
この動画を見る
a=?
b=?
(a>0,b>0)
*図は動画内参照
2022早稲田大学本庄高等学院
整数問題 慶應志木高校2022入試問題解説36問目

単元:
#数学(中学生)#数Ⅰ#数A#2次関数#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
xについての2次方程式
$x^2-(4t-1)x+4t^2-2t = 0$の2つの解をα、βとする
5,α,βを辺にもつ三角形が直角三角形のとき
tの値は?
2022慶應義塾志木高等学校
この動画を見る
xについての2次方程式
$x^2-(4t-1)x+4t^2-2t = 0$の2つの解をα、βとする
5,α,βを辺にもつ三角形が直角三角形のとき
tの値は?
2022慶應義塾志木高等学校
【自力本願⁈ 神のお告げ待ち⁈】因数分解:中央大学附属高等学校~全部入試問題

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$S$を因数分解しなさい.
$S=n^4-5n^3-10n^2+35n+49$
中央大附属高校過去問
この動画を見る
$S$を因数分解しなさい.
$S=n^4-5n^3-10n^2+35n+49$
中央大附属高校過去問
【裏技】池を回って追いこす系
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1周720mの池がある。
Aは40m/分、Bは10m/分で同時に同じ方向へ池に沿って走る。
AがBに追いつくのは 何分後か?
この動画を見る
1周720mの池がある。
Aは40m/分、Bは10m/分で同時に同じ方向へ池に沿って走る。
AがBに追いつくのは 何分後か?
整数問題 慶應志木高校2022入試問題解説35問目

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
x,y,z:素数
$z=80x^2+2xy - y^2$を満たす(x,y,z)の組のうち、
zが2番目に小さくなるものを求めよ
(x,y,z)=▢
2022慶應義塾志木高等学校
この動画を見る
x,y,z:素数
$z=80x^2+2xy - y^2$を満たす(x,y,z)の組のうち、
zが2番目に小さくなるものを求めよ
(x,y,z)=▢
2022慶應義塾志木高等学校
2022年の整数問題 愛工大名電高校2022入試問題解説34問目

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{2022}{2n+1}$が素数になる自然数nのうち最大のものを求めよ。
2022愛知工業大学名電高等学校
この動画を見る
$\frac{2022}{2n+1}$が素数になる自然数nのうち最大のものを求めよ。
2022愛知工業大学名電高等学校
【中学数学】確率の基礎~袋の問題まとめ~【中2数学】

単元:
#数学(中学生)#中2数学#確率
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1) 袋の中に赤玉が2個、白玉が1個、青玉が1個入っている。この袋から同時に2個取り出すとき、2個とも赤玉である確率を求めよ。
(2) 袋の中に赤玉が4個、白玉が2個入っている。この袋から同時に2個取り出すとき、赤玉と白玉が1つずつ取り出される確率を求めよ。
(3) 袋の中に赤、白、青の玉がそれぞれ2個入っている。1回取り出した玉を袋に戻して、2回目を取り出すとき、取り出した2つの玉がどちらも青である確率を求めよ。
(4) 袋の中に赤玉4個、白玉2個が入っている。この袋から2個同時に取り出すとき、少なくとも1個は白玉が取り出される確率を求めよ。
この動画を見る
(1) 袋の中に赤玉が2個、白玉が1個、青玉が1個入っている。この袋から同時に2個取り出すとき、2個とも赤玉である確率を求めよ。
(2) 袋の中に赤玉が4個、白玉が2個入っている。この袋から同時に2個取り出すとき、赤玉と白玉が1つずつ取り出される確率を求めよ。
(3) 袋の中に赤、白、青の玉がそれぞれ2個入っている。1回取り出した玉を袋に戻して、2回目を取り出すとき、取り出した2つの玉がどちらも青である確率を求めよ。
(4) 袋の中に赤玉4個、白玉2個が入っている。この袋から2個同時に取り出すとき、少なくとも1個は白玉が取り出される確率を求めよ。
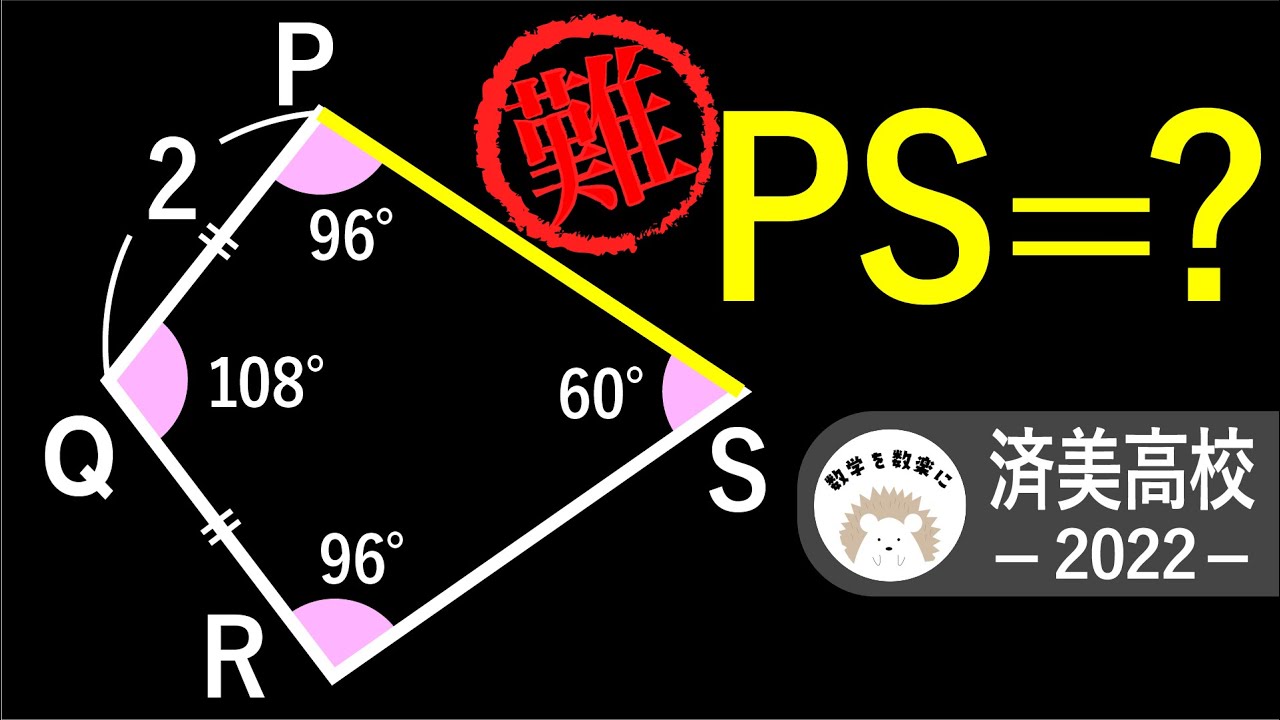
誘導なしだと難しい 済美高校2022入試問題解説33問目
単元:
#数学(中学生)#中1数学#平面図形#角度と面積#平面図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
PS=?
*図は動画内参照
2022済美高等学校
この動画を見る
PS=?
*図は動画内参照
2022済美高等学校
高等学校入学試験問題予想:法政大学第二高等学校~全部入試問題

単元:
#数学(中学生)#中2数学#中3数学#式の計算(展開、因数分解)#2次方程式#確率#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\boxed{1}$
因数分解せよ.
(1)$(x-2y)^2+(x+y)(x-5y)+y^2$
(2)$a=\dfrac{1}{\sqrt5+1},b=\dfrac{1}{\sqrt5-1}$のとき,$(a-4b)(b-4a)=?$
$\boxed{2}$
1~5までの数字が書かれたカードが2枚ずつ合計10枚ある.
(1)これらのカードを袋に入れてその中から同時に2枚取り出すとき,カードの数字の積が偶数となる確率は?
(2)$n$の3以上の自然数$\dfrac{4}{\sqrt n-\sqrt2}$の整数部分が2であるとき,
$n$として考えられる値を全て求めよ.
$\boxed{3}$
$PQ$と$D$の交点を$R$とする.
点$P,Q$の$x$座標を$p,q$とする.
直線$PQ$の傾きが,$C,D$の比例定数$a$と等しく,$R$が線分$PQ$の中点となる.
(1)点$A$の座標を$a$で表せ.
(2)$p+q=?$
(3)点$R$の座標を$a$で表せ.
(4)$p.q$の値
法政第二高校過去問
この動画を見る
$\boxed{1}$
因数分解せよ.
(1)$(x-2y)^2+(x+y)(x-5y)+y^2$
(2)$a=\dfrac{1}{\sqrt5+1},b=\dfrac{1}{\sqrt5-1}$のとき,$(a-4b)(b-4a)=?$
$\boxed{2}$
1~5までの数字が書かれたカードが2枚ずつ合計10枚ある.
(1)これらのカードを袋に入れてその中から同時に2枚取り出すとき,カードの数字の積が偶数となる確率は?
(2)$n$の3以上の自然数$\dfrac{4}{\sqrt n-\sqrt2}$の整数部分が2であるとき,
$n$として考えられる値を全て求めよ.
$\boxed{3}$
$PQ$と$D$の交点を$R$とする.
点$P,Q$の$x$座標を$p,q$とする.
直線$PQ$の傾きが,$C,D$の比例定数$a$と等しく,$R$が線分$PQ$の中点となる.
(1)点$A$の座標を$a$で表せ.
(2)$p+q=?$
(3)点$R$の座標を$a$で表せ.
(4)$p.q$の値
法政第二高校過去問
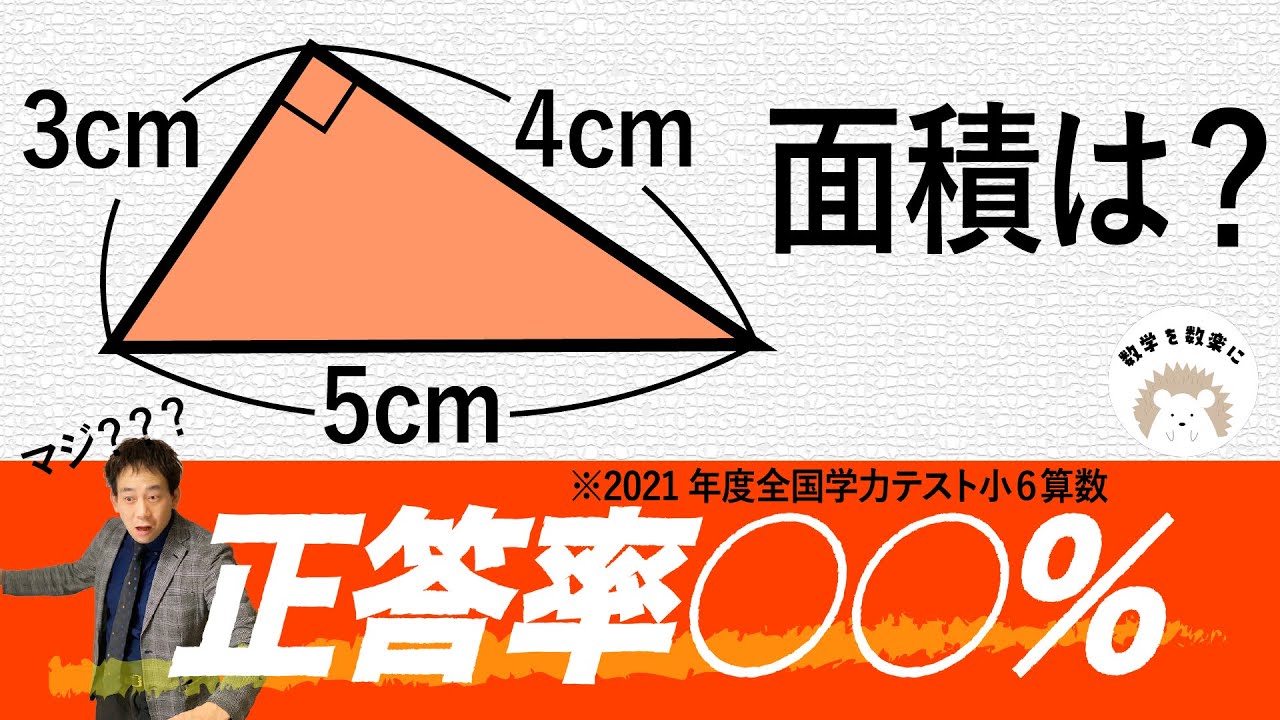
小学6年生は三角形の面積を求められるのか?コメント求む!!後半雑談