 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
数学得意だよって天狗になっている中学生に解かせたい問題 ルートを外せ13

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{24n}$が整数となるような最小の整数nを求めよ。
大阪教育大学附属高等学校天王寺校舎
この動画を見る
$\sqrt{24n}$が整数となるような最小の整数nを求めよ。
大阪教育大学附属高等学校天王寺校舎
【中学数学】連立方程式:連立方程式文章題の発展問題

単元:
#数学(中学生)#中2数学#連立方程式
教材:
#KEYワーク#KEYワーク(数学)中2#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある2桁の自然数がある。
その自然数は1の位の4倍の数より22大きく、10の位と1の位を入れ替えてできる数は元の自然数より18大きい。
元の自然数はいくつか。【連立方程式】
この動画を見る
ある2桁の自然数がある。
その自然数は1の位の4倍の数より22大きく、10の位と1の位を入れ替えてできる数は元の自然数より18大きい。
元の自然数はいくつか。【連立方程式】
【3分で理解!円を伴う図形の基礎】図形:大分県~全国入試問題解法
単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)#大分県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
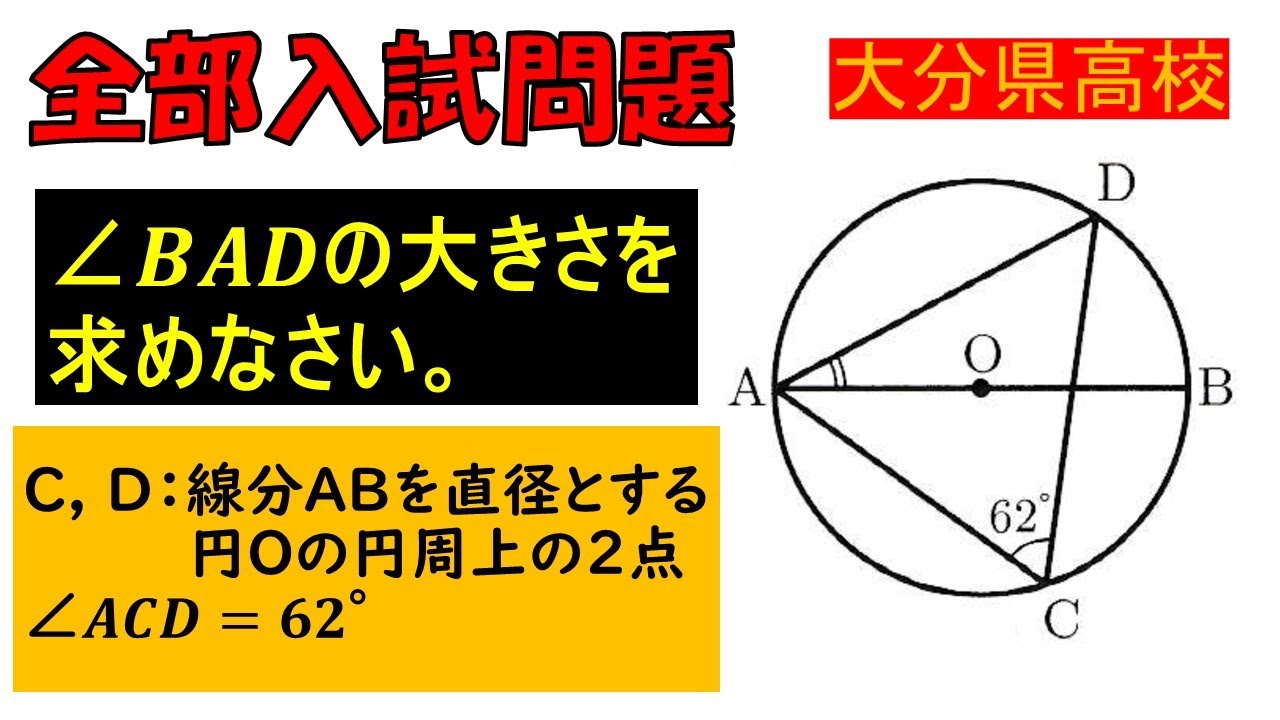
入試問題 大分県の公立高校
$\angle BAD$
の大きさを 求めなさい。
$C, D$: 線分ABを直径とする
円○の円周上の$2$点
$\angle ACD = 62°$
※図は動画内参照
この動画を見る
入試問題 大分県の公立高校
$\angle BAD$
の大きさを 求めなさい。
$C, D$: 線分ABを直径とする
円○の円周上の$2$点
$\angle ACD = 62°$
※図は動画内参照
【裏技】連立方程式こんな解き方あり?

【中学数学】 連立方程式:連立方程式の割合

単元:
#数学(中学生)#中2数学#連立方程式
教材:
#KEYワーク#KEYワーク(数学)中2#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
商品Aと商品Bの仕入れ値の比は45:44である。
また商品Aには20%、商品Bには25%の利益を見込んで定価をつけると、商品Aは商品Bよりも定価が200円安くなった。
この時の商品ABの仕入れ値を求めよ。【連立方程式】
この動画を見る
商品Aと商品Bの仕入れ値の比は45:44である。
また商品Aには20%、商品Bには25%の利益を見込んで定価をつけると、商品Aは商品Bよりも定価が200円安くなった。
この時の商品ABの仕入れ値を求めよ。【連立方程式】
【3分で別解まで分かる!】図形:長崎県~全国入試問題解法
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)#長崎県公立高校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
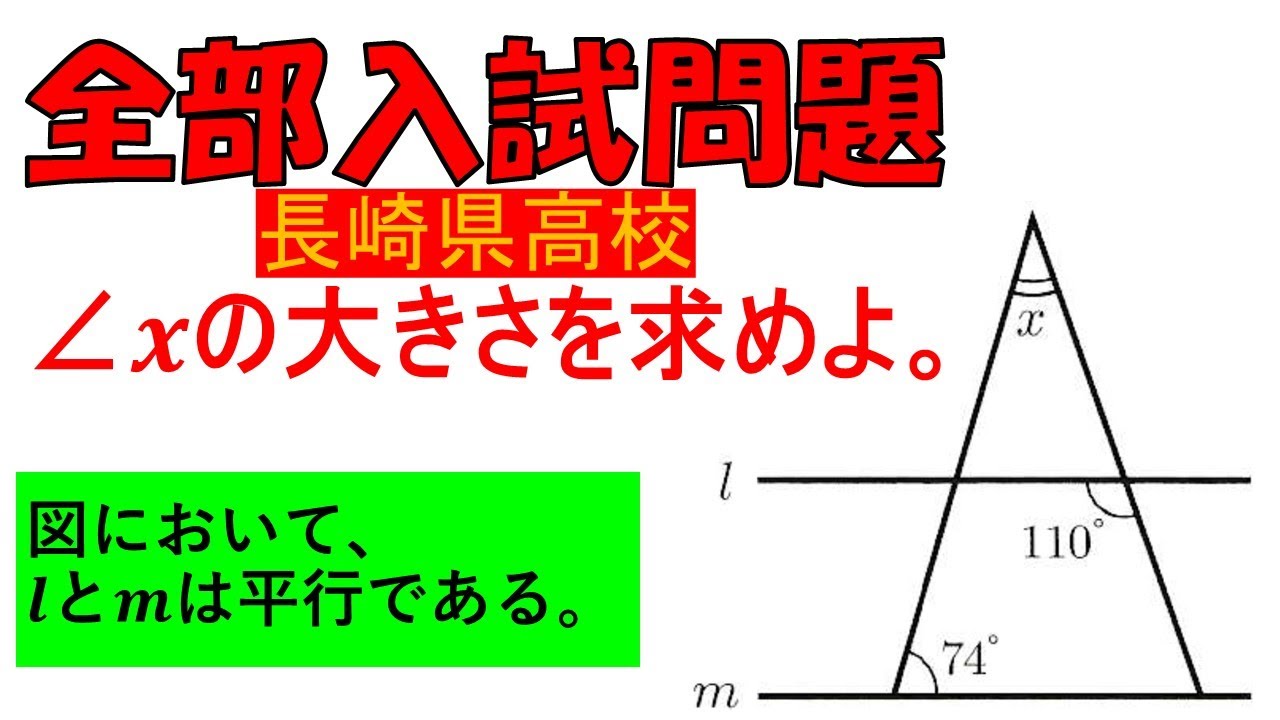
入試問題 長崎県の公立高校
$\angle x$の大きさを求めよ。
図において、$l$と$m$は平行である。
※図は動画内参照
この動画を見る
入試問題 長崎県の公立高校
$\angle x$の大きさを求めよ。
図において、$l$と$m$は平行である。
※図は動画内参照
数学 高校入試 3つの素数 日本女子大学附属高校

単元:
#計算と数の性質#数の性質その他#数学(中学生)#約数・倍数を利用する問題#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
条件を満たす3つの素数は?
・3つの数の積は偶数
・3つの数の和は24
・どの2つの数の差も2以上
日本女子大学附属高等学校
この動画を見る
条件を満たす3つの素数は?
・3つの数の積は偶数
・3つの数の和は24
・どの2つの数の差も2以上
日本女子大学附属高等学校
【中学数学】1次関数の基礎~分からない人はこれを見ろ~ 3-1【中2数学】

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1次関数の式を求めよ
(1)傾き2で、x=4のとき,y=3
(2)変化の割合が5で点(3,2)を通る
(3)(2,-1)(4,-13)を通る
この動画を見る
1次関数の式を求めよ
(1)傾き2で、x=4のとき,y=3
(2)変化の割合が5で点(3,2)を通る
(3)(2,-1)(4,-13)を通る
数学 高校入試 平方根の計算

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{30^4-20^4-10^4} =$
東北学院高等学校
この動画を見る
$\sqrt{30^4-20^4-10^4} =$
東北学院高等学校
【3分で確認、計算のルール!】平方根:福岡大学附属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 福岡大学附属大濠高等学校
$(\displaystyle \frac{6}{\sqrt{ 3 }}-\sqrt{ 18 })(\sqrt{ 12 }+\displaystyle \frac{6}{\sqrt{ 2 }})$
を計算し、簡単にすると▬である。
この動画を見る
入試問題 福岡大学附属大濠高等学校
$(\displaystyle \frac{6}{\sqrt{ 3 }}-\sqrt{ 18 })(\sqrt{ 12 }+\displaystyle \frac{6}{\sqrt{ 2 }})$
を計算し、簡単にすると▬である。
【裏技】円錐の表面積を一瞬で出す

単元:
#算数(中学受験)#数学(中学生)#中1数学#空間図形#立体図形#立体図形その他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
円錐の表面積を一瞬で計算するための解説動画です
この動画を見る
円錐の表面積を一瞬で計算するための解説動画です
高校入試 数学 名古屋高校

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1から30までの自然数の中で6との最大公約数が1となる数は何コ?
名古屋高等学校
この動画を見る
1から30までの自然数の中で6との最大公約数が1となる数は何コ?
名古屋高等学校
【まずは3分、本気で5分!】確率:福岡県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)#福岡県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 福岡県の公立高等学校
4枚の硬貨
A、B、C、D を同時に投げる
↓
少なくとも1枚は、 表が出る確率を求めよ。
※硬貨のそれぞれについて、表と裏の出ることは同様に確からしいとする。
この動画を見る
入試問題 福岡県の公立高等学校
4枚の硬貨
A、B、C、D を同時に投げる
↓
少なくとも1枚は、 表が出る確率を求めよ。
※硬貨のそれぞれについて、表と裏の出ることは同様に確からしいとする。
高校入試 数学 図形 おうぎ形と正方形 創価高校
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
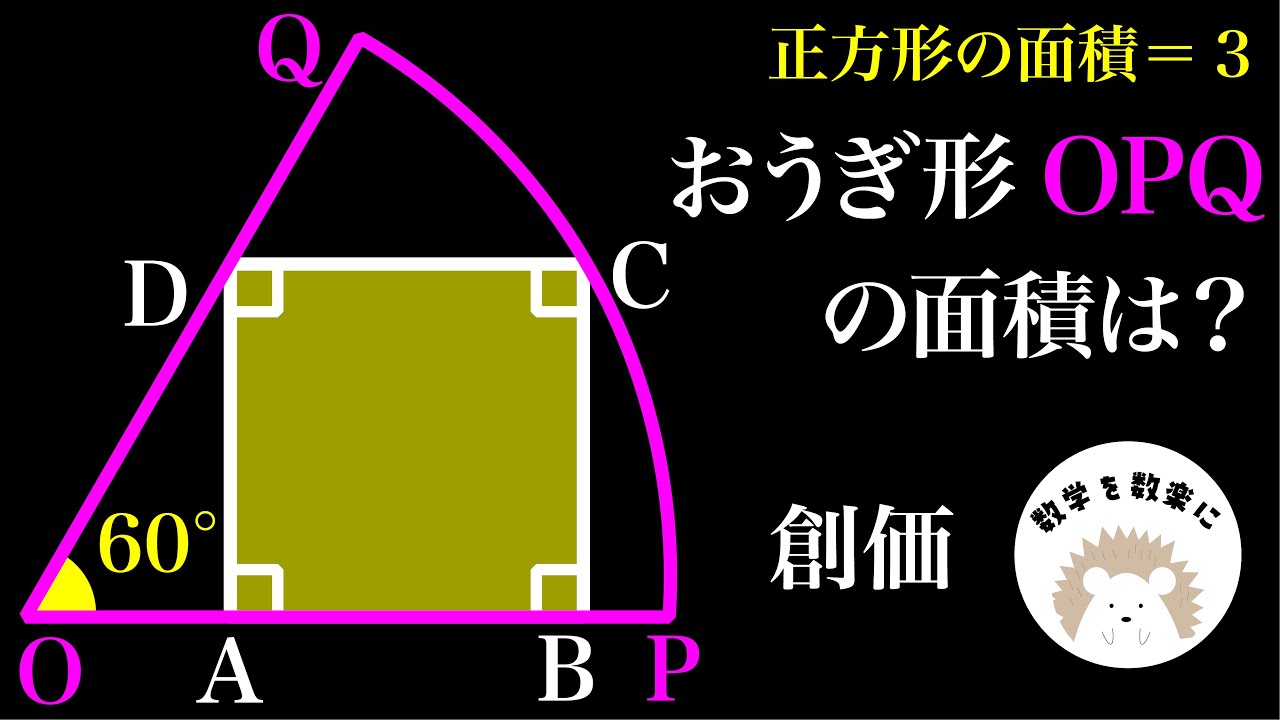
正方形ABCD=3のとき
おうぎ形OPQの面積=?
*図は動画内参照
創価高校
この動画を見る
正方形ABCD=3のとき
おうぎ形OPQの面積=?
*図は動画内参照
創価高校
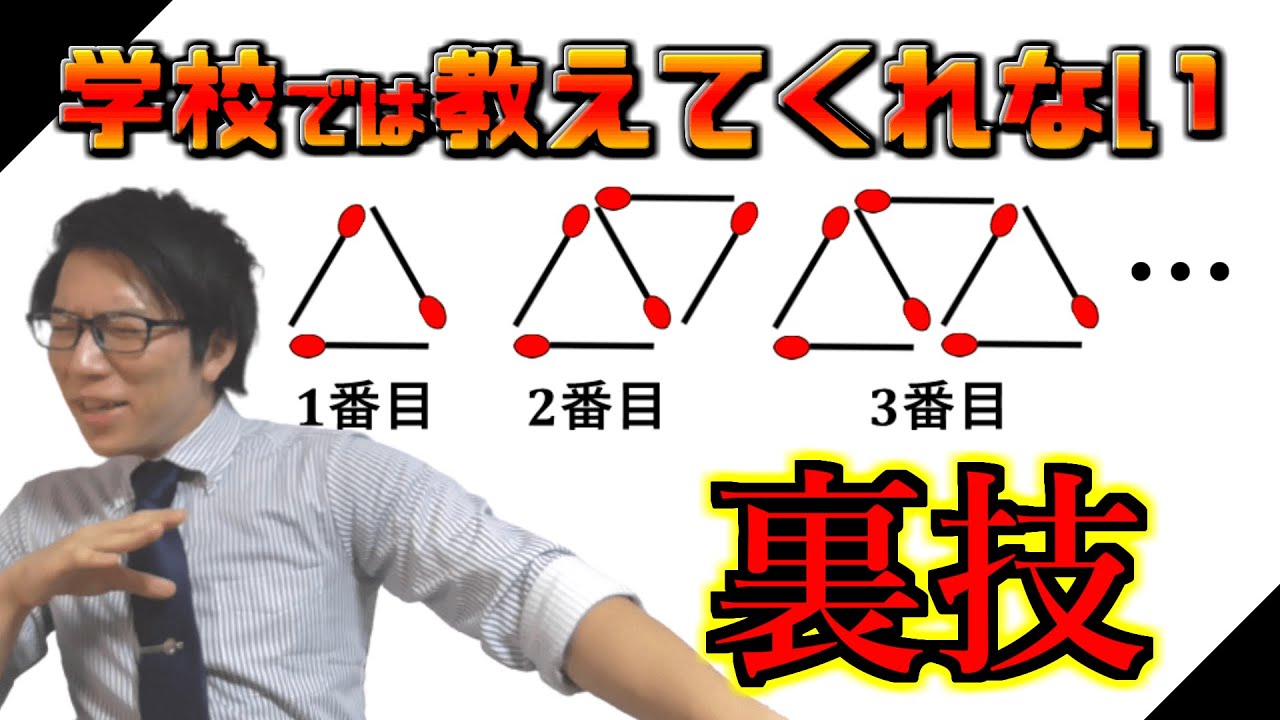
【中学数学】規則性の裏技~n番目を一瞬で求めます~
単元:
#算数(中学受験)#計算と数の性質#数学(中学生)#中1数学#中2数学#中3数学#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
【中学数学】規則性の裏技紹介動画です
この動画を見る
【中学数学】規則性の裏技紹介動画です
【中学数学】連立方程式:基礎の基礎から解説!その6 係数を揃えよう

単元:
#数学(中学生)#中2数学#連立方程式
教材:
#新中学問題集#新中学問題集(数学)2標準編#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の連立方程式を解け。
5x-2y=3
2x-3y=21
この動画を見る
次の連立方程式を解け。
5x-2y=3
2x-3y=21
【数学力!複雑なだけが応用じゃない!】図形:神奈川県公立高校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
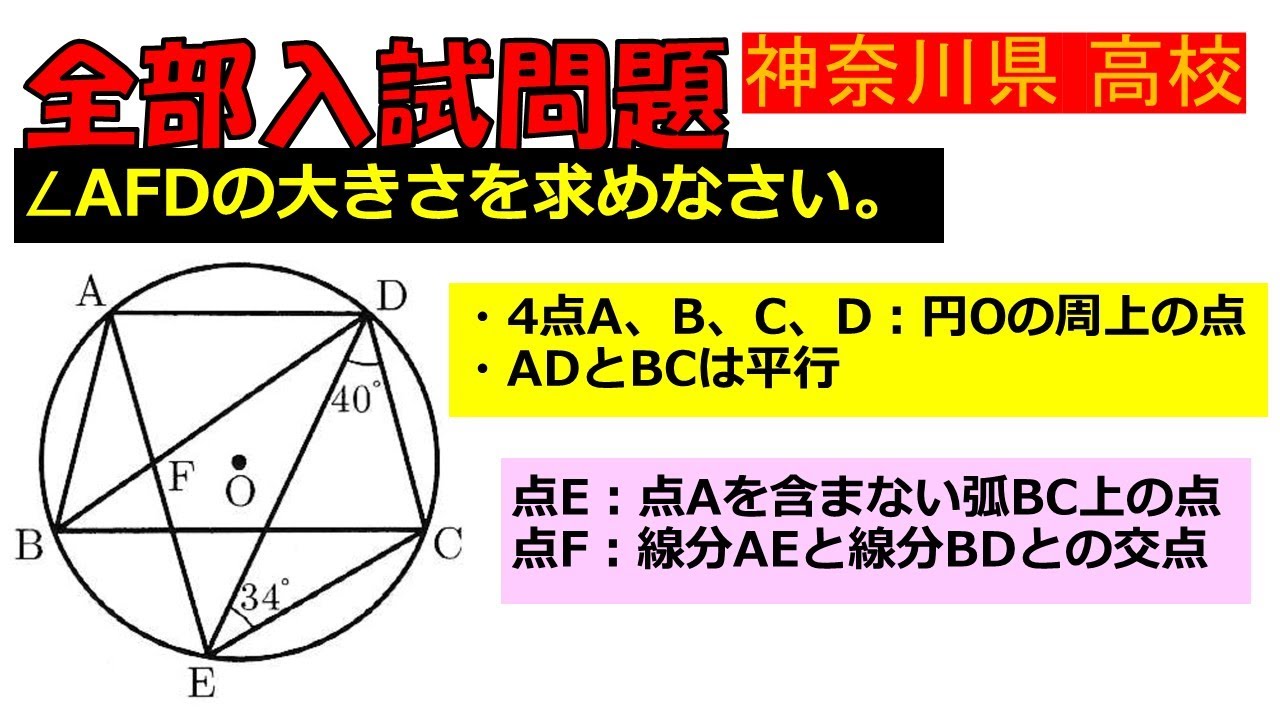
入試問題 神奈川県の公立高等学校
$\angle AFDの大きさを求めなさい。
・4点A、B、C、D:円○の周上の点
・ADとBCは平行
点E:点Aを含まない弧BC上の点
点F:線分AEと線分BDとの交点
※図は動画内参照
この動画を見る
入試問題 神奈川県の公立高等学校
$\angle AFDの大きさを求めなさい。
・4点A、B、C、D:円○の周上の点
・ADとBCは平行
点E:点Aを含まない弧BC上の点
点F:線分AEと線分BDとの交点
※図は動画内参照
X=2022??
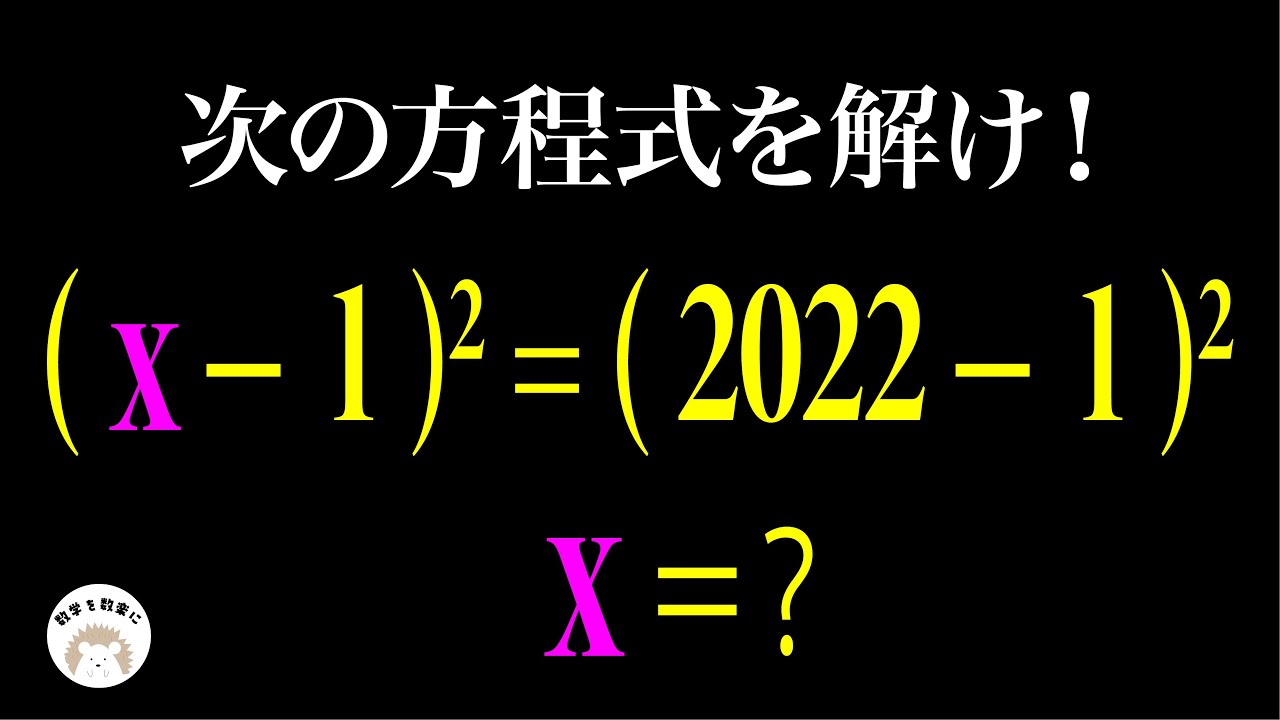
【中学数学】連立方程式:基礎の基礎から解説!その5 係数が揃っている方を消そう

単元:
#数学(中学生)#中2数学#連立方程式
教材:
#新中学問題集#新中学問題集(数学)2標準編#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の連立方程式を解け。
3x-y=10
x+y=6
この動画を見る
次の連立方程式を解け。
3x-y=10
x+y=6
【問題との付き合い方】因数分解・二次方程式:神奈川県公立高等学校~全国入試問題解法【選択式】

単元:
#数学(中学生)#式の計算(展開、因数分解)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 神奈川県の公立高等学校
$(x+6)^2-5(x+6)-24$
を因数分解しなさい。
【2次方程式】
$x^2-3x+1=0$
を解きなさい。
この動画を見る
入試問題 神奈川県の公立高等学校
$(x+6)^2-5(x+6)-24$
を因数分解しなさい。
【2次方程式】
$x^2-3x+1=0$
を解きなさい。
50の18%の暗算仕方

単元:
#算数(中学受験)#計算と数の性質#数学(中学生)#文章題#単位・比と割合・比例・反比例#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
50の18%の暗算仕方 説明動画です
この動画を見る
50の18%の暗算仕方 説明動画です
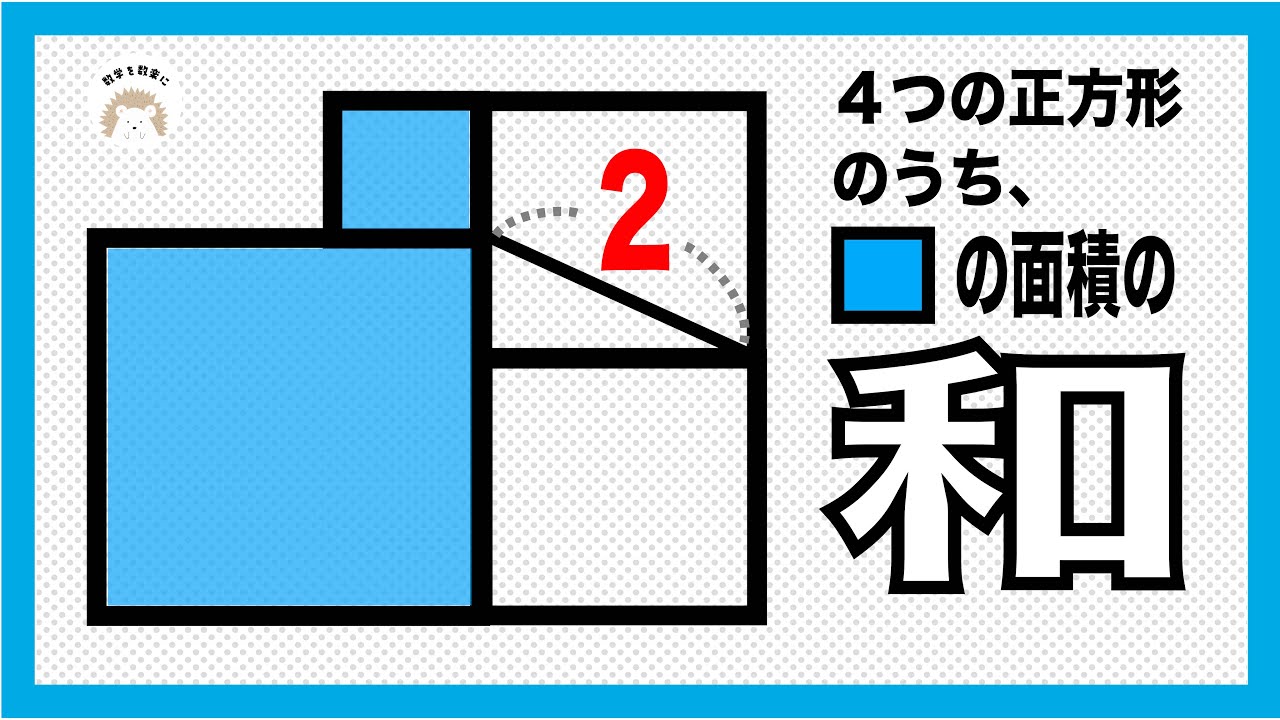
2つの正方形の面積の和
【観たら得をする5分間!】二次関数:埼玉県公立高校~全国入試問題解法
単元:
#数学(中学生)#2次関数#高校入試過去問(数学)#埼玉県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
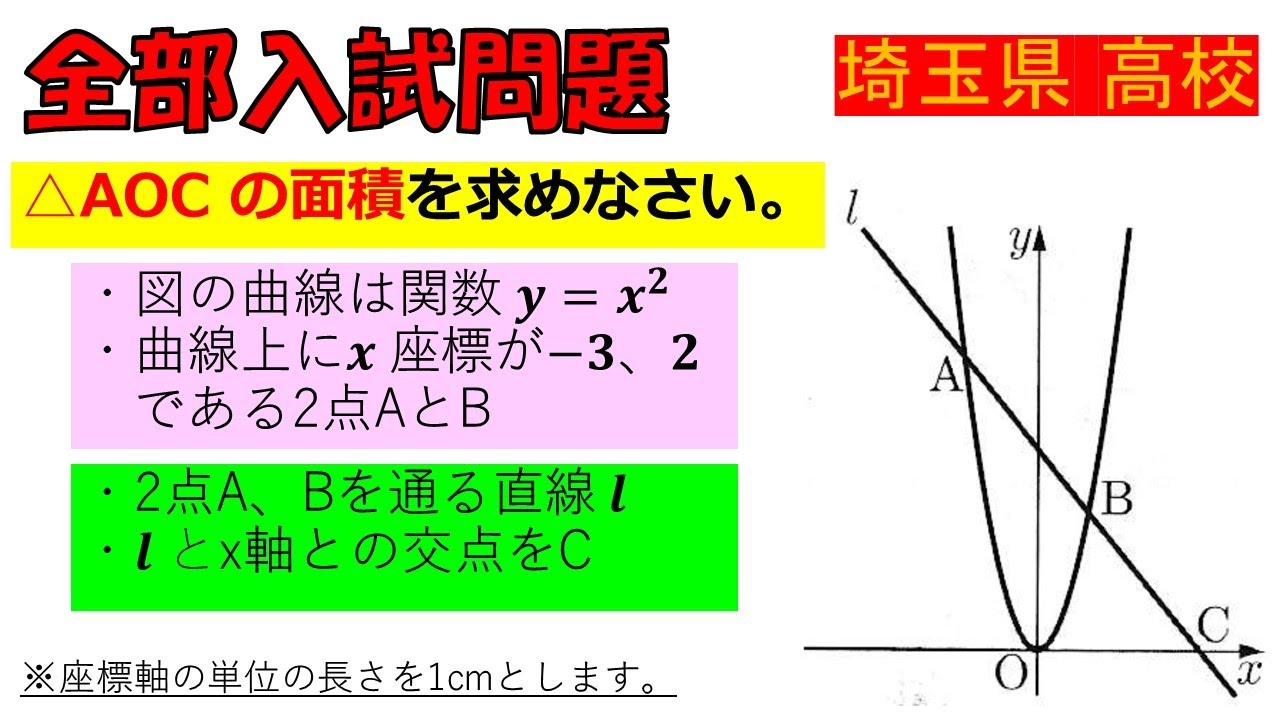
入試問題 埼玉県の公立高校
$\triangle AOC$ の面積を求めなさい。
・曲線は関数$ y = x^2 $
・曲線上に$x$座標が-3、2 である2点AとB
・2点$A$、$B$を通る直線 $ l $
・ $ l $と×軸との交点を$C$
※座標軸の単位の長さを1cmとします。
※図は動画内参照
この動画を見る
入試問題 埼玉県の公立高校
$\triangle AOC$ の面積を求めなさい。
・曲線は関数$ y = x^2 $
・曲線上に$x$座標が-3、2 である2点AとB
・2点$A$、$B$を通る直線 $ l $
・ $ l $と×軸との交点を$C$
※座標軸の単位の長さを1cmとします。
※図は動画内参照
【中学数学】座標上の四角形の面積の裏技~一瞬で求めよう~【中1数学】

複雑な平方根の計算

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{(\sqrt 5 -2)^{100}(5+2 \sqrt 5)^{100}}{5^{50}}$
関西学院
この動画を見る
$\frac{(\sqrt 5 -2)^{100}(5+2 \sqrt 5)^{100}}{5^{50}}$
関西学院
高校入試 整数問題 大阪星光学院

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
x+3y+6z=30を満たす自然数(x,y,z)の組は▢組ある
大阪星光学院高等学校
この動画を見る
x+3y+6z=30を満たす自然数(x,y,z)の組は▢組ある
大阪星光学院高等学校
【3分で数学の知識が1 up!】図形:佐賀県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#空間図形#平面図形#高校入試過去問(数学)#佐賀県立高校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
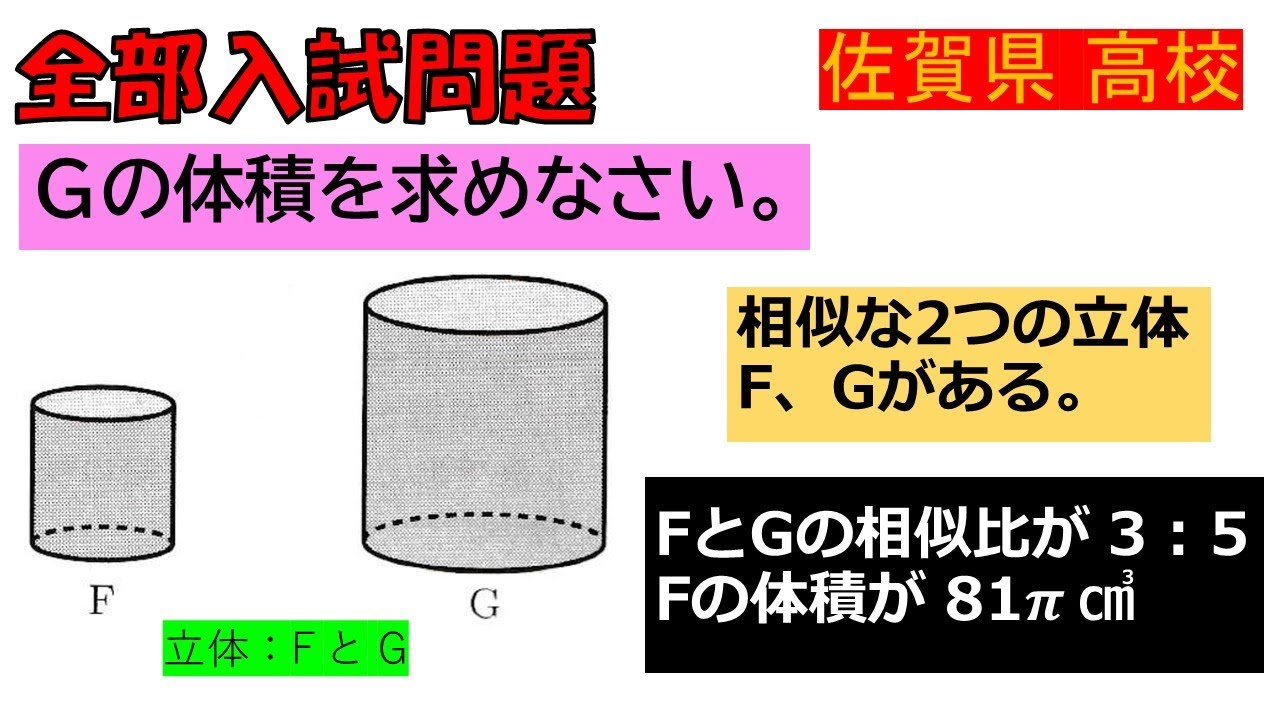
入試問題 佐賀県の公立高校
$G$の体積を求めなさい。
相似な2つの立体 $F$、$G$がある。
$F$と$G$の相似比が$3:5$
Fの体積が $81πcm^3$
※図は動画内参照
この動画を見る
入試問題 佐賀県の公立高校
$G$の体積を求めなさい。
相似な2つの立体 $F$、$G$がある。
$F$と$G$の相似比が$3:5$
Fの体積が $81πcm^3$
※図は動画内参照
平方根 泥臭く解くか華麗に解くか
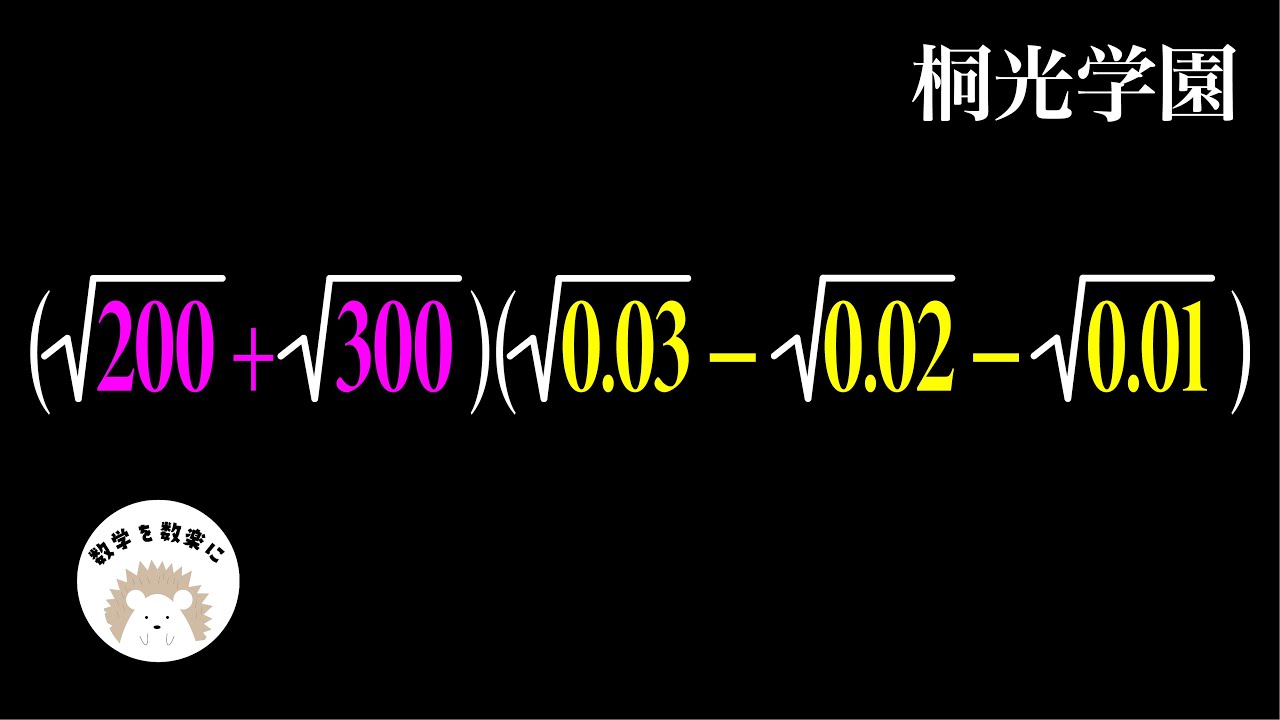
単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\sqrt {200} + \sqrt {300})(\sqrt {0.03} - \sqrt {0.02} -\sqrt {0.01})$
桐光学園高等学校
この動画を見る
$(\sqrt {200} + \sqrt {300})(\sqrt {0.03} - \sqrt {0.02} -\sqrt {0.01})$
桐光学園高等学校
最大値 最小値

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$-3 \leqq x \leqq 1 $ , $2x+y=0$のときxyの最大値と最小値を求めよ
慶應義塾高等学校
この動画を見る
$-3 \leqq x \leqq 1 $ , $2x+y=0$のときxyの最大値と最小値を求めよ
慶應義塾高等学校
この面積求めよ~対角線が垂直に交わる四角形の面積の求め方~

単元:
#算数(中学受験)#数学(中学生)#中1数学#平面図形#平面図形#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
対角線が垂直に交わる四角形の面積の求め方
この動画を見る
対角線が垂直に交わる四角形の面積の求め方
