福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田の数学〜早稲田大学2025人間科学部第2問〜絶対値の付いた関数の最小
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
$a\lt b \lt c$を満たす実数の定数に対して、
すべての実数を定義域とする$x$の関数
$f(x)=\vert x-a \vert + \vert x-b \vert + \vert x-c \vert $を定める。
このとき、$5x+4f(x)$の最小値は
$\boxed{ク}a + \boxed{ケ}b + \boxed{コ}c$である。
また、$f(x)$の最小値が$20$で、
$f(c)=28$かつ$f(10)=31$を満たす$a$の値は
$\boxed{サ}$と$\boxed{シ}$である。
ただし、$\boxed{サ} \lt \boxed{シ}$とする。
$2025$年早稲田大学人間科学部過去問題
この動画を見る
$\boxed{2}$
$a\lt b \lt c$を満たす実数の定数に対して、
すべての実数を定義域とする$x$の関数
$f(x)=\vert x-a \vert + \vert x-b \vert + \vert x-c \vert $を定める。
このとき、$5x+4f(x)$の最小値は
$\boxed{ク}a + \boxed{ケ}b + \boxed{コ}c$である。
また、$f(x)$の最小値が$20$で、
$f(c)=28$かつ$f(10)=31$を満たす$a$の値は
$\boxed{サ}$と$\boxed{シ}$である。
ただし、$\boxed{サ} \lt \boxed{シ}$とする。
$2025$年早稲田大学人間科学部過去問題
福田のおもしろ数学550〜不定方程式の整数解
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x^6+3x^3+1=y^4$
を満たす整数の組$(x,y)$
をすべて求めて下さい。
この動画を見る
$x^6+3x^3+1=y^4$
を満たす整数の組$(x,y)$
をすべて求めて下さい。
福田の数学〜早稲田大学2025人間科学部第1問(3)〜球面が平面から切り取る領域の面積
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(3)座標空間における$2$点
$\left(\dfrac{\sqrt{35}}{2},5,10\right),\left(-\dfrac{\sqrt{35}}{2},10,-4\right)$
を直径の両端とする球面$S$がある。
球面$S$が$xy$平面を切り取る領域の面積は
$\boxed{カ}\pi$である。
また、球面$S$が$z$軸を切り取る線分の長さは
$\sqrt{\boxed{キ}}$である。
$2025$年早稲田大学人間科学部過去問題
この動画を見る
$\boxed{1}$
(3)座標空間における$2$点
$\left(\dfrac{\sqrt{35}}{2},5,10\right),\left(-\dfrac{\sqrt{35}}{2},10,-4\right)$
を直径の両端とする球面$S$がある。
球面$S$が$xy$平面を切り取る領域の面積は
$\boxed{カ}\pi$である。
また、球面$S$が$z$軸を切り取る線分の長さは
$\sqrt{\boxed{キ}}$である。
$2025$年早稲田大学人間科学部過去問題
福田のおもしろ数学549〜無理関数の不定積分その2
単元：
#関数と極限#積分とその応用#関数（分数関数・無理関数・逆関数と合成関数）#不定積分#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
不定積分
$I=\displaystyle \int \sqrt{x^2-1}dx \ (x\gt 1)$を
$x=\sqrt{x^2-1}=t$
と置き換えて求めて下さい。
この動画を見る
不定積分
$I=\displaystyle \int \sqrt{x^2-1}dx \ (x\gt 1)$を
$x=\sqrt{x^2-1}=t$
と置き換えて求めて下さい。
福田の数学〜早稲田大学2025人間科学部第1問(2)〜ルートの2個ある無理方程式の解法
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(2)方程式
$\sqrt{x+510}+\sqrt{x+822}=52$
の解は$x=\boxed{オ}$である。
$2025$年早稲田大学人間科学部過去問題
この動画を見る
$\boxed{1}$
(2)方程式
$\sqrt{x+510}+\sqrt{x+822}=52$
の解は$x=\boxed{オ}$である。
$2025$年早稲田大学人間科学部過去問題
福田のおもしろ数学548〜無理関数の不定積分
単元：
#関数と極限#積分とその応用#関数（分数関数・無理関数・逆関数と合成関数）#不定積分#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
不定積分$I=\displaystyle \int \sqrt{x^2-1}dx \ (x\gt 1)$を
$x=\dfrac{1}{\cos\theta}$と
置き換えて求めて下さい。
この動画を見る
不定積分$I=\displaystyle \int \sqrt{x^2-1}dx \ (x\gt 1)$を
$x=\dfrac{1}{\cos\theta}$と
置き換えて求めて下さい。
福田の数学〜早稲田大学2025人間科学部第1問(1)〜4次式の因数分解と未定係数法
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算（整式・展開・因数分解）#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(1)整式$x^4-13x^2+18x-5$を整数係数の
範囲で因数分解すると
$(x^2+\boxed{ア} x+\boxed{イ})(x^2+\boxed{ウ}x+\boxed{エ})$
となる。
ただし、$\boxed{ア}\lt \boxed{ウ}$とする。
$2025$年早稲田大学人間科学部過去問題
この動画を見る
$\boxed{1}$
(1)整式$x^4-13x^2+18x-5$を整数係数の
範囲で因数分解すると
$(x^2+\boxed{ア} x+\boxed{イ})(x^2+\boxed{ウ}x+\boxed{エ})$
となる。
ただし、$\boxed{ア}\lt \boxed{ウ}$とする。
$2025$年早稲田大学人間科学部過去問題
福田のおもしろ数学547〜複素数の偏角
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
複素数
$(1-\cos 20°-i \sin 20°)^{10}$
の偏角を$0°～360°$の範囲で求めよ。
この動画を見る
複素数
$(1-\cos 20°-i \sin 20°)^{10}$
の偏角を$0°～360°$の範囲で求めよ。
福田の数学〜九州大学2025文系第2問〜円周上の2点との距離の2乗の和の最大値
単元：
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#三角関数#三角関数とグラフ#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
半径$1$の円周$C$上の$2$点$A,B$は
$AB=\sqrt3$をみたすとする。
点$P$が円周$C$上を動くとき、
$AP^2+BP^2$の最大値を求めよ。
$2025$年九州大学文系過去問題
この動画を見る
$\boxed{2}$
半径$1$の円周$C$上の$2$点$A,B$は
$AB=\sqrt3$をみたすとする。
点$P$が円周$C$上を動くとき、
$AP^2+BP^2$の最大値を求めよ。
$2025$年九州大学文系過去問題
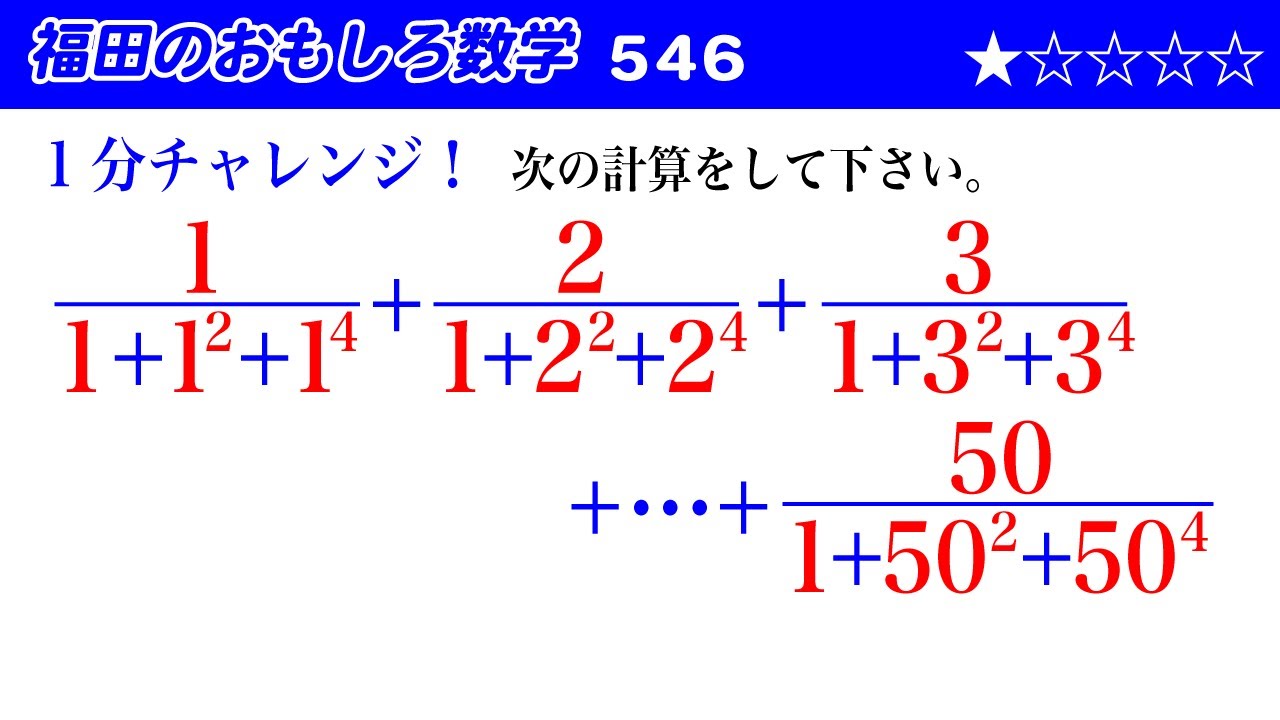
福田のおもしろ数学546〜1分チャレンジ！数値計算の計算
単元：
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
次の計算をして下さい。
$\dfrac{1}{1+1^2+1^4}+\dfrac{2}{1+2^2+2^4}+\dfrac{3}{1+3^2+3^4}+\cdots + \dfrac{50}{1+50^2+50^4}$
この動画を見る
次の計算をして下さい。
$\dfrac{1}{1+1^2+1^4}+\dfrac{2}{1+2^2+2^4}+\dfrac{3}{1+3^2+3^4}+\cdots + \dfrac{50}{1+50^2+50^4}$
福田の数学〜九州大学2025文系第1問〜共通接線
単元：
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
$2$つの曲線
$y=x^3+x^2-x-1,y=x^2$
の両方に接するすべての直線の
方程式を求めよ。
$2025$年九州大学文系過去問題
この動画を見る
$\boxed{1}$
$2$つの曲線
$y=x^3+x^2-x-1,y=x^2$
の両方に接するすべての直線の
方程式を求めよ。
$2025$年九州大学文系過去問題
福田のおもしろ数学545〜最大公約数と最小公倍数の商で定まる数列
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
自然数の列$\{a_n\}$が次の性質を満たしている。
$a_n=\dfrac{Icm(a_{n-1},a_{n-2})}{gcd(a_{n-1},a_{n-2})} \quad (n\geqq 2)$
$a_{560}=560,a_{1600}=1600$のとき
$a_{2025}$を求めて下さい。
この動画を見る
自然数の列$\{a_n\}$が次の性質を満たしている。
$a_n=\dfrac{Icm(a_{n-1},a_{n-2})}{gcd(a_{n-1},a_{n-2})} \quad (n\geqq 2)$
$a_{560}=560,a_{1600}=1600$のとき
$a_{2025}$を求めて下さい。
福田の数学〜九州大学2025理系第5問〜3次方程式の解と確率
単元：
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#複素数と方程式#場合の数#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{5}$
$1$個のさいころを$3$回続けて投げ、
出る目を順に$a,b,c$とする。
整式$f(x)=(x^2-ax+b)(x-c)$
について、以下の問いに答えよ。
(1)$f(x)=0$をみたす実数$x$の個数が
$1$個である確率を求めよ。
(2)$f(x)=0$をみたす自然数$x$の個数が
$3$個である確率を求めよ。
$2025$年九州大学理系過去問題
この動画を見る
$\boxed{5}$
$1$個のさいころを$3$回続けて投げ、
出る目を順に$a,b,c$とする。
整式$f(x)=(x^2-ax+b)(x-c)$
について、以下の問いに答えよ。
(1)$f(x)=0$をみたす実数$x$の個数が
$1$個である確率を求めよ。
(2)$f(x)=0$をみたす自然数$x$の個数が
$3$個である確率を求めよ。
$2025$年九州大学理系過去問題
福田のおもしろ数学544〜1分チャレンジ！微分の計算
単元：
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$y=\sqrt[3]{x+\sqrt{x^2+1}}+\sqrt[3]{x-\sqrt{x^2+1}}$
に対して、
導関数$y'$を$y$で表して下さい。
この動画を見る
$y=\sqrt[3]{x+\sqrt{x^2+1}}+\sqrt[3]{x-\sqrt{x^2+1}}$
に対して、
導関数$y'$を$y$で表して下さい。
福田の数学〜九州大学2025理系第4問〜平面幾何の証明
単元：
#数A#図形の性質#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
半径$1$の円周上に反時計回りに
点$A,B,C,D$を順にとり、
線分$AD$は直径で、$AC=CD$、
$AB=BC$が成り立つとする。
(1)$\angle ACB$を求めよ。
(2)$BC$を求めよ。
(3)線分$AC$と線分$BD$の交点を$E$とするとき、
三角形$BCE$の面積を求めよ。
$2025$年九州大学理系過去問題
この動画を見る
$\boxed{4}$
半径$1$の円周上に反時計回りに
点$A,B,C,D$を順にとり、
線分$AD$は直径で、$AC=CD$、
$AB=BC$が成り立つとする。
(1)$\angle ACB$を求めよ。
(2)$BC$を求めよ。
(3)線分$AC$と線分$BD$の交点を$E$とするとき、
三角形$BCE$の面積を求めよ。
$2025$年九州大学理系過去問題
福田のおもしろ数学543〜2つの球面に引いた接線の長さの等しい点の軌跡
福田の数学〜九州大学2025理系第3問〜剰余類と不定方程式の整数解
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
以下の問いに答えよ。
(1)$n$を整数とするとき、$n^2$を$8$で割った
余りは$0,1,4$のいずれかであることを示せ。
(2)$2^m=n^2+3$をみたす$0$以上の整数の組
$(m,n)$をすべて求めよ。
$2025$年九州大学理系過去問題
この動画を見る
$\boxed{3}$
以下の問いに答えよ。
(1)$n$を整数とするとき、$n^2$を$8$で割った
余りは$0,1,4$のいずれかであることを示せ。
(2)$2^m=n^2+3$をみたす$0$以上の整数の組
$(m,n)$をすべて求めよ。
$2025$年九州大学理系過去問題
福田のおもしろ数学542〜定積分の値の評価
単元：
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\dfrac{1}{3}\lt \displaystyle \int_{0}^{1}x^{(\sin x+\cos x)^2}dx \lt \dfrac{1}{2}$
を証明して下さい。
この動画を見る
$\dfrac{1}{3}\lt \displaystyle \int_{0}^{1}x^{(\sin x+\cos x)^2}dx \lt \dfrac{1}{2}$
を証明して下さい。
福田の数学〜九州大学2025理系第2問〜定積分の計算
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
以下の問いに答えよ。
(1)$y=\tan x$とするとき、
$\dfrac{dy}{dx}$を$y$の整式で表せ。
(2)次の定積分を求めよ。
$\displaystyle \int_{0}^{\frac{\pi}{4}}\dfrac{\tan^4x-\tan^2 x-2}{\tan^2x-4}dx$
$2025$年九州大学理系過去問題
この動画を見る
$\boxed{2}$
以下の問いに答えよ。
(1)$y=\tan x$とするとき、
$\dfrac{dy}{dx}$を$y$の整式で表せ。
(2)次の定積分を求めよ。
$\displaystyle \int_{0}^{\frac{\pi}{4}}\dfrac{\tan^4x-\tan^2 x-2}{\tan^2x-4}dx$
$2025$年九州大学理系過去問題
福田のおもしろ数学541〜条件付き不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x,y,z$は
$x+y+z \geqq xyz$
を満たす非負実数とするとき
$x^2+y^2+z^2 \geqq xyz$
を証明して下さい。
この動画を見る
$x,y,z$は
$x+y+z \geqq xyz$
を満たす非負実数とするとき
$x^2+y^2+z^2 \geqq xyz$
を証明して下さい。
福田の数学〜九州大学2025理系第1問〜平面に垂直なベクトルの絶対値の最小
単元：
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
座標空間内の$3$点$A(1,1,-5),B(-1,-1,7),C(1,-1,3)$を
通る平面を$\alpha$とする。
点$P(a,b,t)$を通り$\alpha$に垂直な直線と
$xy$平面との交点を$Q$とする。
(1)点$Q$の座標を求めよ。
(2)$t$がすべての実数値をとって変化するときの
$OQ$の最小値が$1$以下となるような
$a,b$の条件を求めよ。
ただし、$O$は原点である。
$2025$年九州大学理系過去問題
この動画を見る
$\boxed{1}$
座標空間内の$3$点$A(1,1,-5),B(-1,-1,7),C(1,-1,3)$を
通る平面を$\alpha$とする。
点$P(a,b,t)$を通り$\alpha$に垂直な直線と
$xy$平面との交点を$Q$とする。
(1)点$Q$の座標を求めよ。
(2)$t$がすべての実数値をとって変化するときの
$OQ$の最小値が$1$以下となるような
$a,b$の条件を求めよ。
ただし、$O$は原点である。
$2025$年九州大学理系過去問題
福田のおもしろ数学540〜二項係数の2乗の和
単元：
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${{}_n \mathrm{ C }_0}^2+{{}_n \mathrm{ C }_1}^2+{{}_n \mathrm{ C }_2}^2+\cdots + {{}_n \mathrm{ C }_n}^2=\dfrac{(2n)!}{(n!)^2}$
を証明してください。
この動画を見る
${{}_n \mathrm{ C }_0}^2+{{}_n \mathrm{ C }_1}^2+{{}_n \mathrm{ C }_2}^2+\cdots + {{}_n \mathrm{ C }_n}^2=\dfrac{(2n)!}{(n!)^2}$
を証明してください。
福田の数学〜神戸大学2025文系第3問〜単位円周上の2点と確率
単元：
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#場合の数#三角関数#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
$1$個のさいころを$2$回続けて投げるとき、
出た目の数を順に$a,b$とおく。
座標平面上の$2$点$A,B$を
$A\left(\cos \dfrac{a}{6}\pi,\sin\dfrac{a}{6}\pi\right),\quad B\left(\cos \dfrac{b+6}{6}\pi,\sin\dfrac{b+6}{6}\pi\right)$
とし、原点を$O$とする。
以下の問いに答えよ。
(1)$3$点$O,A,B$が一直線上にある確率を求めよ。
(2)$3$点$O,A,B$が一直線上になく、かつ
三角形$OAB$の面積が$\dfrac{1}{4}$以下である
確率を求めよ。
(3)$2$点$A,B$間の距離が$1$より
大きい確率を求めよ。
$2025$年神戸大学文系過去問題
この動画を見る
$\boxed{3}$
$1$個のさいころを$2$回続けて投げるとき、
出た目の数を順に$a,b$とおく。
座標平面上の$2$点$A,B$を
$A\left(\cos \dfrac{a}{6}\pi,\sin\dfrac{a}{6}\pi\right),\quad B\left(\cos \dfrac{b+6}{6}\pi,\sin\dfrac{b+6}{6}\pi\right)$
とし、原点を$O$とする。
以下の問いに答えよ。
(1)$3$点$O,A,B$が一直線上にある確率を求めよ。
(2)$3$点$O,A,B$が一直線上になく、かつ
三角形$OAB$の面積が$\dfrac{1}{4}$以下である
確率を求めよ。
(3)$2$点$A,B$間の距離が$1$より
大きい確率を求めよ。
$2025$年神戸大学文系過去問題
福田のおもしろ数学539〜部分和がすべて正になるような数列を作れるか
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
総和が$1$である$2025$個の整数が円形に
並んでいる。
ある整数から出発して反時計回りでこれらの
整数を一列に並べ$a_1,a_2,a_3,\cdots, a_{2025}$とする。
これらの部分和$S_n=\displaystyle \sum_{k=1}^{n} a_k \quad (n=1,2,\cdots ,2025)$
がすべて正となるようにできるか？
この動画を見る
総和が$1$である$2025$個の整数が円形に
並んでいる。
ある整数から出発して反時計回りでこれらの
整数を一列に並べ$a_1,a_2,a_3,\cdots, a_{2025}$とする。
これらの部分和$S_n=\displaystyle \sum_{k=1}^{n} a_k \quad (n=1,2,\cdots ,2025)$
がすべて正となるようにできるか？
福田の数学〜神戸大学2025文系第2問〜小数部分と命題の証明
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算（整式・展開・因数分解）#集合と命題（集合・命題と条件・背理法）#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
実数$a$に対して、
$a$を超えない最大の整数を$k$とするとき、
$a-k$を$a$の小数部分という。
$n$を自然数とし、$a_n=\sqrt{n^2+1}$とおく。
以下の問いに答えよ。
(1)$a_n \lt n+1$が成り立つことを示せ。
(2)$b_n$を$a_n$の小数部分とする。
$b_n$を$n$を用いて表せ。
(3)$b_n$を(2)で定めたものとする。
$m,n$を異なる$2$つの自然数とするとき、
$b_m \neq b_n$であることを示せ。
$2025$年神戸大学文系過去問題
この動画を見る
$\boxed{2}$
実数$a$に対して、
$a$を超えない最大の整数を$k$とするとき、
$a-k$を$a$の小数部分という。
$n$を自然数とし、$a_n=\sqrt{n^2+1}$とおく。
以下の問いに答えよ。
(1)$a_n \lt n+1$が成り立つことを示せ。
(2)$b_n$を$a_n$の小数部分とする。
$b_n$を$n$を用いて表せ。
(3)$b_n$を(2)で定めたものとする。
$m,n$を異なる$2$つの自然数とするとき、
$b_m \neq b_n$であることを示せ。
$2025$年神戸大学文系過去問題
福田のおもしろ数学538〜数列の一般項を1つの式で表す
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
数列
$1,1,2,2,3,3,4,4,\cdots $
の一般項を$1$つの式で表せ。
この動画を見る
数列
$1,1,2,2,3,3,4,4,\cdots $
の一般項を$1$つの式で表せ。
福田の数学〜神戸大学2025文系第1問〜3次方程式が異なる3個の実数解をもつ条件
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
$a$を実数とする。
$f(x)=2x^3+ax^2-1$とおくとき、以下の問いに答えよ。
(1)方程式$f(x)=0$は$x=-1$に解にもつとする。
このとき、$a$の値を求め、
方程式$f(x)=0$の解をすべて求めよ。
(2)$a$の値を(1)で求めたものとする。
関数$f(x)$の極限を求めよ。
(3)方程式$f(x)=0$が異なる$3$つの実数解を
もつような$a$の値の範囲を求めよ。
$2025$年神戸大学文系過去問題
この動画を見る
$\boxed{1}$
$a$を実数とする。
$f(x)=2x^3+ax^2-1$とおくとき、以下の問いに答えよ。
(1)方程式$f(x)=0$は$x=-1$に解にもつとする。
このとき、$a$の値を求め、
方程式$f(x)=0$の解をすべて求めよ。
(2)$a$の値を(1)で求めたものとする。
関数$f(x)$の極限を求めよ。
(3)方程式$f(x)=0$が異なる$3$つの実数解を
もつような$a$の値の範囲を求めよ。
$2025$年神戸大学文系過去問題
福田のおもしろ数学537〜2変数関数の極限
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$xy-x^3\tan \dfrac{1}{x}+y^2=0$のとき、
$\displaystyle \lim_{x\to\infty}\dfrac{y}{x}$を求めよ。
この動画を見る
$xy-x^3\tan \dfrac{1}{x}+y^2=0$のとき、
$\displaystyle \lim_{x\to\infty}\dfrac{y}{x}$を求めよ。
福田の数学〜神戸大学2025理系第5問〜連続と微分可能と曲線の長さ
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{5}$
連続関数$f(x)$は$x \geqq 0$で$f(x) \geqq 0$を満たし、
$x \gt 0$で微分可能であり、その導関数$f'(x)$は
連続であるとする。
$t \geqq 1$を満たす$t$に対して、
$y=f(x) \ (1\leqq x \leqq t)$で表される曲線の長さを
$h(t)$とし、$t=1$のときは$h(1)=0$とする。
以下の問いに答えよ。
(1)$t\gt 1$とする。
開区間$(1,t)$で常に$f(x)-xf'(x)=0$が成り立つならば、
閉区間$[1,t]$で$\dfrac{f(x)}{x}$は定数であることを示せ。
(2)$t\geqq 1$を満たす任意の$t$に対して、
$g(t)=h(t)+2$が成り立つとする。
このとき、$f(1)$の値を求めよ。
また、$t\geqq 1$のとき$f(t)$を$t$を用いて表せ。
$2025$年神戸大学理系過去問題
この動画を見る
$\boxed{5}$
連続関数$f(x)$は$x \geqq 0$で$f(x) \geqq 0$を満たし、
$x \gt 0$で微分可能であり、その導関数$f'(x)$は
連続であるとする。
$t \geqq 1$を満たす$t$に対して、
$y=f(x) \ (1\leqq x \leqq t)$で表される曲線の長さを
$h(t)$とし、$t=1$のときは$h(1)=0$とする。
以下の問いに答えよ。
(1)$t\gt 1$とする。
開区間$(1,t)$で常に$f(x)-xf'(x)=0$が成り立つならば、
閉区間$[1,t]$で$\dfrac{f(x)}{x}$は定数であることを示せ。
(2)$t\geqq 1$を満たす任意の$t$に対して、
$g(t)=h(t)+2$が成り立つとする。
このとき、$f(1)$の値を求めよ。
また、$t\geqq 1$のとき$f(t)$を$t$を用いて表せ。
$2025$年神戸大学理系過去問題
福田のおもしろ数学536〜不定方程式の整数解
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\dfrac{13}{x^2}+\dfrac{508}{y^2}=\dfrac{z}{509}$
を満たす正の整数の組
$(x,y,z)$をすべて求めよ。
この動画を見る
$\dfrac{13}{x^2}+\dfrac{508}{y^2}=\dfrac{z}{509}$
を満たす正の整数の組
$(x,y,z)$をすべて求めよ。