 福田次郎
福田次郎
 福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田の数学〜中央大学2023年経済学部第1問(4)〜対数の大小比較

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (4)次の3つの数A, B, Cを小さい順に並べよ。
A=$\frac{1}{2}\log_2\frac{1}{2}$, B=$\frac{1}{3}\log_2\frac{1}{3}$, A=$\frac{1}{6}\log_2\frac{1}{6}$
この動画を見る
$\Large\boxed{1}$ (4)次の3つの数A, B, Cを小さい順に並べよ。
A=$\frac{1}{2}\log_2\frac{1}{2}$, B=$\frac{1}{3}\log_2\frac{1}{3}$, A=$\frac{1}{6}\log_2\frac{1}{6}$
福田の数学〜中央大学2023年経済学部第1問(3)〜三角関数の最大

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$0\leqq x\leqq \require{physics}\flatfrac{\pi}{2}$のとき、次の関数が最大となる$x$の値を求めよ。
$y=\sin ^22x+2\cos^2x$
2023中央大学経済学部過去問
この動画を見る
$0\leqq x\leqq \require{physics}\flatfrac{\pi}{2}$のとき、次の関数が最大となる$x$の値を求めよ。
$y=\sin ^22x+2\cos^2x$
2023中央大学経済学部過去問
福田の数学〜中央大学2023年経済学部第1問(2)〜同じものを含む順列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)E, C, O, N, O, M, I, C, Sの9文字を並べ替えて作ることのできる文字列の個数はC, O, M, M, E, R, C, Eの8文字を並べ替えて作ることのできる文字列の個数と比べて何倍あるか。
この動画を見る
$\Large\boxed{1}$ (2)E, C, O, N, O, M, I, C, Sの9文字を並べ替えて作ることのできる文字列の個数はC, O, M, M, E, R, C, Eの8文字を並べ替えて作ることのできる文字列の個数と比べて何倍あるか。
福田の数学〜中央大学2023年経済学部第1問(1)〜整式の割り算

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)整式$x^3$+$ax^2$+$bx$-3 が$x^2$+$x$-6 で割り切れるとき、定数$a$, $b$の値を求めよ。
この動画を見る
$\Large\boxed{1}$ (1)整式$x^3$+$ax^2$+$bx$-3 が$x^2$+$x$-6 で割り切れるとき、定数$a$, $b$の値を求めよ。
福田の数学〜上智大学2023年理工学部第3問〜対数関数の積分と数学的帰納法

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#数列#数学的帰納法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ $e$を自然定数の底とする。自然数$n$に対して、
$S_n$=$\displaystyle\int_1^e(\log x)^n dx$
とする。
(1)$S_1$の値を求めよ。
(2)すべての自然数$n$に対して、
$S_n$=$a_n e$+$b_n$, ただし$a_n$, $b_n$はいずれも整数
と表されることを証明せよ。
この動画を見る
$\Large\boxed{3}$ $e$を自然定数の底とする。自然数$n$に対して、
$S_n$=$\displaystyle\int_1^e(\log x)^n dx$
とする。
(1)$S_1$の値を求めよ。
(2)すべての自然数$n$に対して、
$S_n$=$a_n e$+$b_n$, ただし$a_n$, $b_n$はいずれも整数
と表されることを証明せよ。
福田の数学〜上智大学2023年理工学部第2問〜逆関数の微分積分

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 関数$f(x)$=$\sin x$ $\left(0≦x≦\frac{\pi}{2}\right)$の逆関数を$g(x)$とする。
(1)関数$g(x)$の定義域は$\boxed{\ \ え\ \ }$である。
(2)$y$=$g(x)$の$x$=$\frac{4}{5}$における接線の傾きは$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$である。
(3)$\displaystyle\int_0^{\frac{1}{2}}g(x)dx$=$\displaystyle\frac{\pi}{\boxed{\ \ キ\ \ }}$+$\boxed{\ \ ク\ \ }$+$\displaystyle\frac{\boxed{\ \ ケ\ \ }}{\boxed{\ \ コ\ \ }}\sqrt{\boxed{\ \ サ\ \ }}$である。
(4)$y$=$g(x)$のグラフと$x$=1および$x$軸で囲まれた図形を$x$軸のまわりに1回転させてできる立体の体積は$\displaystyle\frac{\pi^a}{\boxed{\ \ シ\ \ }}$+$\boxed{\ \ ス\ \ }\pi$ ただし$a$=$\boxed{\ \ セ\ \ }$である。
この動画を見る
$\Large{\boxed{2}}$ 関数$f(x)$=$\sin x$ $\left(0≦x≦\frac{\pi}{2}\right)$の逆関数を$g(x)$とする。
(1)関数$g(x)$の定義域は$\boxed{\ \ え\ \ }$である。
(2)$y$=$g(x)$の$x$=$\frac{4}{5}$における接線の傾きは$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$である。
(3)$\displaystyle\int_0^{\frac{1}{2}}g(x)dx$=$\displaystyle\frac{\pi}{\boxed{\ \ キ\ \ }}$+$\boxed{\ \ ク\ \ }$+$\displaystyle\frac{\boxed{\ \ ケ\ \ }}{\boxed{\ \ コ\ \ }}\sqrt{\boxed{\ \ サ\ \ }}$である。
(4)$y$=$g(x)$のグラフと$x$=1および$x$軸で囲まれた図形を$x$軸のまわりに1回転させてできる立体の体積は$\displaystyle\frac{\pi^a}{\boxed{\ \ シ\ \ }}$+$\boxed{\ \ ス\ \ }\pi$ ただし$a$=$\boxed{\ \ セ\ \ }$である。
福田の数学〜上智大学2023年理工学部第1問(3)〜正四面体を切った断面

単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (3)一辺の長さが2である正四面体OABCにおいて、辺OAの中点をM、辺BCの中点をNとする。
(i)線分MNの長さは$\boxed{\ \ あ\ \ }$である。
(ii)0<$s$<1とし、線分MNを$s$:$(1-s)$に内分する点をPとする。Pを通りMNに垂直な平面で四面体OABCを切った断面は$\boxed{\ \ い\ \ }$であり、その面積は$\boxed{\ \ う\ \ }$である。
$\boxed{\ \ あ\ \ }$の選択肢
(a)1 (b)$\sqrt 2$ (c)$\sqrt 3$ (d)2 (e)$\frac{1+\sqrt 5}{2}$ (f)$\frac{\sqrt 6}{2}$
$\boxed{\ \ い\ \ }$の選択肢
(a)正三角形 (b)正三角形でない二等辺三角形 (c)二等辺三角形でない三角形 (d)長方形 (e)長方形でない平行四辺形 (f)平行四辺形でない四角形
$\boxed{\ \ う\ \ }$の選択肢
(a)$s^2$ (b)$(1-s)^2$ (c)$s(1-s)$ (d)$s\sqrt{1-s^2}$
(e)$2s^2$ (f)$2(1-s)^2$ (g)$2s(1-s)$ (h)$2s\sqrt{1-s^2}$
(i)$4s^2$ (j)$4(1-s)^2$ (k)$4s(1-s)$ (l)$4s\sqrt{1-s^2}$
この動画を見る
$\Large{\boxed{1}}$ (3)一辺の長さが2である正四面体OABCにおいて、辺OAの中点をM、辺BCの中点をNとする。
(i)線分MNの長さは$\boxed{\ \ あ\ \ }$である。
(ii)0<$s$<1とし、線分MNを$s$:$(1-s)$に内分する点をPとする。Pを通りMNに垂直な平面で四面体OABCを切った断面は$\boxed{\ \ い\ \ }$であり、その面積は$\boxed{\ \ う\ \ }$である。
$\boxed{\ \ あ\ \ }$の選択肢
(a)1 (b)$\sqrt 2$ (c)$\sqrt 3$ (d)2 (e)$\frac{1+\sqrt 5}{2}$ (f)$\frac{\sqrt 6}{2}$
$\boxed{\ \ い\ \ }$の選択肢
(a)正三角形 (b)正三角形でない二等辺三角形 (c)二等辺三角形でない三角形 (d)長方形 (e)長方形でない平行四辺形 (f)平行四辺形でない四角形
$\boxed{\ \ う\ \ }$の選択肢
(a)$s^2$ (b)$(1-s)^2$ (c)$s(1-s)$ (d)$s\sqrt{1-s^2}$
(e)$2s^2$ (f)$2(1-s)^2$ (g)$2s(1-s)$ (h)$2s\sqrt{1-s^2}$
(i)$4s^2$ (j)$4(1-s)^2$ (k)$4s(1-s)$ (l)$4s\sqrt{1-s^2}$
福田の数学〜上智大学2023年理工学部第1問(2)〜関数の集合と条件

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (2)$\left\{x|x>0\right\}$を定義域とする関数$f(x)$の集合Aに対する以下の3つの条件を考える。
(P)関数$f(x)$と$g(x)$が共にAの要素ならば、関数$f(x)+g(x)$もAの要素である。
(Q)関数$f(x)$と$g(x)$が共にAの要素ならば、関数$f(x)g(x)$もAの要素である。
(R)$\alpha$が0でない定数で関数$f(x)$がAの要素ならば、関数$\alpha f(x)$もAの要素である。
Aを以下の(i)~(iv)の集合とするとき、条件(P),(Q),(R)のうち成り立つものをすべて解答欄にマークせよ。
(i)$f(1)$=0 を満たす関数$f(x)$全体の集合
(ii)$f(\alpha)$=0 となる正の実数$\alpha$が存在する関数$f(x)$全体の集合
(iii)全ての正の実数$x$に対して$f(x)$>0 が成り立つ関数$f(x)$全体の集合
(iv)定義域$\left\{x|x>0\right\}$のどこかで連続でない関数$f(x)$全体の集合
この動画を見る
$\Large{\boxed{1}}$ (2)$\left\{x|x>0\right\}$を定義域とする関数$f(x)$の集合Aに対する以下の3つの条件を考える。
(P)関数$f(x)$と$g(x)$が共にAの要素ならば、関数$f(x)+g(x)$もAの要素である。
(Q)関数$f(x)$と$g(x)$が共にAの要素ならば、関数$f(x)g(x)$もAの要素である。
(R)$\alpha$が0でない定数で関数$f(x)$がAの要素ならば、関数$\alpha f(x)$もAの要素である。
Aを以下の(i)~(iv)の集合とするとき、条件(P),(Q),(R)のうち成り立つものをすべて解答欄にマークせよ。
(i)$f(1)$=0 を満たす関数$f(x)$全体の集合
(ii)$f(\alpha)$=0 となる正の実数$\alpha$が存在する関数$f(x)$全体の集合
(iii)全ての正の実数$x$に対して$f(x)$>0 が成り立つ関数$f(x)$全体の集合
(iv)定義域$\left\{x|x>0\right\}$のどこかで連続でない関数$f(x)$全体の集合
福田の数学〜上智大学2023年理工学部第1問(1)〜複素数平面と確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#複素数平面#確率#複素数平面#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (1)次の6つの複素数が1つずつ書かれた6枚のカードがある。
$\frac{1}{2}$, 1, 2, $\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}$, $\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}$, $\cos\frac{\pi}{2}+i\sin\frac{\pi}{2}$
これらから無作為に3枚選び、カードに書かれた3つの複素数を掛けた値に対応する複素数平面上の点をPとする。
(i)点Pが虚軸上にある確率は$\displaystyle\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$である。
(ii)点Pの原点からの距離が1である確率は$\displaystyle\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。
この動画を見る
$\Large{\boxed{1}}$ (1)次の6つの複素数が1つずつ書かれた6枚のカードがある。
$\frac{1}{2}$, 1, 2, $\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}$, $\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}$, $\cos\frac{\pi}{2}+i\sin\frac{\pi}{2}$
これらから無作為に3枚選び、カードに書かれた3つの複素数を掛けた値に対応する複素数平面上の点をPとする。
(i)点Pが虚軸上にある確率は$\displaystyle\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$である。
(ii)点Pの原点からの距離が1である確率は$\displaystyle\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。
福田の数学〜上智大学2023年TEAP利用型理系第4問Part2〜不等式の証明と近似値計算

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{4}}$ $e$を自然対数の底とする。$e$=2.718...である。
(1)0≦$x$≦1において不等式1+$x$≦$e^x$≦1+2$x$が成り立つことを示せ。
(2)$n$を自然数とするとき、0≦$x$≦1において不等式
$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}$≦$e^x$≦$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}+\frac{x^n}{n!}$
が成り立つことを示せ。
(3)0≦$x$≦1を定義域とする関数$f(x)$を
$f(x)$=$\left\{\begin{array}{1}
1 (x=0)\\
\displaystyle\frac{e^x-1}{x} (0<x≦1)
\end{array}\right.$
と定義する。(2)の不等式を利用して、定積分$\displaystyle\int_0^1f(x)dx$ の近似値を小数第3位まで求め、求めた近似値と真の値との誤差が$10^{-3}$以下である理由を説明せよ。
この動画を見る
$\Large{\boxed{4}}$ $e$を自然対数の底とする。$e$=2.718...である。
(1)0≦$x$≦1において不等式1+$x$≦$e^x$≦1+2$x$が成り立つことを示せ。
(2)$n$を自然数とするとき、0≦$x$≦1において不等式
$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}$≦$e^x$≦$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}+\frac{x^n}{n!}$
が成り立つことを示せ。
(3)0≦$x$≦1を定義域とする関数$f(x)$を
$f(x)$=$\left\{\begin{array}{1}
1 (x=0)\\
\displaystyle\frac{e^x-1}{x} (0<x≦1)
\end{array}\right.$
と定義する。(2)の不等式を利用して、定積分$\displaystyle\int_0^1f(x)dx$ の近似値を小数第3位まで求め、求めた近似値と真の値との誤差が$10^{-3}$以下である理由を説明せよ。
福田の数学〜上智大学2023年TEAP利用型理系第4問Part1〜不等式の証明と近似値計算

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{4}}$ $e$を自然対数の底とする。$e$=2.718...である。
(1)0≦$x$≦1において不等式1+$x$≦$e^x$≦1+2$x$が成り立つことを示せ。
(2)$n$を自然数とするとき、0≦$x$≦1において不等式
$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}$≦$e^x$≦$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}+\frac{x^n}{n!}$
が成り立つことを示せ。
(3)0≦$x$≦1を定義域とする関数$f(x)$を
$f(x)$=$\left\{\begin{array}{1}
1 (x=0)\\
\displaystyle\frac{e^x-1}{x} (0<x≦1)
\end{array}\right.$
と定義する。(2)の不等式を利用して、定積分$\displaystyle\int_0^1f(x)dx$ の近似値を小数第3位まで求め、求めた近似値と真の値との誤差が$10^{-3}$以下である理由を説明せよ。
この動画を見る
$\Large{\boxed{4}}$ $e$を自然対数の底とする。$e$=2.718...である。
(1)0≦$x$≦1において不等式1+$x$≦$e^x$≦1+2$x$が成り立つことを示せ。
(2)$n$を自然数とするとき、0≦$x$≦1において不等式
$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}$≦$e^x$≦$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}+\frac{x^n}{n!}$
が成り立つことを示せ。
(3)0≦$x$≦1を定義域とする関数$f(x)$を
$f(x)$=$\left\{\begin{array}{1}
1 (x=0)\\
\displaystyle\frac{e^x-1}{x} (0<x≦1)
\end{array}\right.$
と定義する。(2)の不等式を利用して、定積分$\displaystyle\int_0^1f(x)dx$ の近似値を小数第3位まで求め、求めた近似値と真の値との誤差が$10^{-3}$以下である理由を説明せよ。
福田の数学〜上智大学2023年TEAP利用型理系第3問Part2〜容器に水を入れる
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
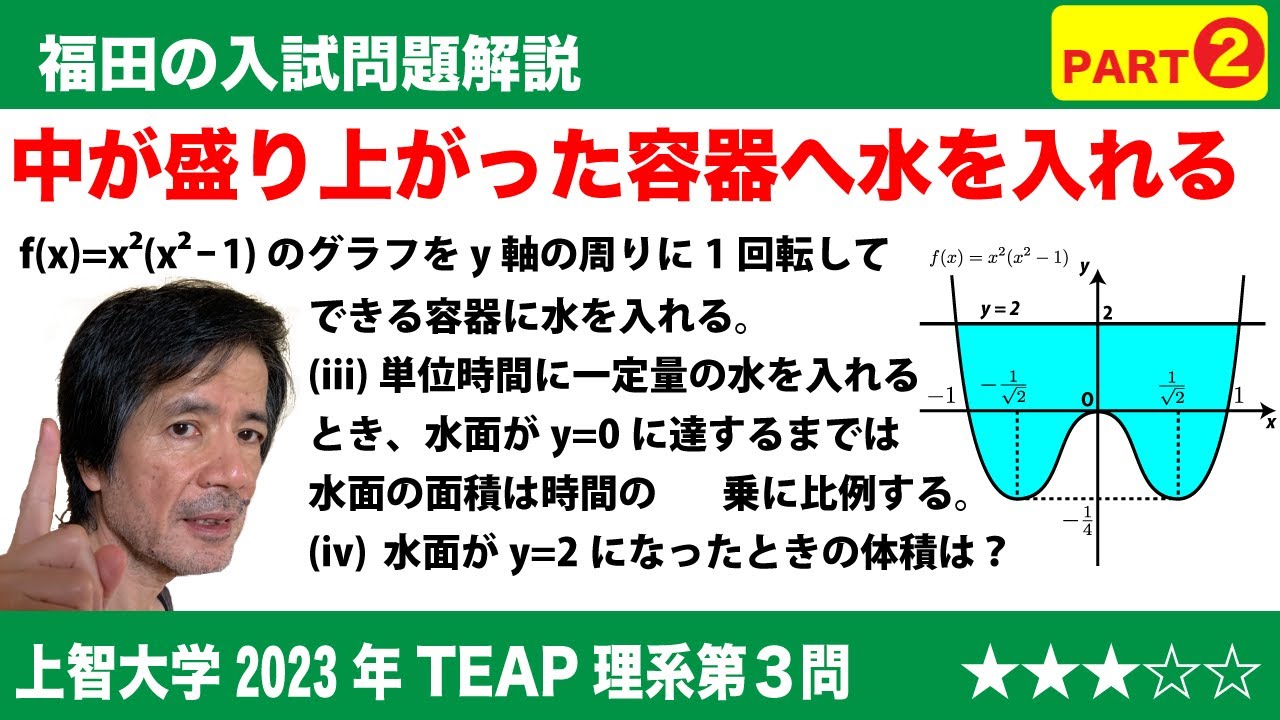
問題文全文(内容文):
$\Large{\boxed{3}}$ $\pi$を円周率とする。$f(x)$=$x^2(x^2-1)$とし、$f(x)$の最小値を$m$とする。
(1)$m$=$\displaystyle\frac{\boxed{\ \ シ\ \ }}{\boxed{\ \ ス\ \ }}$ である。
(2)$y$=$f(x)$で表される曲線を$y$軸の周りに1回転させてできる曲面でできた器に、$y$軸方向から静かに水を注ぐ。
(i)水面が$y$=$a$(ただし$m$≦$a$≦0)になったときの水面の面積は$\boxed{\ \ セ\ \ }$である。
(ii)水面が$y$=0になったときの水の体積は$\displaystyle\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}\pi$ である。
(iii)上方から注ぐ水が単位時間あたり一定量であるとする。水面が$y$=0に達するまでは、水面の面積は、水を注ぎ始めてからの時間の$\displaystyle\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$ 乗に比例して大きくなる。
(iv)水面が$y$=2になったときの水面の面積は$\boxed{\ \ テ\ \ }\pi$であり、水の体積は$\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}\pi$ である。
この動画を見る
$\Large{\boxed{3}}$ $\pi$を円周率とする。$f(x)$=$x^2(x^2-1)$とし、$f(x)$の最小値を$m$とする。
(1)$m$=$\displaystyle\frac{\boxed{\ \ シ\ \ }}{\boxed{\ \ ス\ \ }}$ である。
(2)$y$=$f(x)$で表される曲線を$y$軸の周りに1回転させてできる曲面でできた器に、$y$軸方向から静かに水を注ぐ。
(i)水面が$y$=$a$(ただし$m$≦$a$≦0)になったときの水面の面積は$\boxed{\ \ セ\ \ }$である。
(ii)水面が$y$=0になったときの水の体積は$\displaystyle\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}\pi$ である。
(iii)上方から注ぐ水が単位時間あたり一定量であるとする。水面が$y$=0に達するまでは、水面の面積は、水を注ぎ始めてからの時間の$\displaystyle\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$ 乗に比例して大きくなる。
(iv)水面が$y$=2になったときの水面の面積は$\boxed{\ \ テ\ \ }\pi$であり、水の体積は$\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}\pi$ である。
福田の数学〜上智大学2023年TEAP利用型理系第3問Part1〜容器に水を入れる
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
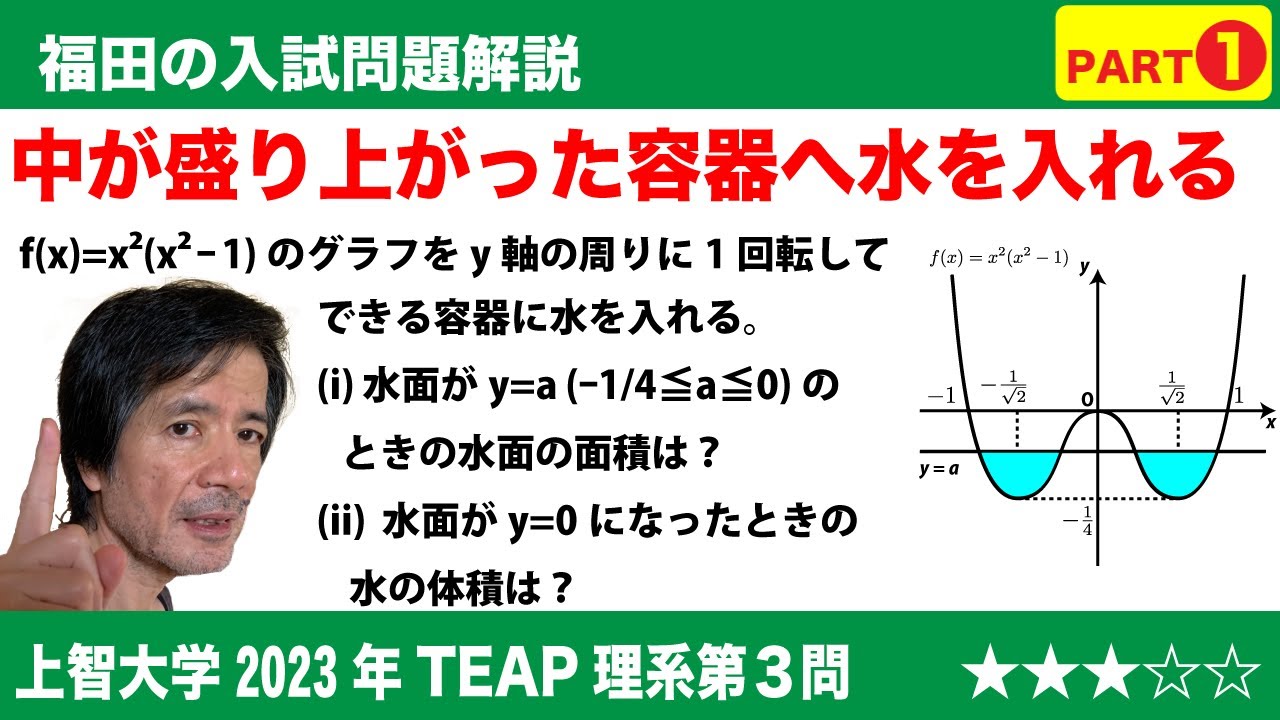
問題文全文(内容文):
$\Large{\boxed{3}}$ $\pi$を円周率とする。$f(x)$=$x^2(x^2-1)$とし、$f(x)$の最小値を$m$とする。
(1)$m$=$\displaystyle\frac{\boxed{\ \ シ\ \ }}{\boxed{\ \ ス\ \ }}$ である。
(2)$y$=$f(x)$で表される曲線を$y$軸の周りに1回転させてできる曲面でできた器に、$y$軸方向から静かに水を注ぐ。
(i)水面が$y$=$a$(ただし$m$≦$a$≦0)になったときの水面の面積は$\boxed{\ \ セ\ \ }$である。
(ii)水面が$y$=0になったときの水の体積は$\displaystyle\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}\pi$ である。
(iii)上方から注ぐ水が単位時間あたり一定量であるとする。水面が$y$=0に達するまでは、水面の面積は、水を注ぎ始めてからの時間の$\displaystyle\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$ 乗に比例して大きくなる。
(iv)水面が$y$=2になったときの水面の面積は$\boxed{\ \ テ\ \ }\pi$であり、水の体積は$\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}\pi$ である。
この動画を見る
$\Large{\boxed{3}}$ $\pi$を円周率とする。$f(x)$=$x^2(x^2-1)$とし、$f(x)$の最小値を$m$とする。
(1)$m$=$\displaystyle\frac{\boxed{\ \ シ\ \ }}{\boxed{\ \ ス\ \ }}$ である。
(2)$y$=$f(x)$で表される曲線を$y$軸の周りに1回転させてできる曲面でできた器に、$y$軸方向から静かに水を注ぐ。
(i)水面が$y$=$a$(ただし$m$≦$a$≦0)になったときの水面の面積は$\boxed{\ \ セ\ \ }$である。
(ii)水面が$y$=0になったときの水の体積は$\displaystyle\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}\pi$ である。
(iii)上方から注ぐ水が単位時間あたり一定量であるとする。水面が$y$=0に達するまでは、水面の面積は、水を注ぎ始めてからの時間の$\displaystyle\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$ 乗に比例して大きくなる。
(iv)水面が$y$=2になったときの水面の面積は$\boxed{\ \ テ\ \ }\pi$であり、水の体積は$\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}\pi$ である。
福田の数学〜上智大学2023年TEAP利用型理系第2問〜立方体の切断と位置ベクトル

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#立体図形#立体切断#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 一辺の長さが2である立方体OADB-CFGEを考える。
$\overrightarrow{OA}$=$\overrightarrow{a}$, $\overrightarrow{OB}$=$\overrightarrow{b}$, $\overrightarrow{OC}$=$\overrightarrow{c}$とおく。辺AFの中点をM、辺BDの中点をNとし、3点O,M,Nを通る平面$\pi$で立方体を切断する。
(1)平面$\pi$は辺AF,BD以外に辺$\boxed{\ \ あ\ \ }$とその両端以外で交わる。
(2)平面$\pi$と辺$\boxed{\ \ あ\ \ }$との交点をPとすると$\overrightarrow{OP}$=$\boxed{\ \ い\ \ } \overrightarrow{a}$+$\boxed{\ \ う\ \ } \overrightarrow{b}$+$\boxed{\ \ え\ \ } \overrightarrow{c}$
(3)断面の面積は$\displaystyle\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}\sqrt{\boxed{\ \ ケ\ \ }}$である。
(4)切断されてできる立体のうち、頂点Aを含むものの体積は$\displaystyle\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。
(5)平面$\pi$と線分CDとの交点をQとする。
(i)点Qは線分CDを$\boxed{\ \ お\ \ }$に内分する。
(ii)$\overrightarrow{OQ}$=$\boxed{\ \ か\ \ } \overrightarrow{a}$+$\boxed{\ \ き\ \ } \overrightarrow{b}$+$\boxed{\ \ く\ \ } \overrightarrow{c}$である。
$\boxed{\ \ い\ \ }~\boxed{\ \ え\ \ }$, $\boxed{\ \ か\ \ }~\boxed{\ \ く\ \ }$の選択肢
(a)0 (b)1 (c)$\frac{1}{2}$ (d)$\frac{1}{3}$ (e)$\frac{2}{3}$ (f)$\frac{1}{4}$ (g)$\frac{3}{4}$ (h)$\frac{1}{5}$
(i)$\frac{2}{5}$ (j)$\frac{3}{5}$ (k)$\frac{4}{5}$ (l)$\frac{1}{6}$ (m)$\frac{5}{6}$
$\boxed{\ \ お\ \ }$の選択肢
(a)1:1 (b)2:1 (c)1:2 (d)3:1 (e)1:3 (f)4:1 (g)3:2
(h)2:3 (i)1:4 (j)5:1 (k)1:5
この動画を見る
$\Large{\boxed{2}}$ 一辺の長さが2である立方体OADB-CFGEを考える。
$\overrightarrow{OA}$=$\overrightarrow{a}$, $\overrightarrow{OB}$=$\overrightarrow{b}$, $\overrightarrow{OC}$=$\overrightarrow{c}$とおく。辺AFの中点をM、辺BDの中点をNとし、3点O,M,Nを通る平面$\pi$で立方体を切断する。
(1)平面$\pi$は辺AF,BD以外に辺$\boxed{\ \ あ\ \ }$とその両端以外で交わる。
(2)平面$\pi$と辺$\boxed{\ \ あ\ \ }$との交点をPとすると$\overrightarrow{OP}$=$\boxed{\ \ い\ \ } \overrightarrow{a}$+$\boxed{\ \ う\ \ } \overrightarrow{b}$+$\boxed{\ \ え\ \ } \overrightarrow{c}$
(3)断面の面積は$\displaystyle\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}\sqrt{\boxed{\ \ ケ\ \ }}$である。
(4)切断されてできる立体のうち、頂点Aを含むものの体積は$\displaystyle\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。
(5)平面$\pi$と線分CDとの交点をQとする。
(i)点Qは線分CDを$\boxed{\ \ お\ \ }$に内分する。
(ii)$\overrightarrow{OQ}$=$\boxed{\ \ か\ \ } \overrightarrow{a}$+$\boxed{\ \ き\ \ } \overrightarrow{b}$+$\boxed{\ \ く\ \ } \overrightarrow{c}$である。
$\boxed{\ \ い\ \ }~\boxed{\ \ え\ \ }$, $\boxed{\ \ か\ \ }~\boxed{\ \ く\ \ }$の選択肢
(a)0 (b)1 (c)$\frac{1}{2}$ (d)$\frac{1}{3}$ (e)$\frac{2}{3}$ (f)$\frac{1}{4}$ (g)$\frac{3}{4}$ (h)$\frac{1}{5}$
(i)$\frac{2}{5}$ (j)$\frac{3}{5}$ (k)$\frac{4}{5}$ (l)$\frac{1}{6}$ (m)$\frac{5}{6}$
$\boxed{\ \ お\ \ }$の選択肢
(a)1:1 (b)2:1 (c)1:2 (d)3:1 (e)1:3 (f)4:1 (g)3:2
(h)2:3 (i)1:4 (j)5:1 (k)1:5
福田の数学〜上智大学2023年TEAP利用型理系第1問(3)〜連立漸化式と極限

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (3)$a_1$=0, $b_1$=6とし、
$a_{n+1}$=$\displaystyle\frac{a_n+b_n}{2}$, $b_{n+1}$=$a_n$ ($n$≧1)
で定まる$a_n$, $b_n$を用いて、平面上の点$P_n$($a_n$, $b_n$)($n$=1,2,3,...)を定める。
(i)点$P_n$は常に直線$y$=$\boxed{\ \ ウ\ \ }x$+$\boxed{\ \ エ\ \ }$上にある。
(ii)$n$を限りなく大きくするとき、点$P_n$は点$\left(\boxed{\ \ オ\ \ }, \boxed{\ \ カ\ \ }\right)$に限りなく近づく。
この動画を見る
$\Large{\boxed{1}}$ (3)$a_1$=0, $b_1$=6とし、
$a_{n+1}$=$\displaystyle\frac{a_n+b_n}{2}$, $b_{n+1}$=$a_n$ ($n$≧1)
で定まる$a_n$, $b_n$を用いて、平面上の点$P_n$($a_n$, $b_n$)($n$=1,2,3,...)を定める。
(i)点$P_n$は常に直線$y$=$\boxed{\ \ ウ\ \ }x$+$\boxed{\ \ エ\ \ }$上にある。
(ii)$n$を限りなく大きくするとき、点$P_n$は点$\left(\boxed{\ \ オ\ \ }, \boxed{\ \ カ\ \ }\right)$に限りなく近づく。
福田の数学〜上智大学2023年TEAP利用型理系第1問(2)〜桁数の評価

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (2)$(2・7・11・13)^{20}$の桁数は$\boxed{\ \ イ\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$ (2)$(2・7・11・13)^{20}$の桁数は$\boxed{\ \ イ\ \ }$である。
福田の数学〜上智大学2023年TEAP利用型理系第1問(1)〜ユークリッドの互除法

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (1)44311と43873との最大公約数は$\boxed{\ \ ア\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$ (1)44311と43873との最大公約数は$\boxed{\ \ ア\ \ }$である。
福田の数学〜上智大学2023年TEAP利用型文系第4問(3)〜線分の通過範囲の面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#面積、体積#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ (3)$a$を定数とする。座標平面上の直線$y$=2$ax$+$\frac{1}{4}$と放物線$y$=$x^2$の2つの交点を$P_1$, $P_2$とする。$a$が0≦$a$≦1の範囲を動くとき、線分$P_1P_2$の通過する部分の面積は$\frac{\boxed{\ \ ル\ \ }}{\boxed{\ \ レ\ \ }}$である。
この動画を見る
$\Large{\boxed{3}}$ (3)$a$を定数とする。座標平面上の直線$y$=2$ax$+$\frac{1}{4}$と放物線$y$=$x^2$の2つの交点を$P_1$, $P_2$とする。$a$が0≦$a$≦1の範囲を動くとき、線分$P_1P_2$の通過する部分の面積は$\frac{\boxed{\ \ ル\ \ }}{\boxed{\ \ レ\ \ }}$である。
福田の数学〜上智大学2023年TEAP利用型文系第4問(2)〜割り算の余りと等差数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ (2)2つの集合
A=$\left\{n|nは3で割ると2余る自然数である\right\}$
B=$\left\{n|nは5で割ると3余る自然数である\right\}$
を考える。A$\cap$Bの要素を小さい順に並べて作った数列の第$k$項は
$\boxed{\ \ ヨ\ \ }k$+$\boxed{\ \ ラ\ \ }$
である。また、A$\cup$Bの要素を小さい順に並べて作った数列の第100項は
$\boxed{\ \ リ\ \ }$
である。
この動画を見る
$\Large{\boxed{3}}$ (2)2つの集合
A=$\left\{n|nは3で割ると2余る自然数である\right\}$
B=$\left\{n|nは5で割ると3余る自然数である\right\}$
を考える。A$\cap$Bの要素を小さい順に並べて作った数列の第$k$項は
$\boxed{\ \ ヨ\ \ }k$+$\boxed{\ \ ラ\ \ }$
である。また、A$\cup$Bの要素を小さい順に並べて作った数列の第100項は
$\boxed{\ \ リ\ \ }$
である。
福田の数学〜上智大学2023年TEAP利用型文系第4問(1)〜命題の真偽と領域

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ (1)実数$x$, $y$に対する次の2つの条件を$p$, $q$を考える。ただし、$r$は正の定数である。
$p$:|$x+y$|≦3 かつ |$x-y$|≦3
$q$:$(x-1)^2$+$(y-1)^2$≦$r^2$
(i)命題「$p$ならば$q$」が真となるような$r$の最小値は$\sqrt{\boxed{\ \ メ\ \ }}$ である。
(ii)命題「$q$ならば$p$」が真となるような$r$の最大値は$\displaystyle\frac{\boxed{\ \ モ\ \ }}{\boxed{\ \ ヤ\ \ }}\sqrt{\boxed{\ \ ユ\ \ }}$ である。
この動画を見る
$\Large{\boxed{3}}$ (1)実数$x$, $y$に対する次の2つの条件を$p$, $q$を考える。ただし、$r$は正の定数である。
$p$:|$x+y$|≦3 かつ |$x-y$|≦3
$q$:$(x-1)^2$+$(y-1)^2$≦$r^2$
(i)命題「$p$ならば$q$」が真となるような$r$の最小値は$\sqrt{\boxed{\ \ メ\ \ }}$ である。
(ii)命題「$q$ならば$p$」が真となるような$r$の最大値は$\displaystyle\frac{\boxed{\ \ モ\ \ }}{\boxed{\ \ ヤ\ \ }}\sqrt{\boxed{\ \ ユ\ \ }}$ である。
福田の数学〜上智大学2023年TEAP利用型文系第3問〜条件付き確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ ある病原菌にはA型、B型の2つの型がある。A型とB型に同時に感染することはない。その病原菌に対して、感染しているかどうかを調べる検査Yがある。
検査結果は陽性か陰性のいずれかで、陽性であったときに病原菌の型までは判別できないものとする。検査Yで、A型の病原菌に感染しているのに陰性と判定される確率が10 %であり、B型の病原菌に感染しているのに陰性と判定される確率が20 %である。また、この病原菌に感染していないのに陽性と判定される確率が10 %である。
全体の1 %がA型に感染しており全体の4 %がB型に感染している集団から1人を選び検査Yを実施する。
(1)検査Yで陽性と判定される確率は$\frac{\boxed{\ \ ネ\ \ }}{\boxed{\ \ ノ\ \ }}$である。
(2)検査Yで陽性だった時に、A型に感染している確率は$\frac{\boxed{\ \ ハ\ \ }}{\boxed{\ \ ヒ\ \ }}$でありB型に感染している確率は$\frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}$である。
(3)1回目の検査Yに加えて、その直後に同じ検査Yをもう一度行う。ただし、1回目と2回目の検査結果は互いに独立であるとする。2回の検査結果が共に陽性であったときに、A型に感染している確率は$\frac{\boxed{\ \ ホ\ \ }}{\boxed{\ \ マ\ \ }}$でありB型に感染している確率は$\frac{\boxed{\ \ ミ\ \ }}{\boxed{\ \ ム\ \ }}$である。
この動画を見る
$\Large\boxed{3}$ ある病原菌にはA型、B型の2つの型がある。A型とB型に同時に感染することはない。その病原菌に対して、感染しているかどうかを調べる検査Yがある。
検査結果は陽性か陰性のいずれかで、陽性であったときに病原菌の型までは判別できないものとする。検査Yで、A型の病原菌に感染しているのに陰性と判定される確率が10 %であり、B型の病原菌に感染しているのに陰性と判定される確率が20 %である。また、この病原菌に感染していないのに陽性と判定される確率が10 %である。
全体の1 %がA型に感染しており全体の4 %がB型に感染している集団から1人を選び検査Yを実施する。
(1)検査Yで陽性と判定される確率は$\frac{\boxed{\ \ ネ\ \ }}{\boxed{\ \ ノ\ \ }}$である。
(2)検査Yで陽性だった時に、A型に感染している確率は$\frac{\boxed{\ \ ハ\ \ }}{\boxed{\ \ ヒ\ \ }}$でありB型に感染している確率は$\frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}$である。
(3)1回目の検査Yに加えて、その直後に同じ検査Yをもう一度行う。ただし、1回目と2回目の検査結果は互いに独立であるとする。2回の検査結果が共に陽性であったときに、A型に感染している確率は$\frac{\boxed{\ \ ホ\ \ }}{\boxed{\ \ マ\ \ }}$でありB型に感染している確率は$\frac{\boxed{\ \ ミ\ \ }}{\boxed{\ \ ム\ \ }}$である。
福田の数学〜上智大学2023年TEAP利用型文系第2問〜空間ベクトルと正八面体

単元:
#数A#大学入試過去問(数学)#図形の性質#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 図のような一辺の長さが1の正八面体ABCDEFがある。
2点P,Qはそれぞれ辺AD, BC上にあり
$\overrightarrow{PQ}$$\bot$$\overrightarrow{AD}$かつ$\overrightarrow{PQ}$$\bot$$\overrightarrow{BC}$
を満たすとする。
(1)$\overrightarrow{AD}$と$\overrightarrow{BC}$のなす角は$\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$である。
(2)|$\overrightarrow{AP}$|=$\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}$, |$\overrightarrow{BQ}$|=$\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$である。
(3)|$\overrightarrow{PQ}$|=$\frac{\boxed{\ \ テ\ \ }}{\boxed{\ \ ト\ \ }}\sqrt{\boxed{\ \ ナ\ \ }}$である。
(4)平面EPQと直線BFの交点をRとすると|$\overrightarrow{BR}$|=$\frac{\boxed{\ \ ニ\ \ }}{\boxed{\ \ ヌ\ \ }}$である。
この動画を見る
$\Large\boxed{2}$ 図のような一辺の長さが1の正八面体ABCDEFがある。
2点P,Qはそれぞれ辺AD, BC上にあり
$\overrightarrow{PQ}$$\bot$$\overrightarrow{AD}$かつ$\overrightarrow{PQ}$$\bot$$\overrightarrow{BC}$
を満たすとする。
(1)$\overrightarrow{AD}$と$\overrightarrow{BC}$のなす角は$\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$である。
(2)|$\overrightarrow{AP}$|=$\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}$, |$\overrightarrow{BQ}$|=$\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$である。
(3)|$\overrightarrow{PQ}$|=$\frac{\boxed{\ \ テ\ \ }}{\boxed{\ \ ト\ \ }}\sqrt{\boxed{\ \ ナ\ \ }}$である。
(4)平面EPQと直線BFの交点をRとすると|$\overrightarrow{BR}$|=$\frac{\boxed{\ \ ニ\ \ }}{\boxed{\ \ ヌ\ \ }}$である。
福田の数学〜上智大学2023年TEAP利用型文系第1問〜三角関数の最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 関数
$y$=2($\sin^3x$+$\cos^3x$)+8$\sin x\cos x$+5 (0≦$x$<2$\pi$)
を考える。$\sin x$+$\cos x$=$t$ とおく。
(1)$y$を$t$の式で表すと
$y$=$\boxed{\ \ ア\ \ }t^3$+$\boxed{\ \ イ\ \ }t^2$+$\boxed{\ \ ウ\ \ }t$+$\boxed{\ \ エ\ \ }$
である。
(2)関数$y$は$t$=$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$において最小値$\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}$をとる。
(3)関数$y$は$x$=$\frac{\boxed{\ \ ケ\ \ }}{\boxed{\ \ コ\ \ }}\pi$において最大値$\boxed{\ \ サ\ \ }$+$\sqrt{\boxed{\ \ コ\ \ }}$をとる。
この動画を見る
$\Large\boxed{1}$ 関数
$y$=2($\sin^3x$+$\cos^3x$)+8$\sin x\cos x$+5 (0≦$x$<2$\pi$)
を考える。$\sin x$+$\cos x$=$t$ とおく。
(1)$y$を$t$の式で表すと
$y$=$\boxed{\ \ ア\ \ }t^3$+$\boxed{\ \ イ\ \ }t^2$+$\boxed{\ \ ウ\ \ }t$+$\boxed{\ \ エ\ \ }$
である。
(2)関数$y$は$t$=$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$において最小値$\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}$をとる。
(3)関数$y$は$x$=$\frac{\boxed{\ \ ケ\ \ }}{\boxed{\ \ コ\ \ }}\pi$において最大値$\boxed{\ \ サ\ \ }$+$\sqrt{\boxed{\ \ コ\ \ }}$をとる。
福田の数学〜青山学院大学2023年理工学部第5問〜定積分で定義された数列と極限

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ $a_n$=$\displaystyle\frac{1}{n!}\int_1^e(\log x)^ndx$ ($n$=1,2,3,...)とおく。
(1)$a_1$を求めよ。
(2)不等式0≦$a_n$≦$\frac{e-1}{n!}$ が成り立つことを示せ。
(3)$n$≧2のとき、$a_n$=$\displaystyle\frac{e}{n!}$-$a_{n-1}$ であることを示せ。
(4)$\displaystyle\lim_{n \to \infty}\sum_{k=2}^n\frac{(-1)^k}{k!}$ を求めよ。
この動画を見る
$\Large\boxed{5}$ $a_n$=$\displaystyle\frac{1}{n!}\int_1^e(\log x)^ndx$ ($n$=1,2,3,...)とおく。
(1)$a_1$を求めよ。
(2)不等式0≦$a_n$≦$\frac{e-1}{n!}$ が成り立つことを示せ。
(3)$n$≧2のとき、$a_n$=$\displaystyle\frac{e}{n!}$-$a_{n-1}$ であることを示せ。
(4)$\displaystyle\lim_{n \to \infty}\sum_{k=2}^n\frac{(-1)^k}{k!}$ を求めよ。
福田の数学〜青山学院大学2023年理工学部第4問〜関数の増減と実数解をもつ条件

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ (1)関数
$y$=$\displaystyle-\frac{\cos3x}{\sin^3x}$ (0<$x$<$\pi$)
の増減と極値を調べ、そのグラフの概形を描け。ただし、グラフの凹凸は調べなくてよい。
(2)$a$を実数の定数とする。$x$についての方程式
$-\cos3x$=$a\sin^3x$
が$\displaystyle\frac{\pi}{6}$<$x$<$\displaystyle\frac{2\pi}{3}$の範囲に実数解をもつような$a$の値の範囲を求めよ。
この動画を見る
$\Large\boxed{4}$ (1)関数
$y$=$\displaystyle-\frac{\cos3x}{\sin^3x}$ (0<$x$<$\pi$)
の増減と極値を調べ、そのグラフの概形を描け。ただし、グラフの凹凸は調べなくてよい。
(2)$a$を実数の定数とする。$x$についての方程式
$-\cos3x$=$a\sin^3x$
が$\displaystyle\frac{\pi}{6}$<$x$<$\displaystyle\frac{2\pi}{3}$の範囲に実数解をもつような$a$の値の範囲を求めよ。
福田の数学〜青山学院大学2023年理工学部第3問〜放物線上の4点で作る四角形の面積の最大
単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#微分法と積分法#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
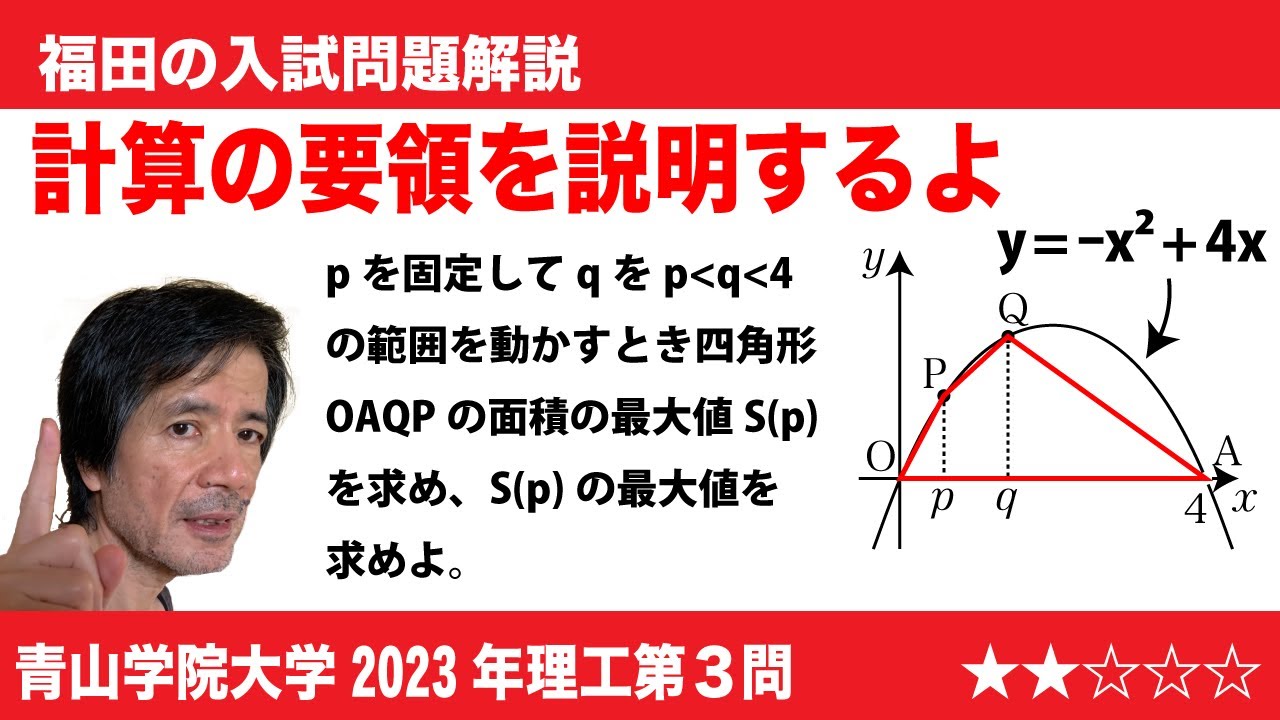
$\Large\boxed{3}$ 点Oを原点とするxy平面上の放物線
$y$=$-x^2$+$4x$
を$C$とする。また、放物線$C$上に点A(4,0), P($p$, $-p^2+4p$), Q($q$, $-q^2+4q$)をとる。ただし、0<$p$<$q$<4 とする。
(1)放物線$C$の接線のうち、直線APと傾きが等しいものを$l$とする。接線$l$の方程式を求めよ。
(2)点Pを固定する。点Qが$p$<$q$<4 を満たしながら動くとき、四角形OAQPの面積の最大値を$p$を用いて表せ。
(3)(2)で求めた四角形OAQPの面積の最大値を$S(p)$とおく。0<$p$<4 のとき、
関数$S(p)$の最大値を求めよ。
この動画を見る
$\Large\boxed{3}$ 点Oを原点とするxy平面上の放物線
$y$=$-x^2$+$4x$
を$C$とする。また、放物線$C$上に点A(4,0), P($p$, $-p^2+4p$), Q($q$, $-q^2+4q$)をとる。ただし、0<$p$<$q$<4 とする。
(1)放物線$C$の接線のうち、直線APと傾きが等しいものを$l$とする。接線$l$の方程式を求めよ。
(2)点Pを固定する。点Qが$p$<$q$<4 を満たしながら動くとき、四角形OAQPの面積の最大値を$p$を用いて表せ。
(3)(2)で求めた四角形OAQPの面積の最大値を$S(p)$とおく。0<$p$<4 のとき、
関数$S(p)$の最大値を求めよ。
福田の数学〜青山学院大学2023年理工学部第2問〜反復試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 白石と黒石を手元にたくさん用意する。表が白色、裏が黒色の硬貨1枚を用いて、机の上で以下の操作を繰り返し行う。ただし、最初の操作は机の上に石が1個もない状態から始めるものとする。
操作:効果を投げ、出た色と異なる色の石が机の上にあればその中の1個を取り除き、なければ出た色と同じ色の石を手元から机の上に1個置く。
とくに、机の上に石が1個もなければ、次の回の操作では出た色と同じ色の石を手元から机の上に1個置く。
(1)3回目の操作後に机の上に石がちょうど3個ある確率は$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$である。
(2)6回目の操作後に机の上に石がちょうど2個ある確率は$\frac{\boxed{\ \ ウエ\ \ }}{\boxed{\ \ オカ\ \ }}$であり、石が1個もない確率は$\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ クケ\ \ }}$である。
(3)6回目の操作後に机の上にある石が2個以下であったときに、8回目の操作後に机の上にある石も2個以下である条件付き確率は$\frac{\boxed{\ \ コサ\ \ }}{\boxed{\ \ シス\ \ }}$である。
この動画を見る
$\Large\boxed{2}$ 白石と黒石を手元にたくさん用意する。表が白色、裏が黒色の硬貨1枚を用いて、机の上で以下の操作を繰り返し行う。ただし、最初の操作は机の上に石が1個もない状態から始めるものとする。
操作:効果を投げ、出た色と異なる色の石が机の上にあればその中の1個を取り除き、なければ出た色と同じ色の石を手元から机の上に1個置く。
とくに、机の上に石が1個もなければ、次の回の操作では出た色と同じ色の石を手元から机の上に1個置く。
(1)3回目の操作後に机の上に石がちょうど3個ある確率は$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$である。
(2)6回目の操作後に机の上に石がちょうど2個ある確率は$\frac{\boxed{\ \ ウエ\ \ }}{\boxed{\ \ オカ\ \ }}$であり、石が1個もない確率は$\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ クケ\ \ }}$である。
(3)6回目の操作後に机の上にある石が2個以下であったときに、8回目の操作後に机の上にある石も2個以下である条件付き確率は$\frac{\boxed{\ \ コサ\ \ }}{\boxed{\ \ シス\ \ }}$である。
福田の数学〜青山学院大学2023年理工学部第1問〜空間ベクトルとと四面体の体積

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#数C#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 座標空間の3点A(0,1,2), B(3,-2,2), C(-1,4,1)が定める平面を$\alpha$とする。
原点Oから平面$\alpha$に垂線を下ろし、$\alpha$との交点をHとする。
(1)$\overrightarrow{AB}$・$\overrightarrow{AC}$=$\boxed{\ \ アイウ\ \ }$
(2)$\triangle$ABCの面積は$\frac{\boxed{\ \ エ\ \ }\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}$である。
(3)$\overrightarrow{AH}$=$\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ クケ\ \ }}$$\overrightarrow{AB}$+$\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$$\overrightarrow{AC}$, $\overrightarrow{OH}$=$\frac{\boxed{\ \ シ\ \ }\sqrt{\boxed{\ \ ス\ \ }}}{\boxed{\ \ セ\ \ }}$
(4)四面体OHBCの体積は$\frac{\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }}$である。
この動画を見る
$\Large\boxed{1}$ 座標空間の3点A(0,1,2), B(3,-2,2), C(-1,4,1)が定める平面を$\alpha$とする。
原点Oから平面$\alpha$に垂線を下ろし、$\alpha$との交点をHとする。
(1)$\overrightarrow{AB}$・$\overrightarrow{AC}$=$\boxed{\ \ アイウ\ \ }$
(2)$\triangle$ABCの面積は$\frac{\boxed{\ \ エ\ \ }\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}$である。
(3)$\overrightarrow{AH}$=$\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ クケ\ \ }}$$\overrightarrow{AB}$+$\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$$\overrightarrow{AC}$, $\overrightarrow{OH}$=$\frac{\boxed{\ \ シ\ \ }\sqrt{\boxed{\ \ ス\ \ }}}{\boxed{\ \ セ\ \ }}$
(4)四面体OHBCの体積は$\frac{\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }}$である。
福田の数学〜慶應義塾大学2023年理工学部第5問(2)〜不定方程式の整数解

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ (2)$f(x)$=$x-$$\displaystyle\frac{1}{x}$とする。自然数$a$,$b$,$c$の組で$a$≦$b$≦$c$かつ$f(a)$+$f(b)$+$f(c)$が自然数であるものの総数は$\boxed{\ \ ト\ \ }$個である。その中で$f(a)$+$f(b)$+$f(c)$の値が最大になるのは($a$,$b$,$c$)=$\boxed{\ \ ナ\ \ }$のときである。
この動画を見る
$\Large\boxed{5}$ (2)$f(x)$=$x-$$\displaystyle\frac{1}{x}$とする。自然数$a$,$b$,$c$の組で$a$≦$b$≦$c$かつ$f(a)$+$f(b)$+$f(c)$が自然数であるものの総数は$\boxed{\ \ ト\ \ }$個である。その中で$f(a)$+$f(b)$+$f(c)$の値が最大になるのは($a$,$b$,$c$)=$\boxed{\ \ ナ\ \ }$のときである。
福田の数学〜慶應義塾大学2023年理工学部第5問(1)〜複素数平面上の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ (1)$\alpha$を±1ではない複素数とする。複素数平面上で$\displaystyle\left|\frac{\alpha z+1}{z+\alpha}\right|$=2 を満たす点$z$全体からなる図形を$C$とする。$C$は$\alpha$が$\boxed{\ \ チ\ \ }$を満たすとき直線となり、$\boxed{\ \ チ\ \ }$を満たさないとき円となる。$\alpha$が$\boxed{\ \ チ\ \ }$を満たさないとき、円$C$の中心を$\alpha$を用いて表すと$\boxed{\ \ ツ\ \ }$となる。$\alpha$が$\boxed{\ \ チ\ \ }$を満たすとき、直線$C$上の点$z$のうち、
その絶対値が最小となるものを$\alpha$を用いて表すと$\boxed{\ \ テ\ \ }$となる。
この動画を見る
$\Large\boxed{5}$ (1)$\alpha$を±1ではない複素数とする。複素数平面上で$\displaystyle\left|\frac{\alpha z+1}{z+\alpha}\right|$=2 を満たす点$z$全体からなる図形を$C$とする。$C$は$\alpha$が$\boxed{\ \ チ\ \ }$を満たすとき直線となり、$\boxed{\ \ チ\ \ }$を満たさないとき円となる。$\alpha$が$\boxed{\ \ チ\ \ }$を満たさないとき、円$C$の中心を$\alpha$を用いて表すと$\boxed{\ \ ツ\ \ }$となる。$\alpha$が$\boxed{\ \ チ\ \ }$を満たすとき、直線$C$上の点$z$のうち、
その絶対値が最小となるものを$\alpha$を用いて表すと$\boxed{\ \ テ\ \ }$となる。



