 福田次郎
福田次郎
 福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田の数学〜千葉大学2023年第6問〜連立漸化式となる確率Part1

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ 1個のさいころを投げて出た目によって数直線上の点Pを動かすことを繰り返すゲームを考える。最初のPの位置を$a_0$=0とし、さいころを$n$回投げたあとのPの位置$a_n$を次のルールで定める。
・$a_{n-1}$=7 のとき、$a_n$=7
・$a_{n-1}$≠7 のとき、$n$回目に出た目$m$に応じて
$a_n$=$
\left\{\begin{array}{1}
a_{n-1}+m (a_{n-1}+m=1,3,4,5,6,7のとき)\\
1 (a_{n-1}+m=2,12のとき)\\
14-(a_{n-1}+m) (a_{n-1}+m=8,9,10,11のとき)\\
\end{array}\right.
$
(1)$a_2$=1 となる確率を求めよ。
(2)$n$≧1について、$a_n$=7 となる確率を求めよ。
(3)$n$≧3について、$a_n$=1 となる確率を求めよ。
この動画を見る
$\Large\boxed{6}$ 1個のさいころを投げて出た目によって数直線上の点Pを動かすことを繰り返すゲームを考える。最初のPの位置を$a_0$=0とし、さいころを$n$回投げたあとのPの位置$a_n$を次のルールで定める。
・$a_{n-1}$=7 のとき、$a_n$=7
・$a_{n-1}$≠7 のとき、$n$回目に出た目$m$に応じて
$a_n$=$
\left\{\begin{array}{1}
a_{n-1}+m (a_{n-1}+m=1,3,4,5,6,7のとき)\\
1 (a_{n-1}+m=2,12のとき)\\
14-(a_{n-1}+m) (a_{n-1}+m=8,9,10,11のとき)\\
\end{array}\right.
$
(1)$a_2$=1 となる確率を求めよ。
(2)$n$≧1について、$a_n$=7 となる確率を求めよ。
(3)$n$≧3について、$a_n$=1 となる確率を求めよ。
福田の数学〜千葉大学2023年第5問〜垂線の足の位置ベクトル

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 点Oを原点とする座標平面において、点Aと点Bが$\overrightarrow{OA}$・$\overrightarrow{OA}$=5, $\overrightarrow{OB}$・$\overrightarrow{OB}$=2, $\overrightarrow{OA}$・$\overrightarrow{OB}$=3を満たすとする。
(1)$\overrightarrow{OB}$=$k\overrightarrow{OA}$ となるような実数$k$は存在しないことを示せ。
(2)点Bから直線OAに下ろした垂線とOAとの交点をHとする。$\overrightarrow{HB}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
(3)実数$t$に対し、直線OA上の点Pを$\overrightarrow{OP}$=$t\overrightarrow{OA}$となるようにとる。同様に直線OB上の点Qを$\overrightarrow{OQ}$=(1-$t$)$\overrightarrow{OB}$となるようにとる。点Pを通り直線OAと直交する直線を$l_1$とし、点Qを通り直線OBと直交する直線を$l_2$とする。
$l_1$と$l_2$の交点をRとするとき、$\overrightarrow{OR}$を$\overrightarrow{OA}$,$\overrightarrow{OB}$,$t$を用いて表せ。
(4)3点O,A,Bを通る円の中心をCとするとき、$\overrightarrow{OC}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
この動画を見る
$\Large\boxed{5}$ 点Oを原点とする座標平面において、点Aと点Bが$\overrightarrow{OA}$・$\overrightarrow{OA}$=5, $\overrightarrow{OB}$・$\overrightarrow{OB}$=2, $\overrightarrow{OA}$・$\overrightarrow{OB}$=3を満たすとする。
(1)$\overrightarrow{OB}$=$k\overrightarrow{OA}$ となるような実数$k$は存在しないことを示せ。
(2)点Bから直線OAに下ろした垂線とOAとの交点をHとする。$\overrightarrow{HB}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
(3)実数$t$に対し、直線OA上の点Pを$\overrightarrow{OP}$=$t\overrightarrow{OA}$となるようにとる。同様に直線OB上の点Qを$\overrightarrow{OQ}$=(1-$t$)$\overrightarrow{OB}$となるようにとる。点Pを通り直線OAと直交する直線を$l_1$とし、点Qを通り直線OBと直交する直線を$l_2$とする。
$l_1$と$l_2$の交点をRとするとき、$\overrightarrow{OR}$を$\overrightarrow{OA}$,$\overrightarrow{OB}$,$t$を用いて表せ。
(4)3点O,A,Bを通る円の中心をCとするとき、$\overrightarrow{OC}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
福田の数学〜千葉大学2023年第4問〜関数の増減と極限

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#関数の極限#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 2つの実数$a$,$b$は0<$b$<$a$を満たすとする。関数
$f(x)$=$\displaystyle\frac{1}{b}\left(e^{-(a-b)x}-e^{-ax}\right)$
の最大値を$M(a,b)$、最大値をとるときの$x$の値を$X(a,b)$と表す。ここで、$e$は自然対数の底である。
(1)$X(a,b)$を求めよ。
(2)極限$\displaystyle\lim_{b \to +0}X(a,b)$ を求めよ。
(3)極限$\displaystyle\lim_{b \to +0}M(a,b)$ を求めよ。
この動画を見る
$\Large\boxed{4}$ 2つの実数$a$,$b$は0<$b$<$a$を満たすとする。関数
$f(x)$=$\displaystyle\frac{1}{b}\left(e^{-(a-b)x}-e^{-ax}\right)$
の最大値を$M(a,b)$、最大値をとるときの$x$の値を$X(a,b)$と表す。ここで、$e$は自然対数の底である。
(1)$X(a,b)$を求めよ。
(2)極限$\displaystyle\lim_{b \to +0}X(a,b)$ を求めよ。
(3)極限$\displaystyle\lim_{b \to +0}M(a,b)$ を求めよ。
福田の数学〜千葉大学2023年第3問〜2次関数と定積分で表された関数

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次関数とグラフ#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 以下の問いに答えよ。
(1)$p$を実数とする。曲線$y$=|$x^2$+$x$-2|と直線$y$=$x$+$p$ の共有点の個数を求めよ。
(2)等式$f(x)$=$x^2$+$\displaystyle\int_{-1}^2(xf(t)-t)dt$ を満たす関数$f(x)$を求めよ。
この動画を見る
$\Large\boxed{3}$ 以下の問いに答えよ。
(1)$p$を実数とする。曲線$y$=|$x^2$+$x$-2|と直線$y$=$x$+$p$ の共有点の個数を求めよ。
(2)等式$f(x)$=$x^2$+$\displaystyle\int_{-1}^2(xf(t)-t)dt$ を満たす関数$f(x)$を求めよ。
福田の数学〜千葉大学2023年第2問〜反復試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 1個のさいころを投げて出た目によって得点を得るゲームを考える。出た目が1,2であれば得点は2、出た目が3であれば得点は1、出た目が4,5,6であれば得点は0とする。このゲームを$k$回繰り返すとき、得点の合計を$S_k$とする。
(1)$S_2$=3 となる確率を求めよ。
(2)$S_3$が奇数となる確率を求めよ。
(3)$S_4$≧$n$となる確率が$\frac{1}{9}$以下となる最小の整数$n$を求めよ。
この動画を見る
$\Large\boxed{2}$ 1個のさいころを投げて出た目によって得点を得るゲームを考える。出た目が1,2であれば得点は2、出た目が3であれば得点は1、出た目が4,5,6であれば得点は0とする。このゲームを$k$回繰り返すとき、得点の合計を$S_k$とする。
(1)$S_2$=3 となる確率を求めよ。
(2)$S_3$が奇数となる確率を求めよ。
(3)$S_4$≧$n$となる確率が$\frac{1}{9}$以下となる最小の整数$n$を求めよ。
福田の数学〜千葉大学2023年第1問〜三角形の面積と軌跡
単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
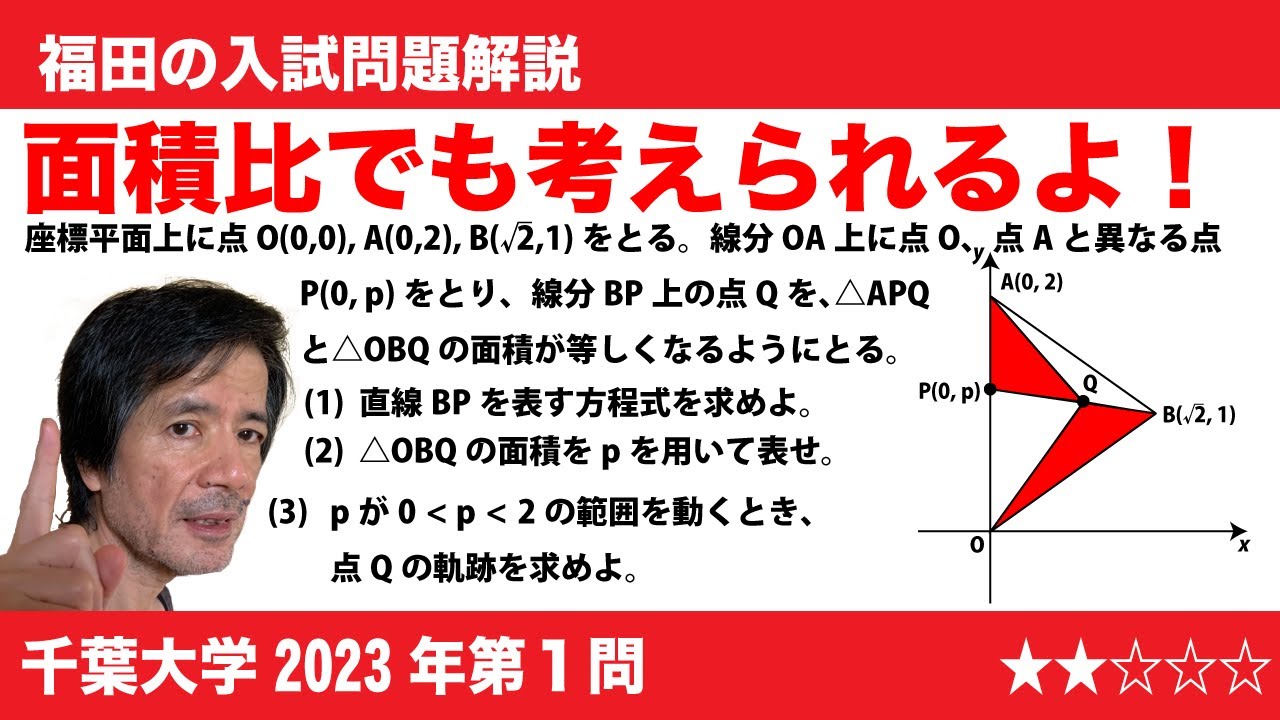
$\Large\boxed{1}$ 座標平面上に点O(0,0), A(0,2), B($\sqrt 2$, 1)をとる。線分OA上に点O、点Aと異なる点P(0,$p$)をとり、線分BP上の点Qを、$\triangle$APQと$\triangle$OBQの面積が等しくなるようにとる。
(1)直線BPを表す方程式を求めよ。
(2)$\triangle$OBQの面積を$p$を用いて表せ。
(3)$p$が0<$p$<2の範囲を動くとき、点Qの軌跡を求めよ。
この動画を見る
$\Large\boxed{1}$ 座標平面上に点O(0,0), A(0,2), B($\sqrt 2$, 1)をとる。線分OA上に点O、点Aと異なる点P(0,$p$)をとり、線分BP上の点Qを、$\triangle$APQと$\triangle$OBQの面積が等しくなるようにとる。
(1)直線BPを表す方程式を求めよ。
(2)$\triangle$OBQの面積を$p$を用いて表せ。
(3)$p$が0<$p$<2の範囲を動くとき、点Qの軌跡を求めよ。
福田の数学〜東京医科歯科大学2023年医学部第3問〜積分で定義された関数と極限

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ $a$,$b$を正の実数、$p$を$a$より小さい正の実数とし、すべての実数$x$について
$\displaystyle\int_p^{f(x)}\frac{a}{u(a-u)}du$=$bx$, 0<$f(x)$<$a$
かつ$f(0)$=$p$を満たす関数$f(x)$を考える。このとき以下の問いに答えよ。
(1)$f(x)$を$a$,$b$,$p$を用いて表せ。
(2)$f(-1)$=$\frac{1}{2}$, $f(1)$=1, $f(3)$=$\frac{3}{2}$のとき、$a$,$b$,$p$を求めよ。
(3)(2)のとき、$\displaystyle\lim_{x \to -\infty}f(x)$, $\displaystyle\lim_{x \to \infty}f(x)$ を求めよ。
この動画を見る
$\Large\boxed{3}$ $a$,$b$を正の実数、$p$を$a$より小さい正の実数とし、すべての実数$x$について
$\displaystyle\int_p^{f(x)}\frac{a}{u(a-u)}du$=$bx$, 0<$f(x)$<$a$
かつ$f(0)$=$p$を満たす関数$f(x)$を考える。このとき以下の問いに答えよ。
(1)$f(x)$を$a$,$b$,$p$を用いて表せ。
(2)$f(-1)$=$\frac{1}{2}$, $f(1)$=1, $f(3)$=$\frac{3}{2}$のとき、$a$,$b$,$p$を求めよ。
(3)(2)のとき、$\displaystyle\lim_{x \to -\infty}f(x)$, $\displaystyle\lim_{x \to \infty}f(x)$ を求めよ。
福田の数学〜東京医科歯科大学2023年医学部第2問PART2〜場合分けされた連立漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ xyz空間において、3点(0,0,0),(1,0,0),(0,1,0)を通る平面$\pi_1$と3点(1,0,0),(0,1,0),(0,0,1)を通る平面$\pi_2$を考える。$x_0$=1, $y_0$=2, $z_0$=-2として、点P${}_0$($x_0$,$y_0$,$z_0$)から始めて、次の手順でP${}_1$($x_1$,$y_1$,$z_1$), P${}_2$($x_2$,$y_2$,$z_2$),... を決める。
・$k$が偶数のとき、$\pi_1$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
・$k$が奇数のとき、$\pi_2$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
このとき、次の問いに答えよ。
(1)$\pi_2$に直交するベクトルのうち、長さが1で$x$成分が正のもの$n_2$を求めよ。
(2)$x_{k+1}$,$y_{k+1}$,$z_{k+1}$をそれぞれ$x_k$,$y_k$,$z_k$を用いて表せ。
(3)$\displaystyle\lim_{k\to\infty}x_k$, $\displaystyle\lim_{k\to\infty}y_k$, $\displaystyle\lim_{k\to\infty}z_k$を求めよ。
この動画を見る
$\Large\boxed{2}$ xyz空間において、3点(0,0,0),(1,0,0),(0,1,0)を通る平面$\pi_1$と3点(1,0,0),(0,1,0),(0,0,1)を通る平面$\pi_2$を考える。$x_0$=1, $y_0$=2, $z_0$=-2として、点P${}_0$($x_0$,$y_0$,$z_0$)から始めて、次の手順でP${}_1$($x_1$,$y_1$,$z_1$), P${}_2$($x_2$,$y_2$,$z_2$),... を決める。
・$k$が偶数のとき、$\pi_1$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
・$k$が奇数のとき、$\pi_2$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
このとき、次の問いに答えよ。
(1)$\pi_2$に直交するベクトルのうち、長さが1で$x$成分が正のもの$n_2$を求めよ。
(2)$x_{k+1}$,$y_{k+1}$,$z_{k+1}$をそれぞれ$x_k$,$y_k$,$z_k$を用いて表せ。
(3)$\displaystyle\lim_{k\to\infty}x_k$, $\displaystyle\lim_{k\to\infty}y_k$, $\displaystyle\lim_{k\to\infty}z_k$を求めよ。
福田の数学〜東京医科歯科大学2023年医学部第2問PART1〜場合分けされた連立漸化式

単元:
#大学入試過去問(数学)#漸化式#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ xyz空間において、3点(0,0,0),(1,0,0),(0,1,0)を通る平面$\pi_1$と3点(1,0,0),(0,1,0),(0,0,1)を通る平面$\pi_2$を考える。$x_0$=1, $y_0$=2, $z_0$=-2として、点P${}_0$($x_0$,$y_0$,$z_0$)から始めて、次の手順でP${}_1$($x_1$,$y_1$,$z_1$), P${}_2$($x_2$,$y_2$,$z_2$),... を決める。
・$k$が偶数のとき、$\pi_1$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
・$k$が奇数のとき、$\pi_2$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
このとき、次の問いに答えよ。
(1)$\pi_2$に直交するベクトルのうち、長さが1で$x$成分が正のもの$n_2$を求めよ。
(2)$x_{k+1}$,$y_{k+1}$,$z_{k+1}$をそれぞれ$x_k$,$y_k$,$z_k$を用いて表せ。
(3)$\displaystyle\lim_{k\to\infty}x_k$, $\displaystyle\lim_{k\to\infty}y_k$, $\displaystyle\lim_{k\to\infty}z_k$を求めよ。
この動画を見る
$\Large\boxed{2}$ xyz空間において、3点(0,0,0),(1,0,0),(0,1,0)を通る平面$\pi_1$と3点(1,0,0),(0,1,0),(0,0,1)を通る平面$\pi_2$を考える。$x_0$=1, $y_0$=2, $z_0$=-2として、点P${}_0$($x_0$,$y_0$,$z_0$)から始めて、次の手順でP${}_1$($x_1$,$y_1$,$z_1$), P${}_2$($x_2$,$y_2$,$z_2$),... を決める。
・$k$が偶数のとき、$\pi_1$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
・$k$が奇数のとき、$\pi_2$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
このとき、次の問いに答えよ。
(1)$\pi_2$に直交するベクトルのうち、長さが1で$x$成分が正のもの$n_2$を求めよ。
(2)$x_{k+1}$,$y_{k+1}$,$z_{k+1}$をそれぞれ$x_k$,$y_k$,$z_k$を用いて表せ。
(3)$\displaystyle\lim_{k\to\infty}x_k$, $\displaystyle\lim_{k\to\infty}y_k$, $\displaystyle\lim_{k\to\infty}z_k$を求めよ。
福田の数学〜東京医科歯科大学2023年医学部第1問PART2〜格子折れ線の個数を数える
単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
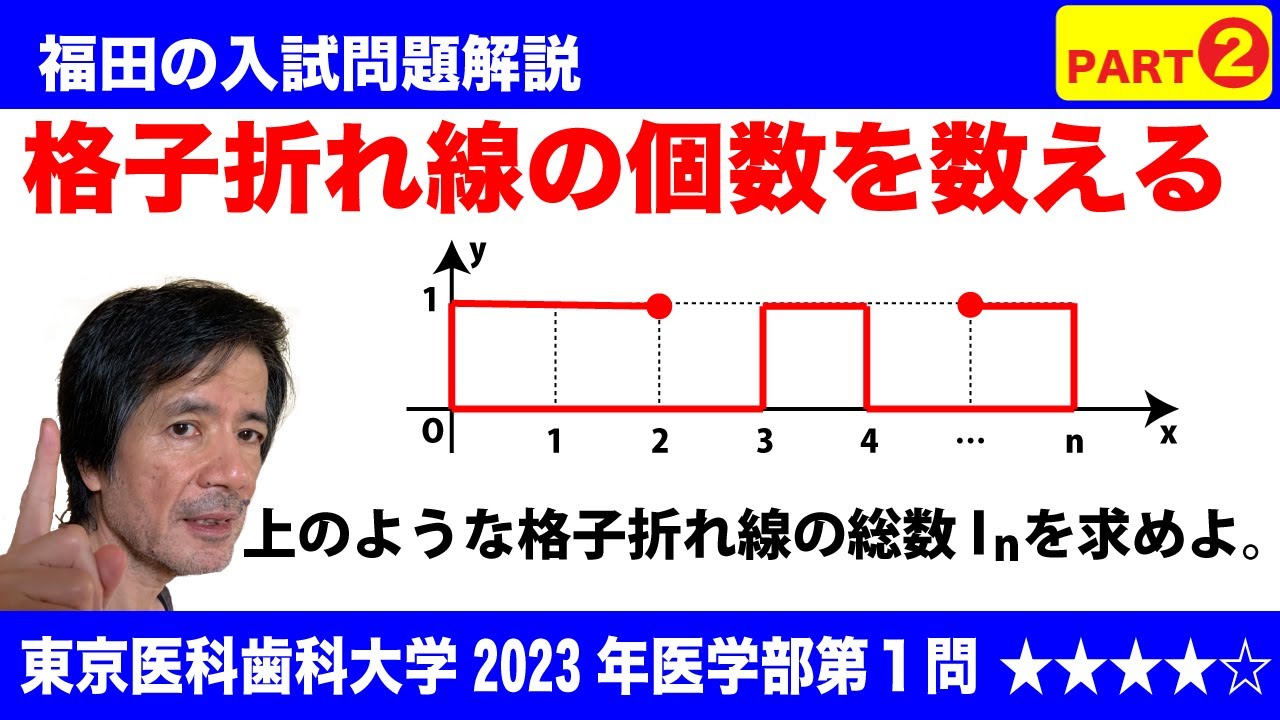
$\Large\boxed{1}$ xy平面において、x座標およびy座標が共に整数であるような点を格子点と呼ぶ。xy平面上の相異なる2つの格子点を端点とする折れ線のうち、x座標またはy座標が等しい格子点どうしを結ぶ線分のみから構成され、かつ同じ点を2度通ることはないものを、格子折れ線と呼ぶ。ここで格子折れ線の向きは考慮せず、端点および通過する点がすべて等しい格子折れ線は同じものとする。また、自然数$n$に対し、
0≦$x$≦$n$ かつ 0≦$y$≦1
を満たす格子点全体の集合を$V_n$とする。さらに、$V_n$に属する格子点をすべて通り、かつ$V_n$に属さない格子点は通らない格子折れ線全体の集合を$L_n$とする。たとえば、7つの格子点(0,1),(0,0),(1,0),(1,1),(4,1),(4,0),(2,0)を順に結んだ折れ線は$L_4$に属する。このとき、以下の問いに答えよ。
(1)$L_1$および$L_2$に属する格子折れ線をすべて図示せよ。
(2)$L_4$に属する格子折れ線のうち、両端点の$x$座標の差が3以上となるものをすべて図示せよ。
(3)$n$≧3のとき、$L_n$に属する格子折れ線のうち、両端点の$x$座標の差が$n$-2となるものの個数を求めよ。
(4)$L_n$に属する格子折れ線の個数$l_n$を$n$を用いて表せ。
この動画を見る
$\Large\boxed{1}$ xy平面において、x座標およびy座標が共に整数であるような点を格子点と呼ぶ。xy平面上の相異なる2つの格子点を端点とする折れ線のうち、x座標またはy座標が等しい格子点どうしを結ぶ線分のみから構成され、かつ同じ点を2度通ることはないものを、格子折れ線と呼ぶ。ここで格子折れ線の向きは考慮せず、端点および通過する点がすべて等しい格子折れ線は同じものとする。また、自然数$n$に対し、
0≦$x$≦$n$ かつ 0≦$y$≦1
を満たす格子点全体の集合を$V_n$とする。さらに、$V_n$に属する格子点をすべて通り、かつ$V_n$に属さない格子点は通らない格子折れ線全体の集合を$L_n$とする。たとえば、7つの格子点(0,1),(0,0),(1,0),(1,1),(4,1),(4,0),(2,0)を順に結んだ折れ線は$L_4$に属する。このとき、以下の問いに答えよ。
(1)$L_1$および$L_2$に属する格子折れ線をすべて図示せよ。
(2)$L_4$に属する格子折れ線のうち、両端点の$x$座標の差が3以上となるものをすべて図示せよ。
(3)$n$≧3のとき、$L_n$に属する格子折れ線のうち、両端点の$x$座標の差が$n$-2となるものの個数を求めよ。
(4)$L_n$に属する格子折れ線の個数$l_n$を$n$を用いて表せ。
福田の数学〜東京医科歯科大学2023年医学部第1問PART1〜格子折れ線の個数を数える
単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
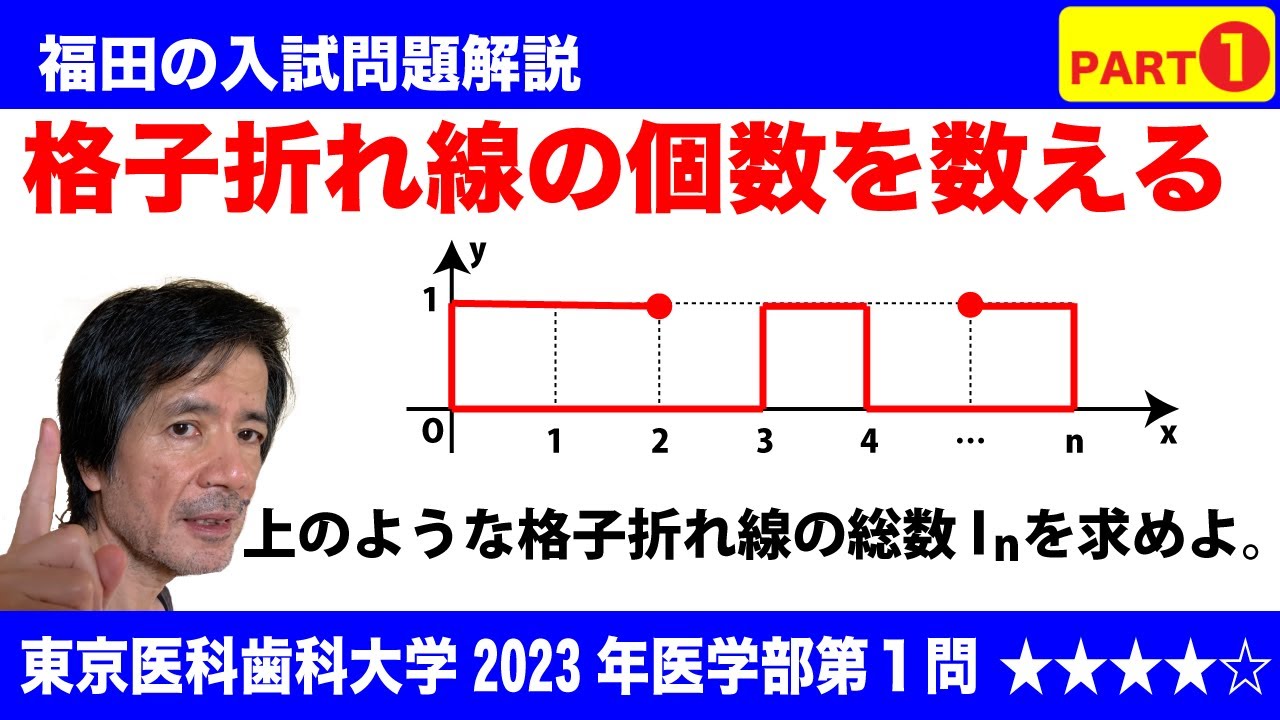
$\Large\boxed{1}$ xy平面において、x座標およびy座標が共に整数であるような点を格子点と呼ぶ。xy平面上の相異なる2つの格子点を端点とする折れ線のうち、x座標またはy座標が等しい格子点どうしを結ぶ線分のみから構成され、かつ同じ点を2度通ることはないものを、格子折れ線と呼ぶ。ここで格子折れ線の向きは考慮せず、端点および通過する点がすべて等しい格子折れ線は同じものとする。また、自然数$n$に対し、
0≦$x$≦$n$ かつ 0≦$y$≦1
を満たす格子点全体の集合を$V_n$とする。さらに、$V_n$に属する格子点をすべて通り、かつ$V_n$に属さない格子点は通らない格子折れ線全体の集合を$L_n$とする。たとえば、7つの格子点(0,1),(0,0),(1,0),(1,1),(4,1),(4,0),(2,0)を順に結んだ折れ線は$L_4$に属する。このとき、以下の問いに答えよ。
(1)$L_1$および$L_2$に属する格子折れ線をすべて図示せよ。
(2)$L_4$に属する格子折れ線のうち、両端点の$x$座標の差が3以上となるものをすべて図示せよ。
(3)$n$≧3のとき、$L_n$に属する格子折れ線のうち、両端点の$x$座標の差が$n$-2となるものの個数を求めよ。
(4)$L_n$に属する格子折れ線の個数$l_n$を$n$を用いて表せ。
この動画を見る
$\Large\boxed{1}$ xy平面において、x座標およびy座標が共に整数であるような点を格子点と呼ぶ。xy平面上の相異なる2つの格子点を端点とする折れ線のうち、x座標またはy座標が等しい格子点どうしを結ぶ線分のみから構成され、かつ同じ点を2度通ることはないものを、格子折れ線と呼ぶ。ここで格子折れ線の向きは考慮せず、端点および通過する点がすべて等しい格子折れ線は同じものとする。また、自然数$n$に対し、
0≦$x$≦$n$ かつ 0≦$y$≦1
を満たす格子点全体の集合を$V_n$とする。さらに、$V_n$に属する格子点をすべて通り、かつ$V_n$に属さない格子点は通らない格子折れ線全体の集合を$L_n$とする。たとえば、7つの格子点(0,1),(0,0),(1,0),(1,1),(4,1),(4,0),(2,0)を順に結んだ折れ線は$L_4$に属する。このとき、以下の問いに答えよ。
(1)$L_1$および$L_2$に属する格子折れ線をすべて図示せよ。
(2)$L_4$に属する格子折れ線のうち、両端点の$x$座標の差が3以上となるものをすべて図示せよ。
(3)$n$≧3のとき、$L_n$に属する格子折れ線のうち、両端点の$x$座標の差が$n$-2となるものの個数を求めよ。
(4)$L_n$に属する格子折れ線の個数$l_n$を$n$を用いて表せ。
福田の数学〜立教大学2023年経済学部第3問〜放物線と直線で囲まれた図形の面積
単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#点と直線#学校別大学入試過去問解説(数学)#面積、体積#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
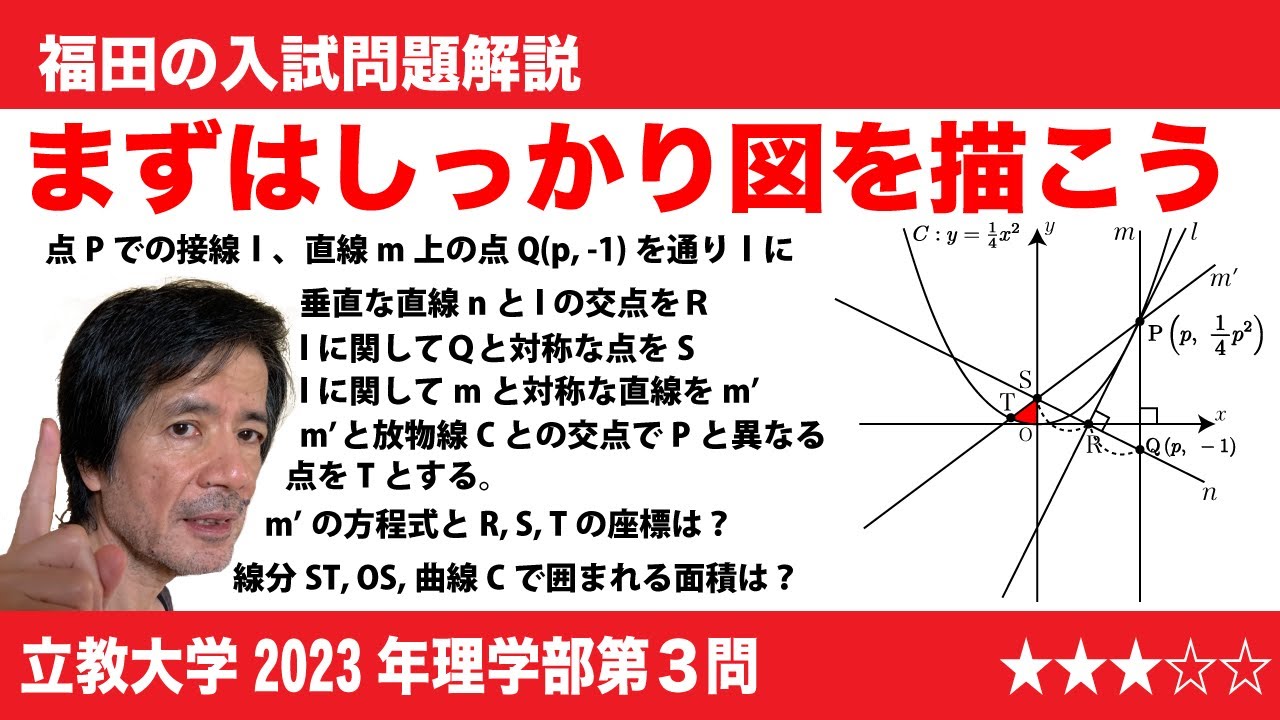
$\Large\boxed{3}$ pを正の実数とする。Oを原点とする座標平面上の放物線C:$y$=$\frac{1}{4}x^2$上の点P$\left(p, \frac{1}{4}p^2\right)$における接線を$l$、Pを通り$x$軸に垂直な直線を$m$とする。また、$m$上の点Q$\left(p, -1\right)$を通り$l$に垂直な直線を$n$とし、$l$と$n$の交点をRとする。さらに、$l$に関してQと対称な点をSとする。このとき、次の問いに答えよ。
(1)$l$の方程式を$p$を用いて表せ。
(2)$n$の方程式およびRの座標をそれぞれ$p$を用いて表せ。
(3)Sの座標を求めよ。
(4)$l$を対象軸として、$l$に関して$m$と対称な直線$m'$の方程式を$p$を用いて表せ。
また、$m'$とCの交点のうちPと異なる点をTとするとき、Tの$x$座標を$p$を用いて表せ。
(5)(4)のTに対して、線分ST、線分OSおよびCで囲まれた部分の面積を$p$を用いて表せ。
この動画を見る
$\Large\boxed{3}$ pを正の実数とする。Oを原点とする座標平面上の放物線C:$y$=$\frac{1}{4}x^2$上の点P$\left(p, \frac{1}{4}p^2\right)$における接線を$l$、Pを通り$x$軸に垂直な直線を$m$とする。また、$m$上の点Q$\left(p, -1\right)$を通り$l$に垂直な直線を$n$とし、$l$と$n$の交点をRとする。さらに、$l$に関してQと対称な点をSとする。このとき、次の問いに答えよ。
(1)$l$の方程式を$p$を用いて表せ。
(2)$n$の方程式およびRの座標をそれぞれ$p$を用いて表せ。
(3)Sの座標を求めよ。
(4)$l$を対象軸として、$l$に関して$m$と対称な直線$m'$の方程式を$p$を用いて表せ。
また、$m'$とCの交点のうちPと異なる点をTとするとき、Tの$x$座標を$p$を用いて表せ。
(5)(4)のTに対して、線分ST、線分OSおよびCで囲まれた部分の面積を$p$を用いて表せ。
福田の数学〜立教大学2023年経済学部第2問〜利息計算と漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 1年目の初めに新規に100万円を預金し、2年目以降の毎年初めに12万円を追加で預金する。ただし、毎年の終わりに、その時点での預金額の8%が利子として預金に加算される。自然数$n$に対して、$n$年目の終わりに利子が加算された後の預金額を$S_n$万円とする。このとき、以下の問いに答えよ。
ただし、$\log_{10}2$=0.3010, $\log_{10}3$=0.4771とする。
(1)$S_1$, $S_2$をそれぞれ求めよ。
(2)$S_{n+1}$を$S_n$を用いて表せ。
(3)$S_n$を$n$を用いて表せ。
(4)$\log_{10}1.08$を求めよ。
(5)$S_n$>513 を満たす最小の自然数$n$を求めよ。
この動画を見る
$\Large\boxed{2}$ 1年目の初めに新規に100万円を預金し、2年目以降の毎年初めに12万円を追加で預金する。ただし、毎年の終わりに、その時点での預金額の8%が利子として預金に加算される。自然数$n$に対して、$n$年目の終わりに利子が加算された後の預金額を$S_n$万円とする。このとき、以下の問いに答えよ。
ただし、$\log_{10}2$=0.3010, $\log_{10}3$=0.4771とする。
(1)$S_1$, $S_2$をそれぞれ求めよ。
(2)$S_{n+1}$を$S_n$を用いて表せ。
(3)$S_n$を$n$を用いて表せ。
(4)$\log_{10}1.08$を求めよ。
(5)$S_n$>513 を満たす最小の自然数$n$を求めよ。
福田の数学〜立教大学2023年経済学部第1問(7)〜集合と座標平面

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (7)座標平面の3つの部分集合
A=$\left\{(x, -2x+2)|xは実数, x<0\right\}$
B=$\left\{(x, 2x+2)|xは実数, x≧0\right\}$
C=$\left\{(x, -x+3)|xは実数\right\}$
に対し、(A$\cup$B)$\cap$C に属する点の座標をすべて求めると$\boxed{\ \ キ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (7)座標平面の3つの部分集合
A=$\left\{(x, -2x+2)|xは実数, x<0\right\}$
B=$\left\{(x, 2x+2)|xは実数, x≧0\right\}$
C=$\left\{(x, -x+3)|xは実数\right\}$
に対し、(A$\cup$B)$\cap$C に属する点の座標をすべて求めると$\boxed{\ \ キ\ \ }$である。
福田の数学〜立教大学2023年経済学部第1問(6)〜関数方程式

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (6)2次式$f(x)$が$f(f(x))$=$f(x)^2$+1 を満たすとき$f(x)$=$\boxed{\ \ カ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (6)2次式$f(x)$が$f(f(x))$=$f(x)^2$+1 を満たすとき$f(x)$=$\boxed{\ \ カ\ \ }$である。
福田の数学〜立教大学2023年経済学部第1問(5)〜共面条件

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (5)$t$を実数とする。座標空間において、3点O(0,0,0), A(1,0,2), B(2,-1,0)の定める平面OAB上に点C($t$+1,$t$,1-$t$)があるとき、$t$=$\boxed{\ \ オ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (5)$t$を実数とする。座標空間において、3点O(0,0,0), A(1,0,2), B(2,-1,0)の定める平面OAB上に点C($t$+1,$t$,1-$t$)があるとき、$t$=$\boxed{\ \ オ\ \ }$である。
福田の数学〜立教大学2023年経済学部第1問(4)〜確率の基本性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (4)大小2個のさいころを同時に投げる。大きいサイコロのでた目を$a$、小さいサイコロのでた目を$b$とするとき、$\displaystyle\frac{a}{b}$が整数になる確率は$\boxed{\ \ エ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (4)大小2個のさいころを同時に投げる。大きいサイコロのでた目を$a$、小さいサイコロのでた目を$b$とするとき、$\displaystyle\frac{a}{b}$が整数になる確率は$\boxed{\ \ エ\ \ }$である。
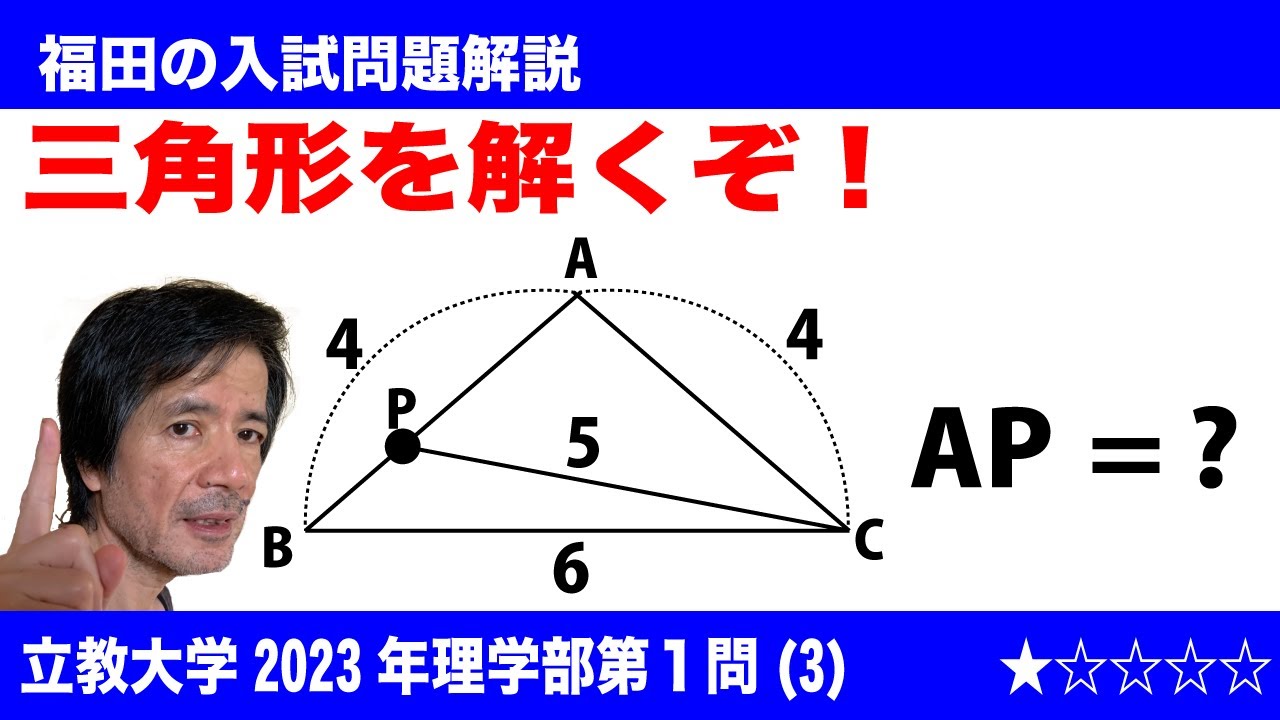
福田の数学〜立教大学2023年経済学部第1問(3)〜三角形を解く
単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)三角形ABCにおいてAB=AC=4, BC=6とする。AB上の点PがCP=5を満たすとき、AP=$\boxed{\ \ ウ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (3)三角形ABCにおいてAB=AC=4, BC=6とする。AB上の点PがCP=5を満たすとき、AP=$\boxed{\ \ ウ\ \ }$である。
福田の数学〜立教大学2023年経済学部第1問(2)〜条件付き最大最小問題

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)2つの実数$x$,$y$が$x^2$+$y^2$=1 を満たすとき、$z$=2$x$+$y$のとりうる値の範囲は$\boxed{\ \ イ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (2)2つの実数$x$,$y$が$x^2$+$y^2$=1 を満たすとき、$z$=2$x$+$y$のとりうる値の範囲は$\boxed{\ \ イ\ \ }$である。
福田の数学〜立教大学2023年経済学部第1問(1)〜三角関数の最小値

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次関数とグラフ#三角関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)関数$y$=4$\cos^2\theta$-$4\sin\theta$-5 の最小値は$\boxed{\ \ ア\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (1)関数$y$=4$\cos^2\theta$-$4\sin\theta$-5 の最小値は$\boxed{\ \ ア\ \ }$である。
福田の数学〜立教大学2023年理学部第4問〜数学的帰納法とはさみうちの原理

単元:
#大学入試過去問(数学)#数列#数学的帰納法#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 正の数列$x_1$,$x_2$,$x_3$,...,$x_n$,... は以下を満たすとする。
$x_1$=8, $x_{n+1}$=$\sqrt{1+x_n}$ ($n$=1,2,3,...)
このとき、次の問いに答えよ。
(1)$x_2$,$x_3$,$x_4$をそれぞれ求めよ。
(2)すべての$n$≧1について($x_{n+1}$-$\alpha$)($x_{n+1}$+$\alpha$)=$x_n$-$\alpha$ となる定数$\alpha$で、
正であるものを求めよ。
(3)$\alpha$を(2)で求めたものとする。すべての$n$≧1について$x_n$>$\alpha$であることを$n$に関する数学的帰納法で示せ。
(4)極限値$\displaystyle\lim_{n \to \infty}x_n$を求めよ。
この動画を見る
$\Large\boxed{4}$ 正の数列$x_1$,$x_2$,$x_3$,...,$x_n$,... は以下を満たすとする。
$x_1$=8, $x_{n+1}$=$\sqrt{1+x_n}$ ($n$=1,2,3,...)
このとき、次の問いに答えよ。
(1)$x_2$,$x_3$,$x_4$をそれぞれ求めよ。
(2)すべての$n$≧1について($x_{n+1}$-$\alpha$)($x_{n+1}$+$\alpha$)=$x_n$-$\alpha$ となる定数$\alpha$で、
正であるものを求めよ。
(3)$\alpha$を(2)で求めたものとする。すべての$n$≧1について$x_n$>$\alpha$であることを$n$に関する数学的帰納法で示せ。
(4)極限値$\displaystyle\lim_{n \to \infty}x_n$を求めよ。
福田の数学〜立教大学2023年理学部第3問〜双曲線と直線の囲む面積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 座標平面上の曲線Cを
C:$y$=$\frac{3}{x}$-8 ($x$>0)
で定める。また$p$を正の定数とし、点$\left(p, \displaystyle\frac{3}{p}-8\right)$におけるCの接線を$l$とする。
さらに、$a$を実数とし、直線$y$=$ax$を$m$とする。このとき、次の問いに答えよ。
(1)$l$の方程式を求めよ。
(2)$l$が原点を通るとき、$p$の値を求めよ。
(3)Cと$m$が異なる2点P,Qを共有するとき、$a$の値の範囲を求めよ。
(4)(3)のとき、Qの$x$座標$x_0$はPの$x$座標$x_1$よりも大きいとする。$x_0$-$x_1$=1であるときの$a$の値を求めよ。
(5)(4)のとき、Cと直線$m$で囲まれる図形の面積を求めよ。
この動画を見る
$\Large\boxed{3}$ 座標平面上の曲線Cを
C:$y$=$\frac{3}{x}$-8 ($x$>0)
で定める。また$p$を正の定数とし、点$\left(p, \displaystyle\frac{3}{p}-8\right)$におけるCの接線を$l$とする。
さらに、$a$を実数とし、直線$y$=$ax$を$m$とする。このとき、次の問いに答えよ。
(1)$l$の方程式を求めよ。
(2)$l$が原点を通るとき、$p$の値を求めよ。
(3)Cと$m$が異なる2点P,Qを共有するとき、$a$の値の範囲を求めよ。
(4)(3)のとき、Qの$x$座標$x_0$はPの$x$座標$x_1$よりも大きいとする。$x_0$-$x_1$=1であるときの$a$の値を求めよ。
(5)(4)のとき、Cと直線$m$で囲まれる図形の面積を求めよ。
福田の数学〜立教大学2023年理学部第2問〜ベクトルの共面条件と共線条件

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 0<$k$1とする。座標空間内の四面体OABCについて、線分ACの中点をD、線分BCの中点をE、線分DEを1:2に内分する点をPとする。また、
線分OPを$k$:1-$k$に内分する点をQとし、Rを$\overrightarrow{CR}$=$l\overrightarrow{CQ}$を満たす点とする。
$\overrightarrow{a}$=$\overrightarrow{OA}$, $\overrightarrow{b}$=$\overrightarrow{OB}$, $\overrightarrow{c}$=$\overrightarrow{OC}$とおいたとき、次の問いに答えよ。
(1)$\overrightarrow{OD}$, $\overrightarrow{OE}$, $\overrightarrow{OP}$を$\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$を用いて表せ。
(2)$\overrightarrow{OR}$を$\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$, $k$, $l$を用いて表せ。
(3)Rが平面OAB上にあるとき、$l$を$k$を用いて表せ。
(4)線分OAの中点をF、線分OBの中点をGとする。Rが線分FG上にあるときの$k$の値を求めよ。
この動画を見る
$\Large\boxed{2}$ 0<$k$1とする。座標空間内の四面体OABCについて、線分ACの中点をD、線分BCの中点をE、線分DEを1:2に内分する点をPとする。また、
線分OPを$k$:1-$k$に内分する点をQとし、Rを$\overrightarrow{CR}$=$l\overrightarrow{CQ}$を満たす点とする。
$\overrightarrow{a}$=$\overrightarrow{OA}$, $\overrightarrow{b}$=$\overrightarrow{OB}$, $\overrightarrow{c}$=$\overrightarrow{OC}$とおいたとき、次の問いに答えよ。
(1)$\overrightarrow{OD}$, $\overrightarrow{OE}$, $\overrightarrow{OP}$を$\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$を用いて表せ。
(2)$\overrightarrow{OR}$を$\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$, $k$, $l$を用いて表せ。
(3)Rが平面OAB上にあるとき、$l$を$k$を用いて表せ。
(4)線分OAの中点をF、線分OBの中点をGとする。Rが線分FG上にあるときの$k$の値を求めよ。
福田の数学〜立教大学2023年理学部第1問(5)〜反復試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (5)表の出る確率が$\frac{2}{3}$、裏の出る確率が$\frac{1}{3}$のコインを投げて、表が出たら+1点を加え、裏が出たら-1点を加える。というルールのゲームを行う。
0点から初めて5回コインを投げ終わった時、得点が3点以上となる確率は$\boxed{\ \ オ\ \ }$である。
2023立教大学理学部過去問
この動画を見る
$\Large\boxed{1}$ (5)表の出る確率が$\frac{2}{3}$、裏の出る確率が$\frac{1}{3}$のコインを投げて、表が出たら+1点を加え、裏が出たら-1点を加える。というルールのゲームを行う。
0点から初めて5回コインを投げ終わった時、得点が3点以上となる確率は$\boxed{\ \ オ\ \ }$である。
2023立教大学理学部過去問
福田の数学〜立教大学2023年理学部第1問(4)〜2次方程式が整数解をもつ条件

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#2次関数とグラフ#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (4)-1≦$\alpha$≦1 とする。$x$に関する方程式
$x^2$-$\frac{3}{2}x$-$\frac{9}{4}$+$\alpha$=0
が整数解をもつとき、$\alpha$の値は$\boxed{\ \ エ\ \ }$である。
2023立教大学理学部過去問
この動画を見る
$\Large\boxed{1}$ (4)-1≦$\alpha$≦1 とする。$x$に関する方程式
$x^2$-$\frac{3}{2}x$-$\frac{9}{4}$+$\alpha$=0
が整数解をもつとき、$\alpha$の値は$\boxed{\ \ エ\ \ }$である。
2023立教大学理学部過去問
福田の数学〜立教大学2023年理学部第1問(3)〜線分上の格子点の個数

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)座標平面上の2点O(0, 0)とP(2023, 1071)について、線分OA上にある点(x, y)でx, yが共に整数であるものの個数は$\boxed{\ \ ウ\ \ }$である。
ただし、線分OPは両端点を含むものとする。
2023立教大学理学部過去問
この動画を見る
$\Large\boxed{1}$ (3)座標平面上の2点O(0, 0)とP(2023, 1071)について、線分OA上にある点(x, y)でx, yが共に整数であるものの個数は$\boxed{\ \ ウ\ \ }$である。
ただし、線分OPは両端点を含むものとする。
2023立教大学理学部過去問
福田の数学〜立教大学2023年理学部第1問(2)〜極値をとる条件

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)関数$f(t)$=$a\cos^3t$+$\cos^2t$が$t$=$\frac{\pi}{4}$で極値をとるとき、$a$=$\boxed{\ \ イ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (2)関数$f(t)$=$a\cos^3t$+$\cos^2t$が$t$=$\frac{\pi}{4}$で極値をとるとき、$a$=$\boxed{\ \ イ\ \ }$である。
福田の数学〜立教大学2023年理学部第1問(1)〜指数方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#指数関数と対数関数#剰余の定理・因数定理・組み立て除法と高次方程式#指数関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)方程式$2^{x+2}$-$2^{2x+1}$+16=0 を解くと$x$=$\boxed{\ \ ア\ \ }$である。
2023立教大学理学部過去問
この動画を見る
$\Large\boxed{1}$ (1)方程式$2^{x+2}$-$2^{2x+1}$+16=0 を解くと$x$=$\boxed{\ \ ア\ \ }$である。
2023立教大学理学部過去問
福田の数学〜筑波大学2023年理系第6問〜複素数平面上の点の軌跡とアポロニウスの円

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ $i$を虚数単位とする。複素数平面に関する以下の問いに答えよ。
(1)等式|$z$+2|=2|$z$-1| を満たす点$z$の全体が表す図形は円であることを示し、その中心と半径を求めよ。
(2)等式
$\left\{|z+2|-2|z-1|\right\}$$|z+6i|$=$3\left\{|z+2|-2|z-1|\right\}$$|z-2i|$
を満たす点$z$の全体が表す図形をSとする。このときSを複素数平面上に図示せよ。
(3)点$z$が(2)における図形S上を動くとき、$w$=$\frac{1}{z}$ で定義される点$w$が描く図形を複素数平面上に図示せよ。
2023筑波大学理系過去問
この動画を見る
$\Large\boxed{6}$ $i$を虚数単位とする。複素数平面に関する以下の問いに答えよ。
(1)等式|$z$+2|=2|$z$-1| を満たす点$z$の全体が表す図形は円であることを示し、その中心と半径を求めよ。
(2)等式
$\left\{|z+2|-2|z-1|\right\}$$|z+6i|$=$3\left\{|z+2|-2|z-1|\right\}$$|z-2i|$
を満たす点$z$の全体が表す図形をSとする。このときSを複素数平面上に図示せよ。
(3)点$z$が(2)における図形S上を動くとき、$w$=$\frac{1}{z}$ で定義される点$w$が描く図形を複素数平面上に図示せよ。
2023筑波大学理系過去問
福田の数学〜筑波大学2023年理系第5問〜関数の増減と極限

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#微分法#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ $f(x)$=$x^{-2}e^x$ ($x$>0)とし、曲線$y$=$f(x)$をCとする。また$h$を正の実数とする。さらに、正の実数$t$に対して、曲線C、2直線$x$=$t$, $x$=$t$+$h$、および$x$軸で囲まれた図形の面積を$g(t)$とする。
(1)$g'(t)$を求めよ。
(2)$g(t)$を最小にする$t$がただ1つ存在することを示し、その$t$を$h$を用いて表せ。
(3)(2)で得られた$t$を$t(h)$とする。このとき極限値$\displaystyle\lim_{h \to +0}t(h)$を求めよ。
この動画を見る
$\Large\boxed{5}$ $f(x)$=$x^{-2}e^x$ ($x$>0)とし、曲線$y$=$f(x)$をCとする。また$h$を正の実数とする。さらに、正の実数$t$に対して、曲線C、2直線$x$=$t$, $x$=$t$+$h$、および$x$軸で囲まれた図形の面積を$g(t)$とする。
(1)$g'(t)$を求めよ。
(2)$g(t)$を最小にする$t$がただ1つ存在することを示し、その$t$を$h$を用いて表せ。
(3)(2)で得られた$t$を$t(h)$とする。このとき極限値$\displaystyle\lim_{h \to +0}t(h)$を求めよ。



