ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
#63 #数検1級1次過去問 #連立方程式
単元：
#数学(中学生)#中２数学#連立方程式
指導講師：
ますただ
問題文全文(内容文)：
$xy \neq 0$のとき、次の連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x+y)(x^2+y^2)=\displaystyle \frac{40}{3}xy \\
(x^2+y^2)(x^4-y^4)=\displaystyle \frac{800}{9}x^2y^2
\end{array}
\right.
\end{eqnarray}$
出典：数検1級1次
この動画を見る
$xy \neq 0$のとき、次の連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x+y)(x^2+y^2)=\displaystyle \frac{40}{3}xy \\
(x^2+y^2)(x^4-y^4)=\displaystyle \frac{800}{9}x^2y^2
\end{array}
\right.
\end{eqnarray}$
出典：数検1級1次
#藤田医科大学(2005) #極限 #Shorts
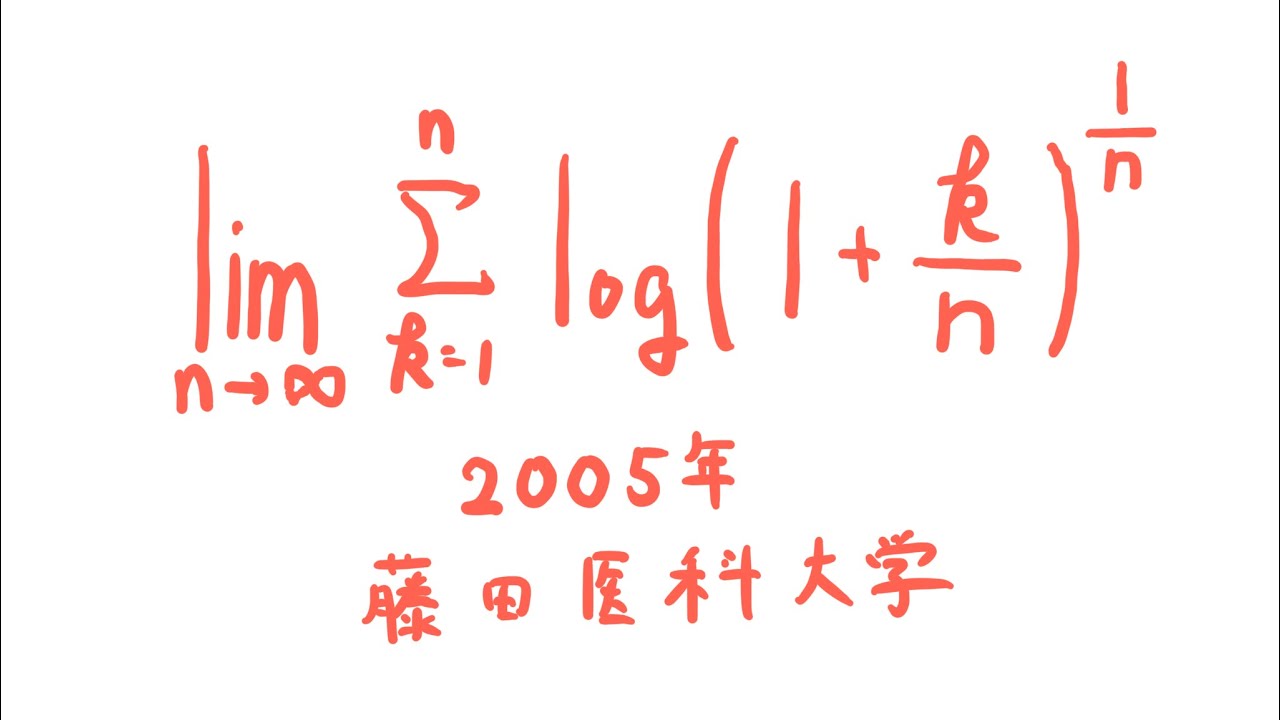
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n log(1+\displaystyle \frac{k}{n})^\frac{1}{n}$
出典：2005年藤田医科大学
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n log(1+\displaystyle \frac{k}{n})^\frac{1}{n}$
出典：2005年藤田医科大学
大学入試問題#792「なぜサムネに『も』をいれてんだ」 #早稲田大学人間科学部(2024)
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x$が実数であるとき$x(x+1)(x+2)(x+3)$の最小値を求めよ。
出典：2024年早稲田大学人間科学部 入試問題
この動画を見る
$x$が実数であるとき$x(x+1)(x+2)(x+3)$の最小値を求めよ。
出典：2024年早稲田大学人間科学部 入試問題
大学入試問題#793「教科書の章末問題！？」 #室蘭工業大学(2018) #数列
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#室蘭工業大学
指導講師：
ますただ
問題文全文(内容文)：
$a_1=\displaystyle \frac{1}{2}, a_{n+1}=\displaystyle \frac{(n+1)a_n}{n+3^na_n}$を満たす数列$\{a_n\}$を求めよ。
出典：2018年室蘭工業大学 入試問題
この動画を見る
$a_1=\displaystyle \frac{1}{2}, a_{n+1}=\displaystyle \frac{(n+1)a_n}{n+3^na_n}$を満たす数列$\{a_n\}$を求めよ。
出典：2018年室蘭工業大学 入試問題
大学入試問題#792「初手が重要！！」 #室蘭工業大学(2020) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#室蘭工業大学
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=\displaystyle \frac{x^2+x-2}{(2x+1)(x^2+x+1)}$と定める。
定積分$\displaystyle \int_{0}^{\frac{\pi}{2}} f(\cos^2x) \sin(2x)dx$の値を求めよ。
出典：2020年室蘭工業大学 入試問題
この動画を見る
$f(x)=\displaystyle \frac{x^2+x-2}{(2x+1)(x^2+x+1)}$と定める。
定積分$\displaystyle \int_{0}^{\frac{\pi}{2}} f(\cos^2x) \sin(2x)dx$の値を求めよ。
出典：2020年室蘭工業大学 入試問題
#62.5 #数検1級1次 #有理化 #Shorts
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
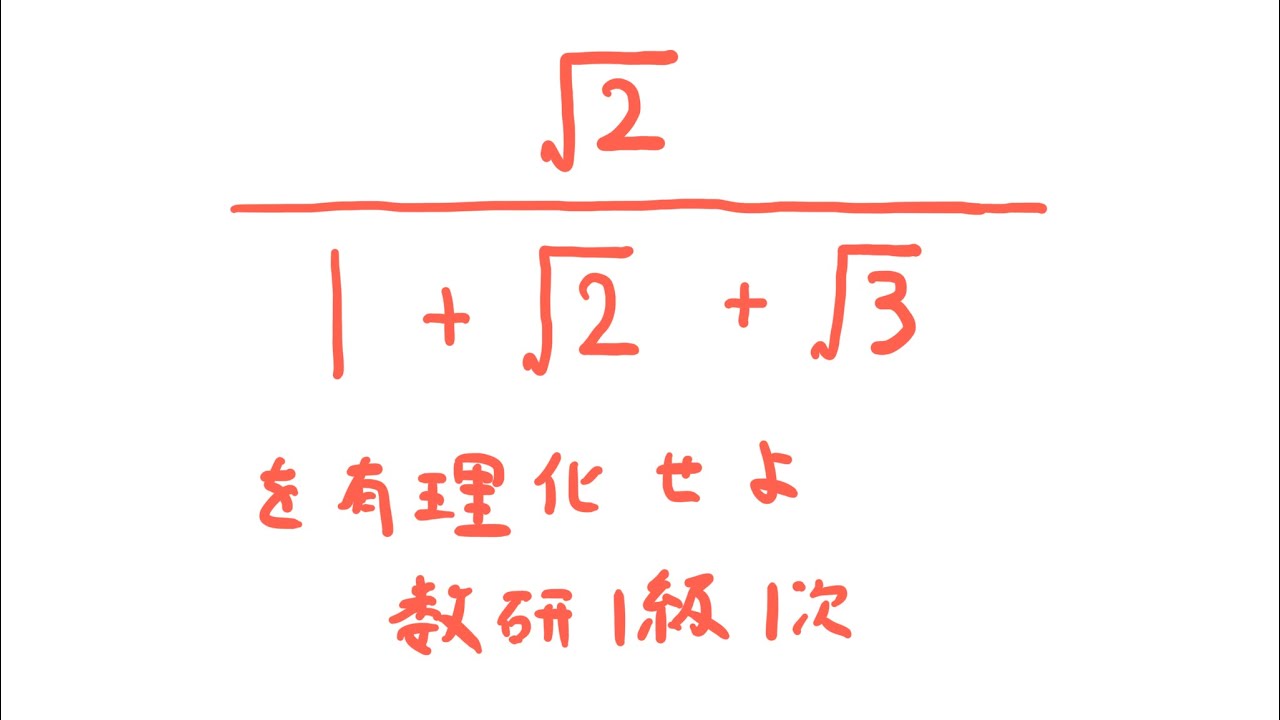
$\displaystyle \frac{\sqrt{ 2 }}{1+\sqrt{ 2 }+\sqrt{ 3 }}$を有理化せよ
出典：数検1級1次
この動画を見る
$\displaystyle \frac{\sqrt{ 2 }}{1+\sqrt{ 2 }+\sqrt{ 3 }}$を有理化せよ
出典：数検1級1次
「安定の良問」 by にっし~Diaryさん #極限
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#関数と極限#数列の極限#関数の極限#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x\{\sin(\displaystyle \frac{1}{x})-\sin(\sin(\displaystyle \frac{1}{x}))\}}{1-x\ \sin(\displaystyle \frac{1}{x})}$
この動画を見る
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x\{\sin(\displaystyle \frac{1}{x})-\sin(\sin(\displaystyle \frac{1}{x}))\}}{1-x\ \sin(\displaystyle \frac{1}{x})}$
#62 #数検1級1次過去問 #因数分解
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
次の式を係数が整数の範囲で因数分解せよ。
$x^6-14x^4+17x^2-4$
出典：数検1級1次
この動画を見る
次の式を係数が整数の範囲で因数分解せよ。
$x^6-14x^4+17x^2-4$
出典：数検1級1次
大学入試問題#791「第一感で大丈夫」 #慶應義塾大学環境情報学部(2024)
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x,y$を正の実数とするとき
$27x+\displaystyle \frac{3x}{y^2}+\displaystyle \frac{2y}{x}$の最小値を求めよ。
また、そのときの$x,y$の値を求めよ。
出典：2024年慶應義塾大学環境情報学部 入試問題
この動画を見る
$x,y$を正の実数とするとき
$27x+\displaystyle \frac{3x}{y^2}+\displaystyle \frac{2y}{x}$の最小値を求めよ。
また、そのときの$x,y$の値を求めよ。
出典：2024年慶應義塾大学環境情報学部 入試問題
大学入試問題#790「解き方はたくさんありそう」 #福島大学(2021) #極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to a } \displaystyle \frac{\sin\ x-\sin\ a}{\sin(x-a)}$
出典：2021年福島大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to a } \displaystyle \frac{\sin\ x-\sin\ a}{\sin(x-a)}$
出典：2021年福島大学 入試問題
#61数検１級１次「よくできた問題」
単元：
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$(x-1)^7-(x^7-1)$を実数係数の範囲で因数分解せよ
出典：数検1級1次
この動画を見る
$(x-1)^7-(x^7-1)$を実数係数の範囲で因数分解せよ
出典：数検1級1次
#高知工科大学(2023) #定積分 #Shorts
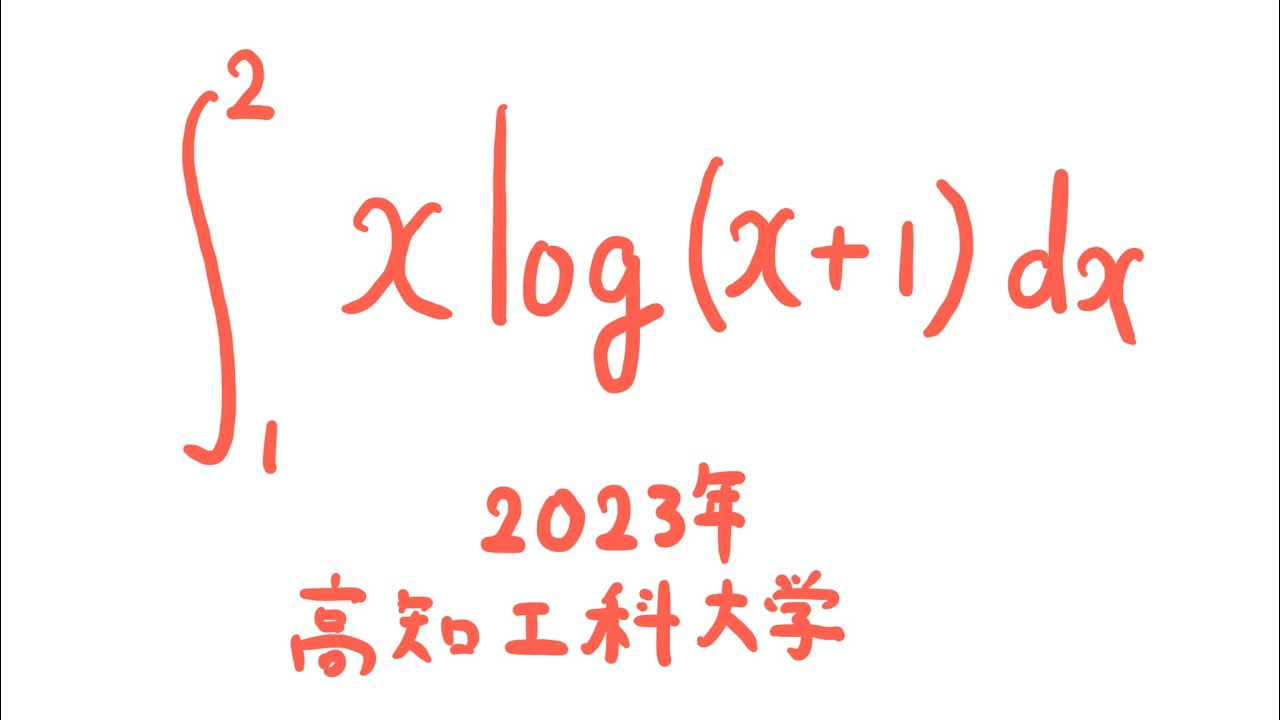
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#高知工科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{2} x\ log(x+1)dx$
出典：2023年高知工科大学
この動画を見る
$\displaystyle \int_{1}^{2} x\ log(x+1)dx$
出典：2023年高知工科大学
大学入試問題#789「落ち着いて解くだけ」 早稲田大学商学部(2024) #整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
不等式
$|\displaystyle \frac{2024n}{1-46n}+44| \lt \displaystyle \frac{1}{2025}$を満たす正の整数$n$の最小値を求めよ。
出典：2024年早稲田大学商学部 入試問題
この動画を見る
不等式
$|\displaystyle \frac{2024n}{1-46n}+44| \lt \displaystyle \frac{1}{2025}$を満たす正の整数$n$の最小値を求めよ。
出典：2024年早稲田大学商学部 入試問題
#高知工科大学(2022) #定積分 #Shorts
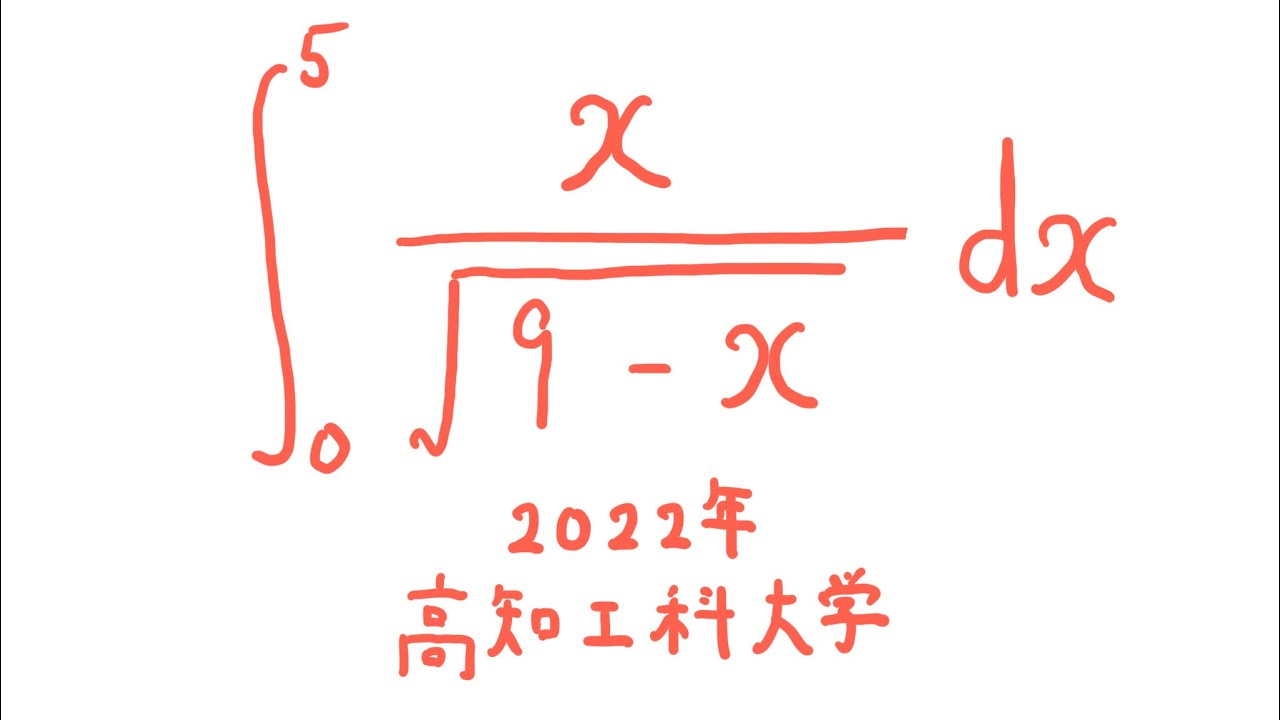
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#高知工科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{5} \displaystyle \frac{x}{\sqrt{ 9-x }} dx$
出典：2022年高知工科大学
この動画を見る
$\displaystyle \int_{0}^{5} \displaystyle \frac{x}{\sqrt{ 9-x }} dx$
出典：2022年高知工科大学
大学入試問題#788「教科書の例題レベル」 慶應義塾大学商学部(2024) #積分方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
等式$f(x)=12x^2+6x\displaystyle \int_{0}^{1} f(t) dt+2\displaystyle \int_{0}^{1} tf(t)dt$を満たす関数$f(x)$を求めよ。
出典：2024年慶應義塾大学商学部 入試問題
この動画を見る
等式$f(x)=12x^2+6x\displaystyle \int_{0}^{1} f(t) dt+2\displaystyle \int_{0}^{1} tf(t)dt$を満たす関数$f(x)$を求めよ。
出典：2024年慶應義塾大学商学部 入試問題
#福島大学(2022) #定積分 #Shorts
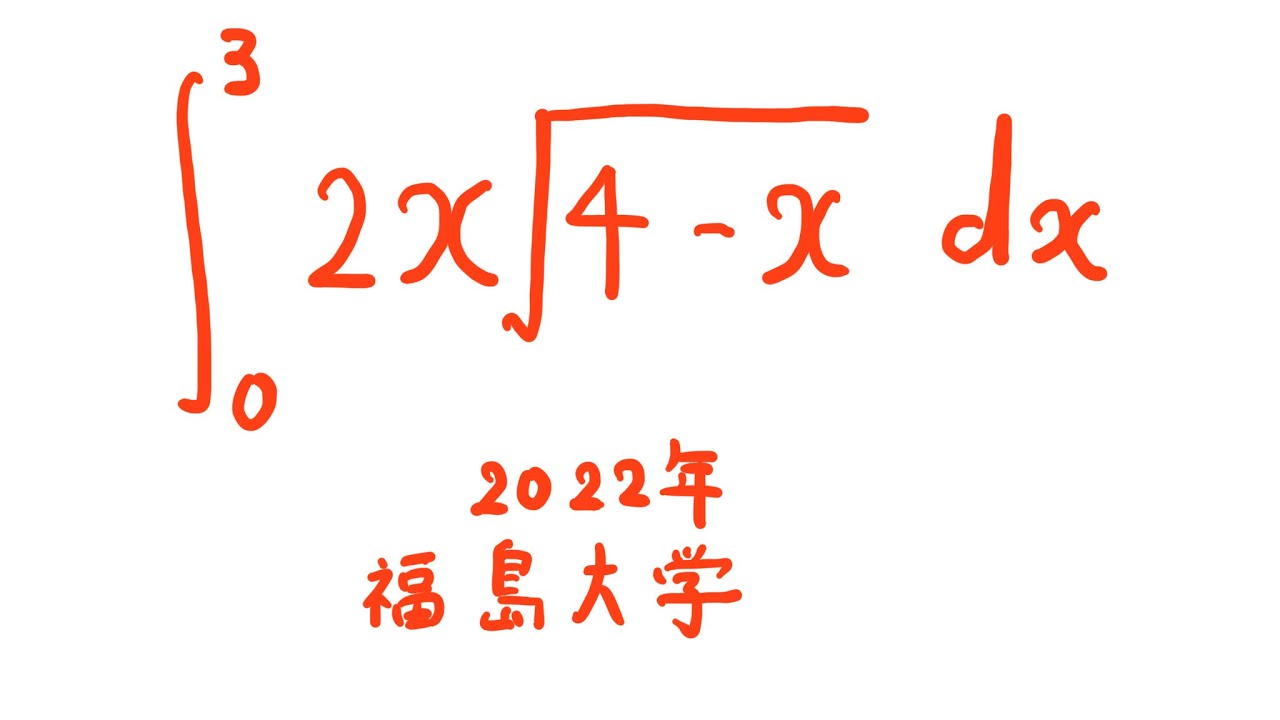
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{3} 2x\sqrt{ 4-x }\ dx$
出典：2022年福島大学
この動画を見る
$\displaystyle \int_{0}^{3} 2x\sqrt{ 4-x }\ dx$
出典：2022年福島大学
#60数検1級1次「ええ問題！落とし穴に注意」 数検1級1次
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
全ての実数$x$について
$\displaystyle \frac{\pi}{2} \lt \tan^{-1}x \lt \displaystyle \frac{\pi}{2}$とするとき、次の値を求めよ。
$\tan^{-1}1+\tan^{-1}2+\tan^{-1}3$
出典：数検1級1次
この動画を見る
全ての実数$x$について
$\displaystyle \frac{\pi}{2} \lt \tan^{-1}x \lt \displaystyle \frac{\pi}{2}$とするとき、次の値を求めよ。
$\tan^{-1}1+\tan^{-1}2+\tan^{-1}3$
出典：数検1級1次
#会津大学(2009) #定積分 #Shorts
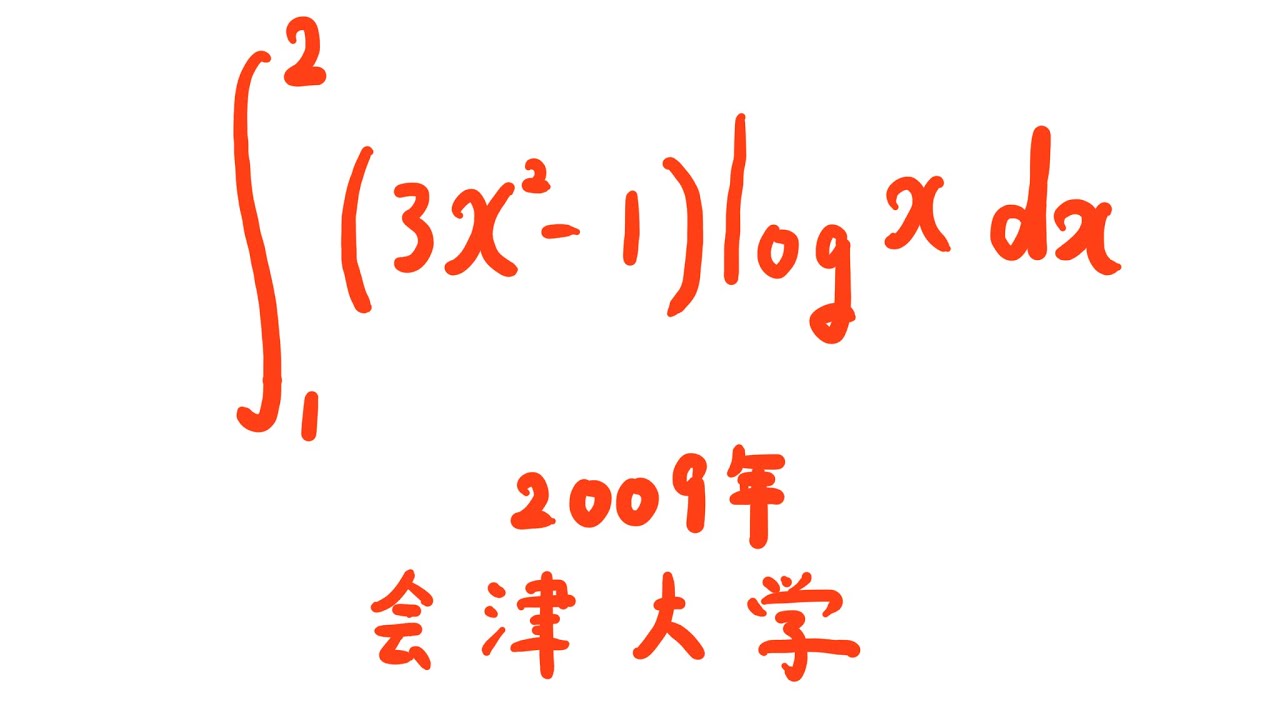
単元：
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{2} (3x^3-1)log\ x\ dx$
出典：2009年会津大学
この動画を見る
$\displaystyle \int_{1}^{2} (3x^3-1)log\ x\ dx$
出典：2009年会津大学
大学入試問題#786「よく出題されている。」 慶應義塾大学商学部(2024) #整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$a \lt b \lt c$ かつ$\displaystyle \frac{1}{a}+\displaystyle \frac{2}{b}+\displaystyle \frac{3}{c}=2$を満たす自然数の組$(a,b,c)$をすべて求めよ
出典：2024年慶應義塾大学商学部 入試問題
この動画を見る
$a \lt b \lt c$ かつ$\displaystyle \frac{1}{a}+\displaystyle \frac{2}{b}+\displaystyle \frac{3}{c}=2$を満たす自然数の組$(a,b,c)$をすべて求めよ
出典：2024年慶應義塾大学商学部 入試問題
#秋田大学(2022) #定積分 #Shorts
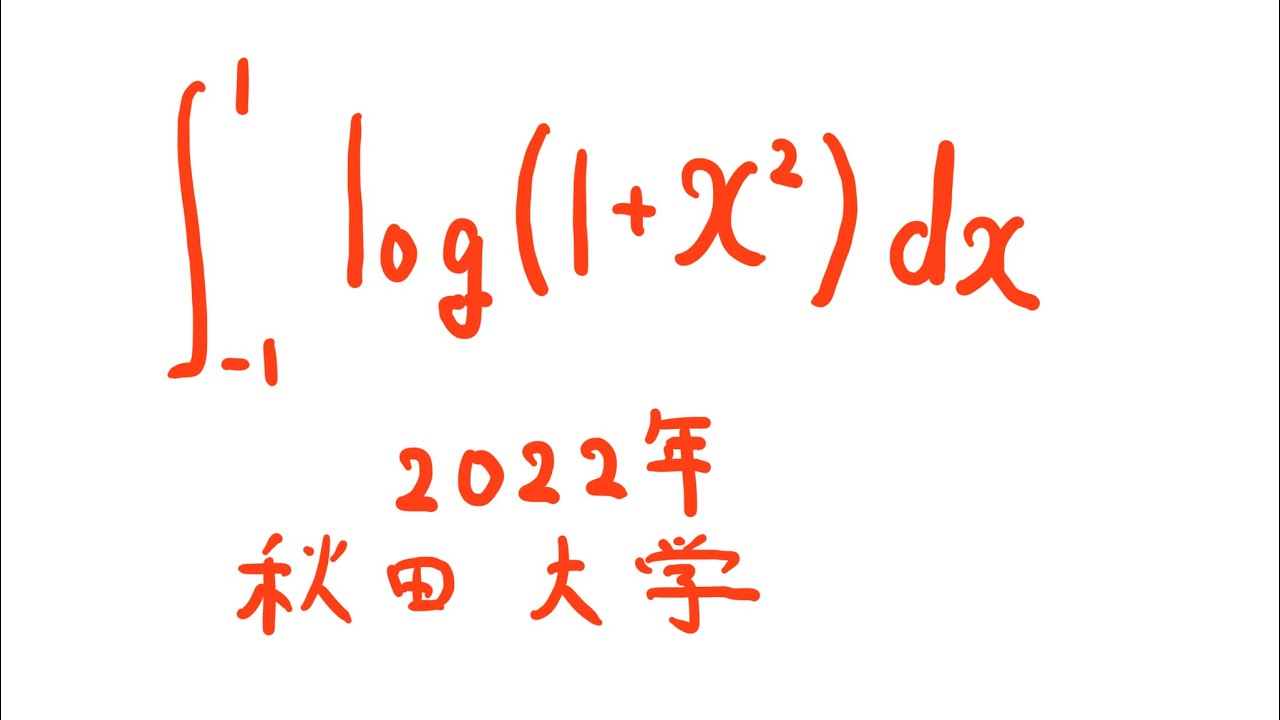
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#秋田大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{1} log(1+x^2) dx$
出典：2022年秋田大学
この動画を見る
$\displaystyle \int_{-1}^{1} log(1+x^2) dx$
出典：2022年秋田大学
#59数検1級1次「国立大の入試問題の代表的な題材」
単元：
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$n$を正の整数とするとき定積分
$\displaystyle \int_{0}^{1} (log_e\ x)^n\ dx$の値を$n$に関する式で表せ。
出典：数検1級1次
この動画を見る
$n$を正の整数とするとき定積分
$\displaystyle \int_{0}^{1} (log_e\ x)^n\ dx$の値を$n$に関する式で表せ。
出典：数検1級1次
大学入試問題#784「解き方は、一択？」 岡山県立大学中期(2011)
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算（整式・展開・因数分解）#学校別大学入試過去問解説(数学)#数学(高校生)#岡山県立大学
指導講師：
ますただ
問題文全文(内容文)：
実数$x,y$が$x^3+y^3=3xy$を満たすとき
$x+y$のとり得る値の範囲を求めよ。
出典：2011年岡山県立大学中期 入試問題
この動画を見る
実数$x,y$が$x^3+y^3=3xy$を満たすとき
$x+y$のとり得る値の範囲を求めよ。
出典：2011年岡山県立大学中期 入試問題
#会津大学(2009) #定積分 #Shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} x\sqrt{ 1-x^2 }\ dx$
出典：2009年会津大学
この動画を見る
$\displaystyle \int_{0}^{1} x\sqrt{ 1-x^2 }\ dx$
出典：2009年会津大学
大学入試問題#783「おもろいタイプ」 岡山県立大学中期(2011) #定積分
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#岡山県立大学
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=\displaystyle \int_{0}^{x} \displaystyle \frac{1}{\sqrt{ 1-t^2 }}\ dt(0 \leq x \leq 1)$において
$\displaystyle \int_{0}^{\frac{1}{2}} f(x)\ dx$を求めよ
出典：2011年青山県立大学中期 入試問題
この動画を見る
$f(x)=\displaystyle \int_{0}^{x} \displaystyle \frac{1}{\sqrt{ 1-t^2 }}\ dt(0 \leq x \leq 1)$において
$\displaystyle \int_{0}^{\frac{1}{2}} f(x)\ dx$を求めよ
出典：2011年青山県立大学中期 入試問題
大学入試問題#782「もう何回目だろうか」 横浜市立大学(2004) #区分求積法
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#横浜市立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty } \{\displaystyle \frac{(2n+1)(2n+2)・・・(2n+n)}{(n+1)(n+2)・・・(n+n)}\}^\frac{1}{n}$
出典：2004年横浜市立大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \{\displaystyle \frac{(2n+1)(2n+2)・・・(2n+n)}{(n+1)(n+2)・・・(n+n)}\}^\frac{1}{n}$
出典：2004年横浜市立大学 入試問題
#宮崎大学(2017) #定積分 #Shorts
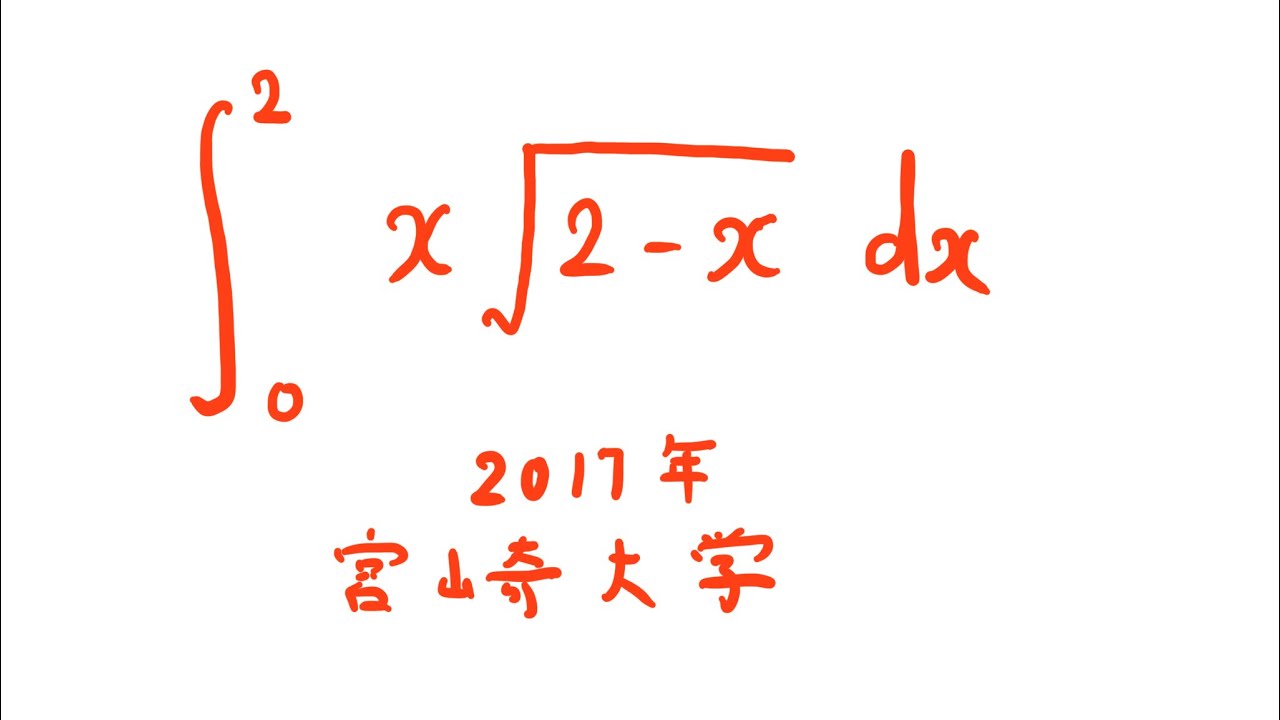
単元：
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{2} x\sqrt{ 2-x }\ dx$
出典：2017年宮崎大学
この動画を見る
$\displaystyle \int_{0}^{2} x\sqrt{ 2-x }\ dx$
出典：2017年宮崎大学
大学入試問題#781「絶対値付きの積分は、なんか苦手！」 久留米大学医学部(2005) #定積分
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#久留米大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}} |\sin\ x-2\sin\ 2x|\ dx$
出典：2005年久留米大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} |\sin\ x-2\sin\ 2x|\ dx$
出典：2005年久留米大学医学部 入試問題
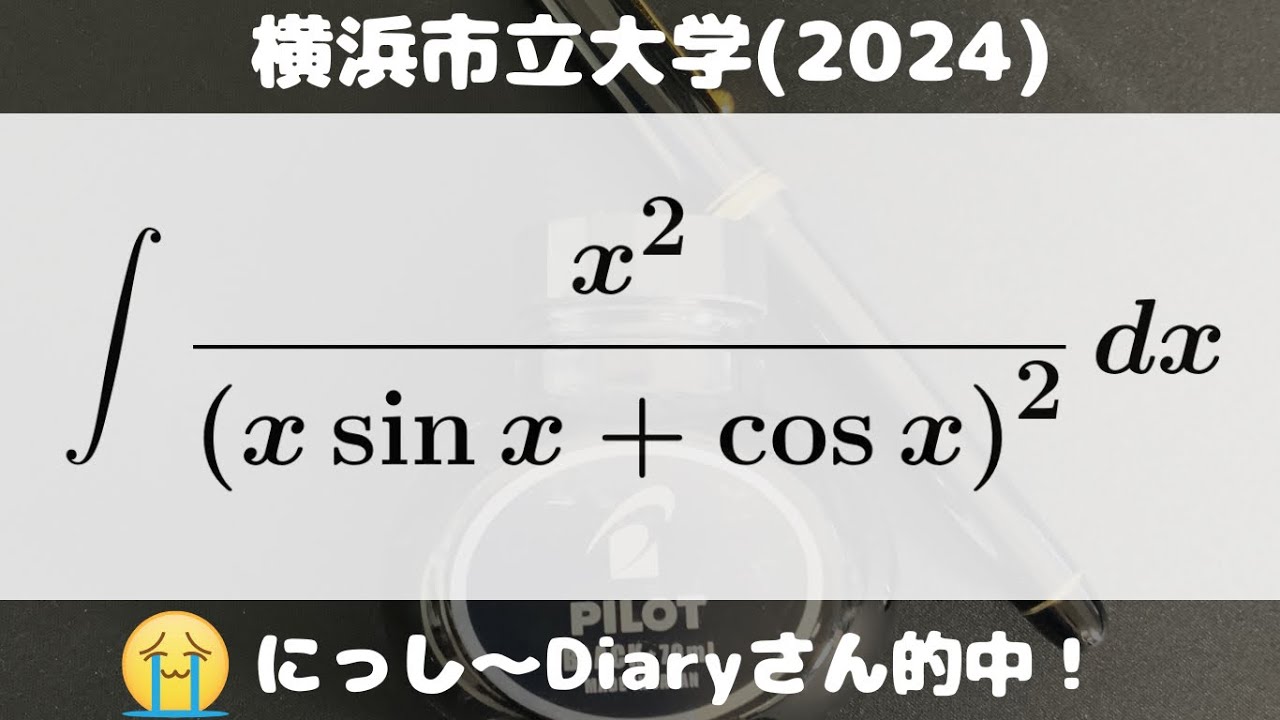
大学入試問題#780「この当て方は、凄すぎ！横浜市立の先生は視聴者かな！？ｗ」 横浜市立大学(2024) #定積分
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#横浜市立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{x^2}{(x\ \sin\ x+\cos\ x)^2} dx$
出典：2024年横浜市立大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x^2}{(x\ \sin\ x+\cos\ x)^2} dx$
出典：2024年横浜市立大学
#広島市立大学(2011) #定積分 #Shorts
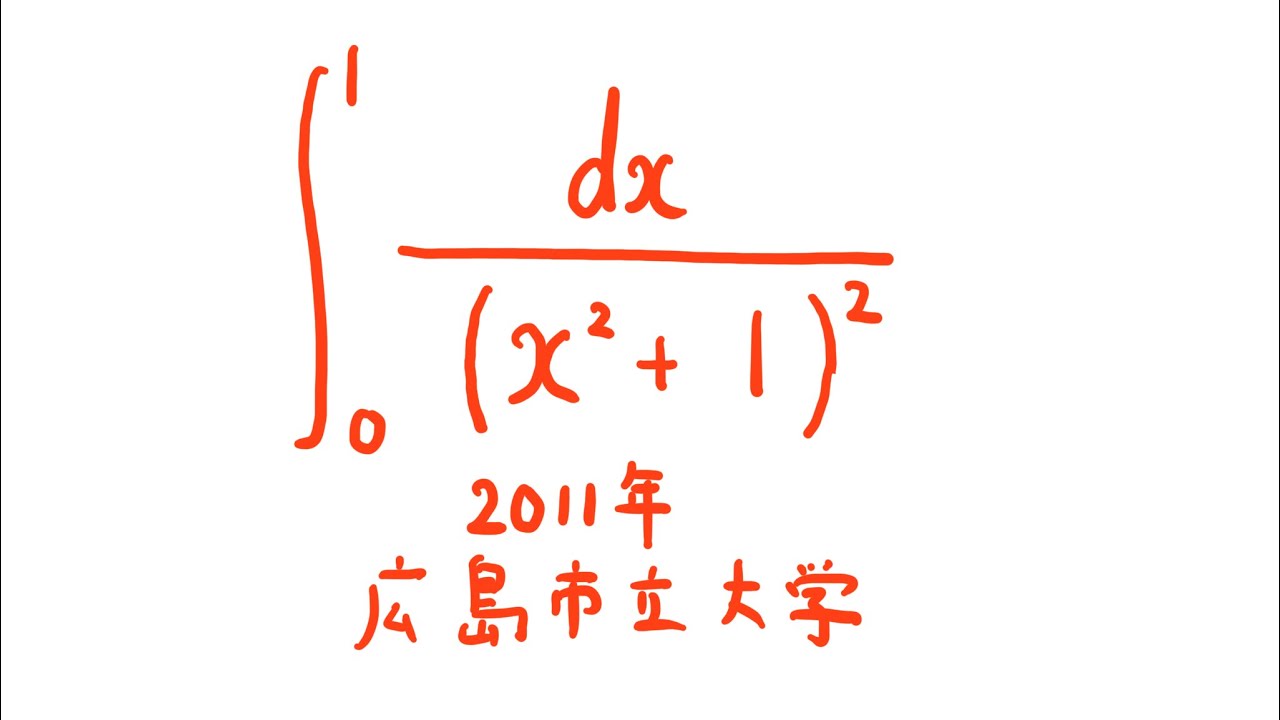
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} \displaystyle \frac{dx}{(x^2+1)^2}$
出典：2011年広島市立大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{dx}{(x^2+1)^2}$
出典：2011年広島市立大学
大学入試問題#779「コメントするなら普通の問題」 青山学院大学(2021) #整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt{ n^2+2n+16 }$ が整数となるような整数$n$をすべて求めよ
出典：2021年青山学院大学
この動画を見る
$\sqrt{ n^2+2n+16 }$ が整数となるような整数$n$をすべて求めよ
出典：2021年青山学院大学