ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
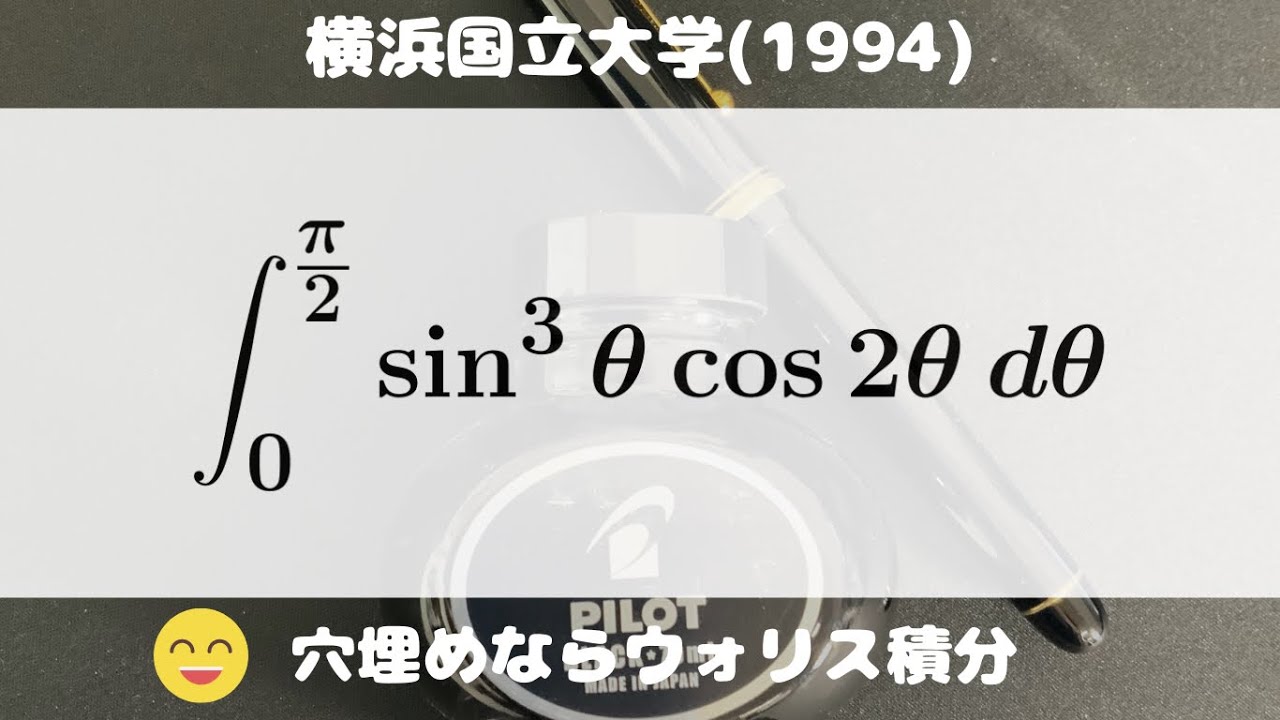
大学入試問題#778「ウォリス積分なら一撃」 横浜国立大学(1994) #定積分
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^3\theta\ \cos2\theta\ d\theta$
出典：1994年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^3\theta\ \cos2\theta\ d\theta$
出典：1994年横浜国立大学 入試問題
大学入試問題#777「どこから手をつける？」 昭和大学医学部(2024)
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算（整式・展開・因数分解）#学校別大学入試過去問解説(数学)#数学(高校生)#昭和大学
指導講師：
ますただ
問題文全文(内容文)：
実数$x,y$が$x^2+xy+y^2=1$を満たすとき
$x+2xy+y$の最大値と最小値を求めよ
出典：2024年昭和大学医学部 入試問題
この動画を見る
実数$x,y$が$x^2+xy+y^2=1$を満たすとき
$x+2xy+y$の最大値と最小値を求めよ
出典：2024年昭和大学医学部 入試問題
大学入試問題#776「シグマの気持ち」 横浜国立大学(1996)
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to +\infty } \displaystyle \frac{1}{n}log\{\displaystyle \frac{n}{n}・\displaystyle \frac{n+2}{n}・\displaystyle \frac{n+4}{n}・・・\displaystyle \frac{n+2(n-1)}{n}\}$
出典：1996年横浜国立大学
この動画を見る
$\displaystyle \lim_{ n \to +\infty } \displaystyle \frac{1}{n}log\{\displaystyle \frac{n}{n}・\displaystyle \frac{n+2}{n}・\displaystyle \frac{n+4}{n}・・・\displaystyle \frac{n+2(n-1)}{n}\}$
出典：1996年横浜国立大学
#広島市立大学(2016) #定積分 #Shorts
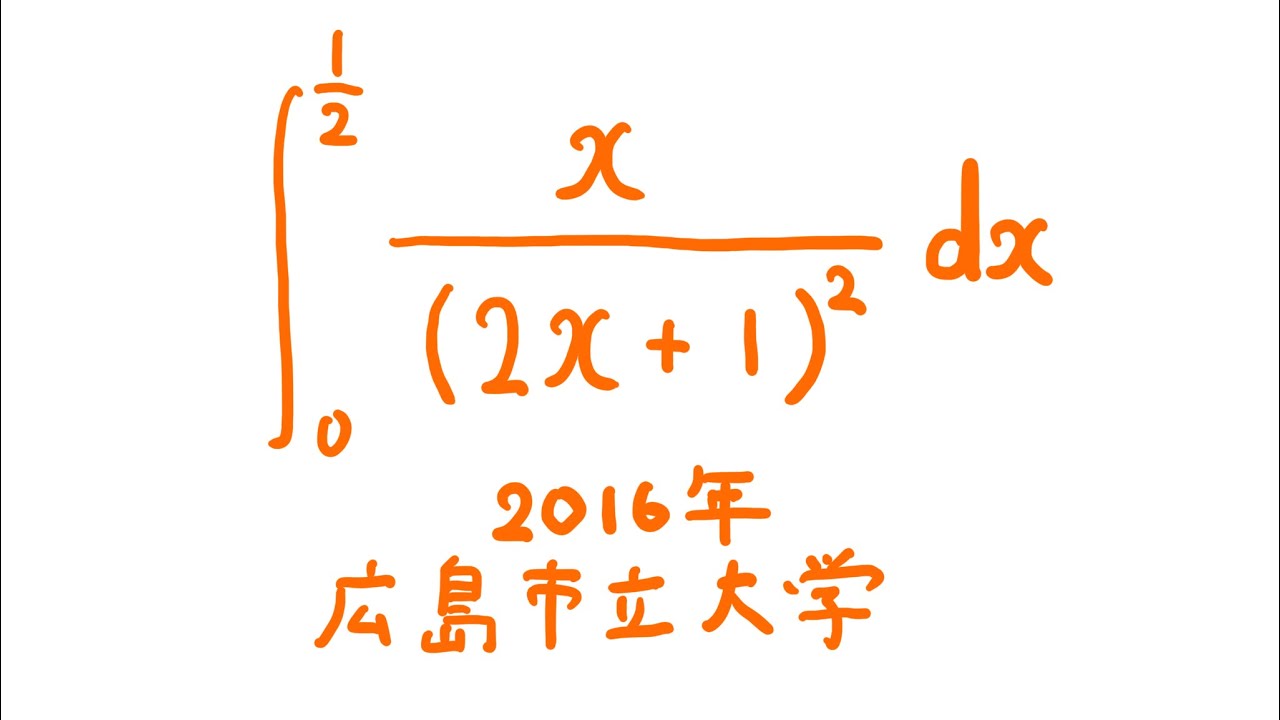
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{1}{2}} \displaystyle \frac{x}{(2x+1)^2} dx$
出典：2016年広島市立大学
この動画を見る
$\displaystyle \int_{0}^{\frac{1}{2}} \displaystyle \frac{x}{(2x+1)^2} dx$
出典：2016年広島市立大学
大学入試問題#775「ほぼ、詰んでる」 横浜国立大学(1998) #定積分
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{2\pi} x^2|\sin\ x|\ dx$
出典：1998年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2\pi} x^2|\sin\ x|\ dx$
出典：1998年横浜国立大学 入試問題
大学入試問題#774「基本的な良問」 横浜国立大学(1998) #定積分
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{e-1} \displaystyle \frac{log(log(x+1))}{x+1} dx$
出典：1998年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e-1} \displaystyle \frac{log(log(x+1))}{x+1} dx$
出典：1998年横浜国立大学 入試問題
#広島市立大学(2016) #定積分 #Shorts
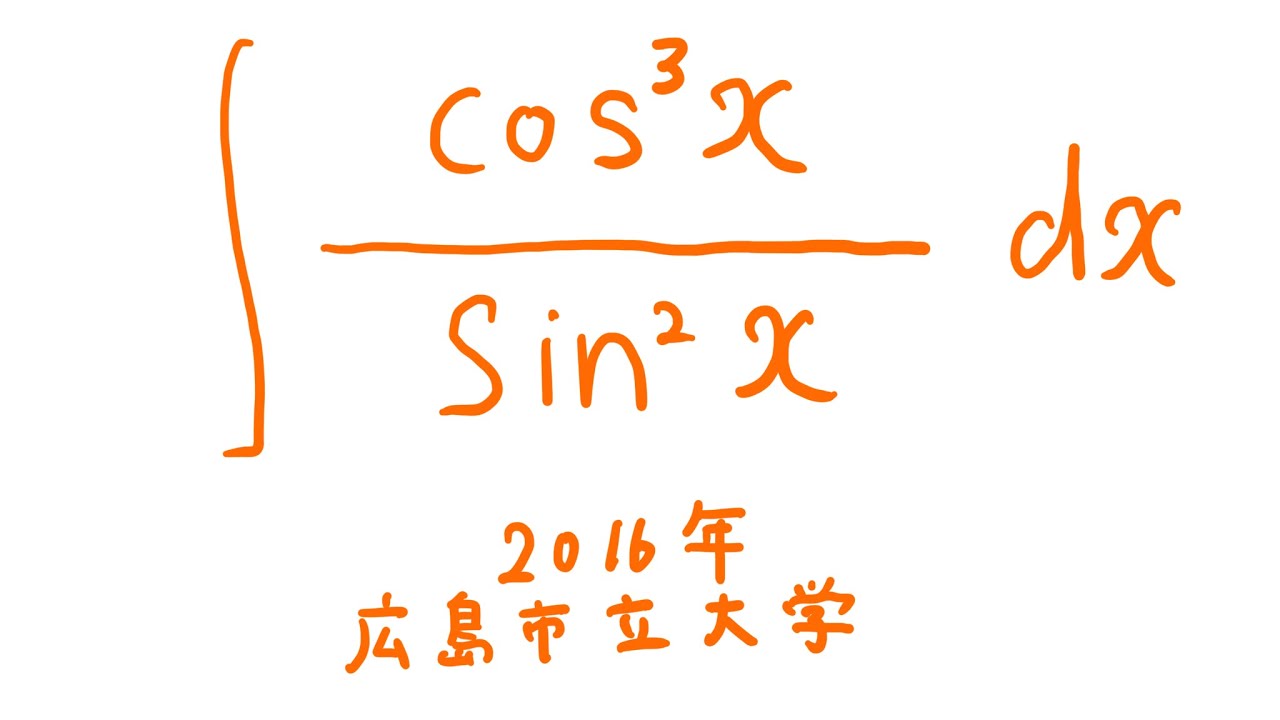
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{\cos^3\ x}{\sin^2\ x} dx$
出典：2016年広島市立大学
この動画を見る
$\displaystyle \int \displaystyle \frac{\cos^3\ x}{\sin^2\ x} dx$
出典：2016年広島市立大学
大学入試問題#773「綺麗な良問」 青山学院大学(2019) #整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師：
ますただ
問題文全文(内容文)：
素数$p.q$および自然数$n$に対し
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}+\displaystyle \frac{1}{pq}=\displaystyle \frac{1}{n}$
が成り立つような$(p,q,n)$の組をすべて求めよ
出典：2019年青山学院大学
この動画を見る
素数$p.q$および自然数$n$に対し
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}+\displaystyle \frac{1}{pq}=\displaystyle \frac{1}{n}$
が成り立つような$(p,q,n)$の組をすべて求めよ
出典：2019年青山学院大学
大学入試問題#772「初手は好みがでそう」 広島市立大学(2012) #不定積分
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{log\ x}{\sqrt[ 3 ]{ x }} dx$
出典：2012年広島市立大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{log\ x}{\sqrt[ 3 ]{ x }} dx$
出典：2012年広島市立大学 入試問題
#会津大学(2023) #定積分 #Shorts
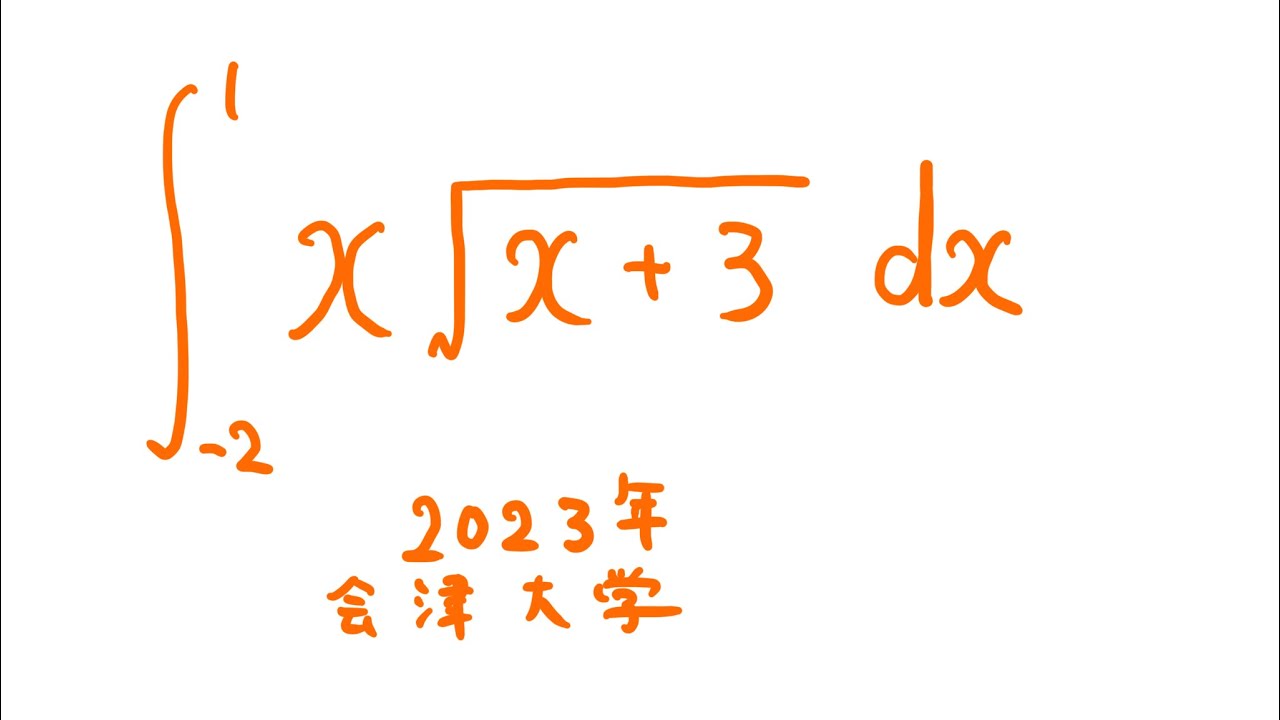
単元：
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-2}^{1} x\sqrt{ x+3 }\ dx$
出典：2023年会津大学
この動画を見る
$\displaystyle \int_{-2}^{1} x\sqrt{ x+3 }\ dx$
出典：2023年会津大学
大学入試問題#771「たぶん良問！」 島根大学後期(2023) #定積分
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#島根大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} \displaystyle \frac{2x-2}{2x^2-2x+1} dx$
出典：2023年島根大学後期 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{2x-2}{2x^2-2x+1} dx$
出典：2023年島根大学後期 入試問題
#会津大学 2020年 #定積分 #Shorts
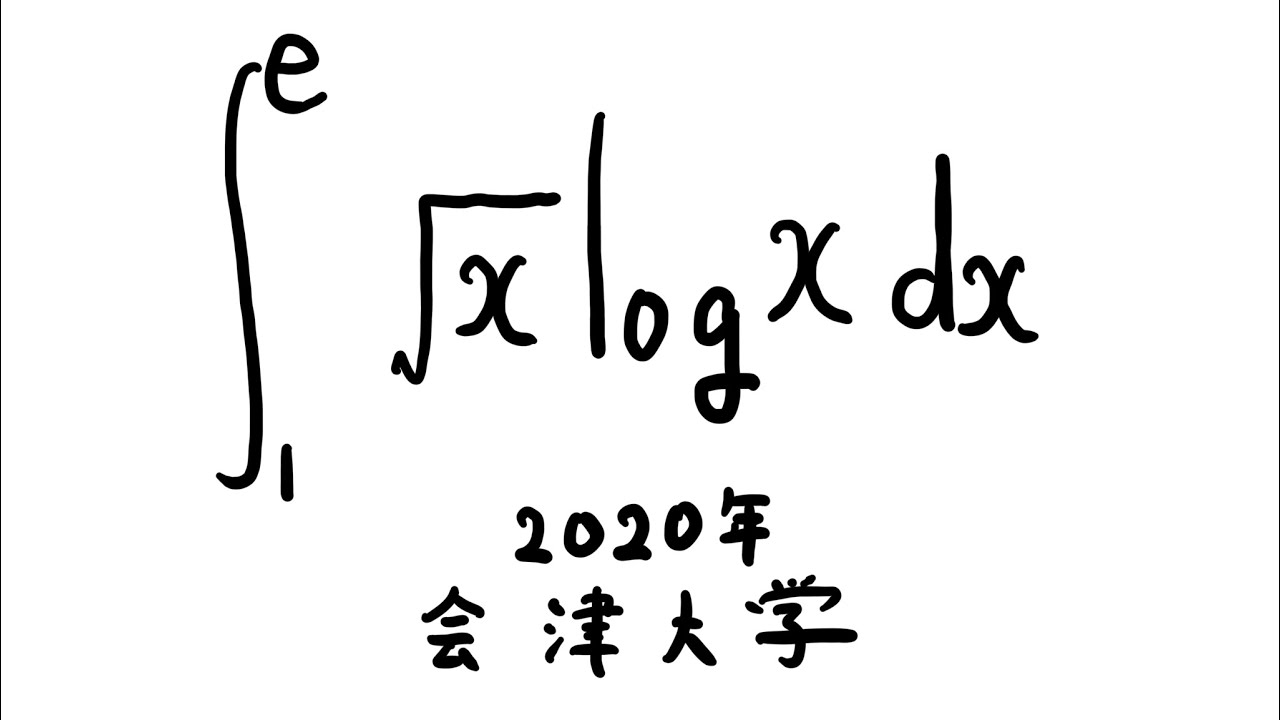
単元：
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{e} \sqrt{ x }\ log\ x\ dx$
出典：2020年会津大学
この動画を見る
$\displaystyle \int_{1}^{e} \sqrt{ x }\ log\ x\ dx$
出典：2020年会津大学
大学入試問題#770「減点注意！」 千葉大学(2003) #微積の応用
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$a$は定数とし、$n$は2以上の整数とする。
関数$f(x)=ax^n log\ x-ax(x \gt 0)$の最小値が-1のとき、定積分$\displaystyle \int_{1}^{e} f(x)\ dx$の値を$n$と$e$を用いて表せ。
出典：2003年千葉大学 入試問題
この動画を見る
$a$は定数とし、$n$は2以上の整数とする。
関数$f(x)=ax^n log\ x-ax(x \gt 0)$の最小値が-1のとき、定積分$\displaystyle \int_{1}^{e} f(x)\ dx$の値を$n$と$e$を用いて表せ。
出典：2003年千葉大学 入試問題
#会津大学 2023年 #定積分 #Shorts
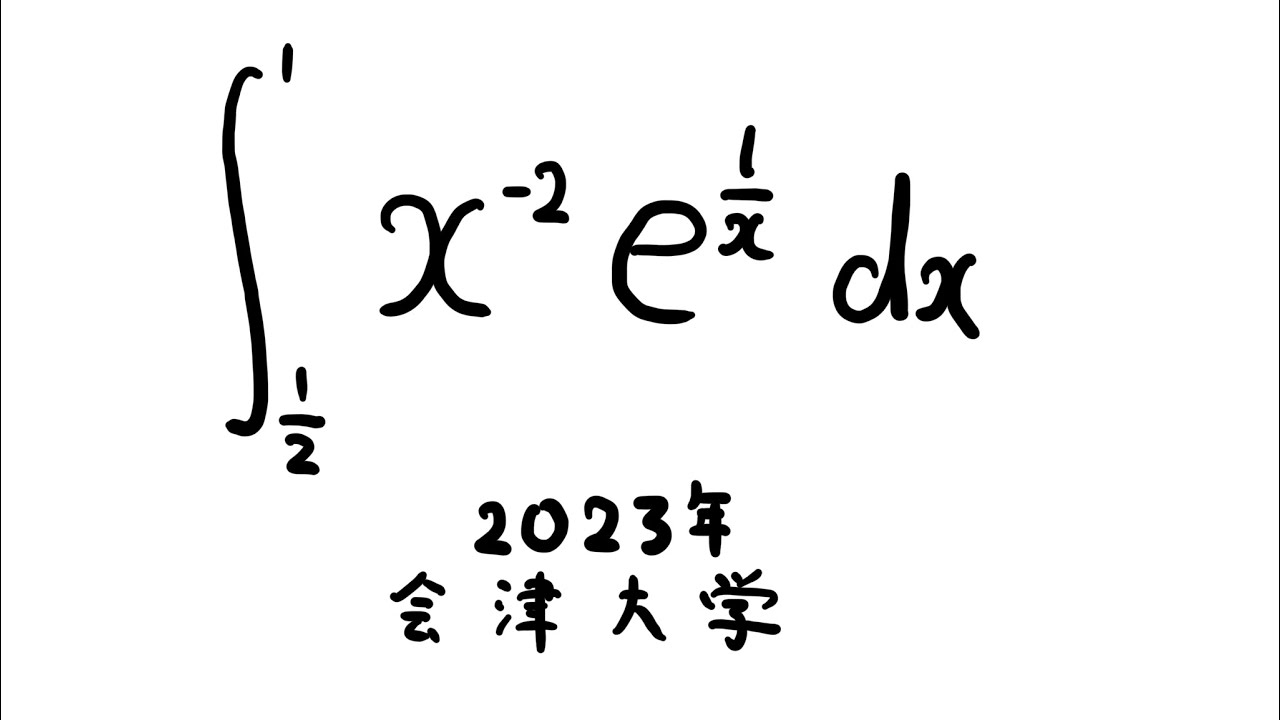
単元：
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{\frac{1}{2}}^{1} x^{-2}e^{\frac{1}{x}} dx$
出典：2023年会津大学
この動画を見る
$\displaystyle \int_{\frac{1}{2}}^{1} x^{-2}e^{\frac{1}{x}} dx$
出典：2023年会津大学
大学入試問題#769「受験生は抑えたい良問」 日本医科大学(2013) #微積の応用
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \frac{3}{2} \leq \displaystyle \lim_{ n \to \infty } (1+\displaystyle \frac{1}{2^2}+・・・+\displaystyle \frac{1}{n^2}) \leq 2$を示せ。
出典：2013年日本医科大学 入試問題
この動画を見る
$\displaystyle \frac{3}{2} \leq \displaystyle \lim_{ n \to \infty } (1+\displaystyle \frac{1}{2^2}+・・・+\displaystyle \frac{1}{n^2}) \leq 2$を示せ。
出典：2013年日本医科大学 入試問題
大学入試問題#768 「ゴリゴリ音がでそう」 千葉大学(2005) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\pi} |3\ \cos\ 2x+7\cos\ x|\ dx$
出典：2005年千葉大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi} |3\ \cos\ 2x+7\cos\ x|\ dx$
出典：2005年千葉大学 入試問題
大学入試問題#767「ほんまに茶番」 #岡山県立大学 (2018) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#岡山県立大学
指導講師：
ますただ
問題文全文(内容文)：
$I=\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{\sin\ x}{\sqrt{ 3 }\ \sin\ x+\cos\ x} dx$
$J=\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{\cos\ x}{\sqrt{ 3 }\ \sin\ x+\cos\ x} dx$
$I$と$J$の値を求めよ。
出典：2018年岡山県立大学 入試問題
この動画を見る
$I=\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{\sin\ x}{\sqrt{ 3 }\ \sin\ x+\cos\ x} dx$
$J=\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{\cos\ x}{\sqrt{ 3 }\ \sin\ x+\cos\ x} dx$
$I$と$J$の値を求めよ。
出典：2018年岡山県立大学 入試問題
大学入試問題#766「基本中の基本」 藤田医科大学(2017) #整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
ますただ
問題文全文(内容文)：
不定方程式
$5x+7y=2017$ を満たす自然数の組$(x,y)$の個数を求めよ。
出典：2017年藤田医科大学 入試問題
この動画を見る
不定方程式
$5x+7y=2017$ を満たす自然数の組$(x,y)$の個数を求めよ。
出典：2017年藤田医科大学 入試問題
大学入試問題#765「まったり解いて大丈夫」 千葉大学(2003) 数列
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
数列$\{a_n\}$を次のように定める。$(n=2,3,・・・)$
$a_1=2$
$a_n=\displaystyle \frac{1}{n}+(1-\displaystyle \frac{1}{n})a_{n-1}$
（1）一般項$a_n$を求めよ
（2）$\displaystyle \sum_{k=1}^n k^2a_k$を求めよ
出典：2003年千葉大学 入試問題
この動画を見る
数列$\{a_n\}$を次のように定める。$(n=2,3,・・・)$
$a_1=2$
$a_n=\displaystyle \frac{1}{n}+(1-\displaystyle \frac{1}{n})a_{n-1}$
（1）一般項$a_n$を求めよ
（2）$\displaystyle \sum_{k=1}^n k^2a_k$を求めよ
出典：2003年千葉大学 入試問題
#宮崎大学 2023年 #定積分 #Shorts
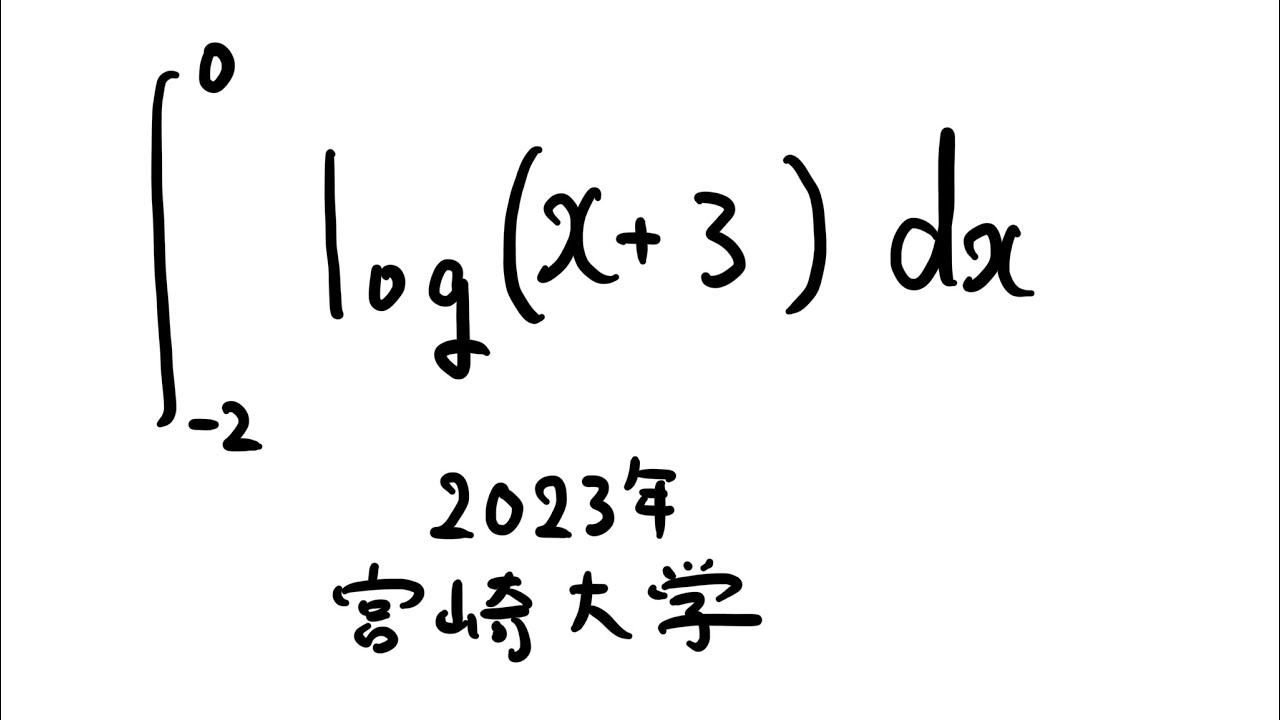
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-2}^{0} log(x+3) dx$
出典：2023年宮崎大学
この動画を見る
$\displaystyle \int_{-2}^{0} log(x+3) dx$
出典：2023年宮崎大学
大学入試問題#764「よく作成できるもんです」 早稲田大学商学部(2024) #数列
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$c$を1でない正の実数とする。
数列$\{a_n\}$が次の条件を満たしている。
$a_1=c,$
$(a_n)^{n+1}・(a_{n+1})^n=c^{-(2n+1)}$
このとき、一般項$a_n$を$c$を用いて表せ。
出典：2024年早稲田大学商学部 入試問題
この動画を見る
$c$を1でない正の実数とする。
数列$\{a_n\}$が次の条件を満たしている。
$a_1=c,$
$(a_n)^{n+1}・(a_{n+1})^n=c^{-(2n+1)}$
このとき、一般項$a_n$を$c$を用いて表せ。
出典：2024年早稲田大学商学部 入試問題
#宮崎大学 2020年 #定積分 #Shorts
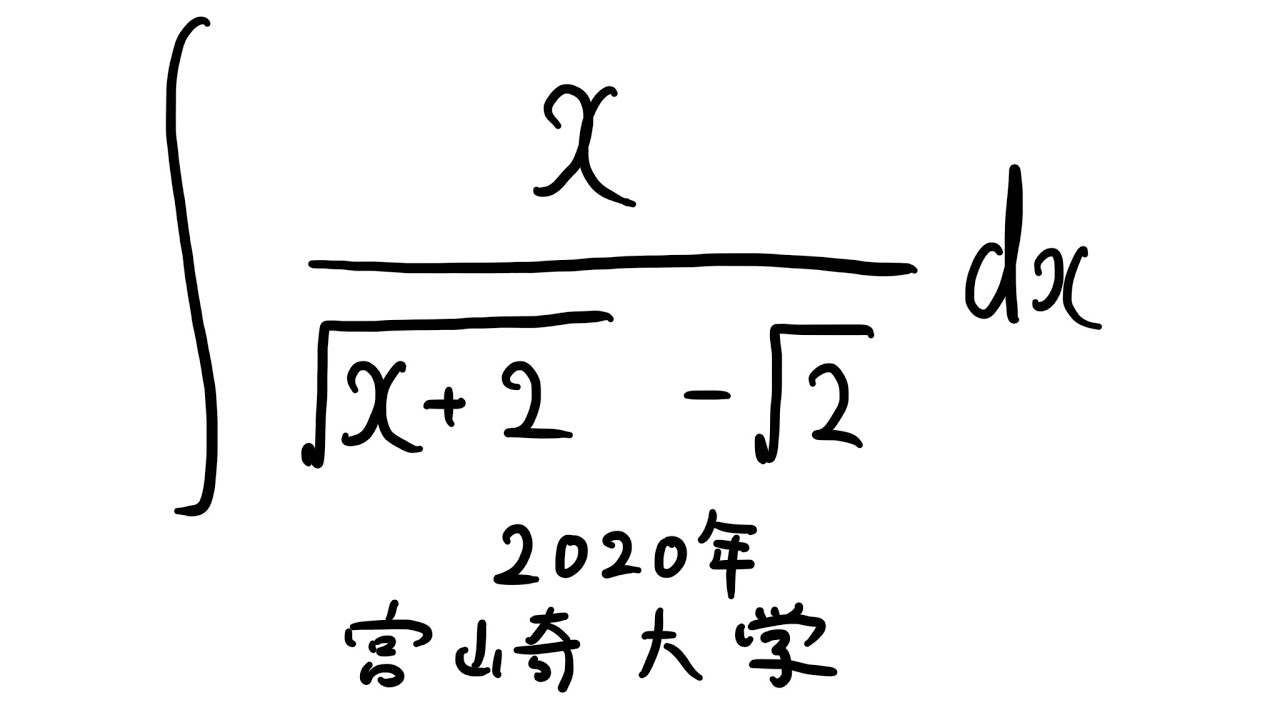
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+2 }-\sqrt{ 2 }} dx$
出典：2020年宮崎大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+2 }-\sqrt{ 2 }} dx$
出典：2020年宮崎大学
大学入試問題#763「読みの入った式変形」 東京理科大学理学部(2003) #複素数
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$0 \lt t \lt 2\pi$とする
$z=\displaystyle \frac{1+\cos\ t+i\ \sin\ t}{1-\cos\ t-i\ \sin\ t}$
（1）$0 \lt t \lt \pi$における$z$の偏角を弧度法で表せ
（2）$\displaystyle \int_{\frac{\pi}{2}}^{\pi} |z|dt$を求めよ。
出典：2003年東京理科大学理学部 入試問題
この動画を見る
$0 \lt t \lt 2\pi$とする
$z=\displaystyle \frac{1+\cos\ t+i\ \sin\ t}{1-\cos\ t-i\ \sin\ t}$
（1）$0 \lt t \lt \pi$における$z$の偏角を弧度法で表せ
（2）$\displaystyle \int_{\frac{\pi}{2}}^{\pi} |z|dt$を求めよ。
出典：2003年東京理科大学理学部 入試問題
#宮崎大学 2020年 #定積分 #Shorts
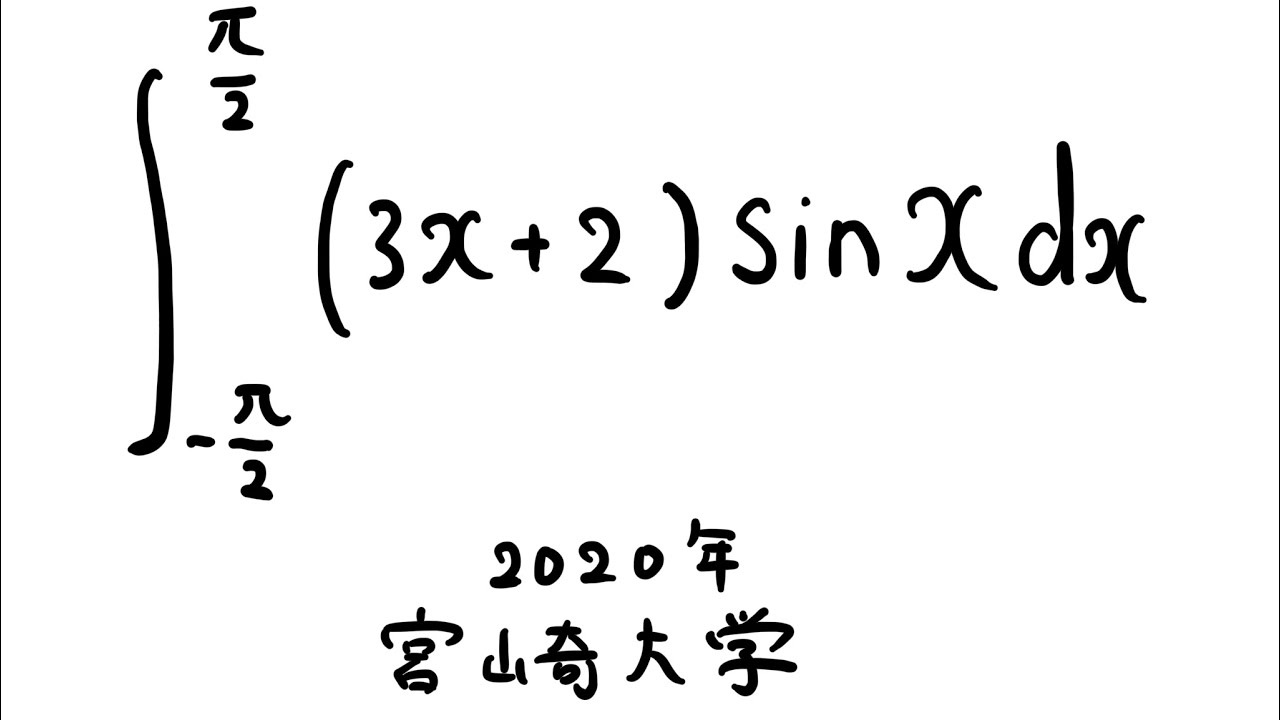
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (3x+2)\sin\ x\ dx$
出典：2020年宮崎大学
この動画を見る
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (3x+2)\sin\ x\ dx$
出典：2020年宮崎大学
大学入試問題#762「再生回数は、期待できない」 東京理科大学工学部(2003) #曲線の長さ
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
曲線$y=(2x+1)\sqrt{ 2x+1 }$の区間$0 \leq x \leq \displaystyle \frac{1}{3}$にある部分の長さを求めよ。
出典：2003年東京理科大学工学部 入試問題
この動画を見る
曲線$y=(2x+1)\sqrt{ 2x+1 }$の区間$0 \leq x \leq \displaystyle \frac{1}{3}$にある部分の長さを求めよ。
出典：2003年東京理科大学工学部 入試問題
#宮崎大学 2022年 #定積分 #Shorts
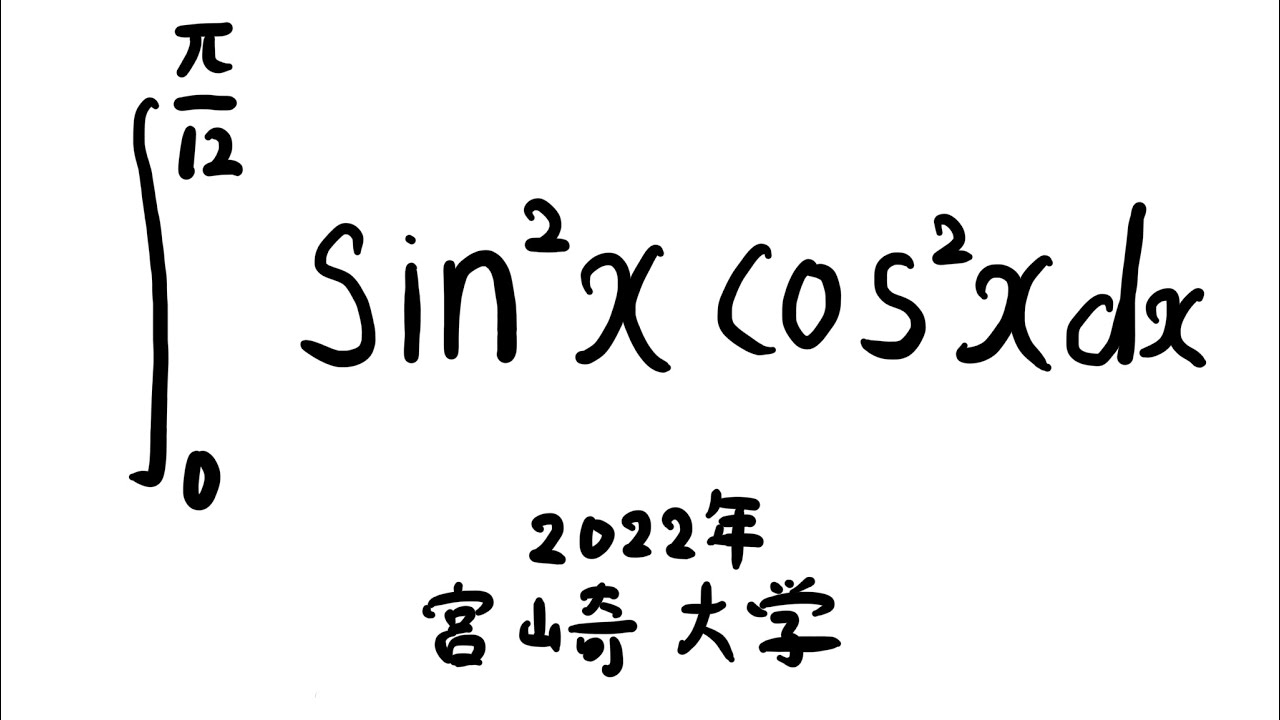
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{12}} \sin^2x\ \cos^2x\ dx$
出典：2022年宮崎大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{12}} \sin^2x\ \cos^2x\ dx$
出典：2022年宮崎大学
大学入試問題#761「微積の入試勉強は、まずこれから！」 東京理科大学理学部(2002) #微積
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
関数$F(x)$を
$F(x)=\displaystyle \int_{0}^{x} (\sin\ t+\cos\ t)^2 dt$と定める。
$F(x),\displaystyle \lim_{ x \to \infty } \displaystyle \frac{F(x)}{x},\displaystyle \lim_{ x \to 0 } \displaystyle \frac{F(x)}{x}$を求めよ。
出典：2002年東京理科大学理学部 入試問題
この動画を見る
関数$F(x)$を
$F(x)=\displaystyle \int_{0}^{x} (\sin\ t+\cos\ t)^2 dt$と定める。
$F(x),\displaystyle \lim_{ x \to \infty } \displaystyle \frac{F(x)}{x},\displaystyle \lim_{ x \to 0 } \displaystyle \frac{F(x)}{x}$を求めよ。
出典：2002年東京理科大学理学部 入試問題
大学入試問題#760「ほぼ一直線」 東京理科大学(2003) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
定積分
$I=\displaystyle \int_{1}^{4} t^2\sin(\displaystyle \frac{\pi}{4}t\sqrt{ t })\ dt$を求めよ。
出典：2003年東京理科大学 入試問題
この動画を見る
定積分
$I=\displaystyle \int_{1}^{4} t^2\sin(\displaystyle \frac{\pi}{4}t\sqrt{ t })\ dt$を求めよ。
出典：2003年東京理科大学 入試問題
大学入試問題#759「サムネみすった」 東京理科大学(2002) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
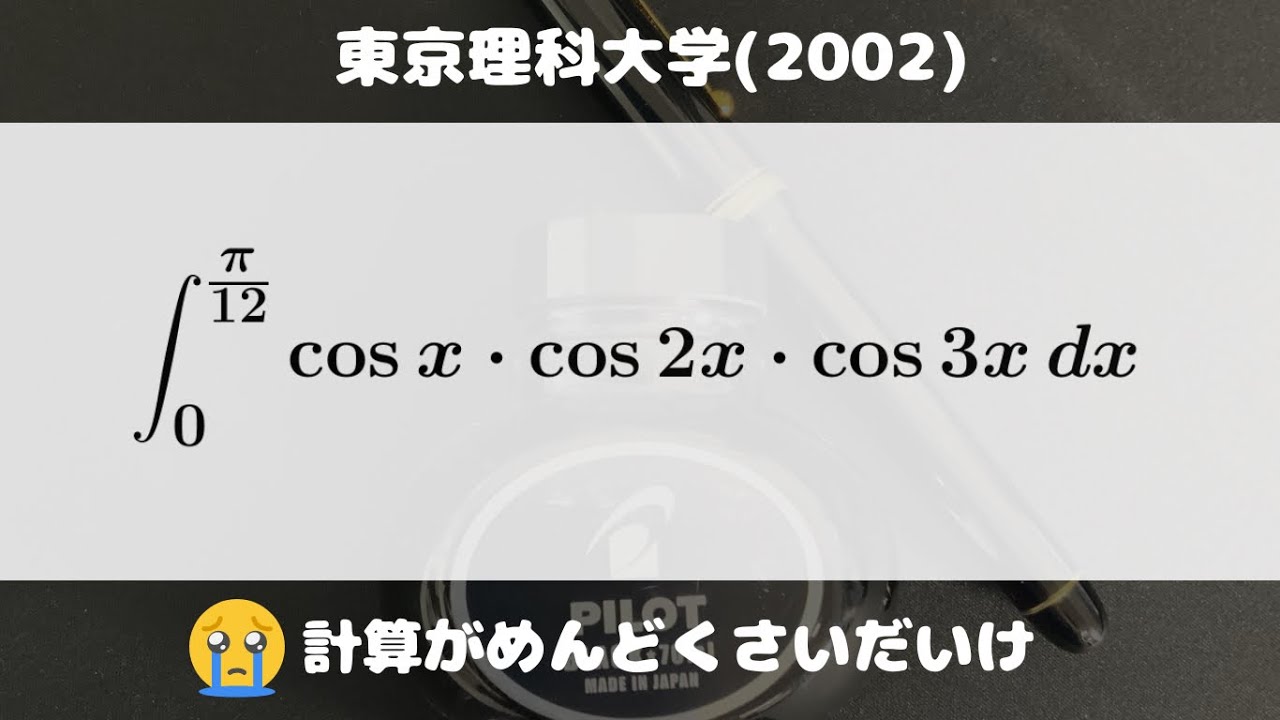
$\displaystyle \int_{0}^{\frac{\pi}{12}} \cos\ x・\cos\ 2x・\cos\ 3x\ dx$
出典：2002年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{12}} \cos\ x・\cos\ 2x・\cos\ 3x\ dx$
出典：2002年東京理科大学 入試問題
#広島市立大学 2010年 #不定積分 #Shorts
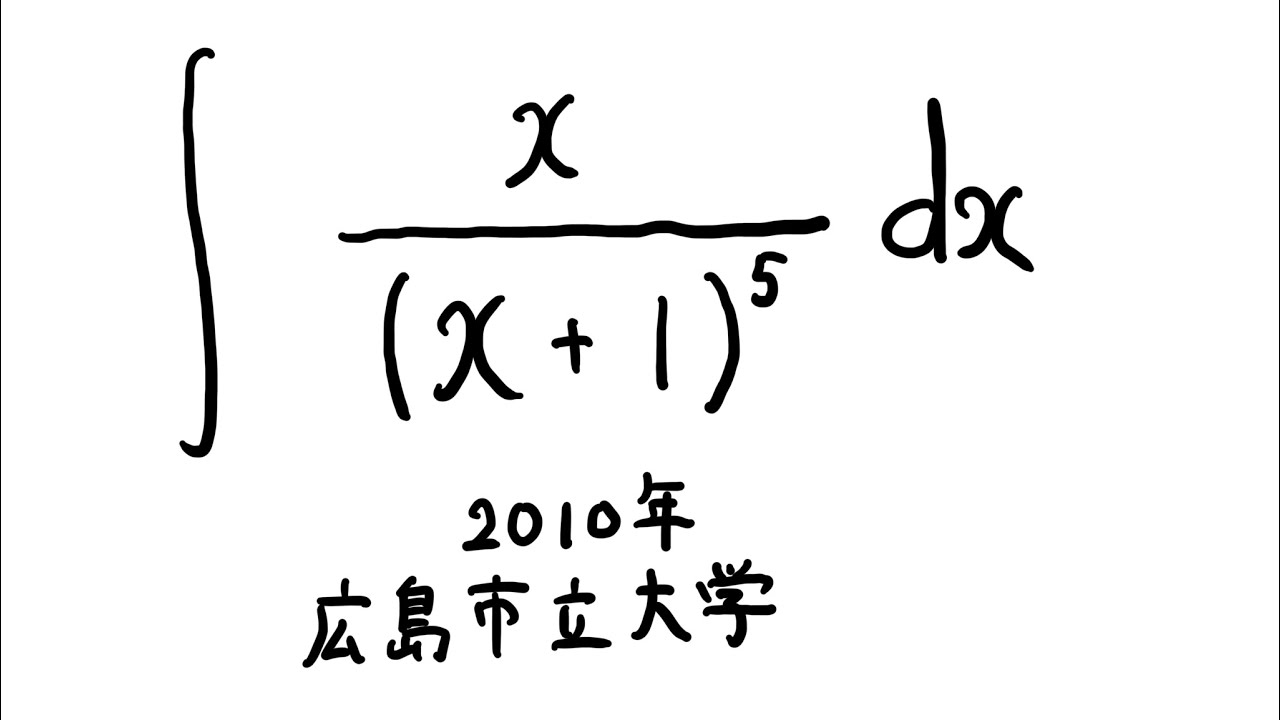
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#広島市立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{x}{(x+1)^5} dx$
出典：2010年広島市立大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{(x+1)^5} dx$
出典：2010年広島市立大学