ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
#37 数検1級1次 過去問 重積分
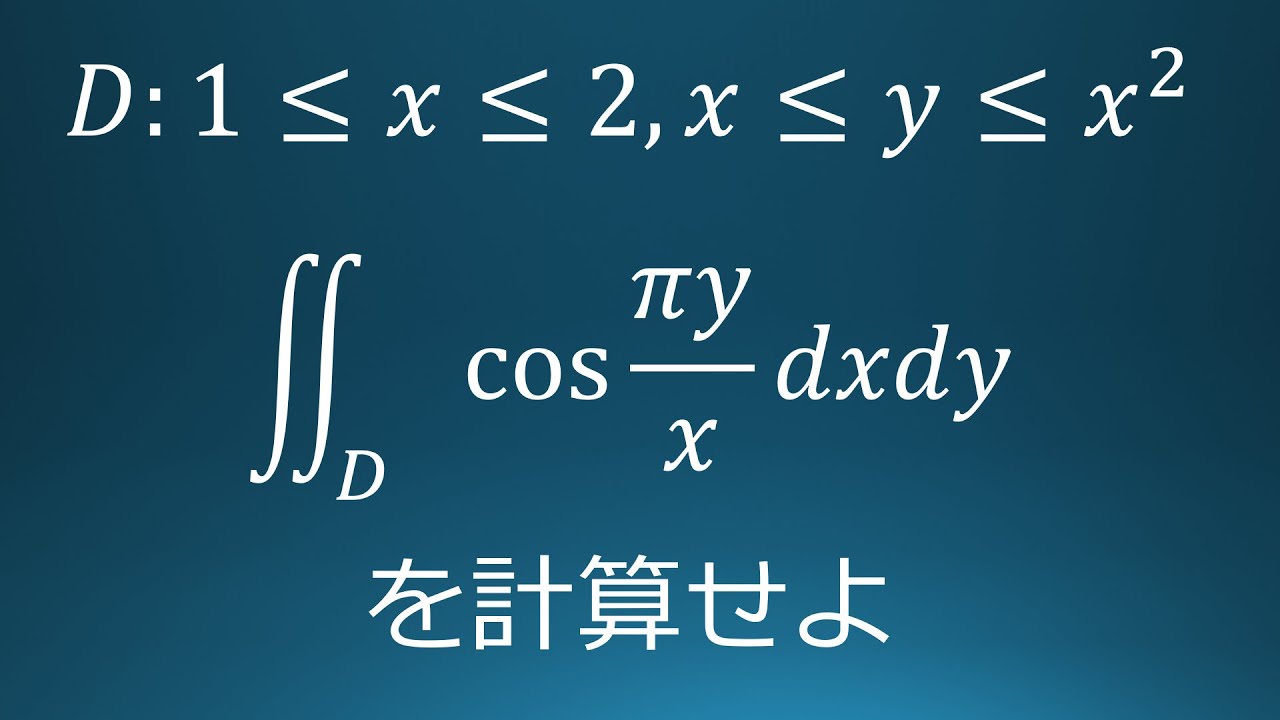
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$D:1 \leqq x \leqq 2,x \leqq y \leqq x^2$
$\displaystyle \int \displaystyle \int \cos\displaystyle \frac{\pi y}{x}\ dxdy$を計算せよ。
この動画を見る
$D:1 \leqq x \leqq 2,x \leqq y \leqq x^2$
$\displaystyle \int \displaystyle \int \cos\displaystyle \frac{\pi y}{x}\ dxdy$を計算せよ。
#36 数検1級1次 過去問 積分
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{1}\sqrt{ \displaystyle \frac{1+x}{1-x} }\ dx$を計算せよ。
この動画を見る
$\displaystyle \int_{-1}^{1}\sqrt{ \displaystyle \frac{1+x}{1-x} }\ dx$を計算せよ。
#35 数検１級１次 過去問 複素数
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数平面#複素数#複素数平面#数学検定#数学検定1級#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt{ 1+\sqrt{ 3 }i }+\sqrt{ 1-\sqrt{ 3 }i }$を簡単にせよ
ただし、外側の平方根の実数部の値は正とする。
この動画を見る
$\sqrt{ 1+\sqrt{ 3 }i }+\sqrt{ 1-\sqrt{ 3 }i }$を簡単にせよ
ただし、外側の平方根の実数部の値は正とする。
#34 数検1級1次 過去問 積分
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\infty}\displaystyle \frac{1}{(x^2+1)^4}\ dx$を計算せよ。
この動画を見る
$\displaystyle \int_{0}^{\infty}\displaystyle \frac{1}{(x^2+1)^4}\ dx$を計算せよ。
#33 数検1級1次 過去問 区分求積法
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{1}{\sqrt{ 2nk-k^2 }}$の極限値を求めよ。
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{1}{\sqrt{ 2nk-k^2 }}$の極限値を求めよ。
13和歌山県教員採用試験（数学：1-(5) 整数問題）
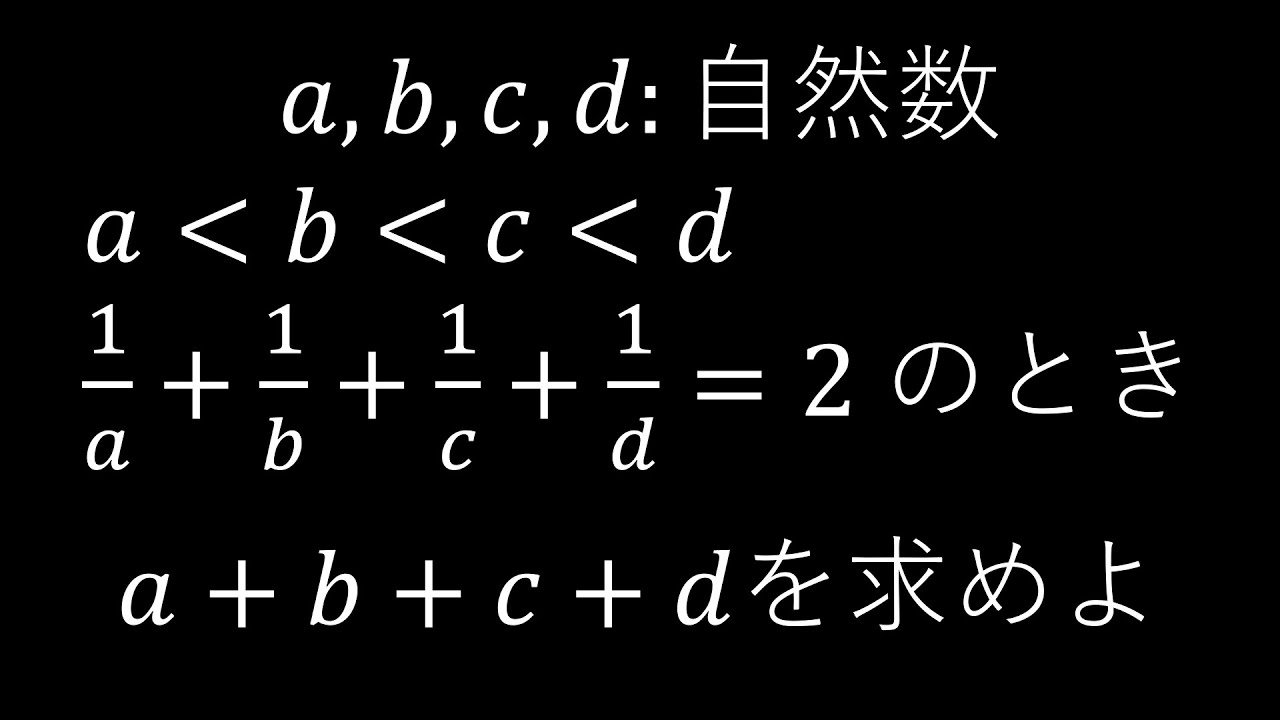
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$a,b,c,d:$自然数
$a \lt b \lt c \lt d$
$\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b}+\displaystyle \frac{1}{c}+\displaystyle \frac{1}{d}=2$を満たすとき$a+b+c+d$の値を求めよ
この動画を見る
$a,b,c,d:$自然数
$a \lt b \lt c \lt d$
$\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b}+\displaystyle \frac{1}{c}+\displaystyle \frac{1}{d}=2$を満たすとき$a+b+c+d$の値を求めよ
#32 数検1級1次 過去問 複素数の方程式
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数平面#複素数#複素数平面#数学検定#数学検定1級#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$z:$複素数
方程式$z^2-z+i\bar{ z }=i$を解け。
この動画を見る
$z:$複素数
方程式$z^2-z+i\bar{ z }=i$を解け。
#31 数検1級1次 過去問 整数問題
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x^3-y^3=331$を満たす正の整数$x,y$を求めよ。
この動画を見る
$x^3-y^3=331$を満たす正の整数$x,y$を求めよ。
#30 数検1級1次 過去問 複雑な定積分
単元：
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
定積分
$\displaystyle \int_{-1}^{1}\displaystyle \frac{x^4+2x^3+4x^2+6x+2}{x^3+2x^2+2x+4}\ dx$を計算せよ。
この動画を見る
定積分
$\displaystyle \int_{-1}^{1}\displaystyle \frac{x^4+2x^3+4x^2+6x+2}{x^3+2x^2+2x+4}\ dx$を計算せよ。
#29 数検1級1次 過去問 解と係数の関係
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x^3+2x^2+4x+7=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^4,\beta^4,\gamma^4$の値を求めよ。
この動画を見る
$x^3+2x^2+4x+7=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^4,\beta^4,\gamma^4$の値を求めよ。
#28 数検1級1次 過去問 Arctanの加法定理
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#三角関数とグラフ#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$\tan^{-1}1+\tan^{-1}2+\tan^{-1}3$の値を求めよ。
この動画を見る
$\tan^{-1}1+\tan^{-1}2+\tan^{-1}3$の値を求めよ。
大学入試問題#44 明治大学(2021) 複素数
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$|z|=2$のとき
$|z^2+iz-1|$のとりうる値の範囲を求めよ。
出典：2021年明治大学 入試問題
この動画を見る
$|z|=2$のとき
$|z^2+iz-1|$のとりうる値の範囲を求めよ。
出典：2021年明治大学 入試問題
大学入試問題#43 津田塾大学(2021) 複素数
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#津田塾大学
指導講師：
ますただ
問題文全文(内容文)：
$|z-5|=|z+5i|$
$|z-2i|=2$を満たす複素数$z$に対して$z^4$を求めよ。
出典：2021年津田塾大学 入試問題
この動画を見る
$|z-5|=|z+5i|$
$|z-2i|=2$を満たす複素数$z$に対して$z^4$を求めよ。
出典：2021年津田塾大学 入試問題
大学入試問題#42 慶應義塾大学(2021) 絶対値の定積分
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$a:$実数
$f(x)=|x|+a$に対して$\displaystyle \int_{-5}^{5}|f(x)|dx$が最小となる$a$の値を求めよ。
出典：2021年慶應義塾大学 入試問題
この動画を見る
$a:$実数
$f(x)=|x|+a$に対して$\displaystyle \int_{-5}^{5}|f(x)|dx$が最小となる$a$の値を求めよ。
出典：2021年慶應義塾大学 入試問題
大学入試問題#41 東海大学医学部(2021) 因数分解
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算（整式・展開・因数分解）#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師：
ますただ
問題文全文(内容文)：
$(a+b+c)^3-a^3-b^3-c^3$を因数分解せよ。
出典：2021年東海大学医学部 入試問題
この動画を見る
$(a+b+c)^3-a^3-b^3-c^3$を因数分解せよ。
出典：2021年東海大学医学部 入試問題
大学入試問題#40 東京理科大学(2021) 数列と極限
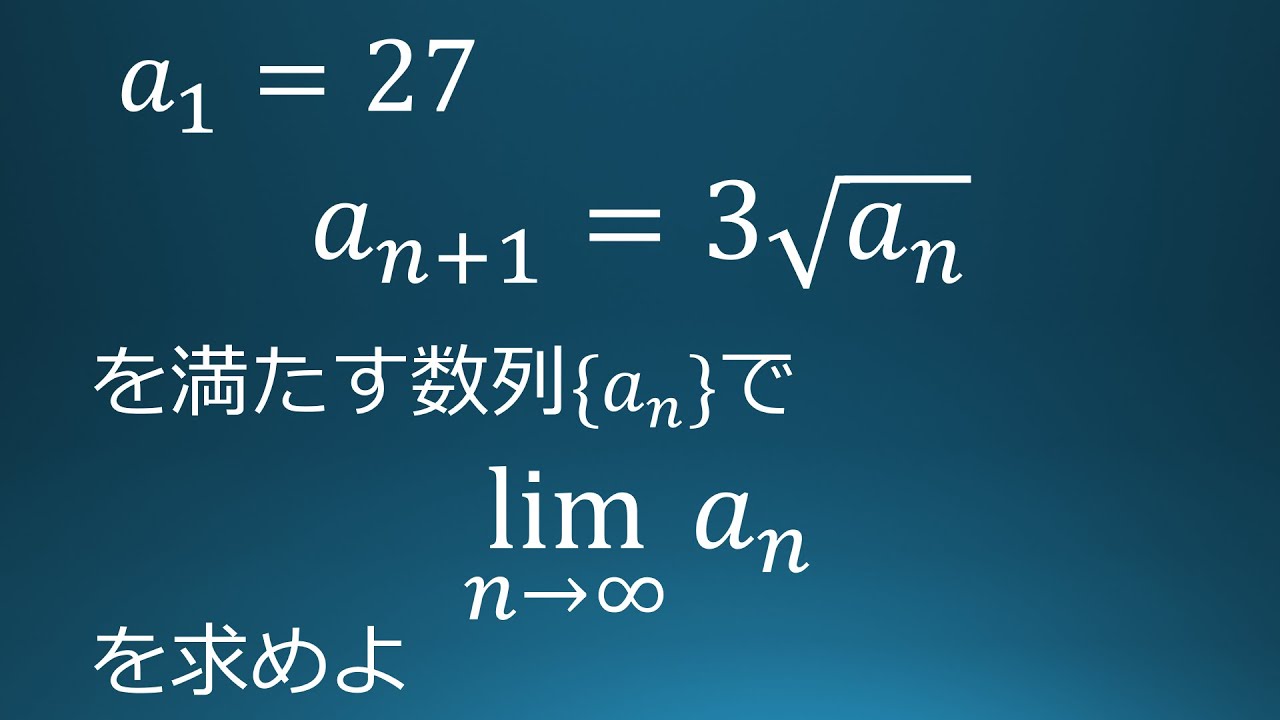
単元：
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$a_1=27$
$a_{n+1}=3\sqrt{ a_n }$を満たす数列$\{a_n\}$において
$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
出典：2021年東京理科大学 入試問題
この動画を見る
$a_1=27$
$a_{n+1}=3\sqrt{ a_n }$を満たす数列$\{a_n\}$において
$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
出典：2021年東京理科大学 入試問題
大学入試問題#39 東海大学医学部(2021) 整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師：
ますただ
問題文全文(内容文)：
$n:$自然数
$n^3+100$が$n+10$で割り切れるような最大の$n$の値を求めよ。
出典：2021年東海大学医学部 入試問題
この動画を見る
$n:$自然数
$n^3+100$が$n+10$で割り切れるような最大の$n$の値を求めよ。
出典：2021年東海大学医学部 入試問題
#27 数検1級1次 過去問 整数問題
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x,y:$正の整数
$x+y=316$
$x:13$の倍数
$y:11$の倍数
をみたす組$(x,y)$をすべて求めよ。
この動画を見る
$x,y:$正の整数
$x+y=316$
$x:13$の倍数
$y:11$の倍数
をみたす組$(x,y)$をすべて求めよ。
#26 数検1級1次 過去問 複雑な方程式
単元：
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y+z=6 \\
x^3+y^3+z^3=36 \\
xyz=6
\end{array}
\right.
\end{eqnarray}$
において、$x \gt y \gt z$を満たす解を求めよ。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y+z=6 \\
x^3+y^3+z^3=36 \\
xyz=6
\end{array}
\right.
\end{eqnarray}$
において、$x \gt y \gt z$を満たす解を求めよ。
#25 数検1級1次 過去問 複雑な方程式
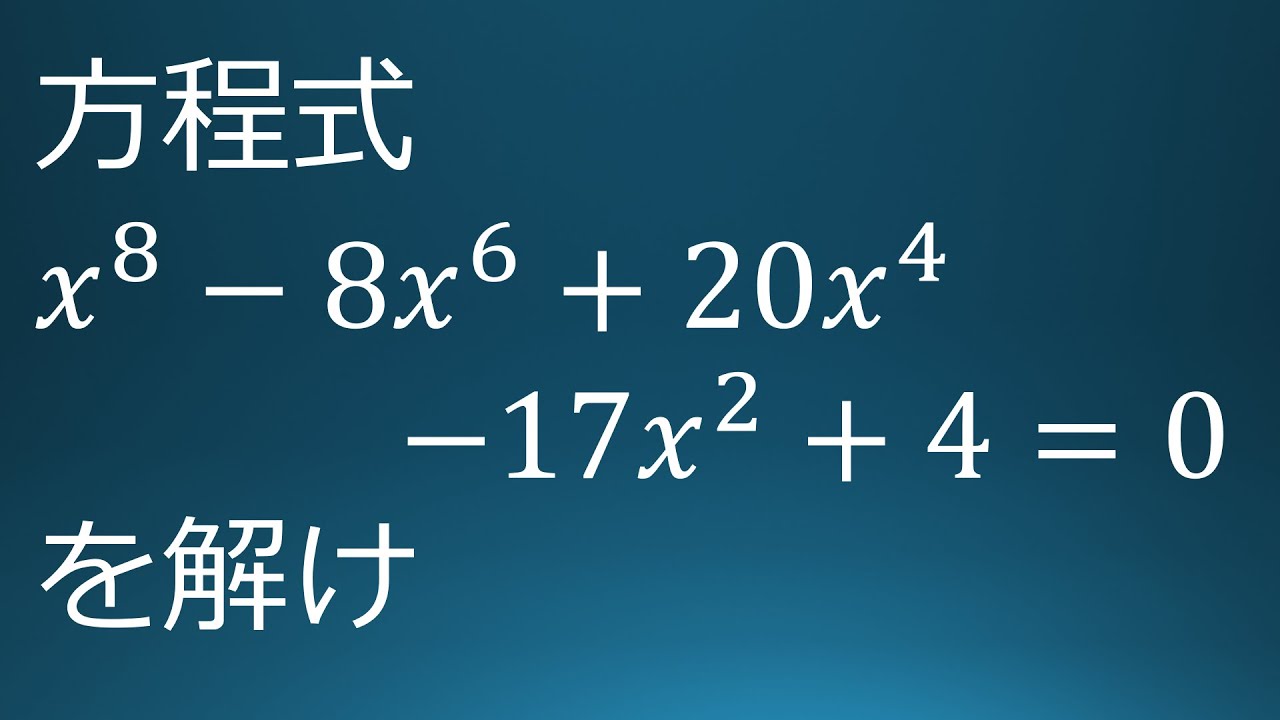
単元：
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
方程式
$x^8-8x^6+20x^4-17x^2+4=0$を解け。
この動画を見る
方程式
$x^8-8x^6+20x^4-17x^2+4=0$を解け。
#24 数検１級１次 過去問 微分方程式
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$2\displaystyle \frac{d^2y}{dx^2}+9\displaystyle \frac{dy}{dx}-35y=-105x-97$の一般項を求めよ。
この動画を見る
$2\displaystyle \frac{d^2y}{dx^2}+9\displaystyle \frac{dy}{dx}-35y=-105x-97$の一般項を求めよ。
#23 数検1級1次過去問 行列
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$A=(\begin{eqnarray}
1\ 2\ 2 \\
2\ 1\ 2 \\
2\ 2\ 1
\end{eqnarray})$
$A^5$を求めよ。
この動画を見る
$A=(\begin{eqnarray}
1\ 2\ 2 \\
2\ 1\ 2 \\
2\ 2\ 1
\end{eqnarray})$
$A^5$を求めよ。
大学入試問題#39 旭川医科大学改(2020) 定積分を利用した不等式の証明
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#旭川医科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$n$は2以上の整数
$n\ log\ n-(n-1) \lt log2+log\ 3+・・・+log\ n$を示せ
出典：2020年旭川医科大学 入試問題
この動画を見る
$n$は2以上の整数
$n\ log\ n-(n-1) \lt log2+log\ 3+・・・+log\ n$を示せ
出典：2020年旭川医科大学 入試問題
#22 数検1級1次 過去問 無限級数
単元：
#数学検定・数学甲子園・数学オリンピック等#関数と極限#関数の極限#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \sum_{i=1}^\infty\ \tan^{-1}\displaystyle \frac{1}{k^2+k+1}$を求めよ。
この動画を見る
$\displaystyle \sum_{i=1}^\infty\ \tan^{-1}\displaystyle \frac{1}{k^2+k+1}$を求めよ。
#21 数検1級1次 過去問 無限級数
単元：
#数学検定・数学甲子園・数学オリンピック等#関数と極限#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \sum_{k=1}^\infty\ \displaystyle \frac{k}{1+k^2+k^4}$を求めよ。
この動画を見る
$\displaystyle \sum_{k=1}^\infty\ \displaystyle \frac{k}{1+k^2+k^4}$を求めよ。
03京都府教員採用試験（数学：4 -(1) 整数問題）
単元：
Warning: usort() expects parameter 1 to be array, bool given in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 269
Warning: Invalid argument supplied for foreach() in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 270
Warning: usort() expects parameter 1 to be array, bool given in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 269
Warning: Invalid argument supplied for foreach() in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 270
指導講師：
ますただ
問題文全文(内容文)：
$m,n:$自然数
$\displaystyle \frac{1}{m}+\displaystyle \frac{1}{n} \geqq \displaystyle \frac{5}{4}$を満たす組$(m,n)$をすべて求めよ。
この動画を見る
$m,n:$自然数
$\displaystyle \frac{1}{m}+\displaystyle \frac{1}{n} \geqq \displaystyle \frac{5}{4}$を満たす組$(m,n)$をすべて求めよ。
06兵庫県教員採用試験（数学：3番 円と直線の関係）
単元：
#数Ⅱ#図形と方程式#円と方程式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
円$c:x^2+y^2=1+m$と直線$l:y=-3x+m$が異なる2点$A,B$で交わる。
$m$は定数
（1）
$m$の値の範囲を求めよ
（2）
弦$AB$の長さの最大値とそのときの$m$の値を求めよ。
この動画を見る
円$c:x^2+y^2=1+m$と直線$l:y=-3x+m$が異なる2点$A,B$で交わる。
$m$は定数
（1）
$m$の値の範囲を求めよ
（2）
弦$AB$の長さの最大値とそのときの$m$の値を求めよ。
大学入試問題#38 日本大学(2021) 三角関数
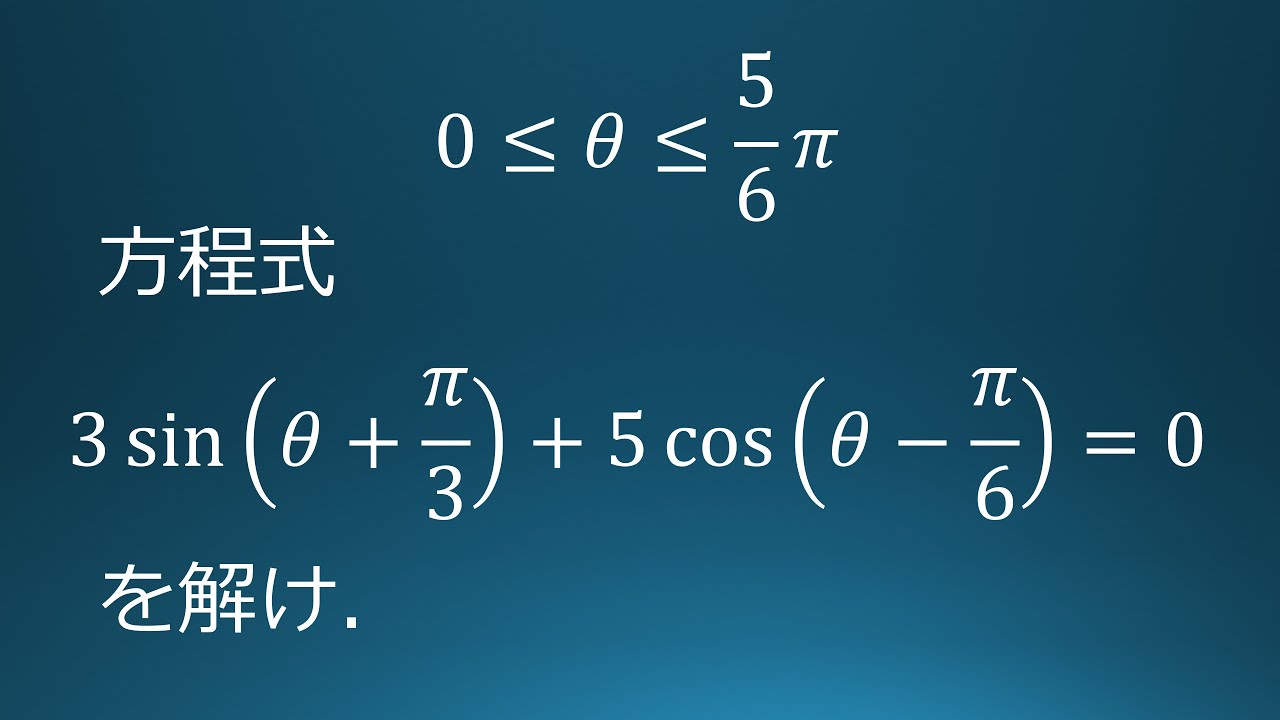
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#日本大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$0 \leqq \theta \leqq \displaystyle \frac{5}{6}\pi$において
方程式
$3\sin(\theta+\displaystyle \frac{\pi}{3})+5\ \cos(\theta-\displaystyle \frac{\pi}{6})=0$を解け。
出典：2021年日本大学 入試問題
この動画を見る
$0 \leqq \theta \leqq \displaystyle \frac{5}{6}\pi$において
方程式
$3\sin(\theta+\displaystyle \frac{\pi}{3})+5\ \cos(\theta-\displaystyle \frac{\pi}{6})=0$を解け。
出典：2021年日本大学 入試問題
大学入試問題#37 早稲田大学(2021) 整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$a,b,c:$実数
$0 \leqq a \leqq b \leqq c$
$a+b+c=7$を満たすとき
$ab,bc,ca$の最大値を求めよ。
出典：2021年早稲田大学 入試問題
この動画を見る
$a,b,c:$実数
$0 \leqq a \leqq b \leqq c$
$a+b+c=7$を満たすとき
$ab,bc,ca$の最大値を求めよ。
出典：2021年早稲田大学 入試問題
16高知県教員採用試験（数学：2-(4) 複素数）
単元：
#複素数平面#複素数平面#その他#数学(高校生)#数C#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\fcolorbox{black}{ #fffff }{$2$}-(4)$
$z^3=8i$
をみたす複素数$z$をすべて求めよ。
この動画を見る
$\fcolorbox{black}{ #fffff }{$2$}-(4)$
$z^3=8i$
をみたす複素数$z$をすべて求めよ。