 ますただ
ますただ
 ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
17東京都教員採用試験(数学 1-3 番 複素数)
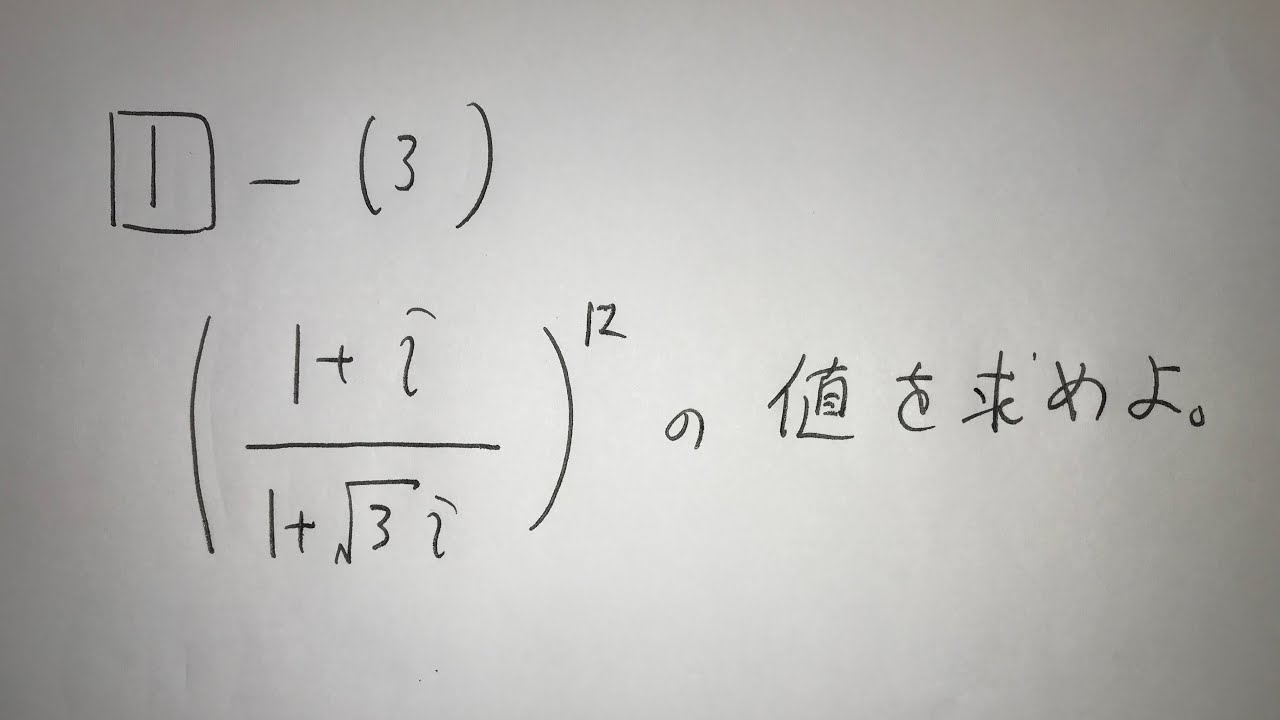
単元:
#複素数平面#複素数平面#その他#数学(高校生)#数C#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(3)
$(\frac{1+i}{1+\sqrt 3 i})^{12}$の値を求めよ。
この動画を見る
1⃣-(3)
$(\frac{1+i}{1+\sqrt 3 i})^{12}$の値を求めよ。
17東京都教員採用試験(数学 1-2 方程式)

単元:
#数Ⅰ#数Ⅱ#数と式#式と証明#式の計算(整式・展開・因数分解)#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
1⃣-(2)
$x^3+\frac{1}{x^3}=0$のとき、$x+\frac{1}{x}$の値を求めよ。
この動画を見る
1⃣-(2)
$x^3+\frac{1}{x^3}=0$のとき、$x+\frac{1}{x}$の値を求めよ。
17東京都教員採用試験(数学1-1番 整数問題)
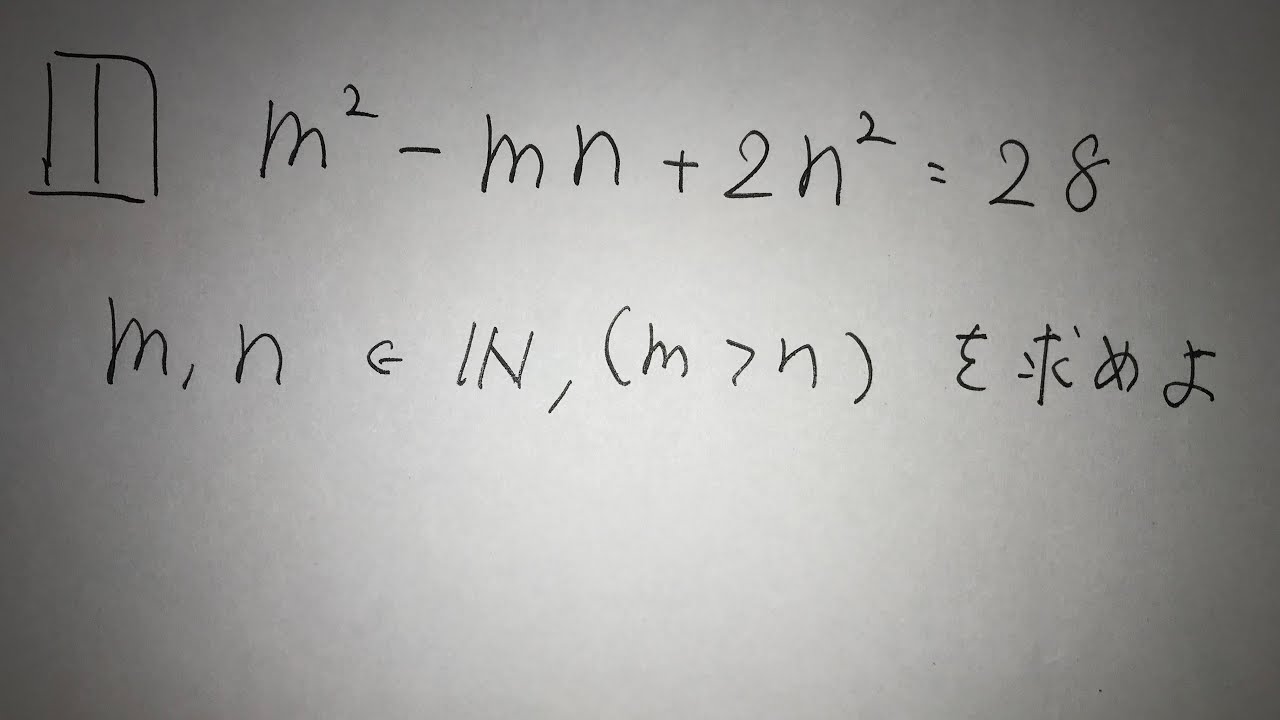
単元:
#数Ⅰ#数A#数Ⅱ#2次関数#式と証明#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
1⃣$m^2-mn+2n^2=28$
$m,n \in \mathbb{ N } (m>n)$を求めよ。
この動画を見る
1⃣$m^2-mn+2n^2=28$
$m,n \in \mathbb{ N } (m>n)$を求めよ。
19東京都教員採用試験(数学:3番x軸回転の体積)

単元:
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
3⃣$f(x)=x \sqrt{4-x^2} \quad (0 \leqq x \leqq 2)$とy=xで囲まれた領域Sの回転体の体積Vを求めよ。
(1)y=f(x)の最大値
(2)y=xと$y=x \sqrt{4-x^2}$ $(0 \leqq x \leqq 2)$で囲まれたSの値を求めよ。
(3)Sの回転体の体積V
この動画を見る
3⃣$f(x)=x \sqrt{4-x^2} \quad (0 \leqq x \leqq 2)$とy=xで囲まれた領域Sの回転体の体積Vを求めよ。
(1)y=f(x)の最大値
(2)y=xと$y=x \sqrt{4-x^2}$ $(0 \leqq x \leqq 2)$で囲まれたSの値を求めよ。
(3)Sの回転体の体積V
00京都府採用試験(数学:3番相加相乗平均)

18兵庫県教員採用試験(数学:2番 ベクトル)
18兵庫県教員採用試験(数学:1-1 確率)

単元:
#数Ⅰ#数A#場合の数と確率#確率
指導講師:
ますただ
問題文全文(内容文):
1⃣-(1)
赤5コ、白7コが入った袋がある。
(1)同時に2コとるとき、玉の色が異なる確率を求めよ。
(2)1コとって、袋にもどさず2コ目をとる。
2コ目が白のとき、1コ目も白の確率を求めよ。
この動画を見る
1⃣-(1)
赤5コ、白7コが入った袋がある。
(1)同時に2コとるとき、玉の色が異なる確率を求めよ。
(2)1コとって、袋にもどさず2コ目をとる。
2コ目が白のとき、1コ目も白の確率を求めよ。
19東京都教員採用試験(数学:1-5 一次変換)

単元:
#その他#その他
指導講師:
ますただ
問題文全文(内容文):
1⃣-(5)
P(x,y)をl:x-3y=0に関して対称移動した点をP'(x',y')とする。
PをP'に移す一次変換を表す行列Aを求めよ。
この動画を見る
1⃣-(5)
P(x,y)をl:x-3y=0に関して対称移動した点をP'(x',y')とする。
PをP'に移す一次変換を表す行列Aを求めよ。
19東京都採用試験(数学:対数)
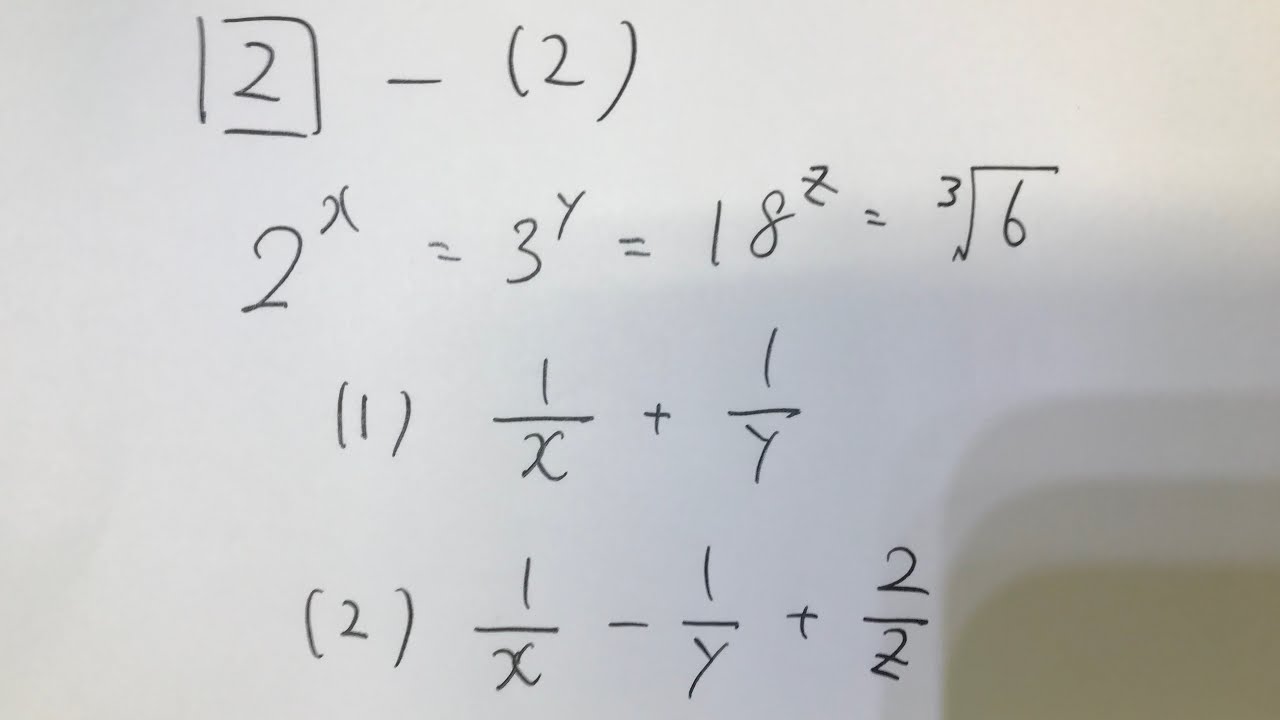
単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
2⃣-(2)
$2^x=3^y=18^z={}^3\sqrt6$
(1)$\frac{1}{x} + \frac{1}{y}$
(2)$\frac{1}{x} - \frac{1}{y}+\frac{2}{z}$
この動画を見る
2⃣-(2)
$2^x=3^y=18^z={}^3\sqrt6$
(1)$\frac{1}{x} + \frac{1}{y}$
(2)$\frac{1}{x} - \frac{1}{y}+\frac{2}{z}$
19東京都教員採用試験(数学:相加相乗平均)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
1⃣(1)
x>0のとき
$\frac{x^2+x+196}{x+1}$
の最小値と、そのときのxの値を求めよ。
この動画を見る
1⃣(1)
x>0のとき
$\frac{x^2+x+196}{x+1}$
の最小値と、そのときのxの値を求めよ。
18東京都教員採用試験(数学:解と係数の関係)
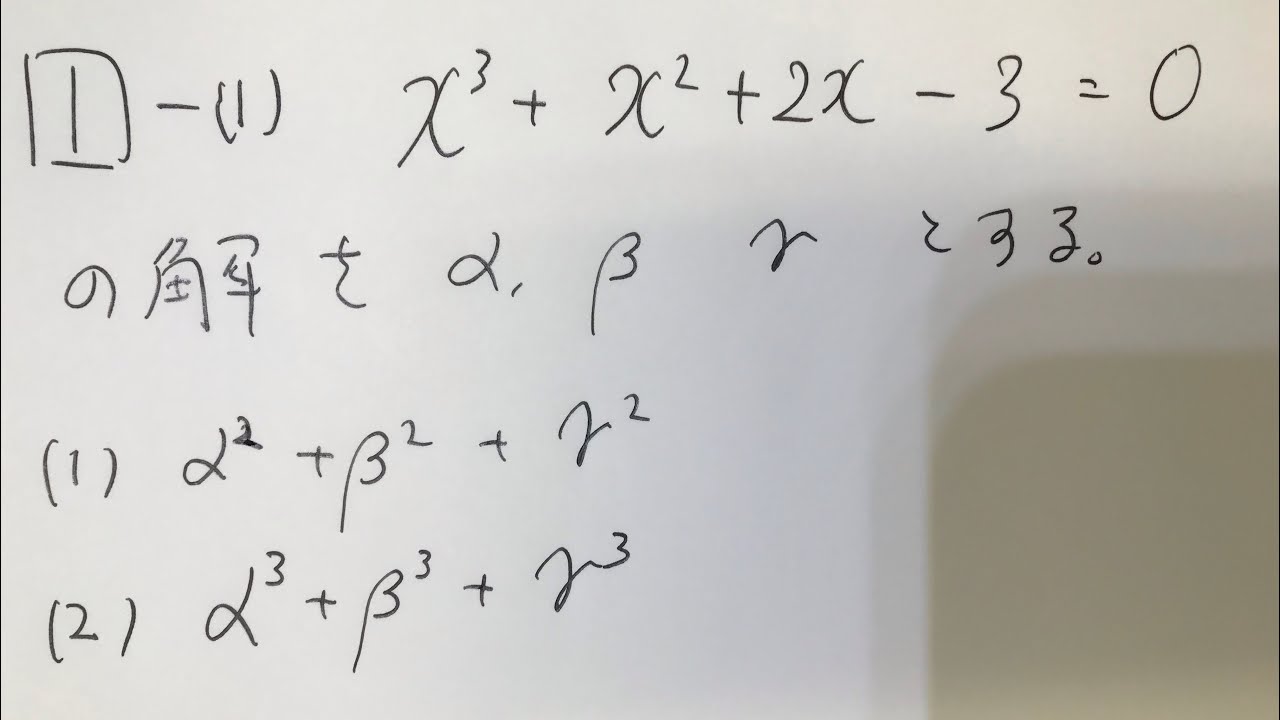
単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
1⃣-(1)
$x^3+x^2+2x-3=0$の解をα、β、γとする。
(1)$α^2+β^2+γ^2$
(2)$α^3+β^3+γ^3$
この動画を見る
1⃣-(1)
$x^3+x^2+2x-3=0$の解をα、β、γとする。
(1)$α^2+β^2+γ^2$
(2)$α^3+β^3+γ^3$
18東京都採用試験(数学:行列)
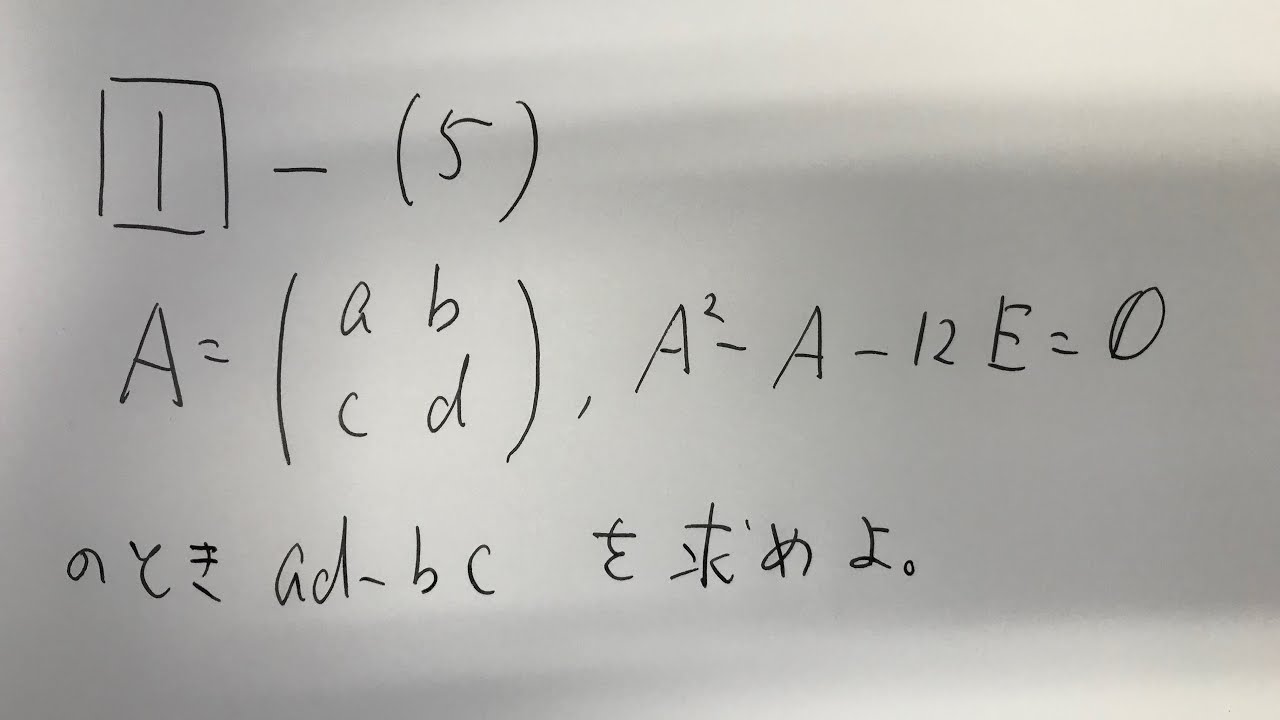
単元:
#その他#その他
指導講師:
ますただ
問題文全文(内容文):
1⃣-(5)
$\begin{eqnarray}
A = \left(
\begin{array}{cccc}
a & b\\
c & d\\
\end{array}
\right)
\end{eqnarray},A^2-A-12E=\emptyset$のときad-bcを求めよ。
この動画を見る
1⃣-(5)
$\begin{eqnarray}
A = \left(
\begin{array}{cccc}
a & b\\
c & d\\
\end{array}
\right)
\end{eqnarray},A^2-A-12E=\emptyset$のときad-bcを求めよ。
18東京都教員採用試験(数学:複素数)

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
1⃣-(4)
Z \in \mathbb{ C } , |Z|=1とする
$w=\frac{z+4}{z-2}$のとき|w|の最大値を求めよ
この動画を見る
1⃣-(4)
Z \in \mathbb{ C } , |Z|=1とする
$w=\frac{z+4}{z-2}$のとき|w|の最大値を求めよ
18東京都教員採用試験(数学:ベクトル)
単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
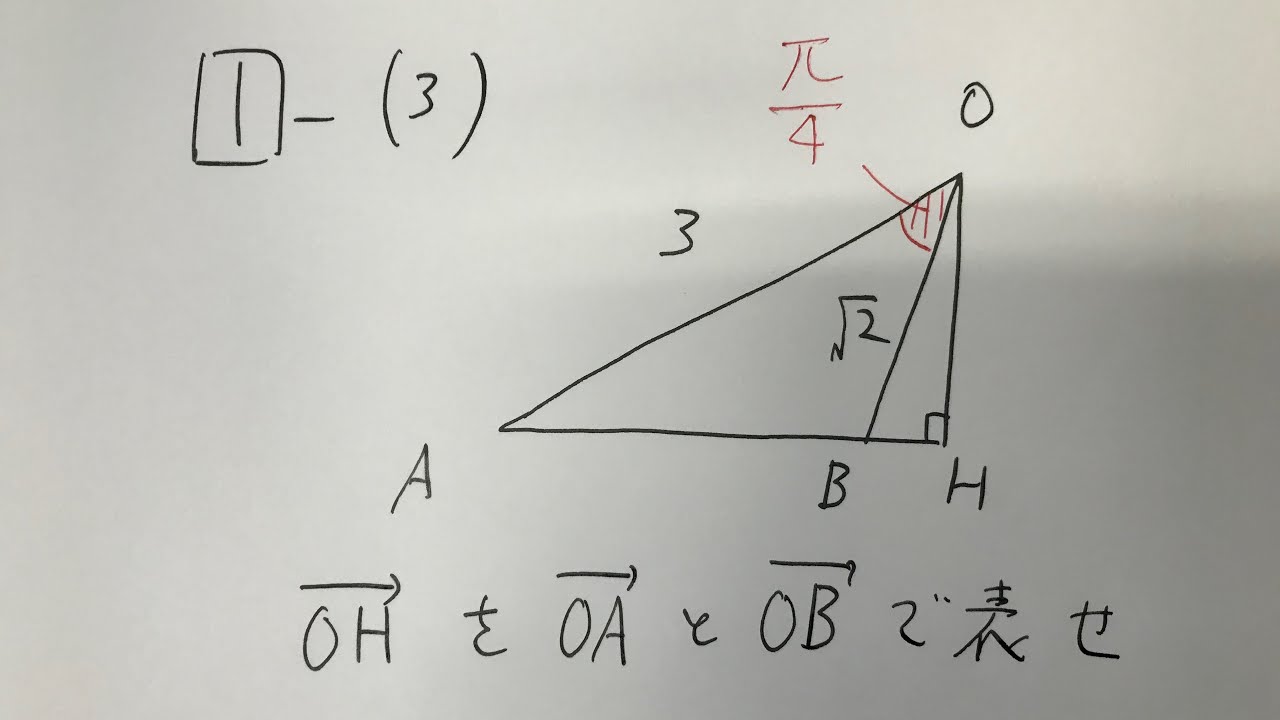
1⃣-(3)
$\overrightarrow{ OH }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$で表せ
*図は動画内参照
この動画を見る
1⃣-(3)
$\overrightarrow{ OH }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$で表せ
*図は動画内参照
18東京都教員採用試験(数学:場合の数、数列)

単元:
#数A#場合の数と確率#場合の数#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(2)
平面上の10コの円は、任意の2コの円も異なる2点で交わり、3コの円は1点で交わらないとき交点の総数を求めよ。
この動画を見る
1⃣-(2)
平面上の10コの円は、任意の2コの円も異なる2点で交わり、3コの円は1点で交わらないとき交点の総数を求めよ。
16大阪府教員採用試験(数学:連立不等式)

単元:
#2次関数#2次方程式と2次不等式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$a \in \mathbb{ R }$,
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 - (a+2)x+2a 0
\end{array}
\right.
\end{eqnarray}
$
を同時に満たす整数がただ1つ存在するようにaの値の範囲を求めよ。
この動画を見る
$a \in \mathbb{ R }$,
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 - (a+2)x+2a 0
\end{array}
\right.
\end{eqnarray}
$
を同時に満たす整数がただ1つ存在するようにaの値の範囲を求めよ。
17大阪府教員採用試験(数学:因数分解・整数問題)

単元:
#数Ⅰ#数A#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
(1)$x^2-6y^2+xy+5x+5y+6$を因数分解せよ。
(2)$x^2-6y^2+xy+5x+5y+9=0$をみたす整数の組(x,y)を求めよ。
この動画を見る
(1)$x^2-6y^2+xy+5x+5y+6$を因数分解せよ。
(2)$x^2-6y^2+xy+5x+5y+9=0$をみたす整数の組(x,y)を求めよ。
20年5月数学検定1級1次試験(行列)

単元:
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師:
ますただ
問題文全文(内容文):
①$A \mathbb{ x }$ =$λ \mathbb{ x }$ ($\mathbb{ x }≠0$)
λをAの固有値
$\mathbb{ x }$をλに関する固有ベクトル
$A \mathbb{ x }$-$λ \mathbb{ x }$=$\emptyset$
$(A-λE) \mathbb{ x } = \emptyset$
det(A-λE) =0
$\because det(A-λE) ≠ 0$ $ \Rightarrow $ $ \mathbb{ x } = \emptyset$となり矛盾する。
②A:3×3のケーリーハミルトンの定理
\begin{eqnarray}
A = \left(
\begin{array}{cccc}
a_{ 11 } & a_{ 12 } & a_{ 13 } \\
a_{ 21 } & a_{ 22 } & a_{ 23 } \\
a_{ 31 } & a_{ 32 } & a_{ 33 }
\end{array}
\right)
\end{eqnarray}
とする
$A^3-(a_{11}+a_{22}+a_{33})A+CA-(detA)E =\emptyset$
$C=a_{11}a_{22}-a_{12}a_{21}+a_{22}a_{33} - a_{23}a_{32}+a_{11}a_{23}-a_{13}a_{21}$
4⃣
\begin{eqnarray}
A = \left(
\begin{array}{cccc}
4 & 1 & 1 \\
1 & 2 & 1 \\
1 & 1 & 2
\end{array}
\right)
\end{eqnarray}
(1)Aの固有値を求めよ。
(2)$A^3-gA^2+18A-12E$を求めよ
この動画を見る
①$A \mathbb{ x }$ =$λ \mathbb{ x }$ ($\mathbb{ x }≠0$)
λをAの固有値
$\mathbb{ x }$をλに関する固有ベクトル
$A \mathbb{ x }$-$λ \mathbb{ x }$=$\emptyset$
$(A-λE) \mathbb{ x } = \emptyset$
det(A-λE) =0
$\because det(A-λE) ≠ 0$ $ \Rightarrow $ $ \mathbb{ x } = \emptyset$となり矛盾する。
②A:3×3のケーリーハミルトンの定理
\begin{eqnarray}
A = \left(
\begin{array}{cccc}
a_{ 11 } & a_{ 12 } & a_{ 13 } \\
a_{ 21 } & a_{ 22 } & a_{ 23 } \\
a_{ 31 } & a_{ 32 } & a_{ 33 }
\end{array}
\right)
\end{eqnarray}
とする
$A^3-(a_{11}+a_{22}+a_{33})A+CA-(detA)E =\emptyset$
$C=a_{11}a_{22}-a_{12}a_{21}+a_{22}a_{33} - a_{23}a_{32}+a_{11}a_{23}-a_{13}a_{21}$
4⃣
\begin{eqnarray}
A = \left(
\begin{array}{cccc}
4 & 1 & 1 \\
1 & 2 & 1 \\
1 & 1 & 2
\end{array}
\right)
\end{eqnarray}
(1)Aの固有値を求めよ。
(2)$A^3-gA^2+18A-12E$を求めよ
20年5月数学検定1級1次試験(微分)
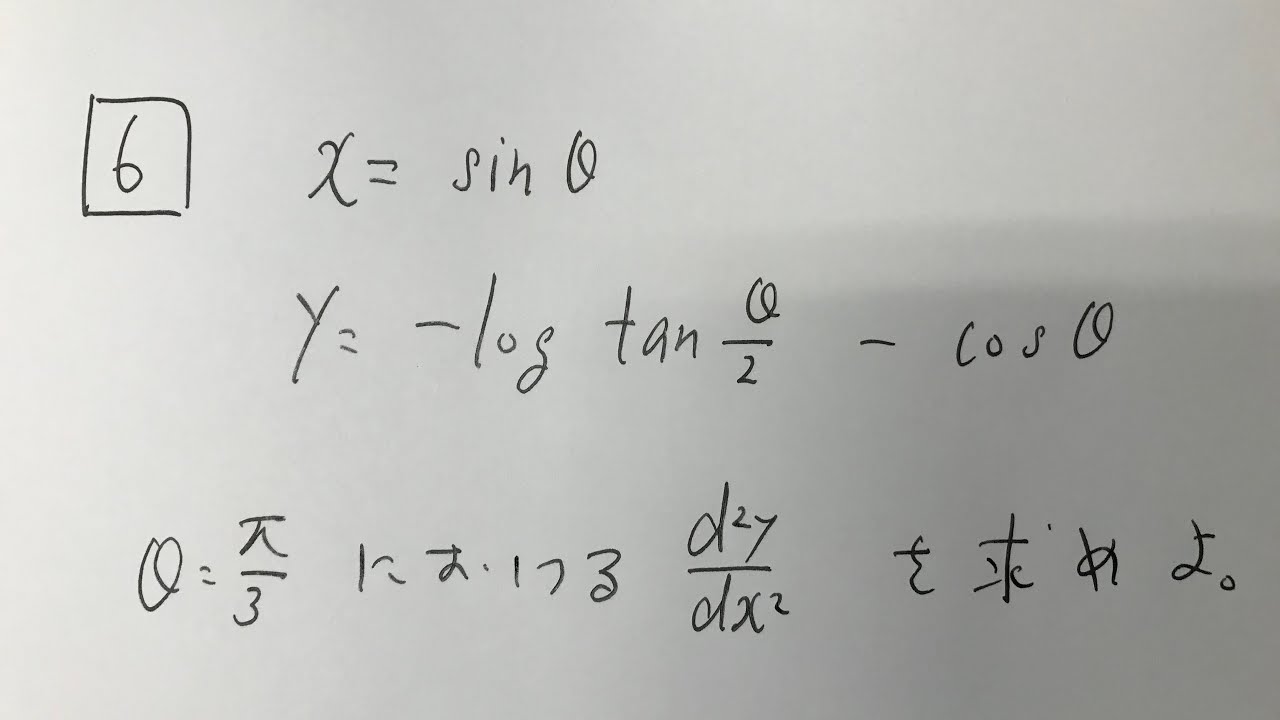
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#三角関数とグラフ#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
6⃣
x=sinθ
$y=-log tan \frac{θ}{2}-cosθ$
$θ=\frac{\pi}{3}$における$\frac{dy}{dx^2}$を求めよ。
この動画を見る
6⃣
x=sinθ
$y=-log tan \frac{θ}{2}-cosθ$
$θ=\frac{\pi}{3}$における$\frac{dy}{dx^2}$を求めよ。
20年5月数学検定1級1次試験(微分)
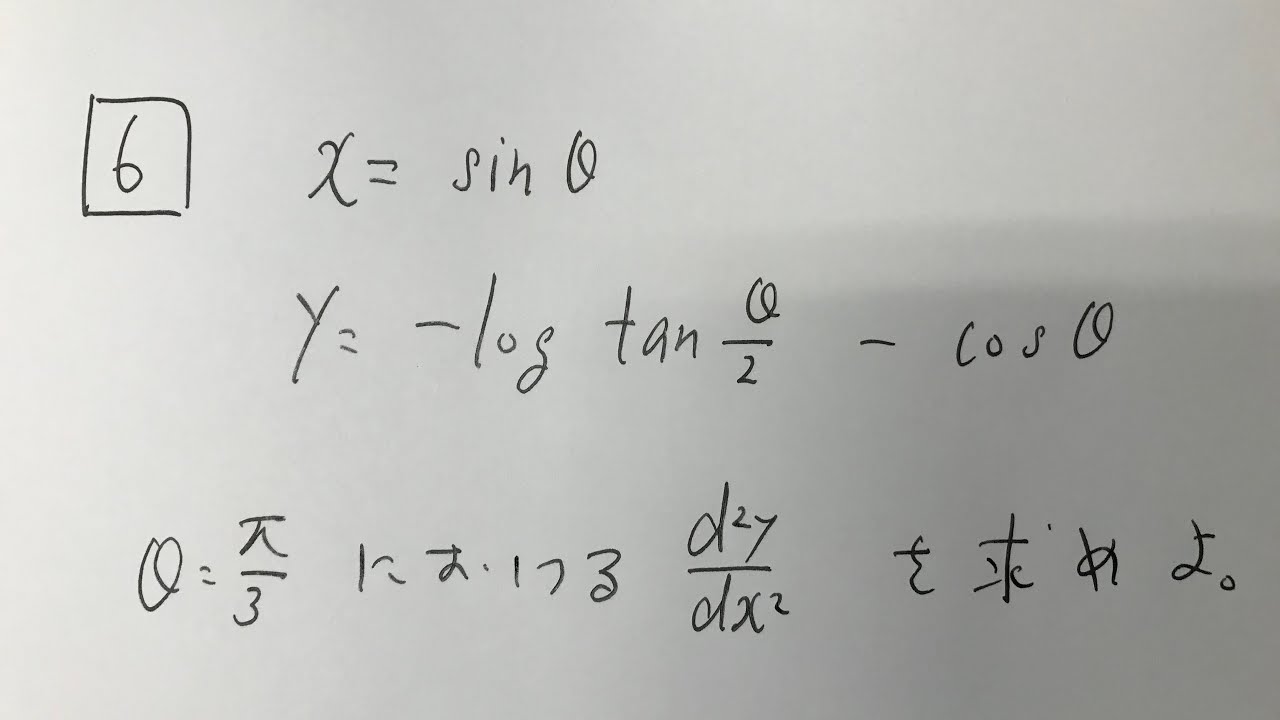
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
$x=\sin\theta$
$y=-1\log\tan\dfrac{\theta}{2}-\cos\theta$
$\theta=\dfrac{\pi}{3}$における$\dfrac{d^2y}{dx^2}$を求めよ.
20年5月数学検定1級1次試験(微分)過去問
この動画を見る
$\boxed{6}$
$x=\sin\theta$
$y=-1\log\tan\dfrac{\theta}{2}-\cos\theta$
$\theta=\dfrac{\pi}{3}$における$\dfrac{d^2y}{dx^2}$を求めよ.
20年5月数学検定1級1次試験(微分)過去問
20年5月数学検定1級1次試験(四面体の体積)

単元:
#数学検定・数学甲子園・数学オリンピック等#空間ベクトル#空間ベクトル#数学検定#数学検定1級#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
3⃣4点 A(1,-4,1),B(2,2,2),C(2,-6,-3),D(3,-2,-1)とする。
四面体ABCDの体積Vを求めよ。
この動画を見る
3⃣4点 A(1,-4,1),B(2,2,2),C(2,-6,-3),D(3,-2,-1)とする。
四面体ABCDの体積Vを求めよ。
20年5月数学検定1級1次試験(四面体の体積)

単元:
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
4点$A(1,-4,1),B(2,2,2),C(2,-6,-3),D(3,-2,-1)$とする.
四面体$ABCD$の体積$V$を求めよ.
$a=\left(\begin{eqnarray}
a_1 \\\
a_2 \\\
a_3
\end{eqnarray}\right)$
$a=\left(\begin{eqnarray}
b_1 \\\
b_2 \\\
b_3
\end{eqnarray}\right)$
$a=\left(\begin{eqnarray}
c_1 \\\
c_2 \\\
c_3
\end{eqnarray}\right)$
20年5月数学検定1級1次試験(四面体の体積)過去問
この動画を見る
$\boxed{3}$
4点$A(1,-4,1),B(2,2,2),C(2,-6,-3),D(3,-2,-1)$とする.
四面体$ABCD$の体積$V$を求めよ.
$a=\left(\begin{eqnarray}
a_1 \\\
a_2 \\\
a_3
\end{eqnarray}\right)$
$a=\left(\begin{eqnarray}
b_1 \\\
b_2 \\\
b_3
\end{eqnarray}\right)$
$a=\left(\begin{eqnarray}
c_1 \\\
c_2 \\\
c_3
\end{eqnarray}\right)$
20年5月数学検定1級1次試験(四面体の体積)過去問
20年5月数学検定1級1次試験(三角関数)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#三角関数とグラフ#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
2⃣
$tan(2Arctan \frac{1}{3} + Arctan \frac{1}{12} )$
この動画を見る
2⃣
$tan(2Arctan \frac{1}{3} + Arctan \frac{1}{12} )$
20年5月数学検定1級1次試験(三角関数)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{2}$
$\tan(2Arc\tan\dfrac{1}{3}+Arc\tan\dfrac{1}{12})$
$Arc\tan a=\tan^{-1}a=t\Leftrightarrow t=\tan a$
$\tan(\tan^{-1}a)=a$
$\tan(\alpha+\beta)=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}$
20年5月数学検定1級1次試験(三角関数)過去問
この動画を見る
$\boxed{2}$
$\tan(2Arc\tan\dfrac{1}{3}+Arc\tan\dfrac{1}{12})$
$Arc\tan a=\tan^{-1}a=t\Leftrightarrow t=\tan a$
$\tan(\tan^{-1}a)=a$
$\tan(\alpha+\beta)=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}$
20年5月数学検定1級1次試験(三角関数)過去問
18大阪府教員採用試験(数学:整数)

単元:
#数A#整数の性質#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2018
x>0の小数部分をbとし、$x^2+b^2 =40$を満たす。
このとき、bの範囲とxの値を求めよ。
この動画を見る
2018
x>0の小数部分をbとし、$x^2+b^2 =40$を満たす。
このとき、bの範囲とxの値を求めよ。
18大阪府教員採用試験(数学:整数)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#その他
指導講師:
ますただ
問題文全文(内容文):
$2018$
$x\gt 0$の小数部分を$b$とし,$x^2+b^2=40$を満たす.
このとき,$b$の範囲と$x$の値を求めよ.
18大阪府教員採用試験(数学:整数)過去問
この動画を見る
$2018$
$x\gt 0$の小数部分を$b$とし,$x^2+b^2=40$を満たす.
このとき,$b$の範囲と$x$の値を求めよ.
18大阪府教員採用試験(数学:整数)過去問
20年5月数学検定1級1次試験(合同式)

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
1⃣
2018 $n ≡ 2$ (mod 1000)をみたす最小の自然数nを求めよ
この動画を見る
1⃣
2018 $n ≡ 2$ (mod 1000)をみたす最小の自然数nを求めよ
20年5月数学検定1級1次試験(合同式)

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}$
$2018n \equiv 2(mod 1000)$をみたす最小の自然数$n$を求めよ.
20年5月数学検定1級1次試験(合同式)過去問
この動画を見る
$\boxed{1}$
$2018n \equiv 2(mod 1000)$をみたす最小の自然数$n$を求めよ.
20年5月数学検定1級1次試験(合同式)過去問
20年5月数検準1級1次試験(楕円)

単元:
#数学検定・数学甲子園・数学オリンピック等#平面上の曲線#2次曲線#数学検定#数学検定準1級#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
6⃣
2点A(0,-3)、B(0,1)から距離の和が6である楕円の方程式を求めよ
この動画を見る
6⃣
2点A(0,-3)、B(0,1)から距離の和が6である楕円の方程式を求めよ
20年5月数検準1級1次試験(楕円)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#図形と方程式#円と方程式#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
2点$A(0,-3),B(0,1)$から距離の和が6である楕円の方程式を求めよ.
20年5月数検準1級1次試験(楕円)過去問
この動画を見る
$\boxed{6}$
2点$A(0,-3),B(0,1)$から距離の和が6である楕円の方程式を求めよ.
20年5月数検準1級1次試験(楕円)過去問



