 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【数Ⅲ】【関数と極限】(1)lim tanx°/x(2)lim sin(x-π)/x-π(3)lim (x-π/2)tanx(4)lim sinπx/x-1(5)lim sin(sinx)/sinx

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の極限を求めよ。
(1) $\displaystyle \lim_{x \to 0} \frac{\tan x^{\circ}}{x}$
(2) $\displaystyle \lim_{x \to \pi} \frac{\sin (x - \pi)}{x - \pi}$
(3) $\displaystyle \lim_{x \to \frac{\pi}{2}} (x - \frac{\pi}{2}) \tan x$
(4) $\displaystyle \lim_{x \to 1} \frac{\sin \pi x}{x-1}$
(5) $\displaystyle \lim_{x \to 0} \frac{\sin (\sin x)}{\sin x}$
(6) $\displaystyle \lim_{x \to \infty} x \sin \frac{1}{2x}$
この動画を見る
次の極限を求めよ。
(1) $\displaystyle \lim_{x \to 0} \frac{\tan x^{\circ}}{x}$
(2) $\displaystyle \lim_{x \to \pi} \frac{\sin (x - \pi)}{x - \pi}$
(3) $\displaystyle \lim_{x \to \frac{\pi}{2}} (x - \frac{\pi}{2}) \tan x$
(4) $\displaystyle \lim_{x \to 1} \frac{\sin \pi x}{x-1}$
(5) $\displaystyle \lim_{x \to 0} \frac{\sin (\sin x)}{\sin x}$
(6) $\displaystyle \lim_{x \to \infty} x \sin \frac{1}{2x}$
【受験算数】長さ8mのバスが、長さ4mの自動車の前を100mの間をあけて走っています。 バスがここから 160m進んだ地点で、自動車にちょうど追いこされました。バスが秒速8mのとき、自動車は秒速何m?

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
長さ8mのバスが、長さ4mの自動車の前を100mの間をあけて走っています。 バスがここから 160m進んだ地点で、自動車にちょうど追いこされました。バスが秒速8mのとき、自動車は秒速何mですか。
この動画を見る
長さ8mのバスが、長さ4mの自動車の前を100mの間をあけて走っています。 バスがここから 160m進んだ地点で、自動車にちょうど追いこされました。バスが秒速8mのとき、自動車は秒速何mですか。
【受験算数】ある中学校で夏休みの予定を調べました。海に行く予定がある人は全生徒の75%,山に行く予定がある人は全生徒の40%でした。海に行く予定がある人の30%は山に行く予定もありました。海に行く…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
第1問 ある中学校で夏休みの予定を調べました。海に行く予定がある人は全生徒の75%,
山に行く予定がある人は全生徒の40%でした。海に行く予定がある人の30%は山に行く予定もありました。
(1)海に行く予定も山に行く予定もある人は全生徒の何%ですか。
(2)海に行く予定も山に行く予定もない人は30人でした。全生徒の人数は何人ですか。
第2問 ある高校で夏休みの予定を調べました。海に行く予定がある人は全生徒の80%,
山に行く予定がある人は全生徒の45%でした。海に行く予定がある人の40%は山に行く予定もありました。
(1)海に行く予定も山に行く予定もある人は全生徒の何%ですか。
(2)海に行く予定も山に行く予定もない人は77人でした。全生徒の人数は何人ですか。
この動画を見る
第1問 ある中学校で夏休みの予定を調べました。海に行く予定がある人は全生徒の75%,
山に行く予定がある人は全生徒の40%でした。海に行く予定がある人の30%は山に行く予定もありました。
(1)海に行く予定も山に行く予定もある人は全生徒の何%ですか。
(2)海に行く予定も山に行く予定もない人は30人でした。全生徒の人数は何人ですか。
第2問 ある高校で夏休みの予定を調べました。海に行く予定がある人は全生徒の80%,
山に行く予定がある人は全生徒の45%でした。海に行く予定がある人の40%は山に行く予定もありました。
(1)海に行く予定も山に行く予定もある人は全生徒の何%ですか。
(2)海に行く予定も山に行く予定もない人は77人でした。全生徒の人数は何人ですか。
【高校化学】次の文中の( )に適当な語句を入れ、下の問いに答えよ。分子が極性分子になるか、無極性分子になるかは、結合の極性と分子の形によって決まる。たとえば、メタン分子 CH₄ の形は(ア)形で

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の文中の( )に適当な語句を入れ、下の問いに答えよ。
分子が極性分子になるか、無極性分子になるかは、結合の極性と分子の形によって決まる。たとえば、メタン分子 CH₄ の形は(ア)形であり、4つの C-H 結合のそれぞれに極性があるが、互いに打ち消し合うため、CH₄ は(イ)分子である。
このように、極性のある結合をもつが、極性分子・無極性分子に分類せよ。ただし、( )内は分子の形状を示している。
① フッ素 F₂(直線形)
② フッ化水素 HF(直線形)
③ 二酸化炭素 CO₂(直線形)
④ 硫化水素 H₂S(折れ線形)
⑤ アンモニア NH₃(三角錐形)
⑥ 塩化メチル CH₃Cl(四面体形)
この動画を見る
次の文中の( )に適当な語句を入れ、下の問いに答えよ。
分子が極性分子になるか、無極性分子になるかは、結合の極性と分子の形によって決まる。たとえば、メタン分子 CH₄ の形は(ア)形であり、4つの C-H 結合のそれぞれに極性があるが、互いに打ち消し合うため、CH₄ は(イ)分子である。
このように、極性のある結合をもつが、極性分子・無極性分子に分類せよ。ただし、( )内は分子の形状を示している。
① フッ素 F₂(直線形)
② フッ化水素 HF(直線形)
③ 二酸化炭素 CO₂(直線形)
④ 硫化水素 H₂S(折れ線形)
⑤ アンモニア NH₃(三角錐形)
⑥ 塩化メチル CH₃Cl(四面体形)
【高校化学】次の文中の( )に適当な語句を入れ、各問いに答えよ。「電子を引きつける強さの尺度」を電気陰性度という。電気陰性度は、一般に、周期表の同一周期では18族を除き、原子番号の大きい原子ほど

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の文中の( )に適当な語句を入れ、各問いに答えよ。
「電子を引きつける強さの尺度」を電気陰性度という。電気陰性度は、一般に、周期表の同一周期では18族を除き、原子番号の大きい原子ほど(ア)くなり、同族元素の原子では、原子番号が大きいほど(イ)くなる。
電気陰性度の異なる2つの原子間で共有結合ができると、1つの原子に電子がより強く引きつけられ、電荷の偏りが生じる。そのような偏りのある結合を、(ウ)結合という。このように、結合した2原子間に電荷のかたよりがあるとき、結合に(キ)があるという。
(1)次の①〜④に示す2つの原子のうち、電気陰性度の大きい原子はどちらか。
① Li と O
② Al と Cl
③ Fe と Cl
④ S と F
(2)次の①〜④に示す結合のうち、結合の極性が最も大きいものはどれか。ただし、各原子の電気陰性度は、O=3.4,H=2.2,N=3.0,F=4.0 である。
① O-H
② N-H
③ F-H
④ F-F
この動画を見る
次の文中の( )に適当な語句を入れ、各問いに答えよ。
「電子を引きつける強さの尺度」を電気陰性度という。電気陰性度は、一般に、周期表の同一周期では18族を除き、原子番号の大きい原子ほど(ア)くなり、同族元素の原子では、原子番号が大きいほど(イ)くなる。
電気陰性度の異なる2つの原子間で共有結合ができると、1つの原子に電子がより強く引きつけられ、電荷の偏りが生じる。そのような偏りのある結合を、(ウ)結合という。このように、結合した2原子間に電荷のかたよりがあるとき、結合に(キ)があるという。
(1)次の①〜④に示す2つの原子のうち、電気陰性度の大きい原子はどちらか。
① Li と O
② Al と Cl
③ Fe と Cl
④ S と F
(2)次の①〜④に示す結合のうち、結合の極性が最も大きいものはどれか。ただし、各原子の電気陰性度は、O=3.4,H=2.2,N=3.0,F=4.0 である。
① O-H
② N-H
③ F-H
④ F-F
【高校化学】アンモニウムイオン NH₄⁺ は、アンモニア分子 NH₃ と水素イオン H⁺ が結合して生じたイオンである。これは、NH₃ 中の窒素原子の(ア)電子対が H⁺ に供与され、結合ができたもの

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
アンモニウムイオン NH₄⁺ は、アンモニア分子 NH₃ と水素イオン H⁺ が結合して生じたイオンである。これは、NH₃ 中の窒素原子の(ア)電子対が H⁺ に供与され、結合ができたものであり、このような結合を(イ)結合という。
このように、他の N-H 間の(ウ)結合と区別ができない結合を、(イ)結合という。
オキソニウムイオン H₃O⁺ の形成や [Cu(NH₃)₄]²⁺ のような錯イオンの形成時にもみられる。
この動画を見る
アンモニウムイオン NH₄⁺ は、アンモニア分子 NH₃ と水素イオン H⁺ が結合して生じたイオンである。これは、NH₃ 中の窒素原子の(ア)電子対が H⁺ に供与され、結合ができたものであり、このような結合を(イ)結合という。
このように、他の N-H 間の(ウ)結合と区別ができない結合を、(イ)結合という。
オキソニウムイオン H₃O⁺ の形成や [Cu(NH₃)₄]²⁺ のような錯イオンの形成時にもみられる。
【高校化学】(ア)塩化水素 HCl(イ)二酸化炭素 CO₂(ウ)メタン CH₄(エ)水 H₂O(オ)アンモニア NH₃(カ)硝酸 HNO₃① 直線形② 折れ線形(V字形)③ 三角錐形④ 正四面体形

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の(ア)〜(カ)の分子の形状を下の①〜⑥から選び、番号で示せ。
(ア)塩化水素 HCl
(イ)二酸化炭素 CO₂
(ウ)メタン CH₄
(エ)水 H₂O
(オ)アンモニア NH₃
(カ)硝酸 HNO₃
① 直線形
② 折れ線形(V字形)
③ 三角錐形
④ 正四面体形
⑤ 三角平面形
⑥ 正八面体形
この動画を見る
次の(ア)〜(カ)の分子の形状を下の①〜⑥から選び、番号で示せ。
(ア)塩化水素 HCl
(イ)二酸化炭素 CO₂
(ウ)メタン CH₄
(エ)水 H₂O
(オ)アンモニア NH₃
(カ)硝酸 HNO₃
① 直線形
② 折れ線形(V字形)
③ 三角錐形
④ 正四面体形
⑤ 三角平面形
⑥ 正八面体形
【高校化学】分子は、それぞれ固有の形状をしている。分子の形状は、含まれる共有電子対、非共有電子対の数によって説明されることがある。たとえば、メタン分子 CH₄ には、共有電子対が(ア)組含まれる。

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の文中の( )に適当な語句や数値を記し、下の問いに答えよ。
分子は、それぞれ固有の形状をしている。分子の形状は、含まれる共有電子対、非共有電子対の数によって説明されることがある。
たとえば、メタン分子 CH₄ には、共有電子対が(ア)組含まれる。これらは互いに反発するが、(イ)形の頂点方向に位置するとき、最も反発が小さくなる。したがって、メタン分子は(イ)形となる。
同様に、アンモニア分子 NH₃ には、(ウ)組の共有電子対と(エ)組の非共有電子対があり、これらが互いに反発して(イ)形をとろうとする。したがって、アンモニアの窒素原子上と水素原子の配置は、(オ)形になる。
(問)同様に考えると、水分子 H₂O はどのような形になると予想されるか。
この動画を見る
次の文中の( )に適当な語句や数値を記し、下の問いに答えよ。
分子は、それぞれ固有の形状をしている。分子の形状は、含まれる共有電子対、非共有電子対の数によって説明されることがある。
たとえば、メタン分子 CH₄ には、共有電子対が(ア)組含まれる。これらは互いに反発するが、(イ)形の頂点方向に位置するとき、最も反発が小さくなる。したがって、メタン分子は(イ)形となる。
同様に、アンモニア分子 NH₃ には、(ウ)組の共有電子対と(エ)組の非共有電子対があり、これらが互いに反発して(イ)形をとろうとする。したがって、アンモニアの窒素原子上と水素原子の配置は、(オ)形になる。
(問)同様に考えると、水分子 H₂O はどのような形になると予想されるか。
【受験算数】ある学年で、すいかが好きな人とメロンが好きな人を調べたところ、すいかが好きな人は学年全体の64%、メロンが好きな人は学年全体の5/7でした。この学年の人数として考えられるもののうち、最も…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
第1問 ある学年で、すいかが好きな人とメロンが好きな人を調べたところ、すいかが好きな人は学年全体の64%、メロンが好きな人は学年全体の5/7でした。この学年の人数として考えられるもののうち、最も少ないものを答えなさい。
第2問 ある学年で、かきが好きな人とくりが好きな人を調べたところ、かきが好きな人は学年全体の4割5分、くりが好きな人は学年全体の4/9でした。この学年の人数として考えられるもののうち、最も少ないものを答えなさい。
この動画を見る
第1問 ある学年で、すいかが好きな人とメロンが好きな人を調べたところ、すいかが好きな人は学年全体の64%、メロンが好きな人は学年全体の5/7でした。この学年の人数として考えられるもののうち、最も少ないものを答えなさい。
第2問 ある学年で、かきが好きな人とくりが好きな人を調べたところ、かきが好きな人は学年全体の4割5分、くりが好きな人は学年全体の4/9でした。この学年の人数として考えられるもののうち、最も少ないものを答えなさい。
【中学受験理科】輪軸②:問1 次の輪軸の図について、①~③にあてはまる数字を答えなさい。なお、輪軸の重さはそれぞれの横に記してあります。また、図に書いてある長さは輪軸の半径を表しています。…

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
問1 次の輪軸の図について、①~③にあてはまる数字を答えなさい。なお、輪軸の重さはそれぞれの横に記してあります。また、図に書いてある長さは輪軸の半径を表しています。
問2 図1でアのおもりを9cm動かすためには、ひもを何cm引けばよいですか。
この動画を見る
問1 次の輪軸の図について、①~③にあてはまる数字を答えなさい。なお、輪軸の重さはそれぞれの横に記してあります。また、図に書いてある長さは輪軸の半径を表しています。
問2 図1でアのおもりを9cm動かすためには、ひもを何cm引けばよいですか。
【高校化学】次の(ア)(オ)の各分子について次の問いに答えよ(ア)F₂ (イ)H₂O (ウ)CO₂ (エ)CH₄ (オ)C₂H₄(1)各分子の電子式を記せ(2)1分子に含まれる共有電子対、非共有電子対

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の(ア)~(オ)の各分子について次の問いに答えよ
(ア)F₂ (イ)H₂O (ウ)CO₂ (エ)CH₄ (オ)C₂H₄
(1)各分子の電子式を記せ
(2)1分子に含まれる共有電子対、非共有電子対の数を求めよ(ない場合は0とせよ)
この動画を見る
次の(ア)~(オ)の各分子について次の問いに答えよ
(ア)F₂ (イ)H₂O (ウ)CO₂ (エ)CH₄ (オ)C₂H₄
(1)各分子の電子式を記せ
(2)1分子に含まれる共有電子対、非共有電子対の数を求めよ(ない場合は0とせよ)
【高校化学】水素原子とフッ素原子の結合様式を図(映像中)に示した図中の▴で表した電子は(ア)と呼ばれ、まず原子はこれを共有しあって結びつく。このような結合を(イ)結合という

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
(ア)~(ウ)の用語を埋め、後の問いに答えよ
水素原子とフッ素原子の結合様式を図(映像中)に示した
図中の▴で表した電子は( ア )と呼ばれ、まず原子はこれを共有しあって結びつく。このような結合を( イ )結合という。フッ化水素におけるフッ素の電子配置はこの時貴ガスの( ウ )と似ている。
(1) フッ化水素1分子に含まれる電子の総数を求めよ
(2) 次の各分子のうち、指定されている原子はどの貴ガス原子と電子配置が似ているか
(a) Cl₂【Cl】 (b)H₂O【O】 (c)CH₄【C】 (d)NH₃【N】
この動画を見る
(ア)~(ウ)の用語を埋め、後の問いに答えよ
水素原子とフッ素原子の結合様式を図(映像中)に示した
図中の▴で表した電子は( ア )と呼ばれ、まず原子はこれを共有しあって結びつく。このような結合を( イ )結合という。フッ化水素におけるフッ素の電子配置はこの時貴ガスの( ウ )と似ている。
(1) フッ化水素1分子に含まれる電子の総数を求めよ
(2) 次の各分子のうち、指定されている原子はどの貴ガス原子と電子配置が似ているか
(a) Cl₂【Cl】 (b)H₂O【O】 (c)CH₄【C】 (d)NH₃【N】
【高校化学】次の(ア)~(エ)についてのちの問いに答えよ(ア)₃Li (イ)₇N (ウ)₁₀Ne (エ)₁₇Cl(1)各原子の電池配置、電子式をかけ(2)各原子の不対電子の数を記せ

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の(ア)~(エ)についてのちの問いに答えよ
(ア)₃Li (イ)₇N (ウ)₁₀Ne (エ)₁₇Cl
(1)各原子の電池配置、電子式をかけ
(2)各原子の不対電子の数を記せ
この動画を見る
次の(ア)~(エ)についてのちの問いに答えよ
(ア)₃Li (イ)₇N (ウ)₁₀Ne (エ)₁₇Cl
(1)各原子の電池配置、電子式をかけ
(2)各原子の不対電子の数を記せ
【高校化学】表(本編中)の名称と組成式を記せ陽イオン K⁺ Fe²⁺ Al³⁺陰イオン Cl⁻ OH⁻ SO₄²⁻ PO₄³⁻

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
表(本編中)の名称と組成式を記せ
陽イオン K⁺ Fe²⁺ Al³⁺
陰イオン Cl⁻ OH⁻ SO₄²⁻ PO₄³⁻
この動画を見る
表(本編中)の名称と組成式を記せ
陽イオン K⁺ Fe²⁺ Al³⁺
陰イオン Cl⁻ OH⁻ SO₄²⁻ PO₄³⁻
【高校物理】点電荷の作る電場と電位:xy平面内の点A(0,a)に、点電荷 + Q を固定した。クーロンの法則の比例定数をkとする。電位の基準を無限遠として、次の各問に答えよ。

単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
xy平面内の点A(0,a)に、点電荷 + Q (>0)を固定した。
クーロンの法則の比例定数をkとする。電位の基準を無限遠として、次の各問に答えよ。
(1) 無限達から点B(0,-a)に、別の点電荷+Qを運んで固定する。この電荷を運ぶのに必要な仕事はいくらか。
(2) (1)の操作後の、x軸上の点 C(√3,0)における電場の強さと向きを求めよ。
(3) (1)の操作後の、点C、および原点Oの電位はそれぞれいくらか。
この動画を見る
xy平面内の点A(0,a)に、点電荷 + Q (>0)を固定した。
クーロンの法則の比例定数をkとする。電位の基準を無限遠として、次の各問に答えよ。
(1) 無限達から点B(0,-a)に、別の点電荷+Qを運んで固定する。この電荷を運ぶのに必要な仕事はいくらか。
(2) (1)の操作後の、x軸上の点 C(√3,0)における電場の強さと向きを求めよ。
(3) (1)の操作後の、点C、および原点Oの電位はそれぞれいくらか。
【受験算数】あるお店の金曜日の売り上げは200000円でした。このお店の土曜日の売り上げは金曜日の売り上げに比べて40%増でした。また、このお店の日曜日の売り上げは土曜日の売り上げと比べて10%減…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
第1問 あるお店の金曜日の売り上げは200000円でした。このお店の土曜日の売り上げは金曜日の売り上げに比べて40%増でした。また、このお店の日曜日の売り上げは土曜日の売り上げと比べて10%減でした。
(1)このお店の土曜日の売り上げは何円でしたか。
(2)このお店の日曜日の売り上げは何円でしたか。
第2問 ある遊園地の木曜日の入場者数は6000人でした。この遊園地の金曜日の入場者数は木曜日の入場者数に比べて20%減でした。また、この遊園地の土曜日の入場者数は金曜日の入場者数と比べて75%増でした。
(1)この遊園地の金曜日の入場者数は何人でしたか。
(2)この遊園地の土曜日の入場者数は何人でしたか。
この動画を見る
第1問 あるお店の金曜日の売り上げは200000円でした。このお店の土曜日の売り上げは金曜日の売り上げに比べて40%増でした。また、このお店の日曜日の売り上げは土曜日の売り上げと比べて10%減でした。
(1)このお店の土曜日の売り上げは何円でしたか。
(2)このお店の日曜日の売り上げは何円でしたか。
第2問 ある遊園地の木曜日の入場者数は6000人でした。この遊園地の金曜日の入場者数は木曜日の入場者数に比べて20%減でした。また、この遊園地の土曜日の入場者数は金曜日の入場者数と比べて75%増でした。
(1)この遊園地の金曜日の入場者数は何人でしたか。
(2)この遊園地の土曜日の入場者数は何人でしたか。
【受験算数】焼く前の牛ヒレ肉の65%は水分で、残りのうちの55%がたんぱく質です。焼く前の牛ヒレ肉200gにふくまれているたんぱく質は何gですか。

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
第1問 焼く前の牛ヒレ肉の65%は水分で、残りのうちの55%がたんぱく質です。
(1)焼く前の牛ヒレ肉200gにふくまれているたんぱく質は何gですか。
(2)たんぱく質77gを牛ヒレ肉でとるには、焼く前の牛ヒレ肉が何g必要ですか。
第2問 焼く前の紅鮭の70%は水分で、残りのうちの75%がたんぱく質です。
(1)焼く前の紅鮭200gにふくまれているたんぱく質は何gですか。
(2)たんぱく質67.5gを紅鮭でとるには、焼く前の紅鮭が何g必要ですか。
この動画を見る
第1問 焼く前の牛ヒレ肉の65%は水分で、残りのうちの55%がたんぱく質です。
(1)焼く前の牛ヒレ肉200gにふくまれているたんぱく質は何gですか。
(2)たんぱく質77gを牛ヒレ肉でとるには、焼く前の牛ヒレ肉が何g必要ですか。
第2問 焼く前の紅鮭の70%は水分で、残りのうちの75%がたんぱく質です。
(1)焼く前の紅鮭200gにふくまれているたんぱく質は何gですか。
(2)たんぱく質67.5gを紅鮭でとるには、焼く前の紅鮭が何g必要ですか。
【高校化学】イオン結晶について(ア)~(エ)に関する語句の正しい語句を選べ一般に(ア.かたく やわらかく)、強い力を加えると割れる融点が(イ.高い 低い)ものが多い固体では電気を(ウ.導く 導かない)

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
イオン結晶について、(ア)~(エ)に関する語句の正しい語句を選べ
一般に(ア.かたく やわらかく)、強い力を加えると割れる
融点が(イ.高い 低い)ものが多い
固体では電気を(ウ.導く 導かない)が、液体や水溶液にすると電気を(エ.導く 導かない)ようになる
この動画を見る
イオン結晶について、(ア)~(エ)に関する語句の正しい語句を選べ
一般に(ア.かたく やわらかく)、強い力を加えると割れる
融点が(イ.高い 低い)ものが多い
固体では電気を(ウ.導く 導かない)が、液体や水溶液にすると電気を(エ.導く 導かない)ようになる
【受験算数】右の図のように、内側の一辺が12個であるよう5列の中空方陣をご石で作り、くさり状につないだ。(1)この外側のご石は何個か。(2)ご石の総数は何個か。

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように、内側の一辺が12個であるよう5列の中空方陣をご石で作り、くさり状につないだ。
(1)この外側のご石は何個か。
(2)ご石の総数は何個か。
この動画を見る
右の図のように、内側の一辺が12個であるよう5列の中空方陣をご石で作り、くさり状につないだ。
(1)この外側のご石は何個か。
(2)ご石の総数は何個か。
【受験算数】右の図のように、内側の一辺が6個であるよう3列の中空方陣をご石で作り、くさり状につないだ。(1)この外側のご石は何個か。(2)ご石の総数は何個か。

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように、内側の一辺が6個であるよう3列の中空方陣をご石で作り、くさり状につないだ。
(1)この外側のご石は何個か。
(2)ご石の総数は何個か。
この動画を見る
右の図のように、内側の一辺が6個であるよう3列の中空方陣をご石で作り、くさり状につないだ。
(1)この外側のご石は何個か。
(2)ご石の総数は何個か。
【中学受験理科】輪軸①:問1 次の輪軸の図について、①~⑤にあてはまる数字を答えなさい。なお、輪軸の重さは考えないものとします。また、輪軸の横に書いてある長さは輪軸の半径を表します。問2 図1~図5…

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
問1 次の輪軸の図について、①~⑤にあてはまる数字を答えなさい。なお、輪軸の重さは考えないものとします。また、輪軸の横に書いてある長さは輪軸の半径を表します。
問2 図1~図5でおもりを10cm動かすためには、それぞれひもを何cm引けばよいですか。ただし、図3はア、図4はイのおもりを10cm動かすものとします。
この動画を見る
問1 次の輪軸の図について、①~⑤にあてはまる数字を答えなさい。なお、輪軸の重さは考えないものとします。また、輪軸の横に書いてある長さは輪軸の半径を表します。
問2 図1~図5でおもりを10cm動かすためには、それぞれひもを何cm引けばよいですか。ただし、図3はア、図4はイのおもりを10cm動かすものとします。
【高校物理】抵抗の合成:抵抗値がいずれもr〔Ω〕の12本の抵抗で、図のような立方体の形の格子をつくる。AとGを電源につないだところ、AからGに向かってI〔A〕の電流が流れた。(1) AD、 DH、 …

単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
抵抗値がいずれもr〔Ω〕の12本の抵抗で、図のような立方体の形の格子をつくる。AとGを電源につないだところ、AからGに向かってI〔A〕の電流が流れた。
(1) AD、 DH、 HG間を流れる電流はそれぞれいくらか。
(2) AG間の電圧はいくらか。
(3) AG間の合成抵抗はいくらか。
この動画を見る
抵抗値がいずれもr〔Ω〕の12本の抵抗で、図のような立方体の形の格子をつくる。AとGを電源につないだところ、AからGに向かってI〔A〕の電流が流れた。
(1) AD、 DH、 HG間を流れる電流はそれぞれいくらか。
(2) AG間の電圧はいくらか。
(3) AG間の合成抵抗はいくらか。
【数C】【平面上の曲線】極座標に関して、次の直線の極方程式を求めよ(1) 点A(2,0)を通り、始線とのなす角が5π/6の直線(2) 点B(1,π/2)を通り、始線とのなす角が2π/3の直線

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
極座標に関して、次の直線の極方程式を求めよ。
(1) 点 $A(2, 0) $を通り、始線とのなす角が $\frac{5}{6}\pi$ の直線
(2) 点 $B(1, \frac{\pi}{2}) $を通り、始線とのなす角が$\frac{2}{3}\pi $の直線
この動画を見る
極座標に関して、次の直線の極方程式を求めよ。
(1) 点 $A(2, 0) $を通り、始線とのなす角が $\frac{5}{6}\pi$ の直線
(2) 点 $B(1, \frac{\pi}{2}) $を通り、始線とのなす角が$\frac{2}{3}\pi $の直線
【数C】【平面上の曲線】次の極方程式の表す円の中心の極座標と半径を求めよ(1) r²-4rsinθ+3=0(2) r²-2√5r(cosθ-sinθ)-6=0

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の極方程式の表す円の中心の極座標と半径を求めよ。
(1) $r^2 - 4r \sin \theta + 3 = 0$
(2) $r^2 - 2\sqrt{5}r(\cos \theta - \sin \theta) - 6 = 0$
この動画を見る
次の極方程式の表す円の中心の極座標と半径を求めよ。
(1) $r^2 - 4r \sin \theta + 3 = 0$
(2) $r^2 - 2\sqrt{5}r(\cos \theta - \sin \theta) - 6 = 0$
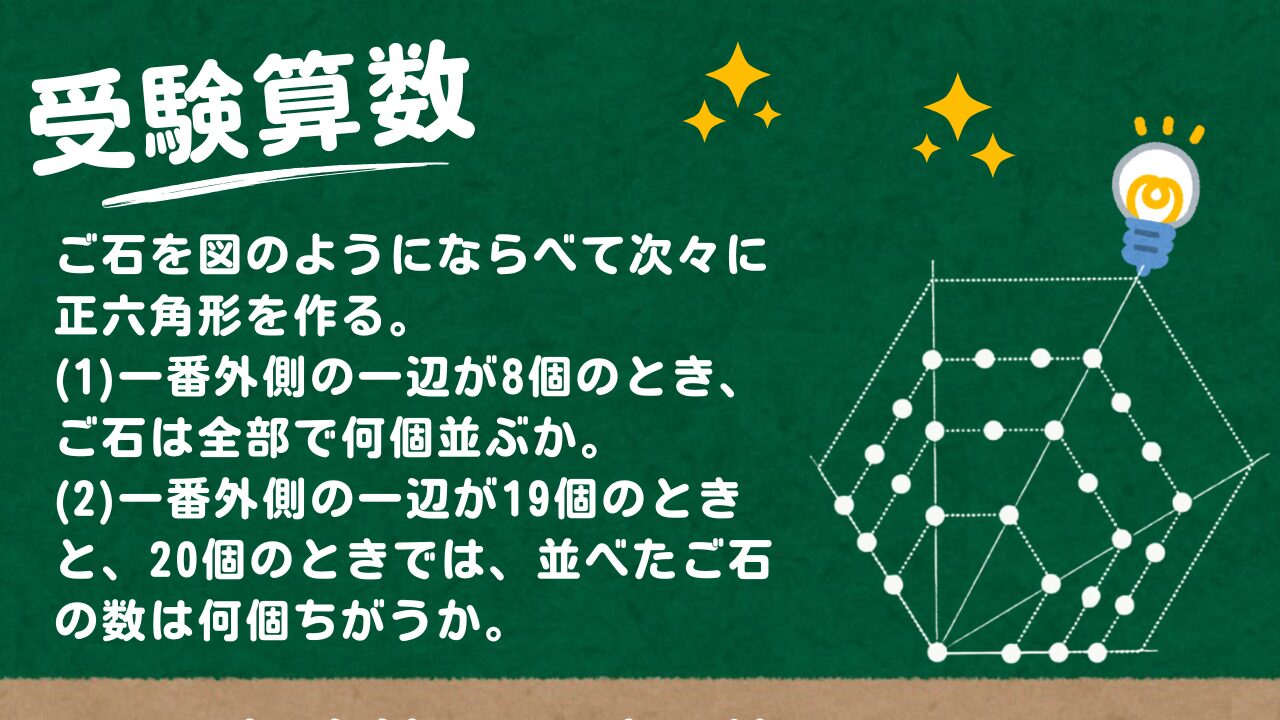
【受験算数】ご石を図のようにならべて次々に正六角形を作る。(1)一番外側の一辺が8個のとき、ご石は全部で何個並ぶか。(2)一番外側の一辺が19個のときと、20個のときでは、並べたご石の数は何個ちがうか
単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
ご石を図のようにならべて次々に正六角形を作る。
(1)一番外側の一辺が8個のとき、ご石は全部で何個並ぶか。
(2)一番外側の一辺が19個のときと、20個のときでは、並べたご石の数は何個ちがうか。
この動画を見る
ご石を図のようにならべて次々に正六角形を作る。
(1)一番外側の一辺が8個のとき、ご石は全部で何個並ぶか。
(2)一番外側の一辺が19個のときと、20個のときでは、並べたご石の数は何個ちがうか。
【受験算数】ご石を図のようにならべて次々に正五角形を作る。(1)一番外側の一辺が9個のとき、ご石は全部で何個並ぶか。(2)一番外側の一辺が16個のときと、17個のときでは、並べたご石の数は何個ちがうか

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
ご石を図のようにならべて次々に正五角形を作る。
(1)一番外側の一辺が9個のとき、ご石は全部で何個並ぶか。
(2)一番外側の一辺が16個のときと、17個のときでは、並べたご石の数は何個ちがうか。
この動画を見る
ご石を図のようにならべて次々に正五角形を作る。
(1)一番外側の一辺が9個のとき、ご石は全部で何個並ぶか。
(2)一番外側の一辺が16個のときと、17個のときでは、並べたご石の数は何個ちがうか。
【受験算数】長方形の土地がある。この土地の北側には6mごとに、西側には8mごとに木を植える計画を立て、その分にあたるなえ木を61本買った。実際は、どちらの側にも7.5mごとに植えたので、なえ木が8本…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
長方形の土地がある。この土地の北側には6mごとに、西側には8mごとに木を植える計画を立て、その分にあたるなえ木を61本買った。実際は、どちらの側にも7.5mごとに植えたので、なえ木が8本残った。土地のかどには必ずなえ木を植えるように計画し、実際に植えました。この土地の面積は何aか。
この動画を見る
長方形の土地がある。この土地の北側には6mごとに、西側には8mごとに木を植える計画を立て、その分にあたるなえ木を61本買った。実際は、どちらの側にも7.5mごとに植えたので、なえ木が8本残った。土地のかどには必ずなえ木を植えるように計画し、実際に植えました。この土地の面積は何aか。
【受験算数】長方形の土地がある。この土地の北側には2mごとに、西側には4mごとに木を植える計画を立て、その分にあたるなえ木を81本買った。実際は、どちらの側にも5mごとに植えたので、なえ木が38本…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
長方形の土地がある。この土地の北側には2mごとに、西側には4mごとに木を植える計画を立て、その分にあたるなえ木を81本買った。実際は、どちらの側にも5mごとに植えたので、なえ木が38本残った。土地のかどには必ずなえ木を植えるように計画し、実際に植えた。この土地の面積は何aか。
この動画を見る
長方形の土地がある。この土地の北側には2mごとに、西側には4mごとに木を植える計画を立て、その分にあたるなえ木を81本買った。実際は、どちらの側にも5mごとに植えたので、なえ木が38本残った。土地のかどには必ずなえ木を植えるように計画し、実際に植えた。この土地の面積は何aか。
【受験算数】チョコレートのいちばん外側のつつみ紙を6枚集めると、新しいチョコレート1個といつでも引きかえられるようなチョコレートがあるとします。次の問いに答えよ。このチョコレートを123個買った人が…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
チョコレートのいちばん外側のつつみ紙を6枚集めると、新しいチョコレート1個といつでも引きかえられるようなチョコレートがあるとします。次の問いに答えよ。
(1)このチョコレートを123個買った人が、つつみ紙で引きかえられるものはすべて引きかえるとすると、買ったものも合わせて全部で何個のチョコレートを手に入れることができるか。
(2)300個のチョコレートを手に入れるためには、少なくとも何個のチョコレートを買えばよいか。
この動画を見る
チョコレートのいちばん外側のつつみ紙を6枚集めると、新しいチョコレート1個といつでも引きかえられるようなチョコレートがあるとします。次の問いに答えよ。
(1)このチョコレートを123個買った人が、つつみ紙で引きかえられるものはすべて引きかえるとすると、買ったものも合わせて全部で何個のチョコレートを手に入れることができるか。
(2)300個のチョコレートを手に入れるためには、少なくとも何個のチョコレートを買えばよいか。
【受験算数】チョコレートのいちばん外側のつつみ紙を4枚集めると、新しいチョコレート1個といつでも引きかえられるようなチョコレートがある。このチョコレートを35個買った人が、つつみ紙で引きかえ…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
チョコレートのいちばん外側のつつみ紙を4枚集めると、新しいチョコレート1個といつでも引きかえられるようなチョコレートがある。
(1)このチョコレートを35個買った人が、つつみ紙で引きかえられるものはすべて引きかえるとすると、買ったものも合わせて全部で何個のチョコレートを手に入れることができるか。
(2)135個のチョコレートを手に入れるためには、少なくとも何個のチョコレートを買えばよいか。
この動画を見る
チョコレートのいちばん外側のつつみ紙を4枚集めると、新しいチョコレート1個といつでも引きかえられるようなチョコレートがある。
(1)このチョコレートを35個買った人が、つつみ紙で引きかえられるものはすべて引きかえるとすると、買ったものも合わせて全部で何個のチョコレートを手に入れることができるか。
(2)135個のチョコレートを手に入れるためには、少なくとも何個のチョコレートを買えばよいか。




