高校入試から見た数学の世界「全部入試問題」by しろたん
高校入試から見た数学の世界「全部入試問題」by しろたん
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【意外と深い…！】整数：愛知県～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
連続する3つの自然数をそれぞれ2乗して足すと365であった。もっとも小さい数を求めなさい。
この動画を見る
連続する3つの自然数をそれぞれ2乗して足すと365であった。もっとも小さい数を求めなさい。
【戸惑うなかれ…！】文字式：京都府～全国入試問題解法
単元：
#数学(中学生)#中１数学#文字と式
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
x=7,y=-6のとき、(x-y)^2-10(x-y)+25の値を求めよ。
この動画を見る
x=7,y=-6のとき、(x-y)^2-10(x-y)+25の値を求めよ。
【分かりやすく感覚的に…！】整数：立命館高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
4851n/2が整数の2乗となる最小の自然数nの値を求めよ。
この動画を見る
4851n/2が整数の2乗となる最小の自然数nの値を求めよ。
【十分な理解がないと…！】文字式：國學院大學久我山高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#文字と式#高校入試過去問(数学)#國學院大學久我山高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
次の文字式を計算しなさい。(-2x/y)^4×(3y/-z^2)^3×(z/2x)^2
この動画を見る
次の文字式を計算しなさい。(-2x/y)^4×(3y/-z^2)^3×(z/2x)^2
【考え方、大切…！】整数：兵庫県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
2つの奇数の積は、偶数になるか、奇数になるか考えなさい。
この動画を見る
2つの奇数の積は、偶数になるか、奇数になるか考えなさい。
【どの解法も大切…！】図形：三重県～全国入試問題解法
shape problems : Shirotan's cute kawaii math show #数学 #高校入試 #勉強 #サイ数学
【直角三角形の全て…！】三平方の定理：徳島県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#三平方の定理
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
三角形ABC:AB=8cm, BC=6cm, CA=xcm。三角形ABCが直角三角形となるようなxの値をすべて求めなさい。
この動画を見る
三角形ABC:AB=8cm, BC=6cm, CA=xcm。三角形ABCが直角三角形となるようなxの値をすべて求めなさい。
【困難はブンカツせよ…！】整数：三重県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
120nの値が整数の2乗となるような自然数nのうち、最も小さい値を求めなさい。
この動画を見る
120nの値が整数の2乗となるような自然数nのうち、最も小さい値を求めなさい。
Shirotan's cute kawaii math show #数学 #高校入試 #勉強 #チャンネル登録をお願いします
単元：
#数学(中学生)#中３数学#２次方程式#高校入試過去問(数学)#巣鴨高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
3つの二次方程式:x^2+ax+b=0, 2x^2+3ax+9b=0, x^2-2x-3=0が同じ正の解をもつとする。このとき、定数a,bの値を求めよ。
この動画を見る
3つの二次方程式:x^2+ax+b=0, 2x^2+3ax+9b=0, x^2-2x-3=0が同じ正の解をもつとする。このとき、定数a,bの値を求めよ。
【よく見てやれば…！】因数分解：成蹊高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
a^2-ac-4b^2+2bcを因数分解せよ。
この動画を見る
a^2-ac-4b^2+2bcを因数分解せよ。
square root: Shirotan's cute kawaii math show #Math #exam #questions #brainteasers
単元：
#数学(中学生)#中３数学#平方根
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
(2√3-3√2)(√2+√3)-2(1/√24-1/6)を計算せよ。
この動画を見る
(2√3-3√2)(√2+√3)-2(1/√24-1/6)を計算せよ。
【形を変えて…！】二次方程式：東京都立墨田川高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#２次方程式
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
二次方程式:(x-3)^2=4x^2を解け。
この動画を見る
二次方程式:(x-3)^2=4x^2を解け。
【落ち着いて考えて…！】文字式：明治大学付属中野高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
√((n^2+515)/(n^2+2))が整数となるような自然数nを求めなさい。
この動画を見る
√((n^2+515)/(n^2+2))が整数となるような自然数nを求めなさい。
【戸惑う人も多い…！】平方根：秋田県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$\sqrt{32}$$-$$\sqrt{50}$$+$$\sqrt{27}$
この動画を見る
$\sqrt{32}$$-$$\sqrt{50}$$+$$\sqrt{27}$
mathematical formula : Shirotan's cute kawaii math show #Math #exam #brainteasers
単元：
#数学(中学生)#中３数学
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$(x-1)(x-2)(x-4)(x-5) = ?$
$x = \frac{7}{3 + \sqrt{2}}$
この動画を見る
$(x-1)(x-2)(x-4)(x-5) = ?$
$x = \frac{7}{3 + \sqrt{2}}$
【少しでも上手く…！】文字式：明治大学付属明治高等学校～全国入試問題解法
単元：
#数学(中学生)#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$x =\sqrt{1103} + \sqrt{1101}$
$ y = \sqrt{1103} - \sqrt{1101}$
のとき
$\left( \frac{1}{2} x^2 y \right)^5 \div \left( \frac{1}{4} x^3 y^2 \right)^3 + x^3 y^7 \cdot xy \div x^4 y^6
$の値は$\boxed{ }$である
この動画を見る
$x =\sqrt{1103} + \sqrt{1101}$
$ y = \sqrt{1103} - \sqrt{1101}$
のとき
$\left( \frac{1}{2} x^2 y \right)^5 \div \left( \frac{1}{4} x^3 y^2 \right)^3 + x^3 y^7 \cdot xy \div x^4 y^6
$の値は$\boxed{ }$である
【意外な盲点…!?】文字式：青森県公立高等学校～全国入試問題解法
単元：
#数学(中学生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$\frac{2x + y - 1}{3} - \frac{3x - 2y + 3}{5}$
この動画を見る
$\frac{2x + y - 1}{3} - \frac{3x - 2y + 3}{5}$
【中学生の方が解ける…!?】図形：駿台甲府高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#数Ⅰ#図形と計量
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
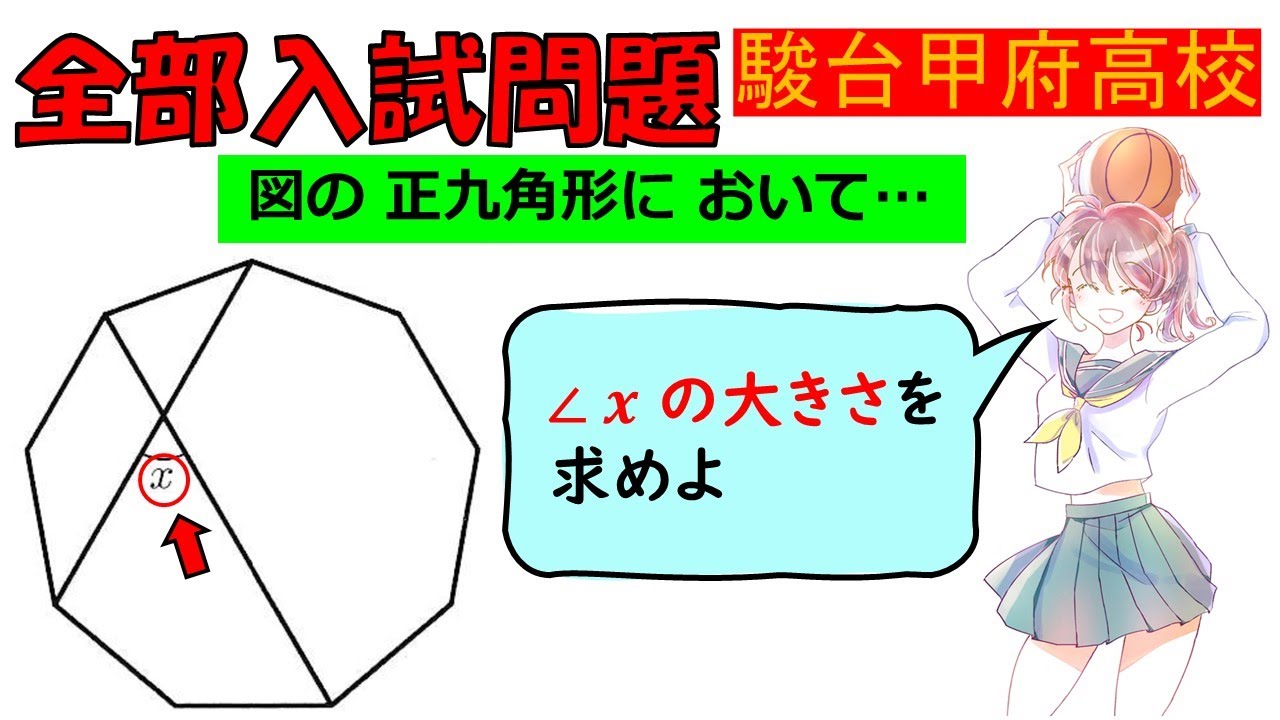
図の正九角形において
$\angle x$の大きさを求めよ
この動画を見る
図の正九角形において
$\angle x$の大きさを求めよ
factorization : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元：
#数学(中学生)#相似な図形#平面図形#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$x^2-\boxed{ }x+14$が$(x-a)(x-b)$の形に因数分解できる。
$\boxed{ }$に当てはまる自然数を二つ書け。
この動画を見る
$x^2-\boxed{ }x+14$が$(x-a)(x-b)$の形に因数分解できる。
$\boxed{ }$に当てはまる自然数を二つ書け。
【考え方が大切…！】二次方程式：山口県～全国入試問題解法
単元：
#数A#整数の性質#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
差が$1$である大小$2$つの正の数がある。これらの積が$3$であるとき
$2$つの数のうち大きい方を求めなさい
この動画を見る
差が$1$である大小$2$つの正の数がある。これらの積が$3$であるとき
$2$つの数のうち大きい方を求めなさい
shape problems : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
【初めの一手は…！】二次方程式：中央大学杉並高等学校～全国入試問題解法
単元：
#数学(中学生)#数Ⅰ#高校入試過去問(数学)#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$4(x - 7)(x - 16)+56 = (x-8)(x-9)$を解きなさい
この動画を見る
$4(x - 7)(x - 16)+56 = (x-8)(x-9)$を解きなさい
【スッキリ理解できる…！】一次関数：駿台甲府高等学校～全国入試問題解法
単元：
#図形と計量#平面図形#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
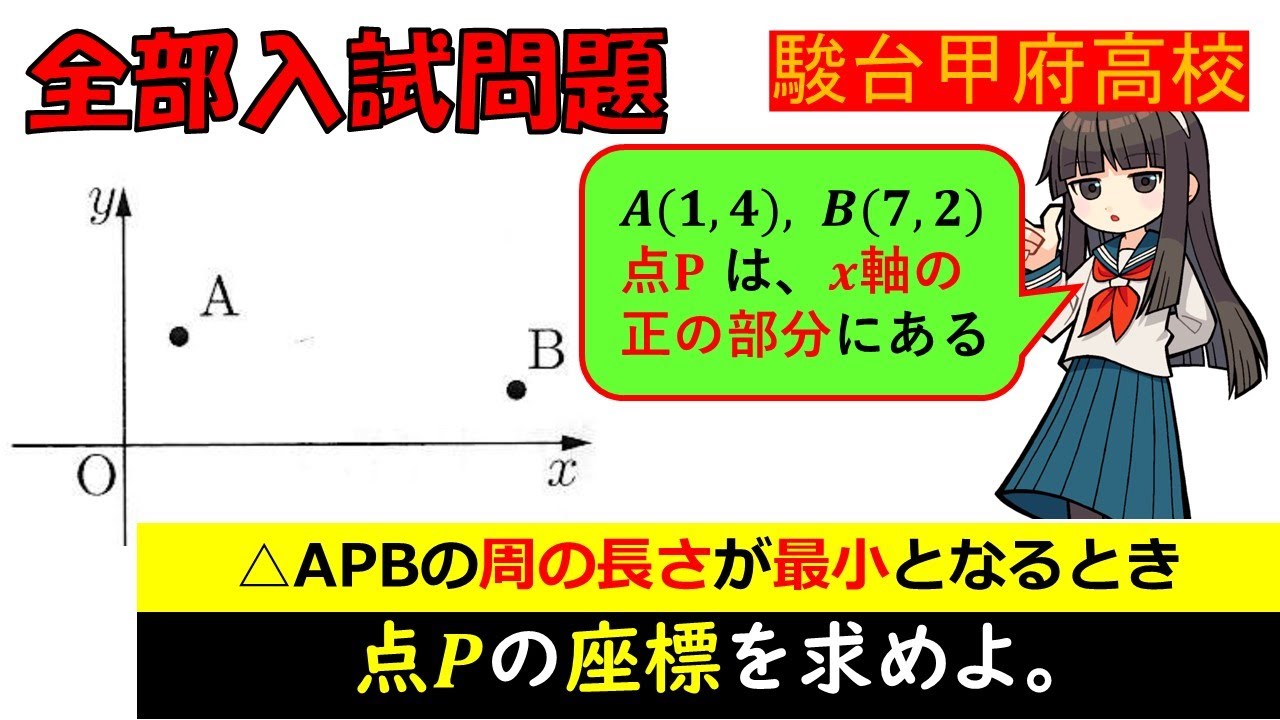
2点$A = (1.4) B = (7.2)$で、$点Pは正の所を動く。$$\triangle APB$の周の長さが最小となるとき点$P$の座標を求めよ
この動画を見る
2点$A = (1.4) B = (7.2)$で、$点Pは正の所を動く。$$\triangle APB$の周の長さが最小となるとき点$P$の座標を求めよ
【入試で必要な発想…！】図形：明治学院高等学校～全国入試問題解法
単元：
#数学(中学生)#数Ⅰ#図形と計量#平面図形#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
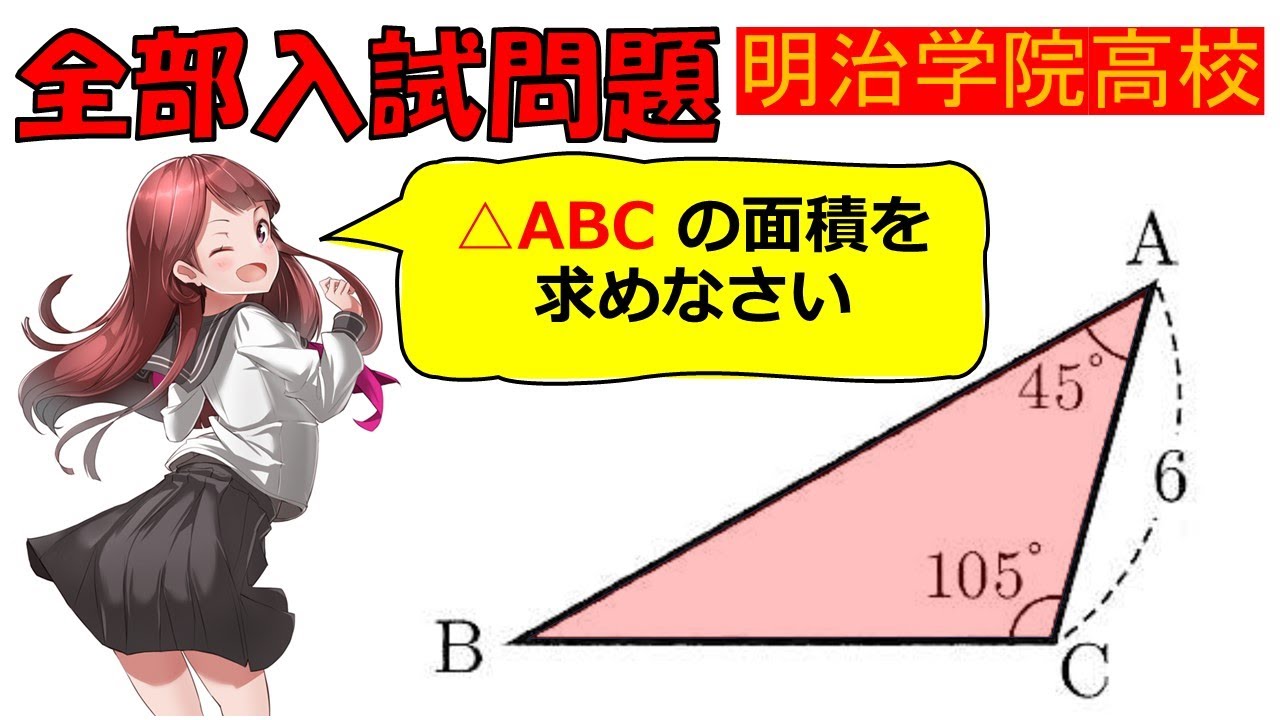
$\triangleABCの面積を求めなさい$
この動画を見る
$\triangleABCの面積を求めなさい$
square root : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元：
#数A#整数の性質#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$\sqrt{12(15-3m)}$が整数になる正の整数$m$を全て求めよ
この動画を見る
$\sqrt{12(15-3m)}$が整数になる正の整数$m$を全て求めよ
【解法は1つでない…！】連立方程式：東京工業大学附属科学技術高等学校～全国入試問題解法
【解法は1つでない…！】連立方程式：東京工業大学附属科学技術高等学校～全国入試問題解法
単元：
#数学(中学生)#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$\begin{eqnarray}
\begin{cases}
(2a-1)x+(b+1)y =-3 \\
(2b+1)x+(a-1)y =11
\end{cases}
\end{eqnarray}$
の解が$x=-1, y=2であるとき定数a,bの値をそれぞれ求めなさい$
この動画を見る
$\begin{eqnarray}
\begin{cases}
(2a-1)x+(b+1)y =-3 \\
(2b+1)x+(a-1)y =11
\end{cases}
\end{eqnarray}$
の解が$x=-1, y=2であるとき定数a,bの値をそれぞれ求めなさい$
【最終兵器…!?】因数分解：ラ・サール高等学校～全国入試問題解法
単元：
#数学(中学生)#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$\frac{x}{12}(9+x)+(19-\frac{5}{3}x)×(1-\frac{x}{4})-\frac{1}{6}(42-x)$を因数分解せよ
この動画を見る
$\frac{x}{12}(9+x)+(19-\frac{5}{3}x)×(1-\frac{x}{4})-\frac{1}{6}(42-x)$を因数分解せよ
【最終兵器…!?】因数分解：ラ・サール高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$\frac{x}{12}(9+x)+(19-\frac{5}{3}x)×(1-\frac{x}{4})-\frac{1}{6}(42-x)$
この動画を見る
$\frac{x}{12}(9+x)+(19-\frac{5}{3}x)×(1-\frac{x}{4})-\frac{1}{6}(42-x)$