数学を数楽に
数学を数楽に
 数学を数楽に
数学を数楽に
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
中央値 2023中央大附属

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
15,a,20,b,11,24
平均値=17 , 中央値=16.5
a=? b=?
(ただし、a<b))
2023中央大学付属高等学校
この動画を見る
15,a,20,b,11,24
平均値=17 , 中央値=16.5
a=? b=?
(ただし、a<b))
2023中央大学付属高等学校
=入れる入れない問題。不等式。初見でよく間違えます。高知学芸

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
不等式1< x < k+2を満たす整数xが2と3だけであるときkの範囲を求めよ。
高知学芸高等学校
この動画を見る
不等式1< x < k+2を満たす整数xが2と3だけであるときkの範囲を求めよ。
高知学芸高等学校
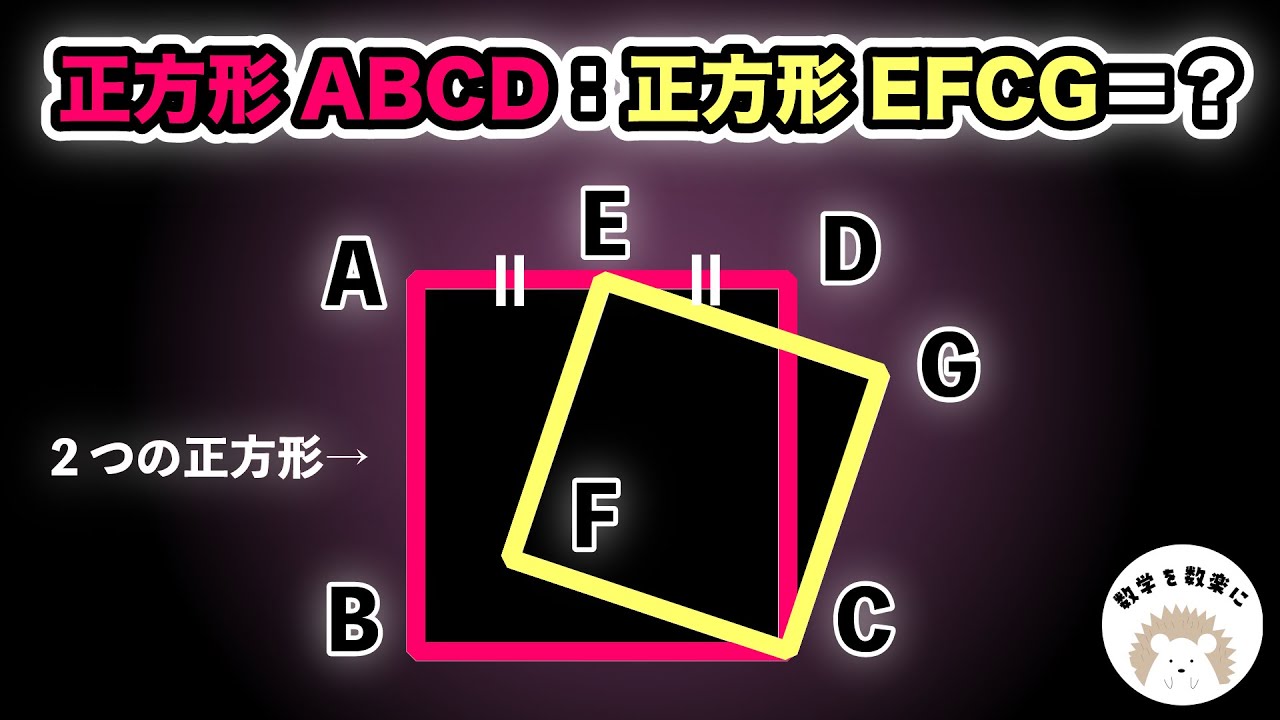
正方形は〇〇形 正方形の面積比
素数に関する問題 明治学院

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
m,nを1ケタの自然数とする。
(m+n)(n-2)が素数となる(m,n)の組はいくつあるか。
明治学院高等学校
この動画を見る
m,nを1ケタの自然数とする。
(m+n)(n-2)が素数となる(m,n)の組はいくつあるか。
明治学院高等学校
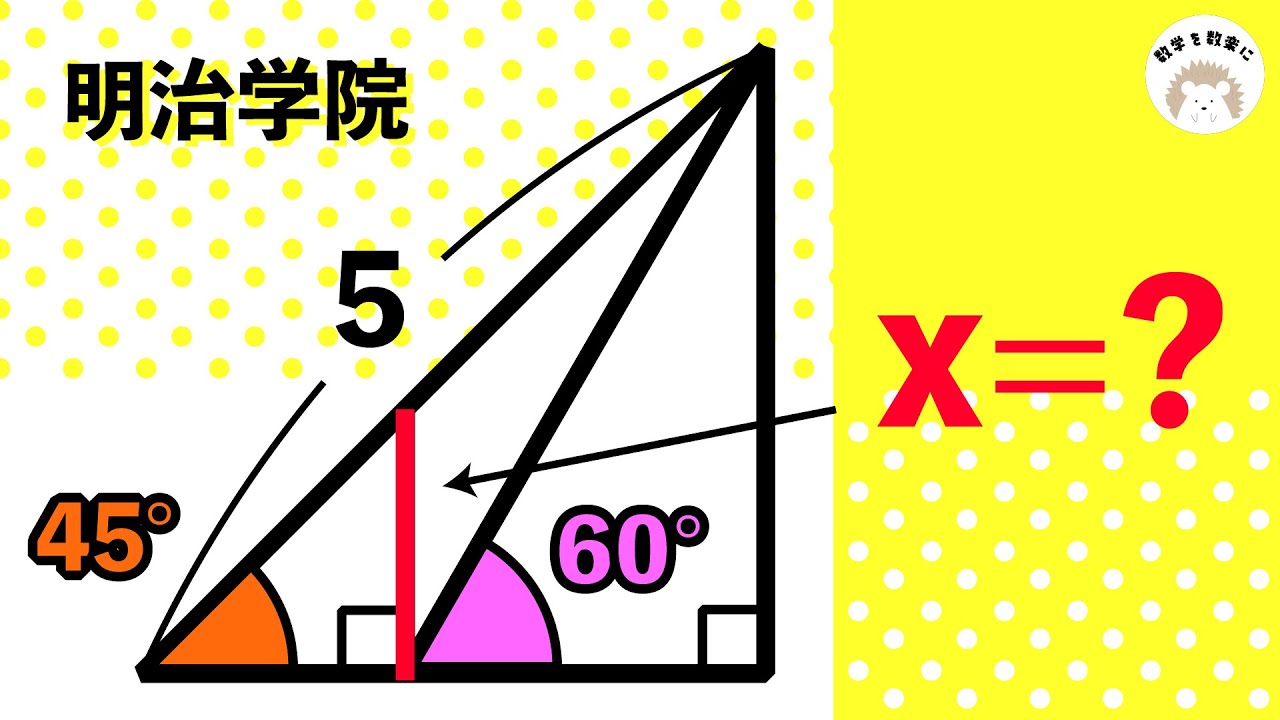
三角定規、比の扱い 明治学院
因数分解できない因数分解

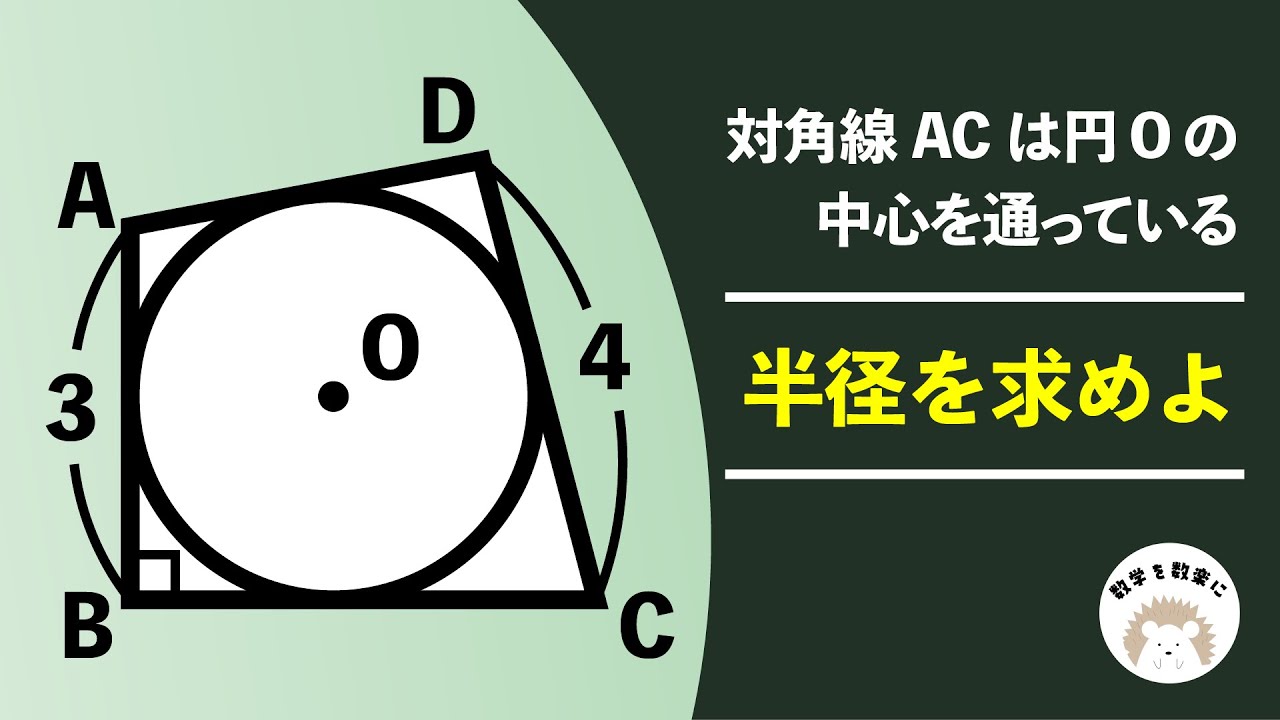
外接四角形
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
対角線ACは円Oの中心を通っている
半径を求めよ
*図は動画内参照
この動画を見る
対角線ACは円Oの中心を通っている
半径を求めよ
*図は動画内参照
分数の中に分数

高校入試だけど3次方程式!? 渋谷幕張高校

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(1)$(x-3)^3$を展開せよ。
(2)$x^3-9x^2+25x-21 = 0$を解け。
渋谷教育学園幕張高等学校
この動画を見る
(1)$(x-3)^3$を展開せよ。
(2)$x^3-9x^2+25x-21 = 0$を解け。
渋谷教育学園幕張高等学校
2通りで解説!!因数分解 朋優学院

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$(a+1)^2+a-b-(b+1)^2$
朋優学院高等学校
この動画を見る
因数分解せよ
$(a+1)^2+a-b-(b+1)^2$
朋優学院高等学校
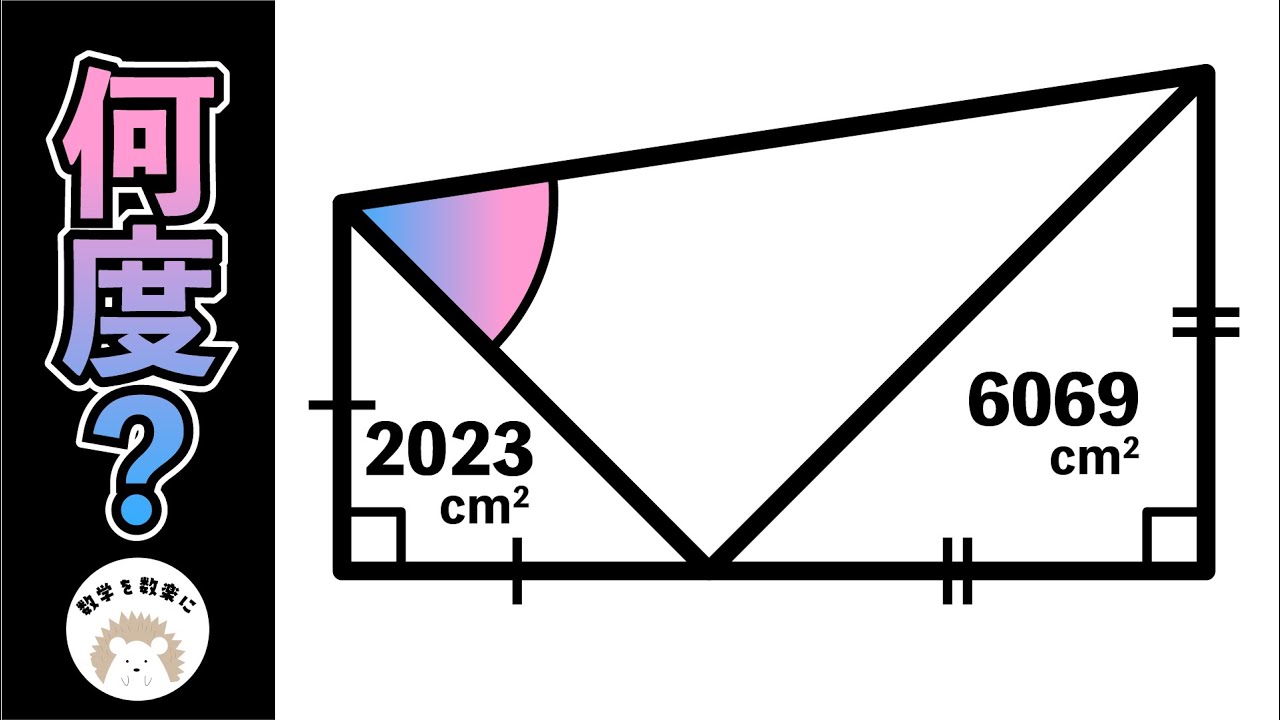
答えは出るでしょう。。。
単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
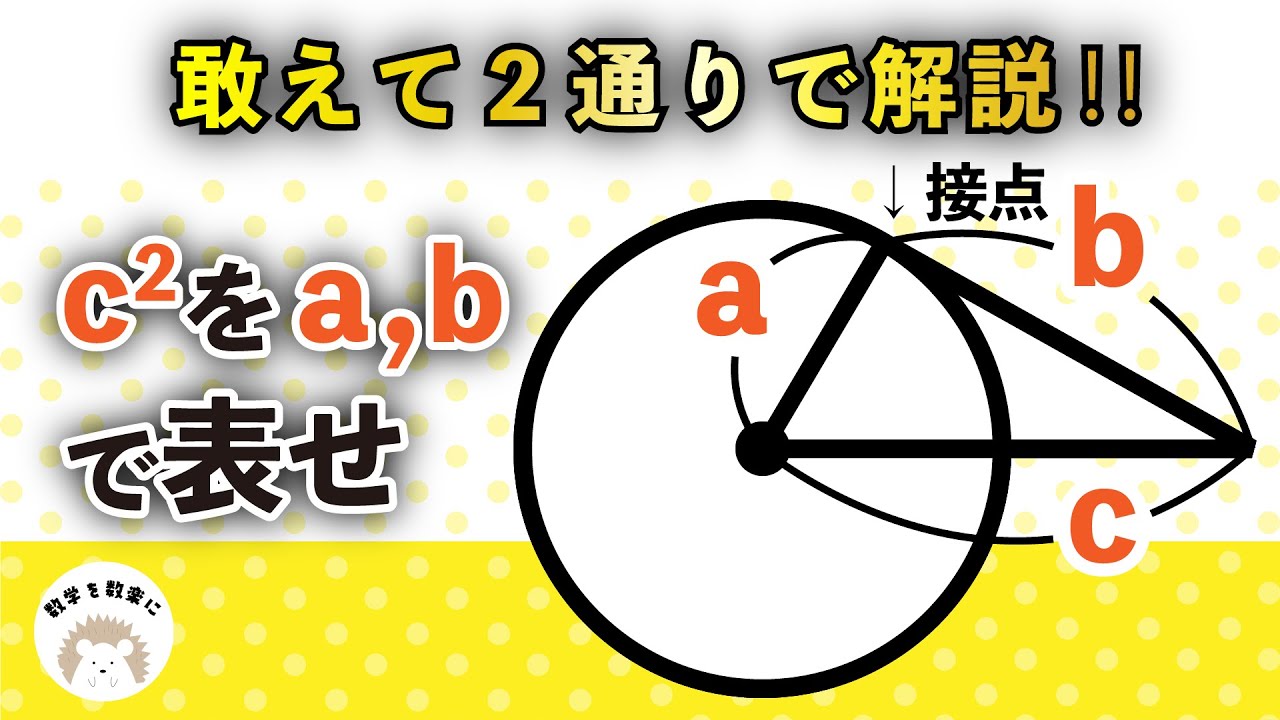
$c^2$をa,bで表せ
*図は動画内参照
この動画を見る
$c^2$をa,bで表せ
*図は動画内参照
気付けば一瞬!!tanθ=❓
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
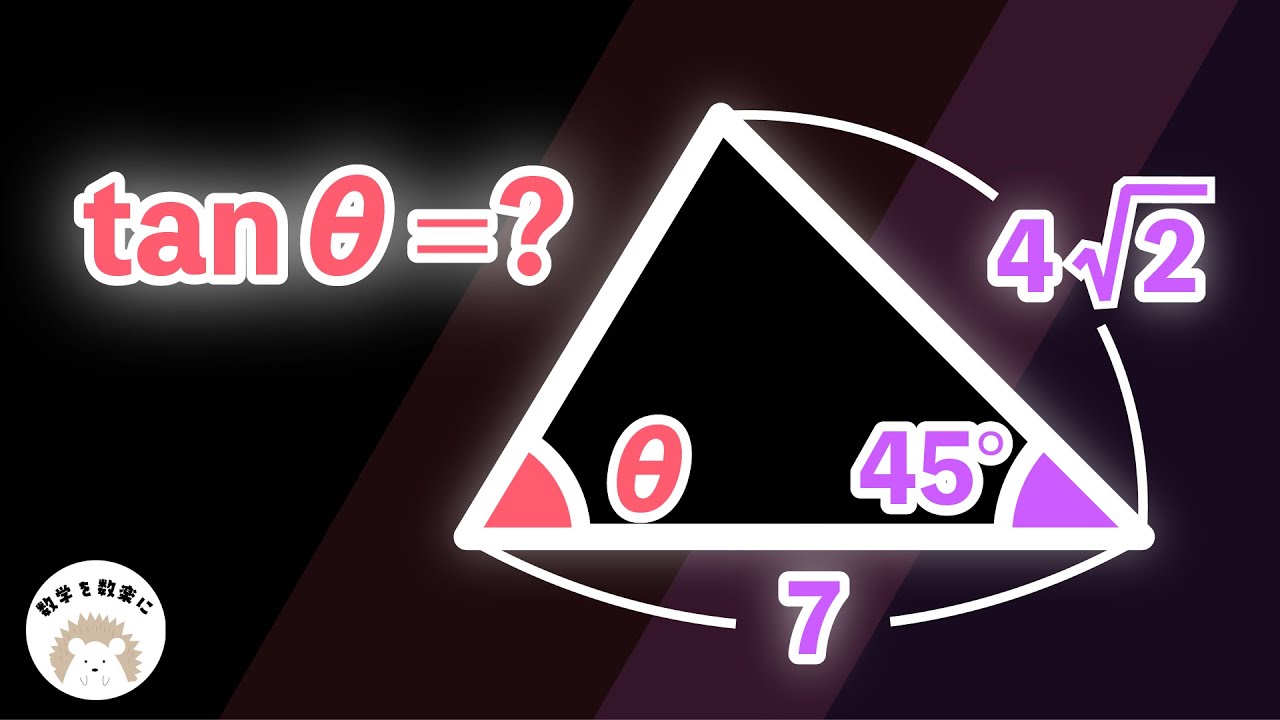
tanθ=?
*図は動画内参照
この動画を見る
tanθ=?
*図は動画内参照
整数問題 昭和学院秀英

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{n^2+2n-1}$の値が整数となるような整数nの値をすべて求めよ。
昭和学院秀英高等学校
この動画を見る
$\frac{1}{n^2+2n-1}$の値が整数となるような整数nの値をすべて求めよ。
昭和学院秀英高等学校
因数分解せよ 昭和学院秀英

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x^3y^3+18-9xy-2x^2y^2$
昭和学院秀英高等学校
この動画を見る
因数分解せよ
$x^3y^3+18-9xy-2x^2y^2$
昭和学院秀英高等学校
実は気付けば一瞬!! √と確率 立命館宇治

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2つのサイコロA,Bを同時に投げ、出た目の数をそれぞれa,bとする。
$a+b=2 \sqrt {ab}$となる確率を求めよ。
立命館宇治高等学校
この動画を見る
2つのサイコロA,Bを同時に投げ、出た目の数をそれぞれa,bとする。
$a+b=2 \sqrt {ab}$となる確率を求めよ。
立命館宇治高等学校
気付けば一瞬!だけど言いたいことを全て言った
面積比の利用 灘高校
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
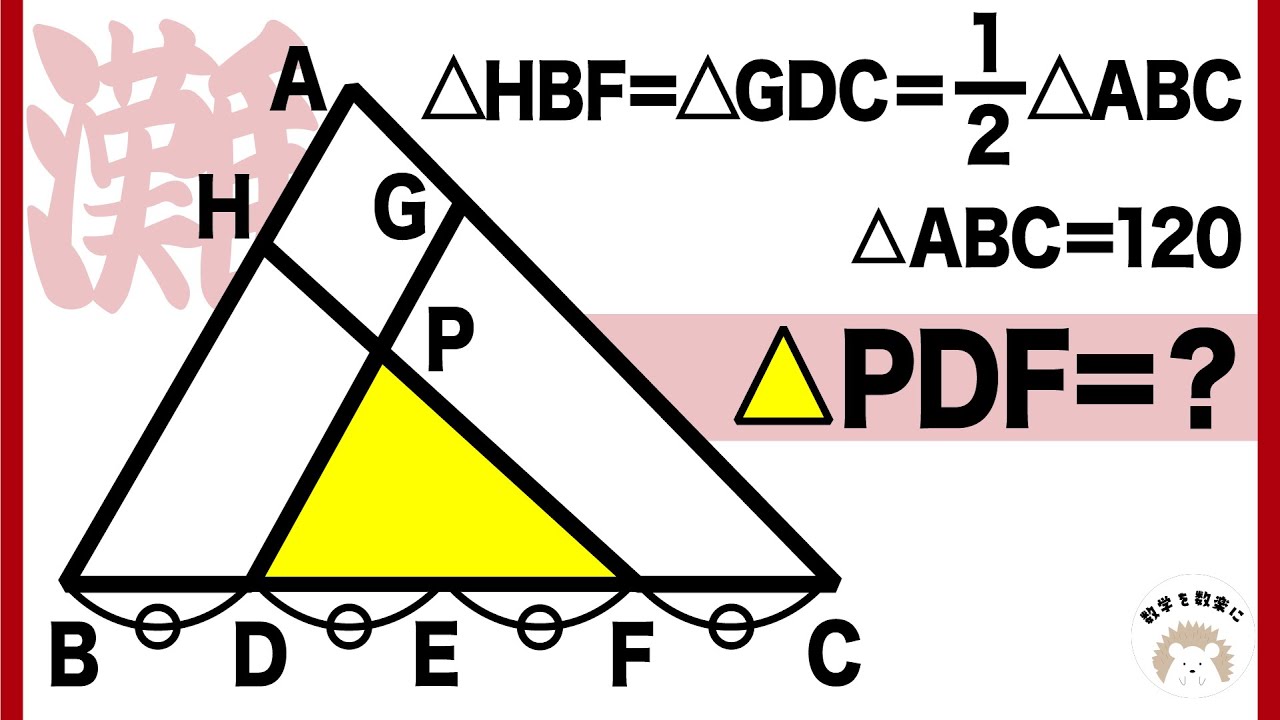
$△HBF=△GDC=\frac{1}{2}△ABC$
$△ABC=120$
$△PDF=?$
*図は動画内参照
この動画を見る
$△HBF=△GDC=\frac{1}{2}△ABC$
$△ABC=120$
$△PDF=?$
*図は動画内参照
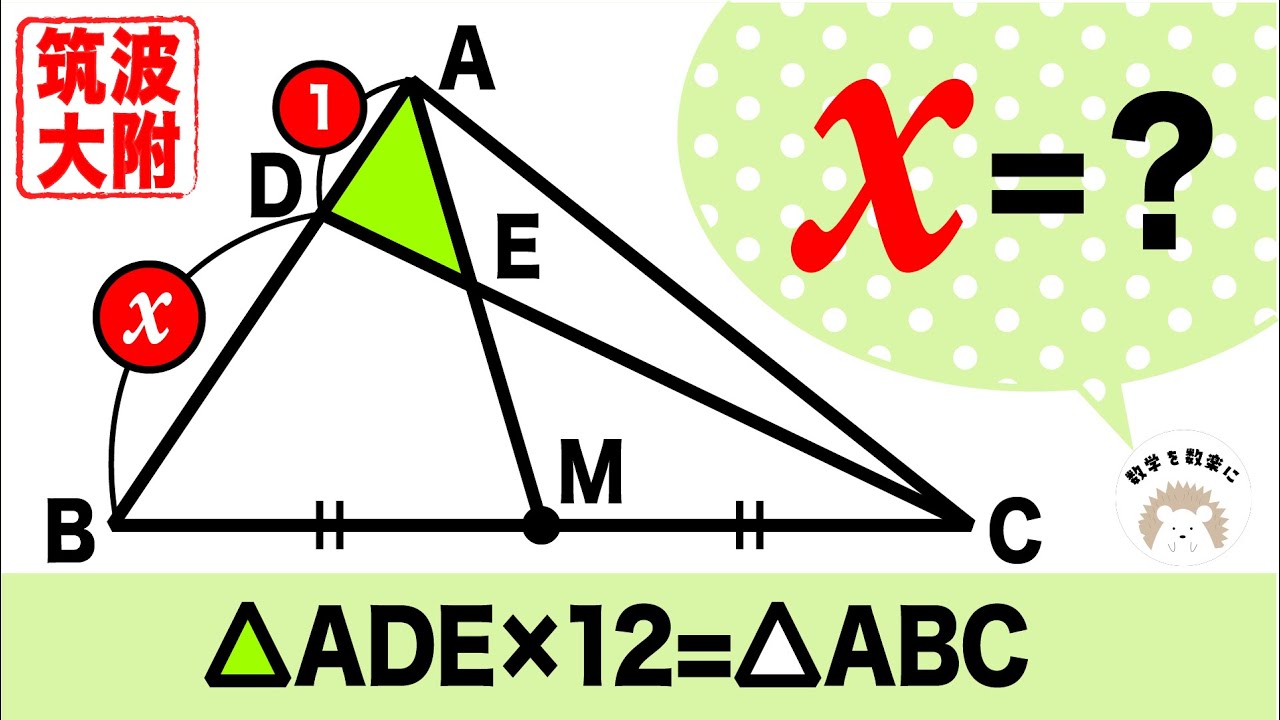
解き方いろいろ 面積比 筑波大附属 訂正はコメント欄に
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$△ADE×12=△ABC$
$x=?$
筑波大学付属高等学校
この動画を見る
$△ADE×12=△ABC$
$x=?$
筑波大学付属高等学校
パズル!!高槻中

単元:
#数A#整数の性質#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
たて、よこ、ななめ3つの数の積は等しいア~カを0でない整数とするとき、オの値を求めよ。
*図は動画内参照
高槻中学校
この動画を見る
たて、よこ、ななめ3つの数の積は等しいア~カを0でない整数とするとき、オの値を求めよ。
*図は動画内参照
高槻中学校
なかなかの難問 江戸川学園取手

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
3辺の長さが$a , 2a , a^2$の直角三角形がある。
この三角形の面積を求めよ。
(1 < a < 2)
江戸川学園取手高等学校
この動画を見る
3辺の長さが$a , 2a , a^2$の直角三角形がある。
この三角形の面積を求めよ。
(1 < a < 2)
江戸川学園取手高等学校
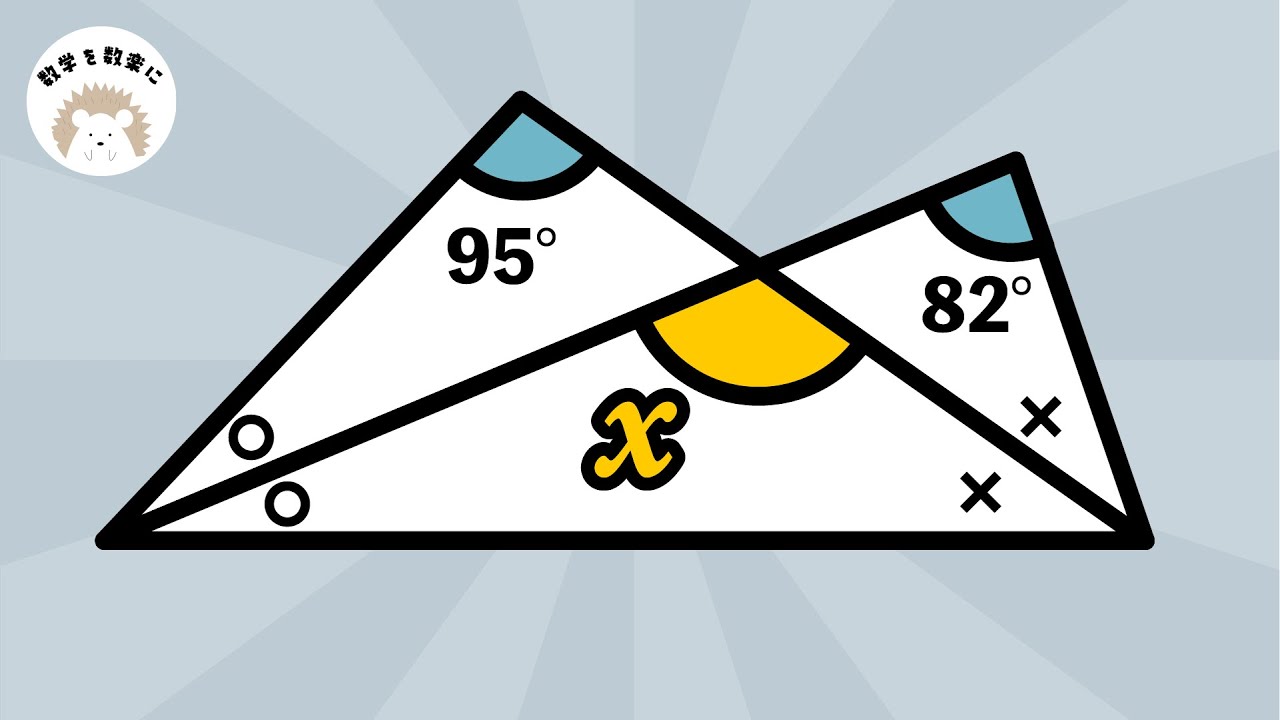
気付けば気持ちいい!角を求めよ
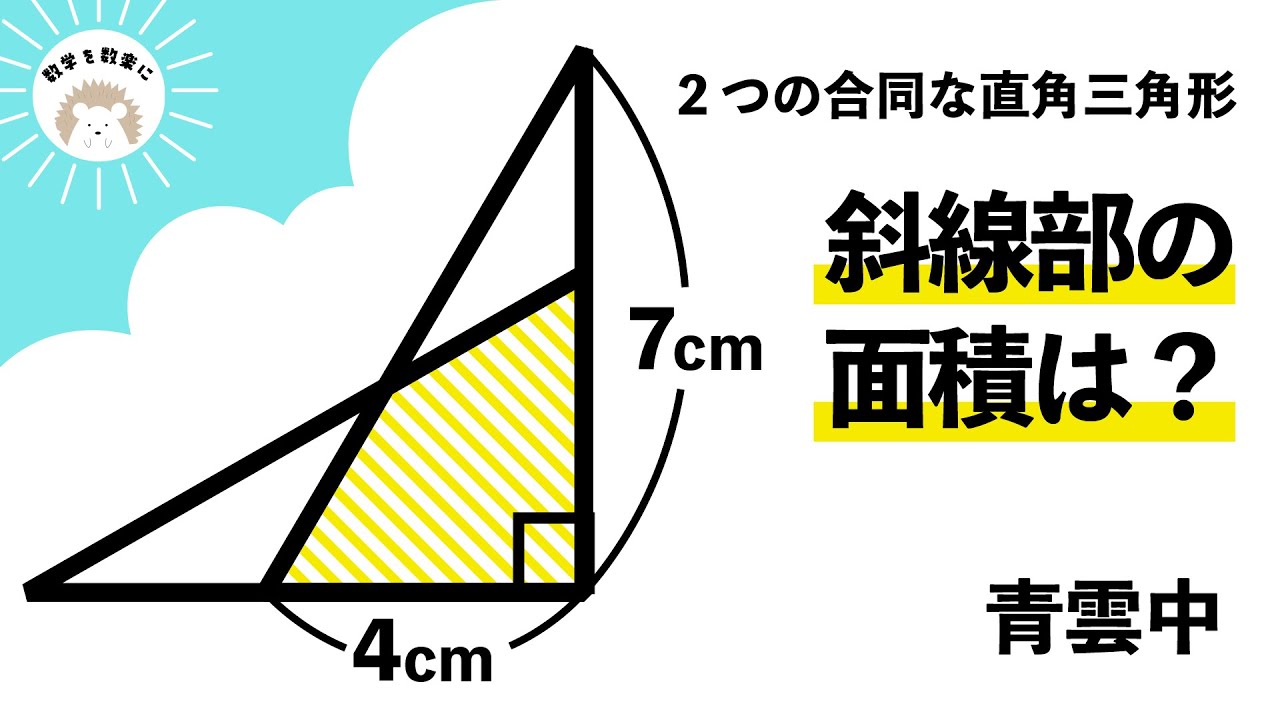
2つの合同な直角三角形 斜線部の面積=❓ 青雲中
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△BDA $\equiv$ △CFA
四角形EFDAの面積は?
*図は動画内参照
青雲中学校
この動画を見る
△BDA $\equiv$ △CFA
四角形EFDAの面積は?
*図は動画内参照
青雲中学校
一度は間違えたことある方程式

指数の方程式
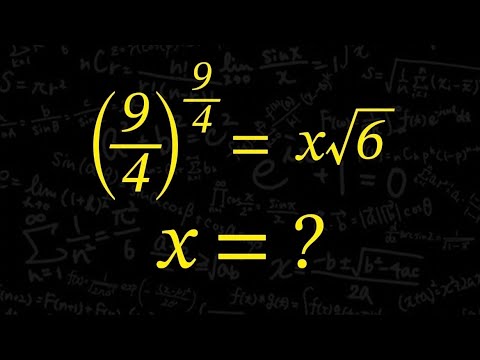
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\frac{9}{4})^{\frac{9}{4}}=x \sqrt 6$
$x=?$
この動画を見る
$(\frac{9}{4})^{\frac{9}{4}}=x \sqrt 6$
$x=?$
気付けば気持ちいい!!連立方程式 慶應義塾

単元:
#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
3x + 2y = 6 \\
6xy = 5
\end{array}
\right.
\end{eqnarray}
慶應義塾高等学校
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
3x + 2y = 6 \\
6xy = 5
\end{array}
\right.
\end{eqnarray}
慶應義塾高等学校
まさかそのまま代入しないよね?因数分解はできないよ。式の値 早稲田実業

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=1+\sqrt 2 + \sqrt 3$のとき
$x^2-2x-4=?$
早稲田実業学校
この動画を見る
$x=1+\sqrt 2 + \sqrt 3$のとき
$x^2-2x-4=?$
早稲田実業学校
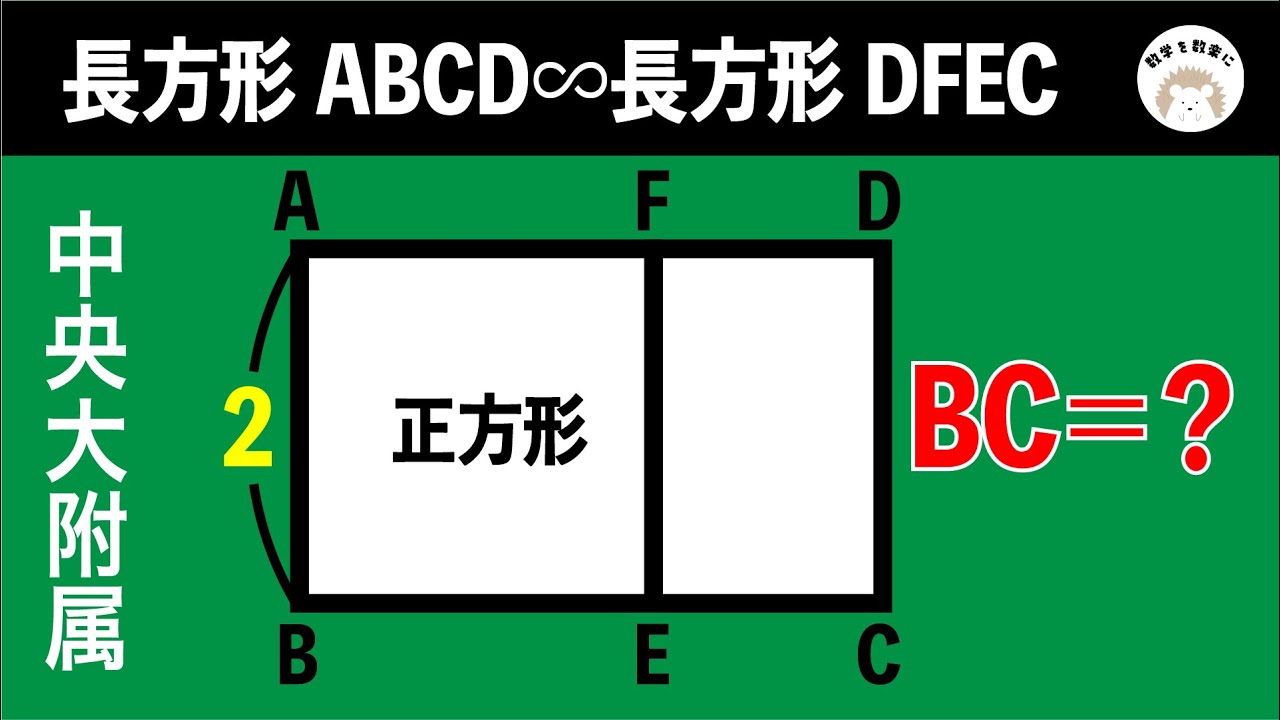
長方形の相似 中央大学附属
560=⭕️✖️⭕️✖️⭕️✖️⭕️ 沖縄尚学

単元:
#数A#整数の性質#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1けたの自然数を4つかけると560になった。
4つの自然数がすべて異なる自然数であるとき、かけた4つの数を求めよ。
沖縄尚学高等学校
この動画を見る
1けたの自然数を4つかけると560になった。
4つの自然数がすべて異なる自然数であるとき、かけた4つの数を求めよ。
沖縄尚学高等学校
長方形の面積=❓ 高校受験
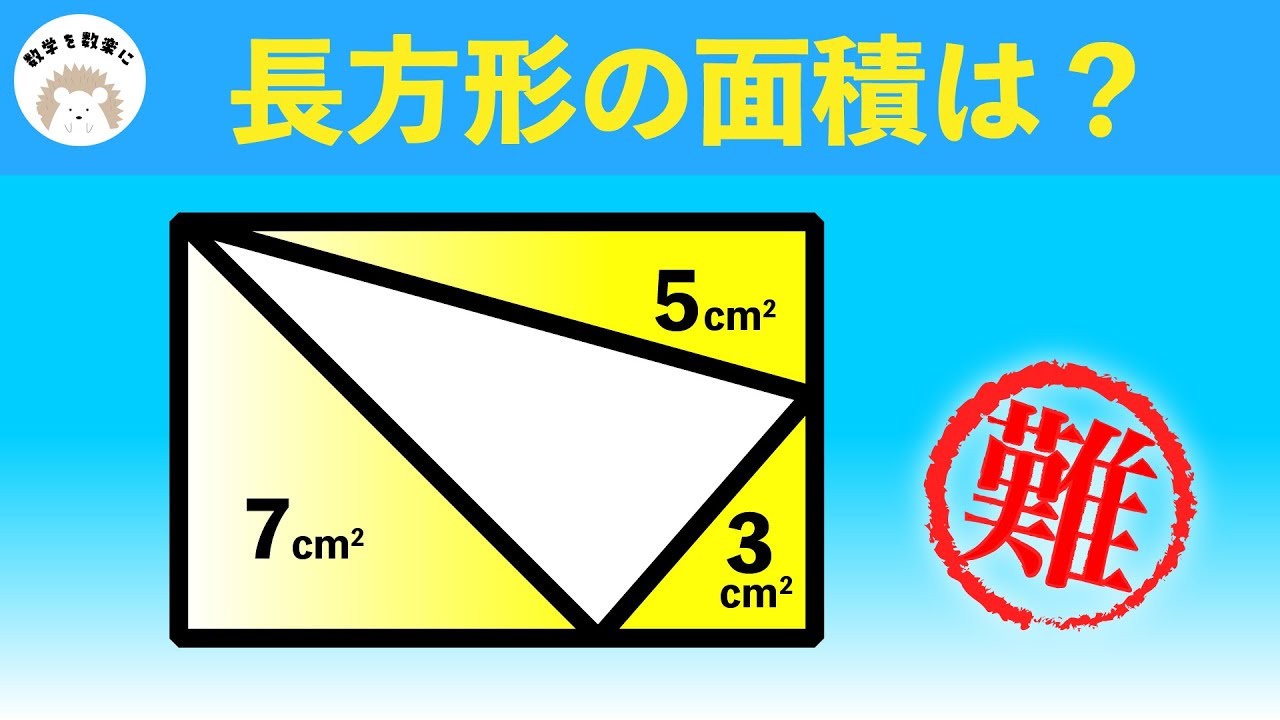
面積と角度