 鈴木貫太郎
鈴木貫太郎
 鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
2021東大 円と3次関数の共有点

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$y=ax^3-2x$と原点が中心で半径$1$の円と$6$つの共有点をもつ$a$の範囲を求めよ.$(a\gt 0)$
2021東大過去問
この動画を見る
$y=ax^3-2x$と原点が中心で半径$1$の円と$6$つの共有点をもつ$a$の範囲を求めよ.$(a\gt 0)$
2021東大過去問
平方根の問題 中学レベル

単元:
#数学(中学生)#中3数学#平方根
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n$を整数とする.
$\sqrt m+\sqrt n=\sqrt{50}$である.
$(m,n)$をすべて求めよ.
この動画を見る
$m,n$を整数とする.
$\sqrt m+\sqrt n=\sqrt{50}$である.
$(m,n)$をすべて求めよ.
ただの3次方程式 複数の解法で

金沢大 指数関数の最大値

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=8^x-4^{x+\frac{1}{2}}+2^x+\dfrac{23}{27}$
$-2\leqq x\leqq a(a\gt -2)$における$f(x)$の最大値が$1$となる$a$の範囲を求めよ.
2020金沢大過去問
この動画を見る
$f(x)=8^x-4^{x+\frac{1}{2}}+2^x+\dfrac{23}{27}$
$-2\leqq x\leqq a(a\gt -2)$における$f(x)$の最大値が$1$となる$a$の範囲を求めよ.
2020金沢大過去問
0.2秒で答えが出る⁉️半円の面積の和

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
大円の半径を1とする.
2つの半円の面積の和を求めよ.
この動画を見る
大円の半径を1とする.
2つの半円の面積の和を求めよ.
岩手大 漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n=1,2,3・・・・$
$a_1=31$
$a_{n+1}=\dfrac{(n+3)a_n-28}{n+2}$
一般項を求めよ.
2020岩手大過去問
この動画を見る
$n=1,2,3・・・・$
$a_1=31$
$a_{n+1}=\dfrac{(n+3)a_n-28}{n+2}$
一般項を求めよ.
2020岩手大過去問
大阪市立大 奇数の和 奇数の平方の和

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)#大阪市立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は3以上の奇数である.
$S_n=1+3+5+・・・・+n$
$T_n=1^2+3^2+5^2+・・・・n^2$
①$S_n$は$n$で割り切れないことを示せ.
②$T_n$が$n$で割り切れるための$n$の条件を求めよ.
2021大阪市立大過去問
この動画を見る
$n$は3以上の奇数である.
$S_n=1+3+5+・・・・+n$
$T_n=1^2+3^2+5^2+・・・・n^2$
①$S_n$は$n$で割り切れないことを示せ.
②$T_n$が$n$で割り切れるための$n$の条件を求めよ.
2021大阪市立大過去問
兵庫医大 普通の基本問題 指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$4^x-2^{x+2}+a^2-3a+4=0$が異なる2つの正の解をもつ$a$の範囲を求めよ.
2019兵庫医大過去問
この動画を見る
$4^x-2^{x+2}+a^2-3a+4=0$が異なる2つの正の解をもつ$a$の範囲を求めよ.
2019兵庫医大過去問
どっちがでかい?

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$2^{3^{100}}$ VS $3^{2^{150}}$
この動画を見る
どちらが大きいか?
$2^{3^{100}}$ VS $3^{2^{150}}$
産業医科大 cos sin 和の値

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\cos\dfrac{2}{7}\pi+\cos\dfrac{4}{7}\pi+\cos\dfrac{8}{7}\pi=\Box$
$\sin\dfrac{2}{7}\pi+\sin\dfrac{4}{7}\pi+\sin\dfrac{8}{7}\pi=\Box$
2019産業医大過去問
この動画を見る
これを解け.
$\cos\dfrac{2}{7}\pi+\cos\dfrac{4}{7}\pi+\cos\dfrac{8}{7}\pi=\Box$
$\sin\dfrac{2}{7}\pi+\sin\dfrac{4}{7}\pi+\sin\dfrac{8}{7}\pi=\Box$
2019産業医大過去問
指数方程式を解け
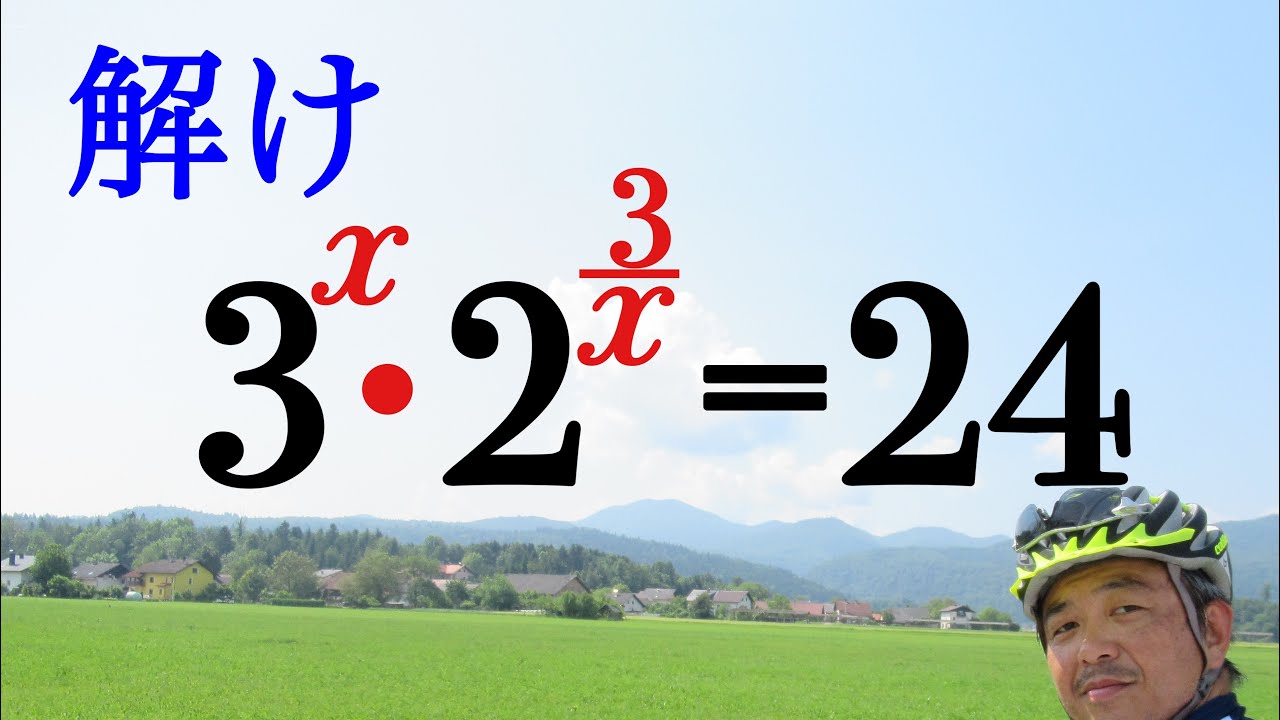
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$3^x・2^{\frac{3}{x}}=24$
この動画を見る
これを解け.
$3^x・2^{\frac{3}{x}}=24$
ただの因数分解 愛知医科大

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
因数分解せよ.
$a^4+2a^3+3a^2+2a+1$
簡単に
$\sqrt{\dfrac{x^4+y^4+(x+y)^4}{2}}$
2019愛知医科大過去問
この動画を見る
因数分解せよ.
$a^4+2a^3+3a^2+2a+1$
簡単に
$\sqrt{\dfrac{x^4+y^4+(x+y)^4}{2}}$
2019愛知医科大過去問
血液型ガチャ 愛知医科大

単元:
#確率分布と統計的な推測#確率分布#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
血液型$AB$の割合を$10$%とする.
$\Box$人以上集めればその中に少なくとも1人以上$AB$型がいる確率が$99$%以上となる.
$\Box$を求めよ.
この動画を見る
血液型$AB$の割合を$10$%とする.
$\Box$人以上集めればその中に少なくとも1人以上$AB$型がいる確率が$99$%以上となる.
$\Box$を求めよ.
東海大(医)バーゼル問題を導く

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
①$(\sqrt x+i)^7$の虚部は?
②$(\sqrt x+i)^7$が実数になる$x$を求めよ.
③②を満たす$x$の和を求めよ.
④$(\sqrt x+i)^{2n+1}$の虚部の$x$の$n$次と$(n-1)$次の係数を求めよ.
⑤$\displaystyle \sum_{k-1}^n \dfrac{1}{\tan^2\dfrac{k}{2n+1}\pi}$
⑥$0\lt \theta \lt \dfrac{\pi}{2}$なら$\sin\theta \lt \theta \lt \tan\theta$
$ \dfrac{1}{\tan^2\theta}\lt \dfrac{1}{\theta^2}\lt \dfrac{1}{\sin^2\theta}$である.
⑦$\displaystyle \sum_{k-1}^{\infty}\dfrac{1}{k^2}$を求めよ.
2018東海大(医)過去問
この動画を見る
①$(\sqrt x+i)^7$の虚部は?
②$(\sqrt x+i)^7$が実数になる$x$を求めよ.
③②を満たす$x$の和を求めよ.
④$(\sqrt x+i)^{2n+1}$の虚部の$x$の$n$次と$(n-1)$次の係数を求めよ.
⑤$\displaystyle \sum_{k-1}^n \dfrac{1}{\tan^2\dfrac{k}{2n+1}\pi}$
⑥$0\lt \theta \lt \dfrac{\pi}{2}$なら$\sin\theta \lt \theta \lt \tan\theta$
$ \dfrac{1}{\tan^2\theta}\lt \dfrac{1}{\theta^2}\lt \dfrac{1}{\sin^2\theta}$である.
⑦$\displaystyle \sum_{k-1}^{\infty}\dfrac{1}{k^2}$を求めよ.
2018東海大(医)過去問
コメント欄はありがたい。本当に2秒で答えが出た

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{1}{\tan\dfrac{\pi}{24}}$の値を求めよ.
2019横浜市立(医)過去問
この動画を見る
$\dfrac{1}{\tan\dfrac{\pi}{24}}$の値を求めよ.
2019横浜市立(医)過去問
横浜市立(医)tanの半角

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{1}{\tan\dfrac{\pi}{24}}$の値を求めよ.
2019横浜市立(医)過去問
この動画を見る
$\dfrac{1}{\tan\dfrac{\pi}{24}}$の値を求めよ.
2019横浜市立(医)過去問
横浜市立(医)ド・モアブルと7倍角

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)ド・モアブルの定理を用いて$\sin7\theta$を$\sin\theta,\cos\theta$およびその累乗を用いて表せ.
(2)$7x^3-35x^2+21x-1=0$を解け.
(3)$\dfrac{1}{\tan^2\dfrac{\pi}{7}}+\dfrac{1}{\tan^2\dfrac{2\pi}{7}}+\dfrac{1}{\tan^2\dfrac{3\pi}{7}}$の値を求めよ.
2016横浜市立(医)
この動画を見る
(1)ド・モアブルの定理を用いて$\sin7\theta$を$\sin\theta,\cos\theta$およびその累乗を用いて表せ.
(2)$7x^3-35x^2+21x-1=0$を解け.
(3)$\dfrac{1}{\tan^2\dfrac{\pi}{7}}+\dfrac{1}{\tan^2\dfrac{2\pi}{7}}+\dfrac{1}{\tan^2\dfrac{3\pi}{7}}$の値を求めよ.
2016横浜市立(医)
新高1生へ 失敗しないたすきがけ因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
因数分解せよ.
$48x^2+5x-18$
$(ax+b)(cx+d)$
この動画を見る
因数分解せよ.
$48x^2+5x-18$
$(ax+b)(cx+d)$
北海道大 微分積分

単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^4+6x^3-24x^2$の変曲点を$P(\alpha,f(\alpha)),Q(\beta,f(\beta))とする.(\alpha \gt \beta)$
$f(x)$の$P$における接線と$f(x)$で囲まれる面積を求めよ.
2021北海道大過去問
この動画を見る
$f(x)=x^4+6x^3-24x^2$の変曲点を$P(\alpha,f(\alpha)),Q(\beta,f(\beta))とする.(\alpha \gt \beta)$
$f(x)$の$P$における接線と$f(x)$で囲まれる面積を求めよ.
2021北海道大過去問
札幌医科大2021 三角関数 複数解法

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\triangle ABC$で$\sin C=2\cos A\sin B$である.
$\triangle ABC$の形を求めよ.
2021札幌医大過去問
この動画を見る
$\triangle ABC$で$\sin C=2\cos A\sin B$である.
$\triangle ABC$の形を求めよ.
2021札幌医大過去問
札幌医科大学2021 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$n$に対し$N=(n+2)^3-n(n+1)(n+2)$が$36$の倍数になるような$n$をすべて求めよ.
2021札幌医大過去問
この動画を見る
自然数$n$に対し$N=(n+2)^3-n(n+1)(n+2)$が$36$の倍数になるような$n$をすべて求めよ.
2021札幌医大過去問
旭川医科大2021 確率漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
コイン2枚 表表+2,表裏+1,裏裏0であり,0からスタートする.
$n$回の合計が
(1)$a_1,b_1,c_1,a_2,b_2,c_2$のとき,求めよ.
(2)$a_{n+1},b_{n+1},c_{n+1}$を,$a_n,b_n,c_n$で求めよ.
(3)$x_{n+1}=\dfrac{1}{4}x_n;\dfrac{1}{4}$を$x_1$を用いて表せ.
(4)$a_n$を求めよ.
2021旭川医大過去問
この動画を見る
コイン2枚 表表+2,表裏+1,裏裏0であり,0からスタートする.
$n$回の合計が
(1)$a_1,b_1,c_1,a_2,b_2,c_2$のとき,求めよ.
(2)$a_{n+1},b_{n+1},c_{n+1}$を,$a_n,b_n,c_n$で求めよ.
(3)$x_{n+1}=\dfrac{1}{4}x_n;\dfrac{1}{4}$を$x_1$を用いて表せ.
(4)$a_n$を求めよ.
2021旭川医大過去問
指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$3^{x^2-2\sqrt5 x}=\dfrac{1}{121}$
この動画を見る
実数解を求めよ.
$3^{x^2-2\sqrt5 x}=\dfrac{1}{121}$
Σと合同式OnlineMathContest

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$1\leqq S,t\leqq 2020$であり,$S$は整数,$t$は奇数である.
$\displaystyle \sum_{k=1}^S k^t$が$S$の倍数となる$(s,t)$の組数を求めよ.
この動画を見る
$1\leqq S,t\leqq 2020$であり,$S$は整数,$t$は奇数である.
$\displaystyle \sum_{k=1}^S k^t$が$S$の倍数となる$(s,t)$の組数を求めよ.
コメント欄はありがたい 素晴らしい別解

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$p,q,r$は自然数である.
$\dfrac{10!}{p!q!r!}$の総和を求めよ.
この動画を見る
$p,q,r$は自然数である.
$\dfrac{10!}{p!q!r!}$の総和を求めよ.
コメント欄はありがたい 素晴らしい別解

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$p,q,r$は自然数であり,$p+q+r=10$である.
$\dfrac{10!}{p!q!r!}$の総和を求めよ.
この動画を見る
$p,q,r$は自然数であり,$p+q+r=10$である.
$\dfrac{10!}{p!q!r!}$の総和を求めよ.
多項定理の応用OnlineMathContest

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$p,q,r$は自然数であり,$p+q+r=10$である.
$\dfrac{10!}{p!q!r!}$の総和を求めよ.
この動画を見る
$p,q,r$は自然数であり,$p+q+r=10$である.
$\dfrac{10!}{p!q!r!}$の総和を求めよ.
方程式 整数解OnlineMathContest

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2-2(m-480)x+4m+97=0$が正整数解のみをもつ整数$m$を求めよ.
この動画を見る
$x^2-2(m-480)x+4m+97=0$が正整数解のみをもつ整数$m$を求めよ.
神様の確率OnlineMathContest

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
白$999$個赤$1001$個のボールを無作為に1個ずつ取り出し,どちらかの色がすべて取り出されたら終了,白が取り出されて終わる確率を求めよ.
この動画を見る
白$999$個赤$1001$個のボールを無作為に1個ずつ取り出し,どちらかの色がすべて取り出されたら終了,白が取り出されて終わる確率を求めよ.
藤田医科大 複素数の計算

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2-x+1=0$
$12x^{2026}+23x^{2025}+34x^{2024}+45x^{2023}+$
$56x^{2022}+67^{2021}$の値を求めよ.
2021藤田医科大過去問
この動画を見る
$x^2-x+1=0$
$12x^{2026}+23x^{2025}+34x^{2024}+45x^{2023}+$
$56x^{2022}+67^{2021}$の値を求めよ.
2021藤田医科大過去問



