北海道大学
北海道大学
福田の1.5倍速演習〜合格する重要問題081〜北海道大学2018年度文系第３問〜確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ 赤色、青色、黄色のサイコロが1つずつある。この3つのサイコロを同時に投げる。赤色、青色、黄色のサイコロの出た目の数をそれぞれR,B,Yとし、自然数s,t,uをs=100R+10B+Y, t=100B+10Y+R, u=100Y+10R+B で定める。
(1)s,t,uのうち少なくとも2つが500以上となる確率を求めよ。
(2)s＞t＞uとなる確率を求めよ。
2018北海道大学文系過去問
この動画を見る
$\Large\boxed{3}$ 赤色、青色、黄色のサイコロが1つずつある。この3つのサイコロを同時に投げる。赤色、青色、黄色のサイコロの出た目の数をそれぞれR,B,Yとし、自然数s,t,uをs=100R+10B+Y, t=100B+10Y+R, u=100Y+10R+B で定める。
(1)s,t,uのうち少なくとも2つが500以上となる確率を求めよ。
(2)s＞t＞uとなる確率を求めよ。
2018北海道大学文系過去問
福田の1.5倍速演習〜合格する重要問題044〜北海道大学2017年度理系第1問〜不等式の証明と整数問題
単元：
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#一次不等式（不等式・絶対値のある方程式・不等式）#整数の性質#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
自然数の2乗となる数を平方数という。
(1)自然数a,n,kに対して、
$n(n+1)+a=(n+k)^2$が成り立つとき、
$a \geqq k^2+2k-1$
が成り立つことを示せ。
(2)$n(n+1)+14$が平方数となるような自然数nを全て求めよ。
2017北海道大学理系過去問
この動画を見る
自然数の2乗となる数を平方数という。
(1)自然数a,n,kに対して、
$n(n+1)+a=(n+k)^2$が成り立つとき、
$a \geqq k^2+2k-1$
が成り立つことを示せ。
(2)$n(n+1)+14$が平方数となるような自然数nを全て求めよ。
2017北海道大学理系過去問
福田の1.5倍速演習〜合格する重要問題043〜北海道大学2017年度文系第３問〜確率漸化式の定番問題
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数B
指導講師：
福田次郎
問題文全文(内容文)：
正四面体ABCDの頂点を移動する点Pがある。点Pは、1秒ごとに、
隣の3頂点のいずれかに等しい確率$\frac{a}{3}$で移るか、もとの頂点に確率1-aで
留まる。初め頂点Aにいた点Pが、n秒後に頂点Aにいる確率を$p_n$とする。
ただし、$0 \lt a \lt 1$とし、nは自然数とする。
(1)数列$\left\{p_n\right\}$の漸化式を求めよ。
(2)確率$p_n$を求めよ。
2017北海道大学文系過去問
この動画を見る
正四面体ABCDの頂点を移動する点Pがある。点Pは、1秒ごとに、
隣の3頂点のいずれかに等しい確率$\frac{a}{3}$で移るか、もとの頂点に確率1-aで
留まる。初め頂点Aにいた点Pが、n秒後に頂点Aにいる確率を$p_n$とする。
ただし、$0 \lt a \lt 1$とし、nは自然数とする。
(1)数列$\left\{p_n\right\}$の漸化式を求めよ。
(2)確率$p_n$を求めよ。
2017北海道大学文系過去問
福田の1.5倍速演習〜合格する重要問題003〜北海道大学2015年文系数学第４問〜隣り合う順列、隣り合わない順列
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
ジョーカーを除く1組52枚のトランプのカードを1列に並べる思考を考える。
(1)番号7のカードが4枚連続して並ぶ確率を求めよ。
(2)番号7のカードが2枚ずつ隣り合い、4枚連続しては並ばない確率を求めよ。
8人の人が一列に並ぶとき、
(1)A,B,Cの3人が連続して並ぶ場合の数を求めよ。
(2)A,B,Cの3人が隣りあわないように並ぶ場合の数を求めよ。
2015北海道大学文系過去問
この動画を見る
ジョーカーを除く1組52枚のトランプのカードを1列に並べる思考を考える。
(1)番号7のカードが4枚連続して並ぶ確率を求めよ。
(2)番号7のカードが2枚ずつ隣り合い、4枚連続しては並ばない確率を求めよ。
8人の人が一列に並ぶとき、
(1)A,B,Cの3人が連続して並ぶ場合の数を求めよ。
(2)A,B,Cの3人が隣りあわないように並ぶ場合の数を求めよ。
2015北海道大学文系過去問
確率×整数問題！さいころの目の最小公倍数や最大公約数【数学 入試問題】【北海道大学】
単元：
#数Ⅰ#数A#場合の数と確率#場合の数#確率#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$n$を2以上の自然数とする。1個のさいころを続けて$n$回投げる試行を行い,出た目を順に$X_1,X_2,･･･,X_n$とする。
(1)$X_1,X_2,･･･,X_n$の最大公約数が3となる確率を$n$の式で表せ。
北海道大過去問
この動画を見る
$n$を2以上の自然数とする。1個のさいころを続けて$n$回投げる試行を行い,出た目を順に$X_1,X_2,･･･,X_n$とする。
(1)$X_1,X_2,･･･,X_n$の最大公約数が3となる確率を$n$の式で表せ。
北海道大過去問
注意ポイントあり！定数分離の良問です【数学 入試問題】【北海道大学】
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
関数 $f(\theta)=\dfrac{1}{\sqrt 2}sin2 \theta-sin \theta+cos\theta$ ($0≦\theta≦\pi)$を考える。
(3)$a$を実数の定数とする。
$f(\theta)=a$となる$\theta$がちょうど2個であるような$a$のい範囲を求めよ。
北海道大過去問
この動画を見る
関数 $f(\theta)=\dfrac{1}{\sqrt 2}sin2 \theta-sin \theta+cos\theta$ ($0≦\theta≦\pi)$を考える。
(3)$a$を実数の定数とする。
$f(\theta)=a$となる$\theta$がちょうど2個であるような$a$のい範囲を求めよ。
北海道大過去問
北大の良問！解けますか？【数学 入試問題】【北海道大学】
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$k$を実数の定数とし、$f(x)=x^3-(2k-1)x^2+(k^2-k+1)x$
$-k+1$とする。
(1)$f(k-1)$の値を求めよ。
(2)$\vert k \vert <2$のとき、不等式$f(x)≧0$を解け。
北海道大過去問
この動画を見る
$k$を実数の定数とし、$f(x)=x^3-(2k-1)x^2+(k^2-k+1)x$
$-k+1$とする。
(1)$f(k-1)$の値を求めよ。
(2)$\vert k \vert <2$のとき、不等式$f(x)≧0$を解け。
北海道大過去問
【良問】整数問題の重要なポイントが詰まりまくった問題【数学 大学入試】
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
(1)整数$m$に対して、$m^2$を4で割った余りは0または1であることを示せ。
(2)自然数$n,k$が$25×3^n=k^2+176$･･････(①)を満たすとき、$n$は偶数であることを示せ。
(3)(2)の関係式(①)を満たす自然数の組($n,k$)をすべて求めよ。
数学入試問題過去問
この動画を見る
(1)整数$m$に対して、$m^2$を4で割った余りは0または1であることを示せ。
(2)自然数$n,k$が$25×3^n=k^2+176$･･････(①)を満たすとき、$n$は偶数であることを示せ。
(3)(2)の関係式(①)を満たす自然数の組($n,k$)をすべて求めよ。
数学入試問題過去問
福田の入試問題解説〜北海道大学2022年文系第４問〜復元抽出と非復元抽出の確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
箱の中に1文字ずつ書かれたカードが10枚ある。そのうち5枚にはA、
3枚にはB、2枚にはCと書かれている。箱から1枚ずつ、3回カードを
取り出す試行を考える。
(1)カードを取り出すごとに箱に戻す場合、1回目と3回目に取り出したカード
の文字が一致する確率を求めよ。
(2)取り出したカードを箱に戻さない場合、1回目と3回目に取り出したカード
の文字が一致する確率を求めよ。
(3)取り出したカードを箱に戻さない場合、2回目に取り出したカードの文字が
Cであるとき、1回目と3回目に取り出したカードの文字が一致する
条件つき確率を求めよ。
2022北海道大学文系過去問
この動画を見る
箱の中に1文字ずつ書かれたカードが10枚ある。そのうち5枚にはA、
3枚にはB、2枚にはCと書かれている。箱から1枚ずつ、3回カードを
取り出す試行を考える。
(1)カードを取り出すごとに箱に戻す場合、1回目と3回目に取り出したカード
の文字が一致する確率を求めよ。
(2)取り出したカードを箱に戻さない場合、1回目と3回目に取り出したカード
の文字が一致する確率を求めよ。
(3)取り出したカードを箱に戻さない場合、2回目に取り出したカードの文字が
Cであるとき、1回目と3回目に取り出したカードの文字が一致する
条件つき確率を求めよ。
2022北海道大学文系過去問
福田の入試問題解説〜北海道大学2022年文系第３問〜直角三角形と内接円
単元：
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
$\angle A=90°,\angle B=60°$である直角三角形ABCにおいて、
その内接円の中心をO、半径をrとおく。また$a=BC$とする。
(1)rをaで表せ。
(2)次の条件を満たす負でない整数k,l,m,nの組を一つ求めよ。
$OA:OB=1:k+\sqrt{l}, OA:OC=1:m+\sqrt{n}$
2022北海道大学文系過去問
この動画を見る
$\angle A=90°,\angle B=60°$である直角三角形ABCにおいて、
その内接円の中心をO、半径をrとおく。また$a=BC$とする。
(1)rをaで表せ。
(2)次の条件を満たす負でない整数k,l,m,nの組を一つ求めよ。
$OA:OB=1:k+\sqrt{l}, OA:OC=1:m+\sqrt{n}$
2022北海道大学文系過去問
福田の入試問題解説〜北海道大学2022年文系第２問〜数列の一般項の最小と部分和の最小
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\left\{a_n\right\}$を$a_1=-15$および
$a_{n+1}=a_n+\frac{n}{5}-2 (n=1,2,3,\ldots)$
を満たす数列とする。
(1)$a_n$が最小となる自然数nを全て求めよ。
(2)$\left\{a_n\right\}$の一般項を求めよ。
(3)$\sum_{k=1}^na_k$が最小となる自然数nを全て求めよ。
2022北海道大学文系過去問
この動画を見る
$\left\{a_n\right\}$を$a_1=-15$および
$a_{n+1}=a_n+\frac{n}{5}-2 (n=1,2,3,\ldots)$
を満たす数列とする。
(1)$a_n$が最小となる自然数nを全て求めよ。
(2)$\left\{a_n\right\}$の一般項を求めよ。
(3)$\sum_{k=1}^na_k$が最小となる自然数nを全て求めよ。
2022北海道大学文系過去問
福田の入試問題解説〜北海道大学2022年文系第１問〜剰余定理と高次不等式の解
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
kを実数の定数とし、
$f(x)=x^3-(2k-1)x^2+(k^2-k+1)x-k+1$
とする。
(1)$f(k-1)$の値を求めよ。
(2)$|k|\lt 2$のとき、不等式$f(x) \geqq 0$を解け。
2022北海道大学文系過去問
この動画を見る
kを実数の定数とし、
$f(x)=x^3-(2k-1)x^2+(k^2-k+1)x-k+1$
とする。
(1)$f(k-1)$の値を求めよ。
(2)$|k|\lt 2$のとき、不等式$f(x) \geqq 0$を解け。
2022北海道大学文系過去問
福田の入試問題解説〜北海道大学2022年理系第５問〜複素数平面上の点の軌跡とドモアブルの定理
単元：
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数C
指導講師：
福田次郎
問題文全文(内容文)：
複素数zに関する次の2つの方程式を考える。ただし、$\bar{ z }$はzと共役な複素数とし、
iを虚数単位とする。
$z\bar{ z }=4 \ldots\ldots$① $|z|=|z-\sqrt3+i| \ldots\ldots②$
(1)①、②それぞれの方程式について、その解z全体が表す図形を複素数平面上に
図示せよ。
(2)①、②の共通解となる複素数を全て求めよ。
(3)(2)で求めた全ての複素数の積をwとおく。このとき$w^n$が負の実数となる
ための整数nの必要十分条件を求めよ。
2022北海道大学理系過去問
この動画を見る
複素数zに関する次の2つの方程式を考える。ただし、$\bar{ z }$はzと共役な複素数とし、
iを虚数単位とする。
$z\bar{ z }=4 \ldots\ldots$① $|z|=|z-\sqrt3+i| \ldots\ldots②$
(1)①、②それぞれの方程式について、その解z全体が表す図形を複素数平面上に
図示せよ。
(2)①、②の共通解となる複素数を全て求めよ。
(3)(2)で求めた全ての複素数の積をwとおく。このとき$w^n$が負の実数となる
ための整数nの必要十分条件を求めよ。
2022北海道大学理系過去問
福田の入試問題解説〜北海道大学2022年理系第４問〜円順列と確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
アルファベットのAと書かれた玉が1個、Dと書かれた玉が1個、Hと書かれ
た玉が1個、Iと書かれた玉が1個、Kと書かれた玉が2個、Oと書かれた玉が
2個ある。これら8個の玉を円形に並べる。
(1) 時計回りにHOKKAIDOと並ぶ確率を求めよ。
(2) 隣り合う子音が存在する確率を求めよ。ここで子音とは、D, H, K の3文字
(玉は4個)のことである。
(3) 隣り合う子音が存在するとき、それがKKだけである条件つき確率を求めよ。
2022北海道大学理系過去問
この動画を見る
アルファベットのAと書かれた玉が1個、Dと書かれた玉が1個、Hと書かれ
た玉が1個、Iと書かれた玉が1個、Kと書かれた玉が2個、Oと書かれた玉が
2個ある。これら8個の玉を円形に並べる。
(1) 時計回りにHOKKAIDOと並ぶ確率を求めよ。
(2) 隣り合う子音が存在する確率を求めよ。ここで子音とは、D, H, K の3文字
(玉は4個)のことである。
(3) 隣り合う子音が存在するとき、それがKKだけである条件つき確率を求めよ。
2022北海道大学理系過去問
福田の入試問題解説〜北海道大学2022年理系第３問〜指数不等式の領域が表す面積の最小
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
以下の問いに答えよ。
(1)連立不等式$x \geqq 2, 2^x \leqq x^y \leqq x^2$の表す領域をxy平面上に図示せよ。
ただし、自然対数の底eが$2 \lt e \lt 3$を満たすことを用いてよい。
(2)$a \gt 0$に対して、連立不等式$2 \leqq x \leqq 6, (x^y-2^x)(x^a-x^y) \geqq 0$
の表すxy平面上の領域の面積をS(a)とする。
$S(a)$を最小にするaの値を求めよ。
2022北海道大学理系過去問
この動画を見る
以下の問いに答えよ。
(1)連立不等式$x \geqq 2, 2^x \leqq x^y \leqq x^2$の表す領域をxy平面上に図示せよ。
ただし、自然対数の底eが$2 \lt e \lt 3$を満たすことを用いてよい。
(2)$a \gt 0$に対して、連立不等式$2 \leqq x \leqq 6, (x^y-2^x)(x^a-x^y) \geqq 0$
の表すxy平面上の領域の面積をS(a)とする。
$S(a)$を最小にするaの値を求めよ。
2022北海道大学理系過去問
福田の入試問題解説〜北海道大学2022年理系第２問〜ベクトルと漸化式
単元：
#大学入試過去問(数学)#平面上のベクトル#数列#平面上のベクトルと内積#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数B#数C
指導講師：
福田次郎
問題文全文(内容文)：
aは$a\neq 1$を満たす正の実数とする。xy平面上の点$P_1,P_2,\ldots\ldots,P_n,\ldots\ldots$および
$Q_1,Q_2,\ldots\ldots,Q_n,\ldots\ldots$が、すべての自然数nについて
$\overrightarrow{ P_nP_{n+1} }=(1-a)\overrightarrow{ P_nQ_n }, \overrightarrow{ Q_nQ_{n+1} }=(0, \frac{a^{-n}}{1-a})$
を満たしているとする。また$P_n$の座標を$(x_n,y_n)$とする。
(1)$x_{n+2}$を$a, x_n, x_{n+1}$で表せ。
(2)$x_1=0, x_2=1$のとき、数列$\left\{x_n\right\}$の一般項を求めよ。
(3)$y_1=\frac{a}{(1-a)^2}, y_2-y_1=1$のとき数列$\left\{y_n\right\}$の一般項を求めよ。
2022北海道大学理系過去問
この動画を見る
aは$a\neq 1$を満たす正の実数とする。xy平面上の点$P_1,P_2,\ldots\ldots,P_n,\ldots\ldots$および
$Q_1,Q_2,\ldots\ldots,Q_n,\ldots\ldots$が、すべての自然数nについて
$\overrightarrow{ P_nP_{n+1} }=(1-a)\overrightarrow{ P_nQ_n }, \overrightarrow{ Q_nQ_{n+1} }=(0, \frac{a^{-n}}{1-a})$
を満たしているとする。また$P_n$の座標を$(x_n,y_n)$とする。
(1)$x_{n+2}$を$a, x_n, x_{n+1}$で表せ。
(2)$x_1=0, x_2=1$のとき、数列$\left\{x_n\right\}$の一般項を求めよ。
(3)$y_1=\frac{a}{(1-a)^2}, y_2-y_1=1$のとき数列$\left\{y_n\right\}$の一般項を求めよ。
2022北海道大学理系過去問
福田の入試問題解説〜北海道大学2022年理系第１問〜絶対値の付いた２次関数の最小値（難）
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#２次関数#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#2次関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
$0 \leqq a \leqq b \leqq 1$を満たすa,bに対し、関数
$f(x)=|x(x-1)|+|(x-a)(x-b)|$
を考える。xが実数の範囲を動くとき、$f(x)$は最小値mをもつとする。
(1)$x \lt 0$および$x \gt 1$では$f(x) \gt m$となることを示せ。
(2)$m=f(0)$または$m=f(1)$であることを示せ。
(3)$a,b$が$0 \leqq a \leqq b \leqq 1$を満たして動くとき、mの最大値を求めよ。
2022北海道大学理系過去問
この動画を見る
$0 \leqq a \leqq b \leqq 1$を満たすa,bに対し、関数
$f(x)=|x(x-1)|+|(x-a)(x-b)|$
を考える。xが実数の範囲を動くとき、$f(x)$は最小値mをもつとする。
(1)$x \lt 0$および$x \gt 1$では$f(x) \gt m$となることを示せ。
(2)$m=f(0)$または$m=f(1)$であることを示せ。
(3)$a,b$が$0 \leqq a \leqq b \leqq 1$を満たして動くとき、mの最大値を求めよ。
2022北海道大学理系過去問
2022北海道大
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数と方程式#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ f(x)=x^3-(2k-1)x^2+(k^2-k+1)x-$
$k+1 $
(1)$ f(k-1)$の値を求めよ.
(2)$ \vert k \vert \lt 2$のとき,不等式 $ f(n)\geqq 0$を解け.
2022北海道大過去問
この動画を見る
$ f(x)=x^3-(2k-1)x^2+(k^2-k+1)x-$
$k+1 $
(1)$ f(k-1)$の値を求めよ.
(2)$ \vert k \vert \lt 2$のとき,不等式 $ f(n)\geqq 0$を解け.
2022北海道大過去問
数学「大学入試良問集」【16−5 複素数平面と軌跡の図示】を宇宙一わかりやすく
単元：
#大学入試過去問(数学)#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数C
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
$z$を複素数とし、$i$を虚数単位とする。
（1）$\displaystyle \frac{1}{z+i}+\displaystyle \frac{1}{z-i}$が実数となる点$z$全体の描く図面$P$を複素数平面上にそれぞれ図示せよ。
（2）$z$が上で求められた図形$P$上を動くときに$\omega=\displaystyle \frac{z+i}{z-i}$の描く図形を複素数平面上に図示せよ。
この動画を見る
$z$を複素数とし、$i$を虚数単位とする。
（1）$\displaystyle \frac{1}{z+i}+\displaystyle \frac{1}{z-i}$が実数となる点$z$全体の描く図面$P$を複素数平面上にそれぞれ図示せよ。
（2）$z$が上で求められた図形$P$上を動くときに$\omega=\displaystyle \frac{z+i}{z-i}$の描く図形を複素数平面上に図示せよ。
練習問題45 北海道大学 微分と積分 教員採用試験 数検準1級
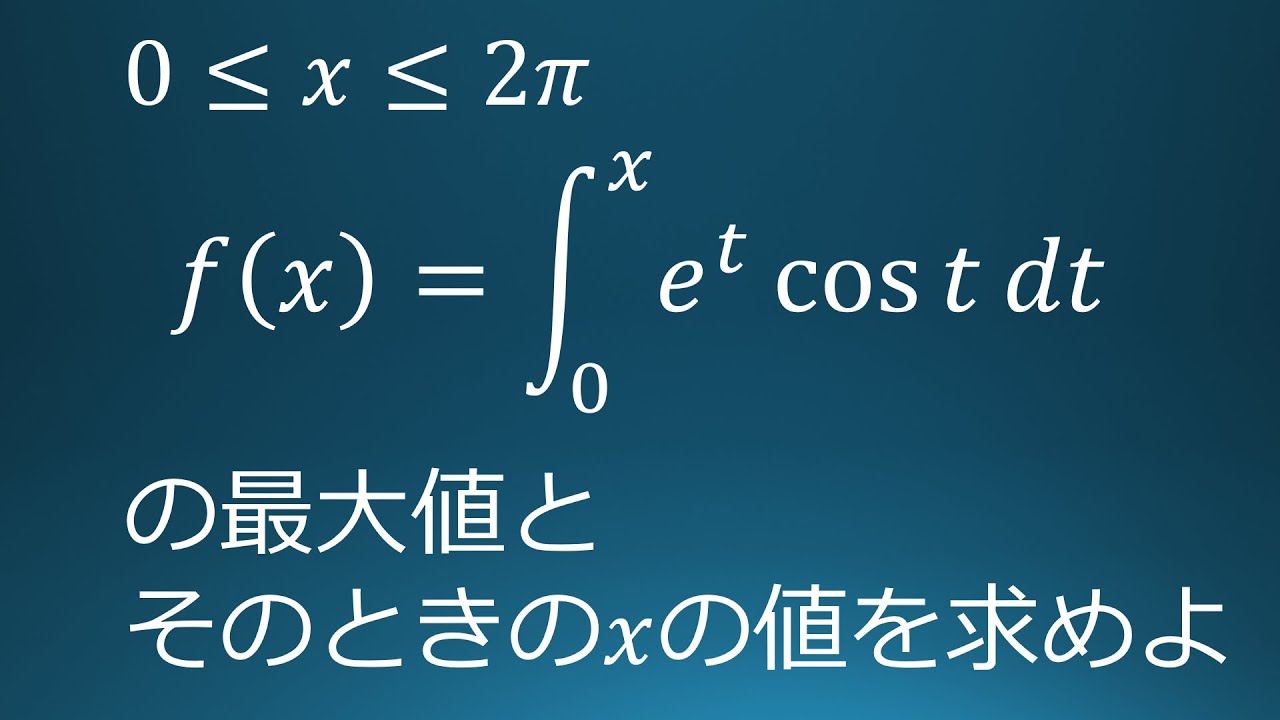
単元：
#大学入試過去問(数学)#数学検定・数学甲子園・数学オリンピック等#微分とその応用#積分とその応用#学校別大学入試過去問解説(数学)#その他#数学検定#数学検定準1級#数学(高校生)#北海道大学#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$0 \leqq x \leqq 2\pi$
関数
$f(x)=\displaystyle \int_{0}^{x}e^t\ cos\ t\ dt$の最大値とそのときの$x$の値を求めよ。
出典：北海道大学 教員採用試験
この動画を見る
$0 \leqq x \leqq 2\pi$
関数
$f(x)=\displaystyle \int_{0}^{x}e^t\ cos\ t\ dt$の最大値とそのときの$x$の値を求めよ。
出典：北海道大学 教員採用試験
有名だけど、意外と狙いやすい大学３選～お買い得な大学、ぶっちゃけます【篠原好】
単元：
#その他#京都大学#京都大学#京都大学#北海道大学#京都大学#青山学院大学#青山学院大学
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
お買い得な大学、ぶっちゃけます
「有名だけど、意外と狙いやすい大学３選」について紹介しています。
この動画を見る
お買い得な大学、ぶっちゃけます
「有名だけど、意外と狙いやすい大学３選」について紹介しています。
良問を出す大学５選～受けなくても、練習問題に最適な大学はコレだ！【篠原好】
単元：
#センター試験・共通テスト関連#共通テスト#共通テスト(現代文)#共通テスト・センター試験#共通テスト(古文)#共通テスト#大阪大学#防衛大学校#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#大阪大学#共通テスト#共通テスト#共通テスト#共通テスト#共通テスト#共通テスト#北海道大学#青山学院大学#青山学院大学
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
受けなくても、練習問題に最適な大学はコレだ！
「良問を出す大学５選」の紹介です。
この動画を見る
受けなくても、練習問題に最適な大学はコレだ！
「良問を出す大学５選」の紹介です。
北海道大 整数
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$n^2+n+14$が平方数となるような$n$(自然数)をすべて求めよ
出典：北海道大学 過去問
この動画を見る
$n^2+n+14$が平方数となるような$n$(自然数)をすべて求めよ
出典：北海道大学 過去問
北海道大 三次方程式 実数解条件
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$f(x)=x^3-3ax^2+bx+c$
一次関数$g(x)$
$f(x)=f'(x)g(x)-6x$を満たす
（1）
$b,c$を$a$で表せ
（2）
$f(x)=0$が相異なる3つの実数解をもつ$a$の範囲を求めよ
出典：2019年北海道大学 過去問
この動画を見る
$f(x)=x^3-3ax^2+bx+c$
一次関数$g(x)$
$f(x)=f'(x)g(x)-6x$を満たす
（1）
$b,c$を$a$で表せ
（2）
$f(x)=0$が相異なる3つの実数解をもつ$a$の範囲を求めよ
出典：2019年北海道大学 過去問
北海道大 双曲線と円の共有点 高校数学 Mathematics Japanese university entrance exam
単元：
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$y=\displaystyle \frac{1}{x}$と、$(a,a)$を中心として$(1,1)$を通る円とが$(1,1)$のみを共有するような$a$の範囲$.(a \neq 1)$
出典：北海道大学 過去問
この動画を見る
$y=\displaystyle \frac{1}{x}$と、$(a,a)$を中心として$(1,1)$を通る円とが$(1,1)$のみを共有するような$a$の範囲$.(a \neq 1)$
出典：北海道大学 過去問
北海道大 対数 不等式 高校数学 Mathematics Japanese university entrance exam
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
（1）
$f(t)=log_{2}t+log_{t}4$の最小値は？
（2）
$k$ $log_{2}t \lt (log_{2}t)^2-log_{2}t+2$が成り立つ$k$の範囲は？
出典：北海道大学 過去問
この動画を見る
（1）
$f(t)=log_{2}t+log_{t}4$の最小値は？
（2）
$k$ $log_{2}t \lt (log_{2}t)^2-log_{2}t+2$が成り立つ$k$の範囲は？
出典：北海道大学 過去問
福田の入試問題解説〜北海道大学2012年理系数学第４問〜２次関数と２次不等式、領域
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{4}}$ 実数$a,b$に対して、$f(x)=x^2-2ax+b,g(x)$$=x^2-2bx+a$ とおく。
(1)$a \ne b$のとき、$f(c)=g(c)$を満たす実数cを求めよ。
(2)(1)で求めた$c$について、$a,b$が条件$a \lt c \lt b$を満たすとする。このとき
連立不等式
$f(x) \lt 0$ かつ $g(x) \lt 0$
が解をもつための必要十分条件を$a,b$を用いて表せ。
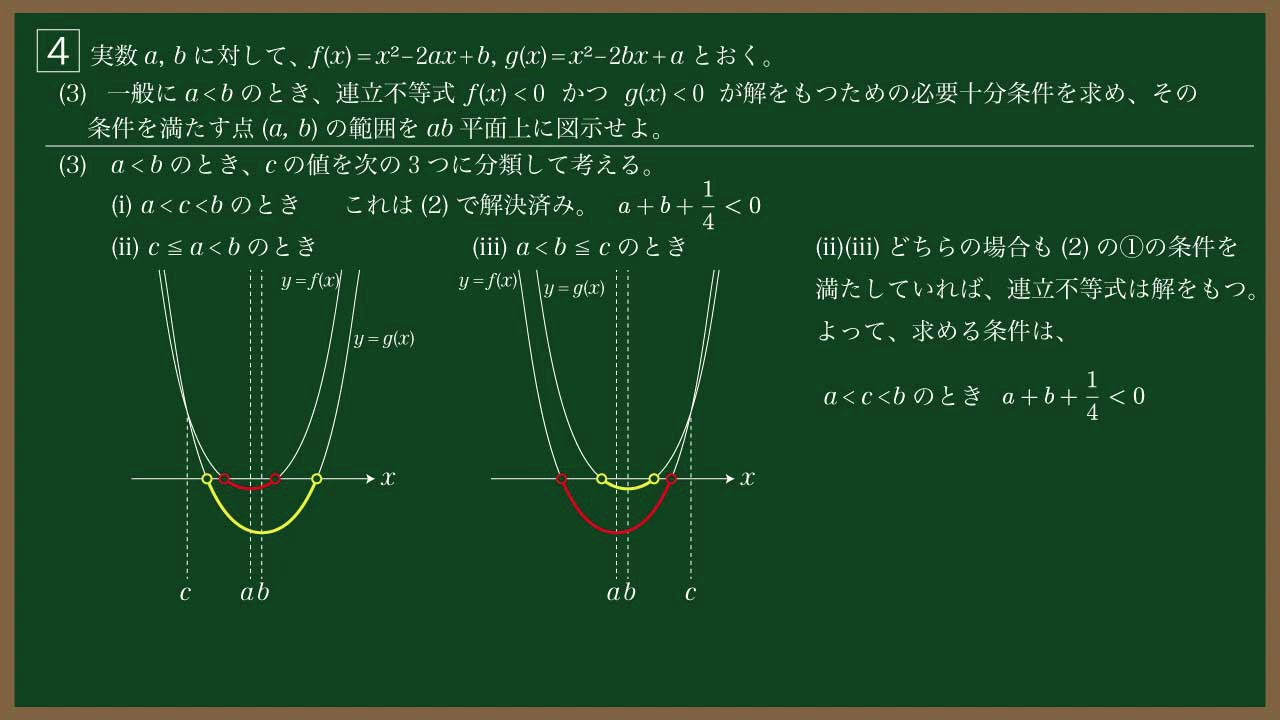
(3)一般に$a \lt b$のとき、連立不等式
$f(x) \lt 0$ かつ $g(x) \lt 0$
が解をもつための必要十分条件を求め、その条件を満たす
点$(a,b)$の範囲を$ab$平面上に図示せよ。
この動画を見る
${\Large\boxed{4}}$ 実数$a,b$に対して、$f(x)=x^2-2ax+b,g(x)$$=x^2-2bx+a$ とおく。
(1)$a \ne b$のとき、$f(c)=g(c)$を満たす実数cを求めよ。
(2)(1)で求めた$c$について、$a,b$が条件$a \lt c \lt b$を満たすとする。このとき
連立不等式
$f(x) \lt 0$ かつ $g(x) \lt 0$
が解をもつための必要十分条件を$a,b$を用いて表せ。
(3)一般に$a \lt b$のとき、連立不等式
$f(x) \lt 0$ かつ $g(x) \lt 0$
が解をもつための必要十分条件を求め、その条件を満たす
点$(a,b)$の範囲を$ab$平面上に図示せよ。
北海道大 二次方程式解と係数 整数 高校数学 Mathematics Japanese university entrance exam
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#２次関数#2次方程式と2次不等式#数学(高校生)#北海道大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
96年 北海道大学過去問
$x^2-2px+p^2-2p-1=0$の２解を$α、β$とする。
$\displaystyle \frac{1}{2}$・$\displaystyle \frac{(α-β)^2-2}{(α+β)^2+2}$が整数となる実数$P$を全て求めよ
この動画を見る
96年 北海道大学過去問
$x^2-2px+p^2-2p-1=0$の２解を$α、β$とする。
$\displaystyle \frac{1}{2}$・$\displaystyle \frac{(α-β)^2-2}{(α+β)^2+2}$が整数となる実数$P$を全て求めよ
北海道大 2次方程式 対数方程式 解の位置関係 Mathematics Japanese university entrance exam
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
'84北海道大学過去問題
m＞2 実数
$x^2-2^{m+1}x+3・2^m=0$・・・①
$2log_2x-log_2(x-1)=m$・・・②
(1)①、②はそれぞれ2つの異なる実数解をもつことを示せ
(2)①の解の1つだけが②の2つの解の間にあることを示せ
この動画を見る
'84北海道大学過去問題
m＞2 実数
$x^2-2^{m+1}x+3・2^m=0$・・・①
$2log_2x-log_2(x-1)=m$・・・②
(1)①、②はそれぞれ2つの異なる実数解をもつことを示せ
(2)①の解の1つだけが②の2つの解の間にあることを示せ
北海道大 積分 高校数学 Mathematics Japanese university entrance exam
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#北海道大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
'02北海道大学過去問題
a,b,cは定数
$f(x)=x^2+ax+b,g(x)=x+c$
(1)$\int_0^1f(x)dx = \int_0^1g(x)dx$となるためのa,b,cの条件
(2)(1)の条件のもとで、$0 \leqq x \leqq 1$における2つの関数f(x)とg(x)の共有点の個数
この動画を見る
'02北海道大学過去問題
a,b,cは定数
$f(x)=x^2+ax+b,g(x)=x+c$
(1)$\int_0^1f(x)dx = \int_0^1g(x)dx$となるためのa,b,cの条件
(2)(1)の条件のもとで、$0 \leqq x \leqq 1$における2つの関数f(x)とg(x)の共有点の個数