藤田医科大学
藤田医科大学
#藤田医科大学2023#定積分
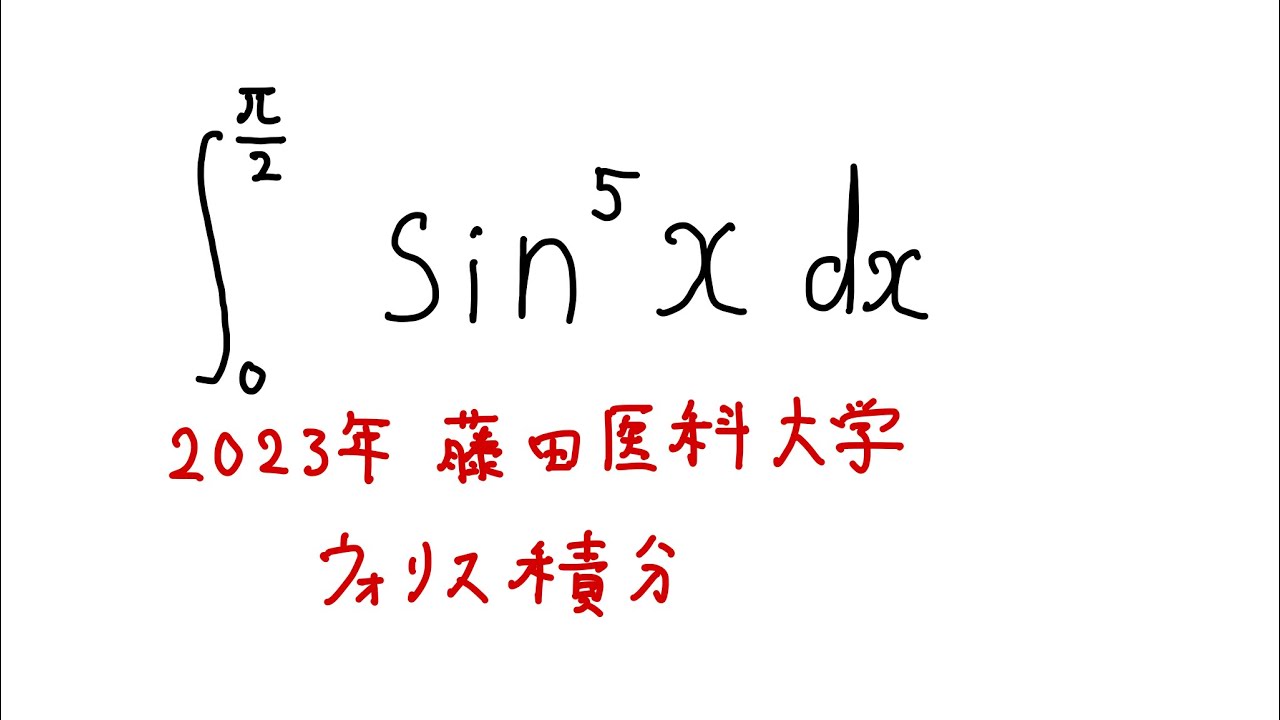
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#藤田医科大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^5x$ $dx$
出典：2023年藤田医科大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^5x$ $dx$
出典：2023年藤田医科大学
#藤田医科大学(2005) #極限 #Shorts
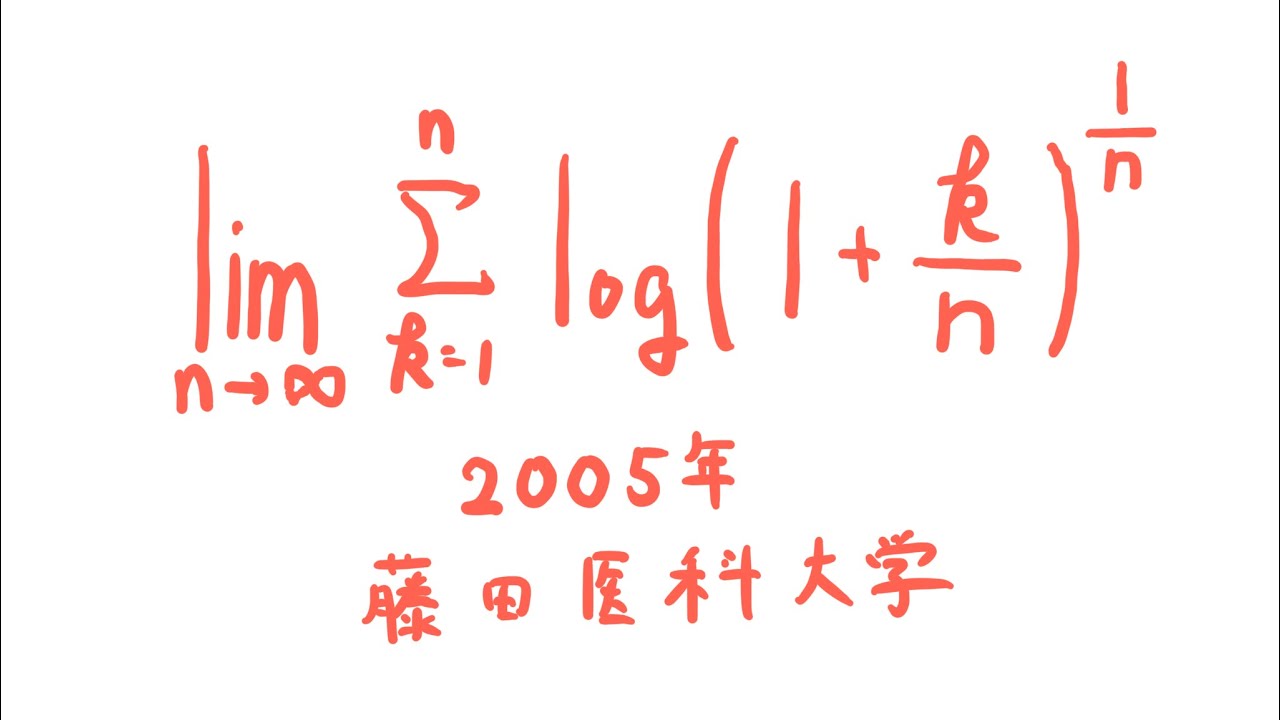
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n log(1+\displaystyle \frac{k}{n})^\frac{1}{n}$
出典：2005年藤田医科大学
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n log(1+\displaystyle \frac{k}{n})^\frac{1}{n}$
出典：2005年藤田医科大学
大学入試問題#766「基本中の基本」 藤田医科大学(2017) #整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
ますただ
問題文全文(内容文)：
不定方程式
$5x+7y=2017$ を満たす自然数の組$(x,y)$の個数を求めよ。
出典：2017年藤田医科大学 入試問題
この動画を見る
不定方程式
$5x+7y=2017$ を満たす自然数の組$(x,y)$の個数を求めよ。
出典：2017年藤田医科大学 入試問題
大学入試問題#756「ほぼ定石通り」 藤田医科大学(2024) #級数
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
ますただ
問題文全文(内容文)：
$a_1=1,\ na_{n+1}=3\displaystyle \sum_{k=1}^n a_k$
１．数列$\{a_n\}$の一般項を求めよ。
２．$\displaystyle \sum_{n=1}^\infty \displaystyle \frac{a_{n+1}}{a_na_{n+2}}$を求めよ。
出典：2024年藤田医科大学 入試問題
この動画を見る
$a_1=1,\ na_{n+1}=3\displaystyle \sum_{k=1}^n a_k$
１．数列$\{a_n\}$の一般項を求めよ。
２．$\displaystyle \sum_{n=1}^\infty \displaystyle \frac{a_{n+1}}{a_na_{n+2}}$を求めよ。
出典：2024年藤田医科大学 入試問題
大学入試問題#738「これはガチ良問！」 藤田医科大学(2024) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-5}^{7} \sqrt{ x^4+2x^3-3x^2-4x+4 }\ dx$
出典：2024年藤田医科大学 入試問題
この動画を見る
$\displaystyle \int_{-5}^{7} \sqrt{ x^4+2x^3-3x^2-4x+4 }\ dx$
出典：2024年藤田医科大学 入試問題
大学入試問題#665「直線的な解答は厳禁」 藤田医科大学(2023) 2024年入学の問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
ますただ
問題文全文(内容文)：
$a,b,x,y$：実数
$a^2+b^2=49$
$x^2+y^2=36$のとき
$ax+by$の最大値を求めよ。
出典：2023年藤田歯科大学 入試問題
この動画を見る
$a,b,x,y$：実数
$a^2+b^2=49$
$x^2+y^2=36$のとき
$ax+by$の最大値を求めよ。
出典：2023年藤田歯科大学 入試問題
大学入試問題#664「三角関数or複素平面」 藤田医科大学(2023) 2024年入学
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \sum_{k=1}^4 \cos\displaystyle \frac{2k}{9}\pi$の値を求めよ
出典：2023年藤田医科大学 入試問題
この動画を見る
$\displaystyle \sum_{k=1}^4 \cos\displaystyle \frac{2k}{9}\pi$の値を求めよ
出典：2023年藤田医科大学 入試問題
大学入試問題#657「第一感は微分だけど」 藤田医科大学(2019)
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
ますただ
問題文全文(内容文)：
$0 \neq x$：実数
$16x^2+\displaystyle \frac{1}{8x^4}$の最小値を求めよ
出典：2019年藤田医科大学 入試問題
この動画を見る
$0 \neq x$：実数
$16x^2+\displaystyle \frac{1}{8x^4}$の最小値を求めよ
出典：2019年藤田医科大学 入試問題
大学入試問題#650「3秒クッキング」 藤田医科大学(2020) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-3}^{3} x(x+\cos^3x) dx$
出典：2020年藤田医科大学 入試問題
この動画を見る
$\displaystyle \int_{-3}^{3} x(x+\cos^3x) dx$
出典：2020年藤田医科大学 入試問題
藤田医科大の問題,数字を変えたら程よい難問になった
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
藤田医科大学みらい入試(改題)
a,b,cは整数
$a^3+b^3-a^2b-ab^2-ac^2-bc^2=704$
を満たすa,b,cを求めよ.
藤田医科大過去問
この動画を見る
藤田医科大学みらい入試(改題)
a,b,cは整数
$a^3+b^3-a^2b-ab^2-ac^2-bc^2=704$
を満たすa,b,cを求めよ.
藤田医科大過去問
藤田医科大 整数の基本問題
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
藤田医科大学みらい入試2024年
a,b,cは整数
$a^3+b^3-a^2b-ab^2-ac^2-bc^2=36$
を満たすa,b,cを求めよ
この動画を見る
藤田医科大学みらい入試2024年
a,b,cは整数
$a^3+b^3-a^2b-ab^2-ac^2-bc^2=36$
を満たすa,b,cを求めよ
投稿した動画とほぼ同じ問題が2024年度入試で出たよ！藤田医科大
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
x+y+z<10
を満たす自然数x,y,zの組をすべて求めよ.
2024藤田医科大過去問
この動画を見る
x+y+z<10
を満たす自然数x,y,zの組をすべて求めよ.
2024藤田医科大過去問
大学入試問題#643「The ミスれない問題」 藤田医科大学(2023)
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt{ x }+\displaystyle \frac{1}{\sqrt{ x }}=\sqrt{ 5 }$のとき
$(x^2-\displaystyle \frac{1}{x^2})^2$の値を求めよ
出典：2023年藤田医科大学 入試問題
この動画を見る
$\sqrt{ x }+\displaystyle \frac{1}{\sqrt{ x }}=\sqrt{ 5 }$のとき
$(x^2-\displaystyle \frac{1}{x^2})^2$の値を求めよ
出典：2023年藤田医科大学 入試問題
大学入試問題#503「微分してもよさげだけど・・・」 #藤田医科大学 (2023) #判別式
単元：
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=\displaystyle \frac{8x^2+5}{x^2-3x+6}$
の最大値を$M$、最小値を$m$とするとき$\displaystyle \frac{M}{m}$を求めよ
出典：2023年藤田医科大学 入試問題
この動画を見る
$f(x)=\displaystyle \frac{8x^2+5}{x^2-3x+6}$
の最大値を$M$、最小値を$m$とするとき$\displaystyle \frac{M}{m}$を求めよ
出典：2023年藤田医科大学 入試問題
藤田医科大 複素数の基本問題
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$Z=1-\sqrt{3}i$
$Z^7+aZ^5-b=0$が成り立つ実数$a,b$を求めよ.
藤田医科大過去問
この動画を見る
$Z=1-\sqrt{3}i$
$Z^7+aZ^5-b=0$が成り立つ実数$a,b$を求めよ.
藤田医科大過去問
2023藤田医科大 １の７乗根の基本問題
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$Z=\cos\dfrac{2}{7}\pi+i\sin\dfrac{2}{7}\piのとき
Z^7=\Box
Z^6+Z^5+Z^4+Z^3+Z^2+Z=\Box
(1-Z)(1-Z^2)(1-Z^3)×(1-Z^4)(1-Z^5)(1-Z^6)=\Box
\Boxを答えよ.$
この動画を見る
$Z=\cos\dfrac{2}{7}\pi+i\sin\dfrac{2}{7}\piのとき
Z^7=\Box
Z^6+Z^5+Z^4+Z^3+Z^2+Z=\Box
(1-Z)(1-Z^2)(1-Z^3)×(1-Z^4)(1-Z^5)(1-Z^6)=\Box
\Boxを答えよ.$
藤田医科大 記数法
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$1,4,6$を使わない自然数を小さい順に
$2,3,5,7,8,9,20,22････$と並べたとき,2023は何番目か?
藤田医科大過去問
この動画を見る
$1,4,6$を使わない自然数を小さい順に
$2,3,5,7,8,9,20,22････$と並べたとき,2023は何番目か?
藤田医科大過去問
藤田医科大学 普通にやれば出るけどね
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\left(-\frac{\sqrt3-1-(\sqrt{3}+1)i}{1+\sqrt{3}i}\right)^5$
これを求めよ.
藤田医科大過去問
この動画を見る
$\left(-\frac{\sqrt3-1-(\sqrt{3}+1)i}{1+\sqrt{3}i}\right)^5$
これを求めよ.
藤田医科大過去問
大学入試問題#448「深夜24時動画ストック０との闘い！」 藤田医科大学(2023) #曲線の長さ
単元：
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$0 \leqq x \leqq \displaystyle \frac{5}{3}$において
曲線$y=2x\sqrt{ x }$の長さを求めよ。
出典：2023年藤田医科大学 入試問題
この動画を見る
$0 \leqq x \leqq \displaystyle \frac{5}{3}$において
曲線$y=2x\sqrt{ x }$の長さを求めよ。
出典：2023年藤田医科大学 入試問題
大学入試問題#445「何度か類題を解いたと思う」 藤田医科大学(2023) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
（1）$\displaystyle \int_{3}^{99} \sqrt{ \sqrt{ 1+x }-1 }\ dx$
（2）$\displaystyle \int_{1}^{3} \sqrt{ \displaystyle \frac{4}{x}-1 }\ dx$
出典：2023年藤田医科大学 入試問題
この動画を見る
（1）$\displaystyle \int_{3}^{99} \sqrt{ \sqrt{ 1+x }-1 }\ dx$
（2）$\displaystyle \int_{1}^{3} \sqrt{ \displaystyle \frac{4}{x}-1 }\ dx$
出典：2023年藤田医科大学 入試問題
藤田医科大 ドモアブルの定理
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#数学(高校生)#藤田医科大学#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(1+i)^n=(1-i)n$をみたす2023以下の自然数nの個数を答えよ.
2023藤田医科大過去問
この動画を見る
$(1+i)^n=(1-i)n$をみたす2023以下の自然数nの個数を答えよ.
2023藤田医科大過去問
大学入試問題#438「積分区間が[0,π/6]なんですけど・・」 藤田医科大学(2023) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{\sin^33x}{\sin^33x+\cos^33x} dx$
出典：2023年藤田医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{\sin^33x}{\sin^33x+\cos^33x} dx$
出典：2023年藤田医科大学 入試問題
大学入試問題#434「基本的な式変形」 藤田医科大学(2023) #式変形
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\alpha=\sqrt{ 6+2\sqrt{ 5 } }$のとき
$\alpha^5-\alpha^4-12\alpha^3+12\alpha^2+16\alpha$の値を求めよ。
出典：2023年藤田医科大学 入試問題
この動画を見る
$\alpha=\sqrt{ 6+2\sqrt{ 5 } }$のとき
$\alpha^5-\alpha^4-12\alpha^3+12\alpha^2+16\alpha$の値を求めよ。
出典：2023年藤田医科大学 入試問題
藤田医科大学 式の最小値
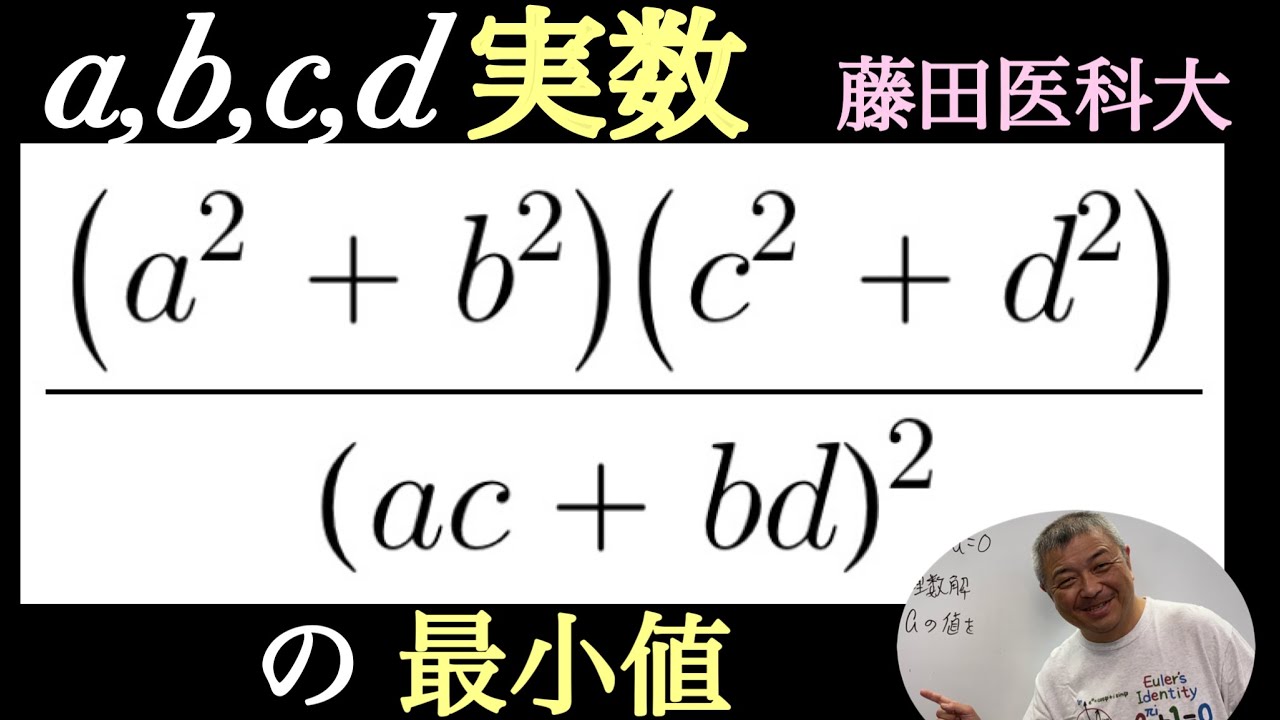
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#複素数平面#数学(高校生)#藤田医科大学#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ a,b,c,dは実数である.
$\dfrac{(a^2+b^2)(c^2+d^2)}{(ac+bd)^2}$の最小値を求めよ.
この動画を見る
$ a,b,c,dは実数である.
$\dfrac{(a^2+b^2)(c^2+d^2)}{(ac+bd)^2}$の最小値を求めよ.
2022藤田医科大の簡単な問題 メインはn個の相加相乗平均の証明
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ x\gt 0$において$\dfrac{x}{2}+\dfrac{2}{x^2}$の最小値を求めよ.
2022藤田医科大過去問
この動画を見る
$ x\gt 0$において$\dfrac{x}{2}+\dfrac{2}{x^2}$の最小値を求めよ.
2022藤田医科大過去問
2022藤田医科大 等差数列の超基本問題
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
公差が０でない整数の等差数列$a_n$がある
$\sum_{ }^{ } a_n$はn=7で
最大値119 $a_n$を求めよ。
藤田医学科大学
この動画を見る
公差が０でない整数の等差数列$a_n$がある
$\sum_{ }^{ } a_n$はn=7で
最大値119 $a_n$を求めよ。
藤田医学科大学
2022藤田医科大 出題意図は「瞬殺せよ」なのかな？
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a_1=5,$
$a_{n+1}=3a_n+2$
$\displaystyle \frac{a_{16}-a_{13}}{a_{12}-a_9}$
の値を求めよ。
2022年藤田医科大学 過去問
この動画を見る
$a_1=5,$
$a_{n+1}=3a_n+2$
$\displaystyle \frac{a_{16}-a_{13}}{a_{12}-a_9}$
の値を求めよ。
2022年藤田医科大学 過去問